Rigidity-driven growth and migration of epithelial cells on microstructured anisotropic substrates

Abstract

The physical properties of the cellular environment are involved in regulating the formation and maintenance of tissues. In particular, substrate rigidity appears to be a key factor dictating cell response on culture surfaces. Here we study the behavior of epithelial cells cultured on microfabricated substrates engineered to exhibit an anisotropic stiffness. The substrate consists of a dense array of micropillars of oval cross-section, so that one direction is made stiffer than the other. We demonstrate how such an anisotropic rigidity can induce directional epithelial growth and guide cell migration along the direction of greatest rigidity. Regions of high tractional stress and large cellular deformations within the sheets of cells are concentrated at the edges, in particular at the two poles of the islands along their long axis, in correlation with the orientation of actin stress fibers and focal adhesions. By inducing scattering activity of epithelial cells, we show that isolated cells also migrate along the direction of greatest stiffness. Taken together, these findings show that the mechanical interactions of cells with their microenvironment can be tuned to engineer particular tissue properties.

The spatial organization of cells, and their migration, are essential for a wide variety of biological processes, including tissue formation, morphogenetic processes (1), responses to wounds, and inflammation (2) or tumor metastasis (3). Cells are subjected to chemical and physical signals from their neighbors (4), from the surrounding fluid (5), and from the extracellular matrix (ECM) (6), and they integrate these various cues to react in an appropriate way. Although it has been shown that many cell types are quite sensitive to mechanical forces, the mechanisms that underlie how these factors affect the organization of tissues need further exploration. Adherent cells exert strong traction forces at their sites of anchorage to the matrix, depending on the size of the adhesive contacts (7–9). Forces can also be transmitted to neighboring cells through adherens junctions (10). The transmission of forces through cell–matrix or cell–cell contacts seems to have a considerable influence on the maturation or disassembly of cell islands (11, 12). Moreover, it has been shown that applying external mechanical forces on cells generates cytoskeletal remodeling and intracellular signaling pathways that affect cellular behaviors (13–17). Specific patterns of cellular growth could also create mechanical stresses inside cellular islands and contribute to the remodeling of epithelial tissues (18).

In particular, recent studies (19–22) have shown that the topographic and physical properties of the surrounding matrix have a significant influence on cell response, as well as on the regulation, formation, and organization of tissues. On substrates structured with grooves, tissue cells become elongated and “crawl” along the direction of the grooves, a phenomenon usually referred to as “contact guidance” (23). Furthermore, a gradient of the rigidity of the substrate can establish the direction of cell migration, because cells tend to move toward the stiffest areas of the substrate (24). In addition, the rigidity of the substrate modifies cell adhesion and cytoskeleton organization (11, 12, 25, 26), as well as net contractile traction forces (24, 25), for many cell types. Soft substrates show diffuse and dynamic adhesion complexes, whereas stable focal adhesions appear on stiff substrates (6, 19, 25). Thus, the mechanical properties of the substrate can influence the spatial organization of cells, their proliferation, the maintenance of tissues, and even cell differentiation (27). However, in all of the systems studied so far, modulation of stiffness was performed on a macroscopic scale.

Here, by using microfabricated substrates with a local anisotropy of rigidity, we present an experimental observation of the influence of a substrate with a microscopic stiffness gradient on tissue growth and cell migration, in correlation with the induced mechanical forces. We studied the response of Madin–Darby canine kidney (MDCK) epithelial cells to a local anisotropy of rigidity by using microfabricated substrates. We demonstrate that such substrates can generate oriented growth patterns of epithelial cells. With the addition of hepatocyte growth factor, which promotes cell scattering (28), we show how cell motility can be influenced by substrate rigidity.

Results

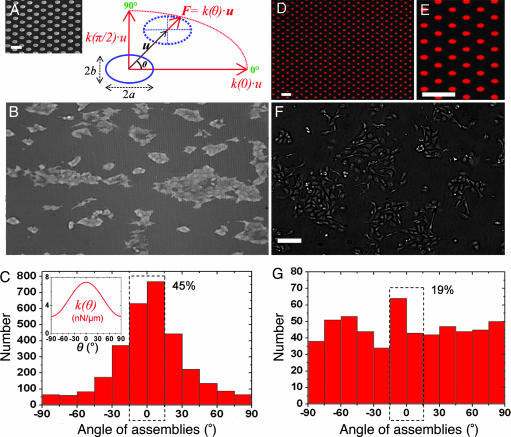
To address how the growth of epithelial cells could be governed by substrate rigidity, we fabricated artificial substrates consisting of a dense array of flexible microposts with oval cross-sections (Fig. 1A). Such “pillars” present a higher resistance to bending along their long axis compared with their short axis. As shown in Fig. 1A, the cross-sections of the pillars can be well fitted by ellipses. Linear elastic theory predicts, for a beam of elliptic cross-section, semimajor (semiminor) axis a (b), and length L, fixed at one end and bent by the application of a shear force F at its free end:

where E is the Young's modulus of the material, θ is the direction of bending, k(θ) is the spring constant, and δu⃗ is the displacement of the free end (see Fig. 1A) (29). Scanning electron micrographs (Fig. 1A) allowed us to determine the geometrical parameters of the pillars. Our microposts presented a form factor on their cross-section a/b ≈ (0.95 ± 0.05 μm)/(0.55 ± 0.05 μm) ≈ 1.72 ± 0.22 and were thus roughly three times stiffer along their major axis [spring constant, k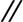 = k(θ = 0°)] than along their minor axis [k_⊥ = k(θ = 90°)]: k 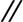= a²/b² k_⊥ ≈ 3k_⊥. Substrates with posts of different heights (3 < L <6.5 μm) forming a dense hexagonal lattice (greatest distance between consecutive posts = 4 μm, center to center; see Fig. 1A) were fabricated with a soft elastomer, polydimethylsiloxane (PDMS), having a Young's modulus of 1.8 ± 0.1 MPa. By varying L, we could modify the spring constant (10 < k 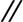< 78 nN/μm) and match the forces exerted by cells (28, 30).

Fig. 1.

Epithelial cell growth on substrates with anisotropic rigidity. (A) Schematic representation of an anisotropic micropillar subjected to a force, F, where u⃗ is the displacement vector of the top of the pillar and θ is the direction of its deflection with respect to the longest semi-axis, a [i.e., the stiffest direction of the substrate (θ = 0°)]. The spring constant, k(θ), depends on the force orientation (see Eq. 1). (Inset) Scanning electron micrograph of an array of oval PDMS pillars. (Scale bar: 5 μm.) (B) MDCK cell islands grown on these substrates and visualized by optical microscopy. The horizontal direction corresponds to the polar axis, θ = 0°. (Image dimensions: length × height = 877 × 512 μm.) (C) Angular distribution of cell assemblies with respect to the stiffest direction (θ = 0°). The dashed rectangle indicates that 45% of the islands are elongated in a 30°-wide sector centered on θ = 0°. (Inset) Profile plot of the stiffness k(θ) for this experiment, computed from Eq. 1. (D) Fluorescence microscopy image of an array of oval patches of Cy3-labeled fibronectin microprinted on a glass coverslip. (Scale bar: 10 μm.) (E) Magnified view of the microprinted patches from D. (Scale bar: 10 μm.) (F) MDCK cells cultured on a microprinted coverslip. (Scale bar: 100 μm.) (G) Angular distribution of cell assemblies on patterned glass. The dashed rectangle indicates that 19% of the islands are elongated in a 30°-wide sector centered on θ = 0°.

These substrates were then surface-treated to promote cell adhesion by mimicking the chemical composition of the ECM. Fluorescently labeled fibronectin, a major component of the ECM that interacts with integrins, was stamped on the tops of the pillars by microcontact printing, and Pluronics (a block copolymer of ethylene oxide and propylene oxide) was adsorbed on the remaining, unstamped regions of the arrays (30). This method allowed us to simultaneously restrict cell adhesion to the tops of the posts and visualize their deflection with fluorescence video microscopy during traction force experiments. We first investigated the role of rigidity in the orientation of cell islands (containing at least five cells) by analyzing the islands' angular spatial distribution. At 24 h after plating MDCK cells on these substrates, we observed elongated cell islands oriented mainly along the direction of greatest stiffness (θ = 0°) (Fig. 1B). To extract their mean orientation, the islands' contours were fitted with ellipses, and the angle between their major axis and the direction θ = 0° was measured. Fig. 1C shows a typical histogram giving the angular orientation distribution of ≈3,000 islands for one experiment. It clearly appears that the large majority of cellular islands are aligned along the stiffest direction (Fig. 1C Inset): 45% of the islands show an orientation angle contained in a 30°-wide sector around θ = 0° (to be compared with 16%, accounting for an isotropic distribution).

We checked that these orientation distributions did not depend on the size of the islands: the same distributions were observed for small (5–10 cells) and large (>20 cells) islands (data not shown). Moreover, control experiments with arrays of cylindrical posts (28) did not show any preferential direction of growth.

One can think of different explanations for the observed growth patterns. Among them, we can attribute this phenomenon to the anisotropic rigidity, but also to contact guidance elicited by the geometry of our substrates, which present a favored direction (23). To uncouple the influence of these two effects, we used the PDMS arrays of anisotropic micropillars as a stamp to print glass coverslips with fluorescently labeled fibronectin (31). To limit cell adhesion to the transferred pattern, the substrates were treated with polyethyleneglycol to passivate the rest of the surface (32). Under these conditions, we obtained an array of oval fibronectin patches printed on glass and offering the same adhesive surface as the micropillar arrays (Fig. 1 D and E). We cultured the cells on such substrates (Fig. 1F) to analyze the angular distribution of cell islands (Fig. 1G). Immunofluorescence staining of the focal adhesion protein vinculin on cellular assemblies cultured on the printed coverslips allowed us to verify that cell adhesion was well restricted to the fibronectin patches (Fig. 2D). On such substrates, presenting the same geometrical anisotropy as the micropillar arrays but no angle-dependent rigidity, we obtained an isotropic angular distribution for the orientation of the islands, as shown in Fig. 1G (19% in a 30°-wide sector).

Fig. 2.

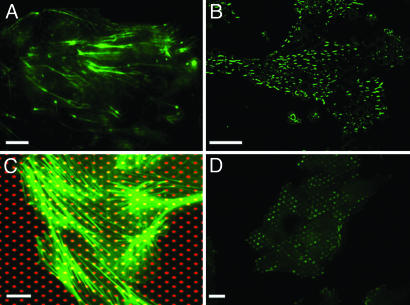
Orientation of the actin cytoskeleton and focal adhesions on microfabricated substrates. (A and B) Immunofluorescence images of filamentous actin (A) and protein vinculin (B) in MDCK cell islands grown on anisotropic PDMS micropillars (stiffest direction, horizontal). (C) Immunofluorescence staining of filamentous actin (green) in cells grown on a glass coverslip microprinted with Cy3-fibronectin (red). (D) Immunofluorescence staining of vinculin on a fibronectin-patterned coverslip (patches oriented horizontally). (Scale bars: 10 μm.)

As a second control experiment, we fabricated substrates with a glassy polymer (polystyrene, PS) identical to those in PDMS (see Materials and Methods and ref. 33) but having a ≈1,000-fold larger Young's modulus. The stiffness of the corresponding microposts was then typically ≈20,000 nN/μm. The posts were so stiff that the cells could not discriminate between the two directions. These substrates were coated with fibronectin and then incubated in a solution of Pluronics, in the same way as the PDMS posts. When plating MDCK cells on these rigid pillars, presenting the same geometrical anisotropy as the micropillar arrays but no angle-dependent rigidity, we obtained a much more uniform angular distribution of cell islands (20% in a 30°-wide sector) than that obtained with flexible micropillars (45% in a 30°-wide sector) [see supporting information (SI) Fig. 6]. The sharp distribution of assembly orientations was thus only observed on the flexible micropillar arrays, showing that spatial patterns of tissue growth followed the direction of highest rigidity. Thus, the orientation of epithelial assemblies was mainly a consequence of the anisotropic substrate elasticity and could not be attributed to contact guidance.

To correlate this phenomenon with a possible reorganization of the spatial distribution of filamentous actin as an intracellular effect of rigidity, we used immunofluorescence staining of microfilaments. As shown in Fig. 2A, a clear orientation of actin stress fibers along the stiffest direction of the micropillar array was observed. This orientation is consistent with a global alignment of focal adhesions in the same direction (vinculin staining, Fig. 2B). In addition, control experiments on glass micropatterned substrates showed no preferential orientation of the actin stress fibers (Fig. 2C) or focal adhesions (Fig. 2D). The substrate stiffness by itself affected the cytoskeleton tension and the orientation of focal adhesions. Pursuing this idea further, we explored whether the orientation of actin stress fibers could set a preferential orientation of cell division on flexible substrates (32). We therefore measured the angle of the mean mitotic axis (the line linking the two daughter cells) during cell divisions with respect to the stiffest direction. This measurement was performed by immunofluorescently staining tubulin so as to visualize the microtubules and thus measure the orientation of the mitotic axis (see SI Fig. 7A). Interestingly, although actin fibers were aligned along the stiffest direction, we did not observe any preferential direction of mitosis for MDCK cells within the islands (SI Fig. 7). This isotropic distribution of the division axis could be attributed to the interactions of cells with their neighbors, which could play a key role in the orientation of the mitotic spindles (34). Consequently, the elongation of cellular assemblies in the direction of maximal rigidity cannot be explained by a preferential orientation of cell division along this direction.

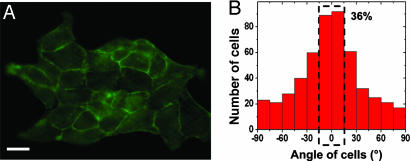
To mutually interact, individual cells must be mechanically coupled and able to transmit tension to their neighbors through intercellular junctions (35–37). The contribution of individual cell elongation within an island to the anisotropic growth process was investigated by using fluorescently labeled actin as an indicator of cell borders (Fig. 3A). The shapes of individual cells within islands were then fitted by ellipses. We found that cells were stretched and mostly oriented in the θ = 0° direction (36% in a 30°-wide sector; Fig. 3B). In addition, by comparing the average ellipticity [defined as 1 − (b/a)] of the cells from the edges vs. that of cells within the core of the islands, it appeared that the cells located at the edges were more elongated (see Fig. 3A and SI Movie 1).

Fig. 3.

Orientation of individual cells within the islands. (A) Immunofluorescence staining of cortical actin showing cell–cell junctions in a MDCK cell island. (Scale bar: 20 μm.) (B) Histogram of the angular orientation of individual cells within the islands. The dashed rectangle indicates that 36% of the islands are elongated in a 30°-wide sector centered on θ = 0°.

To check whether the differential stiffness, k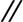/k_⊥, or the absolute rigidity of the substrate was the key parameter in the observed anisotropic growth, we cultured cells on substrates fabricated of oval pillars of two different heights (3.3 and 5.2 μm, respectively), and thus having two different main stiffnesses k 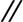(≈56 and ≈15 nN/μm, respectively). In this range of rigidities, comparison of the patterns of tissue formation did not reveal any noticeable difference, implying that the predominant factor in the process is the differential stiffness between directions.

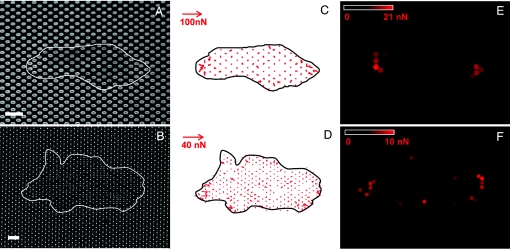
To investigate a possible relationship between the growth patterns and the mechanical tensions within the cellular assemblies, we mapped the traction forces exerted by epithelial monolayers (Fig. 4 A and B). Indeed, the ellipsoidal pillars can be used as microforce sensors by measuring their deflections (see Eq. 1) (Fig. 4). For two different heights of the pillars (L = 4.7 and 3.3 μm) corresponding to different spring constants (k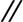 = 19 and 56 nN/μm, respectively), a cartography of the local forces (Fig. 4 C and D) and their magnitude (Fig. 4 E and F) showed that the forces at the edges were significantly greater than those inside the islands, which is consistent with our previous observations (28). Furthermore, the two poles of the islands along the stiffest direction (θ = 0°) exert significantly larger forces compared with the perpendicular direction (Fig. 4 E and F). Reaching typical, instantaneous values of ≈25 nN on the 3.3-μm-long pillars (Fig. 4C) and 13 nN on the 4.7-μm-long ones (Fig. 4D), these high forces are in agreement with our previous results on cylindrical posts on the same cell type (25). In addition, the dynamical formation of elongated patterns showed that the high traction forces at the poles could be due to elongated cells in these regions that pull on the other cells (see SI Fig. 8 and SI Movie 1). This assumption is in agreement with the orientation of filamentous actin and focal adhesions along the stiffest direction of the substrate, which clearly shows a correlation between cytoskeleton organization and the distribution of traction forces.

Fig. 4.

Traction force experiments. (A) Fluorescence microscopy image of the tops of the micropillars coated and labeled with fibronectin-Cy3. (B) Transmission microscopy image of a cell island lying on the micropillars. The positions of the islands are outlined in white. (Scale bars: 10 μm.) (C and D) Maps of the instantaneous traction forces detected within the boundary of the islands at times corresponding to A (C) and B (D) on substrates with two different rigidities: k(θ = 0°) = 56 and 19 nN/μm, respectively. (E and F) Color maps of the average magnitude of the forces applied over a 1-h period by the cellular islands shown in A (E) and B (F), calculated from time-lapse sequences.

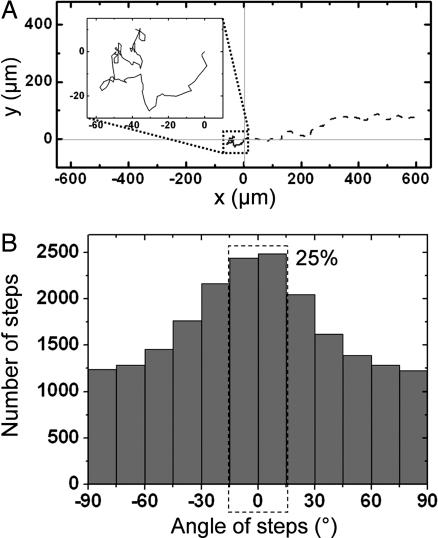
Finally, previous studies have shown that cell migration could be influenced by substrate rigidity (24). We investigated a potential effect of stiffness anisotropy on the dynamics of cellular dissociation/migration. To address this issue, we induced the scattering of MDCK cells from sparse islands by adding hepatocyte growth factor to the medium 24 h after plating the cells on the micropillar arrays (see SI Movie 2). Cells migrating on anisotropic substrates presented a directional motion, whereas a random walk-like motility was observed on substrates fabricated with cylindrical micropillars (Fig. 5A Inset). The analysis of individual cell trajectories (Fig. 5A) allowed us to display the angular distribution of the steps made by each cell between two consecutive images of a time-lapse sequence (Fig. 5B). Cell displacements were again strongly correlated to the stiffest direction of the substrate (Fig. 5B; 25% in a 30°-wide sector), whereas control experiments on hard micropatterned substrates led to an isotropic distribution (see SI Fig. 9). Finally, we quantitatively compared the effects of substrate anisotropy on the orientation of cell migration with the effects on cell-assembly orientation described above (Fig. 1). We fitted the angular distributions shown in Figs. 1C and 5B by the function y = [C·k(θ)]^α, where C and α are constant parameters. Our results indicate that stiffness anisotropy affects the direction of motility (α = 0.72 ± 0.08) but has a much more important effect on cell-assembly orientation (α = 4.2 ± 0.6) (see SI Fig. 10).

Fig. 5.

Effects of anisotropic rigidity on cell migration. (A) Trajectories of two cells over the course of 5-h experiments of hepatocyte growth factor-induced cell migration on pillars having a circular cross-section (solid line) and on pillars having an oval cross-section (dashed line). The starting position of the center of mass was set to (0, 0) for the two cells. (Inset) Magnified view of the path followed by the cell migrating on cylindrical pillars. (B) Histogram of migratory trajectories of individual cells on PDMS anisotropic micropillars. The histogram represents the angular distribution of the displacement vector linking the center of mass of a cell between two consecutive images (at time t and time t + 60 s) with respect to the horizontal direction. The dashed rectangle indicates that 25% of the islands are elongated in a 30°-wide sector centered on θ = 0°.

Discussion

Tissue cells not only adhere to, but also pull on their environment (neighboring cells/substrate) and therefore should adapt to external stimuli. To maintain the stability of a multicellular organism or to induce directionality of tissue growth, it is critical to understand the mechanical signals responsible for such processes. Our substrates, exhibiting a constitutive anisotropic rigidity at a micrometric scale, are a powerful tool to test the hypothesis that mechanical environment plays an essential role in tissue formation. Here, we have demonstrated that both tissue growth and cell migration were oriented along the stiffest direction of such substrates. The alignment of cells could be induced by contact guidance along the topographic features of the substrate. In the present case, because of the small dimensions of the micropillars, we have shown that the key parameter in the orientation of the islands is substrate elasticity. Other experiments such as flow-induced fluid shear stress (38), have shown cell alignment in the direction of the flow, whereas cyclic substrate stretching could induce cell elongation at an angle to the stretch direction (39). This last observation, which seems to contrast with our findings, could probably be attributed to different dynamical interactions at the cell-to-substrate interface, given that the range of deformations in both experiments is completely different.

Moreover, these observations may be understood in terms of differential traction forces exerted by cells on the substrate (24, 25). Through mechanical tensions exerted on the substrate, it appears that cells continuously respond to substrate rigidity by adapting tissue geometry or their direction of migration. In particular, we have shown that the anisotropic growth of cell tissues along the stiffest direction of the substrate (θ = 0°) was correlated with the mapping of the mechanical traction forces and the actin cytoskeleton orientation. Cells located at the poles act as leading cells that exert stronger traction forces (mainly for θ = 0°) and could be responsible for pulling on other cells during tissue growth. Obviously, the mechanical equilibrium conditions that imply a zero force balance on the overall cell island could not explain the preference of cells for greater stiffness. The dynamics of the processes must be included to explain such behavior. Previous studies (11, 12, 20, 25) have shown that cells could remodel their contacts and cytoskeleton by a mechanosensing process at focal adhesions. As theoretically predicted at the scale of a single cell (40), cells orient along the stiffest direction of the substrate in correlation with the direction of higher traction forces. Following the same reasoning, one can argue that the general mechanism underlying our observations could be attributed to a tendency of cell islands to minimize the energy they must invest in the elastic anisotropic medium, providing cell guidance along the direction of maximal stiffness. This assumption is in agreement with the anisotropic distribution of focal adhesions. A plausible mechanism could thus imply different dynamics of cell–matrix contacts, depending on the local rigidity, correlated with traction forces in a similar way that cells respond to external stimuli (19, 20, 41). Further experiments will be necessary to correlate the interplay between the dynamical growth of focal contacts and cellular organization.

In this study, we have focused on the growth of cellular islands. As mentioned in previous studies (13, 21, 37), tissue maintenance is driven not only by cell-to-substrate interactions but also by cell-to-cell interactions. In particular, previous studies (19) have observed that epithelial cells appeared more spread on rigid substrates than on soft ones. Our experiments on substrates with an anisotropic rigidity could describe an intermediate situation in which cells from the edges of the islands exert high traction forces on the substrate along its stiffest direction and pull on the other cells in a way that tends to modify cell–cell interactions. Thus, by implying a rearrangement of cell–cell junctions, the dynamics of the epithelial growth process could suggest a competition between the mechanical signals coming from both types of interactions.

By mimicking tissue dissociation and cell scattering induced by hepatocyte growth factor treatment, our results also address the influence of substrate stiffness on cell locomotion. Epithelial cells that acquired a motile phenotype tended to migrate along the lines of maximal rigidity of their substrate. Previous studies (24) have shown a predominant tendency of cells to migrate toward, and to decrease their velocities on, stiffer regions. Here, it appears that the key parameter in this process of “durotaxis” could be attributed to cell polarization rather than migration. Moreover, recent experiments (42) have shown that the velocity of single MDCK cells after scattering exhibits a biphasic dependence with ECM stiffness, rather than a monotonic decrease. These observations could be relevant to understanding other pathological situations. Indeed, recent studies (43, 44) have shown that increased stiffness of the extracellular matrix may promote malignant behavior by modulating integrin expression.

Finally, our findings suggest specific ways to characterize, control, or engineer cell growth and migratory patterns by tuning cell–matrix interactions, and that such interactions should be taken into account in the engineering of artificial tissues, as well as cell supports and materials used for tissue regeneration. More complex features could be designed in order to obtain more information on the coupling between mechanical processes and cell signaling.

Materials and Methods

Cell Culture.

MDCK cells were maintained at 37°C in a humidified atmosphere (5% CO₂) in Dulbecco's modified Eagle's medium. Cells were plated on substrates 24 h before each experiment, to obtain sparse islands of cells.

Micropillar Surfaces.

The general method for the fabrication and the calibration of PDMS micropillar arrays has been described previously (28). Briefly, a negative replica of the array was fabricated in Si wafers by deep reactive ion etching after a photolithography step and was molded with a heat-curable silicone elastomer (PDMS Sylgard 184; Dow Corning, Midland, MI). Because pillars having a high aspect ratio (L/a ≫ 1) tend to stick irreversibly to each other during the peeling step, some arrays were peeled off in liquid (70% ethanol in water) and were kept in liquid throughout the subsequent steps. For the fabrication of rigid PS pillars, silanized PDMS substrates were molded with the same curable elastomer to obtain a negative replica of the original array of micropillars. After curing (at 65°C for 15 h) and peeling, this replica was laid in PS powder (M ≈ 100,000 Da) on a glass coverslip and then heated under vacuum to above the glass transition temperature of PS (100°C) overnight. Finally, the PDMS replica was peeled off the structured PS.

Surface Treatment.

The plasma-oxidized arrays were first silanized, and the tops of the pillars were coated with fibronectin. A flat PDMS stamp was oxidized in an air plasma cleaner (Harrick Plasma, Ithaca, NY) for 2 min and then incubated with 50 μg/ml fibronectin and 5 μg/ml Cy3-stained fibronectin in PBS for 15 min. The stamp was dried under sterile airflow and deposited gently on the microstructured substrate. Both were left in contact for 15 min to ensure the fibronectin transfer. A similar process was used to treat immersed micropillar substrates that had large aspect ratios. A flat PDMS surface impregnated with fluorescent fibronectin was gently pressed against the substrate, the whole in a PBS bath. After this step, in both cases, the substrates were immersed in 0.1% Pluronics F127 (Sigma–Aldrich, St. Louis, MO) in PBS for 1 h and then rinsed (30).

Microcontact Printing.

First, glass coverslips were silanized. The arrays of PDMS pillars with oval cross-section, described above, were oxidized by plasma treatment and incubated with 50 μg/ml fibronectin and 5 μg/ml Cy3-stained fibronectin in PBS for 15 min. The arrays were then dried and put in contact with a silanized coverslip for 15 min to imprint the pattern. The coverslip was then incubated with 20 mg/ml reactive PEG (mPEG-MAL MW; Nektar Therapeutics, Huntsville, AL) in PBS for 1 h.

Immunofluorescence Labeling.

For vinculin and tubulin fluorescence staining, cells were fixed under standard conditions and then incubated with either a monoclonal mouse anti-vinculin antibody or a monoclonal mouse anti-α-tubulin antibody (Sigma–Aldrich), rinsed, and incubated with a secondary FITC-conjugated sheep anti-mouse IgG antibody (Sigma–Aldrich). For actin labeling, cells were successively permeabilized with 0.1% Triton X-100/0.3 M sucrose in cytoskeleton buffer (CB) for 3 min, then fixed with 4% paraformaldehyde/0.3 M sucrose in CB for 20 min, rinsed with CB, incubated with 50 mM NH₄Cl in PBS for 10 min, rinsed with PBS, incubated with 10% FCS, and finally stained with fluorescein-conjugated phalloidin (Sigma–Aldrich).

Video Microscopy and Image Analysis.

To maintain a controlled temperature (37°C) within the sample, the microscope (equipped with a ×60 immersion objective; Olympus, Rungis, France) was enclosed in an isolated, temperature-controlled box (Ecole Polytechnique Fédérale de Lausanne, Laboratory of Intelligent Systems, Lausanne, Switzerland). As described previously (28), we determined the positions of all of the pillars by using a multiple-particle tracking routine developed in our laboratory. The applied forces were calculated by multiplying the displacements of the pillars and the spring constant k(θ) corresponding to their bending direction (see Eq. 1).

Abbreviations

ECM

extracellular matrix

MDCK

Madin–Darby canine kidney

PDMS

polydimethylsiloxane

PS

polystyrene.