Atomic Force Microscopy Imaging of SWI/SNF Action: Mapping the Nucleosome Remodeling and Sliding

Abstract

We propose a combined experimental (atomic force microscopy) and theoretical study of the structural and dynamical properties of nucleosomes. In contrast to biochemical approaches, this method allows us to determine simultaneously the DNA-complexed length distribution and nucleosome position in various contexts. First, we show that differences in the nucleoproteic structure observed between conventional H2A and H2A.Bbd variant nucleosomes induce quantitative changes in the length distribution of DNA-complexed with histones. Then, the sliding action of remodeling complex SWI/SNF is characterized through the evolution of the nucleosome position and wrapped DNA length mapping. Using a linear energetic model for the distribution of DNA-complexed length, we extract the net-wrapping energy of DNA onto the histone octamer and compare it to previous studies.

INTRODUCTION

DNA is packaged into chromatin in the cell nucleus. The chromatin repeating unit, called the nucleosome, consists of an octamer of the core histones (two each of H2A, H2B, H3, and H4) around which about two superhelical turns of DNA are wrapped (1). The nucleosome core particle (NCP) represents a barrier for the transcription factors binding to their target DNA sequences and interferes with several basic cellular processes (2). Histone modifications, ATP-remodeling machines, and the incorporation of histone variants within chromatin are used by the cell to overcome the nucleosomal barrier and modulate DNA accessibility by the control of nucleosome dynamics (3–6). In this work, we use a single molecule technique (atomic force microscopy (AFM)) to visualize isolated mononucleosomes, to quantify the influence of histone octamer composition (H2A-Bbd variant) on the equilibrium nucleosome conformation, and to map nucleosome mobility induced by a remodeling complex (SWI/SNF).

Chromatin remodeling complexes are used by the cell to overcome the general repression of transcription associated with the DNA organization into chromatin (7–9). To destabilize histone-DNA interaction, remodeling factors (like SWI/SNF) consume the energy from ATP hydrolysis to relocate the histone octamer along the DNA sequence (10,11), and in some cases the ejection of the octamer from the DNA template is observed (12). The molecular motor SWI/SNF is known to mobilize the histone octamer from a central to an end position on short DNA templates (13). Nevertheless, the molecular mechanisms involved in the nucleosome remodeling process have not yet been elucidated.

Histone variants are nonallelic isoforms of the conventional histones. The function of the different histone variants is far from clear, but the emerging general picture suggests that the incorporation of histone variants (14–19) in the nucleosome has a serious impact on several processes, including transcription and repair, and it may have important epigenetic consequences (20–23). H2A.Bbd (Barr body deficient) is an unusual histone variant whose primary sequence shows only 48% identity compared to its conventional H2A counterpart (24). The current view is that H2A.Bbd is enriched in nucleosomes associated with transcriptionally active regions of the genome (24). In recent studies, the unusual properties of this variant nucleosome were described (16,25) using a combination of physical methods and molecular biology approaches. Those results were mainly focused on the biological role of the various histone fold domains of H2A.Bbd on the overall structure, stability, and dynamics of the nucleosome, whereas we concentrate here on the quantification of the subtle modifications in the nucleosome conformation induced by the presence of this histone variant.

Different experimental approaches have been used so far to study the structure and dynamics of the nucleosome, including crystallographic studies by Luger et al. (26), restriction enzyme accessibility assays (27,28), and fluorescence resonance energy transfer measurements (29,30). Additionally, physical models (31) and recent computational efforts were developed to describe the nucleosome dynamics and energetics (32–35). After these numerous contributions, this study combines experimental (AFM) and theoretical tools to bring complementary information regarding the interplay between nucleosome position dynamics and DNA wrapping energetics.

AFM (36) allows direct visualization of chromatin fibers and isolated nucleosomes (37). Several experimental procedures allow us to depose and reproducibly observe all this without any fixing agent, DNA, or chromatin samples (38–44). By scanning the sample with an apex of very high aspect ratio mounted on a flexible lever, the topography of a surface at the nanometric scale can be acquired. Moreover, computer analysis of AFM images enables the extraction of systematic and statistically relevant distributions of structural parameters describing these biological objects (45–47). As the nucleosome is a complex and very dynamic structure, it has been observed that, for a given DNA template, the position of the octamer relative to the sequence (13,48–50) and the length of DNA wrapped around the histone octamer (27–29,51,52) both could change drastically in time.

This article is organized as follows. First, we show that mapping the nucleosome position along with the length of DNA complexed with histones within individual nucleosome is a powerful tool to discriminate between conventional and variant nucleosomes. A model is then proposed to explain these differences quantitatively and to calculate the wrapping energy of nucleosomes in each case. Next, we study nucleosomes in a more dynamic context by observing the action of chromatin-remodeling factor SWI/SNF. To do so, similar mapping of the nucleosome position and DNA-complexed length was used to quantify the impact of ATP-activated remodeling and sliding of nucleosomes. The results suggest experimental insights into the processivity of SWI/SNF on mononucleosomes.

MATERIALS AND METHODS

Preparation of DNA fragments

The 255 basepair (bp) and 356-bp DNA fragments, containing the 601 nucleosome-positioning sequence (53), were obtained by polymerase chain reaction (PCR) amplification from plasmid pGem-3Z-601. For the 255-bp template, the 147-bp-long 601 positioning sequence is flanked by 52 bp on one side and 56 bp on the other side. For the 356-bp template, the 147-bp-long 601 positioning sequence is flanked by 127 bp on one side and 82 bp on the other side. As both 601 DNA templates are built from the same plasmid, the DNA flanking sequences of the short template are included in the long DNA template.

Protein purification, nucleosome reconstitution, and remodeling assays

Recombinant Xenopus laevis full-length histone proteins were produced in bacteria and purified as described (54). For the H2A.Bbd protein, the coding sequences for the H2A and for H2A.Bbd were amplified by PCR and introduced in the pET3a vector. Recombinant proteins were purified as previously described (55).

Yeast SWI/SNF complex was purified as described previously (56), and its activity was normalized by measuring its effect on the sliding of conventional nucleosomes: one unit being defined as the amount of ySWI/SNF required to mobilize 50% of input nucleosomes (∼50 ng) at 29°C during 45 min. Nucleosome reconstitution was performed by the salt dialysis procedure (57). Nucleosomes reconstituted on a 601 nucleosome positioning sequence (20 ng) were incubated with SWI/SNF as indicated at 29°C and in remodeling buffer containing 10 mM Tris-HCl, pH = 7.4, 2.5 mM MgCl₂, and 1 mM ATP. The reaction was stopped after the time indicated, by diluting ∼10 times in TE buffer (Tris-HCl 10 mM, pH = 7.4, EDTA 1 mM) and NaCl 2 mM and deposing the sample onto the functionalized aminopropyltriethoxy silane (APTES)-mica surface.

Atomic force microscopy and surface preparation

For the AFM imaging, the conventional and variant nucleosomes were immobilized onto APTES-mica surfaces. The functionalization of freshly cleaved mica disks (muscovite mica, grade V-1, SPI Supplies, West Chester, PA) was obtained by self-assembly of a monolayer of APTES (aminopropyltriethoxysilane) under argon atmosphere for 2 h (39). Nucleosomes (DNA concentration ∼75 ng/μl) were filtered and concentrated using Microcon centrifugal filters (Millipore, Bedford, MA) to remove free histones from the solution and diluted 10 times in TE buffer, just before deposition onto APTES-Mica surfaces. A 5-μl droplet of the nucleosome solution is applied on the surface for 1 min, rinsed with 1 mL of Milli-Q Ultrapure water (Millipore), and gently dried by nitrogen flow. The samples were visualized by using a Nanoscope III AFM (Digital Instruments, Veeco, Santa Barbara, CA). The images were obtained in tapping mode in air, with silicon tips (Veeco, resonant frequency 250–350 kHz) or diamond-like carbon spike tips (Veeco, resonant frequency ∼150 kHz) at scanning rates of 2 Hz over scan areas 1-μm wide.

This surface functionalization was chosen because it is known to trap three-dimensional (3D) conformation of naked DNA molecules on a two-dimensional (2D) surface (58,59). Moreover, under such experimental conditions, rinsing and drying are thought to have little effect on the observed conformation of biomolecules (60).

Image analysis

We extracted parameters of interest from the AFM images using a MATLAB (The MathWorks, Natick, MA) script essentially based on morphological tools such as binary dilatation and erosion (61–64) and height/area selections. The aim of the first three steps of this algorithm is to select relevant objects:

1. Flattening of the image to remove the piezoelectric scanner thermal drift. The use of a height criteria (h > 0.5 nm, where h is the height of the object) allows us to avoid the shadow artifact induced by high objects on the image.

2. Building of a binary image using a simple thresholding (h > 0.25 nm, where h is the height of the object) and then selection of the binary objects in the good area range (500 < A < 2000 nm², where A is the area of the object).

3. Selection of the objects in the good height range using a hysteresis thresholding (65) ( and where and are the heights of the two thresholds).

These three steps lead to the selection of binary objects whose area is between 500 and 2000 nm² and corresponds in the AFM image to a group of connected pixels whose minimum height is more than 0.25 nm and maximum height is above 1.6 nm. For example, a height criterion is used to reject tetrasomes while events with SWI/SNF still complexed with nucleosomes are removed from analysis by a size criterion. The next steps correspond to measurements in itself:

• 4. Detection of the NCP centroid by shrinking the objects in the binary image.

• 5. Building of a distance map inside the nucleosome with respect to their NCP centroid using a pseudo-Euclidian dilatation-based algorithm.

• 6. Selection of the nonoctamer parts of the nucleosomes (d > d_c, where d is the constraint distance to the NCP centroid and d_c ∼ 7.5 nm is the apparent nucleosome radius) and then thinning the free arm regions using a commercial MATLAB script optimized to avoid most of the branching in the skeleton.

• 7. Selection of the free arm ends and measurement of the free arm lengths.

• 8. Measurement of other parameters of interest like areas, volumes, and mean height of the nucleosomes and the octamers (see Supplementary Material).

These last five steps lead to quick and robust measurements. Indeed the use of morphological tools allows parallel calculation simultaneously on all the objects. Moreover, erosion is a good approximation for the inverse operation of the AFM dilatation due to the finite tip radius and leads to a partial removal of the tip effect (66,67).

The longest arm is named L₊ and the shortest L₋. DNA-complexed length is deduced by L_c = L_tot − L₋ − L₊, where L_tot is either 255 bp for short conventional and variant nucleosomes or 356 bp for long conventional nucleosomes. The position of the nucleosome relative to the DNA template center is calculated as ΔL = (L₊ − L₋)/2. Notice that the position defined this way corresponds to the location of the most deeply buried basepair, which might differ from dyad axis position (strictly defined for symmetric nucleosomes).

Complexed DNA length and nucleosome position distribution construction

For the distribution of DNA-complexed length, well-centered nucleosomes were selected (ΔL* − σ_ΔL/2 ∼ 0 bp < ΔL < 12 bp ∼ ΔL* + σ_ΔL/2 for the 255-bp mononucleosomes where ΔL* is the most probable nucleosome position and σ_ΔL is the standard deviation of the ΔL distribution). To construct the histogram, a 20-bp sliding box was used. For each L₀ in [0, 300 bp], nucleosomes with a DNA-complexed length included in the range [L₀ − 10 bp, L₀ + 10 bp] were counted. After normalization, a smooth distribution is obtained that mathematically represents the convolution of the real experimental distribution with a rectangular pulse 20-bp long.

To obtain the nucleosome position distribution, we selected nucleosomes with a DNA-complexed length, L_c, in a range of width, σ_Lc, around L* = 146 bp (123 bp ∼ L* − σ_Lc < L_c < L* − σ_Lc 169 bp for canonical nucleosomes). Then, the same 20-bp sliding box protocol was used to construct the nucleosome position distribution. The error on the distribution function mean value (standard error) is given by σ_exp/√N, where σ_exp is the standard deviation of the experimental distribution, and N the number of analyzed nucleosomes (central limit theorem).

2D distribution L_c/ΔL construction

To construct the 2D histogram, a 10-bp sliding box was used. For each coordinate (ΔL₀, L₀) in [0, 75 bp] × [0, 300 bp], nucleosomes with a DNA-complexed length included in the range [L₀ − 5 bp, L₀ + 5 bp] and a position included in the range [ΔL₀ − 5 bp, ΔL₀ + 5 bp] were counted. After normalization a smooth distribution is obtained that mathematically represents the convolution of the real experimental 2D distribution with a 10-bp square rectangular pulse.

Reproducibility and experimental errors

We checked that different batches of APTES, nucleosome reconstitutions, ySWI/SNF, and mica surfaces lead to similar results for the sliding assays and for the 2D mapping within the experimental uncertainty. Moreover, we checked by image analysis of the same naked DNA on the same surface and within the same experimental conditions (data not shown) that the whole measurement and analysis process have an experimental error of ∼10 bp in DNA length measurement. Notice that uncertainty on the mean value of length measurements can be much smaller than this resolution as explained in the Supplementary Material Fig. S3.

RESULTS AND DISCUSSION

Simultaneous measurements of DNA-complexed length and nucleosome position

Several biochemical approaches allow accessing either the nucleosome position along a DNA template or the length of DNA wrapped around the histone octamer, but using AFM, we were able to measure them simultaneously. The results are conveniently plotted as 2D histograms of nucleosome position versus DNA-complexed length.

For short and long arm mononucleosomes

We first investigated the influence of the DNA template length on the nucleosome-complexed length distribution for conventional nucleosomes. Indeed, one could expect that the nucleosome positioning efficiency for the 601 DNA template and/or the range of wrapped DNA length could depend on the length of free DNA arms. Using purified conventional recombinant histones, nucleosomes were reconstituted by salt dialysis on 255-bp (short nucleosome) or 356-bp (long nucleosome) DNA fragments containing the 601 positioning sequence. Tapping mode AFM in air was used to visualize the reconstituted particles adsorbed on APTES-mica surfaces, and images of 1 μm² were recorded. A representative image of long mononucleosomes (L_tot = 356 bp) is displayed in Fig. 1 a. Such an image enables us to clearly distinguish the NCP (red part of the complex, h_NCP ∼2 nm) from the free DNA arms (yellow part of the complex, h_DNA ∼0.7 nm) entering and exiting the complex.

FIGURE 1.

AFM visualization of centered mononucleosomes with short and long arms. (a) AFM topography image of mononucleosomes reconstituted on 356 bp 601 positioning sequence. Color scale from 0 to 1.5 nm. Image size is 500 nm. (b) Zoom in of the AFM topography image of a centered mononucleosome and the result of the image analysis. Black line, contour of the mononucleosome. Blue point, centroid of the histone octamer. Blue dot circle, excluded area of the histone octamer. Blue line, skeletons of the free DNA arms. Color scale from 0 to 1.5 nm. X/Y scale bar 20 nm. The longest arm is named L₊ and the shortest L₋. DNA-complexed length is deduced by L_c = L_tot − L₋ − L₊, where L_tot is in this case 356 bp. The position of the nucleosome relative to the center of the sequence is calculated by ΔL = (L₊ − L₋)/2. (c) 2D histogram L_c/ΔL representing the DNA-complexed length L_c along with the nucleosome position ΔL for a short DNA fragment of 255 bp (N = 702 nucleosomes). (d) Probability density function of the DNA-complexed length L_c for a short DNA fragment (255 bp, purple line) and for a long DNA fragment (356 bp, blue line) obtained by selecting the well-positioned nucleosomes (0 < ΔL < 12 bp and 12 < ΔL < 32 bp for the short and long fragments, respectively) and projecting the 2D map along the y axis. (e) Probability density function of the ΔL nucleosome position for a short DNA fragment (255 bp, purple line) and for a long DNA fragment (356 bp, blue line) obtained by selecting nucleosomes having their DNA-complexed length L_c in the range 123 bp < L_c < 169 bp for both fragments, and projecting the 2D map along the x axis.

Precise measurements of the length of each DNA fragment (respectively L₊ and L₋ for the longer and shorter arms) exiting the nucleosome were performed. To measure each “arm” of the mononucleosome, the octamer part is excluded and the free DNA trajectory is obtained (Fig. 1 b) using morphological tools, avoiding false skeletonization by heuristic algorithm (see Materials and Methods). From the total DNA length that is unwrapped around the histone octamer, we get the length of DNA organized by the histone octamer (L_c = L_tot − L₊ − L₋) as well as the nucleosome position with respect to the center of the sequence (ΔL = (L₊ − L₋)/2).

The 2D histogram L_c/ΔL is plotted in Fig. 1 c for 702 conventional short nucleosomes using a 2D sliding box as described in the Materials and Methods section. The maximum of the 2D distribution is positioned at L* = 145 bp and ΔL = 15 bp, in qualitative agreement with the DNA template construction. The 2D mapping is an important tool to study nucleosome mobilization (see the SWI/SNF sliding section), since both variables are highly correlated during nucleosome sliding/remodeling. Quantitative information can, however, also be obtained by projecting such a 2D histogram on each axis. First, we selected well-positioned nucleosomes according to the expected position given by the DNA 601 template construction (0 bp < ΔL < 12 bp for short DNA fragments) and shown their DNA-complexed length probability density function (purple line, Fig. 1 d). This distribution of the DNA length, organized by conventional octamer peaks at L* = 146 ± 2 bp, is in quantitative agreement with the crystal structure of the nucleosome (26) and cryo-electron microscopy (cryo-EM) measurements (25). The broadness of this distribution (σ = 23 bp) might be explained by different nucleosome-wrapping conformations. We will explain later on how this dispersion relates to DNA-histone interaction energies using a simple model.

We used the same approach to study long nucleosomes (2D histogram not shown). Well-positioned long nucleosomes according to the DNA sequence (12 bp < ΔL < 32 bp) have very similar probability distribution (blue line in Fig. 1 d) than that obtained for short nucleosomes showing that the free linker DNA does not significantly affect the organization of complexed DNA for such nucleosomes.

We now select nucleosomes that have a complexed length in the range L* ± σ_Lc, where σ_Lc is the standard deviation of the L_c distribution, and their position distribution is displayed in Fig. 1 e. The peak values for each DNA fragment (9 ± 2 bp and 24 ± 2 bp for short and long nucleosomes, respectively) is close to the expected value from the DNA template construct (2 bp and 22 bp for short and long DNA fragments, respectively). Both distributions have a full width at half-maximum that exceeds 20 bp. This width might arise from several features: asymmetric unwrapping of one of the two DNA arms, AFM uncertainty, or dispersion in octamer position. However, it is not possible with these measurements to determine the contribution of each phenomenon. Next, we can see that the distribution width for longer fragments seems greater. After corrections of artifacts inherent to L₊/L₋ labeling (see Supplementary Material Fig. 2), these two position distributions are very similar, showing that the free linker DNA affects neither the DNA-complexed length nor the positioning of such nucleosomes significantly.

FIGURE 2.

AFM Visualization of centered H2A.Bbd variant and H2A conventional mononucleosome. (a) Probability density function of the DNA-complexed length L_c for a short DNA fragment (255 bp) with conventional H2A (solid thick line) and with variant H2A.Bbd (dotted thick line) nucleosome. Simple model for conventional and variant nucleosomes (solid and dashed thin lines, respectively). (b) Description of the model used to measure the DNA-histone adsorption energies per bp (ɛ_a< and ɛ_a>) and the DNA bending energy per bp (ɛ_b) (dotted line). Representation of the model using the 20-bp sliding box procedure (dotted dashed line). L* corresponds to the most probable DNA-complexed length of the distribution.

We have shown in this section that AFM measurements give comparable estimations with other methods for both the positioning and the DNA wrapping of short 601 mononucleosomes. Furthermore, our experimental approach showed no difference in complexed length probability or nucleosome-positioning dynamics for long and short DNA templates.

For conventional and H2A.Bbd variant mononucleosomes

To investigate the influence of the octamer composition on the wrapping of DNA around the histone octamer, an H2A.Bbd histone variant was used instead of conventional H2A to reconstitute mononucleosomes on a 255-bp DNA fragment. The H2A.Bbd variant nucleosomes were imaged by AFM (25), and using the same analysis as described above, only the well-positioned nucleosomes (ΔL < 12 bp) were selected. Their DNA-complexed length distribution is plotted in Fig. 2 a where it is compared to conventional mononucleosomes reconstituted on the same 601 positioning sequence, 255-bp long, with the same position range selection (ΔL < 12 bp).

The average length of wrapped DNA is clearly different for the variant H2A.Bbd nucleosomes as the distribution peak value is L*_H2A.Bbd = 130 ± 3 bp instead of L*_H2A = 146 ± 2 bp for the conventional nucleosomes. Moreover the standard deviation of the distribution is clearly larger for the H2A.Bbd variant (σ = 41 bp compared to σ = 23 bp for the conventional nucleosomes). These differences show that the H2A.Bbd variant nucleosome is a more labile complex with less DNA wrapped around the octamer, in agreement with previous observations by AFM and cryo-EM (25). The difference in DNA-complexed length suggests that ∼10 bp at each end of nucleosomal DNA are released from the octamer. Therefore, AFM allows us to visualize subtle differences in the nucleosome structure.

Finally, the DNA-complexed length distribution is asymmetric for canonical nucleosomes. This asymmetry can be quantified by measuring their skewness defined as

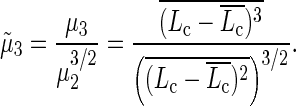We find = −0.57 ± 0.09, the negative sign meaning that nucleosome conformations with subcomplexed DNA, as compared to the mean value 146 bp, are energetically more favorable than with overcomplexed DNA. This can be interpreted within the simple model proposed below, based on relevant structural data information (26). Notice that for variant nucleosomes, the complexed length distribution is nearly symmetric (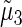≈ 0.01 ± 0.16), and this feature will also be discussed in the modeling section.

Simple model of DNA-complexed length distribution

It has been shown that 14 discrete contacts between DNA and histone octamer are responsible for the stability of the nucleosome (26). The energetic gain at these sites is made through electrostatic interactions and hydrogen bonding. At the length scale of the analysis here, the discreteness of binding sites is not relevant, and it will be replaced by a uniform effective adsorption energy ɛ_a< per unit length in units of kT/bp. The finite number of binding sites, or equivalently the finite DNA length, L*, complexed through these sites (146 bp for canonical nucleosomes, as determined both by these experiments and crystal structure), is due to the specific locations of favorable interactions located at the surface of the histone octamer, forming a superhelical trajectory on which DNA is complexed. DNA wrapping around the histone core involves additional bending penalty characterized by the energy per unit length: 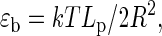where L_p is the persistence length of DNA within classical linear elasticity and R the radius of the histone octamer. The stability of the nucleosome requires that the net energy per unit length is negative (energetic gain), and therefore: ɛ_b < ɛ_a<.

The experimental distributions of DNA-complexed length show that more DNA can be wrapped around the octamer. For these additional basepairs, the net energy per unit length has to be positive, due mainly to bending cost. However, to allow for the possibility of some residual nonspecific (mainly electrostatic) attractive interactions beyond the 14 binding sites, the energetic gain of DNA contacting the octamer surface outside of the 14-site superhelical path has a different value, denoted ɛ_a>. The difference ɛ_a< − ɛ_a> is then representative of the specificity of the 14-site region.

Assuming that the energy reference is given by uncomplexed straight DNA and octamer, the total energy for nucleosome is given by

(1)

The distribution of DNA-complexed length is given by It is maximum for the length L*, which characterizes the region of specific contacts. This length may vary for canonical and variant nucleosomes. The assumptions of energy linearity in wrapped DNA length and of the existence of L* lead to a double exponential distribution. By construction, one has the following constraints between effective energies ɛ_a> < ɛ_b < ɛ_a<.

It should be kept in mind that the effective values ɛ_a>, ɛ_a<, and ɛ_b are representative of nucleosomes adsorbed on a charged flat surface. These values might differ for nucleosomes in bulk solution, as discussed below.

Extraction of the DNA-complexed length parameters

It is possible to extract some parameters from each distribution by using the physical model presented below to interpret the experimental distribution of DNA-complexed length. We found it more reliable to use a global procedure for parameter determination, instead of fitting the multi-variate distribution. Since we expect the DNA-complexed length distribution to be described by a simple double-exponential model, the probability density function can be written as a skew-Laplace distribution whose moments are calculated as

(2)

where L* is the most probable complexed length, ɛ is the relative asymmetry of the skew-Laplace distribution, and σ is the mean decay length. The distribution normalization is taken on the full real axis as a first approximation, thus neglecting finite size effects. Given the experimentally determined μ₁, μ₂, and μ₃ parameters, we extract straightforwardly the parameters L*, ɛ, and σ by numerically solving Eq. 2.

Hence, we are able to measure the parameters L*, ɛ, and σ without any fitting by calculating the first three moments μ₁, μ₂, and μ₃ of the DNA-complexed length statistical series. In our case we thus have

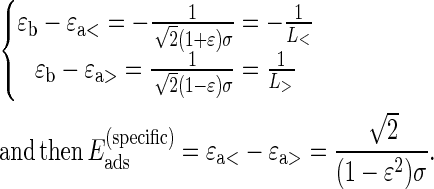To see the adequacy of this model with the experimental distribution, the function P(L_c = L) is drawn for the parameters extracted from the experimental data using the same 20-bp sliding box protocol as for the experimental complexed length distribution (Fig. 2 ).

The results are summarized in Table 1. The values of energies are expressed in units of kT per binding site, assuming 14 such sites along the 147 basepairs of DNA for canonical nucleosomes. Several comments are to be made on these values. First, the measured characteristic decay lengths corresponding to sub-(L_<) and overcomplexed (L_>) DNA lengths (Table 1, b and d) are clearly higher than the intrinsic resolution of our AFM measurements (related to the tip size that corresponds to ∼10 bp, as checked by image analysis of the same naked DNA on the same surface and within the same experimental conditions—data not shown) for both conventional and variant nucleosomes, showing, therefore, the significance of the parameters extracted here. Hence, we are able to quantify the energies of both sub- and overcomplexed DNA length in a mononucleosome. For overcomplexed DNA length, the energy has been converted artificially into units of kT per binding site for the sake of comparison, although the model assumes that there are no such binding sites beyond the 14 sites found in the crystal structure (26). If one assumes that overcomplexed DNA length results solely from bending around the histone core (ɛ_a> = 0), the value found for ɛ_b leads to a persistence length, L_p ∼ 3.5 bp, a value definitely too small for double-stranded DNA. Even more so, this energy is similar in amplitude to the energy of subcomplexed DNA length but with an opposite sign (Table 1, c and e). We conclude that it cannot simply be associated to a bending penalty, therefore justifying a posteriori the assumption of residual attractive interaction between DNA extra length and histone octamer.

TABLE 1.

Summary of model parameters extracted from experimental data as explained in Materials and Methods

	(a) 〈Lc〉 (bp)	(b) Decay length L< (bp)	(c) ɛb− ɛa< (kT per site)	(d) Decay length L> (bp)	(e) ɛb− ɛa> (kT per site)	(f) ɛa<− ɛa> (kT per site)
Conventional nucleosome	146 ± 2	22 ± 1.6	−0.479 ± 0.045	17 ± 1.4	0.61 ± 0.064	1.1 ± 0.072
Variant nucleosome	127 ± 3	31 ± 1.5	−0.33 ± 0.022	27 ± 1.5	0.39 ± 0.026	0.72 ± 0.021
Site exposure model (g)			−3 <…< −0.5
Crystal structure (h)	147					0.8<…<2

All energies are expressed in units of kT per binding site. DNA lengths are expressed in bp. (a) Average complexed length. (b) Characteristic length L_< of exponential decay toward subcomplexed DNA length. (c) Energy per binding site (1/L_<) for subcomplexed DNA length. (d) Characteristic length L_> of exponential decay, toward overcomplexed DNA length. (e) Energy per binding site (1/L_>) for overcomplexed DNA length. (f) Asymmetry of adhesion energy per binding site between sub- and overcomplexed DNA length. (g) Range of values extracted from Polach and Widom's (27,69) data using the site exposure model. (h) Range of values extracted from Davey and Richmond (71) data using x-ray crystal structure of the nuclear core particle. Uncertainty values are determined using the central limit theorem and a propagation of uncertainty calculus detailed in Supplementary Material. N(H2A conventional) = 301 nucleosomes. N(H2A.Bbd variant) = 252 nucleosomes.

The combination of experimental asymmetry of DNA-complexed length distribution and the simple model allows us to quantify the specificity of the 14 binding sites in the nucleosomes (Table 1, f). In particular this can be interpreted as a rough estimation of nonelectrostatic contribution to adhesion energy between DNA and histone octamer.

Comparison of model parameters extracted from data

These values have to be compared to other estimates reported in the literature. The net energetic gain per site can be compared to values extracted from experiments done by the group of J. Widom (68–70). The spirit of these experiments was to probe the transient exposure of the DNA-complexed length in a nucleosome by using different restriction enzymes acting at various well-defined sites along the DNA. The experimental results clearly demonstrate that DNA accessibility is strongly reduced when restriction sites are located far away from the entry or exit of nucleosomal DNA, toward the dyad axis. From the experimental data, the authors extract a Boltzmann weight for different site exposures. This distribution should a priori be similar to the DNA-complexed length distribution obtained in our work, except that only subcomplexed nucleosomes are probed. However, due to the use of different restriction enzymes with different sizes and mechanisms of action, there is an inherent uncertainty in the assignment of precise DNA-complexed length with a free energy of the Boltzmann weight. In other words, only a range of energy per binding site can be extracted from these data. This has to be contrasted with most previous work using Polach and Widom's data, which quote a single value of 2 kT per binding site (31). The range of net energetic gain we are able to estimate out of these data is between 0.5 and 3 kT per binding site. The value we extracted from our own measurements coincides therefore with the lower bound of this range. This might be due to the difference in the type of experiments used.

First, our observations are made on nucleosomes adsorbed on a charged substrate. This might change the energetics of nucleosome opening as compared to its value in solution. A theoretical estimation of this change is currently under progress (Castelnovo et al., unpublished). Another significant difference between Polach and Widom's experiments and our work is the composition of the buffer, which is known to affect the nucleosome stability. In particular, the buffer used for restriction enzyme assays contains more magnesium ions (∼10 mM MgCl₂).

The specificity of DNA binding sites on histone octamer, as determined in Table 1 e can also be compared to values extracted from x-ray experiments performed by Davey et al. (71). Indeed, by counting the hydrogen bonds per binding site found in this structure, one can estimate the specific contribution to the binding energy. These contributions range between 0.8 and 2 kT per binding site (72). Our estimate for conventional nucleosomes falls in this range (1.1 kT per binding site).

Finally, the comparison between canonical and variant nucleosomes shows that both the average complexed length and the energy per binding site are different. The averaged complexed DNA length L_c = 127 pb (Table 1 a) for the variant claims for either the absence or the strong weakening of at least two binding sites. Furthermore, the energy, and therefore the stability of the nucleosome for the remaining binding sites, is reduced (ɛ_H2A.Bbd ∼ 2/3ɛ_H2A), in accordance with other experimental observations (16,25,73). We have shown in this section that a simple model using a linear energy for the DNA-histone interaction can be used to extract from the AFM data two important energetic parameters: the net energetic gain per site and the specific interaction between the DNA and the histone octamer per site. These values are in good agreement with previous biochemical and x-ray studies done on conventional nucleosomes, and for the first time to our knowledge are measured on a variant nucleosome.

Visualization of nucleosome sliding and remodeling by SWI/SNF for conventional and variant nucleosomes

After studying the nucleosomes in their equilibrium state, the same mononucleosomes were visualized in the presence of the SWI/SNF-remodeling factor to validate the possibility for this direct imaging approach to acquire new information on the mechanism and dynamics of nucleosome sliding.

Centrally positioned conventional and variant mononucleosomes (L_tot = 255 bp) were incubated with SWI/SNF at 29°C in the presence or absence of ATP and then adsorbed on APTES-mica surfaces for AFM visualization. In Fig. 3, we report AFM images of mononucleosomes incubated without (Fig. 3 a) and with (Fig. 3 b) ATP for 1 h. The sample containing no ATP is the control experiment to account for possible nucleosome thermally driven diffusion when incubated 1 h at 29°C. The representative chosen set of AFM images of Fig. 3 clearly shows that most of the nucleosomes are centered on the DNA template in the negative control (−ATP), whereas they exhibit end position when SWI/SNF and ATP are present.

FIGURE 3.

AFM visualization of the sliding of centered mononucleosomes by the remodeling complex SWI/SNF. AFM topography image of mononucleosomes reconstituted on 255-bp 601 positioning sequence, incubated at 29°C with SWI/SNF for 1 h (a) in the absence and (b) in the presence of ATP. Color scale from 0 to 1.5 nm. X/Y scale bar 150 nm. Zoom in of the AFM topography image of a (c) centered mononucleosome and (d) end positioned mononucleosome, the result of the image analysis. Black line, contour of the mononucleosome. Blue point, centroid of the histone octamer. Blue line, skeletons of the free DNA arms. Color scale from 0 to 1.5 nm. X/Y scale bar 20 nm.

On AFM images, the SWI/SNF motor is sometimes visible as a very large proteic complex, and if still attached to nucleosome prevents any image analysis of such objects. Our protocol does not include removing SWI/SNF before deposition, even if by diluting the nucleosome/motor mix, one could expect detaching of some motors. Therefore, the motor/nucleosome ratio used in the sliding experiments is kept low with respect to biochemical assays (55) (∼5 times less SWI/SNF per nucleosome).

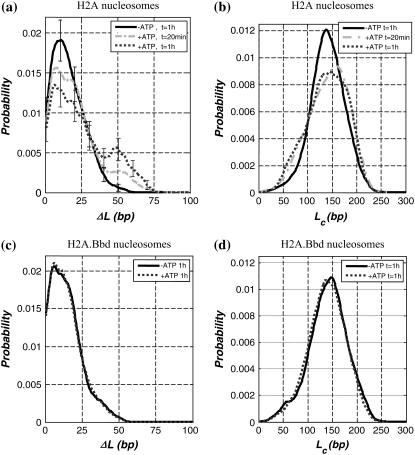
Using the same type of image analysis, we were able to reconstruct 2D histograms L_c/ΔL (using a 2D sliding box as described in the Materials and Methods section) at various time steps during nucleosome sliding: 0 (−ATP), 20 min, and 1 h (Fig. 4). We first notice that in the absence of ATP, SWI/SNF has apparently no effect on the L_c/ΔL map. The 2D distribution exhibits a single peak corresponding to the canonical nucleosome positioned as expected from the DNA template (α state). As a function of time in the presence of remodeling complex and ATP, new states appear: (β) corresponds to an overcomplexed nucleosome having the same mean position ΔL value as (α); this state could result from the capture of extra DNA (a loop of ∼40 bp) inside the NCP induced by SWI/SNF. (β)-state is spread in the ΔL direction, showing that this extra complexed DNA length (∼40 bp) seems to exist for various positions of the nucleosome (0 < ΔL < 30 bp). (γ) is the slided end positioned nucleosome (ΔL ∼ 50 bp) having slightly less DNA wrapped around the histone octamer (L_c ∼ 125 bp). The ΔL distance separating (α)- and (γ)-states is close to the L_c distance between (β) and (α) states, meaning that the slided (γ)-state most likely results from the release of the (β)-state DNA loop (∼40 bp). The fact that slided nucleosomes are subcomplexed, i.e., their dyad has been moved beyond the expected end position, has already been observed in other biochemical studies (74). Similarly, the anisotropic spreading of the (γ)-peak toward higher ΔL and lower L_c is also consistent with this feature. We cannot exclude that a finite size effect of the DNA template could account for this feature. Finally, (δ) is a wide state with a subcomplexed L_c ∼ 75 bp that could correspond to a tetrasome or hexasome. This state could be due to the loss of one wrapped DNA turn either from the (α )-state or the (γ)-state. Nevertheless, one could notice that the (δ)-state is missing on the “+ATP 20 min” map (Fig. 4 b) where only a few nucleosomes have been slided (weak γ-peak), whereas (δ)-state nucleosomes are clearly visible in Fig. 4 c (“+ATP 1 h”). This tends to show that (δ)-state nucleosomes more likely arise from the loss of one DNA turn of the end positioned nucleosome's ((γ)-state).

FIGURE 4.

Evolution of nucleosome L_c/ΔL map during nucleosome sliding by SWI/SNF complex for conventional nucleosome. 2D histogram L_c/ΔL representing the DNA-complexed length L_c along with the nucleosome position ΔL for a conventional nucleosome reconstituted on a short DNA fragment (255 bp) in the presence of remodeling complex SWI/SNF (a) without ATP (1 h at 29°C) (b) with ATP (20 min at 29°C) and (c) with ATP (1 h at 29°C). (d) Representation of the nucleosome L_c/ΔL states for (α), (β), (γ), and (δ) positions as noted on the 2D maps. N(−ATP, 1 h at 29° C) = 692 nucleosomes, N(+ATP, 20 min at 29°C) = 245 nucleosomes, N(+ATP, 1 h at 29°C) = 655 nucleosomes.

We have seen that the 2D mapping of nucleosome position and DNA-complexed length allows us to characterize the new states resulting from the ATP-dependent action of SWI/SNF on our 601 nucleosomes: an overcomplexed state close to the 601 template center (β), a slided state (γ), and a subcomplexed state (δ).

Again, more information can be gained by appropriate projections of these 2D histograms. Nucleosomes having their DNA-complexed length in the range L* ± σ_Lc were selected (L* and σ_Lc are, respectively, the maximum value and the standard deviation of the corresponding complexed length distribution), and their position distribution is plotted in Fig. 5 a. For conventional nucleosomes with SWI/SNF but no ATP, the distributions obtained for nucleosome position (Fig. 5 a) and DNA-complexed length (Fig. 5 b) are very similar to the case without any remodeling complex (Fig. 1 b), showing no effect of thermally driven diffusion of mononucleosomes reconstituted on the 601 positioning sequence in our conditions.

FIGURE 5.

Evolution of nucleosome position and DNA-complexed length distributions during nucleosome sliding by SWI/SNF complex, for conventional and variant nucleosomes. Nucleosome position ΔL (a) and DNA-complexed length L_c (b) distributions as a function of time (0, 20 min, 1 h) in the presence of SWI/SNF, for conventional mononucleosomes reconstituted on 255-bp-long 601 positioning sequence. Nucleosome position ΔL (c) and DNA-complexed length L_c (d) distributions as a function of time (0, 1 h) in the presence of SWI/SNF, for H2A.Bbd variant mononucleosomes reconstituted on the same DNA template. The zero time is given by the control in the absence of ATP (solid line). For each ΔL position distribution, only nucleosomes having their complexed length in the range 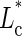± σ_Lc are selected. For the sake of figure clarity, error bars are only depicted on two distributions of graph (a).

When incubation is increased in the presence of ATP (20 min and 1 h), the position distribution of conventional nucleosomes is clearly changed (Fig. 5 a). Indeed, as a function of incubation time, a second peak appears corresponding to the end positioned nucleosomes (ΔL ∼ 50 bp, cf. (γ)-state in Fig. 4 c). After 1 h of SWI/SNF action in the presence of ATP the second peak height has increased at the expense of the primary peak. This corresponds to the situation were one-third of the mononucleosomes are positioned at the end of the DNA template. It is interesting to note that during the remodeling factor action we do not see any significant increase in the amount of nucleosomes in an intermediate position (20 bp < ΔL < 40 bp). This provides experimental evidence that this remodeling factor moves centrally positioned nucleosomes directly to the end of our short DNA template.

Mainly, two situations can explain the bimodal position distribution of nucleosomes after the action of SWI/SNF. The first hypothesis is that the SWI/SNF complex is a processive molecular motor. As it will not detach from the nucleosome before it reaches the end of the DNA template, the elementary step of the SWI/SNF-induced sliding might not be accessible. Indeed, in our experimental conditions, only nucleosomes without SWI/SNF complex attached can be analyzed. The other possibility is that SWI/SNF is weakly processive (SWI/SNF turnover rate is unknown) but with an elementary step of the order of 50 bp, which corresponds to the value measured by us and other approaches (75–77) and happens to be the length of free DNA arms in our case. Therefore, a single step would be enough for the motor to slide a nucleosome to an end position and release the complex.

Nevertheless, another mechanism cannot be excluded by our data, where SWI/SNF action would consist of octamer destabilization followed by thermally driven diffusion toward the end positioned entropically favored. In this situation, ATP-hydrolysis would only be involved in the nucleosome “destabilization” step.

In Fig. 5 b, we show projections of the previous 2D histograms along the DNA-complexed length axis without any selection on their position. For conventional nucleosomes in the presence of SWI/SNF but no ATP, the complexed length distribution is similar to the case with neither SWI/SNF nor ATP. However, the former distribution is larger due to the contribution of different nucleosome positioning. Then after 20 min, the distribution is broader (roughly twice) and shifted toward higher L_c. This might be attributed to the contributions of the different states (β, γ, δ) identified in Fig. 4, b and c. The increase in the L_c mean value is likely due to the statistical weight of the overcomplexed (β)-state.

The same sliding experiment was performed on H2A.Bbd variant nucleosomes in the absence and in the presence of ATP and analyzed through the projection of the 2D histogram L_c/ΔL. No significant effect of SWI/SNF complexes in the presence of ATP on the position distribution of H2A.Bbd variant nucleosomes is observed (Fig. 5 c). This corroborates previous findings using biochemical sliding assays done on 5S and 601 positioning sequences (55). However in AFM measurements, the full position distribution is accessed directly with a resolution better than 10 bp (the size of the AFM tip). This variant nucleosome sliding assay shows the reproducibility of our experimental approach, as not only the position distribution mean value is constant during 1 h in the presence of SWI/SNF and ATP, but also the complete position distribution remains constant (Fig. 5 c). Similarly, SWI/SNF in the presence of ATP does not seem to influence the DNA-complexed length distribution of H2A.Bbd nucleosomes (Fig. 5 d).

CONCLUSION

In summary, we have shown that AFM combined with a systematic computer analysis is a powerful tool to determine the structure of conventional and variant mononucleosomes at equilibrium and after the action of ATP-dependent cellular machineries. With this technique we have simultaneously quantified two important and closely coupled variables: the DNA-complexed length and the position of mononucleosomes along the 601 DNA template. For each of these two distributions, the most probable value is in perfect agreement with measurements done by other methods that give access to one of these two parameters only. In addition, to explain the experimental complexed length distribution, we have developed a simple model that uses the experimental shape of DNA-complexed length distributions to quantify the interaction of DNA with histones. With this model, we extract both the net energetic gain for subcomplexed nucleosomes and the estimation of the nonelectrostatic contribution to the adhesion energy between DNA and histone octamer.

We further show that H2A.Bbd variant and conventional nucleosomes exhibit clear differences in DNA-complexed length and in their ability to be slided by SWI/SNF. Indeed, these variant nucleosomes organize less DNA on average than conventional nucleosomes and present larger opening and closing fluctuations. Moreover, the whole position distribution as well as complexed length distribution remain unchanged, showing the H2A.Bbd variant is neither displaced nor remodeled by the SWI/SNF complex.

Finally, we plotted L_c/ΔL as a 2D map of the nucleosome states. This representation is well suited to highlight the various nucleosome states that appear during the SWI/SNF action. For example, as a function of time, we have evidenced the formation of an overcomplexed state followed by the appearance of a slided state. More quantitative information can be obtained by appropriate projections of the 2D histograms, as for instance the bimodal position distribution induced by SWI/SNF sliding on conventional nucleosomes, suggesting two possible scenarios: a processive action of the molecular motor (no intermediate position visualized) or an elementary stepping length (∼40 bp) of the size of the free DNA arms (∼50 bp). The short length of DNA templates and lack of directionality in our position analysis prevent us from discriminating between these two hypotheses, and further experiments on long oriented mononucleosomes are needed to get more insight into the molecular mechanism of SWI/SNF action. The results here as well as preliminary data on longer oriented templates prove nevertheless that this extension will provide useful information on remodeling mechanisms of SWI/SNF.

A further perspective of this AFM study will be to test the effect of the flanking DNA sequences on the conformation and dynamics of 601 nucleosomes. Nevertheless, to test sequence effects, nucleosomes should be reconstituted on less positioning sequences (5S rDNA for example) or nonpositioning sequences, but this will significantly complicate the nucleosome sliding analysis as the initial position distribution of the nucleosome is expected to be broader in this case.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit http://www.biophysj.org.