Cardiac beat-to-beat alternations driven by unusual spiral waves

Abstract

Alternans, a beat-to-beat temporal alternation in the sequence of heartbeats, is a known precursor of the development of cardiac fibrillation, leading to sudden cardiac death. The equally important precursor of cardiac arrhythmias is the rotating spiral wave of electro-mechanical activity, or reentry, on the heart tissue. Here, we show that these two seemingly different phenomena can have a remarkable relationship. In well controlled in vitro tissue cultures, isotropic populations of rat ventricular myocytes sustaining a temporal rhythm of alternans can support period-2 oscillatory reentries and vice versa. These reentries bear “line defects” across which the phase of local excitation slips rather abruptly by 2π, when a full period-2 cycle of alternans completes in 4π. In other words, the cells belonging to the line defects are period-1 oscillatory, whereas all of the others in the bulk medium are period-2 oscillatory. We also find that a slowly rotating line defect results in a quasi-periodic like oscillation in the bulk medium. Some key features of these phenomena can be well reproduced in computer simulations of a nonlinear reaction-diffusion model.

The spontaneous appearance of one or more reentries on the ventricle is known to be a major cause of ventricular tachycardia (1–5). The self-sustained reentries rotate about their cores very rapidly, emanating a series of action-potential waves that override the normal heart rhythm generated by the natural cardiac pacemaker atrioventricular node. These reentries often destabilize into a turbulent jumble of irregular wavelets and result in cardiac fibrillation leading to a sudden cardiac arrest. Several mathematical model studies have indicated that this instability is closely related to the phenomenon of alternans, a period-2 (p-2) temporal sequence of heart beat (3, 6–8).

Alternans is known to emerge usually when the heart is forced with high-frequency pacing beyond a critical threshold, either by intrinsic pacemakers or extrinsic stimulations. It has been observed in various laboratories and clinical conditions (9–15). In almost all cases, a whole heart, a block of heart tissue, or a quasi-1D cardiac fiber is stimulated with a fast extrinsic pacemaker. Theoretically, the emergence of alternans can be viewed as a period-doubling bifurcation of action potential duration restitution (3, 8). Among others, one spatial feature of alternans is quite noteworthy: line defects termed as “nodal lines” appear in the spatiotemporal alternans state called discordant alternans. The nodal lines are basically a line defect, or a boundary line, across which the phase of p-2 excitation slips by 2π. A series of recent model studies (7, 8) suggest that the nodal lines are a generic feature of alternans in spatially extended cardiac tissues.

In this article, using an in vitro model cardiac system we show that self-sustained p-2 oscillatory cardiac spiral reentries having a well defined line defect can exist. They generate a rhythm of alternans in the bulk medium as they rotate. In other words, alternans can arise and be sustained not by a pacemaker but by spiral reentries. We also show that moving line defects can influence the overall dynamic behavior of the bulk medium. For example, a slowly rotating line defect about a spiral core generates a quasi-periodic-like oscillation in the bulk medium. Some key features of our observations can be reproduced in computer simulations of a generic reaction-diffusion model that supports various complex periodic oscillations.

Optical Recording and Image Analysis

A custom-designed propagation-induced phase contrast imaging scheme (16) has been used to optically map the mechanical contraction patterns of the cultured cardiac tissues noninvasively. Typically, the view field is set to be 28 × 28 mm. Images are captured by a SMD-1M60-20 CCD camera (Dalsa, Waterloo, ON, Canada) with 150-mm FL, 75-mm SLR lens connected to a pair of frame grabber cards (PIXCI D3X, EPIX) in a host computer (dual XEON 2.4 GHZ and 6.5 GB RAM; Intel, Santa Clara, CA). Typically, a sequence of successive images for 30 s (900 frames at 30.0 Hz) is taken at every 20-min interval. The CCD camera is capable of capturing 12-bit monochrome images with spatial resolution of 1,024 × 1,024 pixels at a maximum frame rate of 30 frames per s. The spatial resolution is set at 512 × 512 pixels (with a 2 × 2 binning applied in real time) to keep the recording in a manageable volume. The acquired images are filtered spatiotemporally according to the same protocols used in ref. 17.

A scalar field,

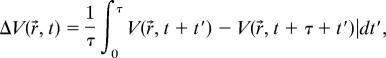is defined to reveal the different temporal periodicity underlying the system. Here, V(r⃗,t) represents the grayscale values of the individual pixels in the filtered images. τ is the period of p-1 oscillation, and technically it is set to be the arithmetic average of τ₁ and τ₂, where τ₁ and τ₂ are the two alternating periods of p-2 time series. For a given pixel, the larger the value of ΔV, the further the location is away from a p-1 dynamics (ΔV = 0).

Experimental Results

Our model cardiac system is a continuously perfused dish containing a confluent isotropic monolayer of rat ventricle cells, which is housed in a small home-built incubation chamber (details in refs. 16 and 17). The spatiotemporal wave activity arising in the cell culture can be monitored almost indefinitely from a very early stage (1 day old) to a mature state (2 weeks or even older). At the early stage, many small wave segments spontaneously emerge without any extrinsic intervention. Previously, it has been demonstrated that this model system can support regular p-1 oscillatory spiral waves (16), identical in many aspects to the ones observed in nonlinear chemical reaction-diffusion systems (18) and various biological media (for example, refs. 19 and 20).

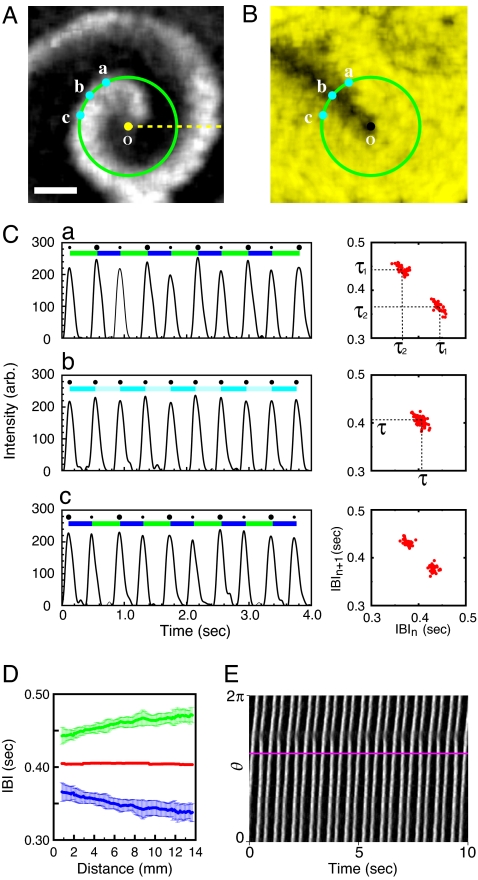
In a series of systematic explorations using various samples under different (density and days in vitro) conditions, we recently found that some reentries can generate alternans. Fig. 1A presents such an example. This particular state has emerged gradually from a previously existing state of p-1 reentries, as the culture matures in the incubation chamber. The snapshot image by itself is very similar to regular p-1 oscillatory spiral waves that form in excitable or simply oscillatory media. However, its dynamical property is rather different for it generates a p-2 oscillation in the bulk medium as it rotates. A typical local time series is presented in Fig. 1Ca. The successive interbeat intervals (IBIs) switch back and forth between two different values, τ₁ and τ₂. The accompanying return map clearly confirms the p-2 oscillatory nature. A significant feature of this p-2 reentry is the existence of a line defect along which the local oscillation is p-1 oscillatory. See the straight black band, which connects the point o (spiral core) and the point b in the overall yellow background of Fig. 1B, which is an image of ΔV(r⃗,t) rendering the local periodicity associated with the reentry of Fig. 1A in color. The brighter the yellow, the farther the local dynamics is away from p-1 oscillation. The local dynamics is p-1 oscillatory only along the line defect, while the bulk medium supports p-2 oscillation, or alternans. As such, the black line structure is termed as line defect, and it is the most salient feature with which a p-2 reentry distinguishes itself from a p-1 reentry.

Fig. 1.

p-2 oscillatory cardiac reentry having a line defect in confluent layer of rat ventricular cells (125.00 h in vitro; cell density: 2.8 × 10³ cells per mm²). (A) Enhanced image acquired through phase-contrast optics. The gray value reflects the degree of contraction (or relaxation). (B) Pseudocolor image visualizing the local periodicity measure ΔV(r,t) for the reentry presented in A. The larger (or brighter yellow) the value of ΔV is, the further the system is away from p-1 dynamics (ΔV = 0, or black). (C) The local time series acquired at a, b, and c, as marked in A and the corresponding return maps of IBI sequences. (D) Variation of τ₁ and τ₂ as a function of the distance from the reentry core along the yellow dashed line in A. (E) Space–time plot confirming the static nature of the associated line defect. Here, the 1D space refers to the green circular loop centered at o in A. The superimposed purple line in E is the trace of the crossing point at which the line defect intersects the circular loop. See [supporting information (SI) Movie 1]. (Scale bar: 6 mm.)

It is important to note that the time series taken in the vicinity of the line defect at the points a and c (Fig. 1C a and c, respectively) are ≈2π out of phase. Namely, the sequential order of τ₁ and τ₂ is reversed in the two time series. This reversal (or 2π phase slip) takes place continuously but rather abruptly, as one crosses the line defect in a transverse direction. Approaching the line defect, τ₁ shrinks while τ₂ increases, and they become identical τ right on the line defect supporting p-1 dynamics (see Fig. 1Cb). In the accompanying return maps, the two groups of dots (Fig. 1Ca) approach and merge together (Fig. 1Cb) only to separate themselves again into another two groups (Fig. 1Cc), as one travels across the line defect. These line defects are in many aspects identical to nodal lines associated with discordant alternans generated by a fast localized, extrinsic pacing (6, 10).

The amount of period detuning, |τ₁ − τ₂ |, rapidly increases in the normal direction away from the line defect and quickly saturates. The period detuning also increases as a smooth function of the radial distance from the reentry core, until it stabilizes more or less beyond the distance of 8–10 mm (see Fig. 1D). Notice that the mean period τ = (τ₁ + τ₂)/2 does not vary for the entire range covered in Fig. 1D. The line defect revealed in Fig. 1D does not move, as illustrated in the space-time plot of Fig. 1E. This static line defect is stable for >2 h until it is overtaken by other wave trains generated from different spiral cores located near the system boundary (data not shown). During this period the spiral core o does not drift nor meander in any significant way.

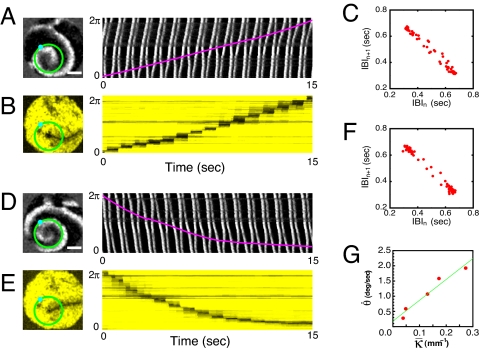
Some line defects associated with p-2 cardiac reentries can be dynamic. For example, the reentry presented in Fig. 2A has a rotating line defect as illustrated in the space-time plots of Fig. 2 A and B. This defect gradually rotates in the same clockwise direction as the associated reentry wave rotation but at a much slower rate, ≈1 turn per 32 turns of the reentry rotation. As a consequence of this slow line defect rotation, the return map of IBIs constructed from a local time series (Fig. 2C) appears as a thin quasi-periodic loop. Notice that there exist two major populations of dots at the two far ends and the data points connecting them are very sparse. In other words, the rotating p-1 line defect that slowly sweeps through an otherwise p-2 oscillatory measurement site produces a quasi-periodic-like local dynamics.

Fig. 2.

p-2 reentries having a rotating line defect. (A) Enhanced phase-contrast snapshot image and 1D space-time plot along the superimposed green circular loop. The culture is t = 114.50 h in vitro. The cell density is 2.3 × 10³ cells per mm². (B) Pseudocolor image visualizing the underlying line defect of the reentry presented in A and 1D space-time activity along the same circular loop. (C) Return map of IBI sequence acquired at the cyan dot marked in A. (D—F) Similar set of images as in A–C but obtained at t = 114.00 h. Note that the chirality of the reentry is reversed. (G) Angular velocity of the line defect (shown in E) versus its mean overall curvature. See SI Movie 2. (Scale bars: 6 mm.)

The reentry presented in Fig. 2A is stable for ≈1 h, beyond which it changes to a new set of reentries. This transition is mediated by some reentry-to-reentry interactions that are primarily based on the rotation periods of the reentries as in the usual entrainment dynamics of p-1 reentries. New reentries constantly emerge and compete as the culture system slowly evolves over time. For example, the p-2 reentry presented in Fig. 2D, which is taken 30 min earlier in the same system, is almost identical to the one presented in Fig. 2A but has the opposite chirality. The reentry in Fig. 2D rotates in a counterclockwise direction, whereas the reentry in Fig. 2A rotates in a clockwise direction. It is important to note that the line defect (see Fig. 2E) associated with the reentry shown in Fig. 2D also rotates slowly in the counterclockwise direction. The quasi-periodic loop-like structure appearing in the return map of Fig. 2F again confirms the line defect rotation. Its angular velocity is not necessarily a constant as can be seen in the space-time plot of Fig. 2E. As Fig. 2G well presents, the angular velocity depends almost linearly on the average curvature of the line defect.

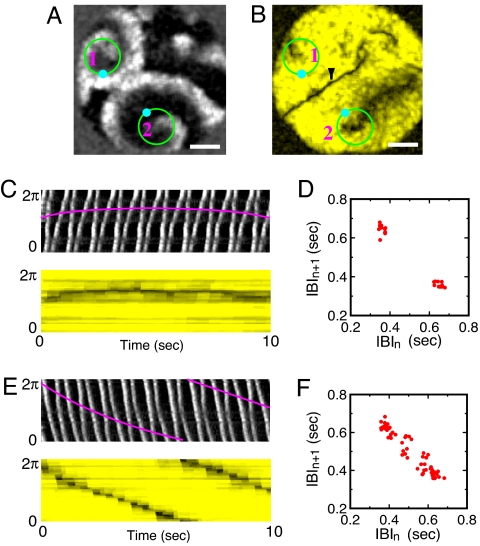
Two or more p-2 reentries can coexist as well, as presented in Fig. 3A. Interestingly, the line defect associated with the reentry marked by 1 is almost static (see Fig. 3C), whereas that of the reentry marked by 2 is dynamic (see Fig. 3E). At this point, there is no clear explanation for this difference. Two things are, nevertheless, frequently observed. First, line defects attached to a reentry core rotates in the same rotational direction of the reentry, whenever they rotate. Second, there is a strong correlation between the overall curvature of line defect and its rotational direction and speed as shown in Fig. 2G. Or, it becomes evident by comparing the static, straight line defect of Fig. 1B with the moving, curved line defects in Fig. 2 B and E. For a curved line defect, the left-right symmetry with respect to the direction of wave propagation is broken. Consequently, “net diffusive ionic flux” across the curved line defect (averaged over a p-2 cycle) is not zero and the line defect moves. This situation has an analogy to the net momentum transfer deriving the shrinkage of “bubbles” in a parametrically driven granular layer (21).

Fig. 3.

Snapshot image showing a pair of p-2 cardiac spiral waves (A) and the underlying structure of line defects (B): one marked by 1 has a static line defect (C and D), whereas the other one marked by 2 has a rotating line defect (E and F). This coexisting state was observed 75 min earlier than Fig. 2A in the same cultured tissue. The thin black line marked by the black arrow in B is a shock boundary where two wave fronts annihilate [i.e., V(r⃗,t) = 0]. See SI Movie 3. (Scale bars: 6 mm.)

Model Simulation

Several key features of the observed p-2 cardiac reentries can be well reproduced by using a simple generic reaction-diffusion model supporting complex oscillations (22, 23). For example, some major features of the p-2 spiral reentry presented in Fig. 1 are reproduced in Fig. 4 by using a three-species 2D Willamowski–Rössler reaction-diffusion model. The model equations are:

where c⃗(r⃗,t) is the concentration vector, D is the diffusion coefficient, and r⃗c⃗(r⃗, t)] describes the following local reaction kinetics:

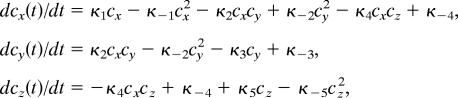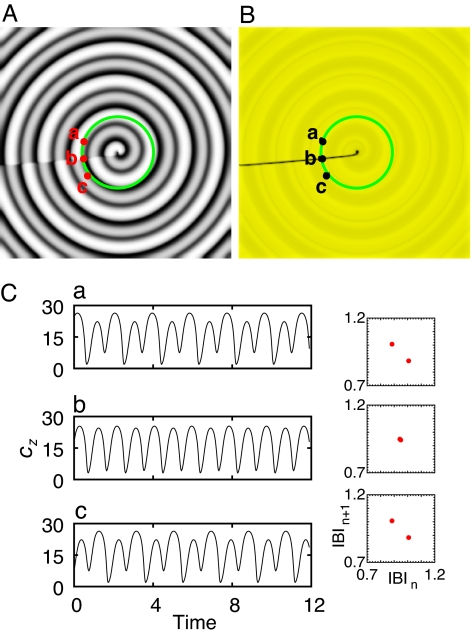
where κ_±i is the rate constant. The Willamowski–Rössler kinetics is well known for its period-doubling bifurcation cascade to chaos. In its simple p-1 oscillatory regime, the model supports a typical p-1 spiral wave. In a p-2 oscillatory regime, as in the case of Fig. 4, the p-1 spiral wave transforms to a p-2 spiral wave, producing a rhythm of alternans. The similarity between the cardiac p-2 reentry of Fig. 1 and the p-2 spiral wave of Fig. 4 is remarkable. They both have a straight, static line defect connecting the core to the boundary. Similar p-2 spiral reentries are also found to exist in a more physiologically relevant model such as the Fenton–Karma model (see ref. 6) (data not shown).

Fig. 4.

Single p-2 oscillatory spiral wave in a model reaction-diffusion system. (A) Gray-scale snapshot image visualizing the scalar field C_Z. (B) A processed image revealing the underlying line defect (black line) of A. The image rendering scheme is the same as in Fig. 1B. (C) Local time series acquired at the positions a, b, and c marked in A and the corresponding return maps of IBIs. The values of rate constants are: κ₁ = 31.2, κ₋₁ = 0.2, κ₂ = 1.50, κ₋₂ = 0.1, κ₃ = 10.8, κ₋₃ = 0.12, κ₄ = 1.02, κ₋₄ = 0.01, κ₅ = 16.5, and κ₋₅ = 0.5. Numerical simulations are conducted with a forward Euler method (DΔt/Δx² = 2 × 10⁴) in a 512 × 512 grids using no flux boundary condition.

Conclusion

In summary, our work demonstrate that some cardiac tissues can support p-2 reentries without any extrinsic intervention. Having some line defects are necessary to resolve the conflict of keeping rotational symmetry of a spiral and the bulk p-2 oscillation simultaneously. Based on our observation, alternans may be viewed as a temporal manifestation of one or more p-2 reentries. In other words, one may view that the spiral cores acting much like a localized fast pacemaker might have caused the temporal rhythm of alternans. On the other hand, it is also possible that the individual myocytes in the culture would support a p-2 oscillation all by themselves even when uncoupled (24) and have provided a base for the p-2 reentries to form. The computer simulation result presented here is more relevant for the latter case.

Finally, we note that a series of recent experimental studies on a Belousov–Zhabotinsky reaction-diffusion system (25, 26) as well have revealed p-2 oscillatory spiral waves that are in many aspects identical to the observed p-2 cardiac reentries discussed here. In all cases, line defects are an essential feature of p-2 spiral reentries. Taken together, p-2 reentries having line defects seem to be an universal feature of any p-2-like oscillatory media. A comprehensive understanding of the spatiotemporal dynamics of line defects and the transition to spatiotemporal chaos mediated by them may shed light on the prevention of cardiac fibrillation.

Abbreviations

IBI

interbeat interval

p-n

period-n.