The electrostatic characteristics of G·U wobble base pairs

Abstract

G·U wobble base pairs are the most common and highly conserved non-Watson–Crick base pairs in RNA. Previous surface maps imply uniformly negative electrostatic potential at the major groove of G·U wobble base pairs embedded in RNA helices, suitable for entrapment of cationic ligands. In this work, we have used a Poisson–Boltzmann approach to gain a more detailed and accurate characterization of the electrostatic profile. We found that the major groove edge of an isolated G·U wobble displays distinctly enhanced negativity compared with standard GC or AU base pairs; however, in the context of different helical motifs, the electrostatic pattern varies. G·U wobbles with distinct widening have similar major groove electrostatic potentials to their canonical counterparts, whereas those with minimal widening exhibit significantly enhanced electronegativity, ranging from 0.8 to 2.5 kT/e, depending upon structural features. We propose that the negativity at the major groove of G·U wobble base pairs is determined by the combined effect of the base atoms and the sugar-phosphate backbone, which is impacted by stacking pattern and groove width as a result of base sequence. These findings are significant in that they provide predictive power with respect to which G·U sites in RNA are most likely to bind cationic ligands.

INTRODUCTION

It is now widely accepted that RNA molecules participate actively in virtually all cellular metabolic processes. Unlike DNA, in which double stranded complementary Watson–Crick (WC) base pairs are obligatory to maintain genetic fidelity, RNA molecules are rich in structural elements comprising non-canonical (i.e. mismatched) base pairs, base triples, junctions, turns, bulges and loops [recently reviewed by Leontis and Westhof (1)]. These structural elements are essential for RNA biological function. Therefore, knowledge of the physicochemical properties of these structural elements will help us understand the molecular basis of RNA folding, stability and function.

One such structural element is the G·U wobble base pair (from here on referred to as a G·U pair), which is the most common non-WC base pair present in RNA. First hypothesized by Crick in 1966 to account for codon degeneracy (2), the G·U pair has been found in nearly all forms of RNA including transfer (t)RNAs (3,4), small nuclear (sn)RNAs (5) and ribosomal (r)RNAs (6,7). Several ribozymes also contain G·U pairs in their structures, such as the Group I and Group II introns (8–10) and the Hepatitis Delta Virus (HDV) ribozyme (11). Furthermore, most of the G·U pairs are highly conserved. Substitution of a G·U pair with other base pairs often has detrimental effects on RNA function. For example, the single G3·U70 pair at the acceptor arm of the Escherichia coli tRNA^Ala is the identity element for aminoacyl-tRNA synthetase recognition. Substitution of this G·U pair with WC base pairs completely abolishes aminoacylation with alanine both in vitro and in vivo (12,13). The G1·U37 wobble pair at the P1 helix of HDV ribozyme is critical for its cleavage reaction. Only an A·C wobble pair, but not WC base pairs, could partially replace the G·U in terms of reactivity (11,14). A G·U pair located in stem I of the mRNA coding for ribosomal protein S15 is an example of the U·G/C·G motif, which serves as the recognition determinant for the binding and autoregulation of S15 (15).

Studies have identified several properties that contribute to the diverse biological function of G·U pairs. First, the geometry of the G·U pair provides unique chemical groups in the major and minor grooves. Among them, the non-hydrogen-bonded amino group of guanine in the minor groove was thought to be important for the 5′ splice site selection of the Group I intron (10,16). Second, the continuous presence of three electronegative groups (guanine N7, guanine O6 and uracil O4) creates a broad region of negative electrostatic potential in the major groove of the G·U pair. This region of electronegative potential is proposed as the recognition site for the binding of metal ions and other positively charged ligands (17–21). In fact, a recently compiled database of metal ion binding sites in RNA structures has shown that the major groove of the G·U pair is the most common metal ion binding motif (22). Third, it has been noted that the presence of the G·U pairs in the A-form RNA helices introduces certain sequence-dependent changes to the structural parameters like the helical twist (23–26). It was proposed that the distortion of the backbone by the G·U pair positions the functional groups of the HDV ribozyme for efficient catalysis (27). Detailed reviews on the structural, chemical and biological properties of RNA structure with G·U pairs can be found elsewhere (19,28).

G·U pairs occur in nearly every class of RNA as single base pair or in tandem form (i.e. adjacent G·U pairs). Most of the G·U pairs found in tRNA are in single form, whereas tandem G·U pairs are commonly observed in rRNA. Analysis of the tandem G·U pairs in rRNAs showed that the sequence 5′-UG-3′/3′-GU-5′ (Motif I) is the most prevalent, followed by 5′-UU-3′/3′-GG-5′ (Motif III) and 5′-GU-3′/3′-UG-5′ (Motif II). Thermodynamic stabilities of RNA structures containing these three motifs follow the same order (29–31).

NMR and X-ray studies have explored the structural features of different motifs for tandem G·U pairs (17,32–34). In Motif I, the six-member ring of the guanine base of the G·U pair stacks directly on top of the six-member ring of the guanine of the opposite strand. In contrast, there is considerable intra-strand stacking between the tandem G·U pairs in Motif II, with the purine ring overlying the pyrimidine ring. Motif III exhibits an intermediate situation between Motif I and Motif II, with a mix of inter- and intra-strand stacking. Data from structural studies suggest that electrostatic interaction, base stacking, hydrogen bonding and the neighboring WC base pairs all contribute to the thermodynamic stabilities of different tandem G·U motifs (17,32–34).

As a result of the strong electrostatic field associated with the high-charge density of the RNA sugar-phosphate backbone, RNA structure and function are highly influenced by electrostatic interactions. The molecular surfaces of RNA molecules display unique electrostatic patterns that are important for recognition and binding of cationic species [for example, see references (18,35)]. Therefore, careful quantitative characterization of electrostatic features of RNA structural elements, such as the G·U pair, is vital for a better understanding of RNA ligand recognition events. Previous studies of the electrostatic features of the G·U pair were focused on the general properties of the major groove of a limited number of structures.

In this research, we seek to provide a more in depth, quantitative analysis of the electrostatic properties of individual G·U pair motifs in order to achieve a detailed understanding of effects contributing to the total electrostatic landscape. The ultimate goal is to predict accurately the likelihood of entrapment of cationic ligands. To accomplish this, we employ the non-linear Poisson–Boltzmann approach, which delivers precise surface and site electrostatic potential values. Our calculations indicated that, in some cases, the major groove of G·U pairs demonstrated enhanced electronegativity over standard GC and AU base pairs. For single G·U pairs, it is sequence dependent, but for tandem G·U pairs, it largely depends on motif conformation. Furthermore, we propose that both the sugar-phosphate backbone and the G·U base atoms contribute significantly to the electronegativity at the major groove of the G·U pairs.

METHODS

Structures

The structures used in the calculations were selected from the Protein Data Bank [PDB (36)] with the help of a database of non-canonical base pairs found in known RNA structures (37). The PDB codes of both NMR and X-ray structures used in this paper are listed in Table 1. The structures contain either single G·U pair or tandem G·U pairs in different motifs. For NMR structures with multiple models, calculations were done on two models with the lowest potential energies as assessed using AMBER8 (38). In all the cases, as the two models showed very similar trends, only the results from the model with the lowest potential energy were presented. All physical coordinates of helical structures used in this study were incorporated into our calculations exactly as experimentally determined (except 1IKD, as noted in Table 1). For each helix containing G·U pair(s), we generated a set of new helices in which both WC GC and AU base pairs replaced the G·U pair(s). These model ideal A-RNA helices (39) were generated using the AMBER8 (38) nucgen utility and were for the purpose of comparison with their G·U counterparts. In one case included in our study, the original structure determination included both G·U (PDB: 434D) and GC (PDB: 435D) helices. The missing hydrogen atoms were added with the program REDUCE (40).

Table 1.

RNA structures from the PDB utilized in the Poisson–Boltzmann calculations

PDB code	Sequences	Structural features
1AJF	5′GACAGGGGA	Tandem G·U; Motif III; P5b helix of Group I intron (51)
	3′CUGUUUCAA
1C0O	5′GGGUCUU	Tandem G·U; Motif II; P5 helix of Group I intron (50)
	3′CCUGGGC
1DFU	5′CCCAUGCGAGAGUAGGGAC	Tandem G·U; Motif I; 5SrRNA/L25 complex (49)
	3′GGGGUGUGAUGGUAGCCGU
1EKA	5′GAGUGCUC	Tandem G·U; Motif I; NMR structure (32)
	3′CUCGUGAG
1GUC	5′GAGGUCUC	Tandem G·U; Motif II; NMR structure (34)
	3′CUCUGGAG
1HLX	5′GGGAUAACUU	Single G·U; P1 helix of Group I intron (23)
	3′CCCUGUUGGC
1IKDa	5′GGGGCUCUU	Single G·U; acceptor stem of E. coli tRNAAla (24)
	3′CCUCGAGGC
1QES	5′GGAGUUCC	Tandem G·U; Motif II; NMR structure (17)
	3′CCUUGAGG
1QET	5′GGAUGUCC	Tandem G·U; Motif I; NMR structure (17)
	3′CCUGUAGG
315D	5′GUAUGUAC	Tandem G·U, Motif I; Crystal Structure (78)
	3′CAUGUAUG
433Db	5′GGUAUUGCGGUACC	Two tandem G·U, Motif III; Crystal structure (52)
	3′CCAUGGCGUUAUGG
434D	5′UAGCUCC 3′AUCGGGG	Single G·U; Crystal structure of acceptor stem of E. coli tRNAAla (26)
472D	5′GUGUUUAC	Tandem G·U, Motif III; Crystal structure (33)
	3′CACGGAUG
435D	5′UAGCCCC 3′AUCGGGG	Mutant of 434D, where G3·U70 was replaced by G3-C70 (26)

^aThe unpaired bases in 1IKD were truncated for easy comparison with its WC RNA counterparts.

^bThere are two tandem G·U pairs in this structure. Only the results of (U5·G24/UU6·G23) were reported here.

Solution to the non-linear poisson Boltzmann equation (PBE)

The electrostatic potentials at the surface (here taken as the solvent-excluded molecular surface defined by a probe radius of 1.4 Å) and atomic sites of isolated G·U, GC and AU base pairs were obtained with the fast multipole-accelerated (41) boundary element solution of the Poisson equation (42). The interior and exterior dielectric constants were fixed at 2 and 80 (25°C), respectively. All default code parameters were employed as described in detail elsewhere (42). For RNA helices, which are now embedded in a solvent medium that contains univalent salt ions corresponding to a salt concentration of 1 M (with an ion exclusion region of 2 Å radius), a novel linear/non-linear Poisson–Boltzmann algorithm was used (Boschitsch and Fenley, unpublished results). Very similar results were also obtained using the hybrid boundary element and finite difference Poisson–Boltzmann solver (with no ion exclusion region) which was employed previously (43). The atomic partial charges and radii were taken from the AMBER94 force field (44). Calculations repeated with the CHARMM27 force field parameters (45) showed the same trend. This similarity indicates that our conclusions were independent of the choice of radii and charge parameters. Formal RNA charges, with a −0.5e charge assigned to each non-bridging phosphate oxygen atom, were employed to examine sequence independent electrostatic features. When formal RNA charges were used, the atomic radii were assigned based on the AMBER94 parameter set.

Visualization

The molecular surfaces were color coded according to electrostatic potential derived from either the Poisson or the non-linear PBE and were rendered using the virtual reality modeling language (VRML) (46). The 3D structures of the RNA base pairs and helices were displayed using the ViewerPro program (Accelrys, Inc., San Diego, CA, USA) and saved in the VRML file format. The 3D structure was then incorporated into the electrostatic potential maps for easy identification. In order to facilitate visual inspection, color mapping of the electrostatic potential was finely scaled as follows: green (most positive), followed by blue, white (neutral), red and yellow (most negative).

Calculations of site and groove electrostatic potentials

The electrostatic potentials surrounding specific atom sites were calculated by taking the average electrostatic potential of sampled grid points outside the molecule around the particular atom. The grid points were sampled by generating two layers of spheres 1.2 and 2.4 Å away from the van der Waals surface of the atom. The electrostatic potentials of the grid points were obtained using the Poisson and PBE approach for the isolated base pairs and RNA helices, respectively, as described above. The electrostatic potential of the major and the minor groove was calculated by averaging the site electrostatic potential of the G·U pair(s) base atoms facing the major/minor groove surface. The atoms facing the major groove include N7(G), O6(G), N4(C), NH4(C) and O4(U). The atoms facing the minor groove include N2(G), N3(G), NH2(G), O2(C) and O2(U).

Calculations of cross-strand phosphate distance

The cross-strand inter-phosphate distance for a given base pair step was computed using the 3DNA program (47).

RESULTS

Electrostatic features of the isolated G·U pair

We began our study of the electrostatic features of the G·U pair by calculating the electrostatic potentials of an isolated G·U pair without the context of the RNA helix, and comparing the results with isolated WC GC and AU base pairs. The calculation was accomplished by use of the Poisson equation as described in Methods. Figure 1 shows the surface electrostatic potential maps for the isolated G·U and WC GC/AU pairs. As shown in the figure, the major groove of the AU base pair is mostly negative along the edge formed by the nitrogen and carbonyl oxygen atoms, with a positive electrostatic potential spot associated with the adenine amino group.

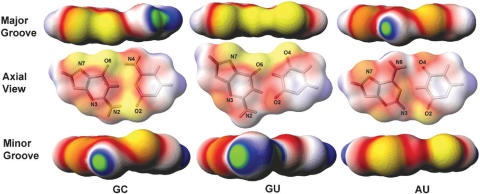
Figure 1.

Surface electrostatic potential maps of an isolated Watson–Crick GC base pair, G·U wobble base pair, and Watson–Crick AU base pair. Each base pair is shown in three aspects, from the major groove edge (top), axial view (center), and minor groove edge (bottom). The axial view is shown with the molecular structure, with key atoms labeled, merged with the potential map, for easy identification. The atomic charge and radii are those from the AMBER94 molecular mechanical force field. The color scheme used in this map is as follows: yellow is the most negative (−1.7 kT/e) and green is the most positive (1.7 kT/e). White is neutral. Red and blue represent negative and positive potentials, respectively. The calculation was performed using the Poisson equation as described in the Methods.

Greater extremes in electrostatic polarity are observed in the major groove of the GC base pair. Deep electronegative potential is seen on the G edge, while the C edge is predominantly electropositive. The polarity observed in the WC base pair is due to the presence of electropositive amino group of adenine and cytosine in the major groove. In contrast, the major groove of the G·U pair is uniformly and strongly negative, since the co-planar N7(G), O6(G) and O4(U) atoms lining the major groove are all electronegative. On the minor groove edge, the non-hydrogen-bonded guanine NH₂ group of the G·U pair created an electropositive region, which is absent in the AU pair and less pronounced in the GC pair. We calculated an average electrostatic potential at the major groove of the isolated G·U pair of −0.4 kT/e, as compared with average electrostatic potentials at the major grooves of GC and AU base pairs of −0.2 and −0.3 kT/e, respectively. The average electrostatic potential at the minor groove of the isolated G·U pair is neutral, whereas for both GC and AU pairs, the value is −0.3 kT/e. Therefore, the overall electrostatic potential of isolated G·U pair is somewhat more negative in the major groove and slightly more positive in the minor groove than for the WC GC/AU base pairs.

In addition to wobble pairs, several X-ray and NMR structures have displayed bifurcated G·U interactions (23,32,48,49). In this arrangement, the O4 of U hydrogen-bonds with hydrogens attached to N1 or N2 of G. The bifurcated G·U positions H5 and H6 of U in the major groove, instead of the electronegative O4. Hence, the surface electrostatic potential of bifurcated G·U displays similar polarity as observed in the WC GC base pair (data not shown).

Use of NLPB Equation for analysis of electrostatic features of RNA helices

Rigorous analysis of RNA electrostatic properties by PBE can identify intense negative electrostatic potential on the RNA molecular surface. Because RNA molecules are highly charged, and often have irregular shapes, the non-linear form of the PBE is the most appropriate method to provide a precise representation of the RNA electrostatic potentials.

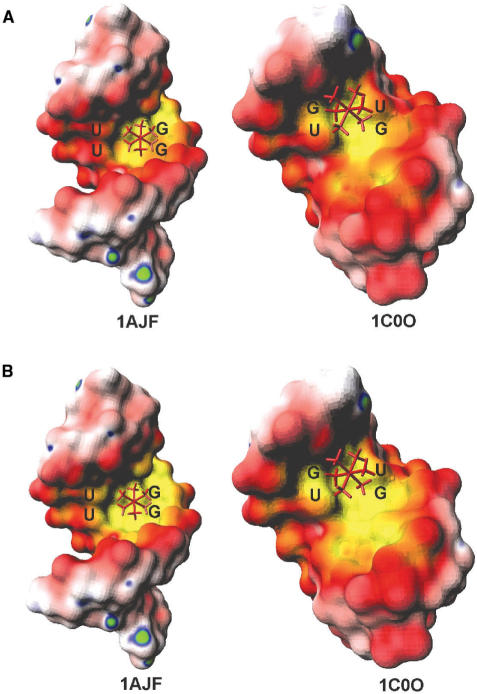
We illustrate this point by calculating the electrostatic surface potential of two helices of the Group I intron that contain tandem G·U pairs [PDB: 1C0O (50) and 1AJF (51)] using both the non-linear PBE and the linear PBE. Figure 2A shows the results for the NLPB treatment for each helix, as well as the cobalt(III)-hexammine ([Co(NH₃)₆]³⁺) ion bound to the RNA in the NMR-derived structure (50,51). Figure 2B shows the corresponding surface maps computed with the linear PBE. Comparison between Figure 2A and B illustrates that the non-linear PBE, as opposed to its linearized version, predicts the metal ion binding sites with far greater precision.

Figure 2.

The surface electrostatic potential maps of P5b (PDB:1AJF) helix and P5 (PDB:1C0O) helix of Group I intron with the bound cobalt hexamine shown as a stick representation. (A) Potential maps were computed using non-linear PBE approach as described in the Methods. (B) Potential maps were computed using linear PBE approach. Enhanced definition of the region of negativity in the major groove of the map shown in (A), which permits greater acuity in identification of the metal ion binding site, is the result of use of the non-linear PBE. The color scheme used in this map is as follows: yellow is the most negative (−6.8 kT/e) and green is the most positive (1.7 kT/e). White is neutral. Red and blue represent negative and positive electrostatic potentials, respectively.

Electrostatic features of the G·U pairs in a RNA helix

In order to examine the impact of base sequence on electrostatic properties of G·U pairs, we divided the RNA helices containing G·U pairs into four categories: (i) RNA helices with a single internal G·U pair; (ii) RNA helices with Motif I tandem G·U pairs (5′-UG-3′ vs. 5′-UG-3′, characterized by purine-purine cross-strand stacking); (iii) RNA helices with Motif II tandem G·U pairs (5′-GU-3′ vs. 5′-GU-3′, with purine-pyrmidine intra-strand stacking); and (iv) RNA helices with Motif III tandem G·U pairs (5′-GG-3′ vs. 5′-UU-3′, with a mix of intra- and inter-strand stacking). We chose three representative RNA helices for each of the four categories and, for the purpose of reference, generated corresponding canonical A-form RNA helices. These helices contained the identical sequence, except for substitution of G·U with both AU and GC (in different structures), each having parameters defined by fiber diffraction data (39). Table 2 lists the electrostatic potential values calculated for the G·U pairs embedded within RNA helices, compared with those of their canonical counterparts. The data in Table 2 indicate that the major groove electrostatic potential of each standard A-form RNA helix is approximately −4.0 ± 0.3 kT/e. This value fluctuates only slightly with different base sequences and stacking patterns. In contrast, the major groove electrostatic potentials of the G·U pairs embedded in RNA helices vary from −4.0 to −6.3 kT/e. For RNA helices containing a single G·U pair, the major groove electrostatic potential is generally considerably more negative than that of the corresponding canonical RNA helices, depending on the specific base sequence.

Table 2.

Total electrostatic potentials (EP in kT/e) of the G·U pairs embedded in RNA helices, compared with their canonical counterparts

RNA helices		EP at the major groove			EP at the minor groove
		GU	GC	AU	GU	GC	AU
Single G·U	1HLX	−4.0	−4.1	−4.0	−1.3	−0.3	−0.5
	1IKD	−5.9	−3.9	−4.2	0.0	−0.1	−0.4
	434Da	−5.1	−4.0	−4.1	0.7	0.0	−0.3
Motif I	1EKA	−3.5	−4.4	−3.6	−1.4	−0.1	−0.3
	1QET	−4.7	−4.4	−3.8	−0.6	−0.2	−0.5
	315D	−4.5	−4.4	−3.8	−0.7	−0.2	−0.5
Motif II	1C0O	−5.9	−3.7	−3.9	−1.0	0.2	−0.1
	1GUC	−6.3	−3.9	−4.0	0.1	−0.3	−0.2
	1QES	−5.1	−4.1	−4.1	0.7	0.0	−0.3
Motif III	1AJF	−5.3	−4.4	−4.4	−0.7	−0.2	−0.6
	433D	−4.9	−4.5	−4.4	−0.9	−0.2	−0.6
	472D	−5.9	−4.0	−3.8	−1.0	−0.1	−0.3

^aNote that the structure of the canonical form of 434D, where the G3·U70 was replaced by G3C70, was already determined by X-ray crystallography (PDB code: 435D).

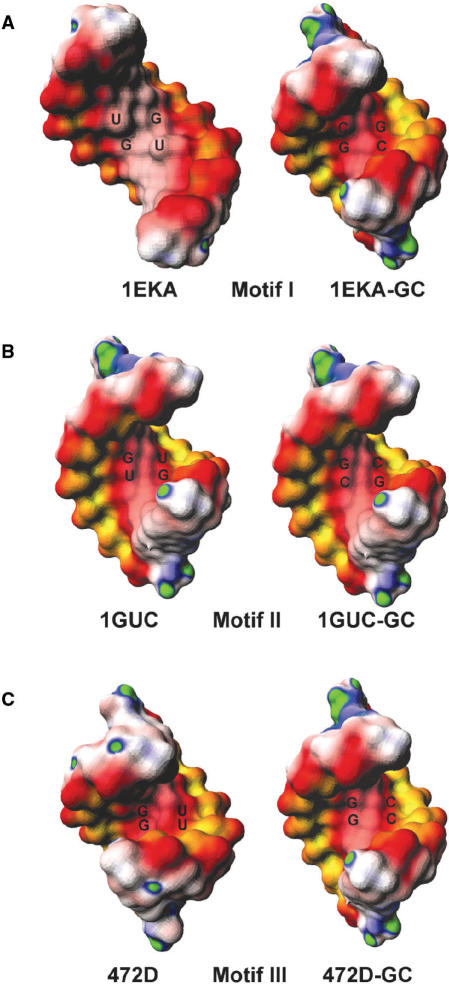
For RNA helices with tandem G·U pairs, the major groove electrostatic potentials are highly influenced by the stacking patterns. Figure 3 shows the surface electrostatic potential maps for one representative RNA helix from each motif compared with its canonical (GC) counterpart. We found that the electrostatic features of Motif I tandem G·U pairs are quite different from those of Motifs II and III (also see Table 2). The electrostatic potential at the major groove of Motif I RNA helices is more positive than (one case) or slightly more negative than (two cases) that of the corresponding WC RNA helix, depending upon groove width (see ahead). However, all of the Motif II and Motif III RNA helices showed enhanced negativity at the major groove, compared with their WC counterparts (GC or AU). We also noted that helices with Motif I are less negative than that of Motif II and Motif III. The most dramatic example was observed between 1EKA and 1GUC. Despite similarities in helical length and the nearest neighbor base pairs, the major groove electrostatic potential of 1GUC is significantly more negative than that of 1EKA (−6.3 kT/e vs. −3.5 kT/e).

Figure 3.

The surface electrostatic potential maps of RNA helices with (A) Motif I G·U pairs (PDB:1EKA), (B) Motif II G·U pairs (PDB:1GUC) and (C) Motif III G·U pairs (PDB:472D). For each motif, comparison between G·U (left) and GC (right) base pairs were made. The potential maps were computed with the non-linear PBE, including the partial charges of all atoms. The color scheme used here is the same as in Figure 2.

Electrostatic potentials at the atomic sites of the G·U pairs

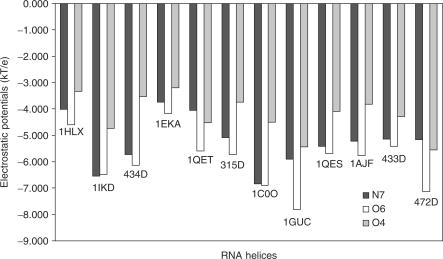
Although the major groove of G·U pairs is uniformly negative in the sense that there is no positive amino group present, a close look at individual base atom sites revealed that electrostatic polarity still exists at the major groove. Figure 4 presented the electrostatic potential at N7(G), O6(G) and O4(U) of the G·U pairs from each RNA helix studied (for RNA helices with tandem G·U pairs, only one G·U pair was shown). For each G·U pair, the average electrostatic potential associated with O6(G) are the most electronegative. In most cases, O4(U) is the least electronegative atom. On average, the difference in potential between O6(G) and O4(U) is 1.7 kT/e. In 434D, the extreme case, the difference between O6(G) and O4(U) is as high as 2.6 kT/e.

Figure 4.

The electrostatic potentials at the atomic sites of guanine N7, guanine O6 and uracil O4 of different G·U pairs in RNA helices.

The sources of negativity at the G·U major groove

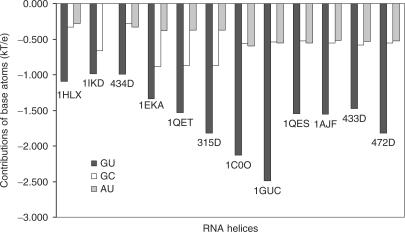
Next, we investigated the sources of the broad region of negative electrostatic potential at the major groove of the RNA helix containing the G·U pair(s). The two most likely sources are the partial charges of the G·U base atoms and the sugar-phosphate backbone charges. To investigate the contributions from the partial charges of the G·U base atoms to the major groove potential, we obtained two major groove electrostatic potential values. The first was calculated with all partial charges included and the other with the partial charges of the G·U base atoms set to zero. The contribution from the G·U base atoms was then defined as the difference between the two electrostatic potential values. As a control, we also calculated the contribution of the corresponding GC/AU base atoms to the major groove potential. Figure 5 illustrates the contributions of the partial charges of the G·U, GC and AU base atoms to the major groove potentials. As is shown, the partial charges of the G·U base atoms make a significant contribution to the total major groove electronegativity, while the base partial charges of the WC GC/AU base pairs have only a small effect. Overall, tandem G·U base atoms contribute around −2.0 kT/e to their major groove electronegativity, whereas the corresponding WC base pairs contribute only about −0.7 kT/e to the major groove electrostatic potential.

Figure 5.

The contributions of the G·U, G·C and A·U base atoms charges to RNA major groove electrostatic potentials. Values were calculated as the difference between the total potential and the potential when the partial charges of the base pairs were set to zero for each base pair. See text for further detail.

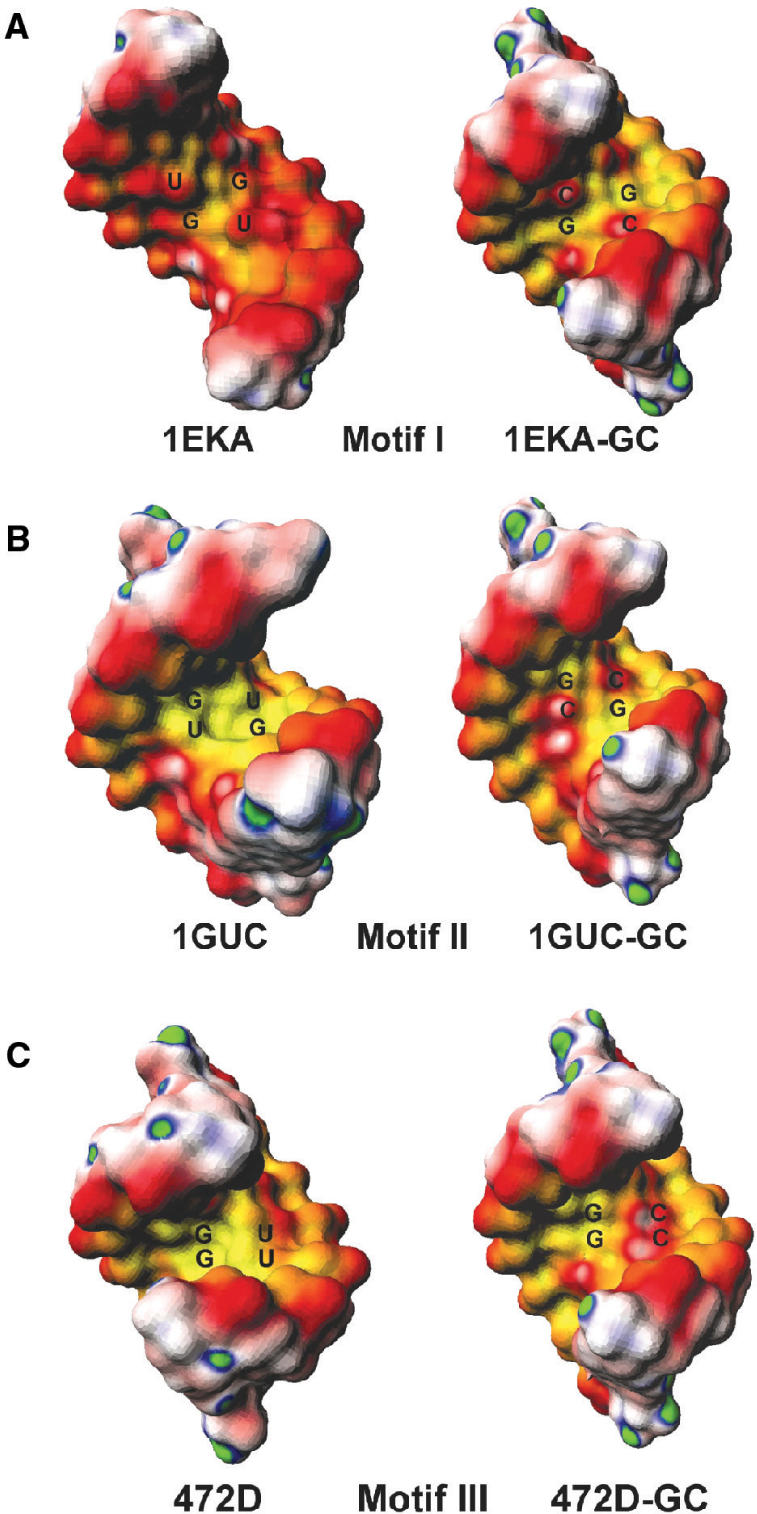
We then examined the contributions of sugar-phosphate backbone to the electronegativity by calculating the ‘formal’ electrostatic potential. The calculation was performed by placing a -0.5e charge on each non-bridging phosphate oxygen atom. Table 3 shows the major groove electrostatic potentials of the G·U pairs derived from these calculations, compared with their canonical counterparts. For the majority of the RNA helices containing G·U pairs, the formal major groove electrostatic potential of G·U pairs is similar to that of the standard A-form RNA helices. However, for some G·U pairs (for example, 1HLX and 1EKA), the formal major groove electrostatic potential is less negative than their canonical counterparts. In particular, we found that most RNA helices with Motif I tandem G·U pairs have less negative formal electrostatic potential than their canonical counterparts. On the other hand, the majority of RNA helices with tandem Motif II and III G·U pairs have similar formal electrostatic potential as their WC counterparts. The gradation of the potential is depicted very clearly in Figure 6. Again, we noticed that helices with Motif I are less negative than that of Motif II and Motif III, when the electrostatic potential were computed with only the sugar phosphate backbone charges included (also see Table 3).

Table 3.

Formal electrostatic potentials (EP in kT/e) of the G·U pairs embedded in RNA helices and the interphosphate distances, compared with their canonical counterparts

RNA helices		EP at the major groove			Cross-strand phosphate distance
		GU	GC	AU	GU	GC	AU
Single G·U	1HLX	−2.2	−3.3	−3.2	19.1	15.2	15.2
	1IKD	−3.5	−3.0	−2.9	14.1	15.2	15.2
	434D*	−2.9	−2.6	−2.8	15.1	15.2	15.2
Motif I	1EKA	−1.9	−3.0	−3.0	19.8	15.2	15.2
	1QET	−2.8	−3.1	−3.0	17.2	15.2	15.2
	315D	−2.5	−3.1	−3.0	18.4	15.2	15.2
Motif II	1C0O	−2.7	−2.9	−2.8	14.1	15.2	15.2
	1GUC	−3.2	−3.0	−3.0	14.9	15.2	15.2
	1QES	−2.9	−2.9	−3.0	16.2	15.2	15.2
Motif III	1AJF	−3.4	−3.2	−3.1	15.1	15.2	15.2
	433D	−2.9	−3.4	−3.3	17.8	15.2	15.2
	472D	−3.3	−3.0	−3.0	15.4	15.2	15.2

Calculation of ‘formal’ potentials is accomplished by ‘turning off ’ charges for the bases and sugars, so that only contributions from the phosphates are considered.

Figure 6.

The surface electrostatic potential maps of RNA helices with (A) Motif I G·U pairs (PDB:1EKA), (B) Motif II G·U pairs (PDB:1GUC) and (C) Motif III G·U pairs (PDB:472D). For each motif, comparison between G·U (left) and GC (right) base pairs were made. The potential maps were computed with the non-linear PBE, including the partial charges of only sugar-phosphate atoms. The color scheme used here is the same as in Figure 2.

In order to investigate the origin of the difference in formal electrostatic potential between the different motifs, we evaluated the inter-strand phosphate-phosphate distance. As shown in Table 3, Motif I had a wider mean cross-strand interphosphate distance than either of the other motifs or than the canonical helices. A wider major groove will result in a lesser concentration of negative potential from the backbone and bases. In contrast, dimensions of the major groove in helices having Motifs II and III are relatively similar to their WC counterparts. In these motifs, the more negative potential is readily apparent.

In summary, G·U base pair atoms, regardless of the motif, contribute to enhancement of the electronegativity in the major groove. However, the different motifs have different groove width, thus different formal electrostatic potential.

The electrostatic features at the G·U minor groove

We focused our study of the electrostatic features of the G·U pair on the major groove, which is the primary binding site for catonic groups in RNA helices. Unlike the major groove, the minor groove potential of standard A-form RNA exhibits a higher degree of dependence on base sequences (Table 2), with the partial charges of the base atoms contributing heavily to the groove potential. In contrast, the G·U base atoms do not make significant contributions to the minor groove potential (data not shown). Although the minor groove electrostatic potential of an isolated G·U pair is more positive than that of isolated WC base pairs, when incorporated into RNA helices, the minor groove electrostatic potential of G·U pairs tends to be more negative than that of the WC base pairs in standard RNA helices (see Table 2). Our results therefore disagree with those of Trikha et al. (52), who performed electrostatic potential analyses of an RNA helix with a Motif III tandem G·U pair and reached the conclusion that the minor groove presented a region of positive potential, which was absent in its canonical counterpart. We were not able to identify the source of discrepancy between our results. However, we noticed that the electrostatic patterns of the WC RNA helix used as the control in their study contradicts standardly accepted electrostatic profile of A-RNA (i.e. the major groove should be more negative than the minor groove).

DISCUSSION

Divalent metal ions are critical for RNA structure and function (53–57). Metal ions can facilitate folding of RNA into a variety of intricate tertiary structures by counter-balancing the repulsion between the negative charges of the sugar-phosphate backbone, and some metal ions participate directly in ribozyme catalysis. Although there is no definitive method for identification of metal ion binding sites in RNA under physiological conditions, location of site bound ions are often inferred from results of X-ray crystallography, NMR or phosphorothioate substitution experiments, among other methods.

However, there is great value in being able to predict likely cationic binding sites based upon computational methods. Techniques such as valence screening, molecular and Brownian dynamics simulations, and microenvironment analysis have been used to identify possible metal ion binding sites (58–62). Given the strength of the NLPB in accurate prediction of the electrostatic features of structured biopolyelectrolytes (59), we have applied this technique to obtain detailed information about the electrostatic potential of G·U base pairs in different structural contexts.

The negative potential of the G·U pair facilitates cationic binding

Numerous experimental studies have identified G·U major groove atoms located within hydrogen bonding distance to metal ions (23,48–51,59,63–66), protein cationic side chains (49,67–70), and aminoglycosidic antibiotics (58,71). It has been suggested that the pronounced negative electrostatic potential at the G·U major groove is an important factor in attracting positively charged ligands (17–19,23). We confirmed that most G·U pairs display enhanced electronegativity at the major groove, ranging from −0.8 to −2.5 kT/e, while some G·U pairs have similar major groove electrostatic potentials to their canonical counterparts.

To show how the enhanced electronegativity facilitates cationic binding, we computed the electrostatic contribution to binding free energy () of [Co(NH₃)₆]³⁺ to P5b helix (PDB:1AJF) and P5 helix (PDB:1C0O) of Group I intron using both all-atom and formal charge sets (method to be published elsewhere). We found that in 1AJF, the major groove becomes more negative when switching from formal charge sets to total charge sets (−3.4 kT/e vs. −5.3 kT/e). Concurrently, becomes more favorable (42.8 kcal/mol vs. 6.3 kcal/mol). A similar effect was observed in 1C0O. So the increase in electronegativity will greatly enhance the binding affinity of positively charged ligands. We emphasize that only measures the electrostatic contributions to binding affinity. Other factors such as hydrophobic, van der Waals and entropic contributions should also be taken into account when estimating binding affinities.

Where do metal ions bind in the major groove of G·U pairs?

Although the major groove of the G·U pairs is negative overall, the surface is still polarized, with the G side more negative than the U side. This is true for both single and tandem G·U pairs. In Motif III, since the two guanines are on the same strand, one side of the helix is more negative than the other side. On the other hand, as the two guanines in Motif II belong to different strands, the center of the G·U pairs is the most negative part of the helix. This prediction agrees with the experimental finding that the cobalt hexammine bound to the Motif II tandem G·U pairs in P5b helix of Group I intron is located at the center of the helix, while the cobalt hexamine bound to the Motif III tandem G·U pairs in P5 helix resides at the guanine side of the helix (50,51) (see Figure 2A). Doudna et al. also showed that a cobalt hexammine ion binds to the guanine side of a tandem G·U pair in the signal recognition particle (72). In fact, many instances have been noted in which sequential guanines in both DNA and RNA are favorable binding sites for cationic ligands (23,51,62,73,74), suggesting that this pattern provides an important biological recognition site.

Why are some G·U pairs in RNA helices more negative than their WC counterparts?

When embedded in a RNA helix, certain single G·U pairs and most Motif I tandem G·U pairs have similar major groove electronegativity to their canonical counterparts (Table 2). However, some single G·U pairs, and most Motif II and Motif III tandem G·U pairs showed enhanced negativity at the major groove, compared with their WC counterparts. Therefore, the natural question is what contributes to the enhanced negativity for certain G·U pairs? Our results show that backbone charges are the dominant source of major groove negativity for standard A-form RNA helices (Table 3, Figure 5), whereas the base atoms only contribute a small fraction. Since standard A-form RNA helices have nearly identical cross-strand phosphate distances, their major groove electrostatic potentials have little variation.

On the other hand, for RNA helices containing G·U pairs, both G·U base atoms and the sugar-phosphate backbone are important in determining the major groove potential. For all G·U pairs, regardless of base sequence or conformation, G·U base atoms contribute more to the major groove negativity than the WC base atoms (Figure 5). When embedded in RNA helices, the cross-strand phosphate distance of certain G·U pairs (1EKA, 1QET and 315D) becomes larger. Correspondingly, the formal electrostatic potentials of these Motif I G·U pairs are less negative than their canonical counterparts (Table 3). The decreased formal electrostatic potentials cancel the enhanced negativity produced by the G·U base atoms. As a result, the total major groove electrostatic potentials of these G·U pairs are similar to their canonical counterparts.

In contrast, the cross-strand phosphate distances of certain single G·U pairs, and most Motif II and Motif III tandem G·U pairs are similar to standard A-form RNA helices, so their formal electrostatic potentials are also similar. Consequently, the net electrostatic negativity is elevated by the enhanced negativity contributed by the G·U base atoms.

We note that other factors such as the neighboring clusters of non-canonical base pairs will change the cross-strand phosphate distances and thus, affect the absolute values of the major groove electrostatic potential. For example, loop E of 5S rRNA contains tandem G·U pairs in Motif I conformation (PDB: 1DFU). Because there are other non-WC base pairs adjacent to the tandem G·U pairs, the cross-strand phosphate distance is similar to standard A-RNA and smaller than other Motif I G·U pairs studied in this paper. As a result of the specific geometry, the formal major groove electrostatic potential of 1DFU is quite negative (−4.2 kT/e vs. −2.4 kT/e), in stark contrast with the other Motif I G·U pairs studied here. The total major groove electrostatic potential for this particular tandem G·U pairs is −6.5 kT/e, far more negative than the other Motif I G·U pairs. Another example in which geometry alters the general pattern is an RNA duplex with non-symmetrical tandem G·U pairs (PDB: 433D). Although the tandem G·U pairs are in Motif III conformation, the cross-strand phosphate distance is larger than standard A-RNA due to the proximity of two tandem G·U pairs. Thus the formal major groove electronegativity is decreased, and the total major groove electrostatic potential is comparable to the WC counterparts. Therefore, we find that geometry of flanking structures exert substantial impact on the overall electrostatic profile and ultimate recognition as a cationic binding site.

Are Motif I G·U pairs effective binding sites for metal ions?

Our results show that the electrostatic potentials at the major groove of G·U pairs in the Motif I conformation are similar to those of the standard A-form RNA. Also, the major groove electrostatic potentials of Motif I tend to be less negative than those of Motif II and Motif III. Although Motif I is the most abundant tandem format in nature, we did not identify many structures of Motif I with experimentally resolved bound metal ions. We therefore can ask if Motif I G·U pairs are effective binding sites for metal ions. The answer is still likely to be yes. First, it has been proposed that the absence of positively charged groups makes the major groove of the G·U pair an attractive target for metal ions, not the absolute value of the electrostatic potential (18). Second, we have shown that the reason that most Motif I G·U pairs have similar major groove electrostatic potential to WC base pairs is the larger cross-strand phosphate distance. Those Motif I G·U pairs with smaller cross-strand phosphate distance (e.g. loop E of 5S rRNA) also have enhanced negative major groove. Third, the factors that contribute to binding affinity are a composite of electrostatics and geometry, as well as hydration and quantum effects. The specifics of interactions with complex ion ([Co(NH₃)₆]³⁺) are often very different from those with hydrated Mg²⁺ (73,75). For example, binding affinity studies by Colmenarejo and Tinoco (50) found that the relative binding affinity of tandem G·U pairs for cobalt hexammine is: Motif II ≈ Motif III > Motif I; for Mg²⁺, the order is changed to Motif I > Motif II > Motif III. The most likely explanation for the variation in binding affinities is that Mg²⁺ binds to Motif I as a partially dehydrated ion, whereas it is not the case for Motif II and Motif III. There may also be surface features favoring one ion over the others. By use of Brownian dynamics, Serra et al. found that all three motifs were likely to bind Mg(II), although the authors have not reported relative binding affinities among the different motifs (76). Additionally, a study by Fan et al. concluded that Motif III binds K⁺ and not Mg²⁺ (77). The non-linear PBE method employed in the present work does not account for ion size/geometry, hydration, ion correlation and quantum mechanical effects.

In conclusion, quantification of localized electrostatic potentials and high-resolution electrostatic surface maps at the grooves of G·U wobble base pairs have provided significant new information about the role of individual chemical groups on the composite profile. What has emerged is that the different stacking patterns associated with various G·U tandem motifs impact directly on electronegativity, contributed by both base atoms and sugar-phosphate backbone. Taken together with energetics studies, these findings will help in the explanation and prediction of in situ cationic binding.