Mechanical Properties of Collagen Fibrils

Abstract

The formation of collagen fibers from staggered subfibrils still lacks a universally accepted model. Determining the mechanical properties of single collagen fibrils (diameter 50–200 nm) provides new insights into collagen structure. In this work, the reduced modulus of collagen was measured by nanoindentation using atomic force microscopy. For individual type 1 collagen fibrils from rat tail, the modulus was found to be in the range from 5 GPa to 11.5 GPa (in air and at room temperature). The hypothesis that collagen anisotropy is due to the subfibrils being aligned along the fibril axis is supported by nonuniform surface imprints performed by high load nanoindentation.

INTRODUCTION

Collagen is the most abundant structural protein in mammals. It is a major component of connective tissue, skin, bone, cartilage, and tendons. Although collagen has been intensively studied for decades, there is still a lack of a convincing and comprehensive structural model for the fibrils and fibers. To date, a simplified, two-dimensional stacking model adapted from Hodge and Petruska (1) is widely used. In the model, five tropocollagen molecules are staggered side-by-side with an offset of D = 67 nm between two neighbors. Since the molecule length is not an exact multiple of D, gap and overlap regions appear (2), resulting in the characteristic D banding pattern of collagen fibrils as seen by transmission electron microscopy (3) and atomic force microscopy (AFM) (4,5). Different three-dimensional models were proposed including modifications of the staggered packing (6–9) or a tubelike (10) or ropelike (11) structure. Nevertheless, recent work by Orgel et al. (12) using x-ray diffraction supports the idea of five staggered tropocollagen molecules being arranged with a right-handed tilt, rather than just axially staggered, to form a microfibril.

The biological function of collagen lies predominantly in its mechanical properties. Hence, there is a fundamental need to determine these at different scales and levels of hierarchy. Information about the mechanical properties of collagen is not only essential to explain the macroscopic biophysics of different tissues but can also contribute to our understanding of the microscopic structure of collagen fibrils themselves. For example, any anisotropy or inhomogeneity of collagen fibrils is likely to manifest itself in a corresponding anisotropy and inhomogeneity of their mechanical properties. Conventional macroscopic technical tools based on direct manipulation and visual observation to determine the mechanical properties are not easily applicable to fibrils of nanoscale dimensions (nanofibrils). Nevertheless, a few techniques have been adapted successfully to the nanoscale such as direct tensile tests with a microelectromechanical system (13,14), three-point bending tests of a suspended fiber (15,16), force spectrometry of a fibril attached between surface and AFM tip (2,16,17), and nanoscale indentation (16,18–23). The stiffness of type 1 collagen by nanoscale indentation was reported recently (24) on the example of sea cucumber tissue in air and at room temperature. Using a spherical tip (R < 50 nm) as indenter, the indentation process was assumed to be purely elastic and the data were analyzed using the Hertzian model (24).

Because of the importance of collagen to mammals, we have chosen in the present work to determine the mechanical properties of individual type 1 collagen fibrils of rat tail tendon in air and at room temperature. The Young's modulus was determined quantitatively using sharp AFM tips (R < 15 nm) in combination with the Oliver and Pharr indentation model (25).

NANOINDENTATION BY AFM THEORETICAL MODEL

In an indentation experiment, the indenter and the sample, both with a characteristic stiffness, are arranged in series. The mathematical expression of two solid bodies brought into contact with each other and subject to elastic deformation is, in this case (26,27),

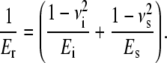(1)

Here, E_r is the reduced modulus of the combined indenter-sample system, E is the Young's modulus, ν is the Poisson's ratio, and i and s refer to the indenter and sample, respectively. The Young's modulus is defined as the ratio of stress to strain (in the literature the inverse quantity called compliance is often used). E_r is also known as indentation or complex modulus. In the case of AFM-based indentation the indenter consists of a silicon AFM tip, which is much stiffer than the biological sample (E_i ≫ E_s). Hence, the reduced modulus is determined only by the Young's modulus of the sample and contains its Poisson's ratio ν_s:

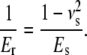(2)

The reduced modulus, E_r, is the quantity determined in the present work, as the Poisson's ratio of collagen is unknown. Deep indentation (tip radius ≪ indentation depth) may result in plastic deformation of the sample during loading if the strain exceeds the material yield point. However, we assumed that, during the unloading process, only the elastic part of the deformation reverts to its initial state, whereas the plastic part remains constant. Therefore, E_r of collagen is determined directly from the unloading force-versus-displacement curves using the Oliver and Pharr model (25).

The following assumptions are made in the model:

1. The deformation during the indentation has an elastic, as well as a plastic, contribution.

2. The indenter is a rigid punch, since (E_i ≫ E_s).

3. The indentation load is applied to a semiinfinite, elastic-plastic half-space (this simplification has been made because the indenter tip radii were approximately five times smaller than the fibril radii, and only indentations located near the center of the fibril were taken into account).

4. The sample material is homogeneous, isotropic, and linear (i.e., the Young's modulus is independent from the strain; these assumptions will be discussed later in Accuracy of the Reduced Modulus Determination).

5. No time-dependent deformation such as creep or viscoelasticity occurs (this has been validated experimentally, as the imprint depth was found to be constant in time; data not shown).

In the following, we define the stiffness, S_F = dF/dh, as the resistance of the material to indentation by an externally applied force, namely the indentation load. Both, the indentation load, F, and the vertical displacement of the indenter, h, are determined directly in an AFM force-distance measurement. The stiffness, S_F, at the inception of unloading is then related to the reduced modulus, E_r (25),

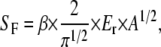(3)

where A is the measured, projected, or cross-sectional contact area, and β is a variable, which takes into account nonaxisymmetry of the indenter and large strains. Being close to unity (25), β has only a small influence compared to the overall experimental inaccuracy, and is therefore neglected in the present work.

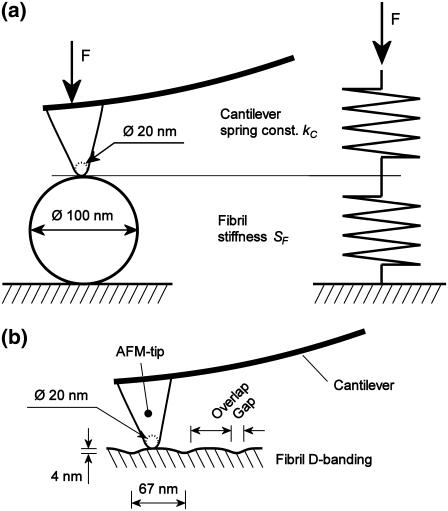
Fig. 1 a shows the indentation setup consisting of indenter and a collagen fibril described by two springs of given spring constant connected in series. The fibril stiffness S_F then follows from

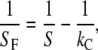(4)

where S is the measured stiffness, also called contact stiffness, and k_C is the cantilever spring constant. The applied force F is calculated by multiplying the cantilever spring constant k_C with the cantilever deflection δ measured in the AFM:

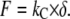(5)

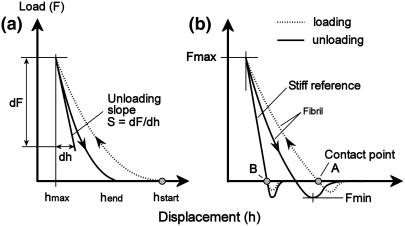
The contact point, which designates the point where the AFM tip first touches the sample surface during loading, is difficult to determine since there is no abrupt increase in cantilever deflection—i.e., the contact point lies in a smooth transition between contact and noncontact (Fig. 2 a). However, in the present work, attractive long-range interfacial forces between AFM tip and sample surface led the tip snap in toward the sample during unloading (Fig. 2 b), thus no smooth transition occurred. Therefore, we define the intersection point between the horizontal (nondeflected cantilever) and the slope (deflected cantilever) as contact point (illustrated in Fig. 2 b as contact points A and B). The indentation depth is defined as the difference in the contact point positions (measured in vertical AFM piezo displacement) between loading a stiff reference sample (Fig. 2 b, contact point B) and loading the fibril (Fig. 2 b, contact point A).

FIGURE 1.

(a) Arrangement of AFM tip, cantilever, and collagen fibril during nanoindentation. The AFM tip being stiff compared to the cantilever and the fibril, the arrangement can be described by two springs connected in series. The dimensions of the AFM tip apex and the fibril diameter are to scale. (b) The longitudinal section of a collagen fibril shows the D-banding structure consisting of an overlap and gap region repeating every ∼67 nm. The dimensions of the AFM tip apex and the fibril D-banding are to scale.

FIGURE 2.

Schematic of typical indentation curves obtained using nanoindentation on an elastic-plastic sample. The slope of the initial unloading curve S = dF/dh is related to the reduced modulus according to Eq. 3. (a) Indentation without attractive interfacial forces. (b) Interfacial forces altering the shape of the curves; the intersection point between the horizontal (nondeflected cantilever) and the slope (deflected cantilever) is defined as the contact point. The indentation is the difference in the contact point positions (measured in vertical AFM piezo displacement) between loading a stiff sample (reference) and loading the fibril.

It has been shown experimentally (25) that unloading curves can be approximated by

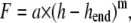(6)

where F is the indenter load, h the vertical displacement of the indenter, h_end the final indentation depth, and m and a are fitting factors (Fig. 2 a). Typically values of the exponent are m = 1 for a flat cylinder and m = 1.5 for a paraboloid of revolution. The depth at which contact is made between indenter and the sample during indentation is defined as contact depth h_C,

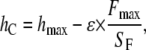(7)

where h_max is the maximum indentation depth and ɛ a constant that depends on the indenter geometry, e.g., ɛ = 1 for a flat punch and ɛ = 0.75 for a paraboloid of revolution. In this work, the constant ɛ is determined by using the experimentally measured exponent m and the following relationship proposed by Oliver and Pharr (25):

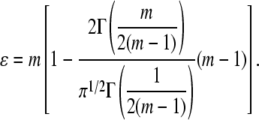(8)

Assuming a spherical indenter with a radius R, the contact area A is given by

(9)

Possible pileup of material (collagen) during indentation increases the contact area and leads to an overestimation of both hardness and Young's modulus (28). An indicator for pileup is the ratio h_end/h_max (Fig. 2); if exceeding 0.7, pileup is likely (25).

MATERIALS AND METHODS

Sample preparation

Type 1 collagen fibrils were dissected from rat tail tendons and stored in phosphate-buffered saline azide at 4°C. An extract of the collagen tendon was sectioned with a scalpel and washed for 5 min in deionized (DI) water. A microscope glass slide (Agar Scientific, Essex, UK) was used as sample substrate. It was cleaned with DI water in an ultrasonic bath for 5 min and subsequently rinsed with ethanol and dried in a stream of nitrogen. A few bundles of collagen fibers were deposited on the glass slide and smeared out manually using tweezers. The sample was then dried in a gentle stream of nitrogen. Several collagen samples, all originating from the same rat tail tendon, were prepared for the experiments.

AFM imaging and force mapping

AFM imaging and indentation of collagen fibrils were performed using a Nanowizard AFM (JPK Instruments, Berlin, Germany). All measurements were taken in air and at room temperature. Aluminum-coated, silicon AFM tips of 150 kHz resonance frequency and 4.5 N/m nominal spring constant (NSC12 tip-C; MikroMasch, Tallinn, Estonia) were used. This cantilever was chosen to match the stiffness of collagen for optimizing sensitivity and signal/noise ratio (SNR).

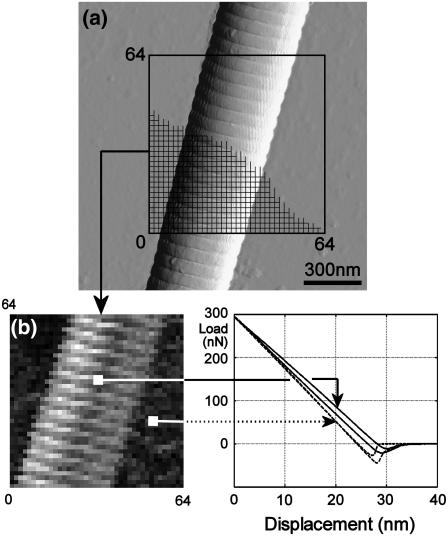
For imaging collagen fibrils without damage, the relatively high stiffness of the cantilevers required use of intermittent contact mode (also known as tapping mode). After taking a topographic image of the fibril, the force mapping mode (also known as force volume mode) was used to perform quasi-static indentations. The 64 × 64 indentation curves, consisting of 256 data points each, were taken on a square area (Fig. 3). The area's dimensions were ∼1.5 × 1.5 μm ± 0.5 μm, optimized in each experiment to balance approximately the number of data points taken on the fibril and on the substrate. The time for both the approach and retraction of the tip was set to 0.2 s (5 Hz), with zero delay in-between.

FIGURE 3.

Stiffness probing. (a) The 64 × 64 indentation curves are taken over a single fibril lying on a stiff substrate. (b) A stiffness map is created where the grayscale value stands for the unloading slope (dark = high stiffness = steep slope; bright = low stiffness = shallow slope). Fibril height: 200 nm.

The loading process was limited to a maximum load, which was chosen individually for each experiment so that the indentation depth was small enough to avoid any influence of the underlying surface. This maximum depth depends on the fibril height, the tip radius, and the ratio of the reduced moduli of the substrate and fibril (29). In the present work, the maximum depth was in the range of 5–10% of the fibril diameter.

Indentation curves taken on glass and on the fibril were selected manually from the force mapping images. To ensure the validity of the assumption of indenting a semiinfinite half-space, only indentation curves located simultaneously at the center of the fibril and at the overlap region of the collagen D-banding (Fig. 1) were considered. The gap's concave geometry is similar to the AFM tip apex; therefore, the contact area between indenter and fibril would increase and the stiffness would be overestimated.

A linear fit was then applied to the rising part of the curves taken on glass, and a nonlinear fit, using the power law model (Eq. 6), was applied to the curves taken on the fibril in the part between F_max and F_min (Fig. 2 b). To calculate the elastic unloading stiffness S, the average slope of the upper quarter of the unloading curve was taken. All calculations were performed using MatLab (The MathWorks, Natick, MA).

Reduced modulus calculation—summary

The measured unloading curve F = F(h) is fitted with Eq. 6, which provides the exponent m, which, in turn, is used in Eq. 8 to determine the constant ɛ. The derivative (slope) of the unloading curve at the inception h_max provides S = dF/dh, which is then used to calculate the fibril stiffness S_F with Eq. 4. The contact depth h_C is calculated with Eq. 7 and provides the contact area A (Eq. 9) for a measured tip radius R. The reduced modulus is then calculated with Eq. 3.

AFM cantilever spring constant determination

For all quantitative AFM force measurements, the cantilever spring constant k_C is needed and has to be determined experimentally for each individual cantilever as commercial cantilevers show a wide variation. Spring constant calibration was performed by first calibrating a rectangular, tipless reference cantilever using the Sader method (30), in which the cantilever dimensions and the resonance frequency are measured. This reference cantilever was then used as a sample of known spring constant k_ref and a force-displacement measurement was performed for each cantilever used in the nanoindentation experiments, as described by Torii et al. (31). The spring constants for the indentation cantilevers k_test were calculated by measuring simultaneously the deflection of the cantilever under test δ_test and the overall deflection of both cantilevers δ_tot. The factor cos θ accounts for the angle between the cantilevers, which was 10° in the present setup:

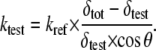(10)

Our nanoindentation experiments required cantilevers of medium stiffness (k = 4.5 N/m) with spring constants similar to the apparent spring constant (contact stiffness) of the fibrils to achieve the best possible sensitivity and SNR. In general, stiffer cantilevers provide a higher SNR. However, high cantilever stiffness in combination with small indentation depth (5–10% of the fibril diameter) results in lower accuracy in determining the unloading slope because of the small cantilever deflection.

The method of Torri et al. (32) has an accuracy of ∼5%. Herein, precise positioning of the tip onto the reference cantilever is the main source of error. Accuracy of the order of 15–20% can be expected from the Sader method (33) and this dominates the overall uncertainty of the cantilever spring constant determination process. However, we used the same reference cantilever for all further calibrations to ensure that this systematic uncertainty of 20% affects all stiffness measurements in the same way.

AFM tip shape determination

The AFM tip radius R was obtained by imaging a tip-shape calibration sample (tip characterization grating TGT01; MikroMasch) consisting of an array of sharp tips. Because the radii of the sample tips and the radii of the AFM tips are in the same range (R ∼ 20 nm) and since we performed nanoindentations with depths less than the AFM tip radius, a mathematical deconvolution of the AFM tip apex was necessary. Assuming a spherical AFM tip apex, its radius was determined visually based on the AFM image. The subtraction of the sample-tip diameter (value given from the manufacturer) from the estimated AFM tip radius deconvolutes the AFM tip apex. For indentation depths smaller than the tip radii, as in the present work, the spherical AFM tip approximation can be used reasonably.

A quantitative error estimation of the described tip characterization technique is difficult since the tip radius estimation is carried out by fitting the AFM image visually to a theoretical tip radius. Based on qualitative consideration, a 20% error in radius seems to be reasonable.

RESULTS AND DISCUSSION

Young's modulus determination

The reduced modulus E_r of individual rat tail tendon type 1 collagen fibrils was found to be in the range from 5 GPa to 11.5 GPa (N = 34). Resulting from the calibration of the reference cantilever's spring constant (see AFM Cantilever Spring Constant Determination), an additional systematic error of ∼20% applies to all measurements in the same way. The typical Poisson's ratio ν of a solid material is in the range of 0–0.5; thus, lower and upper limits for the Young's modulus can be given by 3.75 GPa (ν = 0.5) and 11.5 GPa (ν = 0), respectively. The moduli were measured in air and at room temperature on individual collagen fibrils with diameters between 50 nm and 200 nm.

The large variation of E_r was mainly caused by three factors:

1. Different individual fibrils.

2. Different dehydration state of the fibrils.

3. Uncertainties of the indentation process, mainly the contact area determination.

It was observed that the contribution of factor 2 is ∼30% (see Fibril Dehydration) and factor 3 was estimated to ∼20% (see Accuracy of the Reduced Modulus Determination). Therefore, ∼50% of the variation of E_r can be attributed to variations of the physical properties of individual collagen fibrils (see factor 1).

Correlations between reduced modulus and fibril diameter, AFM tip radius, or AFM tip spring constant were not found. However, the results show a larger standard deviation for stiffer fibrils. This is due to reduced indentation depth on a stiffer fibril for a constant absolute error of the indentation depth determination. Typical depths under a load of 300 nN were 4 nm (5 GPa fibrils) and 2 nm (11.5 GPa fibrils). The absolute accuracy of depth determination was ±0.5 nm.

The exponent m of the power law model (Eq. 6) was found to be in the range from 1.07 ± 0.01 to 1.29 ± 0.01. The higher value can be attributed to a spherical indenter whereas the lower value is likely due to a flat punch. These results are in agreement with earlier works (23,25), where it was shown that m is usually in the range of 1.2–1.6, and independent of the real geometry of the indenter. The constant ɛ (Eq. 8) was found to be 0.83 ± 0.03, which is close to the predicted value 0.75 for a paraboloid of revolution (25). The pileup criterion h_end/h_max was 0.35 ± 0.11, which is well below the critical value 0.7 and hence indicates that no significant pileup occurred.

In Table 1, we compare the Young's modulus measured in the present work to values reported in literature. They are based on Brillouin spectroscopy (34,35), x-ray data (36), force spectroscopy (17), nanotensile tests (13), nanoindentation (24), and steered molecular dynamics simulation of tropocollagen-like molecules (37).

TABLE 1.

Young's modulus of collagen

Collagen fibril (Ref.)	Technique	State of fibril	Young's mod. (GPa)
Rat tail tendon*	Indentation	Different dehydration states	3.75–11.5
Rat tail tendon (34)	Brillouin	In 0.15 M NaCl solution	9.0
Rat tail tendon (34)	Brillouin	At 30% relative humidity	14.7
Rat tail tendon (34)	Brillouin	At 0% relative humidity	21.5
Rat tail tendon (35)	Brillouin	In 0.15 M NaCl solution	5.1
Rat tail tendon (35)	Brillouin	At 50% relative humidity	11.9
Bovine Achilles tendon (36)	X ray	In 0.15 M NaCl solution	2.9 ± 0.1
Bovine Achilles tendon (17)	Spectroscopy	At 0% relative humidity	2–7
Bovine Achilles tendon (17)	Spectroscopy	In phosphate buffered saline	0.2–0.5
Sea cucumber (13)	Tensile test	In water	12 (high strain)
Sea cucumber (24)	Indentation	<45% relative humidity	1–2
Collagen-like peptide (37)	Simulation	—	4.8 ± 1.0

Note: Harley et al. (34) and Cusack and Miller (35) are spectroscopic measurements performed at hyper-sound frequencies in the GHz range.

^*Present work.

One can see that the values obtained in the present work are in reasonable agreement with earlier results obtained by various methods. The main differences can be attributed to the fact that in nanoindentation the Young's modulus represents the lateral elasticity at the surface rather than the bulk, one-dimensional tensile stiffness along the fibril axis reported by others (except (24)). Heim and Matthews observed a lower Young's modulus of single collagen fibrils, which can probably be attributed to the different origin of the collagen and slightly different pretreatment (24). The moduli determined experimentally in Sasaki and Odajima (36) and theoretically in Lorenzo and Caffarena (37) represent the longitudinal modulus of a single tropocollagen molecule rather than a fibril. Considering the lack of knowledge of how the molecules bind to each other and are structurally assembled into a fibril, it is interesting to note that these values are very similar to the experimentally determined fibril modulus in the present work.

Anisotropy of collagen fibrils

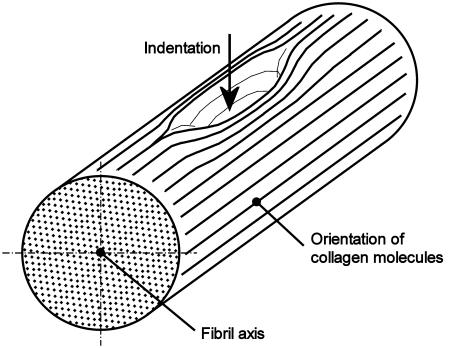
According to the quarter staggered model proposed by Hodge and Petruska (1), fibrils are homogeneous and isotropic in the cross-sectional plane (Fig. 4). However, because of the extreme anisotropy of the tropocollagen molecules lying in the longitudinal fibril direction, the axial mechanical properties of collagen fibrils are likely to be very different from those across to the fibril. For biological reasons, the axial load carrying capacity is most probably much higher than across, which should be reflected in the corresponding Young's moduli.

FIGURE 4.

Indentation imprint assuming the fibril being formed by collagen molecules aligned along the fibril axis. The nonuniformity of the imprint implies an anisotropic fibril structure.

The shape of imprints created by indentation with a sharp tip is shown in Fig. 5. The imprints are clearly anisotropic, being more elongated along the fibril axis than across. The two fibrils used as examples were from the same sample, are similar in diameter, and are aligned perpendicular to each other. The same AFM tip was used for both experiments and its orientation was not changed. This procedure confirms that the anisotropic imprint shape cannot be caused solely by a possible asymmetry of the indenter. The shape of the imprints could be caused by a lateral displacement of the longitudinally aligned molecules (Fig. 4) and this indicates clearly that the mechanical properties of single collagen fibrils are anisotropic. In Fig. 5, the applied load was approximately seven times higher than the load used in the quantitative reduced modulus measurements. The high load-induced pileup (as arrowed in Fig. 5), which altered the contact area and, thus, the indentation model, fails—and no quantitative value can be derived.

FIGURE 5.

Imprints on two similar collagen fibrils with the same individual tip. To eliminate a tip-shape influence on the imprint shape, the fibrils are arranged perpendicular to each other but the tip orientation with respect to the substrate is unchanged. The nonuniform shape of the imprints indicates different material properties in longitudinal and transversal directions. Pileup (arrow) appeared due to the high-load indentations (2 μN). Imprint depth (from left to right): 28 ± 1 nm; 20 ± 1 nm; 28 ± 1 nm; and 29 ± 1 nm.

Fibril dehydration

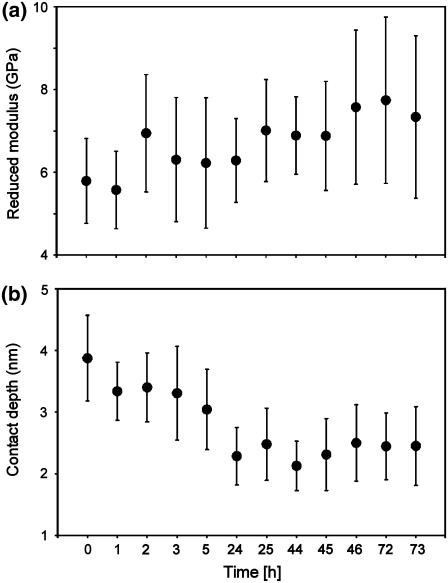
Collagen fibrils contain interstitial water, occurring as tightly bound or bulklike (38–40). The latter would probably evaporate to a certain extent when fibrils are exposed to air or dried with nitrogen during preparation, which could lead to an increase of the stiffness of the fibrils (41). To investigate the effect of dehydration on the fibril stiffness, we performed indentations repeatedly on the same fibril (with each force mapping area being adjacent to the previous one) over a period of three days, starting from the moment the fibril was taken out of the water. The sample was left in the AFM between the measurements and therefore exposed to air at room temperature (T = 23°C, RH = 40 ± 5%). All experimental parameters (AFM tip, maximum applied load, and force map geometry) were kept constant. Fig. 6 a shows a tendency of the reduced modulus to increase slightly from 6 GPa to 7.5 GPa (∼30%) over three days, although the measurement inaccuracy suggests the need for some caution in interpreting the data. However, the indentation depth decreases from 3.5 nm to 2.5 nm (Fig. 6 b), showing that the stiffness effectively increases because the tip and the indentation load are not changed. It should be noted that, most likely, the fibrils were not fully dehydrated under these experimental conditions, but that instead only the outer layer had dried. This is supported by the fact that no reduction in fibril diameter was observed, whereas in previous studies (42) a reduction in diameter was found, suggestive of more thorough drying.

FIGURE 6.

Fibril stiffening due to dehydration. The measurements are taken at the same location on an individual fibril. The error bars represent the random, spatial variation over the area in which the force displacement curves were measured. Fibril diameter: 90 nm. Tip diameter: 30 nm. Applied load: 300 nN. Cantilever stiffness: 12 N/m.

These findings indicate that dehydration of collagen fibrils contributes with 30% to the broad distribution of fibril moduli (see Young's Modulus Determination), containing both hydrated as well as dehydrated fibrils.

Tip shape

The best mathematical fit of the indentation data with Eq. 6 in the dehydration experiments was obtained with m = 1.07 ± 0.01, which is closer to the theoretical value of a flat punch (m = 1) rather than that of a parabolic shape indenter (m = 1.5). However, tip shape determination by AFM imaging revealed a spherical tip apex. Hence, the change in contact area during unloading is not related to the indenter's real tip shape but, instead, depends on the interaction between the tip and the elastic-plastic behavior of the indented sample. In literature, this phenomenon is treated by introducing an effective indenter shape that produces the same normal surface displacement on a flat surface that would be produced by the real indenter shape on the unloaded, deformed surface of the imprint (25). This concept of effective indenter shape does not affect the determination of the fibril stiffness since the contact area at maximum indentation remains constant. The contact area calculation based on Eq. 9 in combination with an estimated radius of a spherical tip apex still provides a reasonable estimation.

Even though the exponent m cannot be used to predict the real tip shape or even the contact area at maximum indentation depth, it is a useful quality parameter to monitor the indentation process itself and detect possible variations of the tip-sample interaction.

Accuracy of the reduced modulus determination

The nominal manufacturer values of both tip shape (tip radius) and cantilever spring constant can often show a large variation of >100% for individual, noncalibrated AFM probes. The accuracy of the reduced modulus depends mainly on the experimental accuracy of the determination of the contact area, A, and of the fibril stiffness, S_F (Eq. 3). The latter is directly proportional to the cantilever spring constant, since the stiffness is force divided by cantilever displacement (Fig. 2), in which the force is simply the product of cantilever deflection and its spring constant (Eq. 5). Since the cantilever deflection and displacement can be measured at very high accuracy, the major contributor to the error of S_F is the spring constant with ∼5% (see AFM Cantilever Spring Constant Determination). To determine the uncertainty of the contact area, the AFM tip radius and the indentation depth must be considered. With ∼20% for the radius determination (see AFM Tip Shape Characterization) and ∼10% for the indentation depth, the relative uncertainty of the contact area, A, is ∼30%. The 10% for the indentation depth is a coarse estimate, since the small indentation depths of only few nanometers, as performed in this work, are very sensitive to the absolute error in the measurement of the cantilever deflection of ∼0.5 nm. The combination of the contact area and the fibril stiffness uncertainties results in a random error of ∼20% for the reduced modulus (Eq. 3). A systematic error of 20% due to the reference cantilever calibration (see AFM Cantilever Spring Constant Determination) must be added to all measurements.

Besides these general, quantitative considerations, the following issues regarding the experimental accuracy have to be addressed: The mechanical properties of single collagen fibrils are anisotropic (see Anisotropy of Collagen Fibrils), which conflicts with the model assumption of an isotropic sample (see Nanoindentation by AFM Theoretical Model). Although anisotropy leads to an elliptical rather than a circular contact area, it was found that, for a broad range of anisotropic materials, the resulting difference in contact area is within 3% (43).

Another possible source of uncertainty of the contact area determination are attractive interfacial forces (long-range attractive force, adhesion force) between AFM tip and sample surface. During sample approach, the long-range attractive force causes the AFM tip to snap in toward the sample surface. Most likely, this point represents the initial point of contact if one assumes that the tip lies perfectly on the surface after snapping in without any deformation of the sample surface. However, for numerical-processing reasons we defined the point during loading, where the adhesion balances the repulsive force (zero cantilever deflection), as initial contact point (Fig. 2 b, contact point A). This can be implemented easily as the intersection point between the horizontal (nondeflected cantilever) and the loading slope (deflected cantilever).

As soon as the tip makes contact with the sample, adhesion force occurs, which increases the effective contact area predicted by the Oliver and Pharr model and, thus, leads to an overestimation of the reduced modulus (44). We stress here that the slope of the initial unloading curve S = dF/dh is not affected by adhesion and therefore does not affect the stiffness determination. To address the change in contact area due to adhesion, it has been suggested to extend the indentation model with an adhesion term. Depending on the material indented, either the Derjaguin-Muller-Toporov or the Johnson-Kendall-Roberts theory is appropriate (23). However, all inaccuracies originating from the attractive interfacial forces were not taken into account in this work, since their contribution is small (adhesion was ∼<5% of the maximum load) compared to the overall large uncertainty of the reduced modulus.

In most commercial AFMs, including the one we have used, the cantilever is tilted down under an angle (typically θ = 10°) to the horizontal. Therefore, two further effects must be considered in indentation experiments:

1. The applied load is nonperpendicular to the surface; however, this is negligible as the load would only have to be multiplied by cos θ, which is close to unity.

2. Lateral motion of the indenter occurs (45).

If the indented material partly constrains lateral movement of the tip, there is an additional nonperpendicular contribution to the applied load, resulting in an asymmetric stress distribution between tip and sample. Additionally, the horizontal part of the nonperpendicular load causes a moment, which, in turn, results in an inclination change at the free end of the cantilever. Since the deflection of a cantilever is derived from the angle at its free end, the actual real deflection readout is inaccurate (46). This is a problem generic to AFM, and affects the entire indentation process.

Considering the large overall uncertainty of the reduced modulus determination and the natural variations of the mechanical properties of collagen fibrils, the effects discussed above are assumed to be less relevant in the present work and thus were not taken into account. However, we believe that quantitative AFM-based nanoindentation studies require awareness of these sources of uncertainty, since they may influence the result significantly.

CONCLUSION

In this work, we present a quantitative investigation of the stiffness of rat tail collagen type 1 fibrils on the nanoscale in air and at room temperature. Using nanoindentation by AFM, together with appropriate models for the indentation process, a Young's modulus between 3.7 GPa and 11.5 GPa was found. This broad range of values is caused by natural variation of the mechanical fibril properties, dehydration, and the accuracy of the calibration of the nanoindentation cantilevers. An additional, systematic error of ∼20% originates from the reference cantilever used to perform this calibration. These results are valid under the assumption that during unloading only elastic deformation occurs and that the sample material is homogeneous, isotropic, and linear. The great advantage of nanoindentation is the small size of the indenter, which is comparable to that of typical biomolecular structures. Using an indenter with tip apex smaller than the collagen fibril diameter, indentation on the fibril surface caused small imprints. Their nonuniform shape indicates an anisotropic material structure of collagen fibrils and supports the hypothesis that the fibrils consist of subfibrils, aligned along the fibril axis. However, this anisotropy can be neglected as its contribution to the overall experimental error is smaller than the variation of the stiffness upon fibril dehydration.