Abstract
Ca2+ liberation through inositol 1,4,5-trisphosphate receptor (IP3R) channels generates complex patterns of spatiotemporal cellular Ca2+ signals owing to the biphasic modulation of channel gating by Ca2+ itself. These processes have been extensively studied in Xenopus oocytes, where imaging studies have revealed local Ca2+ signals (“puffs”) arising from clusters of IP3R, and patch-clamp studies on isolated oocyte nuclei have yielded extensive data on IP3R gating kinetics. To bridge these two levels of experimental data, we developed an IP3R model and applied stochastic simulation and transition matrix theory to predict the behavior of individual and clustered IP3R channels. The channel model consists of four identical, independent subunits, each of which has an IP3-binding site together with one activating and one inactivating Ca2+-binding site. The channel opens when at least three subunits undergo a conformational change to an “active” state after binding IP3 and Ca2+. The model successfully reproduces patch-clamp data; including the dependence of open probability, mean open duration, and mean closed duration on [IP3] and [Ca2+]. Notably, the biexponential distribution of open-time duration and the dependence of mean open time on [Ca2+] are explained by populations of openings involving either three or four active subunits. As a first step toward applying the single IP3R model to describe cellular responses, we then simulated measurements of puff latency after step increases of [IP3]. Assuming that stochastic opening of a single IP3R at basal cytosolic [Ca2+] and any given [IP3] has a high probability of rapidly triggering neighboring channels by calcium-induced calcium release to evoke a puff, optimal correspondence with experimental data of puff latencies after photorelease of IP3 was obtained when the cluster contained a total of 40–70 IP3Rs.
INTRODUCTION
The inositol 1,4,5-trisphosphate receptor (IP3R) acts as a Ca2+ release channel to liberate Ca2+ ions from the endoplasmic reticulum (ER) into the cytosol (1). Structurally, the IP3R is a large (∼30 nm in diameter) homomeric tetramer of four subunits forming a single ion-conducting channel (2). Each subunit is composed of three functionally different domains, including a large cytoplasmic region of amino-terminal IP3-binding domain, a carboxy-terminal channel-forming domain, and a middle coupling modulatory and transducing domain (3,4). Opening of the channel requires binding of the second-messenger inositol 1,4,5-trisphosphate (IP3), which is generated in the cytoplasm in response to the binding of extracellular ligands to plasma membrane receptors. Moreover, gating of the IP3R is biphasically modulated by Ca2+ ions, such that small elevations of cytosolic [Ca2+] promote channel opening, whereas higher [Ca2+] results in inactivation (5). This Ca2+ feedback underlies a process of Ca2+-induced Ca2+ release (CICR), resulting in regenerative liberation of Ca2+ that may either remain restricted to a cluster of IP3R to generate a localized Ca2+ puff (6), or propagate as a saltatory wave across numerous puff sites by successive cycles of Ca2+ diffusion and CICR.
To elucidate the complex spatiotemporal patterns of Ca2+ signals generated by the IP3 pathway, we need to understand the functioning of IP3Rs at the single-molecule level, the spatial arrangement of these receptors in the cell, and their functional interactions via Ca2+ diffusion and CICR. The Xenopus oocyte provides a favorable cell system with which to investigate these topics, by virtue of the wealth of experimental data available regarding both the imaging of IP3-evoked Ca2+ signals in the intact cell (6–8) and patch-clamp recordings of single IP3Rs in the outer membrane of isolated oocyte nuclei (9–12). To bridge these two levels of experimental data, we developed an IP3R model, and used both transition matrix theory and stochastic simulation to predict the behavior of individual and clustered channels.
Models of the IP3R play a central role not only for the understanding channel kinetics, but also as building blocks for constructing larger-scale models of cellular Ca2+ signaling. Several IP3R models (13–19) have been developed to describe experimental data obtained from IP3R reconstituted in bilayer membranes, with broad application of the DeYoung-Keizer model (14) in particular. However, there are significant differences in behavior of the reconstituted IP3Rs versus that of IP3Rs in their native environment of the nuclear envelope, and only a few models have incorporated IP3R data obtained on nucleus membranes. Among these, an allosteric four-plus-two-conformation model was considered by Mak et al. (11). That model postulates that each of the four IP3R monomers has one IP3-binding site and three different functional Ca2+-binding sites on the cytoplasmic side of the channel. Another model was developed by Baran (20), consisting of one activation module and one inhibition module, both allosterically operated by Ca2+, IP3, and ATP, together with one adaptation module, driven by IP3 and Ca2+. However, these two models can predict only the steady-state gating properties, and not the kinetics of individual channel openings and closings.
Thus, there has been no model that could realistically simulate the kinetic behavior of IP3R under physiological conditions in the Xenopus oocyte. Our aim was to develop a dynamic IP3R model that successfully reproduces data obtained from patch-clamp recordings of nuclear IP3Rs, and that is sufficiently simple and computationally tractable for application in future studies simulating the interactions of numerous IP3Rs coupled in a cellular environment by Ca2+ diffusion and CICR. The channel model consists of four identical, independent subunits, each of which has an IP3-binding site, together with one activating and one inactivating Ca2+ binding site. A feature of the model is that channel opening may occur if either three or four of the subunits of the tetramer are in an “activated” state (binding both IP3 and the activating Ca2+ ion, but not the inhibitory Ca2+ ion), and we show how this characteristic can account for the observed biexponential distribution of open times and the dependence of mean open time on [Ca2+]. Moreover, we extend our IP3R channel model to the cellular level by simulating the latency of puffs after step increases of IP3, on the assumption that the stochastic opening of a single IP3R within a cluster rapidly evokes CICR from neighboring channels with high probability to generate a puff. On this basis, we predict that puff sites contain a total of 40–70 IP3Rs.
MODEL
A schematic picture of the IP3R model is shown in Fig. 1, which, from structural studies (2), comprises four identical and independent subunits. Based on experimental observations that the channel open probability is a bell-shaped function of [Ca2+] (5,10,15), we consider two independent Ca2+-binding sites for each subunit; i.e., an activating binding site and an inhibitory site. Consistent with the molecular structure of the IP3R (3,4) and concordant with most previous IP3R models, we also assume a single IP3 binding site in each subunit. The state of each subunit is denoted as (ijk), where the index i represents the IP3-binding site, j the activating Ca2+-binding site, and k the inhibitory Ca2+-binding site. An occupied site is represented as 1, and a nonoccupied site as 0.
FIGURE 1.
Schematic diagram of the model of a single IP3R channel subunit. Each subunit has an activation Ca2+-binding site, an inhibitory Ca2+-binding site, and an IP3-binding site. We label the binding sites by the notation (ijk), where the index i represents the IP3-binding site, j the activation Ca2+-binding site, and k the inhibitory Ca2+-binding site. The number 1 represents an occupied binding site and 0 a nonoccupied site. Additionally we introduce a conformational change between “active” (A-state) and “inactive” (110) states of the subunit. Values for the forward (a) and backward (b) rate constants associated with each transition are listed in Table 1. In the figure, C and I represent the concentrations of Ca2+ and IP3, respectively. The bold arrows indicate the binding of ligands to different sites.
The model further includes a conformational change whereby a subunit in the (110) state (one IP3 and one activating Ca2+ bound) is “inactive”, and must transition to an “active” (A) state before it can contribute to channel opening. This conformational step is analogous to the well-characterized behavior of nicotinic acetylcholine receptors (21), and further implies that the active state is “locked” with respect to agonist binding and dissociation. Observations of ligand-independent flickerings of the IP3R channel to the closed state (11) are consistent with such a conformational change, and the lack of effect of changes in Ca2+ concentration on gating of already open IP3R channels (22) supports the notion that active subunits are locked with respect to ligand binding.
We also assume that the channel is open when either three or four subunits are in an active state. This assumption has previously been applied in some IP3R models (23), and we show here that it can explain the dependence of channel open time on ligand concentration. Although some multimeric channels show distinct conductance levels associated with ligand binding to differing numbers of subunits (24), the Xenopus oocyte IP3R displays only a single major conductance level (11,12), so we distinguish only a single open state, irrespective of whether three or four subunits are active.
Each subunit in the model has nine states, with transitions governed by second-order rate constants ( with
with  ) for binding processes, first-order rate constants (
) for binding processes, first-order rate constants (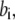 with
with 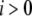 ) for unbinding process, and constant transition rates (
) for unbinding process, and constant transition rates (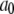 and
and 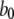 ) applied between the active A-state and the inactive (110) state (Fig. 1). Parameter values used in the model are listed in Table 1. Values for dissociation constants were chosen on the basis of optimal fit to steady-state experimental data from patch-clamped oocyte nuclear IP3R (Fig. 2). For all the binding/unbinding loops given in Fig. 1, the thermodynamic constraint of detailed balance requires that
) applied between the active A-state and the inactive (110) state (Fig. 1). Parameter values used in the model are listed in Table 1. Values for dissociation constants were chosen on the basis of optimal fit to steady-state experimental data from patch-clamped oocyte nuclear IP3R (Fig. 2). For all the binding/unbinding loops given in Fig. 1, the thermodynamic constraint of detailed balance requires that 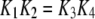 for reaction dissociation constants. The conformation rate changes
for reaction dissociation constants. The conformation rate changes 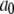 and
and 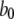 between the (110) and active states of the subunits were chosen to give a maximum channel open probability of ∼0.84, as observed experimentally for Xenopus oocyte nuclei (10,11). The rate constant for IP3 binding was based on experimental measurements of first opening latencies of 0.35 and 0.5 s for IP3R channels in Sf9 cell nuclei at [Ca2+] = 2 μM after step increases in [IP3] from 0 to 10 and 100 μM, respectively (K. Foskett and D. O. Mak; unpublished data). Model simulations of single channel latencies provided a good fit, with predicted corresponding mean latencies of 0.34 and 0.4 s. Rate constants for Ca2+ binding were estimated by iterative fitting of model predictions to published data of Xenopus oocyte IP3R open- and closed-time distributions (10,11).
between the (110) and active states of the subunits were chosen to give a maximum channel open probability of ∼0.84, as observed experimentally for Xenopus oocyte nuclei (10,11). The rate constant for IP3 binding was based on experimental measurements of first opening latencies of 0.35 and 0.5 s for IP3R channels in Sf9 cell nuclei at [Ca2+] = 2 μM after step increases in [IP3] from 0 to 10 and 100 μM, respectively (K. Foskett and D. O. Mak; unpublished data). Model simulations of single channel latencies provided a good fit, with predicted corresponding mean latencies of 0.34 and 0.4 s. Rate constants for Ca2+ binding were estimated by iterative fitting of model predictions to published data of Xenopus oocyte IP3R open- and closed-time distributions (10,11).
TABLE 1.
Parameter values used in the IP3R channel model
| Parameter | Value (unit) | |
|---|---|---|
| Conformation change rate | 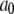 |
540 s−1 |
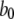 |
80 s−1 | |
| IP3-binding site | 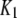 |
0.0036 μM |
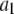 |
60 μM−1 s−1 | |
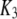 |
0.8 μM | |
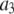 |
5.0 μM−1 s−1 | |
| Activating calcium-binding site | 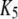 |
0.8 μM |
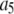 |
150 μM−1 s−1 | |
| Inhibitory calcium-binding site | 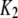 |
16 μM |
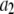 |
0.2 μM−1 s−1 | |
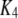 |
0.072 μM | |
 |
0.5 μM−1 s−1 |
In the table, the disassociation constant 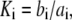 with
with 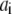 the on-binding rate and
the on-binding rate and 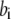 the off-binding rate. Due to the thermodynamic constraint, we have
the off-binding rate. Due to the thermodynamic constraint, we have 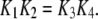
FIGURE 2.
Stochastic and deterministic modeling of IP3R dynamics, and comparison with steady-state experimental data. (A) Example of stochastic simulation of IP3R channel gating (upper), and the corresponding numbers of subunits in the active state (lower) at [IP3] = 10 μM and [Ca2+] = 0.2 μM. Arrows mark openings that are associated with 4-related open states. (B) Graph shows the dependence of steady-state open probability (PO) as a function of [Ca2+] for different concentrations of IP3. Solid curves show results by the deterministic transition matrix theory. The results obtained by stochastic simulation are represented by open symbols ([IP3] = 10 μM (stars), 0.033 μM (circles), 0.02 μM (squares), and 0.01 μM (triangles)). Single-channel patch-clamp experimental data obtained from IP3R on native nuclear membranes by Mak et al. (10,11) were replotted as solid symbols ( [IP3] = 10 μM (stars); 0.033 μM (circles); 0.02 μM (squares); and 0.01 μM (triangles)). (C and D) Mean open time 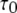 (C) and closed time
(C) and closed time 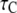 (D), respectively, as functions of [Ca2+] for different concentrations of IP3, as indicated. Solid curves show results obtained with transition matrix theory, and open symbols show stochastic simulation results. Solid stars show corresponding experimental data at [IP3] = 10 μM (10,11).
(D), respectively, as functions of [Ca2+] for different concentrations of IP3, as indicated. Solid curves show results obtained with transition matrix theory, and open symbols show stochastic simulation results. Solid stars show corresponding experimental data at [IP3] = 10 μM (10,11).
We explored the behavior of the IP3R model using both deterministic, matrix transition analysis and stochastic simulation. The deterministic approach provides a rigorous analysis of statistical channel behavior, but cannot reveal the trajectory of openings and closings of an individual IP3R. Because we wish to use the model as a building block to explore the contribution of stochastic single-channel behavior to cellular Ca2+ signaling, we also performed stochastic simulations; an approach that has the further advantage of providing a more intuitive insight into channel behavior.
Deterministic analysis of the IP3R model
The probability of subunits in state (ijk) or (A) is denoted by 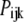 or
or 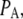 with
with 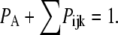 By the mass action kinetics, the equations describing the subunit dynamics are written
By the mass action kinetics, the equations describing the subunit dynamics are written
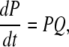 |
(1) |
where Q is the generator matrix (25) of transition rates and P is the vector of probability of subunits. The open probability for an IP3R is then given by
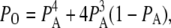 |
(2) |
Mathematically, the equilibrium state is defined by 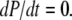 The equilibrium vector w satisfies
The equilibrium vector w satisfies 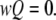 Detailed balance is imposed so that we can solve for w by inspection (26). This is done by calculating all probabilities in terms of their probability relative to state (000). These unnormalized probabilities are denoted
Detailed balance is imposed so that we can solve for w by inspection (26). This is done by calculating all probabilities in terms of their probability relative to state (000). These unnormalized probabilities are denoted 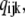 with
with 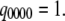 Then
Then
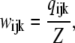 |
(3) |
where each component (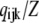 ) gives the equilibrium probability for state (ijk). Z is the normalization factor defined by
) gives the equilibrium probability for state (ijk). Z is the normalization factor defined by 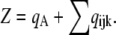 The equilibrium probability (
The equilibrium probability (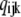 ) of state (ijk) relative to that of state (000) is just the product of forward to backward rates along any path connecting (000) to (ijk). Thus, we can write
) of state (ijk) relative to that of state (000) is just the product of forward to backward rates along any path connecting (000) to (ijk). Thus, we can write
 |
(4) |
and
 |
(5) |
The equilibrium probability for the subunit active state is given by
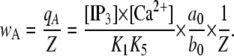 |
(6) |
Since the channel is open if either three or four subunits are active, the equilibrium open probability is a sum of contributions from three and four active subunits:  and
and 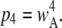 Thus, the open probability at the equilibrium state for an IP3R channel is
Thus, the open probability at the equilibrium state for an IP3R channel is
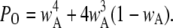 |
(7) |
Because channel states (A, A, A, not-A) are the only open states that connect to closed channel states by any one of three A-states changing to the closed state 110 with rate 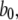 we can directly write the equilibrium probability flux between open and closed states as follows:
we can directly write the equilibrium probability flux between open and closed states as follows:
 |
(8) |
The mean open and closed times are given by
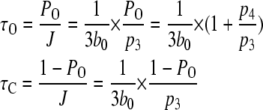 |
(9) |
Equation 9 implies that the channel mean open time varies even though the subunit mean active time is fixed.  has a limiting minimum value of
has a limiting minimum value of 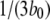 and increases as
and increases as 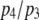 increases. This is to be expected since the channel is open if either three or four subunits are active but closes only when there are precisely three active subunits.
increases. This is to be expected since the channel is open if either three or four subunits are active but closes only when there are precisely three active subunits.
Deterministic solutions presented in Fig. 2 (showing the open probability  mean open time
mean open time 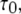 and mean closed time
and mean closed time 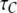 as functions of constant Ca2+ concentration at different IP3) were obtained using Eqs. 7 and 9. Furthermore, we applied the transition matrix theory to predict the open- and closed-time distributions of the channel in steady state and the distributions of the first-opening latency of individual and clustered IP3Rs responding to step IP3 stimulus. The analytic deductions employed to obtain those results will be described in detail in a separate article (J. Shuai, I. Parker, and J. E. Pearson; unpublished).
as functions of constant Ca2+ concentration at different IP3) were obtained using Eqs. 7 and 9. Furthermore, we applied the transition matrix theory to predict the open- and closed-time distributions of the channel in steady state and the distributions of the first-opening latency of individual and clustered IP3Rs responding to step IP3 stimulus. The analytic deductions employed to obtain those results will be described in detail in a separate article (J. Shuai, I. Parker, and J. E. Pearson; unpublished).
Stochastic simulation of the IP3R model
We simulated the stochastic dynamics of this nine-state subunit channel model by a Markov process (27,28), updating the state of the system at small time steps dt. For example, a channel subunit in the (110) state at time t could transition to states (010), (100), (111), or to the active A-state at the next time step 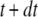 with respective transition probabilities of
with respective transition probabilities of 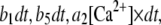 or
or 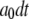 ; otherwise, it remains in the same state. Random numbers homogeneously distributed in [0,1] were generated at each time step and compared with these transition probabilities to determine the state of the channel subunit at the next time step. The IP3R channel is open when three or four subunits are in the A-state. A time step
; otherwise, it remains in the same state. Random numbers homogeneously distributed in [0,1] were generated at each time step and compared with these transition probabilities to determine the state of the channel subunit at the next time step. The IP3R channel is open when three or four subunits are in the A-state. A time step 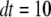 μs was generally used, being much shorter than mean channel open or closed times. The results were not appreciably different when dt was altered between 0.1 and 50 μs, and the close correspondence obtained with results of the deterministic analysis further validates the simulation method.
μs was generally used, being much shorter than mean channel open or closed times. The results were not appreciably different when dt was altered between 0.1 and 50 μs, and the close correspondence obtained with results of the deterministic analysis further validates the simulation method.
RESULTS
Steady-state IP3R dynamics
In this section, we describe the behavior of the single IP3R model under steady-state conditions of given [IP3] and [Ca2+], and demonstrate that our model successfully reproduces the experimental data obtained from patch-clamped IP3R on the Xenopus oocyte nuclear membrane (9–12).
An example of stochastic channel gating
Fig. 2 A illustrates stochastic channel gating, and the corresponding subunit states under conditions [IP3] =10 μM and [Ca2+] = 0.2 μM that result in a mean open probability (PO) of ∼0.4. Because the channel opens when either three or four subunits are active, we can distinguish two different types of channel open state: A3-only openings and A4-related openings. We define A3-only openings as those involving only three simultaneously active subunits throughout the duration of the opening, whereas A4-related openings involve at least one occurrence of all four subunits being active (e.g., openings marked by arrows in Fig. 2 A).
Dependence of open probability on [IP3] and [Ca2+]
The solid symbols in Fig. 2 B show experimental measurements from oocyte nuclei of the dependence of IP3R channel open probability (PO) as a function of cytosolic [Ca2+] for different concentrations of IP3 (10,11). The data follow the well-known “bell-shape” distribution, with increasing concentrations of IP3 producing a rightward shift in the Ca2+ concentration required for maximal PO, and with the maximal PO increasing steeply for IP3 concentrations between 10 and 33 nM. These experimental observations are fit reasonably well by our IP3R model, as shown in Fig. 2 B by results obtained from both deterministic analysis (solid curves) and stochastic simulation (open symbols). An exception is that the model predicts a less steep dependence of PO at low values of [IP3] than was experimentally observed.
A maximal 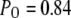 was achieved with the model under optimal conditions ([IP3] > 0.5 μM and [Ca2+] ≈ 3 μM). This corresponds well with measurements from IP3R on the Xenopus oocyte nucleus (10,11), but is much greater than that (PO ≈ 0.2) observed for cerebellar IP3R reconstituted in lipid bilayers (5). Concentrations of IP3 >∼0.5 μM are already saturating, as expected from the relatively high binding affinity (
was achieved with the model under optimal conditions ([IP3] > 0.5 μM and [Ca2+] ≈ 3 μM). This corresponds well with measurements from IP3R on the Xenopus oocyte nucleus (10,11), but is much greater than that (PO ≈ 0.2) observed for cerebellar IP3R reconstituted in lipid bilayers (5). Concentrations of IP3 >∼0.5 μM are already saturating, as expected from the relatively high binding affinity (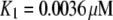 ) in the model.
) in the model.
Mean open and closed time
The mean open (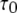 ) and closed (
) and closed ( ) times of the IP3R channel are plotted, respectively, in Fig. 2, C and D, as functions of Ca2+ and IP3 concentrations for the deterministic (solid curves) and stochastic (open symbols) versions of the IP3R model, together with experimental data (solid symbols) from oocyte nuclear receptors at [IP3] = 10 μM (10). It is evident that the dependence of PO upon [Ca2+] and [IP3] described in Fig. 2 B arises primarily through correspondingly large changes in τC, and the model results with 10 μM IP3 fit well to the experimental observations. Additionally, although subject to appreciable scatter, the patch-clamp data also reveal a modest (two- to threefold) increase in τO associated with increasing PO (10). This behavior is reproduced by our model (Fig. 2 C).
) times of the IP3R channel are plotted, respectively, in Fig. 2, C and D, as functions of Ca2+ and IP3 concentrations for the deterministic (solid curves) and stochastic (open symbols) versions of the IP3R model, together with experimental data (solid symbols) from oocyte nuclear receptors at [IP3] = 10 μM (10). It is evident that the dependence of PO upon [Ca2+] and [IP3] described in Fig. 2 B arises primarily through correspondingly large changes in τC, and the model results with 10 μM IP3 fit well to the experimental observations. Additionally, although subject to appreciable scatter, the patch-clamp data also reveal a modest (two- to threefold) increase in τO associated with increasing PO (10). This behavior is reproduced by our model (Fig. 2 C).
Variation of mean open time on [IP3] and [Ca2+]
At first sight, the dependence of predicted τO on ligand concentrations (Fig. 2 C) appears unexpected, given that the transition rate 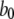 from the active A-state to the closed state (1110) of each subunit is a fixed value, resulting in a constant active dwell time of
from the active A-state to the closed state (1110) of each subunit is a fixed value, resulting in a constant active dwell time of 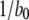 for each subunit. Theory (Eq. 9) indicates that mean open time
for each subunit. Theory (Eq. 9) indicates that mean open time 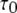 varies with [Ca2+] and [IP3] because the probability for being in the gateway states in which three subunits are active varies with respect to being in the single state with four active subunits. Indeed, the theory is in solid accord with the experimental data, in which the mean open time varies by about a factor of 2. The variation in
varies with [Ca2+] and [IP3] because the probability for being in the gateway states in which three subunits are active varies with respect to being in the single state with four active subunits. Indeed, the theory is in solid accord with the experimental data, in which the mean open time varies by about a factor of 2. The variation in 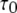 is given by the factor
is given by the factor 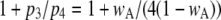 (see Eq. 9). The IP3R is observed to have a maximum
(see Eq. 9). The IP3R is observed to have a maximum 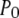 of ∼0.84. To within a few percent,
of ∼0.84. To within a few percent,  takes on its maximum value of 0.84 when
takes on its maximum value of 0.84 when 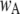 is ∼0.8. This occurs when
is ∼0.8. This occurs when 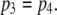 Thus, theory predicts that the channel mean open time varies by a factor of 2, in accord with observation. To further illustrate this point, we analyzed the results of stochastic simulations, and we show below that the variation in mean open time results because there are two populations of channel open states, involving only three simultaneously active subunits, or at least one occurrence of four active subunits.
Thus, theory predicts that the channel mean open time varies by a factor of 2, in accord with observation. To further illustrate this point, we analyzed the results of stochastic simulations, and we show below that the variation in mean open time results because there are two populations of channel open states, involving only three simultaneously active subunits, or at least one occurrence of four active subunits.
We first determined the mean open times associated with each of these conformations. Fig. 3 A shows that mean open times for A3-only openings (T3) and for A4-related openings (T4) change only slightly as a function of [Ca2+] at [IP3] = 10 μM, with respective values of ∼2.6–4.2 and 14.5–15.5 ms. The mean open time TA3 can be intuitively understood because the channel will close when any one of the three active subunits becomes inactive, so that TA3 ≈ 1/(3b0) ≈ 4 ms.
FIGURE 3.
Dependence of 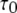 on ligand concentration can be explained by a change in the proportion of openings involving only three active subunits (A3-only openings) and those involving four active subunits (A4-related openings). (A) Stochastic simulation results demonstrating that the mean open times of A3-only and A4-related openings show only a slight dependence on [Ca2+] for [IP3] = 10 μM. (B) The probabilities of A3-only and A4-related openings as functions of [Ca2+]. In both panels, [IP3] = 10 μM.
on ligand concentration can be explained by a change in the proportion of openings involving only three active subunits (A3-only openings) and those involving four active subunits (A4-related openings). (A) Stochastic simulation results demonstrating that the mean open times of A3-only and A4-related openings show only a slight dependence on [Ca2+] for [IP3] = 10 μM. (B) The probabilities of A3-only and A4-related openings as functions of [Ca2+]. In both panels, [IP3] = 10 μM.
Because the mean dwell times of A3- only and A4-related openings have only a slight ligand dependence, the change in mean channel open time with ligand concentration must, therefore, involve also a change in proportion of A3- only and A4-related events. For example, with [Ca2+] at an optimal value of ∼3 μM, each subunit will have a high probability of being in the active state, thereby increasing the probability of finding four active subunits; whereas at lower [Ca2+] the probability of subunits having Ca2+ bound to the activating site is lower, and at higher [Ca2+] there is an increasing chance of subunits becoming inhibited. Thus, the probability for A4-related openings, 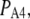 first increases and then decreases with increasing [Ca2+], and the probability for A3-only openings,
first increases and then decreases with increasing [Ca2+], and the probability for A3-only openings, 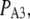 correspondingly follows an inverse relationship (Fig. 3 B).
correspondingly follows an inverse relationship (Fig. 3 B).
The mean open time of the channel, expressed as
 |
(10) |
therefore varies as a function of [Ca2+] and [IP3]. At very low and high [Ca2+], the mean open time 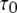 derives almost entirely from the A3-only open state, giving a value of
derives almost entirely from the A3-only open state, giving a value of 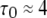 ms. At the optimal value of [Ca2+], ∼3 μM,
ms. At the optimal value of [Ca2+], ∼3 μM, 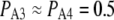 (Fig. 3 B), so that
(Fig. 3 B), so that 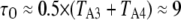 ms.
ms.
Open- and closed-time distributions
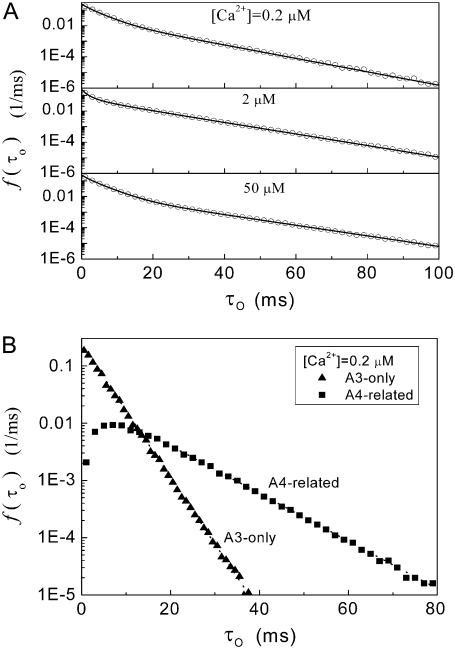
Patch-clamp experimental data show that open-channel dwell times follow a biexponential distribution, with time constants of ∼4 ms and 20 ms (12). This behavior is predicted also by our model with stochastic simulation and deterministic theory, where the open-time distributions at various [Ca2+] are approximated by a sum of two exponentials (Fig. 4 A). These two exponential components can be considered as arising from A3-only and A4-related openings. For example, the distributions of A3-only and A4-related open dwell times are plotted in Fig. 4 B for [Ca2+] = 2 μM and [IP3] = 10 μM. The distribution of A3-only openings is monoexponential, with a time constant of ∼4 ms, and the distribution of A4-related openings approximates an exponential with time constant of ∼12 ms for openings >10 ms. For various [Ca2+] at [IP3] = 10 μM, time constants of A3-only and A4-related exponential open distribution are ∼3–5 and 9–14 ms, respectively.
FIGURE 4.
Distributions of open times predicted by the IP3R channel model. (A) Open-time distributions for basal Ca2+ concentrations at [Ca2+] = 0.2, 2, and 50 μM with [IP3] = 10 μM. Open symbols are results of stochastic simulations, and solid curves were obtained from the transition matrix theory. (B) Distributions of channel open durations involving A3-only and A4-related openings, derived from stochastic modeling at [Ca2+] = 0.2 μM and [IP3] = 10 μM.
Patch-clamp experimental data show that the IP3R channel has at least two closed states, with the time constants ∼1 ms and 10 ms, as well as a long closed kinetic state with time constant of the order of seconds (12). Our model predicts also a rich kinetic behavior for closed dwell times. Three examples of closed-time distributions are plotted in Fig. 5 A for [Ca2+] = 0.2, 2.0, and 200 μM at [IP3] = 10 μM. For [Ca2+] = 0.2 μM (Fig. 5 A, upper), three exponential components can be clearly distinguished at regions  ms,
ms,  ms, and
ms, and 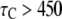 ms, with time constants of 1, 25, and 160 ms, respectively. For [Ca2+] = 2.0 and 200 μM, the distributions can be approximated by two exponential functions: a fast component with time constant 1–3 ms and a slow component with time constants 200–300 ms. The faster component (time constant ∼2 ms) derives largely from immediate, ligand-independent transitions from the (110) state of the model to the active state, as set by the time constant 1/
ms, with time constants of 1, 25, and 160 ms, respectively. For [Ca2+] = 2.0 and 200 μM, the distributions can be approximated by two exponential functions: a fast component with time constant 1–3 ms and a slow component with time constants 200–300 ms. The faster component (time constant ∼2 ms) derives largely from immediate, ligand-independent transitions from the (110) state of the model to the active state, as set by the time constant 1/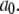 The slower components derive from transitions involving the other seven closed states, and are expected to be correspondingly complex. In practice, we are able to discern only a maximum of three-exponential functions by fitting to predicted closed-time distributions.
The slower components derive from transitions involving the other seven closed states, and are expected to be correspondingly complex. In practice, we are able to discern only a maximum of three-exponential functions by fitting to predicted closed-time distributions.
FIGURE 5.
Multicomponent closed-time distributions of the IP3R channel result in “burst-like” behavior. (A) Closed-time distributions at [Ca2+] = 0.2, 2.0, and 50 μM for [IP3] = 10 μM. Open symbols are stochastic simulations and solid curves are from the transition matrix theory. (B) Two examples of the fluctuation in average channel open probability within a 100-m-running window, respectively, for [Ca2+] = 0.1 and 100 μM and [IP3] = 10 μM.
The multiexponential distributions of closed times lead to a “burst-like” behavior of channel gating. During bursts of rapid openings, short closings arise largely as any one of three active subunits undergoes round-trip transitions through the (110) states, whereas the more prolonged interburst intervals result from subunits entering longer-lived inactive states that require ligand association or dissociation to return to the (110) state. A running average of instantaneous PO with a time window of 100 ms thus shows large fluctuations over time (Fig. 5 B), similar to that observed experimentally (12).
Puff latencies after steps of [IP3]
In this article, we limit consideration of our IP3R model to conditions where [Ca2+] is fixed at given values. The results are therefore not immediately applicable to cellular signaling, where cytosolic [Ca2+] fluctuates widely owing to Ca2+ flux through the IP3Rs themselves. An exception, however, concerns experimental observations of Ca2+ puffs evoked by flash photorelease of IP3, where the mean puff latency shortens with increasing [IP3] (7,8). In this case, the basal cytosolic [Ca2+] remains essentially unchanged before the puff, permitting us to simulate puff initiation by considering the stochastic variability in opening of an IP3R channel after a step increase in [IP3] at constant [Ca2+]. We assume that opening of a single IP3R channel provides sufficient “trigger” Ca2+ to activate neighboring channels and thereby evoke a puff (29), and estimate the number of IP3R clustered at a puff site by fitting the stochastic simulation results to experimental data.
Responses of a single IP3R channel to a step of [IP3]
We first consider the latency of an individual channel after a step increase in IP3 concentration. Initially, the channel is in equilibrium at biologically realistic resting conditions with cytosolic 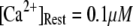 and [IP3] = 0 μM. At time
and [IP3] = 0 μM. At time 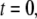 the concentration of IP3 increases instantaneously from 0 μM to
the concentration of IP3 increases instantaneously from 0 μM to 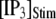 to simulate the rapid photorelease of IP3 by an ultraviolet flash. Examples of three responses to a step
to simulate the rapid photorelease of IP3 by an ultraviolet flash. Examples of three responses to a step 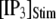 = 10 μM are presented in Fig. 6 A, illustrating the stochastic variability in channel kinetics. Here, we are concerned only with the latency to the first opening of the channel, and disregard subsequent openings. Fig. 6, B and C, plots distributions of channel first-opening latencies for various
= 10 μM are presented in Fig. 6 A, illustrating the stochastic variability in channel kinetics. Here, we are concerned only with the latency to the first opening of the channel, and disregard subsequent openings. Fig. 6, B and C, plots distributions of channel first-opening latencies for various 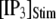 and
and  obtained from simulation and theory. The distributions follow skewed ∩-shaped curves that shift leftward and become narrower with increasing
obtained from simulation and theory. The distributions follow skewed ∩-shaped curves that shift leftward and become narrower with increasing  (Fig. 6 B) and
(Fig. 6 B) and  (Fig. 6 C).
(Fig. 6 C).
FIGURE 6.
Distributions of first-opening latencies for a single IP3R after different steps of [IP3] at various [Ca2+]. (A) Three examples are shown of stochastic simulations for a step of [IP3] from 0 to 10 μM (lower) with [Ca2+] = 0.1 μM. (B and C) Distributions of first-opening latencies after stepwise increases in [IP3] derived from stochastic modeling (open symbols) and theory (solid lines). Results are plotted for different magnitudes of 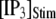 with [Ca2+] = 0.1 μM (B), and for different [Ca2+] with
with [Ca2+] = 0.1 μM (B), and for different [Ca2+] with 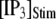 = 10 μM (C).
= 10 μM (C).
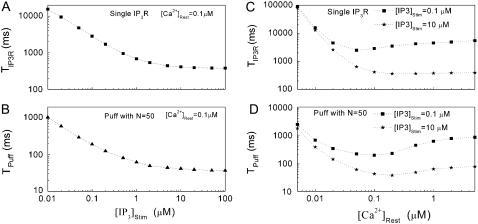
The mean first-opening latency of the channel as a function of  is shown in Fig. 7 A for
is shown in Fig. 7 A for 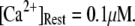 The latency shortens markedly as
The latency shortens markedly as 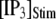 increases from 0 to 5 μM, but then reaches a minimum value of ∼400 ms at higher
increases from 0 to 5 μM, but then reaches a minimum value of ∼400 ms at higher 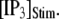 The mean first-opening latency of the channel as a function of
The mean first-opening latency of the channel as a function of 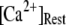 is shown in Fig. 7 C for
is shown in Fig. 7 C for 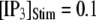 and 10 μM. An interesting observation is that changes in
and 10 μM. An interesting observation is that changes in 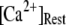 from 0.05 to 0.2 μM cause an increase of the mean minimum latency at low
from 0.05 to 0.2 μM cause an increase of the mean minimum latency at low 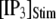 (from ∼2500 to ∼3500 ms for
(from ∼2500 to ∼3500 ms for 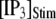 = 0.1 μM), but a decrease of the latency at high
= 0.1 μM), but a decrease of the latency at high 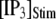 (from ∼650 to ∼350 ms for
(from ∼650 to ∼350 ms for 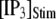 = 10 μM).
= 10 μM).
FIGURE 7.
Mean first-opening latencies for single and multiple IP3R after different steps of 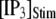 at various [Ca2+]. (A and B) The mean first-opening latency of an individual IP3R channel (A) as a function of
at various [Ca2+]. (A and B) The mean first-opening latency of an individual IP3R channel (A) as a function of 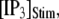 with [Ca2+] = 0.1 μM, and the corresponding latencies for the first opening of any channel among a population of 50 IP3R channels (i.e., the predicted puff latency) (B). (C and D) Corresponding dependence of mean single-channel first-opening latency (C) and puff latency (D) for a cluster of 50 channels as a function of [Ca2+] for
with [Ca2+] = 0.1 μM, and the corresponding latencies for the first opening of any channel among a population of 50 IP3R channels (i.e., the predicted puff latency) (B). (C and D) Corresponding dependence of mean single-channel first-opening latency (C) and puff latency (D) for a cluster of 50 channels as a function of [Ca2+] for 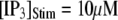 (stars) and
(stars) and 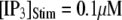 (squares).
(squares).
These results can be understood in terms of the states of the IP3R subunit model. For very small 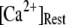 (≤0.01 μM), >85% channel subunits are in the (000) state at
(≤0.01 μM), >85% channel subunits are in the (000) state at 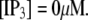 The binding of Ca2+ becomes rate-limiting, so that the latencies are long and have little dependence on
The binding of Ca2+ becomes rate-limiting, so that the latencies are long and have little dependence on  At physiological cytosolic
At physiological cytosolic 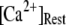 (∼0.1 μM), an important result is that a large proportion of subunits are predicated to be in a Ca2+-inhibited state (e.g., at [Ca2+] = 0.2 μM and
(∼0.1 μM), an important result is that a large proportion of subunits are predicated to be in a Ca2+-inhibited state (e.g., at [Ca2+] = 0.2 μM and  μM, 75% of subunits are in the (001) or (011) states) before flash photorelease of IP3. As a result, changes in basal
μM, 75% of subunits are in the (001) or (011) states) before flash photorelease of IP3. As a result, changes in basal 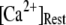 will have dual opposing effects on the latency, with increasing
will have dual opposing effects on the latency, with increasing 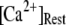 both increasing the steady-state probability of subunits being in Ca2+-inhibited states, and also speeding the binding of Ca2+ to the activating site. At physiological cytosolic
both increasing the steady-state probability of subunits being in Ca2+-inhibited states, and also speeding the binding of Ca2+ to the activating site. At physiological cytosolic 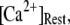 our model shows that these two effects function differently at different
our model shows that these two effects function differently at different 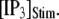 In particular, a fourfold change in
In particular, a fourfold change in 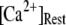 from 0.05 to 0.2 μM results in a small shortening of the mean latency for large
from 0.05 to 0.2 μM results in a small shortening of the mean latency for large  and a small lengthening of the mean latency for small
and a small lengthening of the mean latency for small 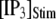 (Fig. 7 C).
(Fig. 7 C).
Responses of clustered IP3Rs to steps of [IP3]
We next extend our simulation from a single IP3R channel to a cluster of N functionally independent channels representing a puff site. Again, the channels are equilibrated at the resting condition ( = 0.1 μM and
= 0.1 μM and 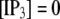 μM), and a step of [IP3], i.e.,
μM), and a step of [IP3], i.e., 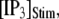 is imposed at time
is imposed at time 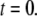 We initially assume that opening of a single channel invariably triggers a puff by CICR, so that the puff latency,
We initially assume that opening of a single channel invariably triggers a puff by CICR, so that the puff latency, 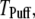 is the interval from t = 0 to the first opening of any channel in the cluster. We then explore the effect of reducing the probability of puff initiation by opening of a single channel.
is the interval from t = 0 to the first opening of any channel in the cluster. We then explore the effect of reducing the probability of puff initiation by opening of a single channel.
The mean puff latency  is plotted as a function of
is plotted as a function of 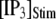 and
and  in Fig. 7, B and D, respectively, for clusters of
in Fig. 7, B and D, respectively, for clusters of  channels. In comparison with the first-opening latency of a single IP3R, the
channels. In comparison with the first-opening latency of a single IP3R, the 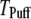 is ∼5–10 times shorter for a given
is ∼5–10 times shorter for a given 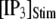 —as expected, since it represents the first among the 50 channels to open—but the general shape of the curve is similar.
—as expected, since it represents the first among the 50 channels to open—but the general shape of the curve is similar.
An interesting observation is that the mean latency for clustered IP3Rs for both large and small 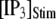 at first shortens as
at first shortens as 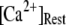 is raised from a low value (0.005 μM), but reaches a minimum at ∼0.1 μM and thereafter actually shows a slight lengthening (Fig. 7 D). An explanation is that binding of Ca2+ to activating sites is rate-limiting at very low
is raised from a low value (0.005 μM), but reaches a minimum at ∼0.1 μM and thereafter actually shows a slight lengthening (Fig. 7 D). An explanation is that binding of Ca2+ to activating sites is rate-limiting at very low 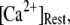 so that the latency first becomes shorter as
so that the latency first becomes shorter as 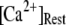 increases from 0.01 μM. However, at higher concentrations (>0.1 μM), there is an increasing likelihood of subunits being in an inhibited state due to
increases from 0.01 μM. However, at higher concentrations (>0.1 μM), there is an increasing likelihood of subunits being in an inhibited state due to 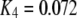 μM (Fig. 1), so that the latency approaches a minimal value set by the dissociation rate
μM (Fig. 1), so that the latency approaches a minimal value set by the dissociation rate 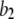 from inhibitory Ca2+-binding sites.
from inhibitory Ca2+-binding sites.
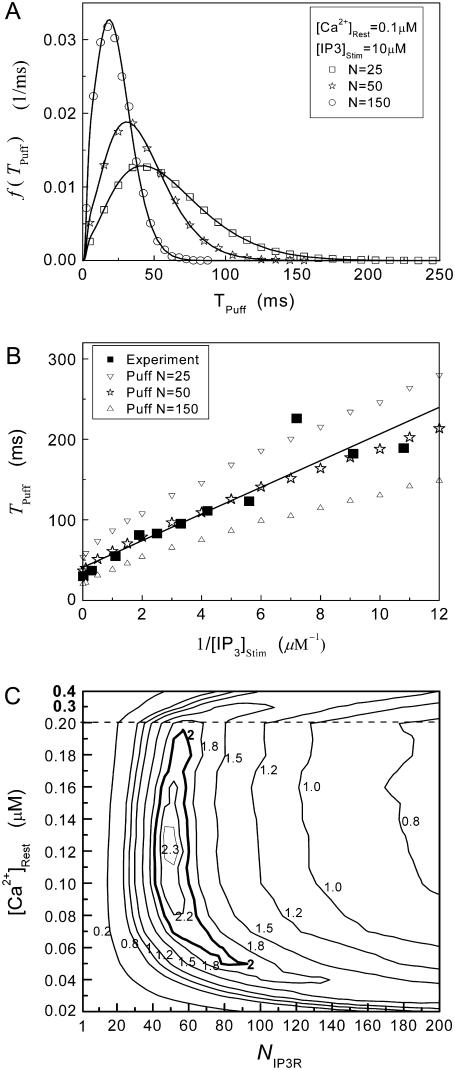
Fig. 8 A shows the puff latency distributions obtained from theory and simulation for 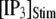 = 10 μM and
= 10 μM and 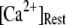 = 0.1 μM considering clusters containing
= 0.1 μM considering clusters containing 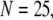 50, and 150 channels. The curves represent the stochastic variability in first-opening latencies, and since they reflect the population behavior of multiple channels, the peaks of the distributions shift to shorter latencies with increasing N while the spread of the distribution narrows.
50, and 150 channels. The curves represent the stochastic variability in first-opening latencies, and since they reflect the population behavior of multiple channels, the peaks of the distributions shift to shorter latencies with increasing N while the spread of the distribution narrows.
FIGURE 8.
Simulation and experimental measurements of puff latencies. (A) Predicted latency distribution of puffs for 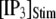 = 10 μM and
= 10 μM and 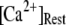 = 0.1 μM, assuming that a puff is evoked by the first opening of any IP3R channel within clusters containing N IP3Rs. The open symbols are for stochastic simulation results with
= 0.1 μM, assuming that a puff is evoked by the first opening of any IP3R channel within clusters containing N IP3Rs. The open symbols are for stochastic simulation results with  (inverted triangles), 50 (stars), or 150 (triangles). The corresponding solid curves are obtained from the transition matrix theory. (B) Predicted mean puff latencies as functions of
(inverted triangles), 50 (stars), or 150 (triangles). The corresponding solid curves are obtained from the transition matrix theory. (B) Predicted mean puff latencies as functions of 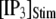 are shown for clusters containing
are shown for clusters containing  (inverted triangles), 50 (stars), and 150 (triangles) channels, with
(inverted triangles), 50 (stars), and 150 (triangles) channels, with 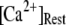 = 0.1 μM. For comparison, experimental data of puff latencies as a function of [IP3] step is replotted as solid squares from Callamaras et al. (7) and Parker et al. (8) after normalizing as described in the text. (C) Goodness of fit of stochastic simulations to the experimental data as functions of both the number of IP3R in a cluster and the resting Ca2+ concentration. Optimal agreement (maximal value of the index
= 0.1 μM. For comparison, experimental data of puff latencies as a function of [IP3] step is replotted as solid squares from Callamaras et al. (7) and Parker et al. (8) after normalizing as described in the text. (C) Goodness of fit of stochastic simulations to the experimental data as functions of both the number of IP3R in a cluster and the resting Ca2+ concentration. Optimal agreement (maximal value of the index  ) is obtained with N ≈ 40–70 and
) is obtained with N ≈ 40–70 and 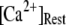 ≈ 0.05–0.2 μM.
≈ 0.05–0.2 μM.
Number of IP3Rs at a puff site
To compare model predictions with the experimental data, the mean puff latency 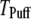 is replotted as a function of
is replotted as a function of 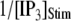 in Fig. 8 B for clusters of
in Fig. 8 B for clusters of 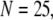 50, and 150 channels at
50, and 150 channels at 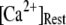 = 0.1 μM, together with experimental data of puff latencies in Xenopus oocytes taken from Callamaras et al. (7) and Parker et al. (8). The experimental puff latency
= 0.1 μM, together with experimental data of puff latencies in Xenopus oocytes taken from Callamaras et al. (7) and Parker et al. (8). The experimental puff latency 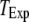 can be fit as a linear function of
can be fit as a linear function of 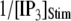 (7),
(7),
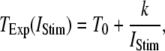 |
(11) |
with the minimal latency 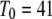 ms and slope
ms and slope 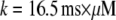 (Fig. 8 B, solid line). Good agreement with these experimental data was obtained by simulating a cluster containing 50 IP3R channels.
(Fig. 8 B, solid line). Good agreement with these experimental data was obtained by simulating a cluster containing 50 IP3R channels.
To better quantify the agreement between model and experimental measurements of puff latencies (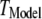 and
and 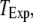 respectively), we introduce an optimal matching function:
respectively), we introduce an optimal matching function:
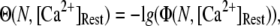 |
(12) |
with
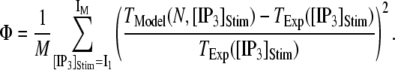 |
(13) |
A larger value of 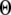 indicates a better match between the modeled puff and the experimental observation.
indicates a better match between the modeled puff and the experimental observation.
The results are depicted graphically in Fig. 8 C by contours of increasing  Here we discuss the optimal function
Here we discuss the optimal function 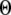 by varying both the channel number N in the cluster and the resting Ca2+ concentration. The resting Ca2+ concentration in cytosol is ∼0.05–0.2 μM. An optimal region in the N-
by varying both the channel number N in the cluster and the resting Ca2+ concentration. The resting Ca2+ concentration in cytosol is ∼0.05–0.2 μM. An optimal region in the N-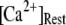 plane obtained with the model also centered at
plane obtained with the model also centered at  = 0.12 μM with N = 55. Our simulation given in Fig. 8 C suggests that the total channel number in a cluster may be in the range of 40 to 70 (considering the contour of
= 0.12 μM with N = 55. Our simulation given in Fig. 8 C suggests that the total channel number in a cluster may be in the range of 40 to 70 (considering the contour of 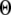 = 2.0 where
= 2.0 where 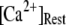 is in the biologically realistic range of 0.05 to 0.2 μM).
is in the biologically realistic range of 0.05 to 0.2 μM).
Effect of reduced triggering probability on puff latency
In the above discussion, the puff latency was calculated assuming that the first opening of any single channel in a cluster invariably triggers a puff by CICR. However, it is likely that brief channel openings may provide insufficient “trigger” calcium to initiate a puff. We thus explored the effect of reducing the probability of puff initiation by reducing the probability, 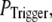 that any given channel opening triggers a puff. Specifically, if the first opening of a channel within a cluster failed to trigger a puff, we then checked whether the next opening event (of the same or a different channel) triggered a puff with the same
that any given channel opening triggers a puff. Specifically, if the first opening of a channel within a cluster failed to trigger a puff, we then checked whether the next opening event (of the same or a different channel) triggered a puff with the same  and so on, until a puff was evoked.
and so on, until a puff was evoked.
Our simulation shows that the average puff latency varies only slightly as a function of trigger probability, 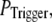 for
for 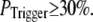 For example, the predicted cluster number N giving a good fit to the experimental data remained at ∼50 for
For example, the predicted cluster number N giving a good fit to the experimental data remained at ∼50 for 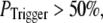 increasing to
increasing to 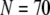 for
for 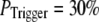 and
and 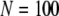 for
for 
DISCUSSION
We propose a dynamic model of the type-1 IP3 receptor in Xenopus oocytes, with the long-term goal of applying the model for stochastic simulations of cellular Ca2+ signaling dynamics within a realistic cytosolic environment. We specifically model the Xenopus oocyte system, as this is the subject of numerous cellular imaging studies (6–8,29) and a wealth of data are available from patch-clamp experiments on oocyte nuclear IP3R (9–12).
Our model assumes that each IP3R channel is comprised of four identical and independent subunits. Like the De Young-Keizer model (14), each subunit consists of two independent Ca2+-binding sites—an activating and an inhibitory binding site—and one IP3 binding site. Furthermore, we assume that a subunit becomes “active” after a conformational change that occurs after both IP3-binding sites and the activating, but not the inhibitory, Ca2+-binding sites are occupied. The channel is open when at least three subunits are in the active state. The model provides a good fit to steady-state experimental data of channel-open probability PO [IP3] (10,11), although it predicts a bell-shaped curve with [Ca2+] even at high concentrations of IP3, different from the “flat-topped” relationship obtained by Mak et al. (11) and Baran (20). Moreover, the model accounts well for the observed distributions of channel-open and -closed dwell times.
With the parameters given in Table 1, our model assumes that there is a negative allosteric interaction between the IP3 site and the inhibitory Ca2+ site, i.e., IP3 binding reduces the affinity of the inhibitory Ca2+ site (from K4 to K2), and Ca2+ binding to the inhibitory site decreases the affinity of the IP3 site (from K1 to K3). The affinity of the activating Ca2+ sites is independent of the inhibitory Ca2+-binding and IP3-binding sites.
In this article, we restrict consideration of the IP3R model to situations where the Ca2+ concentration remains constant; the effects of feedback by Ca2+ flux through the channel will be considered in future publications. Nevertheless, the results provide novel insights into the functioning of both individual IP3Rs and the population behavior of clusters of IP3Rs at puff sites.
Channel opening by three out of four subunits
As is the case for numerous ion channels, the IP3R is a multimer formed from several subunits. In some instances, exemplified by AMPA receptors (24), the single-channel conductance increases in a stepwise fashion as more subunits become active after binding of ligand. However, the Xenopus oocyte IP3R displays only a single major conductance level (11,12), and our model correspondingly incorporates only a single open state. The question then arises as to how many of the four subunits must be active to open the channel.
We assume that the channel is open when either three or four subunits are in an “active” state. This assumption has previously been applied in some IP3R models (23), and we also assume that there is only one conductance state, irrespective of whether three or four subunits are active. An alternative approach to our simple model has been used in allosteric modeling of the tetrameric IP3 and ryanodine receptors (11,30). Such allosteric models are extremely complex because they consider different conductance state with different open probability corresponding to different number of subunits in the active state, which will involve numerous free parameters and be difficult to implement in stochastic simulations. The simulation shows that our simple IP3R model can successfully reproduce two levels of experimental data obtained from patch-clamp of nuclear IP3R and confocal imaging of clustered IP3Rs.
One important consequence of assuming that channel openings occur with either three or four subunits in the active state is that this model successfully predicts the dependence of open dwell time on ligand concentrations, whereas if the channel opening requires all four active subunits to be in the active state, a ligand-independent, constant open dwell time would be expected, since the open time depends only on the backward rate constant b0. The ligand dependence of mean open time can be intuitively understood by distinguishing two types of channel-open state, those involving only three active subunits (A3-only), and those involving four active subunits (A4-related). The mean dwell times in each state are relatively independent of ligand concentration, but A4-related openings are much longer than A3-only openings, since channel closure requires two subunits, rather than just one, to become inactive. Changes in mean channel open time thus derive from changes in the proportion of A3-only and A4-related openings. For example, at very low and very high [Ca2+] the probability of subunits becoming active is small, so almost all channel openings involve only three active subunits and the mean open time thus corresponds to the A3-only dwell time (∼4 ms; Fig. 3 B). Conversely, at optimal [Ca2+] one half of all openings are A4-related, so the channel open time is given by the average of the A3-only and A4-related dwell times (∼9 ms).
The existence of distinct A3-only and A4-related openings may also explain experimental observations that the distributions of mean IP3R channel open times follow two exponential components (12). Mak et al. (12) proposed that these components arise from two kinetically distinguishable open states with different time constants, but our model suggests that they may instead reflect the different mean dwell times of A3-only and A4-related openings.
Furthermore, our model indicates a complex situation for the closed-time distribution. In principle, there are 486 distinct closed states and 9 distinct open states (J. Shuai, I. Parker, and J. E. Pearson; unpublished), but in practice, only two or three major exponential components can be discriminated from experimental or stochastic simulation data. The faster component primarily reflects brief closings caused by any one of the three active subunits undergoing multiple transitions between the active A-state and the inactive (110) state, whereas the slower components involve ligand binding transitions.
Inactivation of IP3R at basal cytosolic [Ca2+]
One feature of the model is that the dissociation constant of the inhibitory Ca2+ binding site increases enormously from 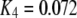 μM to
μM to 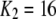 μM after binding of IP3. This scheme is concordant with the conclusion of Mak et al. (10) that the effect of IP3 binding is not to directly activate the channel, as generally assumed, but rather to relieve the channel from Ca2+ inhibition. A distinction, however, is that whereas Mak et al. (10) proposed that the sole action of IP3 is to reduce the effective affinity of the inhibitory Ca2+-binding site, in our model it plays an additional role as an obligate agonist. That is to say, channel opening cannot occur in the absence of IP3 even if the inhibitory Ca2+ sites are unoccupied and the activating sites bind Ca2+ (11).
μM after binding of IP3. This scheme is concordant with the conclusion of Mak et al. (10) that the effect of IP3 binding is not to directly activate the channel, as generally assumed, but rather to relieve the channel from Ca2+ inhibition. A distinction, however, is that whereas Mak et al. (10) proposed that the sole action of IP3 is to reduce the effective affinity of the inhibitory Ca2+-binding site, in our model it plays an additional role as an obligate agonist. That is to say, channel opening cannot occur in the absence of IP3 even if the inhibitory Ca2+ sites are unoccupied and the activating sites bind Ca2+ (11).
An important consequence of the high affinity of the inhibitory Ca2+ binding in the absence of IP3 is that a surprisingly high proportion of IP3R are predicted to be in a Ca2+-inhibited state under basal resting cytosolic conditions with zero [IP3]. For example, with [Ca2+]Rest = 0.1 μM, ∼60% of subunits would be Ca2+-inhibited, resulting in ∼82% of IP3R having two or more subunits in an inhibited state so that the channel cannot immediately open on binding of IP3 and activating Ca2+. Thus, the latency of Ca2+ responses evoked by a step increase of [IP3] will depend strongly on the dissociation of Ca2+ from inhibitory sites, as well the rates of association of Ca2+ and IP3 to activating sites. This is evident in Fig. 7 C, where the mean first-opening latency of a single IP3R initially shortens as 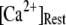 is raised from a low value (0.005 μM), but reaches a minimum at ∼0.05 μM and thereafter actually shows a slight lengthening in response to
is raised from a low value (0.005 μM), but reaches a minimum at ∼0.05 μM and thereafter actually shows a slight lengthening in response to 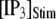 = 0.1 μM. An explanation is that binding of Ca2+ to activating sites is rate-limiting at very low
= 0.1 μM. An explanation is that binding of Ca2+ to activating sites is rate-limiting at very low 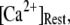 but that at biological concentrations of
but that at biological concentrations of 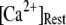 there is an increasing likelihood of subunits being in an inhibited state so that the latency approaches a minimal value set by the dissociation rate
there is an increasing likelihood of subunits being in an inhibited state so that the latency approaches a minimal value set by the dissociation rate 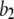 from inhibitory Ca2+-binding sites. Moreover, the magnitude of Ca2+ release will depend on the available fraction of noninactivated IP3R, which in turn will be a function of the resting [Ca2+] before stimulation.
from inhibitory Ca2+-binding sites. Moreover, the magnitude of Ca2+ release will depend on the available fraction of noninactivated IP3R, which in turn will be a function of the resting [Ca2+] before stimulation.
Number of IP3R at a puff site
Finally, we extrapolated our model from the individual IP3R to consider the latency of puffs generated by clusters containing multiple IP3Rs. On the assumptions that IP3Rs within a cluster are independent and that a puff is triggered by whichever channel in the cluster is the first to open, we obtained an optimal fit to experimental measurements of puff latency as a function of [IP3] (7,8) for clusters containing N = 40–70 IP3Rs. This result is affected only slightly by changes of assumed resting Ca2+ concentration within a biologically realistic range of 0.05–0.2 μM.
The conclusion that clusters contain 40–70 IP3Rs likely represents a minimal estimate, since very brief channel openings may fail to initiate a puff, thereby requiring the number of IP3Rs in the model cluster to be increased to match the experimental data. However, this effect becomes appreciable only if the triggering probability is quite low. For example, our simulation shows that if channel openings have a 50% or better chance of initiating a puff (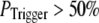 ), a cluster size with
), a cluster size with  still gives a good fitting to the experimental data of puff latency. At smaller
still gives a good fitting to the experimental data of puff latency. At smaller 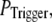 larger values of N are required to obtain a good fit to the experimental data; for example N = 70 for
larger values of N are required to obtain a good fit to the experimental data; for example N = 70 for 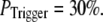 This treatment is simplified compared to the biological situation, where calcium lingering from a channel opening that failed to trigger a puff would likely increase the probability of a subsequent opening to trigger a puff. However, in our simulation, for simplicity, we assume that all the opening events for all the channels in the cluster has the same probability
This treatment is simplified compared to the biological situation, where calcium lingering from a channel opening that failed to trigger a puff would likely increase the probability of a subsequent opening to trigger a puff. However, in our simulation, for simplicity, we assume that all the opening events for all the channels in the cluster has the same probability 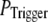 to trigger a puff; and that the resting calcium concentration is always fixed no matter how many opening channels failed to trigger a puff. We plan to address this question more fully in a future study by considering the stochastic dynamics of clustered channels, incorporating the feedback of released Ca2+ ions.
to trigger a puff; and that the resting calcium concentration is always fixed no matter how many opening channels failed to trigger a puff. We plan to address this question more fully in a future study by considering the stochastic dynamics of clustered channels, incorporating the feedback of released Ca2+ ions.
It should be noted that these values estimate the total number of IP3Rs clustered at a puff site. In contrast, most experimental work has used measurements of puff amplitudes to estimate the number of open IP3R channels that contribute to the Ca2+ flux during a puff. For example, we recently capitalized on the discovery of “trigger” events that may represent the opening of a single IP3R channel that initiates a puff (31) to construct a deterministic puff model that predicts the involvement of some 25–35 open channels (29). Thus, it is likely that only a minority of IP3Rs in a cluster open during a puff, as is expected if many receptors are inactivated at resting cytosolic [Ca2+] and Ca2+ dissociates from inhibitory binding sites only slowly on the timescale of puff latencies (a few hundred milliseconds or shorter).
Acknowledgments
This work was supported by National Institutes of Health grants GM 65830 and GM48071.
Editor: Raimond L. Winslow.
References
- 1.Foskett, J. K., C. White, K. Cheung, and D. D. Mak. 2007. Inositol trisphosphate receptor Ca2+ release channels. Physiol. Rev. 87:593–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Taylor, C. W., P. C. da Fonseca, and E. P. Morris. 2004. IP3 receptors: the search for structure. Trends Biochem. Sci. 29:210–219. [DOI] [PubMed] [Google Scholar]
- 3.Bosanac, I., J. R. Alattia, T. K. Mal, J. Chan, S. Talarico, F. K. Tong, K. I. Tong, F. Yoshikawa, T. Furuichi, M. Iwai, T. Michikawa, K. Mikoshiba, and M. Ikura. 2002. Structure of the inositol 1,4,5-trisphosphate receptor binding core in complex with its ligand. Nature. 420:696–700. [DOI] [PubMed] [Google Scholar]
- 4.Bezprozvanny, I. 2005. The inositol 1,4,5-trisphosphate receptors. Cell Calcium. 38:261–272. [DOI] [PubMed] [Google Scholar]
- 5.Bezprozvanny, I., J. Watras, and B. E. Ehrlich. 1991. Bell-shaped calcium-response curves of Ins(1,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 351:751–754. [DOI] [PubMed] [Google Scholar]
- 6.Yao, Y., J. Choi, and I. Parker. 1995. Quantal puffs of intracellular Ca2+ evoked by inositol trisphosphate in Xenopus oocytes. Journal of Physiology-London. 482:533–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Callamaras, N., J. S. Marchant, X. P. Sun, and I. Parker. 1998. Activation and co-ordination of InsP3-mediated elementary Ca2+ events during global Ca2+ signals in Xenopus oocytes. Journal of Physiology-London. 509:81–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Parker, I., Y. Yao, and V. Ilyin. 1996. Fast kinetics of calcium liberation induced in Xenopus oocytes by photoreleased inositol trisphosphate. Biophys. J. 70:222–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mak, D. O., and J. K. Foskett. 1994. Single-channel inositol 1,4,5-trisphosphate receptor currents revealed by patch clamp of isolated Xenopus oocyte nuclei. J. Biol. Chem. 269:29375–29378. [PubMed] [Google Scholar]
- 10.Mak, D. O., S. McBride, and J. K. Foskett. 1998. Inositol 1,4,5-trisphosphate activation of inositol trisphosphate receptor Ca2+ channel by ligand tuning of Ca2+ inhibition. Proc. Natl. Acad. Sci. USA. 95:15821–15825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mak, D. O., S. M. McBride, and J. K. Foskett. 2003. Spontaneous channel activity of the inositol 1,4,5-trisphosphate (InsP3) receptor (InsP3R). Application of allosteric modeling to calcium and InsP3 regulation of InsP3R single-channel gating. J. Gen. Physiol. 122:583–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mak, D. O., and J. K. Foskett. 1997. Single-channel kinetics, inactivation, and spatial distribution of inositol trisphosphate (IP3) receptors in Xenopus oocyte nucleus. J. Gen. Physiol. 109:571–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Atri, A., J. Amundson, D. Clapham, and J. Sneyd. 1993. A single-pool model for intracellular calcium oscillations and waves in the Xenopus laevis oocyte. Biophys. J. 65:1727–1739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.De Young, G. W., and J. Keizer. 1992. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. USA. 89:9895–9899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kaftan, E. J., B. E. Ehrlich, and J. Watras. 1997. Inositol 1,4,5-trisphosphate (InsP3) and calcium interact to increase the dynamic range of InsP3 receptor-dependent calcium signaling. J. Gen. Physiol. 110:529–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sneyd, J., and J. F. Dufour. 2002. A dynamic model of the type-2 inositol trisphosphate receptor. Proc. Natl. Acad. Sci. USA. 99:2398–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Swillens, S., P. Champeil, L. Combettes, and G. Dupont. 1998. Stochastic simulation of a single inositol 1,4,5-trisphosphate-sensitive Ca2+ channel reveals repetitive openings during “blip-like” Ca2+ transients. Cell Calcium. 23:291–302. [DOI] [PubMed] [Google Scholar]
- 18.Fraiman, D., and S. P. Dawson. 2004. A model of the IP3 receptor with a luminal calcium binding site: stochastic simulations and analysis. Cell Calcium. 35:403–413. [DOI] [PubMed] [Google Scholar]
- 19.Sneyd, J., and M. Falcke. 2005. Models of the inositol trisphosphate receptor. Prog. Biophys. Mol. Biol. 89:207–245. [DOI] [PubMed] [Google Scholar]
- 20.Baran, I. 2003. Integrated luminal and cytosolic aspects of the calcium release control. Biophys. J. 84:1470–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hille, B. 2001: Ion Channels of Excitable Membranes, 3rd ed. Sinauer Associates, Sunderland, MA.
- 22.Adkins, C. E., and C. W. Taylor. 1999. Lateral inhibition of inositol 1,4,5-trisphosphate receptors by cytosolic Ca(2+). Curr. Biol. 9:1115–1118. [DOI] [PubMed] [Google Scholar]
- 23.Falcke, M., L. Tsimring, and H. Levine. 2000. Stochastic spreading of intracellular Ca2+ release. Physical Review E. 62:2636–2643. [DOI] [PubMed] [Google Scholar]
- 24.Rosenmund, C., Y. Stern-Bach, and C. F. Stevens. 1998. The tetrameric structure of a glutamate receptor channel. Science. 280:1596–1599. [DOI] [PubMed] [Google Scholar]
- 25.Bruno, W. J., J. Yang, and J. E. Pearson. 2005. Using independent open-to-closed transitions to simplify aggregated Markov models of ion channel gating kinetics. Proc. Natl. Acad. Sci. USA. 102:6326–6331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yang J., W. J. Bruno, W. S. Hlavacek, and J. E. Pearson. 2006. On imposing detailed balance in complex reaction mechanisms. Biophys. J. 91:1136–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shuai, J. W., and P. Jung. 2002. Stochastic properties of Ca2+ release of inositol 1,4,5-trisphosphate receptor clusters. Biophys. J. 83:87–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shuai, J. W., and P. Jung. 2003. Optimal ion channel clustering for intracellular calcium signaling. Proc. Natl. Acad. Sci. USA. 100:506–510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rose, H. J., S. Dargan, J. Shuai, and I. Parker. 2006. “Trigger” events precede calcium puffs in Xenopus oocytes. Biophys. J. 91:4024–4032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zahradnik, I., S. Gyorke, and A. Zahradnikova. 2005. Calcium activation of ryanodine receptor channels–reconciling RyR gating models with tetrameric channel structure. J. Gen. Physiol. 126:515–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shuai, J., H. J. Rose, and I. Parker. 2006. The number and spatial distribution of IP3 receptors underlying calcium puffs in Xenopus oocytes. Biophys. J. 91:4033–4044. [DOI] [PMC free article] [PubMed] [Google Scholar]