Abstract
Infection by membrane-enveloped viruses requires the binding of receptors on the target cell membrane to glycoproteins, or “spikes,” on the viral membrane. The initial entry mechanism is usually classified as fusogenic or endocytotic. However, binding of viral spikes to cell surface receptors not only initiates the viral adhesion and the wrapping process necessary for internalization, but can simultaneously initiate direct fusion with the cell membrane. Both fusion and internalization have been observed to be viable pathways for many viruses. We develop a stochastic model for viral entry that incorporates a competition between receptor-mediated fusion and endocytosis. The relative probabilities of fusion and endocytosis of a virus particle initially nonspecifically adsorbed on the host cell membrane are computed as functions of receptor concentration, binding strength, and number of spikes. We find different parameter regimes where the entry pathway probabilities can be analytically expressed. Experimental tests of our mechanistic hypotheses are proposed and discussed.
INTRODUCTION
Viral entry mechanisms are typically classified as either endocytotic, or as fusogenic (1). In the latter, the virus membrane, after association with the surface of the host cell, fuses and becomes contiguous with the cell membrane. This process is mediated by the binding of cell surface receptors to glycoprotein spikes on the viral membrane surface, forming fusion competent complexes spanning the viral and cell membranes. In endocytosis, the host cell first internalizes the virus particle, wrapping it in a vesicle before acidification-induced fusion with the endosomal membrane can occur. Wrapping can occur only after cell surface receptors, which also act as attachment factors, bind to the viral spikes. Experimentally, both fusion with the cell membrane and internalization can be observed and distinguished using microscopy (2,3).
Many viruses, such as influenza and hepatitis B, use endocytosis as their primary mode of entry (4,5). The surface of an influenza virus is coated with ∼400 hemagglutinin (HA) protein spikes (6). The HA adheres to sialic acid-containing glycoproteins and lipids on the cell surface leading to wrapping of the virus particle. Particle wrapping may also be mediated by the recruitment of pit-forming clathrin/caveolin compounds (7). Cell membrane pinch-off, leading to internalization of the virus, usually requires additional enzymes such as dynamin and endophilin (8). Endosomal acidification oligomerizes the HA, priming them to fuse with the endosomal membrane. Direct fusion of the influenza virus with the host cell membrane is precluded since HA is activated only in the acidic endosomal environment. However, low pH conditions have also been shown to induce the direct fusion of influenza virus with certain cells (9).
Recent experiments on the avian leukosis retrovirus have provided evidence both for a pH-dependent direct fusion mechanism (10,11), and an endocytotic pathway (12). Moreover, the entry pathway of some viruses such as Semliki Forest Virus can be shifted from endocytosis to fusion by acid treatment, but only in certain host cell types (13). In this case, low pH triggering of receptor-primed envelope glycoproteins can initiate fusion before the virus can be wrapped and endocytosed. Vaccinia and HIV (typically infecting cells via fusion after association with the cell surface receptor CD4) have also been shown to exploit both entry mechanisms (7,14–16). For example, fusion-independent mechanisms of HIV-1 capture and internalization in mature dendritic cells, mediated by DC-SIGN (17), can be a significant mode of HIV transmission through dendritic cells and lymphatic tissue (18). Capture by DC-SIGN and CLEC-2 adhesion molecules also internalizes HIV in platelets (19). Thus, depending upon physical conditions and cell type, both entry pathways are potentially accessible to certain viruses. The choice seems to depend on the type of receptors the viruses engages, whether they are receptors/coreceptors that induce fusion (perhaps triggered by low pH), or simply attachment factors such as sialic acid-rich glycoproteins that do not induce fusion. In this latter case, complete wrapping before an irreversible fusion event is more likely to occur, and internalization is favored.
It is not surprising that subtle changes in the interactions between viral membrane proteins and cell receptors dramatically affect the infectivity of a virus, as recently demonstrated for the 1918 influenza virus (20). In this article, we model virus-receptor kinetics and propose a mechanism consistent with experimental observations, which describes viral entry by incorporating both fusion and endocytosis entry pathways in a probabilistic manner. In the next section, we develop a stochastic one-species receptor model for the binding of receptors necessary to start the virus wrapping process. These receptors, upon binding, can induce membrane fusion at each receptor-spike complex. In the Results, we find parameter regimes in which each of the entry mechanisms dominate. Explicit expressions for the entry pathway probabilities, as functions of the relevant kinetic rates, are given in the Appendix. In the Discussion and Summary, we explore the connection between our parameters and experimentally controllable physical conditions such as receptor/coreceptor density, spike density, and cell membrane rigidity. Experimental tests are proposed and extensions of our analysis to more realistically incorporate biological features are discussed.
SINGLE SPECIES RECEPTOR MODEL
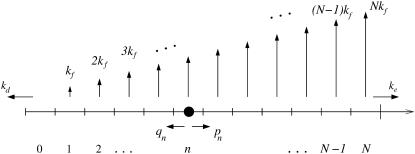
The basic features of our proposed mechanism are shown in Fig. 1. A virus particle initially nonspecifically adsorbed on the cell membrane (without any bound receptors) can spontaneously dissociate with rate kd. Alternatively, mobile receptors in the cell membrane can bind specifically to the glycoprotein spikes (assumed here to be uniformly distributed) on the viral surface. Successive addition of receptors to the viral ligands, when n are already attached, occurs with rate pn. Thus, the binding of the first receptor occurs with rate p0. Similarly, desorption of the nth receptor occurs at rate qn. We consider the adsorption of a single effective receptor or attachment factor to a spike, lumping together the effects of multiple receptor/coreceptor types. This approximation is valid when, for example, coreceptor binding is highly cooperative such as suggested in the HIV infection process where CD4 binding to the gp120 protein spike induces rapid CCR5 coreceptor binding (21).
FIGURE 1.
A schematic of viral entry pathways. (a) A nonspecifically adsorbed virus particle can desorb with rate kd, or it can (b) recruit and specifically bind a receptor. The receptor can immediately initiate membrane fusion with rate kf as shown in panel c, or, it can recruit additional receptor molecules, inducing wrapping of the virus particle. From partially wrapped states (d), the virus can at any stage undergo membrane fusion (e), or, it can completely wrap and internalize the virus particle (f and g).
Receptors not only adhere the cell membrane to the viral membrane, but can also initiate local membrane fusion at each receptor-spike complex with rate kf. Fusion can occur at any time during the receptor recruitment process and is more likely to occur per unit time with more bound receptors. Receptor-spike complexes that are unable to initiate fusion are described by a vanishing fusion rate kf → 0. However, if receptors have high fusogenicity kf, the virus might fuse only after a single receptor has attached. Only if the system reaches a fully wrapped state with N bound receptors (Fig. 1 f), before any fusion event occurs, can pinch-off and endocytosis occur with rate ke. The number of spikes N is typically large, varying among viruses such as HIV (N ∼ 15) (22), SIV (N ∼ 70) (22), and Influenza (N ∼ 400) (6). The path to endocytosis is thus a race between fusion and complete wrapping of a relatively large number N of viral spikes.
States in the model are labeled by the index n (Fig. 2), representing the number of formed receptor-spike complexes. Starting from a nonspecifically adsorbed virus particle denoted by state n = 0, the system progresses along the chain with the appropriate transition rates corresponding to attachment and detachment of cell membrane receptors. The probability Pn(t) of having n bound receptors (or attachment factors) at time t obeys the master equation
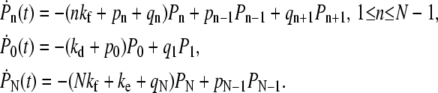 |
(1) |
Although we describe the general viral entry process in terms of recruitment and binding of a single type of receptor, our model encompasses processes involving clathrin or caveolin aggregation and pit formation, typically leading to endocytosis. All of these biologically distinct, but physically similar mechanisms can be analyzed by appropriately interpreting the rates. For example, the nucleation of a clathrin-coated pit can be modeled by effective binding and unbinding rates pn and qn that describe the rates of clathrin addition and removal from the pit. Since individual clathrin molecules are not known to induce membrane fusion, the fusion rate kf = 0, and only endocytosis (or virus dissociation from the cell surface) would occur. The fusion rate is also negligible if the receptor is a simple attachment factor that causes adherence of the membranes, but does not facilitate fusion.
FIGURE 2.
The stochastic process representing the competition between membrane fusion and endocytosis. The states n correspond to the number of receptor-spike complexes formed, while N is the total number of spikes on the virus membrane. Each receptor-spike complex can initiate membrane fusion with rate kf. As more receptors are bound, the total rate of fusion increases linearly. The irreversible pinch-off and endocytosis rate is denoted ke.
The receptor binding and unbinding rates, pn and qn, are related to the cell surface receptor density and the receptor-spike binding strength, respectively. The Markov process shown in Fig. 2 implicitly assumes that the receptor recruitment is not diffusion-limited—the rate of addition of successive receptors is independent of the history of previous receptor bindings.
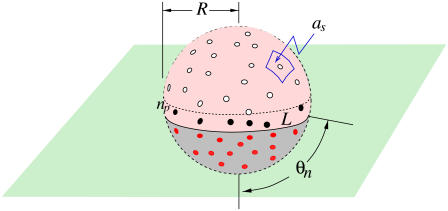
Approximate forms for pn, qn can be physically motivated by considering the number of ways additional receptors can bind or unbind, given that n receptor-spike complexes already exist. As the membrane progressively wraps around the virus particle, the rate of addition of the next receptor is proportional to the number np of unattached spikes bordering the virus-cell membrane contact line L, as shown in Fig. 3.
FIGURE 3.
Schematic of a partially wrapped virus particle. The unbound spikes above the contact region are represented by open circles, while the receptor-bound spikes in the contact region are represented by the red dots. The number np of spikes or spike-receptor complexes near the contact perimeter used to compute pn or qn via Eq. 2 are shown as black dots.
For a large number N of uniformly distributed spikes on a virus particle of radius R, the contact area Ac ≈ 4πR2n/N ≈ 2πR2(1 − cos θn), where 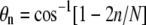 is the angle subtended by the contact line when n receptors are attached. Since the area per spike is as ≈ 4πR2/N, the number of spikes near the contact perimeter L = 2πR sin θn is found from
is the angle subtended by the contact line when n receptors are attached. Since the area per spike is as ≈ 4πR2/N, the number of spikes near the contact perimeter L = 2πR sin θn is found from  Upon using the explicit form for θn, we find the number np of periphery spikes as a function of n ≥ 1 receptor-bound spikes,
Upon using the explicit form for θn, we find the number np of periphery spikes as a function of n ≥ 1 receptor-bound spikes, 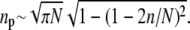 At a stage where n ≥ 1 receptors have bound, ∼np spikes are accessible for additional binding of receptors. Similarly, there are ∼np receptor-spike complexes available for dissociation. Combinatorically, the receptor binding and unbinding rates take the form (23)
At a stage where n ≥ 1 receptors have bound, ∼np spikes are accessible for additional binding of receptors. Similarly, there are ∼np receptor-spike complexes available for dissociation. Combinatorically, the receptor binding and unbinding rates take the form (23)
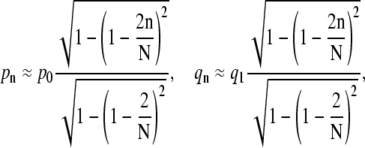 |
(2) |
where 1 ≤ n ≤ N − 1, p0 is the intrinsic rate of binding the first receptor, and q1 = qN is the dissociation rate of an individual receptor-spike complex. Since q1 is a spontaneous receptor-spike dissociation rate, it is independent of receptor density and spike number. If the receptor-spike binding energy is at least a few kBT, we also expect qn to be relatively insensitive to the cell membrane bending rigidity.
A number of physical attributes and biological intermediates can be incorporated into the rate parameters to address more complicated microscopic processes. For example, if thermal fluctuations are rate-limiting, there would be an additional factor in pn, reflecting the probability per unit time that a patch of membrane fluctuates to within a distance of the virus surface spike that allows receptor-spike binding. The dynamics of this process depends on the cell membrane tension and rigidity, the typical spike spacing, and potentially the viscosity of the extracellular environment. For stiff membranes under tension, the wrapping of spherical particles encounters an energy barrier near half-wrapping (24), which can be incorporated into the dynamics by assuming an additional factor in pn that has a minimum near n ≈ N/2. Thus, the energy barrier associated with membrane bending will tend to flatten the n-dependence of pn.
Particular aspects of the entry process can also influence estimates of the other rates. If the viral spikes are mobile and can aggregate to the initial focal point of adhesion, the target cell membrane is not able to fully wrap and endocytosis is prevented. The overall kinetic scheme remains unchanged except with ke ≈ 0. Finally, the recruitment of secondary coreceptors that occurs in, e.g., HIV fusion, can also be developed within our current framework and is put forth in Discussion and Summary. Although some of the physical details described above influence the specific values of pn, we will show that for large N, the qualitative behavior of our model can be summarized by distinct parameter regimes, somewhat insensitive to the precise values of pn, qn.
RESULTS
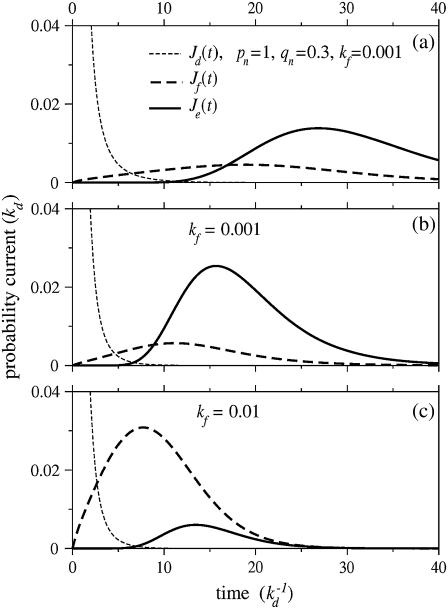
We solved Eq. 1 for the probabilities Pn(t) given an initial condition Pn(t = 0) = δn, 0. Using these probabilities, we find the probability currents through the dissociation, fusion, and endocytosis pathways, Jd(t) = kdP0(t), 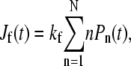 and Je(t) = kePN(t), respectively. Fig. 4 shows the current for each pathway as a function of time (in units of
and Je(t) = kePN(t), respectively. Fig. 4 shows the current for each pathway as a function of time (in units of  ). Note that detachment, fusion, and endocytosis arise sequentially in time. Upon comparing Fig. 4, a and b, we see that changing pn, qn from constant values to the forms in Eq. 2 shifts the currents through the fusion and endocytotic pathways to earlier times. This speedup is simply a consequence of the larger hopping rates pn, qn, especially for n ≈ N/2. Nonetheless, the specific form of pn, qn, provided they are slowly varying in n, only quantitatively affect the timing of the onset of the currents. The dramatic variations in the infection pathway taken come with changes in kf. When the fusion rate kf is increased, endocytosis is suppressed in favor of fusion as shown by Fig. 4, b and c.
). Note that detachment, fusion, and endocytosis arise sequentially in time. Upon comparing Fig. 4, a and b, we see that changing pn, qn from constant values to the forms in Eq. 2 shifts the currents through the fusion and endocytotic pathways to earlier times. This speedup is simply a consequence of the larger hopping rates pn, qn, especially for n ≈ N/2. Nonetheless, the specific form of pn, qn, provided they are slowly varying in n, only quantitatively affect the timing of the onset of the currents. The dramatic variations in the infection pathway taken come with changes in kf. When the fusion rate kf is increased, endocytosis is suppressed in favor of fusion as shown by Fig. 4, b and c.
FIGURE 4.
The currents through each pathway for N = 20 spikes. The thin dashed black curve is the current for desorption, while the thick dashed and solid curves are the currents for fusion and endocytosis, respectively. Time is measured in units of 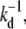 and all rates are normalized with respect to kd. The parameters used in all plots are p0 = 1, q1 = 0.3, and ke = 0.3. (a) The currents for constant pn = 1, qn = 0.3, and fusion rate kf = 0.001. (b) The same parameters except that Eq. 2 is used for the rates pn, qn. (c) The currents with pn, qn as in panel b, except that the fusion rate of each spike-receptor complex is increased to kf = 0.01.
and all rates are normalized with respect to kd. The parameters used in all plots are p0 = 1, q1 = 0.3, and ke = 0.3. (a) The currents for constant pn = 1, qn = 0.3, and fusion rate kf = 0.001. (b) The same parameters except that Eq. 2 is used for the rates pn, qn. (c) The currents with pn, qn as in panel b, except that the fusion rate of each spike-receptor complex is increased to kf = 0.01.
Upon time-integrating the currents, we find the total probabilities 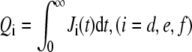 for each pathway. Note that from probability conservation, Qd + Qe + Qf = 1. In Fig. 5, we use the binding and unbinding rates given by Eq. 2 to numerically compute the entry pathway probabilities Qi. Fig. 5 a shows the pathway probabilities as a function of the intrinsic receptor binding rate p0/q1. This ratio is a measure of the density-dependent free energy ΔG of the spike-receptor binding: p0/q1 ∼ eΔG/kT (23). In the simplest limit of extremely low receptor density, (p0 → 0),
for each pathway. Note that from probability conservation, Qd + Qe + Qf = 1. In Fig. 5, we use the binding and unbinding rates given by Eq. 2 to numerically compute the entry pathway probabilities Qi. Fig. 5 a shows the pathway probabilities as a function of the intrinsic receptor binding rate p0/q1. This ratio is a measure of the density-dependent free energy ΔG of the spike-receptor binding: p0/q1 ∼ eΔG/kT (23). In the simplest limit of extremely low receptor density, (p0 → 0), 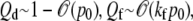 and Qe ∼ 0, and only dissociation can occur. As p0 is increased, the probability of fusion increases at the expense of desorption. Endocytosis remains negligible, as long the states that occur with any appreciable probability are those with small n. Only as p0 ≫ q1 does the probability of endocytosis become appreciable and approach the asymptotic expression given by Eq. 3 in the Appendix.
and Qe ∼ 0, and only dissociation can occur. As p0 is increased, the probability of fusion increases at the expense of desorption. Endocytosis remains negligible, as long the states that occur with any appreciable probability are those with small n. Only as p0 ≫ q1 does the probability of endocytosis become appreciable and approach the asymptotic expression given by Eq. 3 in the Appendix.
FIGURE 5.
Numerical solutions of entry probabilities Qi (all rates normalized by kd). (a) The entry probabilities as a function of p0. Endocytosis arises only for larger p0 > q1, after the fusion probability becomes significant. Parameters used are N = 20, kf = 0.003, and ke = 0.3 (all rates are normalized by kd). (b) The probabilities of dissociation (thin dashed), fusion (thick dashed), and endocytosis (thick solid) as functions of the individual receptor-spike fusion rate kf. Here, q1 = 0.3. The thin dotted curve corresponds to a faster receptor detachment rate (q1 = 2), which prevents endocytosis.
Fig. 5 b shows the total probabilities Qd of dissociation, Qf of fusion, and Qe of endocytosis as functions of the fusion rate kf. For large detachment rates (e.g., q1 = 2 > p0 = 1), Qe ≈ 0, and fusion can occur only at large kf, as shown by the thin dotted curve. For the parameters used, N = 20, p0 = 1, q1 = ke = 0.3 (normalized by kd), the transition from a predominantly endocytotic pathway to a predominantly fusion pathway occurs for 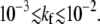 When
When 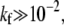 the sum of fusion probabilities over all intermediate states is appreciable, preventing endocytosis. Therefore, only for a particularly small fusion rate kf, and nonnegligible endocytosis rate ke, is internalization possible. We show in the Appendix that generally, if pn > qn, the effective drift of the stochastic system toward the wrapped state renders the partitioning between fusion and endocytosis controlled by the fusion rate kf. If this is the case, the transition from endocytosis to fusion occurs at ∼kf (pn + qn)/N2, as is confirmed by the numerical solution for N = 20 shown in Fig. 5 b.
the sum of fusion probabilities over all intermediate states is appreciable, preventing endocytosis. Therefore, only for a particularly small fusion rate kf, and nonnegligible endocytosis rate ke, is internalization possible. We show in the Appendix that generally, if pn > qn, the effective drift of the stochastic system toward the wrapped state renders the partitioning between fusion and endocytosis controlled by the fusion rate kf. If this is the case, the transition from endocytosis to fusion occurs at ∼kf (pn + qn)/N2, as is confirmed by the numerical solution for N = 20 shown in Fig. 5 b.
Although we have chosen N = 20 as a representative spike number, different viruses and their variants can have a widely varying number of active spikes. In Fig. 6 , we show how the entry pathway probabilities depend on the number N of active viral spikes. As N is increased, the probability for fusion increases at the expense of endocytosis. For N → ∞ and a nonzero kf, Qe → 0, since fusion will likely occur during the infinitely long wrapping processes. For small N, the plotted probabilities must be interpreted with an N-dependent ke. Suppose 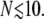 Even if all spikes are receptor-bound, the membrane has an appreciable distance to bend and before full wrapping and endocytosis can occur. Effectively, the fusion rate ke starts to decrease if N gets small such that the rate of membrane fluctuations over a typical interspike distance decreases.
Even if all spikes are receptor-bound, the membrane has an appreciable distance to bend and before full wrapping and endocytosis can occur. Effectively, the fusion rate ke starts to decrease if N gets small such that the rate of membrane fluctuations over a typical interspike distance decreases.
FIGURE 6.
The pathway dependence on receptor association/dissociation rates and the number N of virus spikes. The number of spikes controls which regime of Eqs. 4 or 5 is valid. Large N enhances fusion almost entirely at the expense of endocytosis.
Provided 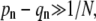 asymptotic analysis of the solutions reveal qualitatively different behaviors depending upon how the fusion rate kf compares with 1/N. If the receptor-spike complex is highly fusion-competent such that
asymptotic analysis of the solutions reveal qualitatively different behaviors depending upon how the fusion rate kf compares with 1/N. If the receptor-spike complex is highly fusion-competent such that 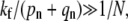 the probability of reaching a completely wrapped (n ≈ N) state is exponentially small and endocytosis cannot occur. Here, the virus pathway is nearly entirely partitioned between dissociation and fusion, as indicated by the asymptotic expressions for Qi given by the expressions in Eq. 4.
the probability of reaching a completely wrapped (n ≈ N) state is exponentially small and endocytosis cannot occur. Here, the virus pathway is nearly entirely partitioned between dissociation and fusion, as indicated by the asymptotic expressions for Qi given by the expressions in Eq. 4.
If 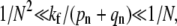 the receptor-spike complex has intermediate fusogenicity. In this case, the time-integrated probability
the receptor-spike complex has intermediate fusogenicity. In this case, the time-integrated probability 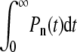 used to construct Qi remains small for n ≈ N and the probability of endocytosis is still exponentially small, despite the smaller kf. In this regime, we find an expression for Qd in Fig. 5. Only when
used to construct Qi remains small for n ≈ N and the probability of endocytosis is still exponentially small, despite the smaller kf. In this regime, we find an expression for Qd in Fig. 5. Only when 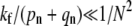 is virus internalization appreciable. Expressions for Qf and Qe in this very weak fusogenicity limit are also displayed in Eq. 5. The expressions we find agree with the exact numerical evaluation of Qd, e, f from solving Eq. 1.
is virus internalization appreciable. Expressions for Qf and Qe in this very weak fusogenicity limit are also displayed in Eq. 5. The expressions we find agree with the exact numerical evaluation of Qd, e, f from solving Eq. 1.
DISCUSSION AND SUMMARY
Fusion can be directly distinguished from endocytosis by imaging fluorescent markers loaded into viruses or model vesicles. Upon fusion, one expects to see an immediate release of marker into the periphery of the target cell. Similarly, single-liposome fluorescence imaging experiments that label and detect vesicle lipids, as they mix with a supported bilayer upon fusion (25), can be used as in vitro model systems for virus fusion. In such experiments, the model parameters pn, qn, kf, ke, kd can be tuned by controlling certain physical chemical properties, enabling one to dissect the mechanism of viral entry. The entry pathways delineated by the different parameter regimes described in the previous section, and by the asymptotic formulae given in the Appendix, provide a framework for analyzing and designing viral entry experiments as well as liposome-based drug delivery protocols.
The receptor density plays the first critical role via the binding rate parameter pn. For low receptor densities and proportionately lower pn (but fixed spontaneous detachment rate qn), the virus particle can only dissociate or fuse. Although lowering receptor concentration decreases the overall entry probability, it can increase Qf /Qe, the fusion probability relative to endocytosis probability (see Fig. 5 a). Only for pn – qn > O(1/N) can the receptor spike complex fusion rate kf become important in determining whether fusion or endocytosis occurs. For endocytosis to occur, the fusion rates must be small such that 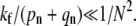 The rate pn can also be substantially decreased by increasing the target membrane surface tension, thereby suppressing the thermal fluctuations of the membrane required to bring cell receptors and viral spikes into proximity.
The rate pn can also be substantially decreased by increasing the target membrane surface tension, thereby suppressing the thermal fluctuations of the membrane required to bring cell receptors and viral spikes into proximity.
The rapid drop-off in endocytosis predicted as the fusion rate is increased from 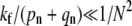 to
to 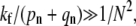 especially for large N, shows that tuning physical conditions (such as pH or temperature) that affect the fusogenicity of receptor-spike complexes, kf, can have a large effect on the viral entry pathway. Recent experiments by Melikyan et al. (26), Henderson and Hope (27), and others have shown a rate-limiting intermediate in the HIV fusion process that can be arrested by lowering temperature. Since CD4 binding was not the rate-limiting step, lowering the temperature decreases kf to a degree presumably much less that (pn + qn)/N2, preventing fusion. If these systems have the necessary endocytotic machinery and support pinch-off, lowering temperature and arresting the receptor-spike fusion complex while retaining the adhesive wrapping of receptor-spike binding would enhance the endocytotic pathway. The effective rate kf can also be lowered by cross-linking (with, e.g., defensins) membrane glycoproteins, rendering their complexes with viral spikes fusion-incompetent (28). However, if the cross-linked glycoproteins retain their attraction for the viral surface, the probability of wrapping and internalization would increase. If an independent measurement or estimate of pn + qn is available, the dependence of kf on temperature, pH, and chemical modification can be probed. Our results also have implications for fusion inhibitors currently being developed to prevent HIV entry. As shown in Fig. 4, the different timing of fusion versus endocytosis may provide a window for the action of fusion inhibitors. However, our findings suggest that endocytosis can still occur even if fusion is prevented.
especially for large N, shows that tuning physical conditions (such as pH or temperature) that affect the fusogenicity of receptor-spike complexes, kf, can have a large effect on the viral entry pathway. Recent experiments by Melikyan et al. (26), Henderson and Hope (27), and others have shown a rate-limiting intermediate in the HIV fusion process that can be arrested by lowering temperature. Since CD4 binding was not the rate-limiting step, lowering the temperature decreases kf to a degree presumably much less that (pn + qn)/N2, preventing fusion. If these systems have the necessary endocytotic machinery and support pinch-off, lowering temperature and arresting the receptor-spike fusion complex while retaining the adhesive wrapping of receptor-spike binding would enhance the endocytotic pathway. The effective rate kf can also be lowered by cross-linking (with, e.g., defensins) membrane glycoproteins, rendering their complexes with viral spikes fusion-incompetent (28). However, if the cross-linked glycoproteins retain their attraction for the viral surface, the probability of wrapping and internalization would increase. If an independent measurement or estimate of pn + qn is available, the dependence of kf on temperature, pH, and chemical modification can be probed. Our results also have implications for fusion inhibitors currently being developed to prevent HIV entry. As shown in Fig. 4, the different timing of fusion versus endocytosis may provide a window for the action of fusion inhibitors. However, our findings suggest that endocytosis can still occur even if fusion is prevented.
Finally, pathways to fusion and endocytosis can diverge for systems that require both primary receptors and secondary receptors (coreceptors). If two species are required, one for adhering cell and viral membranes, and another to induce fusion, endocytosis will be favored, all else being equal. In this case, the initial receptor binding only causes the cell membrane to wrap around the virus particle. An additional coreceptor must diffuse and bind to the spike-receptor adhesion complex to induce fusion. A highly cooperative receptor-coreceptor interaction, such as in HIV fusion involving CD4 and CCR5/CXCR4, is still modeled by Eq. 1, but with the binding rates pn interpreted as an effective binding rate for both classes of receptor, proportional to the product of their surface concentrations. However, if the coreceptor density and/or mobility is limiting (16), the binding of receptors occur first, with coreceptor priming and formation of a fusion competent receptor-spike complex occurring slowly. This allows time for receptor (adhesion molecule) mediated membrane wrapping of the entire virus, enhancing the likelihood of endocytosis. Thus, by maintaining a high adhesion receptor density, and lowering the fusion-enabling coreceptor density, one enhances the endocytotic pathway.
Acknowledgments
The author thanks B. Lee, G. Lakatos, and M. D'Orsogna for valuable discussions.
This work was supported by the National Science Foundation (grant No. DMS-0349195) and by the National Institutes of Health (grant No. K25AI058672).
APPENDIX
Consider the Master Equation (Eq. 1) in the form 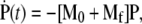 where M0 is the conserved random walk transition matrix involving only kd, pn, qn, and ke, and Mf = kf diag(n) is a decay term arising from fusion. Large N expressions for the entry pathway probabilities Qi can be obtained in different limits.
where M0 is the conserved random walk transition matrix involving only kd, pn, qn, and ke, and Mf = kf diag(n) is a decay term arising from fusion. Large N expressions for the entry pathway probabilities Qi can be obtained in different limits.
In the limit where the receptor binding is irreversible (pn/qn → ∞), Eq. 1 can be solved exactly:
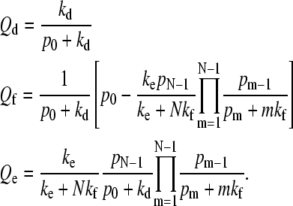 |
(3) |
If qn = 0, the probability of dissociation is fixed by kd and p0, and the remaining current is partitioned between fusion and endocytosis. For a given p0, kf, ke, this limit gives the highest probability of the maximally wrapped state and the highest endocytosis probability.
When  there are two possible limits corresponding to high receptor-spike fusion rates,
there are two possible limits corresponding to high receptor-spike fusion rates, 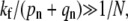 and intermediate fusion rates
and intermediate fusion rates  For
For 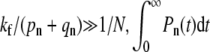 is nonnegligible only for n ≈ 0 and
is nonnegligible only for n ≈ 0 and 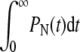 is exponentially small. A small n local analysis of Eq. 1 yields
is exponentially small. A small n local analysis of Eq. 1 yields
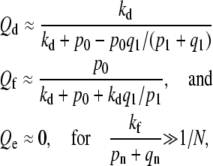 |
(4) |
explicitly showing the absence of endocytosis. The values for Qd and Qf corresponding to the parameter values used in Fig. 6 are Qd ≈ 0.56 and Qf ≈ 0.435, which agree well with the large N limit of the numerical solution.
In an intermediate fusogenicity regime, 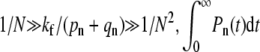 is nearly constant for n ≪ N. However,
is nearly constant for n ≪ N. However, 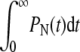 remains small and endocytosis, although still unlikely, occurs with slightly higher probability than in the high fusogenicity limit. In this intermediate limit, one might first attempt perturbation theory for kf = 0 (since its largest element of Mf,
remains small and endocytosis, although still unlikely, occurs with slightly higher probability than in the high fusogenicity limit. In this intermediate limit, one might first attempt perturbation theory for kf = 0 (since its largest element of Mf, 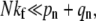 is much smaller than the typical elements of M0). However, as 1/N decreases, so do the spacings between eigenvalues of the zero-fusion transition matrix M0. Heuristically, for perturbation theory to be accurate for slowly varying pN, qN, the largest of the diagonal correction terms, Nkf, must be smaller than (pn + qn)/N, the typical spacing between eigenvalues. First-order perturbation for all Pn(t) is accurate only if
is much smaller than the typical elements of M0). However, as 1/N decreases, so do the spacings between eigenvalues of the zero-fusion transition matrix M0. Heuristically, for perturbation theory to be accurate for slowly varying pN, qN, the largest of the diagonal correction terms, Nkf, must be smaller than (pn + qn)/N, the typical spacing between eigenvalues. First-order perturbation for all Pn(t) is accurate only if 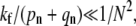 as is explicitly shown by Eq. 3. Upon expanding Qf and Qe (from Eq. 3) in powers of kf, one finds
as is explicitly shown by Eq. 3. Upon expanding Qf and Qe (from Eq. 3) in powers of kf, one finds 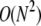 corrections terms. Thus, the expansion is only accurate if
corrections terms. Thus, the expansion is only accurate if 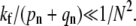 Endocytosis is preempted by fusion or dissociation only when perturbation theory about a nonnegligible Qe fails (when
Endocytosis is preempted by fusion or dissociation only when perturbation theory about a nonnegligible Qe fails (when 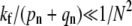 ). Perturbation results, for the few-receptor states n ≈ 0 important for the dissociation probability Qd, are still valid as long as
). Perturbation results, for the few-receptor states n ≈ 0 important for the dissociation probability Qd, are still valid as long as 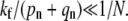 However, the perturbation results that include the flux through larger (n ≈ N) states are accurate only if the receptor-spike complexes are extremely inefficient at initiating membrane fusion, and
However, the perturbation results that include the flux through larger (n ≈ N) states are accurate only if the receptor-spike complexes are extremely inefficient at initiating membrane fusion, and  Thus, for small enough kf /(pn + qn), we find
Thus, for small enough kf /(pn + qn), we find
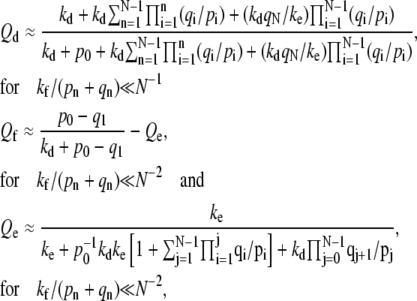 |
(5) |
independent of kf. Equations 3–5 give estimates for the entry probabilities Qd,e,f in the different parameter regimes. For small N such that 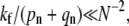 Qe ≈ 0.411, which agrees well with the limit shown in Fig. 6.
Qe ≈ 0.411, which agrees well with the limit shown in Fig. 6.
Editor: Arthur Sherman.
References
- 1.Barocchi, M. A., V. Masignani, and R. Rappuoli. 2005. Cell entry machines: a common theme in nature? Nat. Rev. Microbiol. 3:349–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lakadamyali, M., M. J. Rust, H. P. Babcock, and X. Zhuang. 2003. Visualizing infection of individual influenza viruses. Proc. Natl. Acad. Sci. USA. 100:9280–9285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Markosyan, R. M., F. S. Cohen, and G. B. Melikyan. 2005. Time-resolved imaging of HIV-1 Env-mediated lipid and content mixing between a single virion and cell membrane. Mol. Biol. Cell. 16:5502–5513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cross, K. J., L. M. Burleigh, and D. A. Steinhauer. 2001. Mechanisms of cell entry by influenza virus. Expert Rev. Mol. Med. Aug. 6:1–18. [DOI] [PubMed] [Google Scholar]
- 5.Shekel, J. J., and D. C. H. Wiley. 2000. Receptor binding and membrane fusion in virus entry: the influenza hemagglutinin. Annu. Rev. Biochem. 69:531–569. [DOI] [PubMed] [Google Scholar]
- 6.Masaki, I., T. Mizuno, and K. Kawasaki. 2006. Membrane fusion by single influenza hemagglutinin trimers: kinetic evidence from image analysis of hemagglutinin-reconstituted vesicles. J. Biol. Chem. 281:12729–12735. [DOI] [PubMed] [Google Scholar]
- 7.Dimitrov, D. S. 2004. Virus entry: molecular mechanisms and biomedical applications. Nature Rev. 2:109–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Praefcke, G. J. K., and H. T. McMahon. 2004. The dynamin superfamily: universal membrane tubulation and fission molecules? Nat. Rev. Mol. Cell Biol. 5:133–147. [DOI] [PubMed] [Google Scholar]
- 9.Duzgunes, N., M. C. P. de Lima, L. Stamatatos, D. Flasher, D. Alford, D. S. Friend, and S. Nir. 1992. Fusion activity and inactivation of influenza virus: kinetics of low pH-induced fusion with cultured cells. J. Gen. Virol. 73:27–37. [DOI] [PubMed] [Google Scholar]
- 10.Melikyan, G. B., R. J. O. Barnard, R. M. Markosyan, J. A. T. Young, F. S. S. Cohen, J. Pogorzelski, and A. D. Kogut. 2004. Low pH is required for ASLV Env-induced hemifusion and fusion pore formation, but not for pore growth. J. Virol. 78:3753–3762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mothes, W., A. L. Boerger, S. Narayan, J. M. Cunningham, and J. A. T. Young. 2000. Retroviral entry mediated by receptor priming and low pH triggering of an envelope glycoprotein. Cell. 103:679–689. [DOI] [PubMed] [Google Scholar]
- 12.Diaz-Griffero, F., S. A. Hoschander, and J. Brojatsch. 2002. Endocytosis is a critical step in entry of subgroup B avian leukosis viruses. J. Virol. 76:12866–12876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marsh, M., and R. Bron. 1997. SFV infection in cho cells: cell-type specific restrictions to productive virus entry at the cell surface. J. Virol. 110:95–103. [DOI] [PubMed] [Google Scholar]
- 14.Lai, C., S. Gong, and M. Esteban. 1991. The 32-kiloDalton envelope protein of Vaccinia virus synthesized in E. coli binds with specificity to cell surfaces. J. Virol. 65:499–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schaeffer, E., V. B. Soros, and W. C. Greene. 2004. Compensatory link between fusion and endocytosis of human immunodeficiency virus type 1 in human cd4 T lymphocytes. J. Virol. 78:1375–1383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Platt, E. J., J. P. Durnin, and D. Kabat. 2005. Kinetic factors control efficiencies of cell entry, efficacies of entry inhibitors, and mechanisms of adaptation of human immunodeficiency virus. J. Virol. 79:4347–4356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Su, S. V., P. Hong, S. Baik, O. A. Negrete, K. B. Gurney, and B. Lee. 2004. Dc-sign binds to HIV-1 glycoprotein 120 in a distinct but overlapping fashion compared with icam-2 and icam-3. J. Biol. Chem. 279:19122–19132. [DOI] [PubMed] [Google Scholar]
- 18.Geijtenbeek, T. B., D. S. Kwon, R. Torensma, S. J. van Vliet, G. C. van Duijnhoven, J. Middel, I. L. Cornelissen, H. S. Nottet, V. N. Kewal-Ramani, D. R. Littman, C. G. Figdor, and Y. van Kooyk. 2000. Dc-sign, a dendritic cell-specific HIV-1-binding protein that enhances trans-infection of T cells. Cell. 100:587–597. [DOI] [PubMed] [Google Scholar]
- 19.Chaipan, C., E. J. Soilleux, P. Simpson, H. Hofmann, T. Gramberg, A. Marzi, M. Geier, E. A. Stewart, J. Eisemann, A. Steinkasserer, K. Suzuki-Inoue, G. L. Fuller, A. C. Pearce, S. P. Watson, J. A. Hoxie, F. Baribaud, and S. Pohlmann. 2006. Dc-sign and clec-2 mediate human immunodeficiency virus type 1 capture by platelets. J. Virol. 80:8951–8960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tumpey, T. M., T. R. Maines, N. V. Hoeven, L. Glaser, A. Solórzano, C. Pappas, N. J. Cox, D. E. Swayne, P. Palese, J. M. Katz, and A. García-Sastre. 2007. A two-amino acid change in the hemagglutinin of the 1918 influenza virus abolishes transmission. Science. 315:655–659. [DOI] [PubMed] [Google Scholar]
- 21.Kuhmann, S. E., E. J. Platt, S. L. Kozak, and D. Kabat. 2000. Cooperation of multiple CCR5 coreceptors is required for infections by human immunodeficiency virus type I. J. Virol. 74:7005–7015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhu, P., J. Liu, J. Bess, E. Chertova, J. D. Lifson, H. Grisé, G. A. Ofek, K. A. Taylor, and K. H. Roux. 2006. Distribution and three-dimensional structure of AIDS virus envelope spikes. Nature. 441:847–852. [DOI] [PubMed] [Google Scholar]
- 23.D'Orsogna, M. R., and T. Chou. 2005. Queuing and cooperativity in ligand-receptor binding. Phys. Rev. Lett. 95:170603. [DOI] [PubMed] [Google Scholar]
- 24.Deserno, M. 2004. Elastic deformation of a fluid membrane upon colloid binding. Phys. Rev. E. 69:031903. [DOI] [PubMed] [Google Scholar]
- 25.Yoon, Y. T., B. Okumus, F. Zhang, Y. K. Shin, and T. Ha. 2006. Multiple intermediates in snare-induced membrane fusion. Proc. Natl. Acad. Sci. USA. 103:19731–19736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Melikyan, G. B., R. M. Markosyan, H. Hemmati, M. K. Delmedico, D. M. Lambert, and F. S. Cohen. 2000. Evidence that the transition of HIV-1 gp41 into a six-helix bundle, not the bundle configuration, induces membrane fusion. J. Cell Biol. 151:413–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Henderson, H. I., and T. J. Hope. 2006. The temperature arrested intermediate of virus-cell fusion is a functional step in HIV infection. Virol. J. 3:36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Leikina, E., H. Delanoe-Ayari, K. Melikov, M. S. Cho, A. Chen, A. J. Waring, W. Wang, Y. Xie, J. A. Loo, R. I. Lehrer, and L. V. Chernomordik. 2005. Carbohydrate-binding molecules inhibit viral fusion and entry and crosslinking membrane glycoproteins. Nat. Immunol. 6:995–1001. [DOI] [PubMed] [Google Scholar]