Expression deconvolution: A reinterpretation of DNA microarray data reveals dynamic changes in cell populations

Abstract

Cells grow in dynamically evolving populations, yet this aspect of experiments often goes unmeasured. A method is proposed for measuring the population dynamics of cells on the basis of their mRNA expression patterns. The population's expression pattern is modeled as the linear combination of mRNA expression from pure samples of cells, allowing reconstruction of the relative proportions of pure cell types in the population. Application of the method, termed expression deconvolution, to yeast grown under varying conditions reveals the population dynamics of the cells during the cell cycle, during the arrest of cells induced by DNA damage and the release of arrest in a cell cycle checkpoint mutant, during sporulation, and following environmental stress. Using expression deconvolution, cell cycle defects are detected and temporally ordered in 146 yeast deletion mutants; six of these defects are independently experimentally validated. Expression deconvolution allows a reinterpretation of the cell cycle dynamics underlying all previous microarray experiments and can be more generally applied to study most forms of cell population dynamics.

Cells live in dynamically changing circumstances, both cooperating and competing with other cells for space and resources. The interactions between cells are fundamental to such biological processes as embryogenesis, differentiation and development, and oncogenesis, among others. Disentangling the dynamics of cell populations requires precise identification of cell types (1), ideally based on detailed measurements of molecular markers specific to each cell type (2). Identification of such markers is not trivial. Furthermore, even within a given cell type, cells exist at different stages of the cell cycle (3), presenting an additional layer of complexity to the dynamics of cell populations.

Within a mixed population of cells, one might expect distinct cell types to exhibit distinct programs of transcription (4). Likewise, cells from distinct phases of the cell cycle will exhibit phase-specific transcriptional patterns (5, 6). When transcription levels are measured from a population of cells in a typical experiment, such as by using DNA microarrays (7), the measured transcription actually represents the weighted average of these many independent transcriptional programs.

Here, we ask whether it is possible to deconvolute the DNA microarray data from a cell population to survey the proportions of different cell types, by treating specific transcriptional patterns in DNA microarray data as cell-type specific markers. In this article, we demonstrate that DNA microarray mRNA expression data can be reinterpreted to provide new information about the dynamics of the cells in the original experiments. We focus specifically on identifying yeast cells growing in different phases of the cell cycle. However, the analysis we introduce is generally applicable to any mixed cell population.

Methods

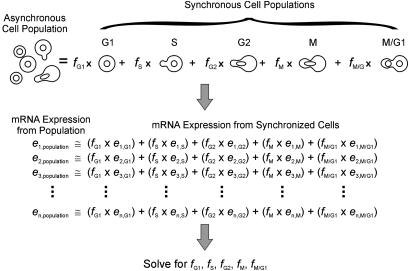
The Method of Expression Deconvolution. Asynchronously growing yeast cells are a mixture of cells in different phases of the cell cycle. Therefore, mRNA expression measurements from asynchronous cells are a mixture of mRNA expression patterns typical of different phases of the cell cycle. By knowing the typical mRNA expression patterns of cells in specific cell cycle phases (G₁, S, G₂, M, and M/G₁), the expression data of asynchronous cells can be modeled as the weighted linear combination of expression data from cells in each phase. The numerical weights associated with each set of phase-specific expression data indicate the proportions of cells in each phase of the cell cycle. This analysis of cell population dynamics, termed expression deconvolution, is diagrammed in Fig. 1.

Fig. 1.

In the method of expression deconvolution, mRNA expression data from a mixed cell population are modeled as the weighted average of expression data from a set of basis experiments, where the weights describe the proportions of each basis cell type in the overall population. As illustrated, expression data from asynchronously grown yeast cells (left data set) are fitas the weighted linear combination of expression data from synchronized cells from specific times in the cell cycle (five right data sets), representing expression characteristic of “pure” populations of cells in each cell cycle phase. A system of linear equations is established, with one equation per gene, and solved for the optimal proportions of cells that best model the expression profile of the cell population.

Specifically, a set of equations is established (one per gene), as illustrated in Fig. 1, in which the expression level of gene i (e_i,population) in the asynchronous cell population equals the fraction of cells in G₁ phase (f_G1) times the expression level of gene i in the G₁ cells (e_i,G1), plus the fraction of cells in S phase (f_S) times the expression level of gene i in the S phase cells (e_i,S), and so on. The cell fractions (f_G1, f_S, etc.) sum to one. From the ≈6,200 genes in yeast, 696 genes exhibit cell cycle-dependent changes in mRNA expression levels (5, 6). Equations are constructed for these 696 genes. Because the genes' typical expression levels are known for each of the phases of the cell cycle (5, 6), this is a straightforward set of equations to solve by standard methods, with 696 equations but only 5 unknowns (the cell fractions). We apply a simulated annealing-based (8) algorithm to identify the proportions of cells optimally satisfying the equations. In this process, the proportions of distinct cell populations are varied randomly to either maximize the Pearson correlation coefficient or minimize the least squares criterion between the expression vector from the mixed cell population and the expression vector represented by the weighted sum of the synchronized cells. The algorithm is implemented in Java 2, and the resulting program DECONVOLUTE is available at http://bioinformatics.icmb.utexas.edu/deconvolute.

Selection of Basis Experiments and Microarray Data. The choice of cell phase-specific expression patterns (termed basis experiments) is clearly important. However, because of the apparently overdetermined nature of the equations, we expect a considerable tolerance for noise in the data. To analyze the yeast cell cycle, basis experiments were chosen from the published data of Spellman et al. (5) as the average of three independent expression arrays measured from cells arrested by three independent methods (listed in Table 1, which is published as supporting information on the PNAS web site, www.pnas.org). Time points were chosen according to the peak expression patterns of genes known to be associated with certain cell cycle phases: the G₁ basis experiments were chosen according to peak expression of the cyclin CLN2, S phase by histone HTA2 expression, G₂ phase by cyclin CLB4 expression, M phase by CLB2 expression, and M/G₁ phase by SIC1 expression.

Expression deconvolution was applied to previously published yeast mRNA expression data obtained from the Stanford Microarray Database (http://genome-www5.stanford.edu/MicroArray/SMD) and Rosetta Inpharmatics (Kirkland, WA). These data include mRNA expression levels from yeast grown in a wide variety of conditions, including asynchronous cultures undergoing sporulation (9), growth at various temperatures (10), DNA damage (11), and disruption of single genes (5, 12). A second set of synchronized cell cycle data (6) was available from Affymetrix-type DNA microarrays. For proper comparison with the Stanford-format microarray basis data, these Affymetrix-type data were converted to ratio form by dividing each positive expression measurement by the average fluorescence intensity for that gene across the time series, and taking the logarithm of these ratios (setting the log ratio equal to 1 for ratios equal to 0). All mRNA expression data vectors were normalized to mean 0, variance 1, before deconvolution.

Calculation of Apparent Timing and Severity of Defects. The apparent timing and severity of a cell cycle defect was calculated from the center of mass of the deconvoluted cell population as follows. The five phases of the cell cycle were modeled as ordered, equally spaced events on a circle of radius 1 centered on the origin of the x-y plane. A particular deconvolution result was interpreted geometrically by positioning the appropriate fraction of cells in the population at each event, then calculating the center of mass of the resulting object. The severity of defect was interpreted as the distance r from the origin o to the center of mass c, normalized with respect to the longest vector possible in that direction. In this manner, asynchronous cells correspond to r ≈ 0, and strongly synchronous cells correspond to r ≈ 1. Deletion strains with r > 0.75 were considered to exhibit severe, temporally localized cell cycle defects. The timing of the defect was interpreted as the angle t made between the x axis and the line oc from the origin to the center of mass. Strains could therefore be ordered by the time of their observed arrest, with cells arrested in G₁ occurring at t = 0°, in S phase occurring at t = 72°, in G₂ phase occurring at t = 144°, in M phase occurring at t = 216°, and in M/G₁ phase occurring at t = 288°, and cells arrested in adjacent phases located at appropriately spaced intermediate timings.

Independent Validation of Arrest Phenotypes. Yeast disrupted in single genes (13) were obtained from Invitrogen as heterozygous diploids and sporulated to obtain haploid cells with and without the gene disruption (detected by growth with/without the antibiotic G418 to select for the gene disruption-specific marker). The haploid yeast were grown in yeast extract/peptone/dextrose (YPD) media and harvested in exponential growth phase (OD ≈ 0.5-0.8), then assayed for DNA content by staining with the DNA-specific dye propidium iodide, followed by flow cytometry with a BD Biosciences FACSCalibur instrument under standard protocols.

Results

Validation of Expression Deconvolution Analysis. We evaluated the ability of expression deconvolution to reveal known cell population dynamics for three sets of control samples: (i) synchronized yeast cells growing in a time course, to test that the analysis correctly detected the cell cycle phases; (ii) yeast deletion mutants with known cell cycle delay phenotypes, to test that expression deconvolution could correctly diagnose the defects; and (iii) simulated cell populations of known proportions.

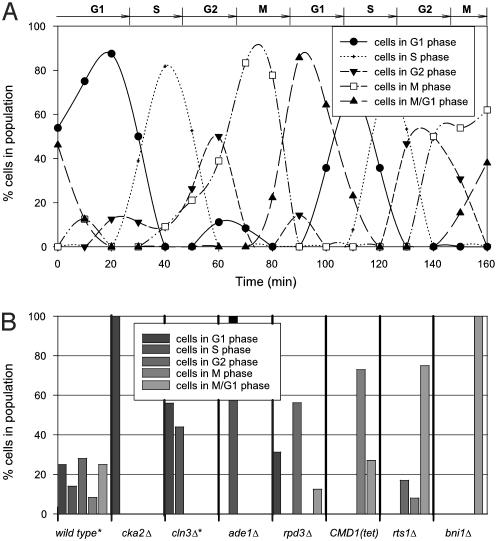
First, we used data from synchronized yeast cells growing in a time course to establish the basis experiments, which represent the expression levels from pure cells in discrete phases of the cell cycle. Synchronous cells growing in G₁, S, G₂, M, and M/G₁ phases were chosen from ref. 5, and form the experiments represented on the right side of the equations in Fig. 1. Then, as a test of the method, an independent cell cycle time course data set was analyzed, collected by different researchers (6) by means of a different DNA microarray technology (Affymetrix arrays). Expression data from each time step was analyzed by expression deconvolution. The percentages of cells estimated to be in each phase of the cell cycle are plotted in Fig. 2A. As expected for synchronized cells, the cell percentages cycle over time. For comparison, the phases determined by microscopy by the original researchers are drawn across the top of Fig. 2 A, and are in agreement with the deconvolution results.

Fig. 2.

Validating expression deconvolution on cells with known population dynamics. (A) Results of deconvoluting mRNA expression of a synchronized cell population. The proportion of cells in each cell cycle phase, measured by expression deconvolution of microarray data (6) and plotted as a function of time, match well with the phases observed by microscopy and FACS analysis (6) marked at the top of the figure. Points are fit with spline curves for ease of interpretation. (B) Application of expression deconvolution to asynchronously grown yeast deletion mutants known to produce full or partial cell cycle arrest phenotypes. Each bar graph shows percentages of cells in different cell cycle phases as estimated by expression deconvolution. Wild-type cells show roughly equal proportions of cells in different phases, but mutant strains show skewed cell populations, suggesting cell cycle delay phenotypes. The mRNA expression data in B are from ref. 12, except those marked with asterisks, which are from ref. 5.

As a second control, public DNA microarray data (5, 12) collected from deletion mutants of yeast genes with known cell cycle defects were analyzed. Unlike the experiment of Fig. 2 A, these cells are grown asynchronously but exhibit specific cell cycle delay defects that are expected to skew the population of cells away from the expected asynchronous distribution. The mRNA expression measurements from each strain were deconvoluted, and the results are plotted in Fig. 2B. Wild-type cells show roughly equal proportions of cells in each phase of the cell cycle, as expected for asynchronously grown cells. However, the cell cycle delay mutants show strongly skewed cell populations as function of the nature of the delay. The agreement with known delay phenotypes indicates that expression deconvolution can accurately measure cell populations, and therefore pinpoint cell cycle defects.

Specifically, cka2Δ cells, previously known to delay with at least 50% unbudded G₁ cells (14), here show a G₁ arrest phenotype when analyzed by expression deconvolution. In contrast, CLN3 is known to be rate limiting for the G₁ to S phase transition (15), and cln3Δ cells are known to have a higher proportion than wild-type cells of unbudded and G₁ phase cells (16). Deconvolution reveals that cln3Δ cells show roughly equal proportions of G₁ and S phase cells, but no other phases. For each of the other strains, the observed deconvolution results match the defects observed by other techniques (17-21), such as the known post-S phase delay of cells overexpressing calmodulin [CMD1 (Tet)], which are defective in nuclear division (22), exhibiting a higher proportion of M and M/G₁ cells in our analysis.

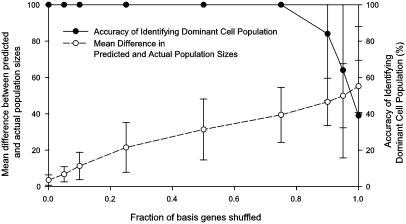
Finally, we attempted to simulate mixed cell populations by randomly combining the basis experiments in different proportions with >50% of the cells drawn from one population. Expression deconvolution was applied to 100 such synthetic cell populations, correctly identifying the dominant cell population in all 100 trials (Fig. 3). As noise was introduced by shuffling increasing fractions of the basis experiments used for deconvolution, the accuracy of identifying the dominant cell population was maintained, but the numerical measurement of the size of the dominant population increased in error, suggesting that when competing transcriptional programs exist, numerical accuracy will depend on the relevance of the basis experiments.

Fig. 3.

Comparing the quantitative and qualitative performance of the algorithm on synthetic data. One hundred cell populations were randomly generated by mixing basis experiments such that >50% of the population derives from one basis experiment. During expression deconvolution, noise was added to the basis experiments used for deconvolution by shuffling, for a given gene, the expression measurements across the basis experiments, simulating the presence of competing transcriptional programs besides the cell cycle. As the fraction of shuffled basis genes increases up to ≈85%, deconvolution correctly identifies the dominant cell population (filled circles), although the error in the numerical estimate of the population's size increases steadily (open circles). Error bar indicates ±1 SD from the mean of the 100 trials.

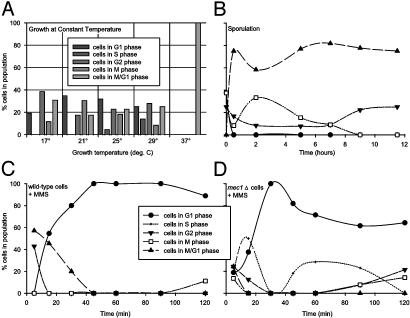
Yeast Population Dynamics Vary with Environmental Stresses. Using expression deconvolution, we measured the population dynamics of yeast cells grown in varying conditions, including steady-state growth at high temperature (10), sporulation (9), and DNA damage (11). First, the mRNA expression profiles of yeast grown under constant temperature conditions (10) were deconvoluted. Cells grown between 17°C and 29°C were asynchronous, implying no apparent cell cycle defect (Fig. 4A). However, cells grown at a constant 37°C displayed cell cycle delay in M/G₁ phase, occurring earlier in the cell cycle than the short-lived G₁ arrest seen in transiently heat-shocked yeast (23).

Fig. 4.

Application of expression deconvolution to yeast grown under varying conditions reveals complex cell population dynamics. Each graph plots the reconstructed distribution of cells in different cell cycle phases. (A) Yeast grown (10) at 17-29°C appear asynchronous, whereas those grown at 37°C delay strongly in M/G₁ phase. (B) Yeast induced to sporulate (9) quickly synchronize with a cell state whose global mRNA expression pattern resembles M/G₁ phase cells. (C and D) Cells challenged with the DNA damaging agent MMS (11) quickly arrest in G₁ phase. Wild-type cells (C) remain arrested, even after 2 h, whereas mec1Δ checkpoint mutant cells (D) progress through the arrest within 40 min. In B-D, points are fit with spline curves for ease of interpretation. All curves follow the legend displayed in C.

Second, expression profiles of sporulating yeast (9) were deconvoluted. The results, plotted as a function of time in Fig. 4B, indicate that the yeast are initially asynchronous, but rapidly exhibit a cell cycle delay phenotype in the first hour of growth under conditions inducing sporulation (growth on potassium acetate and raffinose). Although the cells are undergoing meiosis, the mRNA expression profile of the delayed cells most strongly resembles M/G₁ phase cells, because no meiotic cell expression patterns are included in the basis experiments.

Finally, we deconvoluted the mRNA expression profiles of cells grown in the presence of the DNA alkylating agent methyl methanesulfonate (MMS) (11). DNA damage is known to induce cell cycle arrest in cells, slowing progression through S phase, in a manner dependent on a “checkpoint” pathway (24-26). However, checkpoint mutants (27) can bypass this DNA damage-induced arrest. In Fig. 4C, the deconvolution results are plotted for wild-type cells growing in a time course after treatment with MMS. The cells are initially asynchronous on MMS addition, but rapidly arrest in G₁ phase. The population dynamics of checkpoint mutant cells (mec1Δ) initially resemble wild-type cells (Fig. 4D): At first asynchronous, the cells arrest in G₁ phase within 30 min; however, unlike the wild-type cells, the mec1Δ cells quickly bypass the arrest (cells progressing into S phase are seen within 40 min after DNA damage).

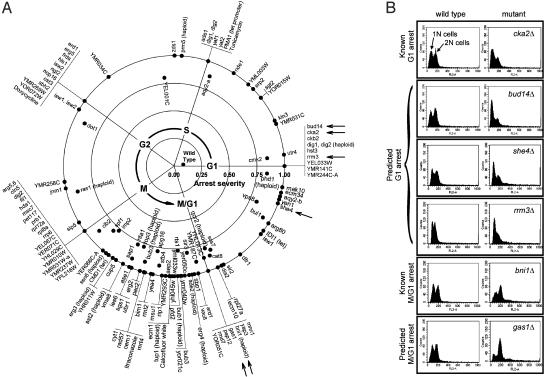
Large-Scale Identification of Cell Cycle Mutants by Using Expression Deconvolution. As expression deconvolution can in principle reveal the precise nature of cell cycle defects in mutant cells, we applied the method to a set of publicly available mRNA expression profiles of 287 yeast deletion mutants and 13 drug-treated cells (12). Of the 300 strains, ≈146 exhibit a strong bias toward a particular cell cycle phase, suggesting that the gene deletions cause, either directly or indirectly, a rate-limiting defect in the cell cycle. The apparent timing and severity of each cell cycle defect was calculated from the center of mass of the deconvoluted cell population distribution. Mutants with >75% of the detectable mRNA expression signal derived from a single cell cycle phase are arranged in Fig. 5A in the observed temporal order of their defects. Defects were identified in all phases of the cell cycle, although ≈60% occur in the M and M/G₁ cycles. Approximately 20% of the genes exhibiting strong cell cycle defects have no known function.

Fig. 5.

(A) One hundred forty-six yeast genes whose deletion confers severe cell cycle delays are plotted, ordered by time of observed cell cycle defect. The timing of each defect, calculated as the center of mass of the deconvoluted cell population, is indicated by the angular position around the circle, with G₁ phase defects at the x axis and with time increasing in a counterclockwise manner. Radial distance from the plot origin indicates defect severity. Asynchronous wild-type cells are therefore plotted near the origin, whereas strong G₁ arrest mutants are at the right-hand boundary. The complete table of deconvolution phenotypes for all 300 strains (12), sorted by defect severity or timing, is available as Table 2, which is published as supporting information on the PNAS web site. Arrows indicate mutants whose defects are independently validated in B. Each horizontal panel in B shows the measured DNA content of two Mat a haploid yeast strains, derived from a single tetrad of a heterozygous diploid yeast strain deleted in the gene labeled at right. Asynchronously grown wild-type cells (Left) show roughly equal proportions of 1N and 2N DNA content, measured by using FACS analysis, whereas deletion mutant strains (Right) show skewed distributions characteristic of the predicted G₁ (top four panels) or M/G₁ (bottom two panels) delay phenotypes.

Of the strongly delayed strains defective in characterized genes, a number of the phenotypes can be rationalized. Disruption of the histone deacetylase HDA1 produces an M phase delay, consistent with its role in maintaining chromatin structure (28-30). Yeast lacking the β-glucan metabolic gene GAS1, known to be slow growing and to harbor cell wall defects (31), delay in M/G₁. Deletion of ZDS1, implicated in establishing cell polarity (32), delays cells in S phase near the approximate time of bud emergence. Deletions of five genes (JNM1, ASE1, BUB3, BIM1, and BNI1) required for proper partitioning of the mitotic spindle during anaphase (33-37) all delay at approximately M phase. Disruptions of SSN6 and TUP1 are known to produce flocculent cells (38), disturbing cell surface properties. Because flocculent cells may imply defects in bud maturation or cell separation, such a phenotype would be consistent with their observed M and M/G₁ defects. Deletions of the ergosterol biosynthesis genes ERG2, ERG3, ERG4, and ERG5 show cell cycle defects, as does treatment with the compound itraconazole or overexpression of IDI1. All disrupt biosynthesis of ergosterol (39-42), an essential component of the plasma membrane, secretory vesicles, and mitochondrial respiration. The deletions presumably affect such cell membrane-related processes, although the defects are distributed across the cell cycle.

A number of known cell cycle delay mutants are recovered, including deletions for the cell cycle kinases CKA2 and CKB2 (producing G₁ phase arrest) (43), the adenine biosynthesis gene ADE1 (defective in S phase, presumably by limiting purines available for DNA synthesis), the cyclin-dependent kinase CLB2, which regulates the G₂/M transition (44) (here, producing M phase delay), and calmodulin (CDM1), which, under a tetracycline-induced promoter, delays in M phase, consistent with its action in nuclear division (45, 46). Lastly, the compound calcofluor white, known to bind preferentially to large-budded cells (47), here produces an M/G₁ phase delay, consistent with disruption of cell wall metabolism.

Several other cellular functions are well represented among the delay mutants, including chromatin silencing and remodeling (ISW1, ISW2, HST3, HDA1, CIN5, DOT1, SIR2, and SIR3), cell wall synthesis (ECM1, ECM10, ECM34, YEA4, and calcofluor white treatment), and ribosome biogenesis, recycling, and rRNA maturation (NOP16, NGL2, FIL1, RRP6, MRT4, RML2, RPL12A, RPL18A, and RPL27A).

Independent Validation of Cell Cycle Mutant Defects. To further support the expression deconvolution results, we independently validated several of the observed cell cycle defects by using established experimental protocols. We tested six yeast mutants, indicated by arrows in Fig. 5A, including four mutants whose deconvolution phenotypes indicated G₁ delay and two mutants exhibiting M/G₁ delay. Two of the strains act as controls [cka2Δ (14) and bni1Δ (21)], in which the cell cycle delay phenotypes were known, and four represent previously undescribed cell cycle delay mutants.

Cell cycle defects were assayed by measuring the DNA content of the six haploid knockout strains by using the DNA-specific dye propidium iodide and f luorescence-activated cell sorting (FACS) to determine the numbers of cells with one (1N) and two (2N) copies of the chromosomes. Each diptych in Fig. 5B represents FACS data from asynchronously grown cells derived from two of the four spores in a single tetrad from a heterozygous diploid yeast deletion mutant.

The FACS analysis confirms that the mutants show defects in DNA content consistent with the deconvolution phenotypes. The bud14Δ, she4Δ, and rrm3Δ strains show excess 1N cells (relative to the wild-type cells derived from the same tetrads), similar to the defect seen in the known G₁ arrest mutant cka2Δ (14). Likewise, the gas1Δ mutant shows an excess of 2N cells, consistent with a post-S phase defect, just as does the M/G₁ defective bni1Δ strain (21).

Discussion

Expression deconvolution provides a theoretical framework for interpreting mRNA expression data that is consistent with known dynamics of cell populations and that sensitively identifies cell growth abnormalities: expression data, which typically represents an average across a cell population, is fit as the linear combination of mRNA expression levels typical of cells in each phase of the cell cycle. The result is the proportion of cells in each phase of the cell cycle

For synchronized cells or those with cell cycle defects, the proportions will be skewed in a manner that characterizes the defect. The analysis therefore provides a genetic screen for cells that are viable but progress abnormally through the cell cycle. Here, expression deconvolution is not detecting hard cell cycle arrests, but is acting as a probe of slowed steps during the cell cycle. By analogy with the recent use of DNA microarrays to distinguish cancer subtypes that were previously indistinguishable (48, 49), we expect this approach to be capable of distinguishing subtle differences in the internal states of cells, because of the reliance on thousands of measurements of gene expression.

Deconvolution accuracy probably depends on the basis profiles' independence from competing transcriptional programs (Fig. 3). In the validation presented here, expression deconvolution correctly modeled synchronized cell phases (Fig. 2 A) and qualitative defects in seven cell cycle mutants (Fig. 2B); six predicted strong cell cycle defects were also independently validated (Fig. 5B). However, the mutants tested in Fig. 5B were not 100% arrested, as predicted, but merely strongly delayed (≈50-80% according to flow cytometry). The algorithm therefore overestimated the precise severity of the defects. We suspect that it may ultimately be desirable to experimentally characterize a set of cell populations to accurately measure the algorithm's numerical error rate.

Some of the observed timings of cell cycle defects plotted in Fig. 5 may correspond not to the times of action of the deleted genes, but to the timings of downstream cellular processes that become rate-limiting in the deletion strains. Genes whose deletion causes cell cycle delay may therefore act earlier in the cell cycle than when the defects are observed. Thus, whereas some mutants delay at logical times (e.g., yeast deleted for the nucleotide biosynthesis gene ADE1 arrest in S phase, and treatment with the cell wall binding dye calcofluor white arrests yeast during cell division in M/G₁ phase), others induce delay at times far from their apparent action (e.g., ade2Δ delaying in M/G₁ phase). The differences in response between ade1Δ and ade2Δ cells may indicate a subtle divergence in the genes' functions, reflected in part by the poor correlation (correlation coefficient = 0.5) in their transcriptional levels across 300 DNA microarray experiments (12). We speculate that genes whose deletions cause delay at precisely the same time in the cell cycle may often induce the same downstream cellular system, and therefore may be functionally linked, perhaps operating in the same upstream pathway.

In the limit of having mRNA expression data for the complete set of viable yeast deletion mutants, we might expect >2,000 deletion strains to exhibit growth defects, by roughly scaling the percentage of cells observed here with delay phenotypes (≈50%). An interesting possibility that arises from this work is that of temporally ordering these ≈2,000 genes by the times at which they induce defects; this would effectively define the set of rate-limiting steps for cell growth and the order in which they occur.

The choice of basis experiments is clearly important. Because a cell population is only interpreted in light of the basis experiments included, it is possible that a strong trend in the data may go undetected. For example, we have not included G₀ stationary phase cell expression patterns in the basis experiments, although it is possible that G₀ phase cells exist in the population. Likewise, we have not included meiotic cells, although the method was applied to sporulating yeast. In this case, the analysis revealed the cell synchronization induced during sporulation, although it is unlikely the cells were actually arrested in M/G₁ phase (Fig. 4B); instead, M/G₁ was the best fit of the existing basis experiments for the meiotic cell expression patterns. Basis experiments might be identified that can distinguish between the meiotic response and the mitotic transcriptional responses, by collecting a time series of DNA microarray data from meiotic cells, followed by choosing an appropriate subset of genes to be fit in the basis experiments. We suspect that choosing the subset of basis experiment genes most strongly associated with the transcriptional program of interest might improve the quantitative accuracy of this approach in the presence of competing transcriptional programs, such as is modeled in Fig. 3.

In this manner, the same expression data could potentially be analyzed for multiple independent trends. For example, one might imagine that diseased cells and healthy cells proceed differently through the cell cycle. A cell population could then be deconvoluted for healthy/diseased cells and for cell cycle phase-specific profiles. We see an important area of future research as defining gene expression signatures that could act as independent basis experiments for a wide variety of cellular states. Ideally, one would then want to experimentally characterize a diverse set of cell samples to test the extent of measurement error under different conditions.

Alternate basis experiments might include healthy/diseased cells, disease subtypes, stress responses, tissue-specific cell types, organisms in an ecological niche, individual mutants, or cells from differing developmental stages. Applications might include toxicology (e.g., fitting with basis experiments derived from drug-treated cells), diagnostics (e.g., deconvoluting tissue sample expression patterns into contributions from different cell types or mixtures of healthy/diseased cells), or infectious processes (e.g., studying the progression of one or more infectious agents through a cell population via the cells' expression patterns). Expression deconvolution may be useful for early diagnosis, where most of the expression profile is derived from healthy cells but a small number of the cells are diseased. The analysis should be applicable to any complex data measured on a cell population, such as proteomics data.