Spatio-temporal analysis of eukaryotic cell motility by improved force cytometry

Abstract

Cell motility plays an essential role in many biological systems, but precise quantitative knowledge of the biophysical processes involved in cell migration is limited. Better measurements are needed to ultimately build models with predictive capabilities. We present an improved force cytometry method and apply it to the analysis of the dynamics of the chemotactic migration of the amoeboid form of Dictyostelium discoideum. Our explicit calculation of the force field takes into account the finite thickness of the elastic substrate and improves the accuracy and resolution compared with previous methods. This approach enables us to quantitatively study the differences in the mechanics of the migration of wild-type (WT) and mutant cell lines. The time evolution of the strain energy exerted by the migrating cells on their substrate is quasi-periodic and can be used as a simple indicator of the stages of the cell motility cycle. We have found that the mean velocity of migration v and the period of the strain energy T cycle are related through a hyperbolic law v = L/T, where L is a constant step length that remains unchanged in mutants with adhesion or contraction defects. Furthermore, when cells adhere to the substrate, they exert opposing pole forces that are orders of magnitude higher than required to overcome the resistance from their environment.

Motility of eukaryotic cells is essential for many biological processes such as embryonic development or tissue renewal, as well as for the function of the immune system (1–4). If misregulated, motility plays an important part in diverse diseases such as cancer, osteoporosis, and mental retardation (3, 4). Many of the deleterious effects result from subtle misregulation of motility and not from its outright absence. The quantitative characterization of these deficiencies may help to improve treatment of such conditions through precise targeting of the cellular motility. Furthermore, understanding and controlling cell migration is important for tissue engineering (3).

Cell migration over surfaces is an integrated physico-chemical process involving the cytoskeleton and its mechanical interaction with the substrate through adhesion regions (4). The amoeba Dictyostelium is a valuable model system for the investigation of cell motility with extensive similarities to higher eukaryotes, in particular to leukocytes (5). Despite the complexity of the various chemical, biological, and mechanical processes involved in eukaryotic cell motility, it has been suggested that cells perform a limited repertoire of motions during their migration: protrusion of the leading edge, formation of new adhesions near the front, cell contraction, and release of the rear adhesions (1). The exact nature and sequence of events making possible this motility cycle are not fully understood yet.

Some of the principal biochemical processes driving the stages of the motility cycle are becoming better known (4). In the front of the cell, localized F-actin polymerization leads to membrane protrusion whereas, in the rear, myosin II (MyoII) motors pull on actin filaments to produce cell contraction (1–3). In Dictyostelium cells, MyoII is not essential for motility, but cells lacking this protein (myoII⁻ cells) move significantly slower than WT cells (6). It has been suggested that MyoII contractility facilitates rear retraction. Supporting this idea are the inability of myoII⁻ cells to move on highly adhesive substrates (7), and their failure to move in the constrained space under a layer of agarose or in a 3D aggregate of cells (8, 9).

Despite significant progress in the understanding of the biochemistry of the cytoskeleton, the analysis of the spatiotemporal events that enable cell movement is in its infancy. So far, the inherent polarity of the cytoskeleton of a motile cell has been studied extensively. This polarity comprises the distribution of structural proteins as well as concentration gradients of activated intermediary signaling molecules such as PI3K, Ras, Rho, or Rac (5), which control various cytoskeletal elements. One less clear aspect is how the initial cellular polarity is generated from weak external or internal cues, and subsequently maintained and coordinated on the cellular level. Similarly, we lack reliable information about the changes in the physical properties of the cell that result from this coordinated regulation. Further understanding requires accurate measurements of these properties as the cell moves and interacts with the substrate under controlled conditions. This requirement is especially challenging in the case of Dictyostelium cells because their relatively small size and fast migration speeds demand high temporal and spatial resolutions. For this reason, the first efforts to quantify the dynamics of the migration of these cells have just started to appear (10–12).

Several methods have been developed to characterize the dynamics of cells as they adhere to the substrate and undergo migration. Most of these methods are based on measurements of the deformation of a flat elastic substrate on which the cells are crawling. To calculate the traction forces from the deformations, Dembo et al. (13, 14) used the classical solution of the elastostatic equation for a homogeneous, semiinfinite medium found by Boussinesq (15). This solution expresses the deformations as functions of the traction forces and has to be inverted. The associated computational problem is numerically stiff and expensive. However, Butler et al. (16) noticed that the inversion of the Boussinesq solution is trivial in Fourier space. As a further improvement, we present herein an exact, computationally efficient solution of the elastostatic equation based on Fourier expansions that expresses the tractions explicitly as functions of the deformations. We take into account the finite thickness of the substrate, which increases the accuracy of the Boussinesq solution and allows for non-zero net forces. We further refine the solution by considering the effect of the distance between the measurement plane and the surface of the substrate.

We use this improved method to study the dynamics of WT and mutant Dictyostelium cells moving up a chemoattractant gradient. We find that these cells produce much larger contractile forces than needed to overcome the resistance from their environment. We also show that the time evolution of the strain energy exerted by the cells on the substrate is quasi-periodic and can be used to identify the stages of the motility cycle. Finally, we demonstrate a remarkably strong correlation between the mean velocity of the cells and the period of the strain energy cycle, which persists for mutants with adhesion and contraction defects.

Results

Stresses on a Finite-Thickness Substrate.

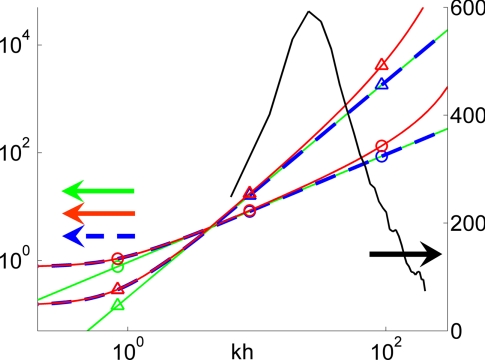
We have examined the behavior of Dictyostelium cells moving up a chemoattractant gradient on the surface of an elastic gelatin matrix containing fluorescent latex beads. As cells move, they deform the substrate, producing time-dependent displacements of the beads. We developed a traction cytometry method to examine this cell movement and to calculate the forces generated by the cells during their movement cycle [see supporting information (SI) Appendix A]. Our traction cytometry method relies on an exact, analytic solution of the elastostatic equation that considers domains of finite thickness as well as non-zero distances between the beads and the free surface of the substrate. These two effects are neglected in the Boussinesq solution that was used in previous works (13, 14, 16–19). Fig. 1 shows the errors associated with the approximations in the Boussinesq solution. The color curves represent the first and second invariants of the matrix that converts the Fourier coefficients of the measured displacements into those of the tangential stresses on the substrate surface [see Eq. SI3 in SI Appendix A]. The data have been plotted as a function of the modulus of the wave number vector $k=\sqrt{{\alpha }^2}+{\beta }^2$ for the representative case when α = β.

Fig. 1.

Spectral analysis of our solution and Boussinesq's solution of the elastostatic equation. The color curves follow the left vertical axis and represent the first (circles) and second (triangles) invariants of the matrix that converts the Fourier coefficients of the measured displacements into those of the tangential stresses on the substrate surface. Green, Boussinesq solution; blue, our solution with h = h₀; red, our solution with h = 1.003h₀. The black curve follows the right vertical axis and shows the spectral energy density of the displacements field in Fig. 2 Top.

Our exact solution differs substantially from Boussinesq's for kh ≤ 4. In this spectral range, the stresses generated by a unit displacement on the surface of the substrate decay slowly with the distance from it and “feel” the bottom of the domain. This effect is especially prominent at k = 0, where our solution yields a positive first invariant that is consistent with a non-zero net force (see Eq. SI4 in SI Appendix A. The semiinfinite thickness approximation was justified previously by the small displacements of the beads relative to h (14, 17, 19). However, this assumption is not correct because the relevant lengthscale to be compared with h is the horizontal lengthscale of the deformation field. There are multiple plausible candidates for this lengthscale, i.e., the typical size of the cell-to-substrate adhesions, the characteristic distance between these adhesions, the size of the cell, the distance between nearby cells, or the horizontal dimensions of the domain in which the deformations are measured. Several of these lengthscales were proposed before (16) but in absence of experimental evidence, it was not possible to identify the proper one. Fig. 1 shows that the appropriate lengthscale to compare with h is the length of the cell. The black curve is the spectral energy density of the displacements measured for an example cell, shown in Fig. 2Top. The spectrum spans the wavenumber range 10 ≤ kh ≤ 100 and peaks at kh ≈ 30, which is equivalent to a length of 26 μm for the corresponding gel thickness, h = 125 μm. This characteristic length is approximately twice the length of the cell in Fig. 2 Top, and the same correlation is observed for all other cells investigated. Therefore, in order for the infinite-thickness approximation to be valid, the cell length must be much smaller than the thickness of the substrate, which was not always the case in earlier studies (13, 14, 16, 17).

Fig. 2.

Analysis of the movement behavior of a Dictyostelium cell migrating up a gradient of the chemoattractant cAMP emitted from a micropipette (see SI Appendix A). The arrows indicate the intensity and direction of the vector data. The color contours indicate their intensity according to the color bars. The black arrow indicates the direction of motion of the cell. (Top) Instantaneous displacements in micrometers. (Middle and Bottom) Instantaneous stresses in pascals; the diagrams on the right show the cell's principal axes and the front (F_f) and back (F_b) pole forces. (Middle) h − h₀ = 0.4 μm; F_f = 156 pN, F_b = 162 pN. (Bottom), h = h₀; F_f = 143 pN, F_b = 149 pN.

The Boussinesq solution also underestimates the stresses at high wavenumbers because it neglects the non-zero distances between the beads and the free surface of the substrate. This approximation introduces a low-pass filter that has the form exp[−k(h − h₀)] for kh ≫ 1 (see SI Appendix B) and significantly damps all features shorter or narrower than 2π/log 2 ≈ 10 times h − h₀. The exponential filter is important at high wavenumbers even when the gap between the beads and the substrate surface is small, as shown in Fig. 1.

The experimental displacement spectrum in Fig. 1 is high in the wavenumber interval where the corrections to the Boussinesq solution because of the gap between the imaged plane of beads and the substrate surface are considerable. This fact is confirmed by Fig. 2 Middle and Bottom, which depicts examples of instantaneous tangential stresses on the surface of the substrate, τ_xz(x,y,h) and τ_yz(x,y,h), computed from the displacements in Fig. 2 Top for positive and zero values of h − h₀. Fig. 2 Middle displays the results obtained by using the finite-thickness solution for h − h₀ = 0.4 μm, showing three localized areas of traction in the front, middle, and back of the cell. The magnitude of the stresses in these areas is ≈50 Pa and decays rapidly with distance. Fig. 2 Bottom shows the same results when using the condition h − h₀ = 0. Although the patterns in the stress field are similar to those in Fig. 2 Middle, their intensity is reduced by >50%. In our experiments, h − h₀ was estimated to be between 0 and 0.4 μm (see SI Appendix A), so the true tangential stresses applied by the cell are in between the values shown in Fig. 2 Middle and Bottom.

Pole Forces.

Fig. 2 Middle Right and Bottom Right shows the overall forces transmitted at the attachment regions in the front and back halves of the cell, which we call pole forces (see Eq. SI5 in SI Appendix A). Because the external and inertial forces acting on the cells are much smaller than the traction forces measured in our experiments, the front and back pole forces always have approximately the same magnitude. They are generally oriented along the direction of polarization and always display a converging or contractile pattern. Therefore, they can be used to quantify the level of cytoskeletal tension of the cell along the direction of polarization. Fig. 2 Middle and Bottom demonstrate that the pole forces are also underestimated when the gap h − h₀ is not considered in the calculations.

Quantitative Evidence for a Regulated Motility Cycle.

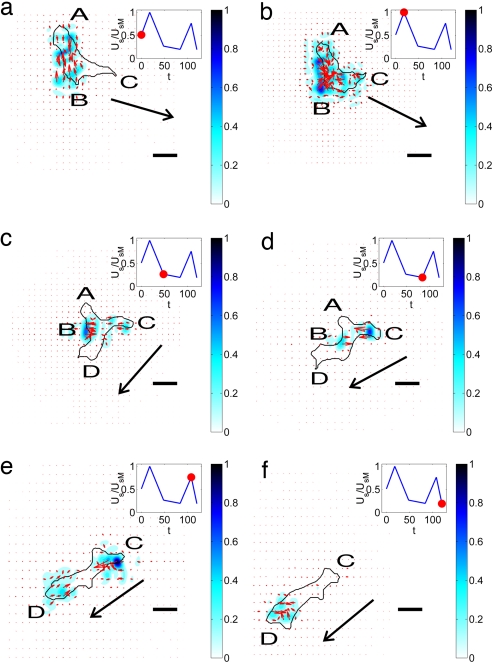
Fig. 3 shows a characteristic time series of images exemplifying the distinct stages that constitute one representative motility cycle of WT Dictyostelium cells. The strain energy imparted by the cell on the substrate (denoted U_s, see Eq. SI6 in SI Appendix A) is also shown on each panel. Note that U_s is approximately periodic, showing successive peaks and valleys. SI Movies 1 and 2 depict longer time-sequences with higher resolution (also see Fig. 5). Although quasi-periodic behaviors in the velocity and shape of migrating Dictyostelium cells have been reported (11, 20), our findings provide strong evidence that the level of force transmitted by the cell to the substrate reflects the regulation of the cell motility cycle.

Fig. 3.

Sequence of images of a moving WT Dictyostelium cell. The black contour is the outline of the cell. The color contours map the magnitude of the stresses produced by the cell relative to their maximum value. The red arrows indicate the magnitude and direction of these stresses. The plot at the upper right corner of each panel indicates the strain energy of the substrate for the selected images. The red circle in that plot indicates the instant of time that corresponds to each panel: (a) t = 0 s; (b) t = 18 s; (c) t = 48 s; (d) t = 84 s; (e) t = 100 s; (f) t = 112 s. (Scale bars: 10 μm.) The arrow indicates the direction of motion of the cell.

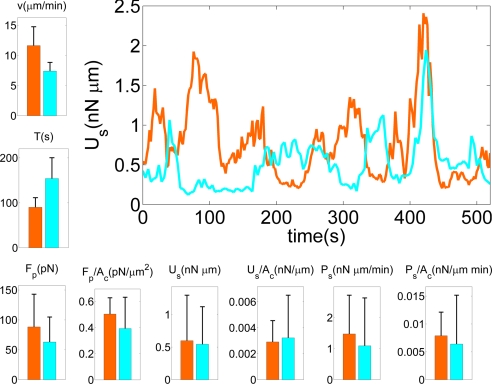
Fig. 5.

The bar plots compare motility statistics for WT (n = 10) and myoII⁻ (n = 6) cells. The black vertical lines indicate the standard deviation. From top to bottom and from left to right: average velocity of the cell centroid (v); average period of the strain energy (T) (single periods are computed from the time autocorrelation function of the strain energy); average magnitude of the pole forces obtained from the integration of the stresses in the front and the back of the cells (F_p); average magnitude of the pole forces normalized with cell area (F_p/A_c); average strain energy (U_s); average strain energy normalized with cell area (U_s/A_c); average elastic power estimated from the average strain energy and its average peak to peak period (P_s); average elastic power normalized with cell area (P_s/A_c). The curve plot on the right of the figure shows examples of the time evolution of the strain energy for a WT (orange) and a myoII⁻ (cyan) cell.

In Fig. 3a, the cell is transmitting its internal tension to the substrate through two discrete attachment regions at A and B, whereas it protrudes a pseudopod at C without producing discernable stresses underneath. The convergence of stresses from two principal areas is a prevalent pattern (Figs. 2 and 3), indicating that the cell is prestretched, consistent with the basic motility model of Lauffenburger and Horwitz (1). The pseudopod at C then attaches to the substrate ≈20 s later (Fig. 3b), leading to an increase of the stresses and U_s. The increase in U_s seems to trigger the detachment of the back of the cell at A (Fig. 3c), which starts a gliding retraction with a subsequent decrease in strain energy. At the same time, a new pseudopod forms at D and glides forward over the substrate. During this phase, which lasts ≈30 s, the attachment at B weakens, and U_s decreases further (Fig. 3d). When the cell finally detaches from B (Fig. 3e), the pseudopod at D attaches to the substrate and U_s rises steeply. After this event, the cell detaches from C and starts a gliding retraction (Fig. 3f) that leads to a sudden decrease in U_s, similar to the transition between Fig. 3 b and c. This quasi-periodic sequence of cell attachment/detachment and force generation is observed in all moving, WT cells and correlates well with the time evolution of the strain energy. Consistent with this result, Uchida et al. (11) observed correlation between the cyclic variation of the cell area and the displacement patterns of beads embedded in the substrate. These authors proposed a motility cycle consisting of two phases in which the cell contracts and extends the substrate alternatively. However, in our experiments, we never observed any expanding stress pattern, just contractile ones. This discrepancy may be due to permanent deformations of their substrates.

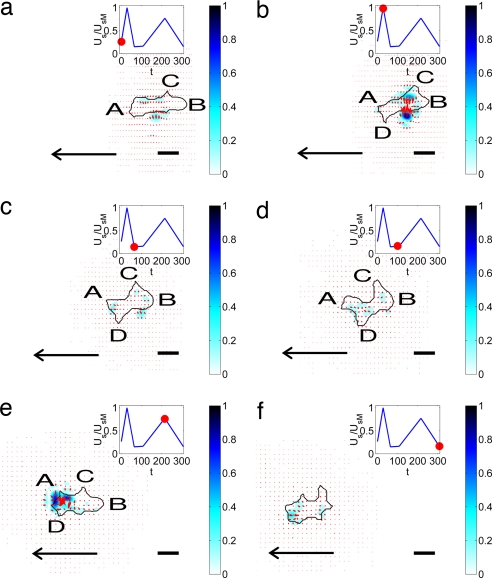
Fig. 4 shows a sequence of images representing the motility cycle of myoII⁻ cells together with the evolution of U_s (see SI Movies 3 and 4). A first comparison of Figs. 3 and 4 suggests that the stages of the cycle are less distinct in myoII⁻ cells than in WT cells. This feature is observed in all of our experiments. In Fig. 4a, the cell is attached weakly to the substrate along its periphery between the front (A) and back (B), and begins to extend a pseudopod at C. The strength of the existing adhesions increases during the following ≈30 s (Fig. 4b), whereas pseudopod C extends and B retracts. Consequently, U_s increases. At the same time, the cell grabs weakly to the substrate near A and protrudes a new pseudopod (D) at its front. Pseudopodia A–D continue gliding while the attachment regions weaken and U_s decays (Fig. 4c). After the strain energy has reached a local minimum, pseudopodia A, C, and D continue extending for ≈40 s in what seems to be a competition to become the dominant protrusion. Eventually, pseudopod A prevails, and the cell slowly retracts pseudopodia B, C, and D (Fig. 4e). The strain energy peaks again when A attaches to the substrate. The stress pattern in Fig. 4e indicates that the cell is clamping the substrate locally at A. This type of pattern is observed repeatedly in the front of all of the myoII⁻ cells studied, and differs from the typical stress distribution observed in WT cells, which is more coordinated along the whole cell body. In the latter case, the stresses transmitted to the substrate at each attachment region are generally unidirectional and compensate for the stresses transmitted by a different pseudopod (Fig. 4). Fig. 4f shows the instant when the cell loosens its adhesion to the substrate, and U_s returns to its baseline.

Fig. 4.

Sequence of images of a chemotaxing myoII⁻ Dictyostelium cell, similar to Fig. 3. (a) t = 0 s. (b) t = 28 s. (c) t = 64 s. (d) t = 100 s. (e) t = 216 s. (f) t = 308 s.

Effects of Cytoskeletal Mutations on the Strain Energy, Magnitude of the Pole Forces, and Migration Speed.

The statistical analysis of the motility parameters of single WT and myoII⁻ cells yields interesting results (Fig. 5 and SI Appendix A). Consistent with ref. 6, we find that the average translation velocity v of the mutants is lower than that of WT cells. The speed of single cells shows little or no correlation with either pole force or strain energy (SI Fig. SI1 in SI Appendix A). The average magnitude of the pole forces transmitted at the attachment regions in the front and back of WT cells, is F_p ∼ 90 pN, but cells lacking MyoII are still able to produce F_p ∼ 60 pN. Not surprisingly, the pole forces and strain energy correlate well with cell area (SI Fig. SI2 in SI Appendix A). These results differ from Uchida et al. (11), who reported that myoII⁻ cells exert much stronger forces on the substrate than WT cells.

Figs. 3 and 4 demonstrate that the time evolution of the strain energy is a simple, quantitative indicator of the stages of their motility cycle. The graph in Fig. 5 compares two representative, 9-min-long time histories of U_s for a WT and a myoII⁻ cell. Both curves show a quasi-periodic behavior, but the periods of U_s for the two cells differ. Although U_s rises and decays 8 times for the WT cell, it only does so 5 times for the mutant cell. MyoII⁻ cells have longer strain energy periods on average. It is immediately apparent from the graph that, whereas the strain energy generated by the mutants grows and decays approximately as fast as in the case of the WT cells, the phases of low U_s last longer. This observation has been confirmed statistically (data not shown). Inspection of the underlying time-lapse sequences reveals that during the phase of low U_s, myoII⁻ cells will typically slow down, partially round up, and start to extend and retract several pseudopodia until one of them becomes dominant (Fig. 4 c, d, and f). WT cells, on the other hand, hardly slow down and rarely lose the preexisting dominant pseudopod. This behavior may be due to MyoII-dependent cortical tension along the lateral and posterior sides of WT cells resulting from MyoII acting as a cross-linker for actin near the plasma membrane that inhibits lateral pseudopod projection and helps maintain the elongated cell shape (21).

The average values of U_s for WT and myoII⁻ cells are similar (Fig. 5), although the error bars indicate a high variability from cell to cell within the two strains. Together with the different magnitudes observed for the pole forces, this result suggests that force production in myoII⁻ cells is less coordinated with polarization than in WT cells. Under such conditions local stresses may cancel each other out and thus reduce the pole forces whereas local strain energies always add up in the calculation of U_s (see also Fig. 6).

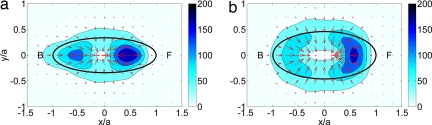
Fig. 6.

Average force field produced by the cells on their substrate, computed in a cell-based reference system rotated to coincide with the instantaneous principal axes of the cells and scaled with the length of their instantaneous major axis, a. The color contours indicate the magnitude of the forces in pN, and the arrows indicate their magnitude and direction. The black ellipses are least squares fits to the average shape of the cells in the cell-based reference system. The front (F) of the cell corresponds to x > 0 and the back (B) corresponds to x < 0. (a) WT cells (n = 10). (b) myoII⁻ (n = 6).

Fig. 5 also compares the average strain power P_s spent by WT and myoII⁻ cells to deform their substrate. For each cell, this power is estimated from the average strain energy, 〈U_s〉, and its period, T, yielding Ps = 4〈U_s〉/T. Consistent with their longer periods, the average strain power exerted by myoII⁻ cells is lower compared with WT cells. In both cell lines, P_s is much higher than the power needed by the cells to translocate, which is given by P_t = Dv, where D is the viscous drag and v is the migration velocity. The drag is estimated by using Stokes law, D = Sμv/d, where μ is the viscosity of water, d is the gap between the cell and the substrate, and S is the area of the horizontal projection of the cell. Assuming a typical value for the gap given by ref. 22, d ≈ 100 nm, the estimated value S ≈ 100 μm², and the average velocity measured in our experiments, we estimate that P_t ≈ 0.003 nN·μm/min, which is <1% of the measured values of P_s for both WT and myoII⁻ cells.

The average force patterns produced by WT and myoII⁻ cells are compared in Fig. 6. Before adding it to the average, the stress field produced by each cell at each instant of time is expressed in a cell-based reference system with its origin at the centroid of the cell and its axes parallel to the directions of its principal moments of inertia. The coordinates are scaled with the instantaneous length of the major axis of the cell, a. This procedure allows us to compile data from different cells at different instants of time into the average. Notice that the coordinates are nondimensional in the cell-based reference system, and, therefore, the stresses have dimensions of force. The average forces generated by WT cells (Fig. 6a) are concentrated in two small regions located on their polarization axis, near the front and the back. These forces form a converging pattern with a clear dominant component along the direction of polarization. MyoII⁻ cells (Fig. 6b) show a different average force pattern with strong forces applied only at the front. This result is consistent with the “clamp-like” pattern observed in the front of the cell in Fig. 4e and supports the idea that MyoII-contraction occurs mainly in the back of the cell. Another interesting difference is that the average forces are more spread out and reach relatively higher values in the periphery of myoII⁻ cells than in WT cells.

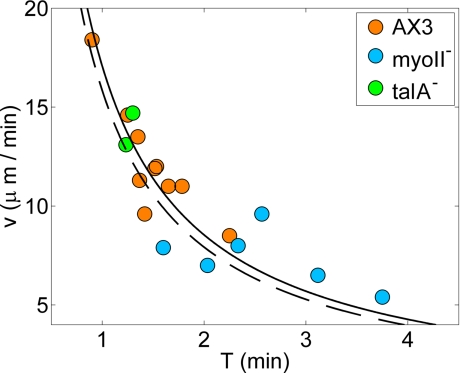
Fig. 7 provides quantitative evidence that the translational velocity v of a cell is determined by the frequency at which it is able to perform the motility cycle described above. Fig. 7 shows a remarkably strong correlation between v and the period T of the strain energy measured over a wide range of translational velocities (5–20 μm/min) and several cell lines. The data fit very well to the hyperbolic law v = L/T, where the constant L has dimensions of length. The values of L obtained for the WT and myoII⁻ cells are very similar, 16 μm and 17 μm, respectively, suggesting that the motility algorithm of the cells from both strains must be similar. These values of L are also approximately equal to the average length of these cells, indicating that the cells move a distance of the order of their length per energy cycle. We have included in Fig. 7 two cells lacking talin A (talA⁻ cells), a conserved protein that mediates cell adhesion (22), showing that their speed is also well described by the same hyperbolic law. The speed of talA⁻ cells is comparable with that of WT cells, even though their average pole forces transmitted to the substrate (≈50 pN) are lower than those transmitted by myoII⁻ cells.

Fig. 7.

Scatter plot of the average velocity of the of WT (orange), myoII⁻ (cyan), and talA⁻ (green) cells plotted versus the peak-to-peak period of the strain energy. The solid and dashed hyperbolas (v = L/T) are least squares fits to the data from WT and myoII⁻ cells. The corresponding values of L are 17 and 16 μm.

Discussion

There have been several attempts to model the underlying physical processes in cell motility by using continuum mechanics approaches (23–25). However, quantitative measurements of the cellular traction forces are still challenging because of the necessary temporal and spatial resolutions. These requirements become especially demanding in the case of Dictyostelium cells because of their relatively small size and high migration speeds. Therefore, only a few studies to quantify the dynamics of the migration of these cells have been performed to date (10–12). In this work, we were able to measure the evolution of the forces and strain energies produced by Dictyostelium cells with high temporal and spatial resolution (Figs. 3 and 4). This approach has enabled us to record the quasi-periodic oscillations of these variables and validate the generally accepted cycle of pseudopod protrusion, adhesion, contraction, and retraction of the back (1).

Our traction cytometry method has allowed us to compute the traction field when the net force exerted by the cell is not zero (see Eq. SI4 in SI Appendix A). In our experiments, the contractile forces produced by Dictyostelium cells were found to be much higher than the viscous drag force they need to overcome to move. Because the cell inertia is negligible, these forces always show a converging pattern and largely cancel each other out at any given time, so that the resultant net thrust force is too small to be measured reliably with our method. There are, however, other conditions in which this net force could be much higher, and the calculation of the net thrust force could greatly benefit from our improved method, i.e., cells under external flow shear (26, 27) or under centrifugal forces (28).

The force patterns generated by myoII⁻ cells are more spread out, less coordinated with the direction of polarization, and closer to the cell periphery than those produced by WT cells (see Fig. 6 and SI Movies 1–4). MyoII⁻ cells exert forces mainly at the front, contrary to WT cells, which generally exert a bi-polar force pattern with two separated foci at the front and back. Despite these differences, the contractile forces exerted by myoII⁻ cells are only ≈30% lower than those exerted by WT cells, and the strain energies produced by cells from both lines are similar. This result suggests that an important contribution to the traction forces is made by actin polymerization (2) with possible contributions from myosin I (29). The importance of MyoII for motility on a flat surface may stem from its function in cytoskeletal organization and cortical integrity (9), rather than from the traction forces produced by its motor activity. A notable fraction of the myoII⁻ cells in our experiments never become organized, remaining round and static. These findings are supported by the observation that the speed of migration of talA⁻ cells is comparable with that of WT cells (Fig. 7), despite the fact that they produce lower traction forces than even myoII⁻ cells, probably because of adhesion defects (22). Consistently, we have observed that the average translation velocity of single cells does not correlate with the average strain energy nor with the average forces they exert, independent of the cell line (see supplementary material). MyoII contraction may only play an essential role in very restrictive environments such as highly adhesive substrates (7) or under high centrifugal forces (28), where higher resistances must be overcome to protrude or retract pseudopodia.

The time analysis of the data reveals that the period of oscillation T of the strain energy and contractile forces correlates remarkably well with the average migration speed v of each cell and follows the hyperbolic law v = L/T, where L is a constant length that does not depend on the cell type. This connection suggests that the frequency and strength of the cellular adhesions plays an important role in the regulation of the cell motility cycle. It also indicates that the basic motility cycle is preserved even in the absence of MyoII, and associates the slower speed of myoII⁻ cells to longer period of the adhesion energy cycle. A more detailed analysis shows that myoII⁻ cells spend longer times attached to the substrate with lower elastic energies than WT cells, whereas the time spent exerting high strain energy is approximately the same in both cases. During the periods of low energy, myoII⁻ cells tend to round up more and exhibit a delay before producing the next dominant pseudopod. These results suggest that attachment and detachment occur at roughly the same rate in both cell lines whereas retraction and protrusion are slower in myoII⁻ cells. Consistently, myoII⁻ cells move on the average slower than WT cells (here measured 7.4 μm/min vs. 12.2 μm/min; see also ref. 6). Variations in the cell contractile forces could alter the energy landscape of the chemical reactions involved in cell attachment and detachment and hence modify their rates, consistent with the Arrhenius–Kramers theory (30), but the observed small differences in these forces do not seem to produce an appreciable effect on those rates. We find impaired retraction of myoII⁻ cells in agreement with the lower forces observed at their back and with previous evidence for the contractile function of MyoII (7). MyoII contraction at the rear is also assumed to contribute indirectly to the front protrusion by facilitating actin depolymerization at the rear (31) and may increase the transport of actin monomers to polymerization sites by driving a convective flow. This protein may also enhance the diffusion of actin monomers, as suggested by evidence that the apparent viscosity of the cytoplasm is lower in WT cells than in myoII⁻ cells (32). Further analysis is required to clarify the precise function of MyoII for Dictyostelium motility.

Materials and Methods

Dictyostelium Culture and Microscopy.

Axenically grown Dictyostelium WT and mutant cells were prepared for chemotaxis as described (33). The cells were seeded onto a gelatin gel as described in SI Appendix A (34). Time-lapse sequences of chemotaxing cells were acquired on an inverted microscope controlled by Metamorph software (Molecular Devices, Downington, PA).

Traction Cytometry.

Cell outlines were determined from differential interference contrast microscopy (DIC) images by using standard image processing techniques. The substrate deformation was obtained from the lateral displacements of carboxylate modified yellow-green 0.1-μm fluorescent latex beads embedded in it by using particle image velocimetry (35). The traction forces were calculated from the displacements after solving the elasticity equation of equilibrium for the finite-thickness substrate. The Young's modulus of the gel was determined from the indentation of a tungsten carbide sphere (36). The average distance of the marker beads from the gel surface was estimated from a Z-stack. For additional details, see SI Appendix A.

Abbreviations

MyoII⁻

myosin II–null

talA⁻

talin A-null.