Structural Transitions and Thermodynamics of a Glycine-Dependent Riboswitch from Vibrio cholerae

Abstract

Riboswitches are complex folded RNA domains found in non-coding regions of mRNA that regulate gene expression upon small molecule binding. Recently, Breaker and coworkers reported a tandem aptamer riboswitch (VCI-II) that binds glycine cooperatively. Here, we use hydroxyl radical footprinting and small-angle x-ray scattering (SAXS) to study the conformations of this tandem aptamer as a function of Mg²⁺ and glycine concentration. We fit a simple three-state thermodynamic model that describes the energetic coupling between magnesium-induced folding and glycine binding. Furthermore, we characterize the structural conformations of each of the three states: In low salt with no magnesium present, the VCI-II construct has an extended overall conformation, presumably representing unfolded structures. Addition of millimolar concentrations of Mg²⁺ in the absence of glycine leads to a significant compaction and partial folding as judged by hydroxyl radical protections. In the presence of millimolar Mg²⁺ concentrations, the tandem aptamer binds glycine cooperatively. The glycine binding transition involves a further compaction, additional tertiary packing interactions and further uptake of magnesium ions relative to the state in high Mg²⁺ but no glycine. Employing density reconstruction algorithms, we obtain low resolution 3-D structures for all three states from the SAXS measurements. These data provide a first glimpse into the structural conformations of the VCI-II aptamer, establish rigorous constraints for further modeling, and provide a framework for future mechanistic studies.

Introduction

The importance of RNA in the expression of proteins as messenger-, transfer- and ribosomal-RNA (mRNA, tRNA, rRNA) has been known for decades. Only more recently, however, has it become increasingly evident that gene regulation not only targets but can also be effected by RNA. One such mechanism of “RNA only” (i.e. without protein interactions) gene regulation are riboswitches. Riboswitches are located in the 5′-untranslated region of mRNAs and undergo conformational changes upon small molecule ligand binding to their aptamer domain. The rearrangement of the aptamer allosterically triggers conformational changes in other parts of the molecule, that either inhibit or promote expression of the gene(s) downstream of the riboswitch.^1–3 This process provides a feedback mechanism for gene regulation that appears to be widespread in prokaryotes and has been suggested to play a role in eukaryotes.⁴ A range of riboswitches has been discovered, both in regard to their small molecule targets and to their mechanism of gene control.^{3, 5–7}

Recently, Breaker and coworkers discovered a riboswitch in Vibrio cholerae that comprises two glycine-binding aptamers joined by a “linker” region.⁸ The secondary structure of this tandem aptamer is shown in Figure 1. Aptamers I and II comprise residues 1–132 and 140–226, respectively. It was demonstrated that the tandem aptamer, termed VCI-II, binds two glycine molecules cooperatively. The full length riboswitch acts as a genetic “on” switch, that controls transcription of the gcvT operon, which codes for proteins that form the glycine cleavage system. The glycine riboswitch is the first example of a naturally occurring tandem aptamer riboswitch that binds its ligand cooperatively.

Fig. 1.

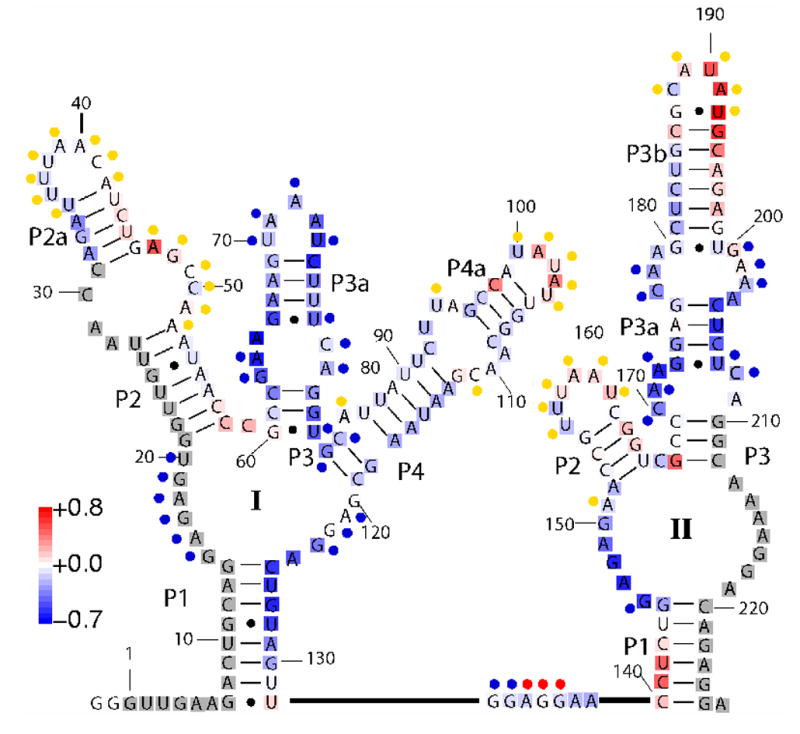
Secondary structure of the VCI-II riboswitch tandem aptamer from Mandal, et. al.⁸ The color code mapped onto the secondary structure overlaying the letters represents relative solvent exposure measured by hydroxyl radical footprinting cleavage for the high glycine B state (average over data points at 10, 25, 50, and 100 mM glycine) compared to the M state (0 mM glycine). Blue indicates residues exhibiting increasing protections upon addition of glycine and red indicates residues exhibiting decreasing protections (increased cleavage) with increasing glycine concentrations. Regions in white display no change in cleavage and regions in gray were not probed. The colored circles next to the letters indicate in-line probing results obtained by Mandal, et. al.⁸ Blue circles correspond to reduced cleavage upon glycine binding, yellow circles mark residues that exhibit unchanged cleavage, and red circles denote increasing cleavage. For details of the footprinting experiment see Figure 3 and the Materials and Methods section. The color scale is indicated by the scale bar on the lower left; the figure was generated by SAFA.⁷⁰

Despite their importance in gene regulation, suggested central role in an early “RNA world”,⁹ and intriguing biochemical properties, relatively little is known about the three-dimensional structure of riboswitches and about the energetic landscape related to their conformations. Atomic resolution structures for three closely related purine binding riboswitches,^{10, 11} for a thiamine pyrophosphate,¹² and for a S-adenosylmethionine binding riboswitch¹³ have been solved in their ligand-bound state. While it is likely that x-ray crystallography and NMR structures of other riboswitches will follow, such atomic level structural information is difficult to obtain for the unfolded and partially folded states that are likely present prior to ligand binding.

Here we use small-angle x-ray scattering (SAXS) and hydroxyl radical footprinting to characterize the structural conformations of the VCI-II riboswitch as a function of magnesium and glycine concentration in aqueous solution. SAXS has been used extensively to study the structure and dynamics of biological macromolecules in solution,^14–16 in particular, SAXS has provided important insights into ion-dependent RNA folding.^17–24 While it does not provide atomic resolution, SAXS can provide global low resolution structural information under (near) physiological conditions. Furthermore, SAXS is well suited to probe unfolded or partially folded structural ensembles, for which information is difficult or impossible to obtain using higher resolution methods such as x-ray crystallography or NMR spectroscopy.

Chemical footprinting using hydroxyl radicals generated by Fe(II)-EDTA Fenton chemistry is complementary to SAXS measurements as it provides a local probe of RNA structure.²⁵ Due to the small size and high reactivity of the hydroxyl radical, cleavage of the solvent accessible backbone of nucleic acids occurs irrespective of sequence and secondary structure,²⁶ and differences in cleavage pattern under different solution conditions can map changes in RNA packing with single nucleotide resolution.^{27, 28}

Our findings provide rigorous constraints for further modeling of the VCI-II construct. Advancing structural insight and understanding the energetic landscape of naturally occurring riboswitches should be an important step toward a more complete, detailed and mechanistic understanding of riboswitch mediated gene control and toward improving the design of engineered RNA switches.

Results and Discussion

We first present SAXS and hydroxyl radical footprinting measurements of the tandem aptamer domain (VCI-II) of the glycine riboswitch from Vibrio cholerae as a function of glycine and Mg²⁺ concentration. Based on these results, we derive a minimal three-state thermodynamic model that can account for the data and provides a framework to understand the energetic coupling between Mg²⁺-dependent folding and ligand binding. Finally, we characterize the structural conformations of the different thermodynamic states, using evidence from footprinting as well as bead reconstruction algorithms to construct low resolution electron density models from SAXS data.

Cooperative glycine binding monitored by SAXS

Solution scattering profiles as a function of Mg²⁺ and glycine concentration were collected as described in the Material and Methods section. Radii of gyration, R_g, were obtained from Guinier analysis of the low angle scattering data. Figure 2 A shows the $R_g^2$ as a function of glycine concentration in the presence of 10 mM MgCl₂. VCI-II undergoes a significant compaction upon glycine binding, from an R_g of about 45 Å to 39 Å. A large structural rearrangement is also suggested by the change in shape of the scattering profile, as discussed further below.

Fig. 2.

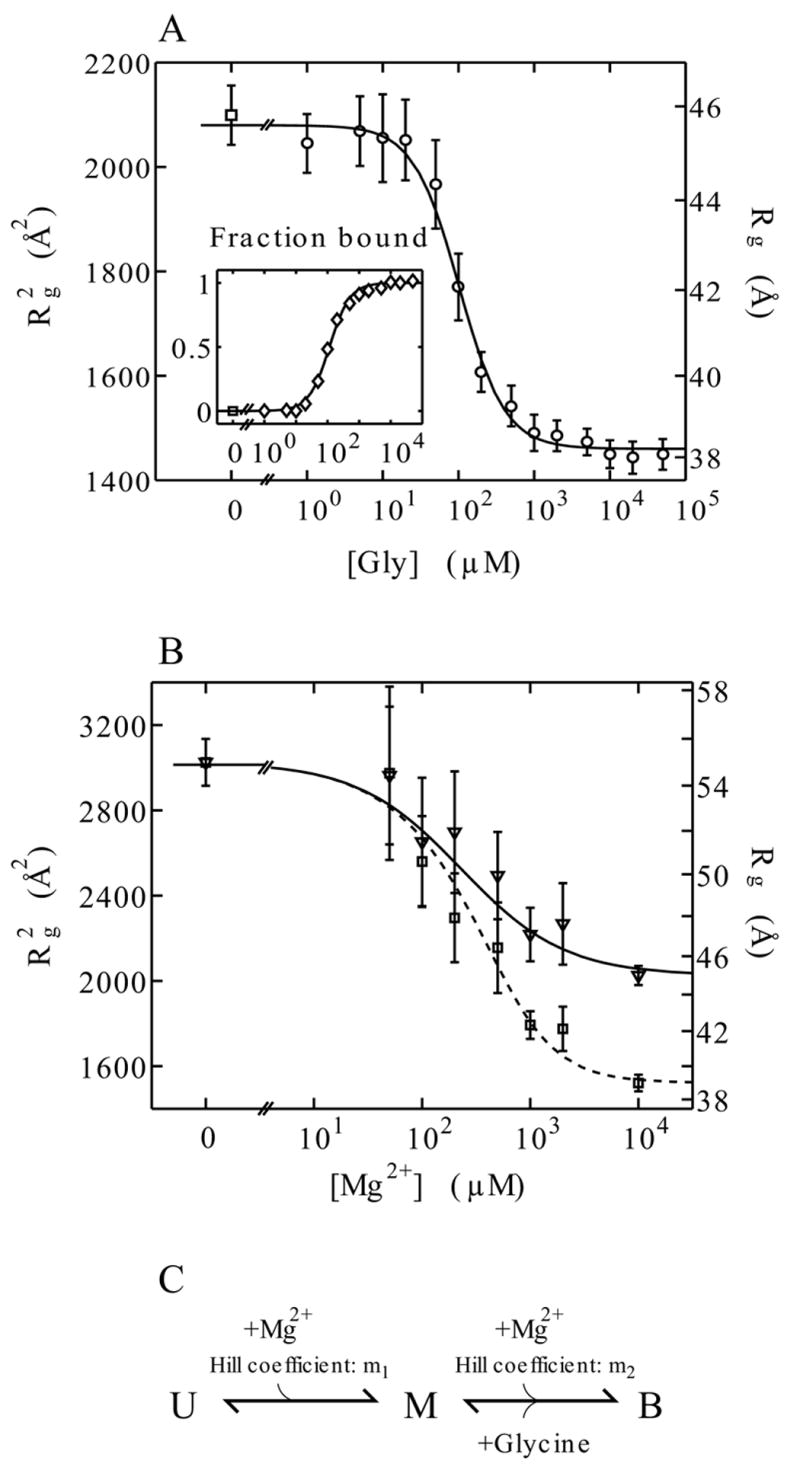
Radii of gyration obtained from Guinier fits to the scattering data and thermodynamic modeling. Panel A: Cooperative binding of glycine to VCI-II measured by SAXS. Radii of gyration at di1erent glycine concentrations (main graph, circles) in the presence of 10 mM Mg²⁺ and Hill fit to the data (solid line), see text. The inset shows the fraction bound obtained from two-state projections of the full scattering profiles (diamonds) and the corresponding Hill fit (solid line). Panel B: Radii of gyration for di1erent Mg²⁺ concentrations in the absence of glycine (triangles) and in the presence of 10 mM glycine (squares). The solid and dashed lines corresponds to the fit of the three-state thermodynamic model as described in the text.

The errors in panel A and B are obtained from Guinier fits with slightly di1erent fitting ranges. The plots show the square of the radii of gyration ( $R_g^2$), as this is the relevant quantity for the fit,³⁰ the right axis shows the corresponding values for R_g.

Panel C: The three-state thermodynamic model of the VCI-II tandem aptamer with unfolded (U), high Mg²⁺ (M), and glycine-bound (B) states.

We model the data as a two-state transition between the state in high magnesium in the absence of glycine, denoted M, and the glycine-bound conformation, denoted B. Following Breaker and coworkers,⁸ we use the Hill equation²⁹ for the fraction bound, $f_B={[\text{Gly}]}^n/({[\text{Gly}]}^n+K_{\text{mid},\text{Gly}}^n)$. K_mid,Gly is the midpoint of the transition, i.e. the glycine concentration at which half maximal binding occurs; n is the Hill coefficient, which provides a measure of cooperativity. A Hill coefficient of two corresponds to both aptamers binding with perfect cooperativity. We fit n and K_mid,Gly to the data, using the Hill equation and the relationship $R_g^2([Gly])=f_M([Gly])R_{g,M}^2+f_B([Gly])R_{g,B}^2$.³⁰ The fit yields K_mid,Gly = 105 ± 15 μM glycine and n = 1.6 ± 0.2. This apparent midpoint has to be corrected for the finite RNA concentration, which was 20 μM for the titration experiments. The free glycine concentration at the midpoint is therefore 85 ± 15 μM, as each of the two aptamers in VCI-II bind one glycine molecule. Errors were obtained from a “bootstrapping” procedure³¹ by generating 1000 synthetic data sets from the experimental data and repeated Hill fits. The Hill model fits the data well (reduced χ² = 0.224, p = 0.996), and the obtained Hill coefficient is in good agreement with the value of n = 1.64 that was measured by Breaker and coworkers⁸ and indicative of cooperative glycine binding.

An alternative to fitting the radii of gyration is to use the entire scattering profiles and to project the data unto the zero and high glycine profiles using the relationship I(q,[Gly]) = f_M ([Gly])I_M (q)+f_B([Gly])I_B(q). The resulting f_B([Gly]) values for these two-state projections are shown in the inset of Figure 2 A, the fit yields a Hill coefficient of n = 1.4 ± 0.2 and an apparent midpoint of K_mid,Gly = 110 ± 15, which is consistent with the fit to the $R_g^2$ data.

Using singular value decomposition (SVD) analysis,^{14, 32} we find the number of signal containing components to be two or possibly three (data not shown). A third signal containing component would suggest the existence of a binding intermediate. Figure S1 of the Supplementary Material shows the experimental scattering profiles along with the fitted two-state projections and the best three-state fit. The data are well fit by a two-state model, but inclusion of a third component does improve the fit.

Hydroxyl radical protections upon glycine binding

To complement the SAXS data, we studied the glycine binding transition using hydroxyl radical footprinting. While SAXS provides information about the global size and shape of a molecule in solution, hydroxyl radical footprinting can probe the local packing of nucleotides. Figure 3 shows a false color rendering of the observed hydroxyl radical protections for VCI-II in 10 mM Mg²⁺ as a function of glycine (an image of a representative gel is shown in Figure S2 of the Supplementary Material). The protections at high glycine (average over data points at 10, 25, 50, and 100 mM glycine) relative to the protection pattern in the absence of glycine (0 mM) are mapped onto the secondary structure in Figure 1 for the residues probed in these experiments (32 to 209).

Fig. 3.

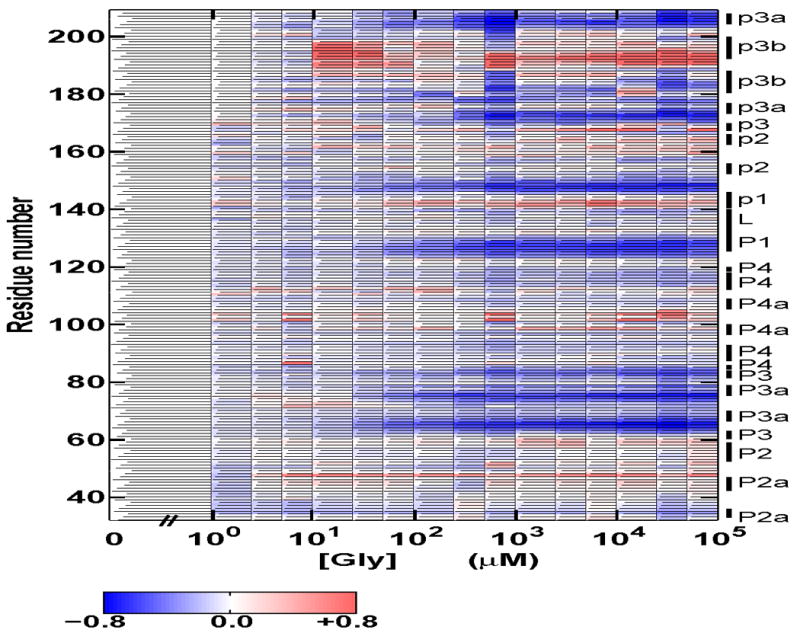
Solvent exposure probed by hydroxyl radical cleavage for residues 32–209 of the VCI-II tandem aptamer in the presence of 10 mM Mg²⁺ as a function of glycine concentration. Data were normalized such that the amount of cleavage at 0 mM glycine corresponds to zero. Blue regions show protections from cleavage upon addition of glycine and red regions show increased cleavage with increasing glycine concentration according to the scale bar show below the graph. The annotation of the sequence to the right follows the nomenclature of Breaker and coworkers.⁸ In this Figure, upper case P corresponds to paired regions in aptamer I, lower case p corresponds to paired region in aptamer II. For clarity we additionally distinguish between regions P2a and P2 and between P4a and P4 in aptamer I, as shown in the secondary structure scheme in Figure 1. For details of data processing and experimental procedures see the Materials and Methods section. Data for residues 34–166 correspond to averages over at least three repeats; data for residues above 166 are from a single experiment and are thus of lower quality.

The data reveal several regions in both aptamer I and II that show systematic protection from hydroxyl radical induced cleavage upon glycine binding, as discussed further below. Figure S3 of the Supplementary Material shows normalized protections for selected residues from these regions and Hill fits to these data. As the footprinting protections were noisier than the SAXS measurements, we fit these data with a fixed Hill coefficient n of 1.4, which corresponds to the value from the two-state projection data. Fits with different values for n in the range from 1.0 to 1.6 gave similar results for the midpoints (data not shown). Different regions of the VCI-II construct exhibit similar midpoints for the glycine induced protections, consistent with cooperative glycine binding (Table S1 of the Supplementary Material). Overall, the fits to the footprinting data give K_mid,Gly = 60 ± 25 μM glycine. This value is somewhat lower than that obtained from the SAXS measurements, but consistent within experimental error.

Mg²⁺-induced structural transitions studied by SAXS

To examine the interplay between magnesium induced folding and glycine binding of the VCI-II construct, we collected SAXS data as a function of magnesium concentration. Figure 2 B shows the radius of gyration as a function of Mg²⁺ in the presence (squares) and absence (triangles) of 10 mM glycine. At 0 mM Mg²⁺ identical scattering profiles are obtained with and without 10 mM glycine (data not shown), and VCI-II adopts a conformation with an R_g of 55 Å, which we denote as the unfolded state, U. Upon addition of Mg²⁺, VCI-II undergoes a significant compaction to an R_g of 45 Å in the absence of glycine (Figure 2 B, triangles) and to 39 Å in the presence of 10 mM glycine (Figure 2 B, squares). These data suggest a U → M transition as a function of Mg²⁺ in the absence of glycine and a transition to the glycine-bound state B in the presence of 10 mM glycine.

Three-state thermodynamic model

We fit a three-state thermodynamic model that accounts for the behavior of the VCI-II construct as a function of Mg²⁺ and glycine concentration. The above data indicate the presence of at least three states, U, M, and B. For convenience, we choose M as our reference state, the model is then parametrized by two free energy differences: ΔG_UM = G_U − G_M is the free energy difference between the unfolded and the more compact state in high Mg²⁺ without glycine and ΔG_BM = G_B − G_M that between the glycine-bound B and the M state. The partition function of the system is Z = 1 + exp(−βΔG_UM) + exp(−βΔG_BM), with β = 1/k_BT, where k_B is the Boltzmann constant and T the absolute temperature. The fractional occupancies, i.e. the relative amount of VCI-II RNA in each of the three states are given by f_U = exp(−βΔG_UM)Z⁻¹, f_M = Z⁻¹, and f_B = exp(−βΔG_BM)Z⁻¹,with the property that f_U + f_M + f_B =1.

To determine the Mg²⁺ and glycine dependence of ΔG_UM and ΔG_BM we assume the thermodynamic scheme presented in Figure 2 C. Let us first consider the U → M transition on the left side of the scheme, which corresponds to the Mg²⁺ titration in the absence of glycine. ΔG_UM does not depend on the glycine concentration, as neither of the two states involves glycine. We model the Mg²⁺ dependence using the Hill equation with the magnesium concentration, [Mg²⁺], as the independent variable, i.e. $f_M={[{\text{Mg}}^{2+}]}^{m_1}/({[{\text{Mg}}^{2+}]}^{m_1}+K_1^{m_1})$, which corresponds to choosing ΔG_UM = m₁k_BTln([Mg²⁺/K₁). K₁ is a constant that corresponds to the magnesium concentration where both states in the U ⇋ M equilibrium are equally populated.

This functional form is often interpreted as “m₁ Mg²⁺ ions binding to the RNA upon folding”. However, one needs to distinguish between several modes of magnesium binding. Most of the ions associated with an RNA molecule remain hydrated and form a diffusively bound ion cloud that screens the electrostatic repulsion between phosphate groups without making specific contact with the RNA. Many fewer, if any, magnesium ions are dehydrated and bound to specific and selective ion binding sites.^{33, 34} Our current experiments do not allow us to distinguish between ions in different binding modes. The parameter m₁ is introduced for mathematical convenience and loosely describes the cooperativity of the magnesium binding and folding transition, but should not be interpreted as the actual number of ions bound.

A fit of the Hill equation to the Mg²⁺ titration in the absence of glycine yields m₁ ≈ 0.85 − 0.9 and K₁ of 200 ± 60 μM magnesium. An m₁ value slightly less than one corresponds to noncooperative binding in the standard Hill formulation. While many RNA molecules show magnesium folding transitions with more apparent cooperativity, a Hill coefficient of about one has been observed for other RNAs.^{35, 36}

In the presence of 10 mM glycine, VCI-II starts out in the same unfolded state, U, at 0 mM Mg²⁺, but the endpoint of the magnesium titration is now the B state with an R_g of 39 Å. The apparent midpoint of the transition is about the same or higher than that for the U ⇌ M transition in the absence of glycine. This observation is incompatible with models in which the M ⇌ B equilibrium does not depend on magnesium as well as glycine, as otherwise the presence of 10 mM glycine (which is at least 100 times greater than the value of K_mid,Gly determined from the glycine titration above) would shift the equilibrium strongly to the B state.

We therefore introduce a second Hill coefficient, m₂, for the dependence of ΔG_BM on magnesium. The M ⇌ B equilibrium on the right side of the scheme in Figure 2 C therefore depends on both glycine and Mg²⁺ with an equilibrium constant K₂ = [B]/([M] [Mg²⁺]^m₂ [Gly]ⁿ) and the free energy difference is ΔG_BM = −k_BTln(K₂ [Mg²⁺]^m₂ [Gly]ⁿ).

In practice, we use the higher signal-to-noise SAXS data for the glycine titration to determine n and K_mid,Gly, which corresponds to K₂ at 10 mM magnesium, as described above (n = 1.6 and K_mid,Gly = 85 μM). We then fit the remaining parameters, m₁, m₂ and K₁, to the magnesium titration data. The fit to the $R_g^2$ data (reduced χ² = 0.361, p = 0.981) yields m₁ = 0.85 ± 0.1, K₁ = 200 ± 50 μM magnesium and m₂ = 2.0 ± 0.5, with errors obtained from a bootstrap procedure (Figure 2 B, solid and dashed line). A fit to two and three-state projections of the full scattering profiles (Figure S4 of the Supplementary Material) gives m₁ = 0.85 ± 0.1, K₁ = 100 ± 30 μM magnesium and m₂ = 2.2 ± 0.5, in fair agreement with the fit to the $R_g^2$ data

The values for m₁ and K₁ are similar to those obtained from a Hill fit to the U ⇌ M equilibrium alone. The fitted values for m₂ are greater than one, which indicates that the M → B glycine binding transition is accompanied by an apparent cooperative association of magnesium ions. Table 1 summarizes the parameters of the three-state model obtained from fits to different data.

Table 1.

Parameter of the three-state thermodynamic model for the VCI-II tandem aptamer as a function of Mg²⁺ and glycine concentration obtained from fits to different data sets (see text). K_mid,Gly and n are the midpoint and Hill coe4cient for glycine binding in 10 mM MgCl₂ and 50 mM MOPS, pH 7. m₁ and m₂ are the magnesium Hill coe4cients for the U → M and M → B transitions, respectively. K₁ is the Mg²⁺ midpoint of the U → M transition.

VCI-II Riboswitch: Parameters of the Three-State Thermodynamic Model
Parameter	$R_g^2$ SAXS data	SAXS profile projections	OH radical footprinting
n	1.6 ± 0.2	1.4 ± 0.1	N.A.†
Kmid,Gly (μM, Glycine)	85 ± 15	90 ± 15	60 ± 25
m1	0.85 ± 0.1	0.85 ± 0.1	N.A.†
K1 (μM, Mg2+)	200 ± 50	100 ± 30	20–250
m2	2.0 ± 0.5	2.2 ± 0.5	N.A.†

^†Hydroxyl radical footprinting data were noisier than the SAXS data and were fit with fixed Hill coefficients (see text).

Hydroxyl radical protections upon addition of Mg²⁺

To further investigate the conformational changes upon addition of Mg²⁺, we complement the SAXS experiments with hydroxyl radical probing data. Figure 4 shows relative protections from cleavage under different magnesium concentrations in the absence (A, left) and presence of 10 mM glycine (B, right) for residues 34–136. The observable protections from cleavage for distinct regions or groups of residues occur at different Mg²⁺ concentrations, with midpoints spanning about an order of magnitude (vide infra). This observation suggests that different regions of the molecule fold relatively independently at different Mg²⁺ concentrations, offering a possible explanation for the low observed Hill coefficient of m₁ = 0.85 and apparent noncooperativity of the U ⇌ M transition: If distinct parts of the molecule fold at different Mg²⁺ concentrations, the global size and shape as measured by SAXS will change only gradually as a function of Mg²⁺.

Fig. 4.

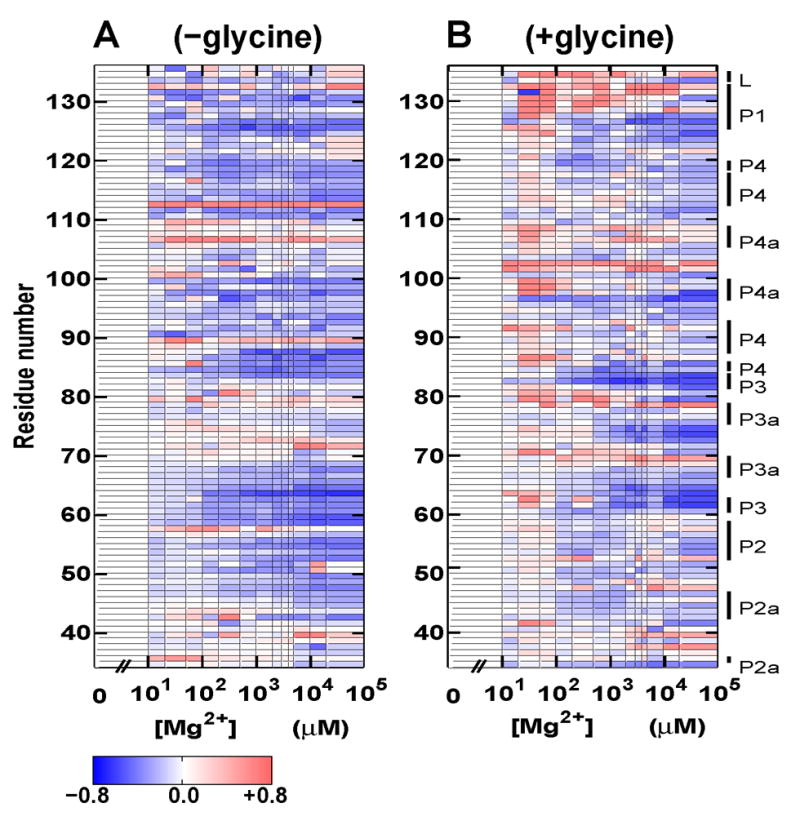
Solvent exposure probed by hydroxyl radical cleavage for residues 34–136 of the VCI-II tandem aptamer as a function of Mg²⁺ concentration. Data in the absence of glycine (A, left) and with 10 mM glycine present (B, right). Data were normalized such that the amount of cleavage at 0 mM Mg²⁺ corresponds to zero (see Materials and Methods). Blue regions show protections from cleavage upon addition of Mg²⁺, and red regions show increased cleavage with increasing Mg²⁺ concentration. The color scale is identical for A and B and shown in the scale bar at the bottom. The annotation of the sequence to the right follows the nomenclature of Breaker and coworkers;⁸ for clarity we additionally distinguish between P2 and P2a and between P4a and P4 in aptamer I (see the secondary structure scheme in Figure 1). For details of data processing and experimental procedures see the Materials and Methods section. Data represent averaged values from at least three repeat measurements.

Since the footprinting data are noisier than the SAXS measurements, we did not fit the three-state thermodynamic model to them. However, the data provide a consistency check for the model parameters. Figure S5 of the Supplementary Material shows Hill fits with a fixed Hill coefficient m₁ = 0.85 to the protections of different residues upon addition of magnesium in the absence of glycine. Individual regions exhibit midpoints between 20 and about 250 μM magnesium (see Table S2), which is consistent with an apparent midpoint of K₁ ≈ 100–200 μM determined by SAXS. To characterize the transition in the presence of glycine without fitting the full three-state model, we use the Hill equation with a fixed Hill coefficient of 1.0 to determine “apparent” midpoints for the Mg²⁺ titrations in the presence of glycine (Figure S6 of the Supplementary Material). The values show significant scatter, but are consistently somewhat higher than those determined for the U → M transition (see Table S3), in agreement with the SAXS data.

Thermodynamic landscape

The fractional occupancies, f_U, f_M and f_B, as a function of glycine and Mg²⁺ concentration from our three-state model are shown as a “thermodynamic landscape” in Figure 5. It is plausible that the VCI-II conformational landscape has more than those three distinct states. In particular, species with a single bound glycine, and folding intermediates, but the present data do not allow us to uniquely identify them. Thus, the three-state model is the minimal thermodynamic model that can account for all data presented here. In the following, we characterize the structure of each of the thermodynamic states using the data from SAXS and hydroxyl radical footprinting.

Fig. 5.

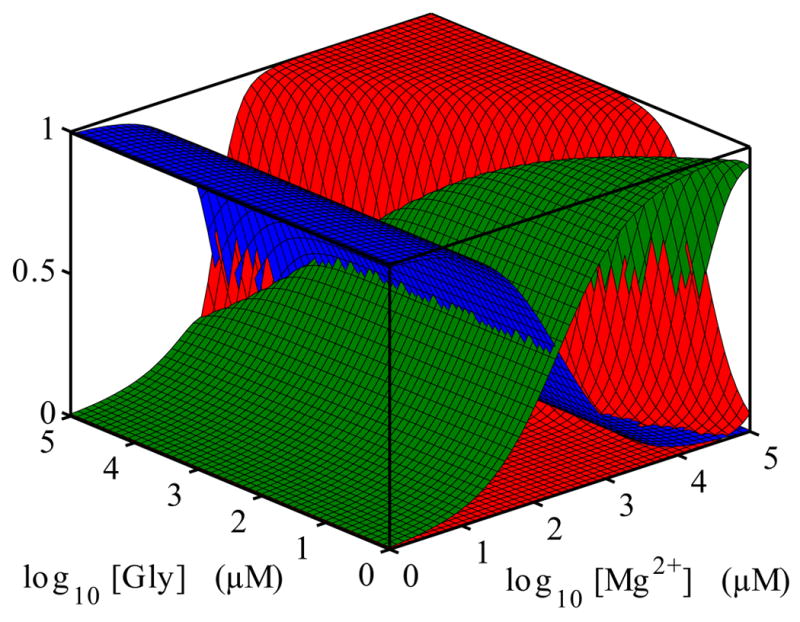
Conformational “landscape” of the VCI-II construct as a function of Mg²⁺ and glycine concentration. The surfaces show the fractional occupancies f_U, f_F and f_B of the unfolded U (blue), folded M (green) and glycine-bound B (red) state. The occupancies are obtained from the thermodynamic model described in the main text. The graph uses the parameters n = 1.6, K_mid,Gly = 85 μM for the for glycine dependence at 10 mM Mg²⁺ and m₁ = 0.85, m₂ = 2 and K₁ = 200μM for the magnesium dependences.

Structural characterization of the unfolded ensemble

Figure 6 A presents scattering profiles for the VCI-II construct under different solution conditions. For clarity, the data are shown as Kratky representations, where the scattering intensity is weighted by momentum transfer (q) squared. Porod’s law³⁰ states that for large q the scattering from an object with a well defined surface falls approximately as q⁻⁴, which leads to a decrease ∝ q⁻² in the Kratky representation for large q. Folded proteins or nucleic acids therefore tend to have a characteristic peak in the Kratky plot.^{14, 15} Kratky showed that the scattering from a random polymer falls like ∝ q⁻¹, which leads to a linear rise at high q in the Kratky plot for completely denatured proteins or nucleic acids.¹⁴

Fig. 6.

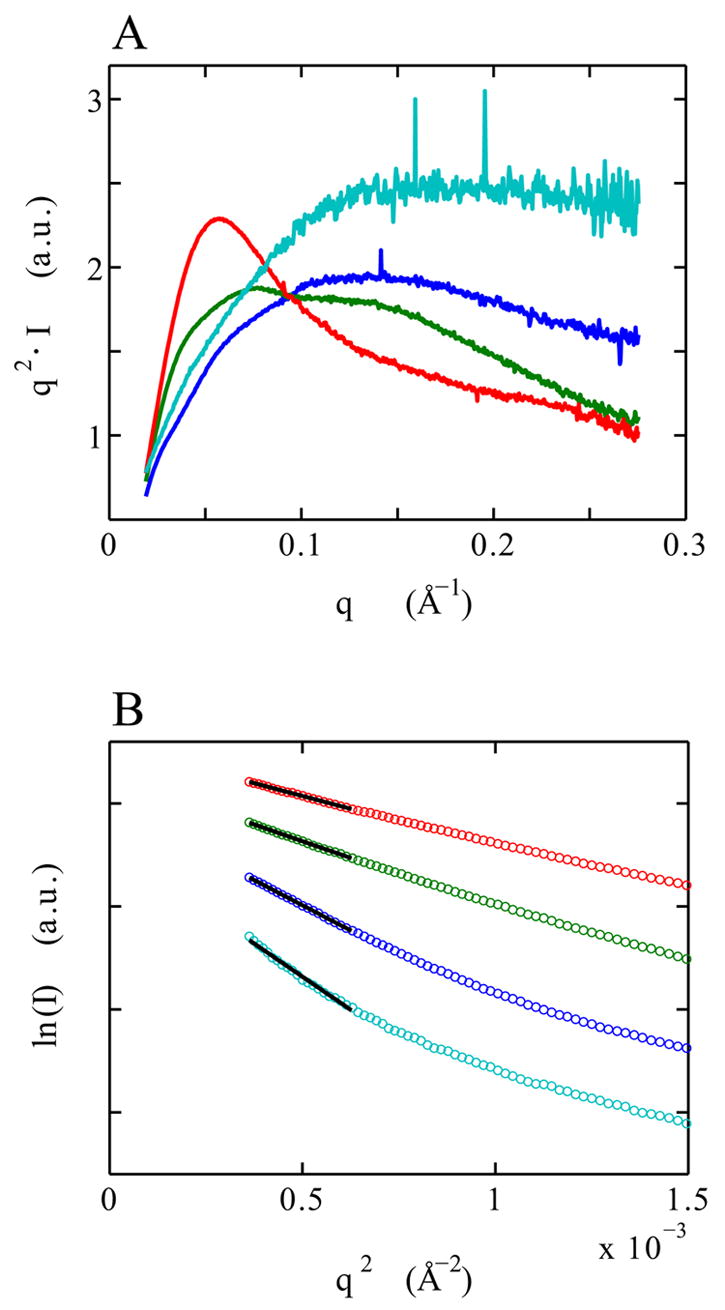
SAXS scattering data for the denatured D (cyan), unfolded U (blue), high Mg²⁺ and no glycine M (green) and glycine-bound B (red) state of the VCI-II riboswitch tandem aptamer. Kratky plots [q² · I(q) as a function of q] of the full scattering profiles (panel A). Guinier plots [ln(I) as a function of q²] of the low q data (circles, panel B) and Guinier fits (black solid lines, panel B). The extend of the black lines indicates the fitting range; the data were vertically o1set for clarity in panel B. The solution conditions under which the profiles were obtained are given in Table 2. The momentum transfer q is equal to q = 4πsin(θ)/λ, where 2θ is the total scattering angle and λ is the x-ray wavelength.

Under conditions that populate the U state (50 mM Na-MOPS buffer without added Mg²⁺) the VCI-II scattering profile exhibits a broad, featureless peak in the Kratky plot, consistent with a heterogeneous ensemble of extended structures (blue profile in Figure 6). However, the RNA is not fully denatured as a rising “tail” in the Kratky plot would be expected for such a state. In 8 M urea (cyan profile in Figure 6) a rising “tail” in the Kratky plot is indeed observed, indicative of denatured, random chain like conformations. This denatured state (D) has a significantly larger radius of gyration R_g and maximum intermolecular distance D_max than the U state, as presented in Table 2. The residual structure in the U state can tentatively be attributed to formed secondary structure.

Table 2.

Geometrical parameters for the VCI-II tandem aptamer under different solution conditions measured by SAXS. The radii of gyration (R_g) were fit by Guinier analysis⁶⁴ (see Figure 6 B), and the maximum intermolecular distances (D_max) were obtained from regularized indirect transforms using the program GNOM⁶⁵ (see the Materials and Methods section). For the very extended denatured state only a lower bound for the R_g could be provided, due to the limited range of validity of the Guinier approximation. The buffer is 50 mM Na-MOPS (3-(N-morpholino)propanesulfonic acid), pH 7.0.

VCI-II Riboswitch: Structural Properties of its Basic Thermodynamic States
State	Solution conditions	Rg (Å)	Dmax (Å)
Denatured (D)	buffer + 8 M urea	≥65	≥220
Unfolded (U)	buffer	55 ± 2	205–215
Folded (M)	buffer + 10 mM Mg2+	45 ± 1	155–165
Bound (B)	buffer + 10 mM Mg2+ + 10 mM Gly	39 ± 1	145–150

Compaction and evidence for partial folding in Mg²⁺

Addition of 10 mM Mg²⁺ to the U state leads to a significant compaction from an R_g of 55 to 45 Å, and a change in maximum intermolecular distance D_max from 210 to 160 Å (Table 2). These differences, the significant change in the shape of the profile, and the appearance of the “shoulder” in the Kratky plot at q ≈ 0.1 Å⁻¹ (Figure 6, green profile) indicate large structural rearrangements of the M state in high Mg²⁺ compared to the U state. Measurements of VCI-II in 150 mM KCl without added Mg²⁺ yield profiles very similar to the U state (data not shown), suggesting that moderate concentrations of monovalent salts are not sufficient to induce the U → M structural transition.

The hydroxyl radical data in Figure 4 A indicate that several regions of the VCI-II construct become protected from cleavage upon addition of Mg²⁺ in the absence of glycine. Due to the small size of the hydroxyl radical, protections correspond to tight packing and do not result from mere compaction without specific contacts.^{22, 28} The hydroxyl radical protections around residues 63–65, 85–87, and 124–126 (see Figure 4 A and Figure S5 of the Supplementary Material) in the M state suggest that the central P1-P2-P3-P4 junction in aptamer I becomes significantly structured even in the absence of glycine. Additional protections around residues 47–48, 95–97 and 117–119 indicate that parts of P2 and P4 become involved in packing interactions upon addition of Mg²⁺.

The SAXS and hydroxyl radical data provide evidence that VCI-II is partially folded in millimolar concentrations of Mg²⁺ in the absence of glycine. Nevertheless, the protected residues around the central P1-P2-P3-P4 junction of aptamer I, 63–65, 85–87, and 124–126, show increased protections upon addition of glycine to the M state, as can be seen from Figures 1 and 3. VCI-II may retain some conformational flexibility in the M state, with certain “packing” contacts partially formed and these contacts may be further enhanced, directly or indirectly, upon binding of glycine.

Glycine-bound structure

Addition of 10 mM glycine in the presence of Mg²⁺ leads to a further compaction and large structural rearrangement to the B state. The R_g changes from 45 Å to 39 Å, and a large peak appears in the Kratky plot at q ≈ 0.05 Å⁻¹ (Figure 6, red profile). The addition of 150 mM KCl does not significantly change the structure of the M or B states (data not shown). The R_g and D_max values are summarized in Table 2.

The glycine-bound conformation shows hydroxyl radical protections in several regions in addition to those observed in the M state (Figure 1, 3 and 4). In aptamer I, the regions sequestered from the solvent upon glycine binding are in the central P1-P2-P3-P4 junction and in the P3 and P3a region, in particular the stem-loop P3a (residues 73–75). In contrast, the P2 and P4 regions show protections upon addition of Mg²⁺ (Figure 4) that exhibit no significant glycine dependence. In aptamer II, glycine-binding induces protections in the single stranded region between P1 and P2 and in the paired regions P3a and P3b as well as in the loops adjacent to P3a and P3b. These findings are in good agreement with the cleavage pattern obtained by Breaker and coworkers in an in-line probing assay.⁸ The in-line probing and hydroxyl radical data are likely to be somewhat related, as in-line probing reports on the rate of spontaneous cleavage, which depends on the sugars adopting a geometry appropriate for cleavage, while hydroxyl radical footprinting measures the accessibility of the sugar moiety.

In summary, the footprinting data indicate that the central P1-P2-P3-P4 junction and the P3 and P3a regions undergo considerable structural changes and form tight packing interactions upon glycine binding, which might suggest that they are part of the glycine binding site in aptamer I. Even though no Mg²⁺ titration footprinting data were obtained, a similar role can be suggested for the P3a regions and the loops adjacent to it and parts of the central P1-P2-P3 junction in aptamer II.

Low resolution structures

To provide further structural insights and constraints, we employ density reconstruction algorithms to obtain low resolution models from the SAXS data for VCI-II in the U, M and B state. Several such algorithms are available,^37–39 and their common strategy is to place uniform point scatterers or “beads” such that their scattering pattern best matches the experimentally measured SAXS profile. The details of how the bead arrangements are generated and updated differ between algorithms. Here we employ the program dammin,³⁸ which imposes a compactness criterion on the solution and updates bead positions using a simulated annealing protocol (see Materials and Methods). Low resolution reconstruction methods have been extensively applied to proteins and protein complexes^38–40 (further examples of applications to protein complexes are found in references41–45). We have tested the applicability of dammin and saxs3d to RNA by using SAXS data of molecules with known structure and found good agreement with the low resolution reconstructions.⁴⁶ For conformations that represent a structural subensemble rather than a precisely defined structure (which is the case for the U and to a lesser extent for the M state, see above) the reconstructions are expected to reproduce the averaged electron density of the ensemble.⁴⁷

The bead reconstructions give excellent agreement with the experimentally observed scattering pattern for all three conformations. Representative fits are shown in Figure S7 of the Supplementary Material. However, the correspondence of 3-D structure to the SAXS scattering profile is not one-to-one. To test the reliability and reproducibility of the reconstructions, we compare i) several independent reconstruction runs (with different random seeds) against the same experimental profile and ii) reconstructions against different experimental profiles from repeat measurements using different RNA batches and concentrations. As a metric to compare bead models with different numbers of beads, we employ the normalized spatial discrepancy (NSD) criterion (see Materials and Methods and reference⁴⁸), which has the property that identical models give a NSD of zero, models of similar shape give NSD values ≈ 1 and models that represent different shapes give values greater than one. Comparing models both across different reconstruction runs against the same data and across reconstructions from different measurements, we found that the models for the B state exhibit pairwise NSD values of 0.6–0.8, models for the M conformation give NSD results of 0.7–0.9 and reconstructions for the U state gave rise to values in the range of 0.9–1.0.

The pairwise NSD values of order one or lower indicate that for each of the conformations all runs converged to structurally similar solutions. Low resolution models for each of the states are presented in Figure 7. The top three rows show different views of the “filtered” consensus models from an averaging procedure outlined in the Materials and Methods section. The last row shows the “filtered” models rendered as beads and the convex hull of all models as a transparent surface.

Fig. 7.

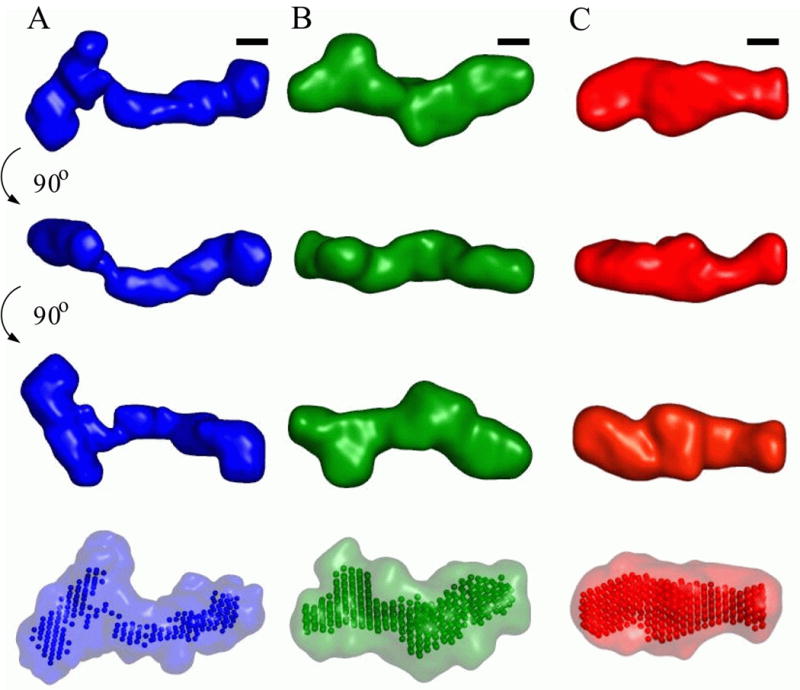
Low resolution structural models for the VCI-II riboswitch tandem aptamer under di1erent solution conditions. Average unfolded conformation (column A, blue), conformation in the presence of 10 mM magnesium and absence of glycine (column B, green) and glycine bound structure (column C, red). The first three columns show the “filtered” structure (see Materials and Methods for details of the reconstruction procedure) for each of the conformations in three di1erent orientations. Black scale bars in each column correspond to 20 Å, the diameter of an A-form RNA helix. The rendered densities were generated by convoluting the bead models with a Gaussian kernel using the program Situs.⁶⁷, ⁶⁸ The last row shows the “filtered” models as beads and the convex hull of all bead models for a given conformation as a transparent surface.

Interestingly, the lowest pairwise NSD values were observed for the B state, for which we expect the structure to be most rigid and well folded. In the cases where structures likely represent conformational ensembles, i.e. for the U and, to a lesser extent, for the M state, slightly higher pairwise NSD values might be indicative of this greater flexibility. However, as different solutions still have pairwise NSD values of order unity, they are classified as “similar” and can be interpreted as an average electron density structure.

Comparing reconstructions for the M state to those for the B state gives NSD values of ≈ 1.0, which is significantly higher than pairwise NSD values of B models or M models amongst another. However, this indicates that the M and B states are still marginally structurally “similar” by the NSD criterion. The NSD between U and B state models is ≈ 1.5 and that between U and M state models is ≈ 1.3, indicating that that the U state is classified as “dissimilar” from both the M and U states.

At present there is no algorithm to uniquely map secondary structure into the low resolution bead models. However, the following general pictures emerges: In the U state at low salt concentration, the electron density is spread out into an elongated shape (Figure 7, column A). The thickness of the elongated middle section is consistent with a single double stranded helix (see the scale bars Figure 7). The overall dimensions are consistent with the secondary structure base pairings being formed and helices being spread apart by electrostatic repulsion. The shape is very roughly that of a “T” (with the top “crossbar” of the T being on the left side of Figure 7, column A). The length of the “stem” of the T is about 150–160 Å, which is consistent with for example the paired regions P2 or P4 and P1 of aptamer I and the paired region P1 of aptamer II being roughly coaxial, or alternatively the paired regions P1 and P3 of aptamer II and P1 of aptamer I being coaxial. Given that aptamer I has more residues and more paired regions, it is suggestive to assign the “stem” of the T shape to aptamer II and P1 of aptamer I and the “crossbar” to P2, P3 and P4 of aptamer I. In 10 mM Mg²⁺ VCI-II adopts a more compact conformation (Figure 7, column B), and the dimensions are suggestive of an increased extent of helix packing in this conformation. However, from the SAXS data alone we cannot distinguish true tertiary packing interactions from a scenario where helices are on average close, but retain some flexibility with respect to their relative positions. Addition of glycine to the folded state causes a significant rearrangement of electron density (Figure 7, column C). In particular, there is a significant shift of density from the periphery toward the middle of the structure, which is also reflected in the observation that the maximum pairwise distant D_max is reduced only by about 7% in going from the M to the B state, but that the radius of gyration is reduced by about 15%. This shift of electron density toward the center region of the molecule might be related to rearrangements upon formation of binding pockets for the two glycine ligands and to molecular contacts involved in allosteric “communication” between the two aptamers. Such allosteric interactions are necessary for cooperative binding of the two aptamers.

Conclusion

The ion-dependent folding of RNA molecules into intricate three-dimensional structures that allow them to carry out their biological function and the free energy landscape associated with these conformations is one of the paradigmatic questions in structural biology. The ability to bind small molecule ligands adds another dimension to this question for riboswitches.

One basic question is to what extent ion-dependent folding and ligand binding are coupled. One extreme scenario is that of in vitro designed RNA aptamers,^49–52 which typically appear to be fairly flexible and unstructured in the absence of their ligand and undergo “ligand-induced” folding.^53–56 At the other end of the spectrum are many small molecule binding proteins, which are folded both in the presence and absence of their ligand and crystal structures have been obtained for both apo and holo forms.⁵⁷ Folding independent of ligand binding is suggested for the glucosamine 6-phosphate binding glmS ribozyme, where the ligand-bound and unbound states in high Mg²⁺ are indistinguishable by hydroxyl radical footprinting and UV cross-linking.⁵⁸ In contrast, limited evidence suggests that a thiamine pyrophosphate binding riboswitch adopts similar conformations without magnesium and in high Mg²⁺ in the absence of its ligand.

The data presented here suggest an intermediate scenario for VCI-II: The addition of Mg²⁺ in the absence of glycine leads to a significant compaction and hydroxyl radical protections suggestive of partial folding. However, parts of the molecule only become involved in tertiary packing upon glycine binding.

The three-state thermodynamic model indicates that the M to B transition requires additional uptake of magnesium ions and predicts a Mg²⁺ dependence of the glycine binding constant. A Mg²⁺-dependent ligand binding constant has been previously observed for the aptamers of purine¹⁰ and thiamine pyrophosphate riboswitches³⁶ and might possibly be a general feature of riboswitches and RNA transitions that condense the negatively charged RNA backbone.

In summary, our results provide a first glimpse into the structure and energy landscape of the VCI-II construct as a function of Mg²⁺ and glycine concentration. It will be interesting to obtain analogous thermodynamic models for other riboswitches and to compare the extent and nature of the observed structural transitions. The models obtained from SAXS measurements and footprinting data establish a minimal thermodynamic framework, provide rigorous structural constraints for further modeling of the VCI-II tandem aptamer, and give early insights into the molecular details of how this fascinating molecule achieves its biological function.

Materials and Methods

RNA preparation

The VCI-II domain of the Vibrio cholerae glycine riboswitch was prepared by T7 RNA polymerase in vitro transcription from PCR generated DNA constructs. The material for hydroxyl radical footprinting was purified on a denaturing 8% acrylamide gel, and the RNA used for SAXS was either gel-purified or purified by phenol-chloroform extraction. Whereas gel purification typically gives better RNA purity, minute contamination with residual acrylamide pieces can give a strong contribution to the SAXS signal, due to the relatively large size of the contaminants.⁵⁹ No such contaminants were observed in this study: SAXS measurements on VCI-II samples purified by gel purification or phenol-chloroform extraction yielded very similar results (see the “SAXS data analysis” section). The final constructs were tested on non-denaturing polyacrylamide gels and no significant RNA contaminations were observed. Samples for hydroxyl radical footprinting were 5′-labeled with [γ-³²P]ATP using phage T4 polynucleotide kinase and repurified by denaturing polyacrylamide gel electrophoresis.

SAXS measurements

All data were taken on the undulator beam line BESSRC CAT 12-ID at the Advanced Photon Source, Argonne, IL, USA, employing a sample-detector distance of 2 m and a x-ray phosphor detector optically coupled to a 3 x 3 mosaic CCD read out. The data were collected using a custom-made thermo-controlled sample holder⁶⁰ at a temperature of 25 °C and an x-ray energy of 12 keV. Details of the measurement and beamline are as described previously.^60–62

SAXS data of the VCI-II glycine riboswitch were collected at RNA concentrations ranging from 0.5 to 5 mg/ml (6 to 60 μM). The samples were dissolved in 50 mM Na-MOPS (3-(N-morpholino)propanesulfonic acid), pH 7.0, with varying concentrations of MgCl₂, glycine and urea added, and equilibrated for 20 min at 50 °C. Samples were flash frozen in liquid nitrogen and stored and shipped at −20 °C. Immediately before data taking, samples were thawed and centrifuged for 10 min at 11,000 g.

As spectroscopic standards we used a 24mer DNA duplex (prepared as described⁶³) at a concentration of 1 mg/ml suspended in 50 mM Na-MOPS with 10 mM MgCl₂ added and 8 mg/ml horse heart cytochrome c as purchased from Sigma in 100 mM acetate, pH 4.6, with 0.5 M GdnHCl added. For each condition, five exposures (1.0 s for RNA and DNA and 0.1 s for cytochrome c) each were taken, data was image corrected, normalized by incident flux and circularly averaged. The five profiles for each condition were averaged to improve signal quality. Appropriate buffer profiles were collected using identical procedures and subtracted for background correction.

The data showed no signs of radiation damage, as tested by comparing scattering profiles of subsequent exposures on the same sample. Profiles for the same buffer conditions at different RNA concentrations are superimposable after scaling by concentration, indicating the absence of significant interparticle interference effects (data not shown).

SAXS data analysis

Scattering intensities were recorded as a function of the momentum transfer q, in the range 0.018 Å⁻¹ < q < 0.3 Å⁻¹, with q = 4π sin(θ)/λ, where 2θ is the total scattering angle and λ the x-ray wavelength, λ = 1.0 Å for all measurements. Radii of gyration, R_g, and forward scattering intensities, I(0), were obtained from background subtracted and averaged profiles by Guinier analysis of the low angle data.^{30, 64} The forward scattering intensity (I(0)) is proportional to the square of the number of excess electrons. It can be expressed in terms of the molecular weight (M) and average electron density contrast (Δρ),³⁰ as I(0) = κc(Δρ)²M², where c is the concentration of the molecular species and κ is a constant that was determined from measurements of a 24mer DNA duplex and horse heart cytochrome c as molecular weight standards of known molecular weight, concentration and electron density contrast.

The molecular weight estimate of 71 ± 6 kDa agree with the theoretical molecular weight for VCI-II of 74 kDa within experimental errors, indicating that the VCI-II construct is monomeric under all studied conditions.

The program GNOM⁶⁵ was used to perform regularized indirect transforms of the scattering data to obtain P(r) functions (a histogram of interatomic distances). The P(r) function has a maximum at the most probable intermolecular distance and goes to zero at D_max, the maximum intramolecular distance. For each measured scattering profile regularized transforms are performed with the input parameter D_max varied in steps of 2 Å. Values of D_max were chosen that yielded solutions that i) fit the experimental data well and ii) have a smooth and strictly positive P(r) function.

Comparing the SAXS data from RNA batches prepared by gel-purifications and phenol-chloroform extractions yielded very similar results. In particular the low angle regions relevant for the Guinier fits are superimposible and show no significant difference. We did observe a tendency for the background subtracted profiles from phenol-chloroform extracted RNA batches to exhibit slightly lower scattering intensity at high angles, q > 0.2 Å⁻¹, compared to RNA constructs that were purified by PAGE. These differences might be due to a slight mismatch of the buffer recorded for background subtraction due to additional salt in the RNA sample or due to a very small scattering contribution from small acrylamide contaminants at high angles. However, the differences do not affect the results presented here and the conclusions obtained.

Modeling of scattering data

The program dammin³⁸ was used to construct 3-D bead models that fit the scattering data. The program employs a simulated annealing procedure and a “compactness criterion”. For each of the basic states three representative scattering profiles were chosen. Ten independent dammin runs were performed for each scattering profile in the “fast” mode, and ten additional runs in the “slow” mode that uses more beads in the reconstruction and a higher number of spherical harmonics to evaluate the scattering pattern. The program was run using default parameters, no symmetry assumptions (P1 symmetry) and the full recorded scattering profiles. Each “fast” reconstruction took 1–2 h of CPU time on a 3.06 GHz Xeon workstation, each of the “slow” reconstruction about 10–12 h. The models resulting from independent runs were superimposed using the program supcomb,⁴⁸ which performs an initial alignment of structures based on their axes of inertia followed by minimization of the normalized spatial discrepancy (NSD). For two sets of points S₁ = {s_1,i, i = 1, ..., N₁} and S₂ = {s_2,i, i = 1, ..., N₂} the NSD is defined as

$$NSD(S_1,S_2)={\left(\frac{1}{2}\left(\frac{1}{N_1{d}_2^2}\sum _{i=1}^{N_1}{\rho }^2(s_{1,i},S_2)+\frac{1}{N_2{d}_1^2}\sum _{i=1}^{N_2}{\rho }^2(s_{2,i},S_1\right)\right)}^{1/2}$$

where ρ(s_1,i, S₂) is minimum value among the distances between s_i,1 and all points from S₂ and d_i is the average distance between neighboring points in S_i. The NSD has the property that it is zero for identical objects and larger than 1 for objects that systematically differ from one another.⁴⁸ The aligned structures were averaged using the program DAMAVER,⁶⁶ giving an effective occupancy of each voxel. Keeping all occupied voxels generates a convex hull of all models (shown as transparent surfaces in the bottom row of Figure 7), filtering at half maximal occupancy provides “filtered” models (rendered in the top three rows in Figure 7). In order to better visualize the results, the reconstructed bead models were converted to electron density maps using real space convolution with a Gaussian kernel with the program Situs.^{67, 68} A kernel width of 6 Å and voxel spacing of 2 Å were employed. Molecular graphics were prepared using the program PyMOL.⁶⁹

Hydroxyl radical footprinting

5′-Radiolabeled RNA (10⁵ counts per minute) was dissolved in 50 mM Na-MOPS (3-(N-morpholino) propanesulfonic acid), pH 7.0, with different concentrations of glycine and MgCl₂ and equilibrated for 20 min at 50 °C. The footprinting Fenton reaction was carried out with final concentrations of 0.1 mM Fe(NH₄)₂(SO₄)₂, 0.062 mM EDTA (Ethylenediaminetetraacetic acid) and 5 mM sodium ascorbate for 60 min at 25 °C. The reaction products were separated on a denaturing 8% polyacrylamide gel, bands were quantitated using storage phosphor imaging (ImageQuant). Autoradiograms were analyzed with single nucleotide resolution using the SAFA (Semi-Automatic Footprinting Analysis) software.⁷⁰ To correct for loading differences across lanes a standardization procedure was employed. The method of Takamoto, et. al.⁷¹ was used to find the best residues for standardization of each gel individually. From all repeat measurements of the same titration the five globally best residues were selected based on their rank order from the Takamoto et. al. procedure and used as standardization residues across all gels for this measurement. The standardization residues were 87, 89, 95, 102, and 122 for the glycine titration, residues 38, 51, 69, 79, and 112 for the Mg²⁺ titration in the absence of glycine and residues 44, 68, 72, 109, and 130 for the Mg²⁺ titration with 10 mM glycine added. The relative protections (or “apparent saturations”) visualized in Figures 1, 3, and 4 were computed as Relative protection = R/R_ref − 1, where R is the standardized intensity and R_ref is the standardized intensity of a references lane. For the Mg²⁺ titration the lanes with no Mg²⁺ were chosen as references; for the glycine titrations those with no glycine were used.