Abstract
B. licheniformis exo-small β-lactamase (ESBL) has two nonsequential domains and a complex architecture. We replaced ESBL serine residues 126 and 265 with cysteine to probe the conformation of buried regions in each domain. Spectroscopic, hydrodynamic, and chemical methods revealed that the mutations do not alter the native fold but distinctly change stability (S-126C > wild-type > S-126/265C > S-265C ESBL) and the features of partially folded states. The observed wild-type ESBL equilibrium intermediate has decreased fluorescence but full secondary structure. S-126C ESBL intermediate has the fluorescence of the unfolded state, no thiol reactivity, and partial secondary structure. S-265C and S-126/265C ESBL populate intermediate states unfolded by fluorescence and thiol reactivity but with full secondary structure. Mass analysis of S-126/265C ESBL in the partially folded state proved that both thiol groups become exposed simultaneously. None of the intermediates is compatible with sequential domain unfolding. Molecular dynamics simulation suggests that the stabilizing effect of the S-126C substitution is due to optimization of van der Waals interactions and packing. On the other hand, destabilization induced by the S-265C mutation results from alteration of the hydrogen-bond network. The results illustrate the large impact that seemingly conservative serine-to-cysteine changes can have on the energy landscape of proteins.
INTRODUCTION
It is a tenet of biochemistry that the three-dimensional (3D) structure of proteins is encoded in the amino acid sequence (1), but the logic of the code is poorly understood. Many studies are carried out to characterize the structure of partially folded states populated transiently or at equilibrium. The impetus for these studies comes from the expectation that knowing the structure of partially folded states will clarify the mechanism of folding (2–4). In this regard, the realization that some partially folded structures result from kinetic traps that slow folding (5) prompts a word of caution. Nonetheless, the impressive improvement in NMR spectroscopy now allows characterizing partially folded states in equilibrium with the native state ensemble (6) and residual structure in largely unfolded states (7). This focuses folding studies on how the molecule is organized in the absence of a fully formed network of tertiary interactions and on the identification of sequence determinants of 3D structure (8).
Insight into partially folded states is also of considerable biotechnological interest. Design, production, and handling of active proteins are plagued with difficulties that can be surmounted with a deep understanding of the properties of these states (9–11). The differential effects of mutations on the properties of partially folded and nonnative states are of particular importance (12–14).
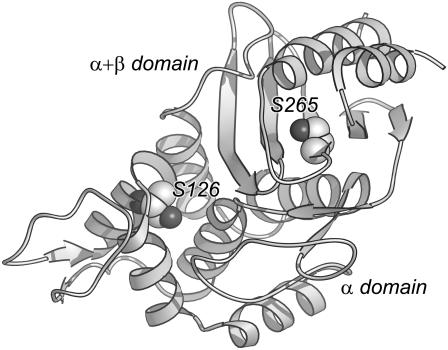
B. licheniformis exo-small β-lactamase (ESBL) (Fig. 1) is a 29.4-kDa, cysteineless protein with two domains and a complex architecture (15,16). The α + β domain (residues 26–60 and 216–295) is discontinuous and comprises a central five-stranded β sheet and three superficial α helices. The α domain (residues 61–215) is a globular array of six helical elements. The catalytic site is located in the interface between the two domains. The general folding properties of ESBL are known: it is a very stable protein that under denaturing conditions populates several partially folded states (17,18).
FIGURE 1.
The structure of ESBL. The cartoon depicts the two domains of the protein and the location of S-126 and S-265. The figure was prepared using Ribbons (21).
In some cases, structural domains are also folding units (19). Given the particular architecture of ESBL and its tendency to adopt partially folded conformations, it is natural to ask whether its two domains fold concertedly or independently. To investigate this issue, we prepared three ESBL variants in which cysteine replaced core serine residues (Fig. 1): S-265C ESBL contains a single cysteine in the α + β domain, deeply buried underneath the C-terminal α-helix; S-126C ESBL contains a cysteine residue deeply buried in the α-domain; and S-126/265C ESBL serves as an additivity control. Serine was mutated to cysteine and not to another amino acid because the introduced sulfhydryl allows the monitoring of the unfolding of each domain by chemical modification. Furthermore, serine and cysteine differ only at the γ atom and have similar side-chain volume, which facilitates molecular dynamics simulations (MDS) of the replacement.
The urea-induced, equilibrium unfolding of the three ESBL variants was monitored in parallel by circular dichroism (CD), tryptophan fluorescence, and thiol-specific chemical reactivity. Thus, at increasing urea concentrations, secondary and tertiary structures were assessed, as well as the solvent accessibility of specific regions of the protein. Moreover, the effects of the mutations on protein conformation were studied by MDS, providing estimates for the ΔG of unfolding comparable to the experimentally determined values.
The results rule out sequential unfolding of the domains, demonstrate that the structure and stability of partially folded states of ESBL is highly sensitive to the introduced mutations, and provide insight into the structural changes that ESBL undergoes to accommodate the oxygen to sulfur replacements.
MATERIALS AND METHODS
General details
Benzylpenicillin (PG) was from Sigma (St. Louis, MO). Protein purity was assessed by sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS-PAGE). Enzymic activity was determined at 25°C (Δɛ240 nm = 570 M−1 cm−1; (20)) in 50 mM sodium phosphate, pH 7.0 supplemented with 1.5 μM bovine serum albumin and containing 0.5 mg/ml benzylpenicillin. Least-square fit was done using Microsoft Excel 2000. Mass spectroscopy (MS) was performed on a VG Quatro II (VG Biotech, Altrinchan, UK) triple quadrupole instrument equipped with an electrospray ionization source. Molecular graphics were prepared using Ribbons (21). Accessible surface area (ASA) was calculated using ACCESS (22,23), with a 1.4-Å probe. Unless otherwise indicated, the nonconsecutive residue numbering system of Ambler (24) was used for the ESBL sequence.
Protein expression and purification
DNA sequences encoding S-126C ESBL, S-265C ESBL, and S-126C/S-265C ESBL were prepared by polymerase chain reaction (PCR) mutagenesis using Pfu DNA polymerase (Stratagene, La Jolla, CA), appropriate primers, and pELB3 as template (17,25). PCR products were cut with restriction enzymes and ligated into the XbaI/BamHI site of pET9a, generating the expression plasmids pELB3S-126C, pELB3S-265C, and pELB3S-126C/S-265C. Protein expression and purification was done as described earlier (17).
Hydrodynamic and optical studies
Analytical size exclusion chromatography (SEC; (17)) was carried out at 22°C using 100 mM sodium phosphate, pH 7.0 (Buffer A). Ultraviolet (UV) absorption and CD spectra were acquired and processed following published procedures (26). Unless otherwise indicated the buffer for optical measurements was 25 mM sodium phosphate, 100 mM sodium fluoride, pH 7.0 (Buffer B) and the temperature was set to 20°C. Near-UV measurements were carried out with a 1.0-cm cell containing 15-μM protein. In the far-UV, cell and protein concentration were 0.1 cm and 1.5 μM, respectively.
Fluorescence measurements were made at 20°C with a K2 ISS spectrofluorometer (ISS, Champaign, IL). Protein solutions (3 μM) were prepared in Buffer A supplemented with 1 mM EDTA. Excitation was at 295 nm (8 nm bandwidth), and data were acquired at 1-nm intervals between 250 and 450 nm. Quantum yield (Q) was calculated as described previously (18).
Equilibrium unfolding
Unfolding transitions as a function of temperature were monitored by CD at 220 nm. Protein concentration was 1.5 μM, and a 1.0-cm cell was used. Buffer B was adjusted to pH 6.0, 6.5, 7.0, 7.5, and 8.0. Temperature was varied from 0°C to 95°C with a rate of 2°C min−1, and the melting curve was sampled at 0.2-min intervals. Assuming an equilibrium with only native (N) and unfolded (U) states (N↔U), data were fitted to the following equations (27):
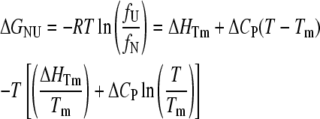 |
(1) |
and
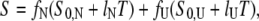 |
(2) |
where fU and fN are the unfolded and folded fractions, Tm is the temperature at which fU = fN, S is the observed CD signal, S0,N and S0,U are the intrinsic spectroscopic signals for the native and unfolded state, respectively, and lN and lU are the slopes for the assumed linear dependence of S0,N and S0,U with the temperature, respectively. The fit was performed simultaneously for all five pH, with a global ΔCP and pH-specific energy and signal parameters.
Isothermal unfolding experiments were carried out incubating the ESBL variants with 0–8 M urea in Buffer A for 3 h at room temperature and then measuring CD, fluorescence, and thiol reactivity. A three-state unfolding mechanism with a partially folded state (I) at equilibrium with N and U was assumed. The raw optical values for 0 and 8 M urea were as expected for native and fully unfolded states, respectively. This allowed normalization of the data to unfolded fractions. The following equations (28) were used in the simultaneous fit of the three normalized signals:
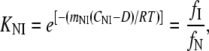 |
(3) |
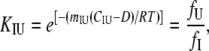 |
(4) |
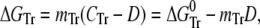 |
(5) |
and
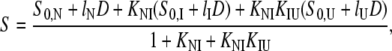 |
(6) |
where fN, fI, and fU are the fractions of native, partially folded, and unfolded state, Tr stands for NI or IU, KTr are equilibrium constants, D is the denaturant concentration, CTr is the denaturant concentration at which ΔGTr is zero, mTr is the slope of the linear dependency of ΔGTr on denaturant concentration, 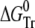 is ΔGTr at zero denaturant concentration, S0 is the value of the signal for each state extrapolated to zero denaturant concentration, and l is the denaturant dependence of the intrinsic signal for each state. The fit was performed with Ci and mi as common parameters for each variant, whereas the parameters related to the signals were specific to each particular probe. The fit was constrained by fixing mNI + mIU = 2.96, the predicted value for a protein the size of ESBL (29). Without this constraint, the fit converges to unreasonably high values of m and ΔG.
is ΔGTr at zero denaturant concentration, S0 is the value of the signal for each state extrapolated to zero denaturant concentration, and l is the denaturant dependence of the intrinsic signal for each state. The fit was performed with Ci and mi as common parameters for each variant, whereas the parameters related to the signals were specific to each particular probe. The fit was constrained by fixing mNI + mIU = 2.96, the predicted value for a protein the size of ESBL (29). Without this constraint, the fit converges to unreasonably high values of m and ΔG.
Thiol accessibility
Chemical reactivity toward 5,5′ dithiobis (2-nitrobenzoic acid) (DTNB) (30,31) was determined at 25°C in Buffer A. Paired solutions supplemented with 1 mM EDTA, urea 0–8 M, and either 6–8 μM protein or 0.78 mg/ml DTNB were prepared. Equal volumes of protein and DTNB solutions were mixed manually or using a stopped flow RX2000 (Applied Photophysics, Leatherhead, Surrey, UK) apparatus. Absorbance was monitored in thermostated cells at 425 nm. Solutions of 2-hydroxy-1-ethanethiol were used to establish the experimental conditions and the effect of urea viscosity on the reaction kinetics. A blank with no protein was run to subtract the absorbance of DTNB.
For mass analysis, solutions of 12 μM S-126/265C ESBL in Buffer A supplemented with 1 mM EDTA, and 0.0, 2.5, or 6.0 M urea were incubated at room temperature for 3 h. Incubations were made under nitrogen to minimize thiol oxidation. Subsequently, 100 μM DTNB was added to all samples, and the incubation was continued for 10 min. The reaction was stopped by protein precipitation with 25% trichloroacetic acid (4°C, 1 h) and centrifugation (14,000 rpm). Modified proteins were redissolved in 0.05% trifluoracetic acid and 6.0 M urea and injected into the HPLC-MS.
Computer simulations
MDS were carried out with GROMACS 3.2 (32) and GROMOS43a1 force field (33). The system was simulated as an isobaric-isothermal ensemble at 300 K and 1 bar, using periodic boundary conditions, 2-fs steps, and weak temperature and pressure coupling (0.1 and 1.0 ps−1 respectively (34)). Cutoff distances for neighbor searching, Lennard-Jones, and Coulombic interactions were 9, 9, and 14 Å, respectively. Long-range interactions were computed with the generalized reaction field method proposed by Tironi et al. (35).
The initial conformation of wild-type ESBL simulation was the PDB structure of Bacillus licheniformis β-lactamase (4BLM). All hydrogen atoms were fixed to the corresponding heavy atom. The protein was embedded in a ∼340-nm3 dodecahedral cell and solvated with ∼9970 water molecules using the extended single point charge (SPC/E) model (36). Conditioning included 1000 energy minimization steps and subsequent linear heating (from 0 to 300 K in 10 ps) by position-restrained MDS. The conditioned system was the starting point for the MDS.
To calculate the changes in energy due to the mutations by thermodynamic integration (37), the 2- and 10-ns unconstrained MDS structures were subjected to free energy perturbation (FEP). The force field parameters for Cβ, Oγ, and Hγ of serine were changed linearly to those corresponding to Cβ, Sγ, and Hγ of cysteine, respectively. The change was linked by λ, a variable ranging from 0.0 for serine to 1.0 for cysteine. Thus, the Hamiltonian associated to each ensemble was expressed as
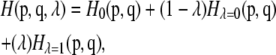 |
(7) |
where p and q are vectors corresponding to generalized momentum and atomic position, respectively, and ΔG of mutation (ΔGS→C) were calculated as
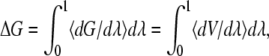 |
(8) |
where V is the potential energy and 〈〉 indicates time average. Numerical integration and error estimation were performed by the extended trapezoidal method (38).
The values of 〈∂V/∂λ〉 were obtained from 11 200-ps MDS intervals, each one with a fixed λ ranging from 0.0 to 1.0 in steps of 0.1. The transitions between consecutive intervals were of 100 ps, in which λ was linearly increased by 0.1. Thereafter, the runs were continued as to span 4.2–5.2 ns simulation time.
To characterize U, two 21-residue ESBL peptides (residues 116–136 and 255–275 for Ser-126 and Ser-265, respectively) were subjected to MDS. Each peptide was included in a dodecahedral box of ∼300 nm3, which suffices to avoid mirror interactions even in the maximally extended conformation. Water molecules were added as above. Initially, peptides were in native conformations. After minimization and position-restrained MDS, the system was heated linearly from 0 to 498 K in 10 ps followed by 1 ns equilibration at the final temperature. The resulting unfolded conformation was used as input for FEP at 300 K as described for the folded state mutations.
Typical atomic root mean-square fluctuations (RMSF) and root mean-square deviation (RMSD) of heavy atoms as a function of residue number were calculated as
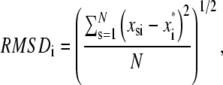 |
(9) |
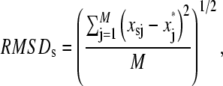 |
(10) |
and
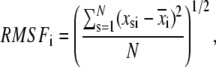 |
(11) |
respectively, where x represent atomic coordinates, the asterisk indicates the reference structure, and subindices i, j, s index α carbons, heavy atoms, and time step, respectively.
RESULTS
Protein purification and characterization
The four ESBL variants showed excellent expression behavior, resulting in 80–250 mg of soluble and enzymatically active protein per liter of culture. Judging from SDS-PAGE analysis, the proteins were purified to homogeneity (not shown). Mass spectrometry results for wild-type, S-126C, S-265C, and S-126/265C ESBL were 29,374 ± 1, 29,391 ± 2, 29,392 ± 2, and 29,408 ± 2 Da, respectively, identical within 1 Da to the masses calculated from the corresponding sequences.
The four variants have indistinguishable far- and near-UV CD spectra (not shown). They also exhibit nearly identical hydrodynamic and spectroscopic properties (Table 1). Benzylpenicillin hydrolysis assays indicated that the S-126→C replacement diminishes the specific activity by 50%, whereas the S-265→C mutation leaves it almost unchanged. (Table 1). Since in the folded state residue 126 is very close to the catalytic Ser-70, the moderately low activity of the variants carrying the S-126C mutation may be due to minor distortions in the active site (see below). Taken together, the above results suggest that the mutations do not significantly change the overall conformation of ESBL.
TABLE 1.
General properties of ESBL variants
| ESBL | RS* | Q† | SH‡ | Specific activity |
|---|---|---|---|---|
| (Å) | (%) | |||
| Wild-type | 25.3 ± 0.7 | 0.24 ± 0.02 | — | 100 |
| S-126C | 25.4 ± 0.8 | 0.26 ± 0.01 | 1.04 ± 0.05 | 52.0 ± 4.5 |
| S-265C | 25.6 ± 1.0 | 0.29 ± 0.01 | 1.07 ± 0.03 | 86.0 ± 5.6 |
| S-126/265C | 25.5 ± 1.1 | 0.29 ± 0.02 | 2.08 ± 0.06 | 53.6 ± 2.9 |
Mean ± SD of 2–3 determinations.
Stokes radius in Buffer A.
Fluorescence quantum yield in Buffer A.
Moles of thiol per mole of protein in 6 M urea at pH 7.0.
In the native state, the cysteine residues of the mutants do not react with DTNB, but they are fully reactive in 6 M urea (Table 1). This is in agreement with the crystallographic structure of ESBL, from which it can be calculated that serine residues 126 and 265 have 0.0% and 4.2% ASA, respectively. Thus, the inertness toward thiol modification provides strong reassurance that the mutants have native side-chain packing and conformational flexibility.
Thermal stability
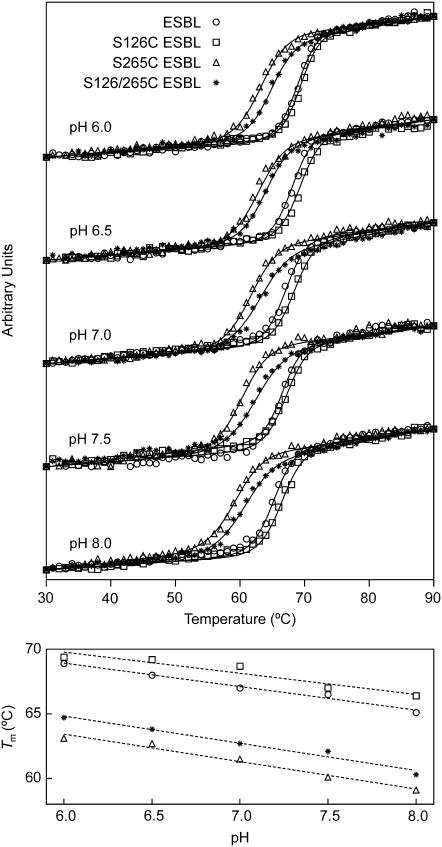
The unfolding transition of the ESBL variants at pH 6.0, 6.5, 7.0, 7.5, and 8.0 was monitored measuring the loss of helical content upon heating at constant rate (Fig. 2). Judging from the >85% signal recovering after reversing the temperature ramp (not shown), unfolding can be treated as reversible. The thermodynamic parameters obtained fitting Eqs. 1 and 2 to the data are listed in Table 2. The high melting temperature of the variants (59°C–69°C) indicates that they are quite stable. The thermal stability of ESBL and its variants decreases as the pH is increased from 6.0 to 8.0. Since deprotonation of histidine typically occurs in a similar pH range, the stability of the molecule may be related to the charge of its lone histidine.
FIGURE 2.
Thermal unfolding. The CD signals at 220 nm of S-126/265C, S-265C, S-126C, and wild-type ESBL as a function of temperature and pH are shown in the upper panel. Lines are the fit to Eqs. 1 and 2 with the parameters shown in Table 2. The dependence of Tm with pH is shown in the lower panel.
TABLE 2.
Thermal unfolding parameters
| Variant | pH °C |
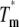 kcal mol−1 kcal mol−1
|
ΔHTm kcal mol−1 K−1 | ΔCP °C | Tx† kcal mol−1 | ΔGTx‡ |
|---|---|---|---|---|---|---|
| Wild-type | 6.0 | 68.9 ± 0.1¶ | 141 ± 2 | 3.9 ± 0.1 | 34.6 ± 0.1 | 7.2± 0.1 |
| 6.5 | 67.9 ± 0.1 | 147 ± 2 | 32.3 ± 0.1 | 7.8 ± 0.3 | ||
| 7.0 | 67.0 ± 0.2 | 140 ± 3 | 32.9 ± 0.1 | 7.2 ± 0.1 | ||
| 7.5 | 66.5 ± 0.1 | 163 ± 3 | 27.2 ± 0.1 | 9.6 ± 0.1 | ||
| 8.0 | 65.1 ± 0.2 | 133 ± 3 | 32.7 ± 0.1 | 6.5 ± 0.2 | ||
| S-126C | 6.0 | 69.3 ± 0.1 | 157 ± 9 | 4.0 ± 0.1 | 32.2 ± 0.1 | 8.7 ± 0.9 |
| 6.5 | 69.2 ± 0.1 | 144 ± 4 | 35.1 ± 0.1 | 7.3 ± 0.5 | ||
| 7.0 | 68.7 ± 0.1 | 148 ± 5 | 33.4 ± 0.1 | 7.8 ± 0.3 | ||
| 7.5 | 67.0 ± 0.1 | 139 ± 4 | 33.9 ± 0.1 | 6.9 ± 0.2 | ||
| 8.0 | 66.4 ± 0.2 | 137 ± 2 | 33.7 ± 0.1 | 6.7 ± 0.3 | ||
| S-265C | 6.0 | 63.1 ± 0.1 | 112 ± 5 | 3.3 ± 0.1 | 36.1 ± 0.1 | 4.6 ± 0.4 |
| 6.5 | 62.7 ± 0.1 | 110 ± 4 | 36.4 ± 0.1 | 4.4 ± 0.2 | ||
| 7.0 | 61.5 ± 0.2 | 109 ± 4 | 35.3 ± 0.1 | 4.3 ± 0.1 | ||
| 7.5 | 60.1 ± 0.1 | 108 ± 3 | 34.1 ± 0.1 | 4.2 ± 0.1 | ||
| 8.0 | 59.1 ± 0.1 | 104 ± 3 | 33.9 ± 0.1 | 4.0 ± 0.3 | ||
| S-126/265C | 6.0 | 64.6 ± 0.1 | 127 ± 7 | 2.9 ± 0.1 | 23.4 ± 0.1 | 7.9 ± 0.2 |
| 6.5 | 63.8 ± 0.1 | 112 ± 5 | 26.0 ± 0.1 | 6.7 ± 0.1 | ||
| 7.0 | 62.7 ± 0.3 | 101 ± 6 | 29.5 ± 0.1 | 5.1 ± 0.2 | ||
| 7.5 | 62.1 ± 0.1 | 95.6 ± 1 | 30.7 ± 0.1 | 4.6 ± 0.3 | ||
| 8.0 | 60.3 ± 0.3 | 93 ± 3 | 29.8 ± 0.1 | 4.3 ± 0.1 |
For a large set of protein-unfolding data it was found that m and heat capacity changes (ΔCP) values and changes in ASA (ΔASA) are correlated (29). Since ΔASA can be accurately predicted from the number of residues, the correlation provides a practical way to estimate the ΔCP of unfolding for any protein; from the data tabulated, estimated ΔCP for ESBL is 4.3 ± 0.2 kcal mol−1 K−1 (95% confidence interval). The ΔCP of ESBL unfolding determined by differential scanning calorimetry is 3.8 kcal mol−1 K−1 (Risso, V. A., et al., unpublished results). Thus a ΔCP of ∼4 kcal mol−1 K−1 can be taken as an indication of full unfolding. This threshold should also be valid for the mutants because the predicted increment in ΔCP for a Ser→Cys replacement (39,40) is negligible. According to this criterion, the data in Table 2 suggest that wild-type and S-126C ESBL exhibit full unfolding, whereas the transition might be incomplete for S-265C and S-126C/S-265C ESBL.
An incomplete transition for mutants that have a compact native state is generally ascribed to the presence of residual structure in the unfolded state. However, if a partially folded state (I) has native helical content, N→I transitions can go unnoticed in CD measurements. Likewise, I→U transitions can be overlooked if I and U are both devoid of secondary structure. Thus, it is also possible that in our experiment CD monitors the full N→U transition of wild-type and S-126C ESBL but only I→U or N→I for S-265C and S-126C/S-265C ESBL.
Another specific effect of the oxygen-sulfur substitution is evident from the thermodynamic stability of the mutants: at pH 7.0, S-126C ESBL is more stable than wild-type ESBL by 0.3 kcal mol−1, whereas S-265C and S-126/265C ESBL are destabilized by ∼2 kcal mol−1.
Urea-induced unfolding
Fig. 3 shows unfolding curves obtained by monitoring fluorescence, far-UV CD, and thiol reactivity. Since the α domain of ESBL concentrates ∼75% of the protein helical structure, the CD signal should be particularly sensitive to changes in that domain. On the other hand, fluorescence informs on the environment of tryptophan residues, of which there are one in the α domain and two in the α + β domain. Lastly, chemical reactivity of Cys-126 and Cys-265—which are deeply buried in the α and α + β domains, respectively—assesses the persistence of native core in the domains.
FIGURE 3.
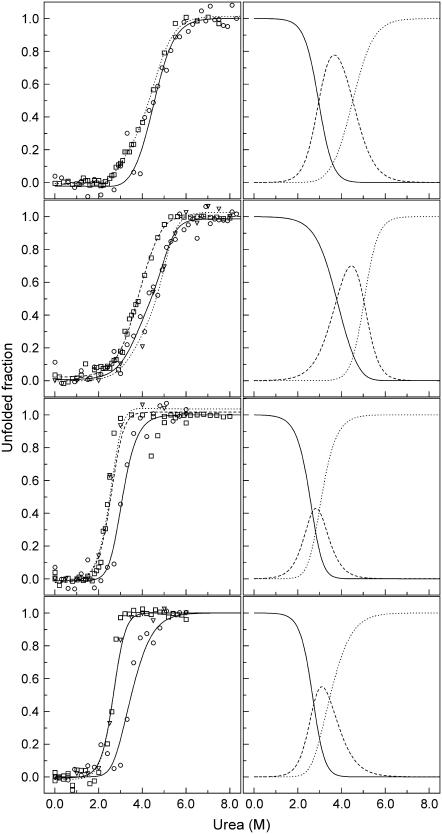
Urea-induced unfolding of wild-type (A), S-126C (B), S-265C (C), and S-126/265C (D) ESBL. Probes were CD (circles), fluorescence intensity (squares), and thiol reactivity (triangles). Lines are the fits to Eqs. 3–10 with the parameters given in Table 3. Left panels show the dependence of the observed and fit signals on urea concentration. Right panels show the calculated fractions for N (solid line), I (dashed line), and U (dotted line).
Unlike thermal unfolding monitored by CD, urea-induced unfolding monitored by the combined probes evidenced partially folded states. To facilitate the comparison of the curves and estimate the fractions of each state, a three-state model (see Materials and Methods) was assumed, and Eqs. 3–10 were fit simultaneously to all the data for each variant (Table 3 and Fig. 3). Since the three-state model may be an oversimplification and more complex equilibria may occur, the calculated curves are discussed only to illustrate general differences between the variants and are not to be taken as supportive of a particular unfolding mechanism.
TABLE 3.
Urea-induced unfolding parameters
| ESBL | 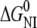 |
CmNI | 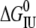 |
CmIU | S0,I,CD | S0,I,FL | S0,I,SH |
|---|---|---|---|---|---|---|---|
| Wild-type | 5.2 ± 1.8 | 3.0 ± 0.1 | 5.5 ± 0.9 | 4.5 ± 0.6 | 0.00 ± 0.09 | 0.18 ± 0.07 | — |
| S-126C | 4.3 ± 0.5 | 3.8 ± 0.1 | 9.1 ± 1.9 | 5.0 ± 0.1 | 0.57 ± 0.08 | 0.96 ± 0.09 | 0.43 ± 0.09 |
| S-265C | 4.1 ± 1.0 | 2.7 ± 0.2 | 4.2 ± 1.4 | 3.0 ± 0.3 | 0.00 ± 0.32 | 1.00 ± 0.28 | 1.05 ± 0.28 |
| S-126/265C | 5.1 ± 0.8 | 2.7 ± 0.1 | 3.8 ± 0.9 | 3.4 ± 0.3 | 0.00 ± 0.22 | 1.01 ± 0.09 | 1.00 ± 0.09 |
CmNI and CmIU are by definition the denaturant concentrations at which the corresponding equilibrium constants are 1. S0,I,CD, S0,I,FL, and S0,I,SH are the intrinsic degree of unfolding (as a fraction) of I measured by CD, fluorescence, and thiol reactivity, respectively. The units of Cm and free energy are M and kcal mol−1, respectively. The parameters were calculated by nonlinear least square fit of the data shown in Fig. 2 as described in Materials and Methods. Errors were calculated from the covariance matrix as described (38).
In ∼3.5 M urea, wild-type ESBL unfolds to a partially folded state with 80% of the native fluorescence intensity and 100% of the native helical content. Between 4 and 6 M urea, the fluorescence and CD curves converge; and, at 4.5 M urea, the average ESBL molecule has 50% of both ellipticity and fluorescence native signals. 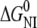 plus
plus 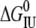 for ESBL is 10.6 kcal mol−1, which is—considering the error associated with each parameter—in reasonable agreement with the value calculated from thermal unfolding.
for ESBL is 10.6 kcal mol−1, which is—considering the error associated with each parameter—in reasonable agreement with the value calculated from thermal unfolding.
In 4.5 M urea, S-126C ESBL populates a partially folded state that is unfolded according to fluorescence and retains ∼40% of the secondary structure. Summing the two transitions, S-126C ESBL is more stable toward denaturation than wild-type ESBL (13.3 vs. 10.6 kcal mol−1), which is also in agreement with the thermal unfolding data. Strikingly, Cys-126 reactivity accompanies the CD rather than the fluorescence curves; and, in 4.5 M urea, only 40% of the molecules are modified by DTNB, which evidences the endurance of the tertiary structure surrounding Cys-126.
The partially folded state of S-265C ESBL is maximally populated at 2.9 M urea. The intrinsic fluorescence and CD signals of this state are equal to those of U and N, respectively. Unlike the case of S-126C ESBL, thiol reactivity of the partially folded state of S-265C ESBL is that of U. Thus, the tertiary structure of this variant seems to break down as a whole, exposing the tryptophan residues and Cys-265.
Judging from the CD and fluorescence curves, the S-265C mutation significantly destabilizes both secondary and tertiary structure relative to the unfolded state. Adding 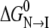 and
and 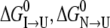 for S-265C ESBL equals 8.3 kcal mol−1, which is 2.3 kcal less than
for S-265C ESBL equals 8.3 kcal mol−1, which is 2.3 kcal less than 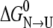 for wild-type ESBL. Since a similar destabilization was observed by thermal denaturation, this confirms that replacing the side-chain oxygen of residue 265 by sulfur is thermodynamically detrimental to the native state.
for wild-type ESBL. Since a similar destabilization was observed by thermal denaturation, this confirms that replacing the side-chain oxygen of residue 265 by sulfur is thermodynamically detrimental to the native state.
As for S-126/265C ESBL, its fluorescence and CD unfolding curves have apparent midpoints at 2.7 and 3.4 M urea, respectively, and—as seen for S-265C ESBL—the thiol reactivity curve matches that of fluorescence. The global stability of S-126/265C ESBL is 8.9 kcal mol−1; thus, the destabilizing effect of the S-265C change prevails over the stabilization of the S-126C change. The partially folded state of S-126/265C ESBL becomes maximally populated at 3.2 M urea and has—as in the case of S-265C ESBL—the fluorescence and thiol reactivity of the unfolded state in a context of native-like secondary structure.
To assess whether the thiol groups become exposed simultaneously, a mass analysis of the DTNB-modified protein was performed. Samples of S-126/265C ESBL were incubated in 0, 2.5, and 6.0 M urea to populate N, N + I, and U, respectively, after which the modification with DTNB was performed. The results were clear cut: in the folded state the chemical modification did not proceed at all, and a single mass corresponding to the unmodified protein was observed; in the unfolded state the reaction yielded an adduct corresponding to the lactamase plus two thionitrobenzoyl (TNB) moieties; and in 2.5 M urea the reaction yielded two products corresponding to the adduct with two TNB moieties and to the unmodified protein. In no case were species with a single TNB moiety detected. This demonstrated that the double mutant unfolds, exposing the two residues of cysteine simultaneously.
Structural modeling
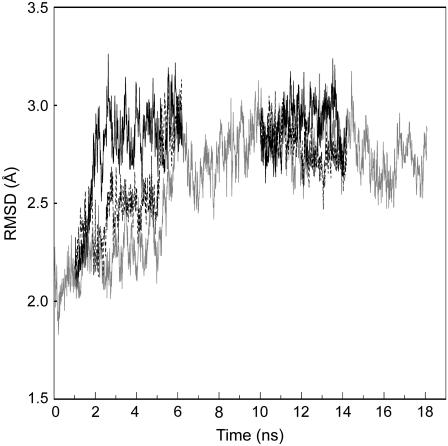
The structure of wild-type ESBL was subjected to 18 ns of MDS, and the coordinates at 2 and 10 ns were used as the starting points of four additional 5.2-ns MDS in which S-126→C and S-265→C mutations were computed. RMSD values of the five runs showed two plateaus: 2.0–2.5 Å and 2.5–3.0 Å at 0–5 and 6–18 ns, respectively (Fig. 4).
FIGURE 4.
Heavy atom displacements in the MDS of wild-type ESBL. RMSD was calculated according to Eq. 10 using the x-ray coordinates as the reference. The 0–18-ns dynamic of wild-type ESBL is shown as a gray line. The initial coordinates for the S-126→C (black line), and S-265→C (dashed line) ESBL FEP mutations were from the 2-ns and 10-ns structures of the wild-type run.
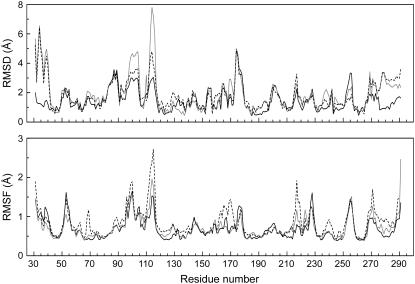
RMSD and RMSF for each residue during the 18-ns MDS of wild-type ESBL are plotted in Fig. 5. Most residues deviated from the reference coordinates <2.0 Å, as expected for thermal fluctuation in the native basin. However, four distinct changes occurred: in the Ω loop (residues 94–119), highly fluctuating residues 94–106 and 110–118 adopted an alternative conformation; the N-terminal helix (residues 31–41) moved ∼2 Å backward along its long axis; the C-terminal helix changed its position slightly as a consequence of the displacement of the N-terminus; and residues 174–176 departed slightly from the native conformation. The above conformational changes were also observed in each of the four Ser→Cys MDS (Figs. 5 and 6), and therefore we interpret them as the adaptation of the crystallographic structure to the simulated solution conditions.
FIGURE 5.
Heavy atom deviation and fluctuation at various intervals during the MDS of wild-type ESBL. Plots for 1–5-, 10–14-, and 14–18-ns intervals are shown as black, gray, and dashed lines, respectively. RMSD and RMSF were calculated by Eqs. 9 and 11.
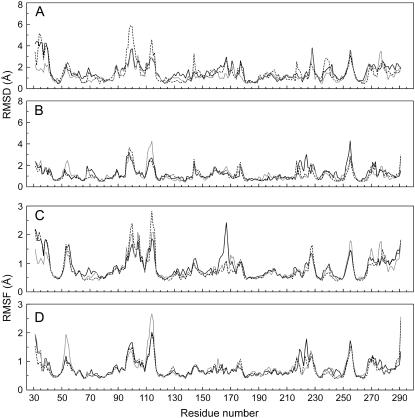
FIGURE 6.
Cα displacements and fluctuations in the mutated structures. Averaged structures corresponding to 6.4–7.4 ns (A and C) and 14.4–15.4 ns (B and D) were compared with the reference wild-type structure. The chosen intervals begin at the end of the simulated mutations and control. S-126→C and S-265→C mutation are represented by black and gray full lines, respectively; the dashed line corresponds to wild-type ESBL.
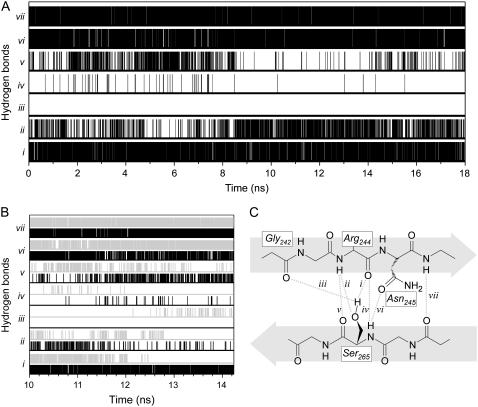
Three specific conformational effects were observed in the two MDS of each mutant. First, as happens in the control, in the S-126→C runs, Ser-265 Oγ formed a new hydrogen bond to Arg-244 N (Fig. 7). Second, in the S-265→C runs, the mutated side chain populated an alternative rotamer, lost the two γ-atom hydrogen bonds to Arg 244, and established a new one between the Sγ and the O atom of Gly-242 (Fig. 7). Concomitantly, residues 276–280—which connect strand β3 to the C-terminal helix and are located on top of Ser-265—departed slightly from the original conformation. Third, in the two S-126→C mutations, residues 222–224 departed from the reference, but neither the rotamer nor the hydrogen-bond status of side chain 126 changed significantly during the simulations (not shown).
FIGURE 7.
Hydrogen-bond inventory for residue 265. (A) Wild-type MDS. (B) S-126→C (black), and S-265→C (gray) MDS starting at 10-ns (identical trends were observed for the S→C mutations starting at 2 ns, not shown). (C) Diagram of the bonds referred to in A and B.
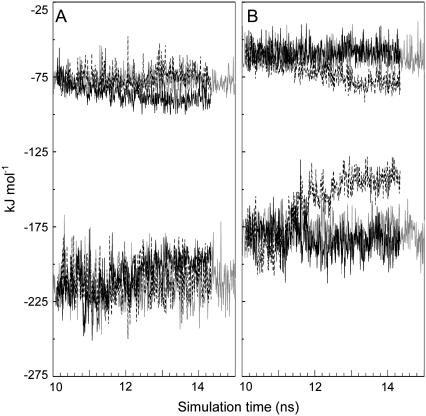
It is also worth noting that the Coulombic and van der Waals energies for all the interactions within 9 Å of side chains 126 and 265 showed specific differences (Fig. 8). For the S-126→C mutation van der Waals and Coulombic energies decreased and increased, respectively, nearly canceling each other. For S-265→C the components varied in the same fashion, but the Coulombic term is larger, causing a net destabilizing effect. Finally, the average number of contacts established by the 126 γ atom within a 5-Å radius sphere was larger for the S-126C ESBL than for wild-type and S-265C ESBL (not shown).
FIGURE 8.
Local energy changes during the mutations. The interaction energies of the atoms within spheres of 9.0-Å radius centered at the side chains 126 (A) or 265 (B) were summed. Van der Waals (upper traces) and couloumbic (lower traces) interactions are shown. Traces in gray correspond to wild-type ESBL; black and dotted lines refer to S-126→C and S-265→C mutations, respectively. Although only the runs starting at 10 ns are shown, identical trends were observed for the mutations started at 2 ns.
Thermodynamic modeling
The difference in unfolding free energy (ΔΔGNU) between wild-type ESBL and the mutants was calculated by FEP and thermodynamic integration (37) assuming the following cycle:
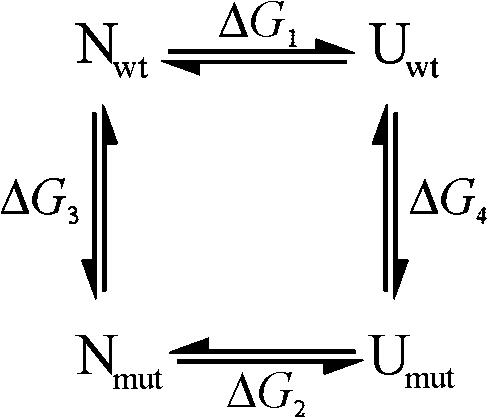 . .
|
Computing ΔΔGNU as ΔG2 − ΔG1 is infeasible because of the vastness of the conformational space of the unfolded state. Provided that the only relevant differences in the unfolded state between the wild-type and the cysteine mutants are circumscribed to the mutating residues and their sequential neighbors, ΔΔGNU can be estimated by the calculation of ΔG4 − ΔG3. To that end, the effects of the mutation on the folded state were simulated for the whole molecule, whereas the effects on the unfolded state were modeled for the mutated residue flanked by the corresponding 10-residue sequence at each side.
Integration of the time average derivative of the energy, 〈∂V/∂λ〉, yielded the energy changes listed in Table 4. In the unfolded state either of the two mutations destabilized the chain by nearly the same energy amount, indicating that contributions from neighboring residues were negligible or equally averaged and that most of the effect came from solvation and intraresidue effects.
TABLE 4.
Calculated stability changes upon the S→C mutations
| S-126C | S-265C | |
|---|---|---|
| NS→C, 2 ns | 16.5 ± 0.1 | 19.1 ± 0.1 |
| NS→C, 10 ns | 17.0 ± 0.1 | 20.1 ± 0.1 |
| US→C | 18.4 ± 0.1 | 18.3 ± 0.1 |
| ΔΔGN→U, 2 ns | 1.9 ± 0.2 | −0.7 ± 0.2 |
| ΔΔGN→U, 10 ns | 1.4 ± 0.2 | −1.7 ± 0.2 |
See Materials and Methods and the thermodynamic cycle depicted in the text.
Both mutations destabilized the native state as well. But the S-126C mutation destabilized the folded state less than the unfolded state and the S-265C mutation did the converse. Therefore ΔGNU,S-126C > ΔGNU,wt and ΔGNU,S-265C < ΔGNU,wt. ΔΔGNU calculated by integration of the curves for mutations starting at 2 ns were 1.9 ± 0.2 and −0.7 ± 0.2 kcal/mol for S-126C and S-265C, respectively; the cognate values for the 10-ns mutations were 1.4 ± 0.2 and −1.7 ± 0.2 kcal/mol. These values are in good agreement with the results for thermal and urea-induced unfolding experiments reported above.
DISCUSSION
This research builds upon the single-atom difference between the amino acids serine and cysteine, for which site-specific mutagenesis turns into atom-specific mutagenesis. It has been previously observed that this single-atom difference affects function and structure of proteins in a context-dependent fashion. Chou and co-workers studied three Ser-to-Cys mutants of trp repressor with altered affinity for tryptophan and/or DNA (41). In another work, four single-site Cys-to-Ser mutants of the DNA packaging machine of bacteriophage P22 exhibited important differences in stability and assembly kinetics (42). Also, in an insightful computational study (43), it was shown that a Ser-to-Cys replacement in the L1 loop of the core domain of p53 may cause a local conformational change and the destabilization of the protein, explaining the cancer susceptibility phenotype related to this mutation. In all the above cases, the impact of the Ser-to-Cys replacement seems to stem from differences in hydrogen-bonding propensities, hydrophobicity, and packing, which triggers conformational changes. Herein, we report that three serine-to-cysteine ESBL variants fold properly into stable native states but exhibit differences in global stability and in the intermediates populated at equilibrium under partially denaturing conditions.
In previous studies (18), we characterized ESBLCΔ9, a truncated variant that lacks nine residues in the α + β domain. It was found that ESBLCΔ9 folds into a compact intermediate that retains some degree of secondary structure but lacks tertiary interactions, suggesting that the α domain is unable to complete its fold without the cooperation of the α + β domain. In agreement, more recent results evidenced that the two domains of ESBL do not significantly populate N if expressed independently (V. A. Risso and M. R. Ermacora, unpublished results).
In this work, the spectroscopic and chemical features exhibited by the equilibrium intermediates confirm that they are not the combination of one native domain with the other in a partially folded state, i.e., the two canonical domains fold in concert. Nonetheless, the parallelism between the CD signal and chemical reactivity for S-126C ESBL and the correlation between CD, fluorescence, and chemical reactivity for S-265C ESBL suggest that the degree of structure persistence is strongly influenced by the core mutations. Particularly, an α-helical cluster involving cysteine 126 was identified that resists unfolding more than the tertiary structure monitored by fluorescence.
No comparable partially folded states at equilibrium were observed for the ESBL variants: wild-type ESBL populates a very structured I, with full secondary structure and almost native fluorescence; S-126C ESBL partially folded state is unfolded by fluorescence and 40% folded by CD; and S-265C intermediates are unfolded by fluorescence but retain full CD signal. Furthermore, thiol exposure in the partially folded states also differs between variants. This result suggests that the mutations have specific effects on the structures in the partially unfolded state ensemble, changing their relative stability and sorting out which will be observable in each case. Particularly, we propose that the S-126C mutation strongly stabilizes a tightened and reduced version of the array of helices in the α domain. Conversely, despite having native-like secondary structure, the S-265C partially folded state would be destabilized because the thiol group becomes solvated.
MDS allowed modeling the energetic and structural effects of the mutations on the native state with atomic resolution. According to geometrical considerations, the Oγ atom of Ser-126, deeply buried in the α domain, establishes only van der Waals interactions. The transformation Oγ→Sγ results in no significant differences in conformation for residue 126, but a better packing of the atoms surrounding Cys-126 suggests a diffuse improvement of multiple interactions. This improvement may be the product of the greater hydrophobic character of the thiol group (44–46), in agreement with the decrease in the van der Waals energy observed in Fig. 8. For a buried position and compared to cysteine, a serine side chain establishing no hydrogen bonds may seem a suboptimal choice from a structural point of view. However, too tight packing may affect the flexibility of the active site and reduce catalytic efficiency, suggesting a reasonable explanation for the diminished specific activity of the S-126C mutant and for the evolutionary conservation of serine at position 126.
Ser-265 is buried in the α + β domain, at hydrogen-bond distance to the Arg-244 O and Arg-244 N atoms. MDS showed that, as the mutation to cysteine progresses, the native rotamer becomes unstable, changes ∼90°, and forms a new hydrogen bond at the expense of two original ones. In the new conformation, the cysteine side chain improves its van der Waals interactions, but this is not enough to compensate for the hydrogen bond and Coulombic loses. Thus, for ESBL, having a cysteine at position 265 can be considered structurally detrimental.
We also attempted to model the double mutation S-126/265C as two sequential processes (wild-type→S-126C→S-126/265C and wild-type→S-265C→S-126/265C). The results were in good agreement with the individual mutations reported above (i.e., the S-126C mutation stabilizes the S-265C mutant and the S-265C mutation destabilizes the S-126C mutant; not shown). Not withstanding, these results were not presented in detail herein because the errors involved in the calculation are large compared to the net energy changes.
The finding that the energy of the unfolded state of ESBL is increased almost equally by either of the two mutations (Table 4) is most revealing and suggests that, for the unfolded chain, the adverse effect upon stability is mainly mediated through protein-solvent interactions and by protein-protein intraresidue (1–4 bonded) interactions. A preliminary attempt to estimate the relative contribution of these two terms along the simulations suggests that both are significant and Coulombic in character (not shown).
If the peptide model adopted in this work for the unfolded state is a faithful representation of the unfolded state of ESBL, the above result means that most of the effects of the mutations on stability should result from interactions in the native state. The simulation shows that the mutation at either of both positions destabilized the native state. Therefore, the opposite net effect observed in 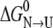 is due to the fact that the destabilization is less for S-126→C than for S-265→C. The above mentioned preliminary calculations here again suggest that the effect may be mediated mainly by intraresidue Coulombic effects. On the other hand, small-range nonbonded Coulombic effects seem to be opposite for the two variants: stabilizing for S-126→C and destabilizing for S-265→C. In the latter case, the loss of a hydrogen bond would explain most of the destabilizing effect, and therefore would be the main factor involved in S-265C ESBL relative instability.
is due to the fact that the destabilization is less for S-126→C than for S-265→C. The above mentioned preliminary calculations here again suggest that the effect may be mediated mainly by intraresidue Coulombic effects. On the other hand, small-range nonbonded Coulombic effects seem to be opposite for the two variants: stabilizing for S-126→C and destabilizing for S-265→C. In the latter case, the loss of a hydrogen bond would explain most of the destabilizing effect, and therefore would be the main factor involved in S-265C ESBL relative instability.
The behavior of the system studied herein may be revealing general trends for serine-to-cysteine mutagenesis of core residues. Substitution of hydrogen-bonded, core Oγ with sulfur is likely to result in the loss of that bond and in a less stable folded state. This effect would not be compensated for by the unfavorable solvation of the thiol group in the unfolded state. Additionally, compensatory effects due to the hydrophobic nature of sulfur must be expected, which may make the change less unfavorable.
The trend for core serine Oγ not involved in hydrogen bonds would be different. In this case, the mutation can lead to a more stable native state because the hydrophobic sulfur atom can interact better with nonpolar atoms. As explained above, the mutation destabilizes the unfolded state, and both effects add together to make 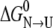 of the mutant larger. Hopefully, more studies of serine-to-cysteine core mutations will be available in the near future to establish the predictive value of these considerations in protein engineering.
of the mutant larger. Hopefully, more studies of serine-to-cysteine core mutations will be available in the near future to establish the predictive value of these considerations in protein engineering.
Summarizing, this work illustrates the ability of serine-to-cysteine core mutations to influence the folding landscape of a protein. Moreover, virtual modeling of the thermodynamic effects of the mutations on the native and unfolded state successfully accounted for the experimental observations. Thus this atom-specific mutation holds great promise to study protein folding by a combination of experimental and theoretical approaches.
Acknowledgments
We thank Prof. Anthony Fink for providing the wild-type lactamase gene and many suggestions on this protein. We also thank Lic. Inés Burgos and Dr. Gerardo Fidelio for making available to us their DSC instrument.
This work was supported by grants from Consejo Nacional de Investigaciones Cientificas y Técnicas, Universidad Nacional de Quilmes, and Agencia de Promoción Cientifica y Tecnológica.
Javier Santos and Valeria A. Risso contributed equally to this work.
Editor: Ruth Nussinov.
References
- 1.Anfinsen, C. B. 1973. Principles that govern the folding of protein chains. Science. 181:223–230. [DOI] [PubMed] [Google Scholar]
- 2.Levinthal, C. 1968. Are there pathways for protein folding? J. Chem. Phys. 65:44–45. [Google Scholar]
- 3.Levinthal, C. 1969. How to fold graciously. In Mossbauer Spectroscopy in Biological Systems: Proceedings of a Meeting Held at Allerton House. J. T. P. DeBrunner and E. Munck, editors. University of Illinois Press, Monticello, IL. 22–44.
- 4.Rumbley, J., L. Hoang, L. Mayne, and S. W. Englander. 2001. An amino acid code for protein folding. Proc. Natl. Acad. Sci. USA. 98:105–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Laurents, D. V., and R. L. Baldwin. 1998. Protein folding: matching theory and experiment. Biophys. J. 75:428–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Maity, H., M. Maity, M. M. Krishna, L. Mayne, and S. W. Englander. 2005. Protein folding: the stepwise assembly of foldon units. Proc. Natl. Acad. Sci. USA. 102:4741–4746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ackerman, M. S., and D. Shortle. 2002. Robustness of the long-range structure in denatured staphylococcal nuclease to changes in amino acid sequence. Biochemistry. 41:13791–13797. [DOI] [PubMed] [Google Scholar]
- 8.Gebhard, L. G., V. A. Risso, J. Santos, R. G. Ferreyra, M. E. Noguera, and M. R. Ermácora. 2006. Mapping the distribution of conformational information throughout a protein sequence. J. Mol. Biol. 358:280–288. [DOI] [PubMed] [Google Scholar]
- 9.Kuhlman, B., and D. Baker. 2000. Native protein sequences are close to optimal for their structures. Proc. Natl. Acad. Sci. USA. 97:10383–10388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Misura, K. M., and D. Baker. 2005. Progress and challenges in high-resolution refinement of protein structure models. Proteins. 59:15–29. [DOI] [PubMed] [Google Scholar]
- 11.Hecht, M. H., A. Das, A. Go, L. H. Bradley, and Y. Wei. 2004. De novo proteins from designed combinatorial libraries. Protein Sci. 13:1711–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shortle, D., and A. K. Meeker. 1989. Residual structure in large fragments of staphylococcal nuclease: effects of amino acid substitutions. Biochemistry. 28:936–944. [DOI] [PubMed] [Google Scholar]
- 13.Hughson, F. M., D. Barrick, and R. L. Baldwin. 1991. Probing the stability of a partly folded apomyoglobin intermediate by site-directed mutagenesis. Biochemistry. 30:4113–4118. [DOI] [PubMed] [Google Scholar]
- 14.Craig, S., M. Hollecker, T. E. Creighton, and R. H. Pain. 1985. Single amino acid mutations block a late step in the folding of beta-lactamase from Staphylococcus aureus. J. Mol. Biol. 185:681–687. [DOI] [PubMed] [Google Scholar]
- 15.Moews, P. C., J. R. Knox, O. Dideberg, P. Charlier, and J. M. Frère. 1990. Beta-lactamase of Bacillus licheniformis 749/C at 2 Å resolution. Proteins. 7:156–171. [DOI] [PubMed] [Google Scholar]
- 16.Knox, J. R., and P. C. Moews. 1991. Beta-lactamase of Bacillus licheniformis 749/C. Refinement at 2 Å resolution and analysis of hydration. J. Mol. Biol. 220:435–455. [DOI] [PubMed] [Google Scholar]
- 17.Frate, M. C., E. J. Lietz, J. Santos, J. P. Rossi, A. L. Fink, and M. R. Ermácora. 2000. Export and folding of signal-sequenceless Bacillus licheniformis beta-lactamase in Escherichia coli. Eur. J. Biochem. 267:3836–3847. [DOI] [PubMed] [Google Scholar]
- 18.Santos, J., L. G. Gebhard, V. A. Risso, R. G. Ferreyra, J. P. Rossi, and M. R. Ermácora. 2004. Folding of an abridged beta-lactamase. Biochemistry. 43:1715–1723. [DOI] [PubMed] [Google Scholar]
- 19.Garel, J. R. 1992. Folding of large proteins: multidomain and multisubunit proteins. In Protein Folding. T. E. Chreighton, editor. W. H. Freeman, New York.
- 20.Jansson, J. A. T. 1965. A direct spectrophotometric assay for penicillin β-lactamase (penicillinase). Biochim. Biophys. Acta. 99:171–172. [DOI] [PubMed] [Google Scholar]
- 21.Carson, M. 1997. Ribbons. Methods Enzymol. 277:493–505. [PubMed] [Google Scholar]
- 22.Richards, F. M. 1977. Areas, volumes, packing and protein structure. Annu. Rev. Biophys. Bioeng. 6:151–176. [DOI] [PubMed] [Google Scholar]
- 23.Richards, F. M. 1985. Calculation of molecular volumes and areas for structures of known geometry. Methods Enzymol. 115:440–464. [DOI] [PubMed] [Google Scholar]
- 24.Ambler, R. P., F. W. Coulson, J. M. Frere, J. M. Ghuysen, B. Joris, M. Forsman, G. Tiraby, and S. G. Waley. 1991. A standard numbering scheme for the class A β-lactamases. Biochem. J. 276:269–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Studier, F. W., and B. A. Moffatt. 1986. Use of bacteriophage T7 RNA polymerase to direct selective high-level expression of cloned genes. J. Mol. Biol. 189:113–130. [DOI] [PubMed] [Google Scholar]
- 26.Clerico, E. M., and M. R. Ermácora. 2001. Tryptophan mutants of intestinal fatty acid-binding protein: ultraviolet absorption and circular dichroism studies. Arch. Biochem. Biophys. 395:215–224. [DOI] [PubMed] [Google Scholar]
- 27.Fersht, A. 1999. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. W. H. Freeman, New York.
- 28.Santoro, M. M., and D. W. Bolen. 1992. A test of the linear extrapolation of unfolding free energy changes over an extended denaturant concentration range. Biochemistry. 31:4901–4907. [DOI] [PubMed] [Google Scholar]
- 29.Myers, J. K., C. N. Pace, and J. M. Scholtz. 1995. Denaturant m values and heat capacity changes: relation to changes in accessible surface areas of protein unfolding. Protein Sci. 4:2138–2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Riddles, P. W., R. L. Blakeley, and B. Zerner. 1983. Reassessment of Ellman's reagent. Methods Enzymol. 91:49–60. [DOI] [PubMed] [Google Scholar]
- 31.Silverstein, R. M. 1975. The determination of the molar extinction coefficient of reduced DTNB. Anal. Biochem. 63:281–282. [DOI] [PubMed] [Google Scholar]
- 32.Lindahl, E., B. Hess, and D. v. d. Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Mod. 7:306–317. [Google Scholar]
- 33.van Gunsteren, W. F., S. R. Billeter, A. A. Eising, P. H. Hünenberger, P. Krüger, A. E. Mark, W. R. P. Scott, and I. G. Tironi 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. Hochschulverlag AG an der ETH Zurich and BIOMOS b.v, Zurich, Groningen.
- 34.Berendsen, H. J. C., J. P. M. Postma, W. F. v. Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 35.Tironi, I. G., R. Sperb, P. E. Smith, and W. F. v. Gunsteren. 1995. A generalized reaction field method for molecular dynamics simulations. J. Chem. Phys. 102:5451–5459. [Google Scholar]
- 36.Berendsen, H. J. C., J. R. Grigera, and T. P. Straatsma. 1987. The missing term in effective pair potentials. J. Phys. Chem. 91:6269–6271. [Google Scholar]
- 37.Beveridge, D. L., and F. M. DiCapua. 1989. Free energy via molecular simulation: applications to chemical and biomolecular systems. Annu. Rev. Biophys. Biophys. Chem. 18:431–492. [DOI] [PubMed] [Google Scholar]
- 38.Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 1992. C: The Art of Scientific Computing. Cambridge University Press, New York.
- 39.Makhatadze, G. I., and P. L. Privalov. 1993. Contribution of hydration to protein folding thermodynamics. I. The enthalpy of hydration. J. Mol. Biol. 232:639–659. [DOI] [PubMed] [Google Scholar]
- 40.Privalov, P. L., and G. I. Makhatadze. 1990. Heat capacity of proteins. II. Partial molar heat capacity of the unfolded polypeptide chain of proteins: protein unfolding effects. J. Mol. Biol. 213:385–391. [DOI] [PubMed] [Google Scholar]
- 41.Chou, W. Y., and K. S. Matthews. 1989. Serine to cysteine mutations in trp repressor protein alter tryptophan and operator binding. J. Biol. Chem. 264:18314–18319. [PubMed] [Google Scholar]
- 42.Rodriguez-Casado, A., and G. J. Thomas Jr. 2003. Structural roles of subunit cysteines in the folding and assembly of the DNA packaging machine (portal) of bacteriophage P22. Biochemistry. 42:3437–3445. [DOI] [PubMed] [Google Scholar]
- 43.Pan, Y., B. Ma, R. B. Venkataraghavan, A. J. Levine, and R. Nussinov. 2005. In the quest for stable rescuing mutants of p53: computational mutagenesis of flexible loop L1. Biochemistry. 44:1423–1432. [DOI] [PubMed] [Google Scholar]
- 44.Nagano, N., M. Ota, and K. Nishikawa. 1999. Strong hydrophobic nature of cysteine residues in proteins. FEBS Lett. 458:69–71. [DOI] [PubMed] [Google Scholar]
- 45.Roseman, M. A. 1988. Hydrophilicity of polar amino acid side-chains is markedly reduced by flanking peptide bonds. J. Mol. Biol. 200:513–522. [DOI] [PubMed] [Google Scholar]
- 46.Lomize, A. L., M. Y. Reibarkh, and I. D. Pogozheva. 2002. Interatomic potentials and solvation parameters from protein engineering data for buried residues. Protein Sci. 11:1984–2000. [DOI] [PMC free article] [PubMed] [Google Scholar]