Varying environments can speed up evolution

Abstract

Simulations of biological evolution, in which computers are used to evolve systems toward a goal, often require many generations to achieve even simple goals. It is therefore of interest to look for generic ways, compatible with natural conditions, in which evolution in simulations can be speeded. Here, we study the impact of temporally varying goals on the speed of evolution, defined as the number of generations needed for an initially random population to achieve a given goal. Using computer simulations, we find that evolution toward goals that change over time can, in certain cases, dramatically speed up evolution compared with evolution toward a fixed goal. The highest speedup is found under modularly varying goals, in which goals change over time such that each new goal shares some of the subproblems with the previous goal. The speedup increases with the complexity of the goal: the harder the problem, the larger the speedup. Modularly varying goals seem to push populations away from local fitness maxima, and guide them toward evolvable and modular solutions. This study suggests that varying environments might significantly contribute to the speed of natural evolution. In addition, it suggests a way to accelerate optimization algorithms and improve evolutionary approaches in engineering.

A central question is how evolution can explain the speed at which the present complexity of life arose (1–17). Current computer simulations of evolution are well known to have difficulty in scaling to high complexity. Such studies use computers to evolve artificial systems, which serve as an analogy to biological systems, toward a given goal (6, 9, 18). The simulations mimic natural evolution by incorporating replication, variation (e.g., mutation and recombination), and selection. Typically, a logarithmic slowdown in evolution is observed: longer and longer periods are required for successive improvements in fitness (6, 9, 18) [similar slowdown is observed in adaptation experiments on bacteria in constant environments (19, 20)]. Simulations can take many thousands of generations to reach even relatively simple goals, such as Boolean functions of several variables (9, 18). Thus, to understand the speed of natural evolution, it is of interest to find generic ways, compatible with natural conditions, in which evolution in simulations can be speeded.

To address this, we consider here the fact that the environment of organisms in nature changes over time. Previous studies have indicated that temporally varying environments can affect several properties of evolved systems such as their structure (6), robustness (21), evolvability (22, 23), and genotype-phenotype mapping (10, 24). In particular, goals that change over time in a modular fashion (18), such that each new goal shares some of the subproblems with the previous goal, were found to spontaneously generate systems with modular structure (18).

Here, we study the effect of temporally varying environments on the speed of evolution. We tested the speed of in silico evolution when the goal changes from time to time, a situation which might be thought to make evolution more difficult. We considered a variety of scenarios of temporally varying environments. The speed of evolution is defined as the number of generations needed, for an initially random population, to achieve a given goal. We find that temporally varying goals can substantially speed evolution compared with evolution under a fixed goal (in which the same goal is applied continuously). Not all scenarios of varying goals show speedup. Large speedup is consistently observed under modularly varying goals (MVG), and, in some conditions, with randomly varying goals (RVG). A central aim was to find how the speedup scales with the difficulty of the goal. We find that the more complex the goal, the greater the speedup afforded by temporally varying goals. This suggests that varying environments may contribute to speed up natural evolution.

Results

We compared evolution under a fixed goal to evolution under four different scenarios of temporally varying goals: MVG and three different scenarios of RVG.

In MVG, we considered goals that can be decomposed into several subgoals (18). The goal changes from time to time, such that each new goal shares some of the subgoals with the previous goal. For example, the two subgoals described by the functions f(x, y) and h(w, z) can be combined by a third function g to form a modular goal with four inputs: G = g(f(x, y), h(w, z)). Modular variations of such a goal were generated by changing one of the functions g, f, or h. For example, consider the subgoals made of the exclusive-OR (XOR) function: f = x XOR y and h = w XOR z. One goal can be formed by combining these, using an OR function, G1 = g(f, h) = f OR h = (x XOR y) OR (w XOR z). A modular variation of this goal is G2 = g′(f, h) = f AND h = (x XOR y) AND (w XOR z) generated by changing the function g from g = OR to g′ = AND. A different modular variation is to G3 = g(f′, h) = (x EQ y) OR (w XOR z), by changing the function f from f = XOR to f′ = EQ (equals). In this way, a large number of modular goals can be generated.

In addition to MVG, we also examined periodic changes between a given goal G1 and a randomly selected goal R (6), and then back to G1 and so on. We considered two different scenarios of such RVG: in the first scenario, the goals change periodically between G1 and the same random goal R. This is called RVG_c, where c stands for constant random goal. In the second scenario, a new random goal is chosen every time the goal changes. This is called RVG_v, where v stands for varying random goal.

Finally, we examined a scenario where the goal switches periodically from a given goal G1 to a situation with no fitness selection and only neutral evolution. This scenario is called VG₀.

To compare the speed of evolution under a fixed goal with evolution under varying goals, we used standard genetic algorithms (25–27) to evolve networks that are able to make computations. The simulations start with a population of random networks. Each network in the population is represented by a genome that represents the nodes and connections in the network. Evolution proceeds toward a defined goal: to compute a specific output based on inputs. Each network is evaluated to compute its fitness, defined as the fraction of all possible input values for which the network gives the desired output. Networks with higher fitness are given a higher probability to replicate. Standard genetic operations [mutations and crossovers (recombination)] are applied to alter the genomes. As generations proceed, the fitness of the networks in the population increases, until a perfect solution to the goal is found [more details in Methods and supporting information (SI) Appendix]. For generality, we used four different types of well studied network models, including Boolean logic circuits, integrate-and-fire neural networks, and networks of continuous functions (Table 1). In addition to the computational models, we also considered a well studied structural model of RNA (28–32). In this model, we used genetic algorithms to evolve RNA molecules toward a specific secondary structure.

Table 1.

Evolution under varying environments: Speedup comparison summary

Model	Building blocks	Fold-Speedup for the hardest goals (Smax), mean ± SE
		MVG	RVGV	VG0	RVGC
1 Logic circuits	NAND gates	95 ± 45	45 ± 20	2.5 ± 2	<1
2 Feed-forward logic circuits	NAND, OR, AND	265 ± 150	160 ± 80	190 ± 90	1.3 ± 0.3
3 Feed-forward neural networks	Integrate-and-fire neurons	700 ± 450	10 ± 5	1.5 ± 1	<1
4 Feed-forward circuits	Continuous functions	60 ± 10	3 ± 1	3 ± 2	<1
5 RNA secondary structure	Nucleotides A, U, G, and C	25 ± 5	<1	<1	<1

Speedup results of evolutionary simulations of four different network models and a structural model of RNA. S_maxis defined as the speedup of the hardest goals (all goals with T_FG > G_max/2). S_max (mean ± SE) under four different varying goals scenarios are shown for each of the models. Bold, mean (S_max) > 3.

We begin with a detailed description of one case, and then summarize the results for all models. We start with combinatorial logic circuits made of NOT AND (NAND) gates. Circuits of NAND gates are universal in the sense that they can compute any logical function. They serve as the basic building blocks of current digital electronics. We evolved circuits built of NAND gates toward a fixed goal G1 made of three XOR operations and three AND operations acting on six inputs, G1 = [(x XOR y) AND (w XOR z)] AND [(w XOR z) AND (p XOR q)] (see SI Appendix, section 1.1). Starting from random circuits, the median time to evolve circuits that perfectly achieve this goal was T_FG = 8 × 10⁴ ± 2 × 10⁴ generations (the subscript FG corresponds to fixed goal).

Next, we applied MVG, in which goals were changed every E = 20 generations. In MVG, during the simulation, each new goal was similar to G1 except that one of the three AND operations was replaced with an OR or vice versa (see SI Appendix, section 1.1). Evolution under these changing goals rapidly yielded networks that adapt to perfect solutions for each new goal within a few generations. The median time to find perfect solutions for G1, from initial random population, was T_MVG = 8 × 10³ ± 1.5 × 10³ generations. This time was much shorter than in the case of a fixed goal, reflecting a speedup of evolution by a factor of ≈10, S = T_FG/T_MVG ≈ 10 (see Fig. 1a, arrow). Although the goals changed every 20 generations, a perfect solution for goal G1 was found faster than in the case where the goal G1 was applied continuously.

Fig. 1.

Evolution speedup under varying goals. The five panels show the speedup of different model systems. Each graph describes the speedup of evolution under MVG compared with fixed goal, versus the median time to evolve under a fixed goal (T_FG). Each point represents the speedup, S = T_FG /T_MVG, for a given goal. (a) Model 1: general logic circuits. (b) Model 2: feed-forward logic circuits. (c) Model 3: feed-forward neural networks. (d) Model 4: continuous function circuits. (e) Model 5: RNA secondary structure. Speedup scales approximately as a power law with exponents in the range α = 0.7 to α = 1.0. T₀ is the minimal T_FG value to yield S > 1 (based on regression). SEs were computed by using the bootstrap method.

We repeated this for different modular goals made of combinations of XOR, EQ, AND, and OR functions. The different goals each had a different median time to reach a solution under fixed goal evolution, ranging from T_FG = 2 × 10² to T_FG = 3 × 10⁶ generations. Thus, the difficulty of the goals, defined as the time needed to solve them “from scratch,” spanned about four decades. We find that the more difficult the fixed goal, the larger the speedup afforded by MVG (Fig. 1a). A speedup of ≈100-fold was observed for the hardest goals. The speedup S appeared to increase as a power-law with the goal complexity, S ∼ (T_FG)^α with α = 0.7 ± 0.1.

Next, we studied the other three scenarios of temporally varying goals on each one of the different goals. Again, the goals changed every 20 generations. The random goals were random Boolean functions. We found that under RVG_v, there was also a significant speedup, and under VG₀ and RVG_c there was a slowdown for most goals (Table 1, SI Appendix, section 3).

The second model we studied was feed-forward combinatorial circuits made of three logic gate types: AND, OR and NAND gates (Model 2). We evolved circuits toward the goals mentioned for model 1, and used similar MVG scenarios. We found that MVG speeded up evolution by a factor of up to 10³. Again, the more difficult the goal, the faster the speedup. The speedup scaled as S ∼ (T_FG)^α with α = 0.7 ± 0.1 (Fig. 1b). RVG_v and VG₀ also showed speedup, but smaller than under MVG; RVG_C showed a slowdown for all goals (Table 1).

In the two network models described above, the nodes compute logic functions. We also evolved networks in which the nodes compute real (non-Boolean) continuous functions (Models 3 and 4), and found similar conclusions. Model 3 used neural networks of integrate-and-fire nodes. In these networks, edges between nodes have weights. Each node sums the inputs multiplied by their weights, and outputs a one (fires) if the sum exceeds a threshold. The goals were to identify input patterns (SI Appendix, section 1.3). We find that MVG showed the highest speedup, and scaled with goal difficulty with exponent α = 0.8 ± 0.1 (Fig. 1c and Table 1).

In the last network model (Model 4), each node computes a continuous function of two inputs x and y: xy, 1 − xy and x + y − xy (see SI Appendix, section 1.4). The goals were polynomials of six variables. The variables were continuous in the interval between 0 and 1. We found that MVG showed the highest speedup, whereas the other scenarios showed virtually no speedup (Table 1). The speedup afforded by MVG increased with goal complexity (exponent α = 0.7 ± 0.1, Fig. 1d).

In the RNA secondary structure model, genomes are RNA nucleotide sequences, and the goal was a given secondary structure. We used standard folding algorithms (33) to determine the secondary structure of each sequence. The fitness of each molecule was defined as 1 − d/B, where d is the structural distance to the goal and B is the sequence length (see Methods). The goals were RNA secondary structure such as a tRNA structure; MVG were generated by modifications of hairpins in the original structure (see SI Appendix, section 1.5). Under MVG, the fitness increased significantly faster than under a fixed goal (SI Appendix, section 1.5), whereas all other scenarios showed slowdown (Table 1). The speedup afforded by MVG increased with goal complexity, with an exponent of α = 1.0 ± 0.2 (Fig. 1e).

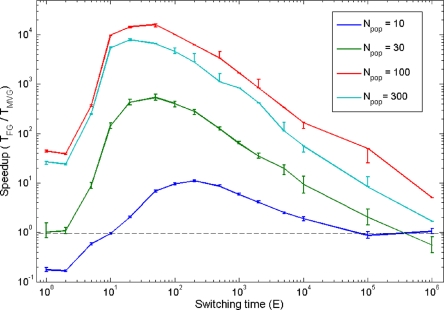
We next examined the effects of the simulation parameters on the speedup. We find that speedup under MVG occurs for a wide range of switching times (the number of generations between goal switches). For efficient speedup, the switching time of the goals should be larger than the minimal time it takes to rewire the networks to achieve each new goal and shorter than the time it takes to solve a fixed goal. In the present examples, the former is usually on the order of a few generations, and the latter is usually 10³ generations or larger. We thus find that the range of switching times with significant speedup typically spans several orders of magnitude (Fig. 2). Furthermore, speedup occurred for a wide range of population sizes, mutation and recombination rates, and selection strategies (see SI Appendix, section 6). We find a similar speedup also by using a hill-climbing algorithm (34) (see SI Appendix, section 7) instead of genetic algorithms. The fact that speedup is found in two very different algorithms suggests that it is a feature of the varying fitness landscape rather than the precise algorithm used.

Fig. 2.

Effect of frequency of goal switches on speedup. Speedup (±SE) is shown under different frequencies of goal switches and with various population sizes (N_pop). Results are for goal G1 = (x XOR y) OR (w XOR z), using a small version of model 2, with 4-input and 1-output goals (see Methods). In the MVG scenario, the goal switched between G1 and G2 = (x XOR y) AND (w XOR z) every E generations. The dashed line represents a speedup of S = 1.

Speedup is observed given that the problem is difficult enough, and that solutions for the different modular goals differ by only a few genetic changes in the context of the genotype used (otherwise the population cannot switch between solutions in a reasonable time). We found empirically that almost all modular goals of the form discussed above that require more than a few thousand generations to solve showed speedup under MVG.

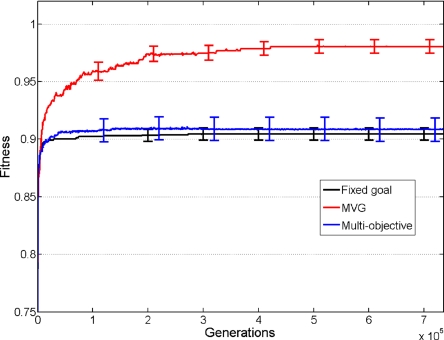
Next, we asked whether the observed speedup under MVG is due to goal modularity, goal variation, or both. For this purpose, we considered multiobjective optimization (35) in which the different variants of the modularly varying goals were represented as simultaneous (nonvarying) objectives. We compared the speed of evolution of MVG with both objectives: weighted multiobjective optimization and pareto multiobjective optimization (26) (SI Appendix, section 5). We find that the multiobjective scenarios showed virtually no speedup, whereas the equivalent MVG scenario showed speedup (Fig. 3 and SI Appendix, section 5). Thus, multiple modular goals by themselves, with no temporal variation, are not sufficient for speedup to occur.

Fig. 3.

Fitness as a function of time in MVG, fixed goal and multiobjective scenarios. Maximal fitness in the population (mean ± SE) as a function of generations for a 4-input version of model 1 for the goal G1 = (x XOR y) AND (w XOR z). For the MVG and multiobjective case, the second goal was G2 = (x XOR y) OR (w XOR z). For MVG, data are for epochs where the goal was G1. For multiobjective evolution, in which two outputs from the network were evaluated for G1 and G2, fitness of the G1 output is shown. Data are from 40 simulations in each case.

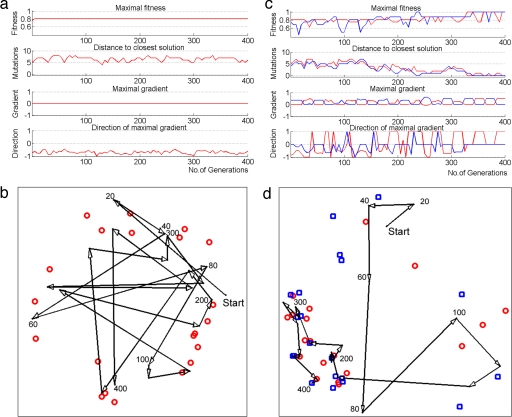
Finally, we aimed to discern the reason for the observed speedup in evolution. To address this, we fully mapped the fitness landscape of a version of model 2 with 4 inputs and 1 output by evaluating all 3 × 10¹¹ possible genomes (see Methods). Such full enumeration allowed us to track the evolving networks and their distance to the closest solution. We find that during evolution toward a fixed goal, the population became stuck at fitness plateaus (11) for long times. These plateaus are typically many mutations away from the closest solution for the goal. The maximal fitness gradient, defined as the maximal change in fitness upon a mutation, is zero in the plateau. Moreover, the gradient typically points away from nearby solutions (Fig. 4 a and b). This explains why it takes a long time to find solutions under a fixed goal. RVG_v seems to help by pushing the population in a random direction, thereby rescuing it from fitness plateaus or local maxima. We find that MVG has an additional beneficial effect: each time that a goal changes, a positive local gradient for the new goal is generated (Fig. 4c). Strikingly, we find that this gradient often points in the direction of a solution for the new goal. Thus, the population rapidly reaches an area in the fitness space where solutions for the two goals exist in close proximity (Fig. 4 c and d). In this area, when the goal switches, the networks rapidly find a solution for the new goal just a few mutations away (Fig. 4d).

Fig. 4.

Trajectories and fitness landscapes in fixed goal and MVG evolution. (a) A typical evolution simulation in a small version of model 2, toward the fixed goal G1 = (x XOR y) OR (w XOR z). Shown are properties of the best network in the population at each generation during simulation: fitness; distance to closest solution (the required number of mutations to reach the closest solution); maximal fitness gradient; and average direction of the maximal gradient. −1, away from the closest solution; +1, toward the closest solution. (b) The trajectory of the fittest network, shown every 20 generations (arrowheads). The trajectory was mapped to two-dimensions by means of multidimensional scaling (44), a technique that arranges points in a low dimension space while best preserving their original distances in a high-dimension space (the 38-dimensional genome space where each axis corresponds to one bit in the genome). Red circles describe the closest solutions. Numbers represent generations. (c) Same as in a but for evolution toward MGV, switching between G1 and G2 = (x XOR y) AND (w XOR z) every 20 generations. Properties of best circuit under goal G1 and G2 are in red and blue, respectively. (d) Trajectory of evolution under MVG. Red circles describe the closest G1 solutions, and blue squares describe the closest G2 solutions.

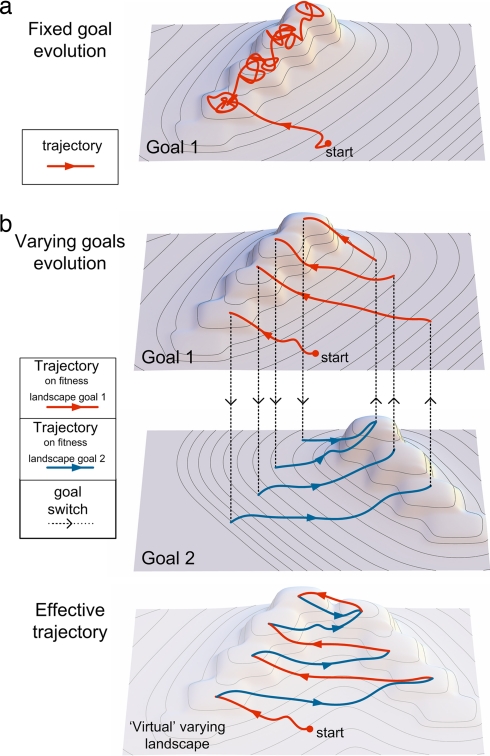
These findings lead to a schematic picture of how speedup might be generated (Fig. 5). Under a fixed goal, the population spends most of the time diffusing on plateaus or stuck at local maxima (Fig. 5a). Under MVG, local maxima or plateaus in one goal correspond to areas with a positive fitness gradient for the second goal (Fig. 5b). Over many goal switches, a “ramp” is formed in the combined landscape made of the two fitness landscapes, that pushes the population toward an area where peaks for the two goals exist in close proximity (Fig. 5b). It seems that this effect of MVG is different from a purely randomizing force [such as temperature in the language of Monte Carlo and simulated-annealing optimization algorithms (36)]. The effect may be related to the modular structure of the solutions found with MVG, with modules that correspond to each of the shared subgoals (18).

Fig. 5.

A schematic view of fitness landscapes and evolution under fixed goal and MVG. (a) A typical trajectory under fixed goal evolution. The population tends to spend long periods on local maxima or plateaus. (b) A typical trajectory under MVG. Dashed arrows represent goal switches. An effectively continuous positive gradient on the alternating fitness landscapes leads to an area where global maxima exist in close proximity for both goals.

Discussion

Our simulations demonstrate that varying goals can speed up evolution. MVG seemed to speed evolution in all models, and showed the highest speedup factor. We find that speedup increases strongly with the complexity of the goal. Not all types of temporally varying goals show speedup. RVG_V sometimes shows speedup, but this depends on the model and the fitness landscape. In contrast, RVG_C and VG₀ showed no speedup in most cases. The results thus highlight the ability of MVG to speed up evolution, based on variations between goals that share subgoals rather than between goals that do not.

Natural evolution usually occurs in temporally and spatially changing environments. These changes are often modular in the sense that similar biological subgoals are encountered in each new condition. On the level of the organism, for example, the same subgoals, such as feeding, mating, and moving, must be fulfilled in each new environment but with different nuances and combinations. On the level of cells, the same subgoals such as adhesion and signaling must be fulfilled in each tissue type but with different input and output signals. On the level of proteins, the same subgoals, such as enzymatic activity, binding to other proteins, regulatory input domains, etc., are shared by many proteins but with different combinations in each case. On all of these levels, goals seem to have shared subgoals that vary from condition to condition (niches, tissues, etc.).

The present study demonstrates the impact that varying environments might have on the speed of evolution. In all cases studied, the more complex the problem at hand, the more dramatic the speedup afforded by temporal variations. Although the present study aimed at understanding the speed of biological evolution, it may also apply to evolutionary approaches in engineering and to optimization algorithms (26, 36–39).

Methods

Genetic Algorithms Description.

We used standard genetic algorithms (26, 27) to evolve four network models and a structural model of RNA. The settings of the simulations were as follows. A population of N_pop individuals was initialized to random binary genomes of length B bits (random nucleotide sequences of length B bases in the case of RNA). In each generation, the L individuals with highest fitness (the elite) passed unchanged to the next generation [elite strategy, see SI Appendix, section 1]. The L least fit individuals were replaced by a new copy of the elite individuals. Pairs of genomes from the nonelite individuals were recombined (using crossover probability of P_c), and then each genome was randomly mutated (mutation probability P_m per genome). The present conclusions are generally valid also in the absence of recombination (P_c = 0). Each simulation was run until fitness = 1 was achieved for the goal (or for all goals in case of MVG). If the fitness was not achieved in G_max generations, T was set at G_max. We note that speedup occurred under a wide range of parameters (see SI Appendix, sections 1 and 6). The simulations did not include sexual selection (40), developmental programs (41), exploratory behavior (1, 4), evolutionary capacitance (42), or learning (43). For example, organisms seem to have mechanisms for facilitated phenotypic variation (1) that may further speed evolution. The impact of these effects on evolution under varying environments can in principle be studied by extending the present approach. For a detailed description of the algorithm, models, goals, and MVG schedules, see SI Appendix, section 1. Simulations were run on a 60-central processing unit computer grid.

Combinatorial Logic Circuits Composed of NAND Gates (Model 1).

Circuits were composed of up to 26 2-input NAND gates. Feedbacks were allowed. Goals were 6 inputs and 1- or 2-output Boolean functions composed from XOR, EQ, AND, and OR operations. The goal was of the form G = F(M1,M2,M3) where M1, M2, and M3 were two-input XOR or EQ functions. F was composed of AND and OR functions. The varying goal changed in a probabilistic manner every 20 generations by applying changes to F.

Feed-Forward Combinatorial Logic Circuits Composed of Several Gate Types (Model 2).

Circuits were composed of four layers of 8,4,2,1 gates (for the 1-output goals) or three layers of 8,4,2 gates (for the 2-output goals); the outputs were defined to be the outputs of the gates at the last layer. Each logic gate could be AND, OR, or NAND. Only feed-forward connections were allowed. Goals and MVG scenarios were similar to model 1.

Model 2, Small Version.

Circuits were composed of three layers of 4,2,1 gates; the output was that of the single gate at the third layer. Goals were 4 inputs, 1-output Boolean functions.

Neural Network Model (Model 3).

Networks were composed of seven neurons arranged in three layers in a feed-forward manner. Each neuron had two inputs, summed its weighted inputs and fired if the sum exceeds a threshold. Inputs to the network had three levels: low, medium, and high. The goal was to identify input patterns. MVG scenario: The goal was a combination R of two 2-input subgoals (S1, S2). R switched between AND and OR every 20 generations. In total we evaluated 15 goals composed of different combinations of eight different 2-input subgoals.

Continuous Function Circuits (Model 4).

Circuits were composed of four layers of 8,4,2,1 gates (for the 1-output goals) or three layers of 8,4,2 gates (for the 2-output goals). The outputs were those of the nodes at the last layer. Connections were allowed only to the next layer. Three types of 2-input continuous functions implementing: xy, 1 − xy, x + y − xy were used. Inputs had values between 0 and 1. A goal was defined by a multivariate polynomial (of six variables). MVG scenario: The goals were composed of three subgoals (T1, T2, and T3) combined by a function (U) on their output. T_i were bilinear functions of one of the forms: x + y − 2xy or 1 − x − y + 2xy. The varying goal switched in a probabilistic manner every 20 generations by applying changes on U.

RNA Secondary Structure (Model 5).

We used standard tools for structure prediction (33) available at www.tbi.univie.ac.at/RNA/, and the “tree edit” structural distance (33). The goals were the secondary structure of the Saccharomyces cerevisiae phenylalanine tRNA and a synthetic structure composed of three hairpins. For MVG, three modular variations of each of the two goals were constructed by changing each of the three hairpins in the secondary structure into an open loop. Goals changed every 20 generations.

Abbreviations

Gn

goal n

MVG

modularly varying goals

NAND

NOT AND

RVG

randomly varying goals

XOR

exclusive-OR.