Hydrodynamic Interactions between Two Swimming Bacteria

Abstract

This article evaluates the hydrodynamic interactions between two swimming bacteria precisely. We assume that each bacterium is force free and torque free, with a Stokes flow field around it. The geometry of each bacterium is modeled as a spherical or spheroidal body with a single helical flagellum. The movements of two interacting bacteria in an infinite fluid otherwise at rest are computed using a boundary element method, and the trajectories of the two interacting bacteria and the stresslet are investigated. The results show that as the two bacteria approach each other, they change their orientations considerably in the near field. The bacteria always avoided each other; no stable pairwise swimming motion was observed in this study. The effects of the hydrodynamic interactions between two bacteria on the rheology and diffusivity of a semidilute bacterial suspension are discussed.

INTRODUCTION

An interesting aspect of bacterial suspensions is that bacteria exhibit various types of collective motions. Recently, Dombrowski et al. (1) observed a mesoscale structure in a suspension of Bacillus subtilis in which a B. subtilis cell tended to swim in the same direction as its neighbors, generating a flow pattern larger than the scale of an individual cell but smaller than the scale of the container used in the experiment. The mesoscale structure changed its direction randomly in a manner reminiscent of turbulence, so they named this phenomenon “slow turbulence”. Mendelson et al. (2) also observed mesoscale motions of whorls and jets generated by B. subtilis experimentally. In their experiment, populations of B. subtilis were placed in a water film above an agar gel. It has been demonstrated that the diffusion in such suspensions is considerably enhanced by the mesoscale structures (3). Another well-known collective motion of bacteria is the band formation observed for magnetotactic bacteria. Magnetotactic bacteria contain intracytoplasmic Fe₃O₄ particles, and the magnetic dipole is oriented more or less parallel to the axis of motility of the cells (4). Spormann (5) and Carlile et al. (6) reported a migration phenomenon in suspensions of unidirectional magnetotactic bacteria swimming in narrow glass tubes subjected to magnetic fields in which thousands of cells formed a stable band perpendicular to the swimming direction.

Although the collective motions of bacteria are interesting and important when discussing suspension properties, such as rheology and diffusivity, the fundamental mechanism for these motions is still unknown. Analytical models have been proposed at a number of levels to better understand the mechanism of collective motions. Vicsek et al. (7) proposed an analytical model to express self-ordered motion in systems of particles with biologically motivated interactions. In their model, particles were driven with a constant absolute velocity and assumed the average direction of motion of the particles in their neighborhood at each time step with some random perturbations added. Ramaswamy and his co-workers (8,9) constructed hydrodynamic equations for suspensions of self-propelled particles, which considered the effect of swimming particles by adding force dipoles to the fluid momentum equation. Lega and Passot (10) applied a continuum model in the form of a mixture theory to two-dimensional bacterial populations. They triggered the motion of the mixture by applying a random external force to the particle. More recently, Hernandes-Ortiz et al. (11) performed direct simulations of large populations of confined hydrodynamically interacting swimming particles. In their model, the swimming motion of bacteria was modeled using three point forces per bacteria.

Although the results obtained from these studies are valuable and consistent with experimental observations, the near-field fluid dynamics have not been treated precisely. Even the latest works by Hernandes-Ortiz et al. (11) used three point forces to model swimming bacteria and neglected the torque balance of the swimming particles. Modeling a bacterium as a point force or stresslet is sufficient for discussing the far-field hydrodynamic interactions because higher moments decay rapidly if the distance between the particles is great enough. In the near field, however, all multipole moments contribute to the hydrodynamic interactions, and one cannot simplify the phenomena using the first few moments.

Ishikawa et al. (12,13) have shown both experimentally and analytically that the near-field interaction is important for discussing the stability of swimming motions, the trajectories of swimming cells, and the stresslet generated by the cells. Since the stability of swimming motions dominates the length and timescales of the coherent structure, the near-field hydrodynamic interaction should be treated precisely when discussing the collective motion of cells in the suspension. The change in trajectories also dominates the chaos or randomness of cell swimming so that the near-field hydrodynamic interactions again should be treated precisely when discussing the diffusivity of the suspension (14). Another important macroscopic quantity for a cell suspension is the particle stress tensor, which is dominated by the stresslet of the cells. Therefore, the near-field interaction must be treated precisely when examining the rheology of the suspension (15).

Some previous studies have solved the flow field around bacteria precisely. Phan-Thien and his group have reported the flow field around a solitary bacterium (16), the interaction between a bacterium and a wall (17), and the interaction between two bacteria fixed parallel to each other or straightly aligned in space (17,18). However, these studies did not discuss the trajectories of the two swimming bacteria and the stability of their swimming motions. Moreover, one cannot tell from these studies how the two-cell interaction affects the macroscopic quantities of the suspension, such as the rheology and diffusivity.

In this article, we solve the hydrodynamic interactions between two swimming bacteria precisely. We show the trajectories of two interacting bacteria and the stresslet for the first time to our knowledge. These are essential quantities when discussing the diffusivity and rheology of bacterial suspensions. We also show that a parallel swimming motion is unstable, which, to our knowledge, is a new finding that is important to the stability of collective motions in bacterial suspensions. Lastly, we discuss the effect of hydrodynamic interactions between two bacteria on the rheology and diffusivity of a bacterial suspension in a semidilute regime.

METHOD

Bacterial model

We used the same bacterial model as Phan-Thien and his group (16,17). The details of the model have been presented elsewhere, so only a brief explanation is given here. A bacterium is assumed to be neutrally buoyant because the sedimentation velocity for typical aquatic bacteria is much less than the swimming speed. The center of buoyancy of the bacterium is assumed to coincide with its geometric center. Consequently, the model bacterium is force free and torque free. The Reynolds number based on the swimming speed and body length is usually <10⁻³, so the flow field around the bacterium is assumed to be a Stokes flow.

Brownian motion is not considered, since typical bacteria have a body length, including flagella, of 2–10 μm (19) and are too large for Brownian effects to be important for the near-field interaction between bacteria. When two bacteria are far apart, however, we need to discuss carefully the effect of Brownian motion because it is one of the main factors for a real solitary bacterium to change its orientation. Berg (20,21) reported that the angular diffusion of Escherichia coli is ∼10° in 0.5 s. We should note that the orientation change of a real bacterium can be generated not only by the Brownian motion but also by the asymmetry of flagella shape, the shape change of flagellar bundle, deviation of the central axis of flagellar spiral from the body axis, interaction between bacteria, interaction between a bacterium and a wall, chemotaxis, and so on. Thus we cannot say that the angular diffusion observed in E. coli is due solely to Brownian motion. By assuming that the body length of E. coli is ∼2 μm and the swimming speed is ∼20 μm, solitary E. coli changes its orientation ∼10° after swimming five times longer than its body length. In this study, we do not discuss trajectories longer than seven times body length, and the orientation change is much larger than 10°. Thus, the effect of hydrodynamic interaction dominates the orientation change of two interacting bacteria in the parameter range used in this study.

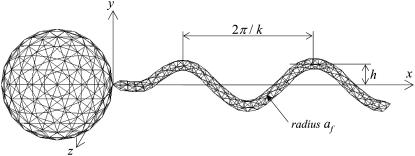
The geometry of a bacterium is modeled as a spherical cell body (or later as a spheroidal cell body, see Fig. 15) with a single helical flagellum, as shown in Fig. 1. Though the geometry employed in this study is simple, a number of real bacteria, notably eubacteria such as Photobacterium phosphoreum and Pseudomonas aeruginosa, have roughly a spheroidal cell body with a single helical flagellum. Many bacteria have several flagella attached at points distributed over the surface of the cell. When such bacteria are swimming, the separate flagella come together in a synchronous flagellar bundle, which propels the cell. Since the clearance between flagella in a bundle is very small, Brennen and Winet (19) mentioned in their review article that whether the principal propulsive unit is a single flagellum or a bundle has relatively minor effects on the external hydrodynamics. Thus, the flagellar geometry used in this study could be appropriate to a flagellar bundle too.

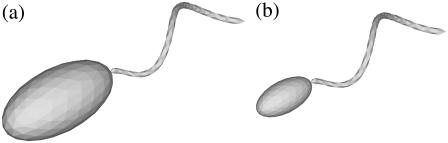
FIGURE 15.

Two bacterial shapes with an ellipsoidal cell body with an aspect ratio of 2.0.

FIGURE 1.

Shape parameters for a bacterial model with 360 and 320 triangle elements for the flagellum and spherical body, respectively. The total number of elements per bacterium is 680. (a) Shape A (h = 0.77, k = k_E = 1.3, and a_f = 0.1), (b) shape B (h = 0.77/2), and (c) shape C (h = 0.77/2, k = 2.6).

The bacterial model swims by executing a helical wave down its flagellum. Let r be the position vector relative to the contact point between the spherical cell body and the flagellum, and let the x axis coincide with the central axis of the helix. The position of any point along the centerline of the flagellum was derived by Higdon (22) and is given parametrically by

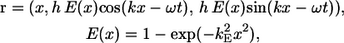(1)

where h is the amplitude, k is the wave number, ω is the angular frequency of the helical wave, and k_E is a constant that determines how quickly the helix grows to its maximum amplitude. We also assume that the flagellum is a cylindrical filament of cross sectional radius a_f. Phan-Thien et al. derived the position vector for any point on the surface of the flagellum (16).

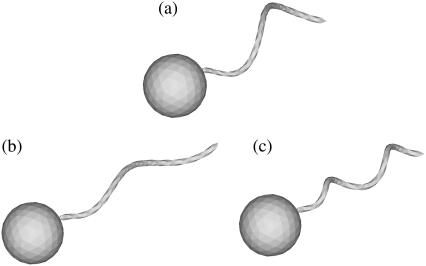
In this study, we used three flagellum shapes, as shown in Fig. 2. Shape A (Fig. 2 a) had parameter values of h = 0.77, k = k_E = 1.3, and a_f = 0.1. The length of the flagellum, which can be obtained from a line integral along its centerline, was 7.0. These values were set so that the bacterium was highly efficient in terms of swimming power consumption (cf. Phan-Thien et al. (16)). Shapes B and C have the same flagellum length, but h = 0.77/2 for shapes B and C and k = 2.6 for shape C. These parameters were used to determine the effect of h and k on the trajectories.

FIGURE 2.

Three bacterial shapes used in this study. (a) t = 0, (b) t = 70, (c) t = 100, (d) t = 140, (e) t = 200, and (f) t = 330.

Since some bacteria have ellipsoidal cell bodies, we also evaluated the effect of the aspect ratio of the cell body by selecting two ellipsoidal shapes, as shown in Fig. 15. Shapes D and E had the same flagellum as shape A, but the length of the major axis a_x and minor axis a_y were 2 and 1 for shape D and 1 and 0.5 for shape E, respectively.

Basic equations

The hydrodynamic interactions between two swimming bacteria were computed in an infinite fluid otherwise at rest. Since the Stokes flow field was assumed, the velocity field was developed instantaneously by the given boundary conditions. The numerical method used was similar to the one used by Ishikawa et al. (13), so only a brief explanation is given here.

When there are two bacteria in an infinite fluid, the Stokes flow field around the bacteria can be given in integral form as (23)

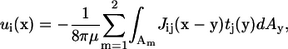(2)

where u(x) is the velocity at position x, μ is the viscosity, A_m is the surface of bacterium m, J is the Oseen tensor, and t is the traction force. The bacteria are assumed to be force free and torque free, so that

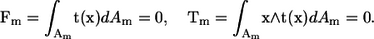(3)

On the surface of the body, the velocity field takes the form

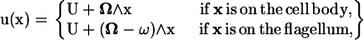(4)

where U and Ω are the translational and rotational velocities of the cell body, respectively. The flagellum rotates with respect to the rest frame with an angular velocity of (Ω − ω). Both U and Ω are determined as a part of the problem, so that Eqs. 2 and 3 are satisfied. Recently, Ishikawa and Hota investigated the hydrodynamic interactions between real microorganisms experimentally (12); the results showed that the interactions were mainly hydrodynamic. Therefore, the rotational motion of the flagellum relative to the spherical cell body was assumed to be invariant throughout the interactions. These governing equations were nondimensionalized using the radius of the spherical body, a, the angular velocity, ω, and the fluid viscosity, μ. We should note that a typical bacterium has the body length of ∼1–3 μm and the flagellar length of ∼3–6 μm. The typical angular velocity of a cell body when its flagellum is tethered is ∼100–1000 s⁻¹ (19).

Numerical method

The boundary element method was used to discretize the equations (cf. Ishikawa et al. (13)). The computational mesh generated on the surface of the bacterial model is shown in Fig. 1, where 360 triangle elements were generated for each flagellum and 320 elements were generated for each spherical body. The total number of elements per bacterium was 680. Both ends of the flagellum were assumed to be cones in the same manner as Phan-Thien et al. (16). The integration in Eq. 2 was performed on a triangular element using 28-point Gaussian polynomials. The singularity in the integration was solved analytically (23). The time marching was performed using the fourth-order Runge-Kutta method. The accuracy of this numerical method was verified by comparing our swimming velocities, swimming power, and trajectories for a solitary bacterium with previous solutions (16,24). Trial computations for the mesh convergence showed that the difference between the swimming velocities obtained using 680 and 2330 elements per bacterium was <2%.

In a previous study (13), we verified how accurately this method reproduced the lubrication forces between two nearby spheres. The results for shearing and squeezing motions agreed well with analytical solutions using lubrication theory when the gap between the two surfaces ɛ was >0.01 units. Fortunately, in this article, most of the computations were performed for bacteria that were separated by at least 0.01 units, including flagella, so we could accurately resolve the interactions with 680 elements per bacterium. Only when two bacteria initially faced each other (as shown in Fig. 6) did they come closer than 0.01 units. To avoid numerical errors due to the small gap and prohibitively small time steps for the computations, we introduced a short-range repulsive force given by

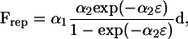(5)

where α₁ and α₂ are dimensionless coefficients and d is the unit vector passing through the minimum separation points on the two surfaces. This form of the interparticle force corresponds to charged particles interacting through colloidal forces at a constant surface charge (25) and has also been used in previous research (T. Ishikawa and T. J. Pedley, unpublished). The coefficients used in this study were α₁/(μa²ω) = 0.1 and α₂ = 100. The minimum separation obtained with these parameters was in the range 10⁻²–10⁻³ units. The effect of the repulsive force on the trajectories was very small because it acts only in the very near field and changes the distance between particles by only 10⁻² units. The repulsive force had no effect in this study except when two bacteria were initially facing each other (see Fig. 6).

FIGURE 6.

Sequences a–d showing the interactions between two shape A bacteria initially facing each other at a distance of five units, as shown in a.

RESULTS

We begin by introducing interesting features of the trajectories for three initial orientations: a), two bacteria initially placed parallel, b), two bacteria initially facing each other, and c), two bacteria initially placed at right angles. Let the x direction be e₁, where e₁ is the orientation vector of bacterium 1. Let two orientation vectors, e₁ and e₂, and the center of spherical cell bodies, r₁ and r₂, be in the same x-y plane. Although our initial conditions were restricted to two dimensions, i.e., e₁, e₂, r₁, and r₂ were in the same plane, their motions are not restricted to that plane because a bacterium swims with a spiral trajectory due to its asymmetric flagellum shape, as discussed by Keller and Rubinow (24).

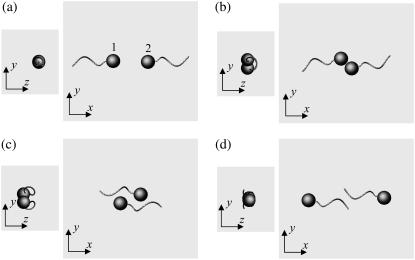
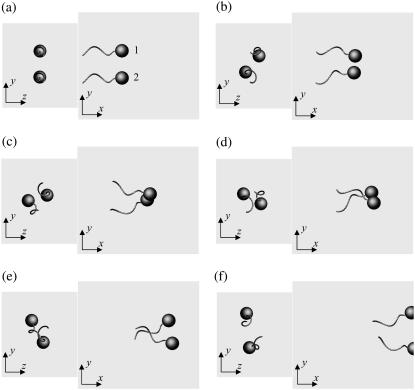
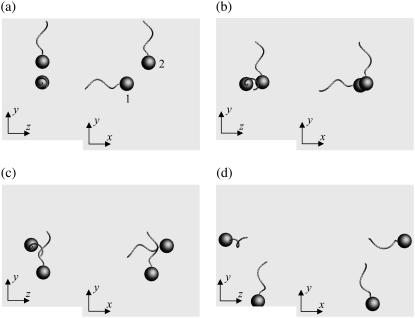
Fig. 3 shows the interactions between two shape A bacteria that were initially placed parallel to each other at a distance of four units, i.e., |r₁ − r₂| = 4. Here, t is the time, and t = 0 (Fig. 3 a) shows the initial conditions. As the two bacteria approach, they rotate in a clockwise direction in the z-y plane and eventually avoid each other. The interactions are fully three dimensional and show complex orientation changes that were generated only by the hydrodynamic interactions.

FIGURE 3.

Sequences a–f showing the interactions between two shape A bacteria initially placed in parallel at a distance of four units, as shown in a.

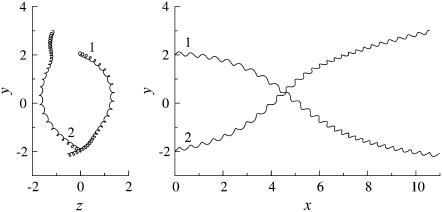
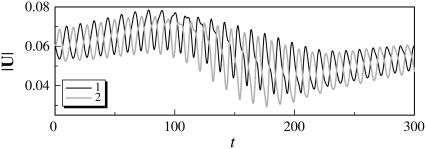
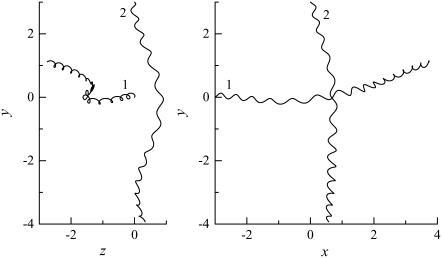
The trajectories of this case are shown in Fig. 4. The bacteria did not swim in a straight line, but formed a spiral with a width of ∼0.1 units. The trajectories twisted as the bacteria approached each other. The final swimming directions were considerably different from the initial swimming directions. The swimming velocities were also affected by the hydrodynamic interactions. Fig. 5 shows the change in the length of the translational velocity vectors, |U|, with time for this case. Since two bacteria interacted hydrodynamically, even at t = 0, the |U| values oscillated from the start of the simulation. The phases of the bacteria oscillations were opposite to each other, but their mean values were similar. The amplitude was large between t = 140–200, when the two flagella were in proximity to each other. The swimming motions were affected by the phase of the flagella relative to the orientation of the two bacteria.

FIGURE 4.

Trajectories of interacting bacteria (shape A, initially parallel).

FIGURE 5.

Temporal change in the length of the translational velocity vectors (shape A, initially parallel). (a) t = 0, (b) t = 70, (c) t = 120, and (d) t = 200.

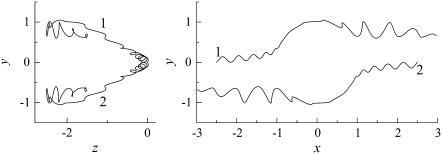
Fig. 6 shows the interactions between two shape A bacteria that were initially facing each other at a distance of five units, i.e., |r₁ − r₂| = 5 (see Fig. 6 a). In this case, the two bacteria were very close initially. Then, they passed each other while maintaining a small gap between the two spherical bodies and finally avoided each other. The trajectories for this case are shown in Fig. 7. The trajectories showed strong asymmetry, although the two bacteria were placed on the same x axis initially. This asymmetry arose from the initial conditions of the two bacteria and the shape of the flagellum. Since a bacterium generates a spiral trajectory, the two bacteria initially facing each other do not collide at the top of their spherical bodies. In addition, the two bacteria can rotate even if they do collide at the top of their spherical bodies since their flagella are not axisymmetric. The interactions were again three dimensional and exhibited complex orientation changes.

FIGURE 7.

Trajectories of interacting bacteria (shape A, initially facing each other). (a) t = 0, (b) t = 60, (c) t = 130, and (d) t = 250.

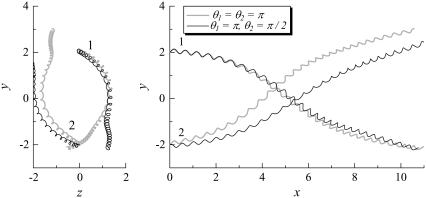
Fig. 8 shows the interactions between two shape A bacteria that were initially placed at right angles to each other at a distance of 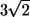units, i.e., 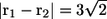(see Fig. 8 a). In this case, the two bacteria were close initially but then changed their orientations as the two flagella approached. Once again, the bacteria avoided each other. The trajectories for this case are shown in Fig. 9. Again, the interactions showed complex orientation changes.

FIGURE 8.

Sequences a–d showing the interactions between two shape A bacteria, initially placed at right angles to each other, as shown in a.

FIGURE 9.

Trajectories of interacting bacteria (shape A, initially at right angles). (a) θ₁ = θ₂ = π, and (b) θ₁ = π, θ₂ = π/2.

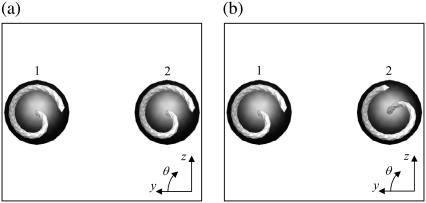
We rotated the flagellum of bacteria 2 for the parallel swimming case of Fig. 3 to observe the effect of the phase of the flagella relative to the orientation of the two bacteria. Let θ be the angle from the y axis in the y-z plane, as shown schematically in Fig. 10. We changed θ₂ from π to π/2. The resulting trajectories, which are compared in Fig. 11, changed considerably, and the final swimming directions differed for these two cases. Therefore, the interactions between two bacteria are affected not only by the orientation vectors but also by the phase of the flagella.

FIGURE 10.

Two initial conditions for parallel swimming cases, in which the angle of flagellum 2 relative to that of flagellum 1 differs.

FIGURE 11.

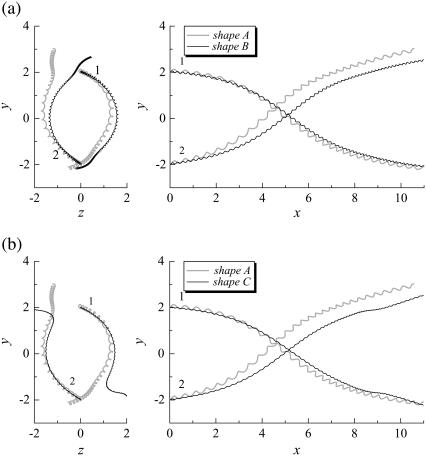
Effect of the flagella phase on the trajectories of interacting bacteria (shape A, initially parallel). (a) Comparison between shapes A and B. (b) Comparison between shapes A and C.

We also investigated the effect of the bacterial shape. The parallel swimming case in Fig. 3 was computed using shape B and shape C bacteria (cf. Fig. 2). The resulting trajectories are compared with the shape A bacteria trajectory in Fig. 12. Again, the trajectories changed considerably, and the final swimming directions differed for each case. Therefore, the bacterial shape also affected the interactions between the two bacteria. However, the general tendencies of the interactions, such as the direction of the twist in the trajectories, were similar for all the bacterial shapes and flagella phases.

FIGURE 12.

Effect of flagella shape on the trajectories of interacting bacteria (initially parallel).

Next, we investigate the rheology of a bacterial suspension in dilute and semidilute regimes. For any concentration of particles, there is a relation between the deviatoric part of the bulk stress and the conditions at the surfaces of the individual particles. Batchelor (26) derived this relation as

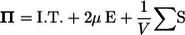(6)

where I.T. stands for an isotropic term and E is the bulk rate of the strain tensor. The last term is the particle bulk stress, which is expressed as a summation of the stresslet S in a fluid occupying volume V. The stresslet, S, which is the symmetric part of the hydrodynamic stress, is defined as (26)

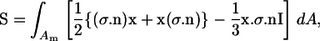(7)

where σ is the stress tensor, n is the outward normal vector, x is the position vector, and I is the unit tensor.

The stresslet of a shape A, B, or C solitary bacterium can be calculated from Eq. 7, and the results are as follows:

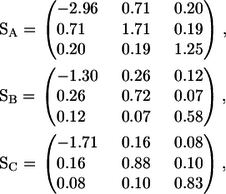(8)

where the x axis coincides with the direction of the orientation vector, and the y and z axes are taken as shown in Fig. 13. Since a bacterium generates a thrust force from behind the body, the xx component is negative, whereas the yy and zz components are positive.

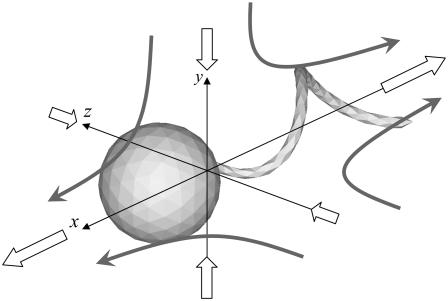
FIGURE 13.

Velocity field generated by the stresslet of a solitary bacterium. The large open arrows indicate the stresslet on each coordinate axis, and the shaded arrows schematically indicate the direction of the generated flow.

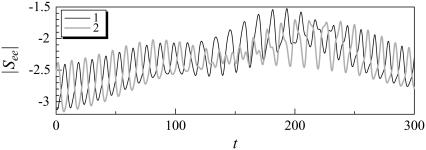
Although the stresslet for a solitary bacterium gives a first-order correction to the bulk stress in terms of the volume fraction, c, one must consider the hydrodynamic interactions between bacteria to calculate the bulk stress in a nondilute suspension. The next term in the asymptotic expression for the particle bulk stress in terms of c is O(c²), which can be obtained by considering the interactions between just two bacteria (see Batchelor and Green (27)). Fig. 14 shows the temporal change in the stresslet component S_ee for interacting shape A bacteria initially placed parallel to each other (the same condition is shown in Figs. 3–5), where S_ee indicates the stresslet component in the direction of its orientation vector. The stresslets oscillate in a similar manner with the velocities shown in Fig. 5. These oscillations and changes in the stresslets are generated by the hydrodynamic interactions.

FIGURE 14.

Temporal change in the stresslet component S_ee for interacting shape A bacteria, initially parallel. (a) shape D (a_x = 2, a_y = 1), and (b) shape E (a_x = 1, a_y = 0.5).

The effect of the aspect ratio of a bacterial cell body should also be considered, since some bacteria have ellipsoidal bodies rather than spherical bodies. There are several ways to change the shape of the cell, such as keeping the major or minor axis constant, keeping the surface area constant, or keeping the volume constant, while fixing the flagellum shape. Here, we show the results obtained when the major or minor axes were kept constant. (The results obtained when the surface area or volume were kept constant were straightforward, so they are omitted here.) We calculated the stresslet for a solitary bacterium with shape D and E ellipsoids, as shown in Fig. 15. The flagellum remained the same as that of shape A. The results are as follows:

(9)

where the x axis coincides with the direction of the orientation vector, and the y and z axes are as shown in Fig. 13. The shape D stresslet was greater than the shape A stresslet, whereas the shape E stresslet was less than the shape A stresslet. The difference was mainly due to the size difference of the cell bodies. Although the values of the stresslet components changed with the body shape, the general tendencies, such as the ratios of S_xx, S_yy, and S_zz, were similar. Therefore, the general tendencies of the interactions between two bacteria were also similar, regardless of the aspect ratio.

DISCUSSION

These results show that a parallel swimming motion of bacteria is unstable and breaks down easily in three dimensions. This instability arises from the three-dimensional flow field around the bacterium due to the asymmetric and helical flagellum shape. Previous studies that discussed the collective motion of bacteria did not consider this parallel swimming motion instability. Guell et al. (28) explained the band formation mechanism for magnetotactic bacteria using the flow field generated by the point stresslet. (If the bacteria are force free and torque free, they can be approximated as a point stresslet when determining far-field interactions.) The stresslet of a bacterium is negative in the direction of the orientation vector because it generates thrust force from behind. Consequently, the velocity field generated by the stresslet attracts two bacteria in a parallel swimming motion.

Our results show that such a parallel swimming motion generates twisting trajectories and does not persist. We also performed trial computations with different initial conditions and different bacterial shapes, but we did not observe any stable pair swimming motions. This is because all multipole moments were considered in this study, whereas Guell et al. considered the stresslet only (28). Other studies, such as Hatwalne et al. (9) and Hernandes-Ortiz et al. (11), also modeled bacteria as point forces or stresslets, and the near-field interactions were not solved precisely. Therefore, the near-field interactions differed from the far-field interactions, and one must deal with them precisely when discussing the collective motion of bacteria.

Next, we discuss the rheology of a bacterial suspension in dilute and semidilute regimes. The stresslet for a solitary bacterium gives the bulk stress in a dilute suspension in which the hydrodynamic interactions between bacteria can be neglected. If the orientation of the bacteria in a dilute suspension is isotropic, the particle bulk stress also becomes isotropic. If the bacteria have a preferred direction due to chemotaxis, phototaxis, thermotaxis, etc., the particle stress tensor is no longer isotropic and the bacteria have direct contributions to the stress field. From Eq. 8, the diagonal components of the stresslet for a solitary bacterium increase with h and k, where h is the amplitude and k is the wave number as shown in Fig. 1. Therefore, bacteria have more influence on the suspension rheology as h and k increase.

Another interesting feature of Eq. 8 is that the yy component is greater than the zz component. The velocity field generated at x due to a point stresslet at the origin of the coordinate system is given by (cf. Durlofsky et al. (29))

(10)

Therefore, the far-field disturbed velocity in the y direction is greater than that in the z direction when the stresslet is given by Eq. 8. This is one reason the trajectories of two bacteria become three dimensional. Previous studies discussing the interactions between bacteria did not consider the asymmetry of the stresslet. For example, Hatwalne et al. (9) assumed an axisymmetric stresslet for a bacterium to discuss the rheology of suspensions. Hernandes-Ortiz et al. (11) also assumed an axisymmetric stresslet to discuss the collective motions of bacteria. If one averages the stresslet of a bacterium over time, the stresslet becomes axisymmetric to the swimming direction. However, if one considers the interactions between bacteria or physical quantities in nondilute suspensions, one must consider the asymmetry because it affects the interactions and eventually the microstructures in the suspension.

In the case of a nondilute suspension, one must consider the hydrodynamic interactions between bacteria to calculate the bulk stress. The next term in the asymptotic expression for the particle bulk stress in terms of c is O(c²), which can be obtained by considering the interactions between just two bacteria. We see from Fig. 14 that the stresslet value changes considerably during the interactions, becoming about half of its time-mean value at t = 190. Such changes in the stresslet contribute to the bulk stress of the suspension directly. By contrast, the previous studies modeled a bacterium using a point stresslet, and changes due to hydrodynamic interactions were not considered. Since the stresslet changes dramatically as two bacteria approach each other, the near-field interactions must be computed precisely to evaluate the rheology of the suspension.

Lastly, we discuss the self-diffusion of the bacteria in a semidilute suspension. Understanding the diffusive behavior of bacteria is important to obtain a better continuum model for a bacterial suspension. Therefore, the self-diffusivity of swimming cells has been investigated both experimentally (3,11,30,31) and numerically (T. Ishikawa and T. J. Pedley, unpublished). In a semidilute suspension, Locsei et al. (32) showed that the self-diffusion coefficient could be predicted using a simple gas model based on the hydrodynamics of two-body interactions. In the model, the mean value of the change in the swimming direction during an interaction is the key parameter. This can be obtained by averaging the change in the swimming direction over all possible initial orientations. (These computations were not performed here because they are beyond the scope of our study.)

From Figs. 4, 7, and 9, the change in the swimming direction was strongly affected by the initial orientations, and the final direction was determined by the near-field fluid dynamics between the two bacteria. The change in the swimming direction was also strongly affected by the angle and shape of the flagellum (see Figs. 11 and 12). Therefore, a precise hydrodynamic treatment is required to calculate the self-diffusion of bacteria in a suspension accurately. Previous studies by Vicsek et al. (7) and Lega and Passot (10) used a random external force to express the hydrodynamic interactions between swimming particles. In our study, the directional changes of swimming bacteria were calculated deterministically using hydrodynamics. Therefore, the diffusive process was described by the chaotic motions of the interacting bacteria, not by random motions. We expect that our method can be used to predict the self-diffusivity quantitatively in the near future.