Interactions of Cationic-Hydrophobic Peptides with Lipid Bilayers: A Monte Carlo Simulation Method

Abstract

We present a computational model of the interaction between hydrophobic cations, such as the antimicrobial peptide, Magainin2, and membranes that include anionic lipids. The peptide's amino acids were represented as two interaction sites: one corresponds to the backbone α-carbon and the other to the side chain. The membrane was represented as a hydrophobic profile, and its anionic nature was represented by a surface of smeared charges. Thus, the Coulombic interactions between the peptide and the membrane were calculated using the Gouy-Chapman theory that describes the electrostatic potential in the aqueous phase near the membrane. Peptide conformations and locations near the membrane, and changes in the membrane width, were sampled at random, using the Metropolis criterion, taking into account the underlying energetics. Simulations of the interactions of heptalysine and the hydrophobic-cationic peptide, Magainin2, with acidic membranes were used to calibrate the model. The calibrated model reproduced structural data and the membrane-association free energies that were measured also for other basic and hydrophobic-cationic peptides. Interestingly, amphipathic peptides, such as Magainin2, were found to adopt two main membrane-associated states. In the first, the peptide resided mostly outside the polar headgroups region. In the second, which was energetically more favorable, the peptide assumed an amphipathic-helix conformation, where its hydrophobic face was immersed in the hydrocarbon region of the membrane and the charged residues were in contact with the surface of smeared charges. This dual behavior provides a molecular interpretation of the available experimental data.

INTRODUCTION

Antimicrobial peptides are short peptides that are lethal toward a broad spectrum of pathogens, but are quite inactive on normal eukaryotic cells (1). Accumulated data suggest that, regardless of the origin and diversity of the antimicrobial peptides in their primary and secondary structure (2,3) antimicrobial activity is a result of specific interactions with pathogenic membranes and not by direct association with a receptor (4–6). Therefore antimicrobial peptides may either complement existing antibiotics or even possibly replace them (7,8). However, the precise mechanism of action of antimicrobial peptides is incompletely understood.

In order for a peptide to partition into the membrane-water interface of its host bacteria, it must overcome a significant free energy barrier. This barrier can be reduced if the peptide assumes an ordered secondary structure, where backbone hydrogen bonds are satisfied (9). Exposure to water-membrane interfaces has indeed been shown to actually induce secondary structure in membrane-active peptides (10). There clearly must be a final stage, at which the peptide is in close contact with the membrane before lysis. This stage has been studied but there is no conclusive opinion regarding the actual mechanism by which antimicrobial peptides disrupt the membrane. Numerous studies, conducted on various native antimicrobial peptides, emphasize the importance of properties that are inherent to the peptide, such as net positive charge, chain length, amino acid composition, and amphipathicity (11,3)

The Shai-Matsuzaki-Huang model may explain the activity mechanism of most antimicrobial peptides (12–14). The model proposes that the peptides interact with the membrane's surface by electrostatic attraction until a carpeting of the membrane occurs and the peptides incorporate into the membrane. The membrane structure is then altered, resulting in a strain within the bilayer. This is followed by a phase transition and formation of pores, through which peptides and lipids can migrate into the inner leaflet. Following these changes in the bilayer structure, the membrane collapses into fragments and lyses. Recently, a new model was suggested that uses the detergent-like features of the antimicrobial peptides (11). In this model, the effect of peptide structure, membrane composition and peptide/lipid ratio on the membrane morphology are considered and are described in terms of a phase diagram. In this complex diagram, the former mechanisms of pore formation, proposed by the Shai-Matsuzaki-Huang model, are special cases.

Molecular dynamics (MD) simulations are often used to study the interactions of membrane-active peptides with lipids, but the current computer power limits the timescale of processes that can be traced with such a direct approach (15,16). Thus, we introduced a coarse-grained model that described the interaction between a hydrophobic peptide and a membrane (17). In that work, the peptide was represented as a chain of amino acids, each of which was described as two interaction sites, and the water-membrane environment as a structureless smooth hydrophobicity profile. The model reproduced dynamic and thermodynamic properties of the peptide-membrane interaction. However, it was limited only to the study of the interactions of hydrophobic peptides with electrostatically neutral membranes, made of zwiterionic lipids. Here, we present a developed model that accounts for Coulombic interactions between charged peptides and anionic membranes. To this end, an additional energy term was added to the potential, which provides attraction of positively charged residues to—and repulsion of negatively charged residues from—the membrane-water interface. This term reflects the content of the charged amino acids in the peptide and their structural context. It also reflects the chemical composition of the membrane in terms of the ratio of charged versus zwiterionic lipids. It thus allows us to investigate the impact of changes of the amino acid sequence of the peptide and the phospholipids composition of the membrane on peptide-membrane interactions. The model was calibrated using the heptalysine, i.e., K₇ (Table 1).

TABLE 1.

The sequences of the peptides that were used in this work

K7	GGGKKKKKKKGG
K5	GGGKKKKKGG
K3F2	GGGKFKFKGG
Magainin2 (Mag2)	GIGKFLHSAKKFGKAFVGEIMNS-NH2
Penetratin (pAntp)	RQIKIWFQNRRMKWKK

Hydrophobic residues are in bold, polar residues are in italics, and titratable residues are underlined.

The robustness of the model over a range of values of the parameters was examined using the polylysine peptides K₅ and K₃F₂ and the amphipathic peptide Magainin2 ((Mag2); Table 1). Mag2 is an antimicrobial peptide, which is secreted from the skin of the frog Xenopuse laevis. It is highly potent against bacteria, virus, and fungi, but nonhemolytic. Its analog pexiganan was suggested as an agent against infected diabetic foot ulcers (18,8). Mag2 was studied using different biophysical methods, it was found to be unfolded at the aqueous phase prebinding, and to become helical upon absorption onto the membrane (reviewed in Bechinger (19)). Its affinity to membranes with different lipid compositions was also studied and its preferential binding to anionic membrane shown (20,21), thus making it a good candidate for this study.

A further validation was performed on penetratin, which is a cell-penetrating peptide that enters the cell in a nonendocytotic or receptor/transporter mediated way. It is a fragment of the Drosophila transcription factor Antennapedia, which corresponds to its third helix and contains 16 residues (Table 1). According to the NMR structure of the whole Antennapedia protein in complex with double-stranded DNA (22), the third helix (pAntp) is bound to the DNA major groove. It has recently been suggested that pAntp enters the cell via direct interaction with the membrane, and hence experiments were performed to find its binding constant to membranes of different compositions. The pAntp peptide is composed of seven cationic residues, and only few hydrophobic residues. Its structure in a nonpolar medium composed of trifluoroethanol/water mixture (9:1) was solved by NMR (23); it revealed a bent irregular helix between residues 4 and 12, whereas the ends of the peptide were unwound. The positive charges were spread around the main axis of the peptide, and did not manifest an amphipathic distribution; a canonical α-helix model of the peptide was also not amphipathic. In NMR experiments in a polar environment (trifluoroethanol/water mixture of 1:9), an ordered structure of the peptide was not detected and circular dichroism (CD) measurements indicated a low helix content (23).

We calculated the free energy of membrane association of these peptides, and studied structural and dynamical aspects of their association with lipid bilayer models. All the peptides have been studied experimentally and their interaction with membranes was well characterized. However, as the studies were performed by different research groups using various experimental setups, there was no uniform data set to which we could refer, thus making the calibration of the model a nontrivial task. As shown in Results and Discussion below, the simulations were overall in accord with the available experimental data, but some deviations were observed.

METHODS

We present here an extension of the model from our earlier work (17) to account for the Coulombic interaction between charged residues and anionic phospholipids. A new term ΔG_Coul (described below) was added to the equation that describes the total free energy difference between a peptide in the membrane and in the aqueous phase (ΔG_tot)

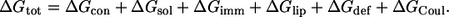(1)

The first five free energy terms on the right-hand side of the equation, and the approach taken to calculate them, were described in details in Kessel et al. (17) and Shental-Bechor et al. (24). Generally speaking, ΔG_con is the free energy change due to membrane-induced conformational changes in the peptide. It was calculated as a sum of the internal energy changes between the water and membrane-bound states of the peptides, as well as the entropy changes between the states.

ΔG_sol is the free energy of transfer of the peptide from water to the membrane. It accounts for electrostatic contributions resulting from changes in the solvent's polarity, as well as for nonpolar (hydrophobic) effects, which result from both differences in the van der Waals interactions of the peptide with the membrane and aqueous phases, and from solvent structure effects. ΔG_imm is the free energy penalty resulting from the confinement of the external translational and rotational motion of the peptide inside the membrane. ΔG_lip is the free energy penalty resulting from the interference of the peptide with the conformational freedom of the aliphatic chains of the lipids in the bilayer. The incorporation of these three terms into the energy calculations is discussed below.

In Eq. 1, ΔG_def is the free energy penalty associated with fluctuations of the membrane width around its resting (average) value of 30 Å. A harmonic potential was used, as described earlier (17).

Gouy-Chapman theory and the calculation of ΔG_Coul

The last term in Eq. 1 accounts for the electrostatic interaction between anionic phospholipids and titratable residues of the peptides. A classical way to account for this interaction is provided by the Gouy-Chapman theory (25–27). This theory used a simplified description of the charged headgroup region and considered it as a surface of smeared charges with a constant charge density, which is located at a distance z_GC from the membrane midplane (depicted by the dashed dotted line in Fig. 1). The theory describes how the electrostatic potential φ(z) (measured in units of k_BT/e, where k_B is Boltzmann constant, T is the temperature, and e is electron charge) depends on the distance z from the membrane midplane in an electrolyte solution.

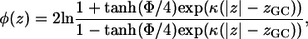(2)

where κ is the inverse of the Debye length. 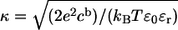c^b is the number of monovalent anions per unit volume in bulk, ɛ₀ is the permittivity in vacuum, and ɛ_r is the dielectric constant in water (taken as 80). The potential on the plane of smeared charges Φ depends on the charge density of the membrane σ, and on the molarity of the solution [K⁺]:

(3)

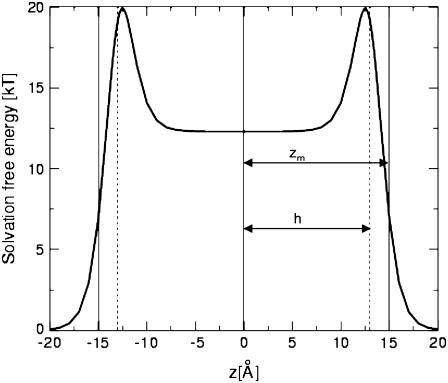
FIGURE 1.

The weighted electrostatic potential energy φ_w(z) as a function of the distance from the bilayer midplane z (Eqs. 6A and 6B). The distance between the bilayer midplane and the hydrophobicity profile's torque point (p^s(z)) is marked as z_m (vertical solid line). The plane of the smeared charge is depicted by the vertical dashed-dotted line; z_GC is the distance between this plane and the membrane midplane, h is the width of the sigmoidal function χ(z) and is depicted by the vertical dashed line. An equilibrated membrane bilayer composed of POPC molecules (coordinates were taken from http://moose.bio.ucalgary.ca. Molecular graphics image was produced using the UCSF Chimera package from the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, CA). The aliphatic lipid chains are colored in cyan of various brightness, depending on depth, and the phosphates are orange. The hydrophobic core of each leaflet of the bilayer spans 15 Å, and the charged phosphate atoms fluctuate around their equilibrium position at a distance of ∼20 Å from the membrane midplane, which coincides with the position of the surface of smeared charges.

N is Avogadro number. The charged surface is represented by its charge density—σ, which is smeared over the membrane plane. The magnitude of σ is determined by the composition of the phospholipids in the membrane and can be calculated from the mol fraction of the anionic phospholipids f_a using Eq. 4:

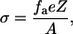(4)

where Z is the valence of the anionic lipid and A is the area occupied by one phospholipid in the membrane—taken as 70 Ų (26).

A titratable residue interacts Coulombically with the charged membrane only when the residue is in its charged form. However, due to the large desolvation free energy penalty associated with the transfer of a charge from water to oil (28), the titratable residues typically switch into their neutral forms upon approaching the nonpolar environment of the membrane. We arbitrarily chose to describe the dependence of the charge state of the titratable residues on their distance from the membrane midplane as a sigmoidal function χ_i(z), which is similar to the membrane polarity profile p of our earlier work (17) (also see below).

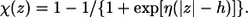(5)

In Eq. 5, η is the transition steepness, and h is the distance between the membrane midplane and the torque point of the sigmoidal function and in general it represents the width of the hydrophobic region of the membrane. A value of 15 Å is commonly used as the hydrophobic width of a monolayer (17). However, h and η are free parameters of the model, and their values were determined by series of calibration simulations that are described in Results and Discussion below and were set to η = 1 and h = 13 Å. As a result, the weighted electrostatic potential of the i-th residue φ_w_i(z), (Fig. 1) is:

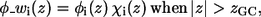(6a)

(6b)

The electrostatic interaction energy between the peptide and the membrane's charges is a sum over the contributions of each residue:

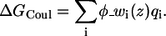(7)

A full positive (negative) charge was assigned to the side-chain interaction site of Lys, Arg (Asp and Glu), and to the C_α of the N-terminal (C-terminal, unless amidated).

Solvation, immobilization, and lipids perturbation

The solvation free energy of transferring the peptide from the aqueous phase into the membrane and the immobilization and lipids perturbation contributions were calculated as described in Kessel et al. (17). A hydrophobicity scale that was developed by Kessel and Ben-Tal (9) was used. This scale is based on Δg_i, the free energies of transfer of the amino acids from the aqueous phase into lipid bilayers. The hydrophobicity scale was incorporated into the reduced model as described in details in Kessel et al. (17). In short, the polarity at a distance z from the membrane midplane p^s(z) was described by the sigmoidal function:

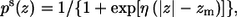(8)

where η is the transition steepness, and z_m is the distance between the membrane midplane and the torque point of the sigmoidal function; z_m represents the width of the hydrophobic region of the membrane and a value of z_m = 15 Å was used here. In this work we used η values between 0.8 and 1.1 to describe the sharpness of the hydrophobicity profile. These values correspond to an interface region that ranged from 4 to 6 Å, which is typical for phosphatidylserine (PS) lipids. The value of η used in this work is larger than the value of 0.5 that was used in our earlier studies of the interactions of M2δ with membranes (17). Because this parameter may influence the interaction energy, we repeated the calculations of the membrane binding energy of M2δ with η = 0.8, 1.0, and 1.1 and obtained values that were within the error range of the earlier calculations (data not shown).

An exception to the general solvation scheme was the treatment of the titratable residues and the peptide's termini, because of their capacity to shift between charged and neutralized forms. When a titratable residue was charged, the free energy required for its transfer from the aqueous phase into the membrane—Δg_i was taken as 64 kT (28). This is due to the excessive free energy penalty associated with the transfer of a full charge from the aqueous phase into the hydrocarbon region of the bilayer. When the residue was neutralized, the Δg_i values that were reported in Table 1 of Kessel et al. (17) were used. A gradual transition between the charged and neutral form of the residue, based on χ_i(z) of Eq. 5 was introduced, and the weighted contribution of the solvation, immobilization, and lipid perturbation free energy terms for a titratable residue was:

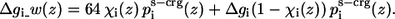(9)

The polarity profile of the charged side-chain solvation is given by:

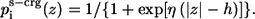(10)

p^s-crg(z) and p^s(z) are similar sigmoidal functions and initially we assumed that identical values should be used for the free parameters in both. However, the calibration tests that we conducted showed that the value of h—the width of the hydrophobicity profile of the charged residues—should be smaller (h = 13 Å) than z_m—the width of the hydrophobicity profile of the neutral residues (z_m = 15 Å). This choice provides sufficiently wide energy wells for the titratable residues. A possible interpretation of the formulation in Eq. 9 is that the neutral and charged states are at equilibrium with each other, and that the sigmoidal function describes the fractions of titratable residues that are in the charged state at each distance z from the membrane. For example, Fig. 2 exhibits Δg_w(z) of a lysine residue. Δg_w of lysine is zero at large z value far from the membrane; it increases to a maximal value near the membrane surface. From that point, the amount of charged lysine is reduced and the solvation energy reduces to a constant value of 12.3 kT in the hydrophobic core. This value corresponds to the solvation free energy penalty of transfer of a neutralized lysine from water into the membrane core. The implications of the curve are discussed further below.

FIGURE 2.

The solvation free energy of lysine as a function of the distance z between its side-chain interaction site and the bilayer midplane. The distance between the bilayer midplane and the hydrophobicity profile's torque point (p^s(z)) is marked as z_m (vertical solid line); h, the width of the sigmoidal function χ(z), is depicted by the vertical dashed lines. See also the main text.

Sampling protocol

The simulations were carried out in reduced temperatures in the range of 1.2–1.4. The reduced temperature is a scaling parameter that effectively controls the system's temperature, and the temperature range was set following our previous work (24) in which the experimentally determined Zimm-Bragg parameters and percent helicity were accurately reproduced.

To calculate the membrane interaction energy of each peptide, we simulated the peptides both in water and in membrane environments. The values were averaged over four different simulations of 50,000 Monte Carlo (MC) cycles each. In water simulations, the peptide was subjected solely to internal conformational modifications. In membrane simulations, additional external rigid body rotational and translational motions were also generated to allow the peptide to change its location in, and orientation with respect to, the membrane. New conformations were generated by simultaneously perturbing the generalized coordinates. The maximal step of the virtual backbone's torsion angle was 3° and 0.5° for both the side chain's torsion angle and its angle with respect to the backbone. New configurations were generated by perturbing both the Euler angles that describe the peptide orientation by a maximal step of 5°, and the Cartesian coordinates of its geometric center by a maximal step of 0.5 Å. A detailed description of the sampling protocol is available in Kessel et al. (17) and Shental-Bechor et al. (24).

Initial structures

K₇, K₅, and K₃F₂

These peptides were built in extended conformations using InsightII (Accelrys, San Diego, CA). Since we used a reduced representation of the amino acids, the torsion angles of the residues at the ends of the chain were ill-defined. This affected the stability of the peptide and was especially pronounced in short peptides. To overcome this pitfall, three glycine residues were added at the N-terminal and two more at the C-terminal.

Magainin2

We used model number 1 of Protein Data Bank (PDB) entry 2MAG (29).

Penetratin (pAntp)

The peptide was modeled as a canonical α-helix using InsightII (Accelrys).

The sequences of the peptides are provided in Table 1. Clustering of conformations and the calculation of the average helicity were carried out following the methodology described in Shental-Bechor et al. (24).

RESULTS AND DISCUSSION

The model contains several parameters and we first calibrated them. The parameters that have the strongest effect on the nature of the binding of antimicrobial peptides to membranes concern the structure of the membrane-water interface, where the peptides reside. These parameters are z_GC, the location of the surface charges in the membrane, and η, the slope of the transition (Eqs. 5, 6, 8, 9, and 10). Simulations with polylysine peptides (Table 1) were very useful for the calibration of z_GC, because the available experimental evidences indicated that the peptides interact with the membrane, in essence, based on the Coulombic attraction alone (26,30,31). To determine the value of η, we used Mag2 (Table 1) that interacts with membranes both electrostatically and hydrophobically. pAntp (Table 1) was subsequently used as a test case, as it is a well-studied peptide and ample structural and thermodynamic data regarding its interaction with membrane are available in the literature.

K₇

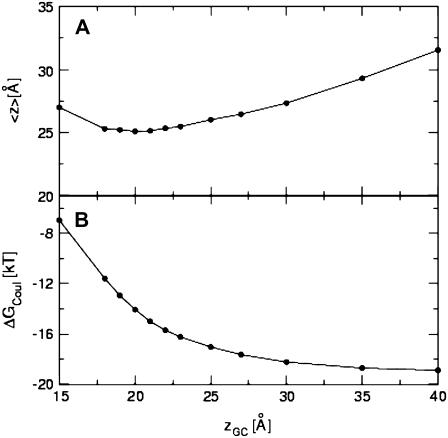
As a first step in the establishment of the model, we determined the optimal distance between the membrane midplane and the plane of smeared charges z_GC, based on the magnitude of the free energy of binding of heptalysine to the membrane. To this end, the binding free energy of heptalysine to a membrane composed of 33% anionic lipids was calculated at a reduced temperature of c = 1.3. The peptide was initially located with its geometrical center at a distance of 40 Å from the membrane midplane in an extended conformation. To check the dependence of the energy on z_GC we repeated the calculations using values of 15–40 Å, keeping c = 1.3 and η = 1.0. The results are depicted in Fig. 3, A and B. The average distance of the peptide from the membrane throughout four different simulations, 〈z〉, was stable at its minimal value of around 25 Å for z_GC values of 18–23 Å (Fig. 3 A). Higher 〈z〉 values were obtained for larger or smaller z_GC values. The Coulombic interactions increased in magnitude with z_GC and reached a saturated value of −19 kT, when z_GC was >35 Å, that is, when the surface charges were in the aqueous phase (Fig. 3 B). The total free energy was lower in magnitude than the Coulombic component by 1–2 kT (data not shown).

FIGURE 3.

Determination of the location of the surface of smeared charges. (A) The average distance between the centroid of the K₇ peptide and the membrane midplane versus z_GC, the distance between the membrane midplane and the surface of smeared charges. (B) The dependence of the Coulombic free energy in z_GC. The standard deviations in 〈z〉 and the energy are negligible.

The free energy of heptalysine binding to vesicles composed of 33% phosphateidylglycerol (PG) lipids was measured by McLaughlin and his co-workers (26), who reported a value of −11.6 kT. This value was reproduced in our simulations at z_GC values in the range of 19–20 Å (−11.9 ± 0.4 and −13.2 ± 0.4 kT, respectively). Thus, the rest of the calculations were carried out using z_GC = 20 Å (Fig. 1), which implies that the charges coincide approximately with the phosphate groups of the lipids (Fig. 1; (10)).

The various components of the membrane-binding free energy at c = 1.3 and z_GC = 20 Å are listed in Table 2. The dominant Coulombic attraction between the basic residues and the acidic lipids provides a favorable contribution of about −15 kT to the binding free energy. The collective energetic penalty, due to the other free energy components, amounts to ∼2 kT.

TABLE 2.

The total and components of the free energy of interaction between K₇ and a membrane composed of 33% acidic lipids at different reduced temperatures, c

Reduced temperature	ΔGtot* (kT)	ΔGcon† (kT)	ΔGsol‡ (kT)	ΔGCoul§ (kT)	〈z〉¶ (Å)
1.2	−13.7 ± 0.5	−0.2 ± 0.55	1.09 ± 0.01	−15.14 ± 0.06	24.93 ± 0.09
1.3	−13.2 ± 0.4	0.6 ± 0.4	1.09 ± 0.01	−15.37 ± 0.04	24.92 ± 0.05
1.4	−14.0 ± 0.2	−0.2 ± 0.3	1.10 ± 0.01	−15.39 ± 0.08	24.91 ± 0.1

The results that were obtained using the value of c that was used throughout the calculations are marked in bold fonts. The values represent averages and standard deviations that were calculated based on four different simulations. The position of the surface of smeared charges was z_GC = 20 Å and η = 1.0.

^*The total free energy.

^†The conformation free energy.

^‡The solvation free energy.

^§The Coulombic free energy.

^¶The average value of the z-coordinate of the centroid of the chain; the membrane midplane was at z = 0.

We also examined the robustness of the model to temperature changes and calculated the binding free energy at reduced temperature c in the range 1.2–1.4 while keeping z_GC = 20 Å. Binding free energy values between −13 and −14 kT were obtained (Table 2).

During the simulations in water and near the anionic membrane, heptalysine was unstructured and the conformational free energy was about zero. Thus, on average, it resided in extended conformation with its principal axis approximately parallel to the membrane plane, which may explain the success of Poisson-Boltzmann (PB) calculations, based on such peptide-membrane configuration, to reproduce its measured membrane-binding free energy (26). An energy minimum of −11.6 kT was found in these calculations. At the minimum, the peptide, which was taken in a fixed extended conformation, resided flat on the membrane, with a distance of ∼2.5 Å between the van der Waals surfaces of the peptide and membrane, which corresponds to one layer of water molecules; the solvation component of the interaction was zero. A comparable peptide location was found in our work and the solvation contribution to the binding free energy at c = 1.3 was ∼1.1 kT, which reflects the variety of allowed conformations in the simulation.

Control simulations demonstrated that the peptide did not bind to neutrally charged membranes, and resided at a distance of ∼38 Å from the membrane midplane (data not shown).

K₅ and K₃F₂

We calculated the binding free energy of K₅ to a membrane composed of 33% anionic lipids. Along the simulation, the peptide was absorbed onto the surface of the membrane, with its geometrical center at ∼25.5 Å from the membrane midplane in an ensemble of unstructured conformations. As with K₇, on average, the peptide was in an extended conformation with its principal axis parallel to the membrane surface. The binding free energy was −9.6 ± 0.8 kT. Similar results have been obtained by Ben-Tal et al. (26), who reported a value of −8.6 kT based on both measurements and PB calculations. In these calculations, the peptide was found to be absorbed onto the membrane surface, with a distance of ∼2.5 Å between the van der Waals surfaces of the peptide and the lipid bilayer, which is comparable to our observation. Electron paramagnetic resonance (EPR) experiments showed that capped pentalysine (labeled with nitroxide) bind to a membrane composed of 33% PS lipids and 67% phosphatidylcholine (PC) with a free energy value of −5.7 kT (30). This value is smaller in magnitude than the measured and calculated values reported above. The EPR measurements also showed that the peptide was absorbed onto the membrane surface. The same location with respect to the membrane, and a binding free energy value of −5.6kT, were found in MD simulations that were combined with continuum solvent scheme for the solvation and Coulombic interactions (27). This value is essentially identical to the EPR measurements but somewhat smaller in magnitude then the value that was obtained using our MC simulations and the values that were measured and calculated by McLaughlin and co-workers (26).

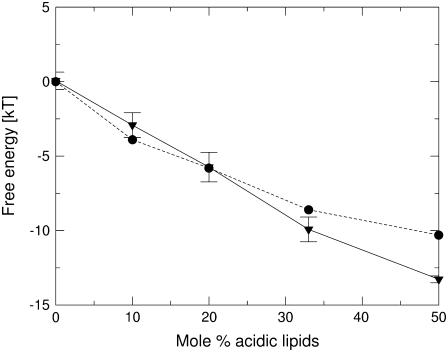
We calculated the binding free energy of K₅ to membranes with different fraction of anionic lipids and compared the results to the experimental data of reference (26) (Fig. 4). As expected, and in agreement with the measurements, the binding free energy became more negative as the fraction of anionic lipids increased, reaching the value of −13.3 ± 0.2 kT in a membrane composed of 50% anionic lipids. The peptide did not exhibit binding to a neutrally charged membrane; ΔG_tot = 0 ± 0.6 and 〈z〉 = 37 ± 2 Å, which is also in accordance with the observation that no binding was recorded in experiments with pure-PC membranes (26). The calculated binding free energy of the peptide to a membrane composed of 50% anionic lipids is ∼3 kT more negative than the measured value, but the reasons for this difference are unknown.

FIGURE 4.

The free energy of binding of pentalysine to bilayers as a function of the mol % of acidic lipids. The calculated values are marked as triangles, connected by the solid line and the experimentally determined values of reference (26) are marked as circles, connected by the dotted line. The membrane affinity of the peptide increases with the mol % acidic lipid, as it should.

The binding free energy of capped K₃F₂ labeled by nitroxide to a membrane composed of 33% PS lipids (and 67% PC) was also measured by EPR (30). The binding free energy increased in magnitude so that K₃F₂ bound the membrane a bit stronger than K₅, with binding free energy of −6.4 kT. K₃F₂ was found at the level of the phosphate group of the lipids, deeper than K₅. A very similar binding free energy value of −6.7 kT was obtained in MD simulations of K₃F₂ (27).

In our simulations however, K₃F₂ was found with its geometric center at ∼26 ± 2 Å from the membrane midplane, similar to pentalysine, and its binding free energy was only −5.0 ± 0.8 kT, which makes the interaction of K₃F₂ with the membrane less favorable than that of K₅. In contrast to the observations of Victor and Cafiso (30) and Lazaridis (27), in our simulations the Phe groups did not interact with the hydrophobic core of the membrane. The discrepancy between our calculated value and the experimental value may result from the differences in the peptide sequence. First, in the experiments the peptide contained a hydrophobic labeling group that might have increased the hydrophobicity of the peptide and therefore made the interaction with the membrane core more favorable. Second, in the simulations we had to add Gly residues to minimize the influence of the peptide ends. However, it is possible that K₃F₂ is too short and the effect of the uncertainty in the structure and energy contributions of the end residues is too pronounced in such a short peptide. This structural uncertainty may have prevented the favorable solvation interactions of the Phe groups with the hydrophobic core of the membrane.

Solvation profile of Lys and the change of protonation state

The problem of modeling the transition between titration states near the membrane is common to all computational studies. A possible approach, which was used before, was to treat the titratable residues as charged when calculating the Coulombic interactions, and as neutral when calculating solvation contributions. For example, the interaction energies of many cationic residues was successfully reproduced (27), which implies that this, inconsistent, approach is practically sufficient to describe the energetics of the system.

In this study we attempted to give a physically more accurate description of the system, and modeled the probability of the transition between the two titration states. The function that we used to describe the solvation of the titratable residues has a maximum (of 20 kT for Lys; Fig. 2) at |z| = 12.5 Å, which is at the membrane-water interface. At this z-value, the Coulombic contribution to the free energy is −1.5 kT. Thus, the free energy value at this region is higher than that at the hydrophobic core of the membrane. This is in contradiction to the expectation of the solvation energy profile of a charged residue; the energy maximum could have been avoided if titration would have taken place a few angstroms further away from the membrane. However, typically, a titratable residue such as Lys would reside in its charged form where it benefits from the Coulombic interaction with the membrane surface charges, i.e., 20 Å from the membrane midplane. At this position, it is solvated by water and the desolvation penalty is essentially zero.

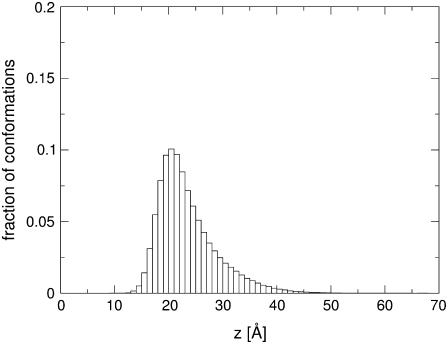
Fig. 5 shows a histogram of the position of the Lys residues of Mag2 during four simulations. Indeed, it is evident that during the simulations the average position of the residues is +21 Å, which is in the vicinity of the surface of smeared charges. According to Eq. 5, at this position, ∼100% of the titratable residues are in the charged state. Thus, the shape of the solvation profile of the titratable residues at the core of the membrane and near it (in particular around z = 12.5 Å, near the pick in the solvation energy curve; Fig. 2) is insignificant within the scope of this study because the peptide does not sample this region at all.

FIGURE 5.

A histogram of the position along the membrane-normal of the side-chain interaction site of the Lys residues of Mag2 during four simulations.

However, it is clear that in the future we will have to optimize the model to include the change in the titration state in a more accurate manner that would be feasible for the study of all possible peptides. A possible way to do that is to add another free parameter to the model that will replace h in Eq. 5. That means that the midpoint of the titration curve χ(z) will be different than that of the polarity profile curve . The new parameter will obviously have to be calibrated, which we wanted to avoid at this point.

Magainin2 (Mag2)

Simulations of Mag2 were performed in the aqueous phase and in the presence of a membrane, and the free energy of membrane association was calculated. The simulations were carried out in a range of reduced temperatures and with membranes with different values of the parameter η that characterizes the width of the water-membrane interface.

Simulations in water

We calculated the effective conformational energy of Mag2 in water at reduced temperatures c = 1.2, 1.3, and 1.4, from four repetitive simulations with different, randomly chosen, initial conformations, in each case. During the simulations, the energy fluctuated and the peptide adopted conformations with low helicity, in correlation with experimental data (19). The exception was c = 1.2, in which the helicity of the peptide in the aqueous phase was relatively high (43 ± 4%), in accord with the results that we obtained for polyalanine and polyalanine-like peptides that contain basic residues (24). The average effective internal energy and entropy are listed in Table 3.

TABLE 3.

The average effective internal energy (E_con), entropy (S_con), and average helicity of Mag2 in water at different values of the reduced temperature, c

Reduced temperature	Econ (kT)	T×Scon (k)	Helicity (%)
1.2	−64 ± 2	59 ± 2	43 ± 4
1.3	−47 ± 1	67 ± 0.5	24 ± 2
1.4	−37 ± 2	70.7 ± 0.7	13 ± 2

The values represent averages and standard deviations that were calculated based on four different simulations. The results that were obtained using the value of c that was used throughout the calculations are marked in bold fonts.

Simulations in a membrane composed of 30% acidic lipids

We carried out simulations of Mag2 with a membrane composed of 30% acidic (and 70% neutral) lipids at reduced temperatures in the range 1.2–1.4, using Mag2's NMR structure (model 1) as the initial structure. In this conformation, Mag2 is an amphipathic helix. It was initially placed on the membrane surface with its nonpolar residues pointing toward the membrane core and its geometric center 20 Å away from the membrane midplane, i.e., in line with the surface charges and the phosphate groups of the lipids. The results are listed in Table 4. The interaction energy at c = 1.3 was −11.0 ± 1.0 kT; decomposition shows that it was composed of −8.8 kT from the Coulomb term, −1.0 kT from the solvation term, and −1.3 kT from the conformational term.

TABLE 4.

The total and components of the binding free energy between Mag2 and a membrane composed of 30% acidic lipids in the “inner” and “outer” groups of conformations and in the whole trajectory, calculated at different reduced temperatures

Reduced temperature	Group	ΔGtot* (kT)	ΔGcon† (kT)	ΔGsol‡ (kT)	ΔGCoul§(kT)	〈z〉¶ (Å)	N‖(%)
1.2	outer	−6.2 ± 0.2	1.8 ± 0.3	0.17 ± 0.06	−8.6 ± 0.1	28.4 ± 0.1	45 ± 3
	inner	−11.5 ± 0.4	3.2 ± 0.6	−5.9 ± 0.3	−9.27 ± 0.09	18.9 ± 0.2	34 ± 2
	whole	−8.9 ± 0.5	1.6 ± 0.4	−2.1 ± 0.2	−8.93 ± 0.04	24.5 ± 0.3	100
1.3	outer	−7.8 ± 0.9	0.11 ± 0.9	0.11 ± 0.04	−8.48 ± 0.07	28.34 ± 0.06	56 ± 3
	inner	−16 ± 1	−2.7 ± 0.5	−5.0 ± 0.7	−9.32 ± 0.08	19.3 ± 0.2	21
	whole	−11 ± 1	−1.3 ± 0.7	−1.0 ± 0.3	−8.76 ± 0.08	25.8 ± 0.3	100
1.4	outer	−8.2 ± 0.9	−0.3 ± 0.8	0.1 ± 0.01	−8.41 ± 0.02	28.4 ± 0.03	63 ± 2
	inner	−15 ± 2	−3.4 ± 1.24	−2.68 ± 0.6	−9.7 ± 0.1	20.2 ± 0.2	10 ± 1
	whole	−9.6 ± 0.7	−1.0 ± 0.6	−0.33 ± 0.1	−8.68 ± 0.08	26.8 ± 0.2	100

The values represent averages and standard deviations that were calculated based on four different simulations. The position of the surface of smeared charges was z_GC = 20 Å and η = 1.0. The results that were obtained using the value of c that was used throughout the calculations are marked in bold fonts.

^*The total free energy.

^†The conformation free energy.

^‡The solvation free energy.

^§The Coulombic free energy.

^¶The average value of the z-coordinate of the centroid of the chain; the membrane midplane was at z = 0.

^‖The fraction of conformations (in percent) in each group.

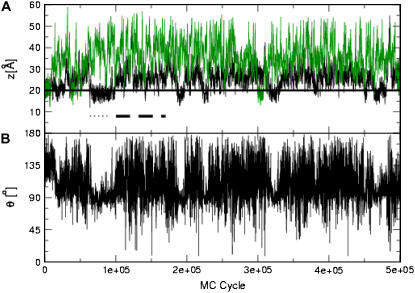
The black curve in Fig. 6 A shows the distance between the peptide's geometric center and the membrane midplane during one representative simulation. The peptide departed from the membrane surface and then interacted with the membrane core again. The membrane-bound conformations that were generated during the simulation can be segregated into “outer” and “inner” groups. A representative conformation of each group is presented in Fig. 7. The “outer” group included conformations, the average geometric center of which was 25 Å < z < 35 Å from the membrane midplane. In these conformations, the peptide was electrostatically bound to the membrane with four of its lysine residues pointing toward the membrane surface and the nonpolar residues embedded in the aqueous phase. The conformations in this group were mostly unstructured, for example, the RMSD between the conformations of the peptide in the part of the trajectory that is marked by the dashed line in Fig. 6 A was 4.6 Å.

FIGURE 6.

Mag2 interaction with neutral and charged membranes. (A) The distance z between the peptide centroid and the membrane midplane versus the number of MC cycles. Two representative simulations are presented: the black curve marks the results obtained with a negatively charged membrane containing 30% acidic lipids, and the green curve corresponds to simulations with a neutrally charged membrane of 100% zwiterionic lipids. The solid horizontal line marks the location of the surface of smeared charges of the membrane. The dashed and dotted lines represent parts of the trajectory obtained with the negatively charged membrane, in which the conformations correspond to the “outer” and “inner” states, respectively. (B) The projection angle θ of the peptide's end-to-end distance vector and the membrane normal versus the number of MC cycles, from the simulation with the negatively charged membrane.

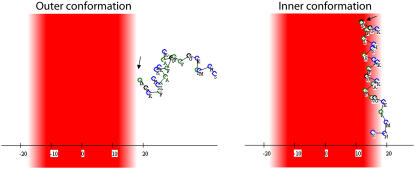
FIGURE 7.

Representatives of the “outer” (left) and “inner” (right) conformations of the Mag2 simulation of Fig. 6 A. The membrane hydrophobicity profile is color-coded so that dark-red represents the most highly hydrophobic region of the lipid chains, pale-red represents the membrane-water interface, and the aqueous phase is white. The hydrophobic residues are marked in green and the rest of the residues in blue. The peptide's N-terminus is marked with an arrow.

The “inner” group was composed of conformations in which the peptide was adsorbed deeper on the membrane surface, at predominantly helical structures, with their average geometric center at z < 25 Å from the membrane midplane. The conformations were very similar to each other and to the NMR structure that was used as the initial conformation. For example, the RMSD between the peptide conformations in the part of the trajectory that is marked by the dotted line in Fig. 6 A was 2.5 Å.

The projection angle θ of the peptide's end-to-end distance vector onto the membrane normal along the simulation is presented in Fig. 6 B. One can see that in the inner group of conformations (e.g., the dotted line in Fig. 6 A) the peptide was aligned parallel to the membrane with its tilt angle around θ = 90° with minimal variations. The nonpolar residues of the peptide were immersed in the hydrophobic core of the membrane, while the lysine residues pointed outward, toward the aqueous phase and the surface of smeared charges (Fig. 7 B). In this state, the peptide was bound to the membrane through a combination of favorable contributions of the solvation and Coulombic components of the free energy.

From a rough partitioning of the trajectory into the two groups of conformations, one can get a general idea of the free energy components of the interaction of the peptide with the membrane in the two states. The average values in each group of conformations are reported in Table 4. On average, the total binding free energy of the peptide in the “inner” group was more negative. The solvation component was negative in the group of “inner” conformations and larger in magnitude than in the “outer” group.

The binding free energy that was calculated using this model at the reduced temperature c = 1.3 and with η = 1 was −11.1 ± 1.0 kT. This free energy value was in agreement with the equilibrium affinity constant that was measured for Mag2 binding to 30% PG mono- and bilayers using surface plasmon resonance (SPR) (21); a binding constant of K = 10.9 × 10⁴ M⁻¹ was reported, which is equivalent to −11.6 kT (calculated as −ln(K)). A less negative binding free energy value of −7.6 kT was measured by calorimetric titration (32), and represents the binding constant between peptides right near the membrane surface and membrane-bound peptides. This is not the apparent binding affinity but rather the “hydrophobic binding constant”, which might explain the discrepancy between the experimental values. The measured hydrophobic binding constant should be comparable to the difference in free energy between the peptide in the inner and the outer states that were calculated in the simulations. This free energy difference originates mainly from the interaction of the peptide with the membrane in the inner state, which reflects predominantly the hydrophobic effect. In the simulations, the value was −16 kT − (−7.8 kT) = −8.2 kT, which is close to the measured value.

In MD simulations only the inner state of Mag2 was detected and the corresponding binding energy was −13.8 kT (27). In that work, the peptide was initially placed on the membrane surface with its hydrophobic region facing into the membrane in a conformation that resembles the inner state. During the simulations, the peptide did not change its conformation and orientation with respect to the membrane, which might explain why the outer state, i.e., the state of membrane binding that is governed by the Coulombic attraction, was overlooked.

Simulations in neutral membranes

The binding free energy of Mag2 to a neutrally charged membrane was calculated using the model that was described in our earlier publication (17), that is, the model that was used here with the Coulombic term in Eq. 1 set to zero. Mag2 did not seem to bind efficiently to the membrane; the binging free energy was −0.7 ± 0.9 kT, and the peptide was located with its geometrical center ∼36 Å away from the membrane's midplane (the green line in Fig. 6 A).

However, a close examination of the simulation trajectory revealed short episodes (2.6 ± 0.9% of the conformations in the trajectory) in which the peptide was tightly adsorbed onto the membrane surface with its nonpolar face immersed in the hydrophobic region of the membrane. Taking only these conformations into account, the total binding free energy was −7.0 ± 3.0 kT. This is comparable to the value of -9.1 kT that was calculated in MD simulations (27), which represent the binding of the peptide to the membrane in a conformation that resembles the inner conformation of our MC simulations. Binding free energies of −7 kT and −6.8 kT to a PC/cholesterol (10:1) monolayer and bilayer, respectively, were measured by SPR (21). These values represent membrane binding energy of the peptide in various conformations and not only in the inner conformation of the simulations; therefore the origin of the apparent agreement of the results is unclear. In calorimetric titration experiments (32), however, the binding free energy of Mag2 to small unilamellar vesicles made of PC was −11.6 kT, which is much stronger than other measured or computed values.

In rigid body simulations, using the helical conformation of the peptide from the PDB, the inner conformation was pronounced and the same binding free energy was recorded. This suggests that the interaction of Mag2 with neutral membranes is challenged by the entropy. In rigid body simulations, where the conformational entropy was not taken into account, the inner orientation could be easily found by the peptide. Rigid body simulations are somewhat similar to imposing harmonic constraints on the backbone in MD simulations.

Recent full atom MD simulations of Mag2 in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) membrane were reported (15). In that work, the peptide was placed 10 Å away from the phosphate atoms in the water region parallel to the membrane in two orientations, one with the hydrophobic face and the other with the cationic face toward the membrane. Along the 50-ns simulation both peptides immersed in the membrane interface, where the one with the hydrophobic face pointing toward the lipids bound deeper into the headgroup region than the one with the cationic face. These final conformations are similar to the inner and outer conformations that were found in our MC simulations. However, in contrast to our MC simulations, in the MD simulations these orientations were found only as a result of the initial positioning of the peptide. In the timescale of the MD simulations, the transition from the water region to both membrane-bound conformations and the transition between the two states could not be observed. Furthermore, the MD simulations could not produce a quantitative estimate of the binding free energy, and used indirect measures to conclude that of the two states, the one with the peptide that faced its hydrophobic side to the membrane was more stable. These are two advantages of the reduced model over full atom models.

Sensitivity of the calculations to the model parameters

We repeated the simulations of the interaction of Mag2 with several membrane models that differed in the steepness of the transition from polar to nonpolar environment η, and used various values of the reduced temperature. The same qualitative behavior was evident in all the simulations, but the relative abundance of the conformations in which the peptide inserted deeper into the membrane depended on the value of η. When η was small (η = 0.8) and the transition from the aqueous phase to the hydrocarbon core of the membrane was moderate, these conformations appeared rarely. This trend was strengthened as the reduced temperature increased. Based on these results we concluded that using the set of parameters c = 1.3, η = 1, and z_GC = 20 Å, the experimental data were best reproduced. However, similar results were obtained using parameters in the ranges 1.2 < c < 1.4, 0.8 < η < 1.1, and 19 Å < z_CG < 20 Å, emphasizing the robustness of the model.

Penetratin (pAntp)

We calculated the free energy of pAntp (Table 1) binding to membranes with acidic lipid concentrations between 0 and 40% at reduced temperature c = 1.3 and with membrane polarity profile η = 1. The results are presented in Table 5. The binding free energy depended strongly on the membrane acidity. A value of −14.0 ± 1.5 kT was obtained for pAntp binding to a membrane composed of 40% acidic lipids compared to only −2.9 ± 0.5 kT to a membrane composed of 10% acidic lipids, and no binding was observed to a neutral membrane. The dependence of the magnitude of the binding free energy on the acidic lipid concentration, which is expected theoretically, was also observed experimentally ((33); Table 5). However, it is too pronounced in the calculations in comparison with the experiments. Overall, our model reflected the selective binding of the pAntp to acidic membrane and approximately reproduced its binding free energy to a membrane composed of 40% acidic lipids. However, the model considerably underestimated the membrane binding affinity at lower concentrations of the acidic lipid. Probably, the structural complexity of pAntp, which includes both basic and hydrophobic residues, but does not form a simple amphipatic structure, and the neglect of membrane effects like lipid demixing and creation of anionic lipid clusters as a response to the presence of cationic peptide (34–36) may explain the discrepancy between the experimental results and the calculations.

TABLE 5.

The total and components of the membrane-binding free energy of pAntp to acidic membranes at a reduced temperature of c = 1.3

%PG	ΔGtot* (kT)	ΔGcon† (kT)	ΔGsol‡ (kT)	ΔGCoul§ (kT)	〈z〉¶ (Å)	−kTln(Kapp)‖ (kT)
10	−2.9 ± 0.5	0.5 ± 0.5	0.13 ± 0.02	−4.02 ± 0.04	30.1 ± 0.2	−9.7
20	−9.1 ± 0.7	−0.9 ± 0.7	0.30 ± 0.06	−9.0 ± 0.05	27.0 ± 0.2	−14.2
30	−11.9 ± 1.1	0.4 ± 1.1	0.48 ± 0.02	−13.26 ± 0.09	25.3 ± 0.3	−15.3
40	−14.4 ± 1.5	1.5 ± 1.7	0.46 ± 0.07	−16.8 ± 0.2	24.3 ± 0.3	−16.0

The values represent averages and standard deviations that were calculated based on four different simulations. The position of the smeared surface charge was z_GC = 20 Å and η = 1.0.

^*The total free energy.

^†The conformation free energy.

^‡The solvation free energy.

^§The Coulombic free energy.

^¶The average value of the z-coordinate of the centroid of the chain; the membrane midplane was at z = 0.

^‖As measured by Persson et al. (33).

The binding free energies of pAntp to a neutral membrane and to a membrane composed of 40% negatively charged lipids were calculated in MD simulations (27). According to these simulations, pAntp did not bind to the neutral membrane, in accordance with the experimental results and our simulations. However, the binding energy to a membrane composed of 40% acidic lipids was −9.5 ± 3.0 kT, a significantly less negative value than the measured binding energy value of −16.0 kT and the value of −14.4 ± 1.5 kT that we calculated.

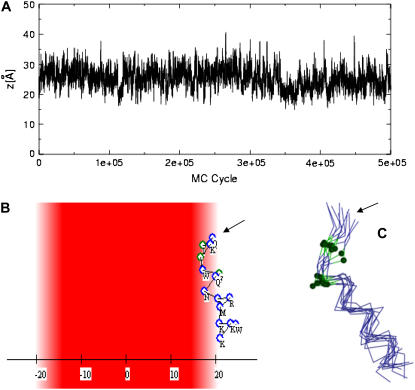
Because of the nonamphipatic structure of pAntp, its interaction with the membrane in simulations at reduced temperature c = 1.3 was mainly due to the Coulombic attraction. Simulations at lower reduced temperature can increase the probability of lower energy conformations that were rare because of the large entropy penalty. Indeed, in simulations that were conducted with lower values of the reduced temperature (c = 1.2), the peptide was more helical and it was possible to observe more clearly different modes of its interaction with the membrane. The vast majority of the conformations were bound to the membrane solely by the Coulombic attraction. Some conformations, however, were closer to the membrane and characterized by negative solvation free energy, too (Fig. 8 A). In these conformations Ile-3 and Ile-5 were inserted into the membrane, which was enabled by the unwinding of the helix at the N-terminal as presented in Fig. 8, B and C, this allowed both Ile residues (marked in green in Fig. 8 C) to be in contact with the membrane. This conformation of the peptide and orientation with respect to the membrane resembles one of the conformations that were observed in MD simulations (27) in that Ile-3 and Phe-5 partially inserted into the hydrophobic core of the membrane.

FIGURE 8.

Interaction of the pAnt peptide with membranes. (A) The distance z between the centroid of pAntp and the membrane midplane as a function of the simulation's cycle in a representative simulation at low reduced temperature c = 1.2. (B) A representative conformation from the inner group of conformations. The peptide and membrane were represented using the scheme of Fig. 7. The peptide's N-terminus is marked with an arrow. (C) A cluster of conformations from the inner group of conformations. The peptides are represented using a C_α trace model, and Ile-3 and Ile-5, which partition into the hydrocarbon region of the membrane, are marked in green. The peptide's N-terminus is marked with an arrow.

CONCLUSIONS

In this work, we extended a model of peptide-membrane interaction that was described in our earlier studies (17,24) to include the Coulombic interaction between negatively charged phospholipids and positively charged peptides, using the Gouy-Chapman theory. The model was implemented within the framework of an MC simulation method for sampling both internal degrees of freedom of the peptides and external degrees of freedom that determine its location and orientation with respect to the membrane. The new model was checked over several well-characterized test cases, and was proved useful to describe the thermodynamic properties of the systems. For the most part, the simulations reproduced the measured values of the binding free energy of the peptides to the membrane and the structural features, such as the helix content of the peptide and its orientation in the membrane.

The model takes into account the hydrophobic and unionic nature of the lipid bilayer as well as structural and physicochemical properties of the peptide. Thus, it can accommodate the peptide in several regions of the energy landscape. Basic peptides, such as heptalysine, exhibit only one mode of interaction; they reside outside the polar headgroups region of the membrane to avoid the high desolvation free energy penalty, while their basic residues interact Coulombically with the acidic lipids. We refer to it as the “outer state”. More complex peptides, such as Mag2 and pAntp, which contain both charged and hydrophobic surfaces, explore more possibilities. They were detected primarily in two states (Fig. 7): one was similar to the outer state of the basic peptides and in the other one, termed “inner”, the peptides resided closer to the membrane with their hydrophobic residues immersed in the hydrocarbon region of the membrane and their basic residues snorkeling out into the polar headgroups region, interacting Coulombically with the acidic lipids. This is in agreement with the finding of Shai and co-workers (21,37) of two states of binding of Mag2 with membrane composed of 30% PS (and 70% neutral) lipids.

The MC simulations gave us a glance at the dynamics of the transition between these states (Figs. 6, A and B, and 8 A). Because of the stochastic nature of the simulations, it is difficult to describe the exact dynamics of the process, but one can surely conclude that there are two different states of binding. This is an advantage of this MC model over the recently published MD studies (27). The MD model can be thought of as the full-atom equivalent of our model in the way that it estimates the contributions of the various components of the binding free energy. In principle, the MD free energy values are more accurate than ours because of the full-atom description. However, the MD simulations were limited to the vicinity of a known (or predicted) location of the peptide on the membrane surface and the protocol that was used does not allow the exploration of other states. This is presumably the reason why only the “inner state” was observed in these simulations, while the “outer state” was overlooked.

The model contains several parameters. The magnitude of the surface charge density, σ, was calculated from the mol fraction of the anionic phospholipids according to Eq. 4. This allowed us to mimic various biological systems with different lipids compositions. In addition, the model also contains several parameters that were calibrated, such as the reduced temperature (c) and the features of the membrane structure (η and z_GC). This could impede the robustness of the model. However, the simulations were repeated with several values, and the results were quite stable in the range that was examined. In this respect, it is interesting to note that a change of the reduced temperature of the simulation may give an insight of the interaction, as in the case of the imperfect amphipathic peptide pAntp.

The model utilizes a very simple description of the membrane as a continuum structureless medium, which is characterized by its polarity profile and surface charge density. The capacity of the membrane to deform was also included in this description. These are three important features of the lipid bilayer. However, other membrane characteristics are missing in the model, which are expected to play a major role in membrane lysis. From experimental data, it is evident that Mag2 acts as a detergent and imposes a positive curvature on the membrane to induce lysis (38,39). Similarly, the inherent curvature of the lipids affects the lysis process. For instance, it was shown that lysis of membranes that are composed of the acidic lipid PG occurs at 1:100 Mag2/lipid ratio (40). A 10 times larger peptide/lipid ratio was required for the lysis of membranes that are composed of the acidic lipid PS. PG membranes behave differently than PS membranes; this is attributed to the inherent curvature strain of the lipids: PS but not PG lipids are known to form hexagonal structures (with negative curvature) and therefore facilitate membrane lysis. Our model lacks the description of the membrane curvature and we therefore cannot observe the mechanical influence of the peptide on the membrane's structure and the peptide binding.

In a bilayer, the charged lipids are spread over the plane roughly homogenously. This homogenous charge density may be disrupted when an oppositely charged peptide approaches the membrane. A cluster of positively charged residue on the peptide surface may induce migration of negatively charged lipids into the interaction zone and a migration of neutral lipids away from this zone to obtain a more favorable binding energy (34,35) as was suggested to be the mechanism of action of the lipid PIP₂ (36). In this respect it is noteworthy that the lipids' demixing, which changes the local charge density in the membrane and hence changes the local membrane composition, may affect the stability of the membrane and facilitate its lysis. The more favorable binding energy may increase the local peptide concentration on the membrane surface, and may also have an effect on membrane stability and the lysis process. All these effects should be included in our model.

An important step in membrane lysis by antimicrobial peptides is the pore forming stage, which is common to all the models (11). The pore forming step depends on the concentration of the peptide near the membrane surface; a critical concentration is required for pore formation and membrane lysis (41). Our simulation box contains only a single peptide molecule, and the model does not account for the cooperative effect of the increase in peptide concentration. This is a pronounced disadvantage of all simulation methods over the experiments, especially when studying a concentration-dependent process. On the other hand, a close examination of a single peptide can give insight on the molecular basis of the process, as we did here.

In this context it is important to notice that peptide-concentration effects on membrane stability can be studied using a complementary approach, in which the lipids are described in molecular details. However, for that, one has to assume a simplified and predefined peptide geometry; all the peptides are treated the same, regardless of their amino acid sequences. For example, Zemel et al. used such approach in their studies of the interaction of amphipathic and pore-forming helical peptides with lipid bilayers (42).

Some antimicrobial peptides interact specifically with special components in the plasma membrane. For example, human β-defensin has the ability to bind lipopolysaccharide and thereby prevents bacterial infection (43). The glycopeptide vancomicine and other type of antimicrobial peptide as nisin antibiotics target lipid II, a membrane-anchored bacterial cell-wall precursor (44). By blocking the lipid II cycle, the bacterial cell-wall is affected and the antimicrobial activity is achieved. These, clinically important, antimicrobial agents cannot be studied using our model since the specific membrane components that they target are not presented in our simplistic membrane presentation.

In conclusion, the model that was developed is capable of exploring the folding and the interactions with the membrane of a variety of peptides with different physicochemical characteristics. It was proved to be useful in exploring the folding of helical peptides in water and the membrane association of hydrophobic and amphipathic-cationic peptides. The success of the model in the reproduction and interpretation of existing data suggests that it may be useful in the design of new helical peptides that associate with membranes. β-Peptides are another class of peptides that are still not included in the model, but nevertheless have a significant biological role. In the future it should be possible to adapt the model to deal with such peptides too.