Hybrid Stochastic and Deterministic Simulations of Calcium Blips

Abstract

Intracellular calcium release is a prime example for the role of stochastic effects in cellular systems. Recent models consist of deterministic reaction-diffusion equations coupled to stochastic transitions of calcium channels. The resulting dynamics is of multiple time and spatial scales, which complicates far-reaching computer simulations. In this article, we introduce a novel hybrid scheme that is especially tailored to accurately trace events with essential stochastic variations, while deterministic concentration variables are efficiently and accurately traced at the same time. We use finite elements to efficiently resolve the extreme spatial gradients of concentration variables close to a channel. We describe the algorithmic approach and we demonstrate its efficiency compared to conventional methods. Our single-channel model matches experimental data and results in intriguing dynamics if calcium is used as charge carrier. Random openings of the channel accumulate in bursts of calcium blips that may be central for the understanding of cellular calcium dynamics.

INTRODUCTION

Calcium signaling regulates numerous cellular functions as diverse as gene expression, secretion, muscle contraction, and synaptic plasticity. A major class of Ca²⁺ signals are triggered by the binding of extracellular ligands to cell surface receptors, resulting in the activation of well-known second messenger pathways (1–5) to evoke Ca²⁺ release from intracellular storage compartments—principally the endoplasmic reticulum (ER) and the sarcoplasmatic reticulum. Information is encoded in the spatiotemporal patterning of the resulting increases in cytosolic Ca²⁺ concentration, which may be organized as localized transients (6), propagating waves (7–11), and global oscillations (1,12–15).

Inositol 1,4,5-trisphosphate (IP₃) receptor channels (IP₃R) are present in the ER membrane and regulate the liberation of Ca²⁺ in response to the binding of Ca²⁺ and IP₃ to receptor sites on the channel: that is to say, the open probability of the IP₃R channel depends on the cytosolic calcium concentration as well as the IP₃ concentration (see (16–19) for reviews). This feedback provides a self-amplifying release mechanism (calcium-induced calcium release), so that the calcium flux increases nonlinearly with concentrations of IP₃ and Ca²⁺. In particular, Ca²⁺ released by one channel diffuses in the cytosol and thus increases the open probability of neighboring channels, thereby enabling complex spatiotemporal signals.

Experimental observation of local, random release events called “puffs” indicates that IP₃R channels are grouped into clusters on the ER membrane containing a few tens of channels (20–23), whose opening is concerted by local diffusion of Ca²⁺ and calcium-induced calcium release between adjacent channels. These clusters in turn are randomly distributed across the ER membrane at spacings of a few micrometers. Puffs are now considered to be elemental events of Ca²⁺ signaling (24), underlying global oscillations and waves. Subsequent theoretical studies demonstrated that the observed local calcium elevations are not random due to the small numbers of Ca²⁺ ions, but rather due to the random binding and dissociation of Ca²⁺ and IP₃ at the regulatory binding sites of the IP₃R (see (11,25–29) and (30) for the ryanodine receptor channel).

It is therefore important for the understanding of calcium signaling, to develop accurate models for stochastic transitions of single channel states. The available experimental data are of two categories: First, there are patch-clamp experiments of single channel currents. IP₃Rs are inserted into bilayer membranes or are studied in the nuclear membrane and exposed to fixed concentrations of Ca²⁺ and IP₃. It is crucial to note that in these experiments a charge carrier different from calcium is used, so that the ions moving through the channel do not bind to receptor sites on the channel and thereby modify the channel gating. Recordings of single-channel currents are then analyzed to obtain, for instance, open probabilities, mean open and mean close times. Several IP₃R models (31–36) have been developed to describe experimental data obtained from IP₃Rs reconstituted in bilayer membranes, with the De Young-Keizer model (32) in particular being widely applied. However, there are significant differences in behavior of the reconstituted IP₃Rs versus that of IP₃Rs in their native environment of the nuclear envelope (37,38), and only a few models have incorporated IP₃R data obtained for the latter (39,40). On the other hand, models that do exist for nuclear receptors are not dynamic models, i.e., they cannot elucidate channel kinetics. Therefore, we have developed a DeYoung-Keizer-like model based on data obtained from patch-clamp of nuclear IP₃Rs that consistently reproduces experimental data (41). The model comprises four identical, independent subunits, each with nine different states. A channel opens when at least three of its subunits undergo a conformational change to an active state after binding IP₃ and Ca²⁺.

In a second type of experiment, one studies IP₃R channels under physiological conditions in intact cells by using fluorescent indicator dyes to monitor Ca²⁺ liberation into the cytosol. The resolution of such imaging techniques is sufficient to detect presumptive single-channel signals (christened “blips”) (6,21), but it is difficult to study these events in isolation because the opening of one channel usually triggers openings of multiple adjacent channels in the cluster (42). Because the blips form the smallest fundamental building block from which cellular calcium signals are generated, it is important to understand the behavior of IP₃Rs under physiological conditions where the gating of an individual channel is modulated by the large (>1000-fold) changes in local Ca²⁺ concentration that result from Ca²⁺ flux through that channel.

To that end, we simulate stochastic IP₃R channel state dynamics under conditions of no Ca²⁺ feedback (K⁺ as the charge carrier), and where Ca²⁺ is the charge carrier. The latter events we refer to as “blips with calcium carrier.” The transitions during a patch-clamp experiment (i.e., no Ca²⁺ feedback) can be simulated by a Markovian scheme with constant transition rates. A standard method (two-state Markovian scheme) is to compile a list of all transitions of the channel in models such as the DYK, and fix a sufficiently small time-step dt. The occurrence of each of the stochastic transitions during a specific simulation time step is determined by comparison of a computer random number with the product of the corresponding rate and dt (27,43). Another, much more efficient method, is the so-called Gillespie algorithm, which determines the time of each transition by using one random number, while a second random number is used to determine the specific next reaction that is to occur (44). Thus, it needs as many steps (and twice as many random numbers) as transitions occurring, which is far less than for the standard method.

While the Gillespie method provides an efficient means for the study of stochastic channel transitions, the simulation of blips with calcium carrier poses a number of additional problems, which we will briefly outline.

1. The spatiotemporal evolution of free calcium and calcium-binding buffers needs to be simulated simultaneously with the evolution of channel states. In this work, we consider the diffusion and chemical reactions of these species as deterministic processes. This strategy should be principally proven by simulating the full system stochastically and comparing the results with those from the reduction approach. In view of the large number of calcium ions and buffer proteins our assumption is, however, generally accepted (35,43,45) and we will not address its validity in the current publication.

2. The spatial extent of a channel is ∼10–30 nm. Strong currents of calcium through the membrane lead to very localized calcium concentrations around an open channel. On the other hand, released calcium diffuses rapidly over distances of several micrometers. To cope with the resulting range of length scales we chose the finite element method and resolve the calcium profile at nanometer scales close to the channel mouth, while utilizing larger and computationally more tractable grid lengths far from the channel.

3. The timescale of calcium flux upon opening of a channel is in microseconds. This timescale cannot be ignored since the binding of calcium to the channel can occur on timescales as short as tens of microseconds. However, simulations need to trace the evolution for many seconds to achieve statistically significant estimates of stochastic channel gating. This gap of timescales necessitates an efficient time-stepping method including time adaptivity for both the stochastic and deterministic equations of our model.

4. A fourth problem, which is at the focus of this article, is that huge and fast concentration changes upon channel openings and closings have a strong impact on the stochastic dynamics of channel binding and unbinding. As mentioned above, the rate of calcium binding may increase by three orders of magnitude upon channel opening owing to the enormous local calcium concentration increase. This implies that the classical Gillespie algorithm, which rests on the assumption of time-independent rates between succeeding stochastic events, cannot be used. Instead, we chose a special, so-called hybrid method to couple stochastic and deterministic simulations. This method was described recently for ordinary differential equations (ODEs) coupled to Markov processes (46,47) and allows for an adaptive step-size integration of the deterministic equations while at the same time accurately tracing the stochastic reaction events.

In this article, we describe the application of the hybrid method introduced by Alfonsi et al. (46) to the calcium system and thus for the first time, to our knowledge, to a spatially extended system described by partial differential equations (PDEs). A second novelty of our approach is the following: The hybrid method assumes that all stochastic events cause a change in the deterministic variables, which is not the case in the Ca²⁺ system. A special feature of the Ca²⁺ system is that the binding/unbinding of Ca²⁺ ions and IP₃ may not change the open/close state of a channel. Therefore, we devised a new hybrid method by combining the adaptive simulation scheme of the deterministic reaction-diffusion dynamics and the simulation technique for stochastic binding/unbinding of Ca²⁺ and IP₃, which may or may not change the open/close change of the channel. In this article, we describe in detail our hybrid method and, as an example, simulations of calcium blips for a single IP₃R channel. We also compare our hybrid simulation results to results obtained with a simpler method, which uses the Euler scheme for Ca²⁺ diffusion simulation and the two-state Markovian approach with sufficiently small time steps for the stochastic channel dynamics (43,48,49), exploiting spherical symmetry properties of a reduced problem. We find good agreement between both methods and conclude that the fastest method for blip simulations would be a hybrid code for stochastic Gillespie transitions coupled to a simulation of a reduced one-dimensional reaction-diffusion equation. On the other hand, our final aim is the simulation of Ca²⁺ release from channel clusters, where spherical symmetry cannot be used. Thus, in the future we will take full advantage from our three-dimensional finite element/hybrid method.

The article is organized as follows: First, we introduce the basic model of calcium dynamics, which includes the description of all deterministic processes by partial differential equations and the stochastic model of channel state transitions, and discuss the adaptive scheme to solve the deterministic and stochastic equations involving the newly developed hybrid algorithm. We then present results of simulations, first for the purely stochastic model of a single channel with a carrier different from calcium, and then the results for simulations of the full set of equations with calcium as carrier. In the conclusions, we analyze the efficiency and accuracy of the method and briefly discuss the relevance of our results for present problems in calcium dynamics.

MODEL OF CALCIUM DYNAMICS

In the following we will describe each of the components of the model and the equations that we use. As sketched above the model will consist of PDEs for concentration fields and a Markovian description of discrete stochastic quantities. The concentration fields are the calcium concentration in the cytosol and the buffer concentrations. Stochastic quantities are the discrete states of channel subunits, which determine the open/close state of a channel. The coupling works in the following way: random opening and closing of the channels causes fluctuations of certain source terms in the PDEs, while concentrations enter the transition rates of the Markov processes.

Partial differential equations for the concentration fields

The calcium concentration is determined by diffusion, the transport of calcium through the ER membrane, and the binding and unbinding of buffer molecules. Here we do not include buffers within the ER. In the cytosol, we consider three types of buffers: an exogenous mobile buffer with slow reaction kinetics; a stationary buffer with fast kinetics; and an exogenous dye buffer.

All buffers are assumed to be distributed homogeneously at initial time. Total concentrations of mobile, stationary, and dye buffer are denoted by B_m, B_s, and B_d, the amount of buffer bound to calcium by b_m, b_s, and b_d, respectively. Experimentally, the amounts of exogenously added mobile and dye buffers are controlled. The amount of endogenous stationary buffer, comprising contributions from different calcium stores such as mitochondria, is not well characterized.

The buffers are subject to binding and unbinding of calcium, which is modeled using mass-action kinetics:

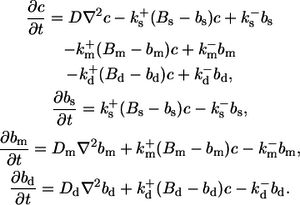(1)

Here, the 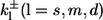denote the on and off rates of calcium reacting with the corresponding buffer proteins. The equations are solved in a domain next to an idealized plane membrane patch of (8 μm)². In the direction perpendicular to the membrane, we consider a spatial extent of 5 μm. All boundary conditions except for c at the membrane are no-flux conditions. The boundary condition for c at the ER membrane models the transport through the ER membrane,

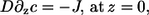(2)

and comprises three contributions:

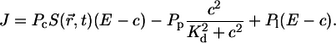(3)

Calcium moves from the ER to the cytosol through IP₃ receptors and by a small leak contribution, which are modeled by terms with coefficients P_c and P_l, respectively. In the other direction, calcium is resequestered into the ER by pumps (P_p). The action of pumps is assumed to be cooperative in calcium and modeled with a quadratic c dependence. K_d is the dissociation constant of the pumps.

The first term in Eq. 3 represents the current through the channel. The current in the open state of the channel was found to depend on the cross-membrane difference of the Ca²⁺ concentration (50). For values of the cross-membrane difference in a physiological environment, the current can be approximated by a linear dependence on (E − c), where E denotes the concentration of free Ca²⁺ in the ER. Furthermore, it was found that the current I through a single channel in the open state is ∼0.1 pA under physiological conditions, an estimate obtained by analysis of patch-clamp experiments on single IP₃ channels expressed on membrane bilayers (50) and detailed simulations of the physiological situation (51). The current through an open channel is modeled by a boundary term, which is constant and non-zero in a specified channel region. Following Thul and Falcke (51), we model the source area of a channel by a disk of radius R_s = 6 nm. This radius is an approximation for the radius of the Donnan potential down to which we can assume lumenal and cytosolic diffusion properties to hold (52). The corresponding total current through this membrane area is derived from

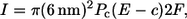(4)

where F is the Faraday constant. With a Ca²⁺ concentration in the ER of E = 700 μM and neglecting c, which is close to zero if the channel is closed, we obtain a cross-membrane difference of 700 μM, resulting in P_c = 6.32 × 10⁶ nm/s.

The position of the model channel in the box of coordinates (0, 8 μm) × (0, 8 μm) × (0, 5 μm) is given by 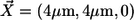in the center of the ER membrane. The channel flux term in Eq. 3 is controlled by the channel state through the factor 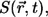which is defined by

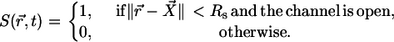Stochastic model of channel gating

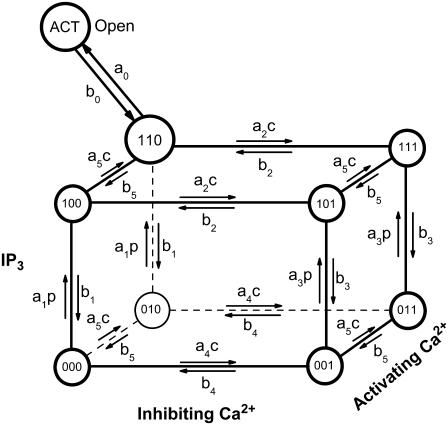
To discuss the dynamics of a single IP₃R we adopt a version of a newly developed stochastic model for the gating of subunits (41), which is based on the DeYoung-Keizer model (32,53). According to the DeYoung-Keizer model, an IP₃R consists of four identical subunits. There are three binding sites on each subunit: An activating site for Ca²⁺, an inhibiting Ca²⁺ site, and an IP₃ binding site (see Fig. 1). The three binding sites allow for eight different states X_ijk of each subunit. The index i indicates the state of the IP₃ site, j the one of the activating Ca²⁺ site, and k the state of the inhibiting Ca²⁺ site. An index is 1 if an ion is bound and 0 if not. Rates of transitions involving binding of a molecule are proportional to the concentration of the respective molecule.

FIGURE 1.

The stochastic model of channel gating is given by 26 possible transitions of each of the four subunits. The values p and c denote the concentrations of IP₃ and Ca²⁺, respectively.

A further transition from X₁₁₀ to a state denoted by X_ACT is introduced. It represents a conformational change of the subunit related to the channel opening. We assume that the channel is open if at least three of the subunits are in the X_ACT state.

The binding and dissociation of Ca²⁺ and IP₃ as well as the conformational change are stochastic events rendering the opening and closing of the channel a stochastic process. That stochastic process is coupled to the concentration of cytosolic Ca²⁺ since the binding probabilities per unit time depend on it, and vice versa, the open/close state of a channel determines the concentration field.

We associate stochastic variables X₀₀₀, X₀₀₁, … , X_ACT with each channel. These variables count the numbers of subunits that are in the respective state, with the sum of all nine variables equal to 4.

Estimation of the calcium concentration on the cytosolic face of the membrane is crucial for comparison with experiments where calcium is used as charge carrier. Due to the strong gradients of calcium around an open channel, the exact position of regulatory Ca²⁺ binding sites may be important for the transition rates in the model. Here, however, we do not study this dependence and simply assume that each of the Ca²⁺ binding processes is determined by the Ca²⁺ concentration in the center of the channel.

Numerical method

Our numerical method consists of a coupled solver for the deterministic set of PDEs and the stochastic solver. In view of the multiple scales in length and time, we employ an unstructured finite element method and an adaptive linear implicit time-stepping for the deterministic part. The stochastic solver is based on the Gillespie method (44), which is adaptive in the sense that its time step follows the evolution of transition probabilities. A complication arises since the usual Gillespie method solves stochastic processes where the so-called propensities are constant during subsequent transitions (see below). However, for channels with Ca²⁺ as carrier, the propensities may change rapidly due to channel openings and closings. This problem is solved by devising the hybrid method described in Simulation with Calcium as Carrier: Bursts of Blips.

Finite element method for integration of the partial differential equations

We discretized the spatial domain by linear finite elements (tetrahedra). This method is particularly useful when spatial resolution needs to be very high in some regions only. For our simulations of calcium blips, we employ a grid with a very fine resolution in the channel area of radius 6 nm. There the grid length is smaller than 1 nm. With increasing distance from the channel, the grid is coarsened up to 500 nm. The grid consists of ∼30,000 points. Details of the method and the spatial gridding procedure can be found in a forthcoming publication.

The finite element discretization results in a coupled set of ODEs, which are solved by a Krylov-W method with three stages (55). This method is a linear-implicit Runge-Kutta method of order 2, with an embedded scheme of order 1. Solutions of both orders are used to calculate an approximation of the time-stepping error and to adapt the temporal time step. The arising linear systems are solved by the BiCGSTAB method (56).

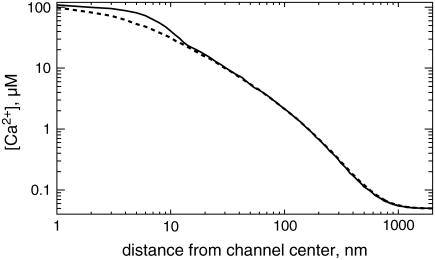
The stationary Ca²⁺ concentration gradient around an open channel is shown in Fig. 2. Here we have plotted [Ca²⁺] against the distance from the channel center on the membrane and vertical to the membrane. The maximum calcium concentration at the channel is ∼112 μM.

FIGURE 2.

The stationary Ca²⁺ concentration for an open channel directly at the ER membrane (solid) and perpendicular to the membrane (dashed) as calculated with the finite element discretization.

Hybrid algorithm

The algorithm is based on a recently introduced approach for simulating hybrid models of chemical reaction kinetics in spatially homogeneous systems (46). For the sake of clarity, we introduce our hybrid method for a single channel system—the generalization to multichannel systems will be obvious.

Recall that X₀₀₀, X₀₀₁, … , X_ACT are random variables counting the number of subunits that are in the respective state. The channel changes its state if the occupation of one of the binding sites changes. Such changes are modeled as stochastic events, denoted by R₁, … ,R_m. The event dynamics is defined in terms of the associated propensity functions α₁, … , α_m that characterize the probability per unit time that the corresponding event takes place. The propensities are proportional to the number of subunits X_su in the corresponding subunit state of the transition, hence α_i = X_sur_i, where r_i denotes the transition rate. For instance, denoting the transition from X₁₀₀ to X₁₀₁ by R₁, we define a propensity α₁ = X₁₀₀a₂c (see Fig. 1). The product α_idt is the probability that the event R_i occurs in a given infinitesimal time interval dt.

The Gillespie algorithm allows for simulation of stochastic event systems (44). Given the actual time t, the probability that the next stochastic event occurs in the infinitesimal time interval [t + τ, t + τ + dt] and is an R_i event, is given by

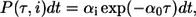(5)

where 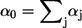is the sum of all propensities. The probability density P(τ, i) can be realized by drawing two random numbers r₁ and r₂ from a uniform distribution in the interval [0, 1], and choosing τ and i such that

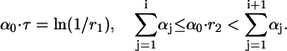(6)

In this way, the next event to occur is R_i, and it will occur after time τ.

The Gillespie method rests on the assumption that during successive stochastic events the propensities α_i do not change. However, when linking the stochastic channel dynamics to the calcium dynamics, we expect the propensity α_i to change in time due to its dependence on the local calcium concentration c. This effect will be particularly strong for openings and closings of channels, since after such events the local calcium concentration c changes dramatically by three or four orders of magnitude.

To resolve this problem we adopt the recently introduced hybrid method by Alfonsi et al. (46). Within their setting the time τ to the next stochastic event is determined by solving

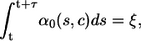(7)

with ξ = ln(1/r₁), where the sum of propensities α₀ may explicitly depend both on time s and the local calcium concentration. Note that the above equation simplifies to the equation, which determines τ in Eq. 6 in the case of constant α₀. To determine the time of the next reaction τ, Eq. 7 is conveniently rewritten in differential form by introducing a variable g(τ) and solving

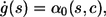(8)

with initial condition g(0) = 0, along with the deterministic equations for c and buffers. A reaction then occurs whenever g(s) reaches the value ξ. As before the specific event, R_i, is determined based on a second random number r₂, satisfying the second condition in Eq. 6 with propensities evaluated at the event time t + τ.

A special feature of the calcium system is that not all stochastic events change the open/close state of a channel. An event resulting in an opening or closing of the channel occurs only if the number of subunits in the state X_ACT changes between 2 and 3 and will be called a “channel transition” in the following. A channel transition has an impact on the local calcium concentration c, while nonchannel transitions do not change the local calcium concentration. Below, the algorithmic realization of our hybrid approach is given. Along the computation of the deterministic part of the calcium dynamics, the stochastic events are traced via Eq. 7 or 8. If a non-channel transition occurs, the stochastic event is performed. The stochastic channel dynamics is updated correspondingly, while there is no influence on the calcium concentration. On the other hand, if a channel transition takes place, both the channel and the calcium dynamics do change. This typically requires a readjustment of the deterministic time step.

The outline of the algorithmic realization is as follows (here we use only c as deterministic variable):

1. Initialization

   Set t_old = 0, Δt > 0, c_old = c₀, X = X₀, g_old = 0 and   draw a uniform random number r₁ in [0,1] defining ξ = ln(1/r₁).

2. Deterministic step

   Compute c_new and g_new based on c_old, g_old, and Δt.

   If the local error criterion (provided by the Krylov-W method) is not met, reduce the step size Δt and go to 2., otherwise define t_new = t_old + Δt and set the new step size Δt according to the time-stepping code prediction.

3. If g_new < ξ (no stochastic event),

   Set c_old = c_new, g_old = g_new, t_old = t_new, and go to 2.

   Else (g_new ≥ ξ, some stochastic event occurs in the time interval [t_old, t_new]),

   Determine the event time t_s ∈ [t_old, t_new] by (linear) interpolation, and compute the corresponding calcium concentration c_s at the event time t_s by (linear) interpolation.

   Draw a uniform random number r₂ in [0, 1] and determine the stochastic event R_i according to Eq. 6 based on c_s.

   If the next event R_i is not a channel transition,

   Perform the stochastic event R_i to determine the new channel state X.

   Set g_old = 0 and recompute g_new based on c_s, g_old and the remaining time (t_new – t_s).

   Draw a new uniform random number r₁ in [0, 1] defining ξ = ln(1/r₁), and go to 3.

   Else (the next event R_i is a channel transition),

   Perform the channel transition R_i to determine the new channel state.

   Set g_new = 0, and draw a new uniform random number r₁ in [0, 1] defining ξ = ln(1/r₁).

   Set t_new = t_s, and define new step size Δt = Δt_channel (a sufficiently small number).

   Set c_old = c_s, and go to 2.

Note that Δt_channel should be smaller than or similar to the timescale of stochastic transitions after a channel opening/closing, since we linearly interpolate the deterministic solution to determine stochastic transitions between succeeding deterministic time steps. Therefore, fast changes of the deterministic variables after a channel opening/closing need to be approximated numerically at timescales comparable to the stochastic transitions. In our simulations described below, Δt_channel is set to 10⁻⁵ s.

RESULTS FOR THE DYNAMICS OF A SINGLE CHANNEL

Simulations with fixed calcium concentration

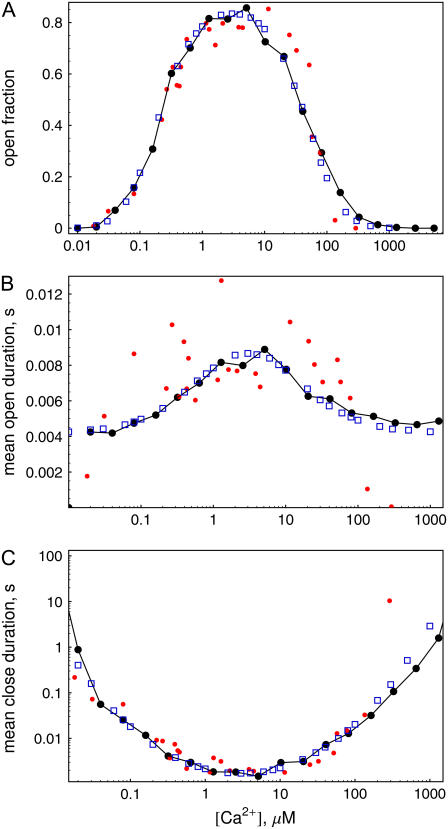
In this section, we present results of simulations to test the hybrid method applied to the calcium system. We begin with simulations where the calcium concentration in the cytosol is held fixed to a certain value. Fig. 3, a–c, show the open fraction, mean open time, and mean close time for different calcium concentrations in the cytosol. The connected dots correspond to runs with the hybrid program for 100 s each. The IP₃ level was set to 10 μM in these simulations. The plot of the open probability (Fig. 3 a) clearly shows the bell-shaped curve typical for IP₃ receptor channels. Further, one can observe a distinct maximum in the mean open time and a minimum in the mean close time for cytosolic calcium concentrations at ∼5 μM.

FIGURE 3.

Open fraction (a), mean open (b), and mean close time (c) versus cytosolic [Ca²⁺] for [IP₃] = 10 μM. (Connected large dots) Hybrid simulations for runs of 100 s. (Small dots) Data from experimental work of Mak et al. (38). (Blue squares) Two-state Markovian method for runs of 10⁵ s.

Our model of channel gating was originally obtained by fitting the experimental data of Mak et al. (38). Their results are shown in Fig. 3 by small dots. A detailed description of the parameter estimation by fitting to experimental data can be found in a forthcoming publication (41).

We also compared our results to those from simulations based on a standard Markovian method and found satisfying agreement. This data is shown in Fig. 3 by blue squares.

Simulation with calcium as carrier: bursts of blips

We will now present hybrid simulations of our model for a calcium carrying channel. In this problem, the resting free calcium concentration is set to 0.05 μM, but the opening of the channel and the ensuing calcium current lead to large local cytosolic values of [Ca²⁺] of ∼110 μM, thereby vastly increasing the probability of further Ca²⁺ binding.

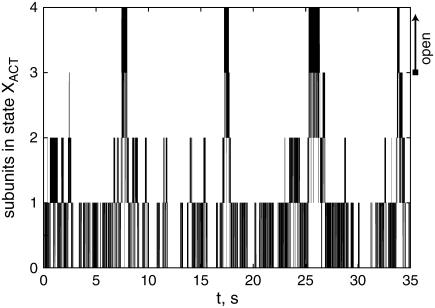
Fig. 4 shows the evolution of the number of activated subunits for a test run of 35 s. Here the IP₃ concentration was set to 0.1 μM. During the 35-s interval, there are five bursts of channel openings and closings, which are typical for all runs that we have performed. These bursts consist of rapid openings and closings on a millisecond timescale reflecting the transitions between the states X₁₁₀ and X_ACT.

FIGURE 4.

The evolution of the number of subunits in state X_ACT for a simulation run with [IP₃] = 0.1 μM. The channel is open if X_ACT = 3 or 4. The resting concentration of Ca²⁺ was 0.05 μM.

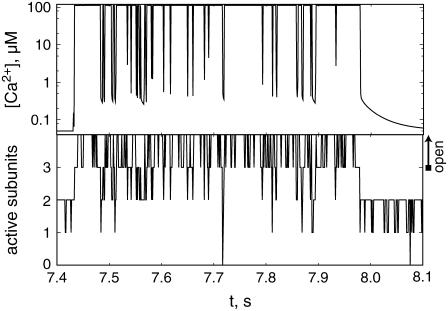
The evolution of a typical burst is shown in Fig. 5 in terms of the number of subunits in the active state X_ACT and the Ca²⁺ concentration at the channel mouth. The first opening of the channel after ∼7.43 s leads to a rapid increase of the local Ca²⁺ concentration, which reaches a stationary value within a few microseconds. Since activation is a fast process provided that the Ca²⁺ concentration is high, all four subunits are activated within a short time. The switching of subunits between the states X₁₁₀ and X_ACT leads then to the repeated openings and closings of the channel lasting ∼550 ms.

FIGURE 5.

The Ca²⁺ concentration at the channel mouth and the number of subunits in the active state, X_ACT, during the second burst shown in Fig. 4. After the last closing of the burst, residual Ca²⁺ decays in ∼100 ms.

It is less clear what causes the termination of a burst. We observed that often the termination of a burst is related to inhibition of one subunit, leaving three noninhibited and activated subunits. The deactivation of one further subunit causes the Ca²⁺ concentration to collapse to values below 1 μM within 1 or 2 ms, leaving only residual calcium around the channel, which persists for ∼100 ms (see Fig. 5). Consequently, the probability for subsequent binding of Ca²⁺ to activating sites is small, which can lead to a prolonged closure of the channel.

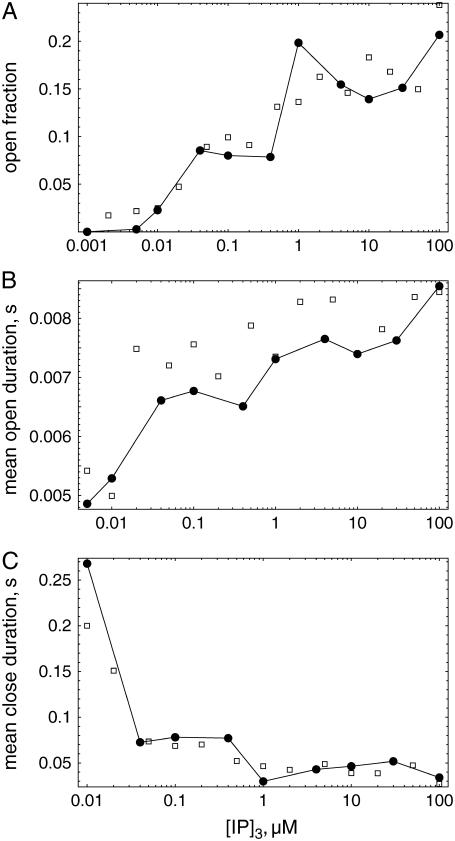
We have made a series of simulations to determine the open fraction, mean open time, and mean close time for different IP₃ concentrations. The open fraction is shown in Fig. 6 a. It increases with increased levels of [IP₃]. The values are always far from the maximum 80% found for channels without Ca²⁺ carrier (compare Fig. 3).

FIGURE 6.

Open fraction (a), mean open duration (b), and mean close duration (c) versus IP₃ concentration using calcium carrier. (Circles) Hybrid simulations (simulation time: 200 s); (squares) simulation with two-state Markovian method (150 s).

Fig. 6, b and c, show the estimated mean open and mean close times for different IP₃ concentrations. The mean open time depends significantly on the IP₃ concentration and increases from ∼5 to 8 ms. The mean close time reaches values of ∼200 ms for small IP₃ concentration and reduces to ∼40 ms for larger IP₃ concentration.

We have again compared the results of our simulations using the hybrid method with results of the two-state Markovian method. To calculate the cytosolic Ca²⁺ concentration we exploited spherical symmetry to simplify the Laplace operator according to the numerical scheme introduced by Smith et al. (57). The spatial grid distance used in these simulations was dx = 15 nm. Results of these simulations, supporting the data obtained by the hybrid method, are shown in Fig. 6 by squares.

Inspection of time series showed that the duration of bursts depends on the IP₃ concentration. For small concentration values, below those of the example shown in Fig. 4, we find typical burst durations of 300 ms and less. This behavior is presumably related to the binding of IP₃ to <4 subunits if the IP₃ concentration is low. Then the chance for the termination of a series of blips is much higher than with all four subunits available for activation.

CONCLUSIONS

In this article, we have described the first computational approach to intracellular calcium dynamics, which takes into account the coupling of stochastic and deterministic evolution equations in an accurate and efficient way. The strong localization of Ca²⁺ ions around an open channel necessitates the use of finite elements. This method has also been successfully used by other groups (58–60). Here we concentrated on the additional problem of fast temporal scales, which arise from the channel gating and local relaxation of calcium concentrations. The hybrid algorithm to reliably link the stochastic transitions to deterministic concentration variables was described in detail in this article. The hybrid method is an extension of the exact Gillespie method for chemical master equations, and is in general used to accelerate the update of species with large quantities. We have adapted the hybrid method of Alfonsi et al. (46) to simulate DYK-type schemes where only a few of the transitions lead to direct changes in deterministic concentrations. Furthermore, to our knowledge we have used the hybrid method for the first time in conjunction with reaction-diffusion equations, that is, in systems, where the concentration variables exhibit spatial dependence. The results of extensive simulations were compared with results of a standard two-state method. This method gives accurate results for sufficiently small time-steps. Using a time step of 10⁻⁵ s for the two-state method, a satisfactory agreement of both methods was found.

The advantage of the hybrid method is a much larger typical time step and a reduced number of required random numbers. For a run of 35 s as shown in Fig. 4, the two-state Markovian method needed 3,500,000 steps and 3,500,000 random numbers. The hybrid simulation required ∼36,400 steps of the deterministic solver for the same run, where most of the steps are required for output at every millisecond, and two random numbers per transition, i.e., at ∼12,000 random numbers (for the run shown in Fig. 4, we found ∼6000 stochastic transitions.)

We note that, within the current problem of single-channel simulations, a one-dimensional spatial discretization of a spherically symmetric channel can be used, as was done in our simulations using the two-state method. This approach has the advantage of speeding up the deterministic simulation step considerably compared to the fully three-dimensional simulations used with the hybrid code. Therefore we found that the total simulation times using the hybrid code were higher than for the two-state method based on the one-dimensional model exploiting spherical symmetry. However, the ultimate goal of our research is the simulation of one or several clusters of channels. We plan to simulate the release of calcium from ∼20 to 60 channels per cluster, which are located on a plane membrane patch. Here, spherical symmetry cannot be used, and the full advantage of hybrid modeling is apparent.

A possible improvement of our simulation technique regards the time step for the deterministic equation. Here we use an implicit solver, which allows large time steps even if fast relaxation processes occur. However, we need to accurately trace the evolution of propensities and thus of the Ca²⁺ concentration and cannot, in the current computer code, take advantage of large time steps. The use of time-stepping techniques with dense output may mitigate this problem (61). Such methods allow large time steps but provide the solution at intermediate times with much higher accuracy than the linear interpolation that we are using in the current code.

We want to stress that the hybrid method can be generalized for use in models of many different biochemical systems. Fast timescales and the existence of processes with large and small numbers of molecules often prohibit efficient simulation of the complete chemical master equation. The solution that we propose is the simulation of ODEs or PDEs coupled to stochastic molecular processes, which are expected to introduce relevant fluctuations. We have shown in this article that the coupling of both systems can be efficiently performed with the hybrid method.

We are aware of the fact that such a method, in principle, needs to be validated solving the channel as well as the calcium and the buffer dynamics fully stochastically, according to the reaction-diffusion master equation (62–64). Due to the large amount of calcium and buffer molecules in the system, this would not even be feasible on supercomputers, since the computational effort scales with the number of reactions (including diffusion as a first-order, i.e., pseudo reaction; see, e.g., (64)). However, pursuing along a similar line as in Alfonsi et al. (46), we may justify our new approach. Since calcium and dye buffer concentrations are high, as are the diffusion and binding rate constants for calcium-dye binding processes, the resulting propensities will be large. As a consequence, all diffusion reactions as well as the calcium dye-binding processes can be modeled deterministically. However, the propensities corresponding to the channel dynamics will be small to moderate, since the associated rate constants are small. This finally results in the herein presented model, a deterministic reaction-diffusion model for calcium and the dye buffer, coupled to a stochastic model of the channel kinetics. The proposed algorithmic realization is therefore based on the same theoretical justification as the method in Alfonsi et al. (46).

We finally discuss the relevance of our work for the understanding of calcium dynamics. First of all, our model uses an additional active state compared to the DYK model. This additional state enables us to fit short mean open and mean close times, which were found in experimental data and which could not be fitted using the DYK model. Furthermore, we found that the existence of the additional conformational change results in bursts of rapid openings and closings if calcium is used as a carrier, similar to that found by Swillens et al. (35). In this and in further respects the nine-state model for subunit dynamics will be a better model for ongoing studies of calcium dynamics. For instance, the existence of two timescales of activity inherent to the nine-state model (i.e., the mean open time and the duration of a burst) may well have consequences for the dynamics of clusters of channels and will be studied in more detail in the future.

APPENDIX

In Table 1 we provide the complete list of parameters of our model.

TABLE 1.

List of parameters

Parameter	Value	Unit
Channel flux coefficient P	6.32 × 106	nm s−1
Single channel radius Rs	6	nm
Pump flux coefficient Pp	40000	nm μM s−1
Pump dissociation coefficient Kd	0.2	μM
Ca2+ concentration in ER, E	700	μM
Ca2+ concentration in cytosol at rest, c0	0.05	μM
Leak flux coefficient	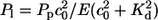3.36	nm s−1
Diffusion coefficient D of free cytosolic Ca2+	200	μm2 s−1
Diffusion coefficient Dm of mobile buffer	200	μm2 s−1
Diffusion coefficient Ddye of dye buffer	15.0	μm2 s−1
On-rates of fast buffers:
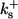
	50	(μM s)−1
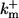
	5	(μM s)−1
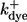
	150	(μM s)−1
Dissociation constants of buffers :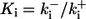
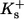
	2	μM
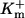
	0.15	μM
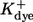
	2	μM
Total concentrations of buffers:
Bs	80	μM
Bm	300	μM
Bdye	40	μM
Subunit kinetics, note bi = aidi
IP3 binding
a1, a3	80	(μM s)−1
d1	0.008	μM
d3	0.5	μM
Inhibiting, with IP3
a2	0.04	(μM s)−1
d2	12	μM
Inhibiting, without IP3
a4	0.4	(μM s)−1
d4	0.192	μM
Activating
a5	15	(μM s)−1
d5	0.8	μM
Open conformational transition
a0	550	μM
b0	80	μM