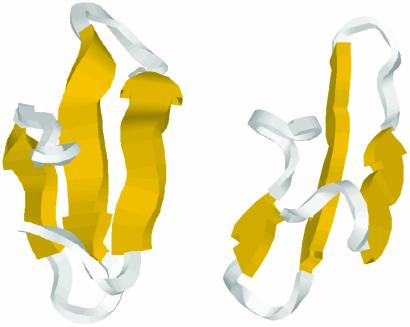Coarse-grained sequences for protein folding and design

Abstract

We present the results of sequence design on our off-lattice minimalist model in which no specification of native-state tertiary contacts is needed. We start with a sequence that adopts a target topology and build on it through sequence mutation to produce new sequences that comprise distinct members within a target fold class. In this work, we use the α/β ubiquitin fold class and design two new sequences that, when characterized through folding simulations, reproduce the differences in folding mechanism seen experimentally for proteins L and G. The primary implication of this work is that patterning of hydrophobic and hydrophilic residues is the physical origin for the success of relative contact-order descriptions of folding, and that these physics-based potentials provide a predictive connection between free energy landscapes and amino acid sequence (the original protein folding problem). We present results of the sequence mapping from a 20- to the three-letter code for determining a sequence that folds into the WW domain topology to illustrate future extensions to protein design.

An important insight into the protein folding problem is the recognition that native-state topology often plays a dominant role in the kinetics of the folding process (1, 2). This concept implies that the subtlety of interactions among 20 different amino acids that give rise to cooperative formation of native structure through backbone hydrogen bonding and specific side-chain packing of the native-state core can often be suppressed and effectively replaced by coarse-grained descriptions that capture the overall topology and spatial distribution of local and nonlocal contacts.

Minimalist proteins are coarse-grained models that use an α-carbon trace to represent the protein backbone in which structural details of the amino acids and aqueous solvent have been integrated out and replaced with effective bead–bead interactions. In these models, the potential energy functions for bead–bead interactions are typically Gō model potentials, which require direct knowledge of native-state tertiary contacts (3). These models are particularly useful in the study of proteins for cases when sequence is unimportant relative to the effects of native-state topology for determining folding rate and mechanism.

However Go bead models avoid the more difficult aspect of the protein folding problem, namely its dependence on amino acid sequence. Therefore, it is not surprising that these idealized models can lack a quantitative connection to experiment in some cases (4, 5). Physics-based models return to the original problem of confronting the complexity of amino acid sequence and corresponding interplay of physical interactions that give rise to the particulars of protein stability and kinetics and therefore do not require knowledge of native-state tertiary contacts (6–11). They are more generally applicable, especially when sequence details are equally important to topology, such as that found for two members of the ubiquitin fold class, the Ig-binding proteins L and G.

Proteins L and G are two single-domain proteins that have little sequence identity and yet identical fold topologies, consisting of a central α-helix packed against a four-strand β-sheet composed of two β-hairpins (12). Experimental evidence indicates that protein L folds in a two-state manner through a transition state involving a native-like β-hairpin 1 and largely disrupted β-hairpin 2 (13–15). Protein G, on the other hand, folds through a possible early intermediate (16, 17), followed by a rate-limiting step that involves formation of β-hairpin 2 (18).

The differences between proteins L and G illustrate the delicate balance between energetic and topological frustration in the folding of proteins and suggest that a model capable of distinguishing them would require a level of resolution that captures the differences in primary sequence. The question we explore here is: can a coarse-grained sequence description and design approach be used to capture the differences in folding mechanism between two proteins that adopt the same fold topology?

In this work, we present the results of sequence design on our off-lattice minimalist bead model that uses three residue types: hydrophobic, hydrophilic, and neutral. We start with a minimalist sequence that folds to the correct α/β fold topology and build on it through sequence mutation to produce two new minimalist sequences that reproduce the differences in folding mechanism seen experimentally for proteins L and G. Ultimately, a difference of only three bead types is required to differentiate between minimalist proteins L and G to exhibit the correct difference in their folding mechanism.

When the designed reduced letter code sequences are aligned alongside their respective counterpart sequences of the real protein L or protein G, we find ≈75% sequence identity. This alignment indicates that there is in actuality rather high sequence identity between proteins L and G at a coarse-grained sequence level, which is clearly minimal at the resolution of a 20-letter code (18). This degree of sequence identity shows that the patterning of hydrophobic and hydrophilic beads is largely preserved in the sequence design to fold to the target topology and suggests that it is the patterning that is the physical origin for the success of relative contact-order descriptions of folding kinetics.

We conclude that a minimalist three-letter code sequence is capable of discriminating between the primary structure for proteins L and G that is responsible for the two proteins folding through such distinctly different folding mechanisms. To demonstrate that the sequence mapping from a 20-letter letter amino acid code to the three-letter reduced code is sufficient for determining the folding to a target topology, we perform this sequence mapping for the WW domain and provide preliminary evidence that it folds to the experimentally observed β-sheet topology by using our physically motivated model.

Methods

Inspired by early efforts of Thirumalai and coworkers (6, 19, 20), our group has developed a more comprehensive minimalist model that is general to α-helical, β-sheet, and mixed α/β protein topologies. We have previously explored its use for members of the ubiquitin α/β fold class (8, 9, 21). The protein chain is modeled as a sequence of beads of three flavors: hydrophilic, hydrophobic, and neutral; these are designated by L, B, and N, respectively. The total potential energy function is

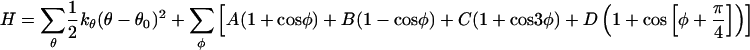[1]

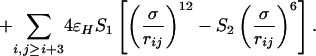In the above equation, θ is the bond angle, φ is the dihedral angle, and r_ij is the distance between beads i and j. ε_H sets the energy scale and gives the strength of hydrophobic contact. The bond angle term is a stiff harmonic potential with force constant k_θ = 20ε_H/rad², and θ₀ = 105°. Each dihedral angle in the chain is designated to be one of the following three types: helical (designated by H), with A = 0, B = C = D = 1.2ε_H; extended (designated by E), with A = 0.9ε_H, C = 1.2ε_H, B = D = 0; or turn (designated by T), with A = B = D = 0, C = 0.2ε_H. The dihedral potentials are in large part responsible for maintaining the secondary structure topology. For both proteins L and G, the β1 region begins at bead 1 and terminates at bead 21, and the α helix covers the bead range from 23 to 35, whereas the β2 region covers the bead range from 37 to 56.

The nonlocal interactions are determined by: S₁ = S₂ = 1 for B–B interactions; S₁ = 1/3 and S₂ = –1 for L–L and L–B interactions; and S₁ = 1 and S₂ = 0 for all N–L, N–B, and N–N interactions. The attractive forces in the model responsible for collapse are due to the interactions between hydrophobic beads (B–B interactions). The interactions among all other combinations of beads are repulsive, although different strengths of repulsion are used depending on the bead types involved.

We use constant-temperature Langevin dynamics in the lowfriction limit to perform simulations for characterizing the thermodynamics and kinetics of folding. Bond lengths are held rigid by using the RATTLE algorithm (22). All simulations are performed in reduced units, with mass m, length σ, energy ε_H, and k_B all set equal to unity.

The free energy landscape is characterized with the multidimensional histogram technique (23–25). We collect multiple six-dimensional histograms over energy E, radius of gyration R_g, and native-state similarity parameters χ, χα, χβ₁, and χβ₂. χ is given by

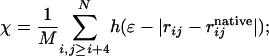[2]

here the double sum is over beads on the chain, and r_ij and 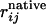are the distances between beads i and j in the state of interest and the native state, respectively. h is the Heaviside step function, with ε = 0.2 to account for thermal fluctuations away from the native-state structure. M is a constant that satisfies the conditions that χ = 1 when the chain is identical to the native state and χ ≈ 0 in the random coil state. The remaining χ parameters are specific to their respective elements of secondary structure. That is, χα involves summation over beads in the helix, and χβ₁ and χβ₂ involve summation over beads in the first and second β-sheet regions, respectively.

From the histogram method, we get the density of states as a function of six-order parameters, Ω(V, R_g,χ, χα, χβ₁, χβ₂), which can be used to calculate thermodynamic quantities. In constructing the free energy surfaces, we collect histograms at 15 different temperatures: 1.20, 0.90, 0.70, 0.62, 0.60, 0.55, 0.50, 0.48, 0.46, 0.44, 0.42, 0.41, 0.40, 0.39, and 0.38. We run three independent trajectories at each temperature and collect 10,000 data points per trajectory.

The kinetics of the folding process can be characterized by calculating a large number of first-passage times (the time required for a folding trajectory to cross into the native basin of attraction). The first-passage times are calculated by taking an initial high-temperature random coil structure and evolving it at the folding temperature of interest until recording the time that it enters the native basin of attraction. We subtract off an initial correlation time in which the high-temperature chain is briefly equilibrated at the target temperature (this is the computational dead time during the kinetics run).

On the basis of theoretical work (2, 26, 27), one criterion for the foldability of heteropolymer sequences is the requirement of having a significant energy gap between the native-state and average misfold energies. Our sequence design strategy makes use of this concept by creating a misfold library generated from multiple trajectories at temperatures near the collapse temperature. To then obtain optimal new sequences, we attempt to maximize the energy gap, ΔE_design = 〈E_misfold〉 –E_native. The library is quenched before use, ensuring that member structures are at local minima on the potential energy surface. The structures collected in this way are representative of misfold traps and not the barriers separating minima. Maximizing ΔE_design for misfolds located at barriers could be expected to adversely affect folding kinetics, because trapping could become more substantial.

Results

Our original work on a minimalist representation of an α/β fold topology produced a sequence that adopts the correct native fold but exhibits at least two folding pathways, each of which corresponds to either a protein-L-like mechanism or a protein-G-like mechanism (8, 9). In light of this fact, this original α/β sequence will be called the “L/G” sequence to indicate it has properties of both proteins L and G, distinguishing it from our two new distinct sequences for proteins L and G.

Initially, we began our search for mutations to improve the L/G sequence by aligning it against the real protein sequences and proposing mutations that move the L/G sequence toward being more L- or G-like. The alignments are performed by using secondary structure as a rough guide. This process also requires categorization of amino acids as either L, B, or N. Shown in Table 1 is the general mapping between the 20- and three-letter codes, with the interpretation of the three flavors as simply hydrophobic, hydrophilic, or neutral. There is, of course, ambiguity in the mapping from a 20- to a three-letter code. Lysine can be viewed as either hydrophilic or hydrophobic, depending on the structural context. The long lysine side chain can participate in the hydrophobic core through its four methylene groups, whereas its amino group typically resides on the surface, which imparts its typical hydrophilic character. Important hydrogen bonds in the native structure might result in two hydrophilic amino acids (designated as an L bead) becoming two hydrophobic B beads in our reduced-letter code, i.e., emphasizing that an attractive interaction exists. However, in general, the mapping used in Table 1 is a good first approximation to the original sequence.

Table 1. Sequence mapping between 20-letter (20) amino acid and coarse-grained three-letter (3) code.

20	3	20	3	20	3	20	3
Ala	B	Met	B	Gly	N	Asn	L
Cys	B	Val	B	Ser	N	His	L
Leu	B	Trp	B	Thr	L	Gln	L
Ile	B	Tyr	B	Glu	L	Lys	L
Phe	B	Pro	N	Asp	L	Arg	L

Tables 2 and 3 contain the sequence alignments for the L/G minimalist reduced code against the amino acid sequences of proteins L (2PTL) and G (2GB1), as well as possible errors in the assignments. We do not consider an L→NorN→L mapping as an error, because both L and N interact through repulsive potentials (see Methods); errors arise only from L→B, N→B, B→N, and B→L mappings, because the fundamental interaction potential changes from attractive to repulsive, or vice versa. Overall, we find ≈65–75% sequence identity between 2PTL and 2GB1 and our model L/G sequence.

Table 2. Sequence alignment for the B1 domain of protein L (Protein Data Bank ID code 2PTL) (first line) against reduced code of minimalist model for protein L/G (second line).

	Protein L mapping
1°2PTL	VTIKANLIFANGSTQTAEFKGTFEKATSEAYAYADTLKKDNGEYTVDVADKGYTLNIKFAG
1°model L/G	LBLBLBLBBNNNL BBLBBBBBNN NLLBLLBBLLBNB LBLBLBB NNNBBBLBLBLBL
1°model L	LBLBLBLBBNNNB BBLBLBBBNN NLLBLLBBLLBNB LBLBLBL NNNLBBLBLBBBL
2°2PTL	CCCEEEEECSSSCCEEEECCBSSHHHHHHHHHHHHHTCSSSCCEEECCBTTTTEECEEECC
2°model L	EEEEEETEHTHE EEEEEEEHHE HHHHHHHHHHEHT EEEEEEE TTTEEEEEEEE

Possible error candidates in mapping are shown in bold. The third line shows the new sequence for protein L, with differences from L/G shown in bold. Also shown is the secondary structure alignment for the B1 domain of protein L (fourth line) against reduced code of minimalist model for protein L (last line).

Table 3. Sequence alignment for the B1 domain of protein G (Protein Data Bank ID code 2GB1) (first line) against reduced code of minimalist model for protein L/G (second line).

	Protein G mapping
1°2GB1	MTYKLILNGKTLKGETTTEAVDAATAEKVFKQYANDNGVDGEWTYDDATKTFTVTE
1°model L/G	LBLBLBLBBNNNLBBLBBBBBNNN LLBLLBBLLBNBLBLBLBB NNNBBBLBLBLBL
1°model G	LBLBLBLBBNNNLBBLBLBBBNNN LLBLLLBLLBNBBBLBBBB NNNLBBLBLBLBL
2°2GB1	CEEEEEEECSSCEEEEEEECSSHHHHHHHHHHHHHHTTCCSEEEEETTTTEEEEEC
2°model G	EEEEEETEHTHEEEEEEEEHHEH HHHHHHHHHEHTEEEEEEE TTTEEEEEEEE

Possible error candidates in mapping are shown in bold. The third line shows the new sequence for protein G, with differences from L/G shown in bold. Also shown is the secondary structure alignment for the B1 domain of protein G (fourth line) against reduced code of minimalist model for protein G (last line).

Further improvements in sequence consist of proposing mutations and threading the new sequences through a (quenched) misfold database and subsequently looking for those mutations that give a favorable ΔE_design. To address the feasibility of using errors in the sequence alignments as a guide for proposing new mutations, we began initially by aligning protein L and using solely these errors to improve the sequence. In the case of protein G, all possible single mutations were investigated during the design process, and we did not restrict ourselves to errors solely from the alignment.

Starting from the original L/G sequence and proceeding through a series of mutations, we arrived at the new sequences for proteins L and G. Note that these mutations are only in the primary sequence, and that all proteins share the same secondary structure topology (dihedral sequence). Each new sequence required a series of five point mutations from the original L/G sequence. Shown in Tables 2 and 3 are the mutations used to obtain the new sequences. The energy of the original L/G native state is –32.4ε_H, whereas for the new protein L, the native-state energy is –28.8ε_H, and for protein G the native-state energy is –26.9ε_H. The energy distribution of the misfold library is well separated from these native state energies.

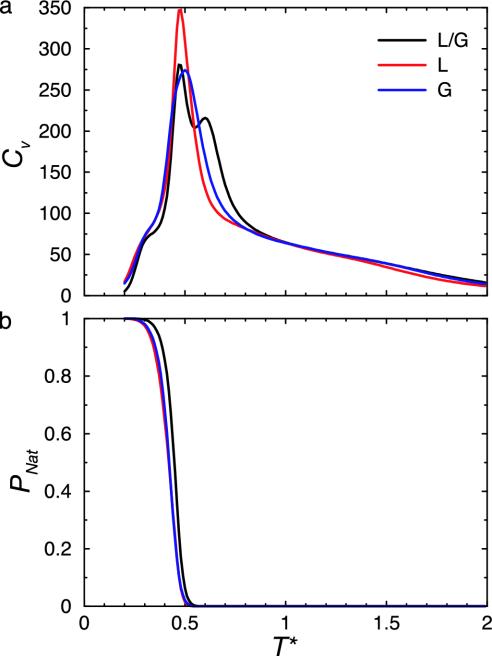
Two of the five point mutations for L and G are common to both sequences (B18L and B47L), which serve to make the proteins more foldable and appear to clean up thermodynamic aspects of the original sequence. This is evident in a comparison of the heat capacity curves (Fig. 1a) for proteins L/G, L, and G. The sharper transitions in these thermodynamic signatures are evidence for greater cooperativity in folding. From the melting curves (Fig. 1b), we see that the folding temperature [the value of T for which P_Nat(T) = 0.5] is lowered for L and G relative to the L/G sequence.

Fig. 1.

Comparison of thermodynamic data for the new optimized sequences of proteins L and G to that of original L/G sequence. (a) Heat capacity C_v vs. temperature T for the original nonoptimal L/G, L, and G sequences. The new L and G sequences show increased cooperativity. (b) Fraction of chains in the native state, P_Nat, vs. temperature, T, for the L/G, L, and G sequences. At the folding temperature, T_f, the distribution of population between the folded and unfolded states is equal, that is, P_Nat(T_f) = 0.5.

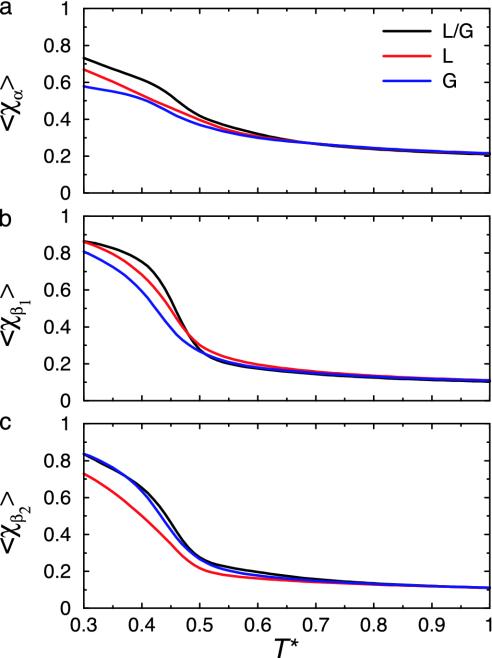
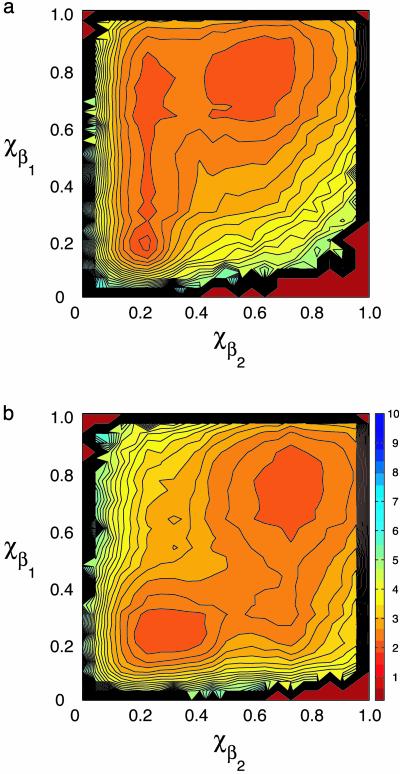
The remaining three mutations are different for proteins L and G and hence are responsible for differentiating the folding of protein L from G. Their main consequence appears to be changing the relative thermodynamic stability of elements of secondary structure. Fig. 2 shows the native-state similarity parameters for the α-helix and two β-sheet regions as a function of temperature. For χα, the stability is reduced in the new L and G sequences relative to L/G. Of more interest are the changes in stability of χβ₁ and χβ₂. By looking at the mutations listed in Table 2, we see that the protein L reduced letter code introduces a net attraction into β-hairpin 1 and a net repulsion into β-hairpin 2. From Fig. 2, it can be seen that the result is a new L sequence in which the second β-sheet region (β₂) is destabilized relative to the β₂ region in the original L/G sequence. Likewise for the new G sequence, it can be seen that the mutations for the reduced code in protein G appear to introduce net stabilization into β-hairpin 2. Consequently, we get a sequence that favors a greater degree of β₂ ordering at higher temperature relative to the original L/G sequence (Fig. 2). This behavior is also reflected in the free-energy projections along χβ₁ and χβ₂ for L and G (shown in Fig. 3). From these projections there is a minimum free-energy path from the unfolded to folded ensembles that involves either formation of β-hairpin 1 then β-hairpin 2 (protein L), or β-hairpin 2, and then β-hairpin 1 (protein G).

Fig. 2.

Thermodynamic measures of the formation of native-state secondary structure. (a) Average native-state similarity of the α helix 〈χα〉 vs. temperature T. Stability of the α helix is reduced for new L and G sequences compared with original L/G sequence. (b) Average native-state similarity of the first (N-terminal) β-sheet region 〈χβ₁〉 vs. temperature T. Stability of β₁ region is reduced for new L and G sequences relative to original L/G sequence. Note that the stability is reduced further for G than for L. (c) Average native-state similarity of the second (C-terminal) β-sheet region 〈χβ₂〉 vs. temperature T. Stability of β₂ region is similar for L/G and G sequences but reduced for the L sequence.

Fig. 3.

Projection of free-energy surfaces onto order parameters χβ₁ and χβ₂. (a) Free-energy contour plot for protein L as a function of native-state similarity of the second (C-terminal) β-sheet region χβ₂ and first (N-terminal) β-sheet region χβ₁ at the folding temperature. Note the minimum free-energy path connecting the unfolded and folded ensembles proceeds through a transition state in which the β₁ region is native and the β₂ region is largely disrupted. (b) Free-energy contour plot for protein G as a function of native-state similarity of the second (C-terminal) β-sheet region χβ₂ and first (N-terminal) β-sheet region χβ₁ at the folding temperature. For G, the minimum free-energy path connecting the unfolded and folded ensembles proceeds through a transition state in which the β₂ region is native-like and the β₁ region is disrupted. Contour lines are spaced k_BT apart.

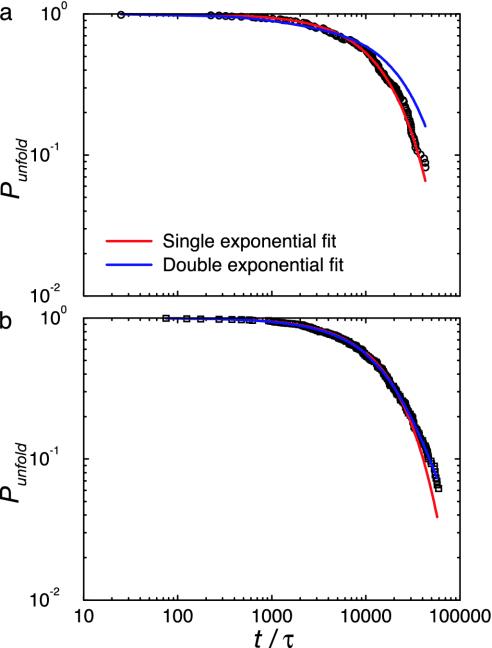
Looking at folding kinetics around the folding temperature, shown in Fig. 4a, we see different behavior for L and G (values given in Table 4). The kinetics for protein L is well fit by a single exponential. Thus, as reported for protein L in the literature, our minimalist-model protein L shows all of the signs of being a cooperative two-state folder. For protein G, the story is not as straightforward. We find that protein G folds slower than protein L by a factor of two, qualitatively consistent with experiment. The kinetics in protein G is better fit by a double rather than single exponential (Fig. 4b). The fit shows a fast folding event, involving ≈80% of the population, and a slow folding event that involves the remainder of the population. These results are consistent with differences in folding kinetics reported for proteins L and G, which we will analyze in greater detail elsewhere (S.B. and T.H.-G., unpublished work).

Fig. 4.

Kinetic data with fits for proteins L and G. (a) Fraction of unfolded states P_unfold as a function of time t for protein L at the folding temperature. The best fit of the data is to a single exponential. (b) Fraction of unfolded states P_unfold as a function of time t for protein G at the folding temperature. The best fit for these data is to a double exponential. Fit parameters are given in Table 4.

Table 4. Parameters for kinetic fits at folding temperature.

	T	A0	1-A0	τ0	τ1	χ2/10-4
L	0.42	1.0	0	15700	0	3.43
G	0.41	0.81	0.19	13700	46400	0.353

Equation fit is A₀exp(-t/τ₀) + (1 - A₀)exp(-t/τ₁).

To illustrate that the mapping from the 20-letter amino acid sequence to three-letter reduced code can result in a protein model that folds to the correct topology, we consider preliminary studies on the prototype β-sheet protein, the WW domain. We focus on one specific member, the Pin WW domain, for which extensive experimental thermodynamic and kinetic analysis of its folding has been reported by Gruebele and coworkers (28). The 20-letter amino acid sequence, KLPPGWEKRMSRSSGRVYYFNHITNASQWERPSGN, was mapped to the following three-letter code: LBBBNBLLLBNLNNNLBBBBLLBNLBNLBLLBNNL.

Sequence design with the misfold library described in the Methods section was used to determine the following sequence: LBBNNBLBLBNLNNNLBBBBLLNNLBNBBLLBNNL, which reliably folded to the correct β-sheet topology as the lowest energy structure (Fig. 5). Furthermore, we find the same network of residue–residue contacts of hydrophobic groups in the strand regions with the coil ends that is thought to stabilize the Pin WW domain (28).

Fig. 5.

Minimalist model of the native state topology for Pin WW domain (Right) and the NMR solution structure (Left), showing the very similar arrangement of secondary and tertiary structure.

Conclusion

Experiments on proteins L and G have previously shown that protein L favors a pathway involving formation of the first (N-terminal) β-hairpin, followed by formation of the second (C-terminal) β-hairpin (13–15). Protein G involves the sequential formation of secondary structure in the opposite order, namely β-hairpin 2 followed by β-hairpin 1 (18), and may involve the formation of populated intermediates (16, 17). This situation prompts the question of what changes of the protein G sequence are necessary to modify its kinetics to be more two-state with rate-limiting formation of the first β-hairpin, or alternatively, what changes to protein L would induce its mechanism of folding to be like that of protein G. Nauli et al. (29) address this question by using a computer-based design strategy that allows them to reengineer the protein G sequence, resulting in a new protein that folds 100 times faster and by a mechanism more faithful to wild-type protein L.

We answer this question in the context of our model by using a library of misfolds to quantify the consequences of sequence mutations and show that it is possible to design sequences that involve distinctly different folding mechanisms for minimalist representations of proteins L and G. It is important to note we do not a priori design a sequence to match the primary structure of naturally occurring protein. However, we find that our sequence design protocol has evolved sequences faithful to the primary structure of the real protein, assuming reasonable definitions of residues considered to be hydrophilic, hydrophobic, and defining small or ambiguous amino acids as neutral. After mapping the 20-letter code to a three-letter code and seeking optimal alignments in secondary and primary structure, we find ≈70–75% sequence identity in the cases we have considered within the ubiquitin fold class. Errors in sequence mappings were used to suggest mutations that actually corresponded to new sequences exhibiting differences in protein L and protein G folding mechanisms. Despite looking at all possible point mutations for protein G, the final outcome resulted in the selection of mutations (based on the ΔE_design criterion) that were in fact all beads corresponding to errors in the alignment. Therefore, it further strengthens our case that we can perform a sequence mapping onto our minimalist code, which could allow for the study of novel proteins whose structure is not yet known.

The main result of this paper is that sequence design with a three-letter reduced code is capable of translating the differences in primary sequence for proteins L and G into the expected differences in thermodynamic and kinetic properties. Heretofore, minimalist models have been appreciated for their ability to capture attributes relating to fold topology. Our physics-based model provides insight into the physical origin of how amino acid sequence patterning of hydrophobic and hydrophilic beads favors the formation of a target topology. This work restores the connection between free energy landscapes and amino acid sequence, the original protein folding problem. Another possible implication drawn from our simple model is that evolutionary perspectives of sequence conservation of a folding nucleus might be reexamined by considering the conservation of the overall patterning in the sequence (30, 31). Perhaps the patterning is tolerant to a small number of mutations, which would manifest as residues poorly conserved being found in the folding nucleus (31), also consistent with the robustness of fold topologies to mutation (32, 33).

We show that our minimalist model can also capture attributes explicitly depending on primary sequence that favors one folding mechanism over another. The differences in amino acid sequence could be manifested as explicit atomic representation of side chains (34, 35). However, studies have shown that simple patterning of polar and nonpolar residues is sufficient to produce compact states with significant secondary structure (36, 37). Additionally, active mutants of barnase have been found in which the hydrophobic core has been completely redesigned by incorporating random hydrophobic reassignments (38). These results point to the fact that explicit representation of side-chains may not be necessary.

The applicability of a three-letter code is also of interest because of the computational complexities inherent in protein design (39). For a sequence of N amino acid residues and 20 choices per residue with r rotamers each, the number of design possibilities scales as (r × 20)^N. This neglects any additional complexity introduced by including backbone rearrangements, the incorporation of which can change results appreciably (40). The cost of protein design can be greatly reduced by the mapping of amino acid sequences into our three-letter minimalist code. Note that the idea of using a reduced set of amino acids in protein design is not new and in fact has been shown to be successful in a number of experimental studies (41). However, because our simplified model is computationally tractable, we are able to incorporate not only native-state structure into our design technique but also unfolded structures (misfolds) as well. This ability is significant in light of emerging experimental evidence that unfolded structures can have nontrivial influence on protein design (42).

Finally, we provide preliminary evidence that the mapping from the 20-letter amino acid sequence to a three-letter reduced code results in a sequence that reliably folds into one of the members of the WW domain topology. Furthermore, examination of this lowest-energy structure from simulated annealing reveals that it forms a specific network of hydrophobic contacts consistent with the origin of stabilizing contacts observed experimentally for the Pin WW domain (28). We will report on our results on WW domain folding elsewhere.