A new approach to estimate parameters of speciation models with application to apes

Abstract

How populations diverge and give rise to distinct species remains a fundamental question in evolutionary biology, with important implications for a wide range of fields, from conservation genetics to human evolution. A promising approach is to estimate parameters of simple speciation models using polymorphism data from multiple loci. Existing methods, however, make a number of assumptions that severely limit their applicability, notably, no gene flow after the populations split and no intralocus recombination. To overcome these limitations, we developed a new Markov chain Monte Carlo method to estimate parameters of an isolation-migration model. The approach uses summaries of polymorphism data at multiple loci surveyed in a pair of diverging populations or closely related species and, importantly, allows for intralocus recombination. To illustrate its potential, we applied it to extensive polymorphism data from populations and species of apes, whose demographic histories are largely unknown. The isolation-migration model appears to provide a reasonable fit to the data. It suggests that the two chimpanzee species became reproductively isolated in allopatry ∼850 Kya, while Western and Central chimpanzee populations split ∼440 Kya but continued to exchange migrants. Similarly, Eastern and Western gorillas and Sumatran and Bornean orangutans appear to have experienced gene flow since their splits ∼90 and over 250 Kya, respectively.

Although central to evolutionary biology, the question of how species form remains largely open. In fact, the very definition of species is a subject of active debate (Hey 2006). The most common definition is the “biological” one, in which species are defined as groups of interbreeding organisms that are reproductively isolated from other populations. The introduction of this concept >60 yr ago transformed the study of speciation into a research program to examine the conditions under which reproductive isolation emerges and to uncover its genetic architecture (Mayr 1963).

Accumulating evidence suggests that incipient species arise primarily in populations with restricted gene flow, as alleles (or combination of interacting alleles) that contribute to reproductive isolation reach fixation (e.g., Wittbrodt et al. 1989; Sawamura et al. 1993; Ting et al. 1998; Wang et al. 1999; Fossella et al. 2000; Barbash et al. 2003; Presgraves et al. 2003; Coyne and Orr 2004a). The speciation process initiates after two populations become completely isolated from one another (i.e., are in allopatry) or as they continue to exchange migrants (i.e., in parapatry).

Under a model of allopatric speciation, the process occurs through the homogeneous divergence of the genome. Shortly after the split, the two populations share alleles due to the persistence of ancestral polymorphism (more so if the ancestral population size is large). Eventually, however, the shared alleles are lost or reach fixation and the two populations start to accumulate fixed differences, either by genetic drift or due to differential adaptation (Coyne and Orr 2004a). Under a simple allopatric model with no selection, it will take approximately 9–12N generations (where N is the effective size of the descendant population) for the genealogies of >95% of loci to be reciprocally monophyletic and, hence, for the two populations not to share alleles that are identical by descent (Hudson and Coyne 2002). Given these assumptions, humans and common chimpanzees should almost never share alleles (as they are thought to have diverged ∼ 20–25N generations ago) (Wall 2003; Hobolth et al. 2006; Patterson et al. 2006), while bonobos and common chimpanzees are expected to share alleles at ∼50% of loci (since they are estimated to have diverged ∼ 4N generations ago; Won and Hey 2005).

If the incipient species are in parapatry, however, divergence is not believed to occur homogeneously across the genome but instead in a number of stages (Wu 2001). First, alleles that cause a decrease in hybrid fertility or viability reach fixation in the parental populations. The populations may continue to exchange migrants, but in the genomic regions carrying functionally divergent or incompatible alleles, gene flow is selected against and hence effectively restricted. By contrast, in unlinked (or loosely linked) genomic regions, alleles can be brought in by migrants with no associated fitness costs. Thus, at neutral loci, populations share alleles longer than expected under allopatric speciation. Eventually, reproductive isolation factors accumulate in sufficient numbers as to prevent gene flow throughout the genome—the final stage of speciation. This model predicts variation in the number of shared alleles and levels of divergence along the genomes of closely related species. While shared alleles are also expected under a model of recent allopatric speciation, greater variation is expected along the genome under parapatry, such that, with enough data, the two scenarios should be distinguishable.

In these simple speciation models, the salient parameters are the split times, effective population sizes, and, in the case of parapatry, the gene flow rates. Thus, learning about these parameters should greatly deepen our understanding of speciation. This realization has motivated the development of statistical methods to estimate the parameters from multilocus patterns of polymorphism in closely related species.

Existing methods all assume that genetic variation data are available from both populations, at a number of independently-evolving loci, but differ in their assumptions about gene flow and recombination, and in whether they use all the polymorphism data or summaries. Loosely, they can be classified into two groups. The first set assumes an extreme model of allopatry, in which a panmictic (i.e., randomly mating) ancestral population instantaneously splits into two panmictic descendant populations, with no subsequent gene flow. In this model, there are four parameters: the three effective population sizes and the split time. The parameters are estimated using summaries of the polymorphism data, either by a moment estimator (Wakeley and Hey 1997; Kliman et al. 2000) or by maximum likelihood (Leman et al. 2005; Putnam et al. 2007). While, in its current version, the method of Leman et al. (2005) can only be applied to one, non-recombining locus, other methods can be applied to multiple loci and incorporate recombination (Wakeley and Hey 1997; Putnam et al. 2007). They use highly summarized versions of the data, however, at the potential cost of much information. Moreover, in the presence of gene flow after the split, their estimates will be biased—the ancestral effective population size will tend to be overestimated (Wall 2003) and the split time underestimated (Leman et al. 2005).

The second set of methods considers a more general model, often called the “isolation-migration” model, in which there is gene flow between incipient species throughout the genome, either at fixed (Hey and Nielsen 2004) or locus-specific rates (Won and Hey 2005). The parameters are estimated from all the polymorphism data at a single locus (Nielsen and Wakeley 2001) or at multiple loci (Hey and Nielsen 2004), using Markov Chain Monte Carlo (MCMC). The Hey and Nielsen method, henceforth called IM, has been applied to a number of species, from Heliconius (Bull et al. 2006) to cichlids (Hey et al. 2004; Won et al. 2005). These applications suggest that speciation often occurs in the presence of some gene flow (Hey 2006).

While IM considers a wide range of models, it assumes that haplotypes are known and that there is no intralocus recombination. Although not ideal, the first assumption is not restrictive, as a two-step procedure can be used in which haplotype phase is inferred (e.g., using the program PHASE; Stephens et al. 2001) and then IM is run on the phased data. In contrast, the assumption of no recombination is more limiting, because the method can only be applied to autosomal loci by excluding segments or haplotypes with evidence for recombination. This practice is likely to bias estimates of the parameters, as excluding segments with visible recombination will tend to lead to shorter genealogical histories (Hey and Nielsen 2004). Moreover, if intralocus recombination is not taken into account, a small variance in divergence times across segments may be confounded with a small ancestral effective population size (Takahata and Satta 2002). The assumption of no intralocus recombination represents an especially severe limitation in species in which the ratio of recombination to mutation is thought to be high (e.g., Drosophila melanogaster, Andolfatto and Wall 2003; or Papilio glaucus, Putnam et al. 2007). In such species, any segment with polymorphisms in a sample is likely to have experienced numerous recombination events in its genealogical history, making recombination hard to ignore (Hudson and Kaplan 1985; Nordborg and Tavare 2002).

To overcome this limitation, we developed a new Bayesian approach to estimate parameters of an isolation-migration model from recombining loci. We have in mind data sets similar to the ones most commonly collected to date: short noncoding sequences distributed throughout the genome. Our approach is to summarize the polymorphism data at each locus by four statistics known to be sensitive to the parameters of interest (Wakeley and Hey 1997; Leman et al. 2005). We then estimate the posterior probability of the parameters given these summaries using MCMC. Simulations suggest that, in the absence of recombination, our method performs as well or almost as well as the full likelihood approach. Moreover, the approach presents the advantage of being quite flexible in the demographic model that it can consider and in allowing for intralocus recombination.

We illustrate the potential of our method by applying it to multilocus polymorphism data from noncoding loci in chimpanzees, gorillas, and orangutans. Very little is known about the evolutionary history of great apes, in part because of a poor fossil record. Chimpanzees, the closest living relatives of humans, are classified into two species, common chimpanzees (Pan troglodytes) and bonobos (Pan paniscus), both found exclusively in Africa. The two chimpanzee species were thought to have diverged as a result of the formation of the River Congo 1.5–3.5 million years ago (Mya) (Beadle 1981; Myers Thompson 2003), but recent estimates of their split time based on genetic data appear to be too recent for this scenario to be plausible (Fischer et al. 2004; Won and Hey 2005). Common chimpanzees are usually subdivided further into three (or sometimes four) “subspecies,” including Eastern (P. troglodytes schweinfurtheii), Central (P. troglodytes troglodytes), and Western (P. troglodytes verus) (Hill 1969). The meaning of the term “subspecies” is unclear, at least to us, but the labels are thought to correspond to the most pronounced population structure within the species. This view is supported by a recent analysis of 310 microsatellites, which found three populations within common chimpanzees, which correspond to the three subspecies, and little evidence of recent gene flow between them (Becquet et al. 2007).

Gorillas, in turn, are classically subdivided into two subspecies: Western (Gorilla gorilla) and Eastern gorilla (Gorilla beringei), found in western and central African forest, respectively (Groves 1970). Some controversy surrounds this classification: The range of the two populations does not currently overlap in the wild; but on the basis of morphological and genetic diversity, it has been proposed that the subspecies should be elevated to the rank of species (e.g., Grubb et al. 2003). Here, we refer to Western and Eastern gorillas as subspecies or populations. A recent application of IM to polymorphism data from the two gorilla populations suggests that they split between 0.08 and 1.6 Mya and experienced low levels of gene flow since (Thalmann et al. 2006).

Even less is known about the history of orangutans (Pongo pygmaeus), currently found only in Indonesia and Malaysia, but whose range is thought to have spanned much of southeast Asia until recently (Smith and Pilbeam 1980). Some taxonomies consider Sumatran (P. p. abelii) and Bornean (P. p. pygmaeus) orangutans to be subspecies (e.g., Groves 1971), and others to be species (e.g., Zhi et al. 1996). Again, these populations do not overlap in their range, so that the classification is based on morphology and behavior, as well as on patterns of genetic diversity. The islands of Sumatra and Borneo were fully formed 500 thousand years ago (Kya) but were reconnected by land bridges during the two last glaciations, ∼130–200 Kya and ∼10–100 Kya, respectively (Muir et al. 2000; Hughes et al. 2006). Estimates of the average time to the most recent common ancestor for both populations based on mitochondrial DNA (mtDNA) and a small number of microsatellites and autosomal and X-linked loci are ∼1.5–2.5 Mya (Zhi et al. 1996; Kaessmann et al. 2001; Zhang et al. 2001), but to our knowledge, there are no published estimates of the population split time.

Here, we analyze a compilation of multilocus polymorphism data recently published in the three great ape species (Yu et al. 2003; Fischer et al. 2006; Thalmann et al. 2006), refining population parameter estimates for chimpanzees and gorillas and providing the first estimates for orangutans.

Results

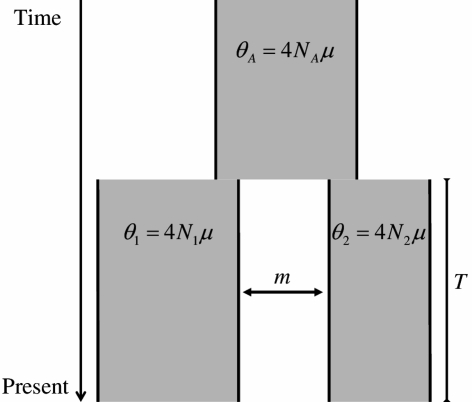
We developed a method that estimates the demographic parameters of an “isolation-migration” model from recombining loci (Fig. 1). There are five parameters of interest: the population mutation rates for the two descendant populations, θ₁ and θ₂, and the ancestral population, θ_A; the time since the populations split in generations, T; and the migration rate, m. To estimate these parameters, the method requires resequencing data from two populations (or closely related species) at independently-evolving loci, and an outgroup sequence. Briefly, the polymorphism data for each locus are summarized by the four statistics studied by Wakeley and Hey (1997), as these carry information about the divergence time and other parameters of interest (Wakeley and Hey 1997; Leman et al. 2005). We choose the parameters of the model from prior distributions, and for each locus, we generate a set of genealogies under a model with those parameters. We then estimate the likelihood by calculating the probability of the data summaries at all the loci given the set of genealogies and the parameters. Finally, we obtain a sample from the posterior distribution of the parameters given the data summaries using MCMC (see Methods). Thus, our method follows a number of Bayesian approaches that use summaries of the data but differs in that we update the parameters using MCMC (for more details, see Methods). Hereafter, we refer to our method as MIMAR: MCMC estimation of the isolation-migration model allowing for recombination.

Figure 1.

The “isolation-migration” model, in which two populations diverged T generations ago from a common ancestral population. The parameters θ₁, θ₂, and θ_A are the population mutation rates per base pair for populations 1 and 2 and the ancestral population, respectively. The split time in generations is T, and m is the symmetrical migration rate between populations per generation (for details, see Methods).

Performance of MIMAR under the allopatric model

In order to assess the performance of our method, we generated 30 simulated data sets, each consisting of 20 non-recombining loci, with parameter values applicable to Drosophila species in which related studies have been conducted (Llopart et al. 2005; see Methods). Supplemental Figure S1 shows the 30 posterior distribution samples for the four parameters of interest. As can be seen, the posterior distributions estimated by MIMAR for θ₁, θ₂, and T are centered around their true values with relatively little variance, suggesting that the summaries that we use contain enough information to estimate these parameters precisely and accurately. However, for these parameters, 20 non-recombining loci do not seem to contain as much information about the ancestral effective population size, leading to a wider posterior distribution estimate for θ_A. This does not appear to be a feature of our statistics, since the use of IM yields similar results, even though it is based on the full polymorphism data set (data not shown). As expected, our estimates of θ_A become more precise with larger data sets (data not shown).

Comparison to IM for the case of no recombination

Next, we studied the performance of MIMAR by generating 30 simulated data sets under the allopatric model for 20 non-recombining loci, but this time drawing the parameters from prior distributions (for details, see Methods); the parameter values are, as above, applicable to Drosophila species. The results confirm that the estimates of θ₁, θ₂, and T are precise and have very little bias, while the estimates of θ_A are less precise (Table 1; Supplemental Fig. S2).

Table 1.

Performance of MIMAR and IM

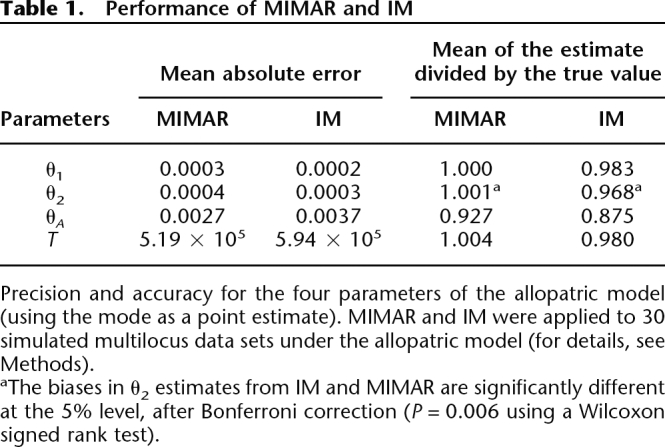
Precision and accuracy for the four parameters of the allopatric model (using the mode as a point estimate). MIMAR and IM were applied to 30 simulated multilocus data sets under the allopatric model (for details, see Methods).

^aThe biases in θ₂ estimates from IM and MIMAR are significantly different at the 5% level, after Bonferroni correction (P = 0.006 using a Wilcoxon signed rank test).

We analyzed the same simulated data sets with IM to compare the estimates from MIMAR, which are based on summaries, with a full likelihood approach (since IM does not allow for recombination, we set the intralocus recombination rate to 0 when generating the 30 data sets). We found that the two methods perform similarly well, in terms of both accuracy and precision (see Table 1). For example, the mean absolute error over the 30 simulated data sets for the estimate of T is 5.19 × 10⁵ using MIMAR and 5.94 × 10⁵ using IM. Similarly, if we consider the estimate divided by the true value as a measure of bias, the mean over the 30 data sets is 1.004 for MIMAR and 0.980 for IM. Similar results were obtained for all parameters, with the possible exception of the current effective population sizes, for which MIMAR appears to yield slightly more reliable estimates (see Table 1). Moreover, we found that the two methods have similar coverage: For both, the central 95th percentiles of the marginal posterior distribution sample for T included the true value in 29 out of 30 cases; for θ_A, this occurred in 29 out of 30 cases for IM and 30 out of 30 cases for MIMAR. We also compared the results of MIMAR and IM on larger simulated data sets of 100 loci and found that, in this case, IM outperformed MIMAR. However, with such large data sets, both methods provided highly accurate and precise estimates (data not shown).

In the comparison, we ran both methods long enough for them to appear to have reached convergence (Supplemental Fig. S3). For the same number of iterations of the MCMC, IM was two to three times faster than MIMAR (data not shown).

Assessing the evidence for gene flow

To assess our ability to distinguish a model with gene flow from one without, we generated 20 simulated data sets (each consisting of 40 recombining loci) under both an allopatric and a parapatric model, with parameter values applicable to apes. In the parapatric model, we fixed the expected number of migrants M = 4N4N₁m to 1, which corresponds to an average of 11 migration events in the history of the sample. We applied MIMAR to the 40 data sets, allowing for recombination and sampling the expected number of migrants from the prior ln (M) ∼ U[−5, 2] (for details, see Methods). When applied to data sets generated under a model with no gene flow, MIMAR suggested no migration (using the criterion that the mode of the marginal posterior distribution, 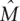, be < 0.1) in 14 out of 20 cases; moreover, in one out of the six cases in which 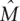≥ 0.1, most of the posterior probability mass for M was close to 0 (data not shown). For the data sets simulated with gene flow, there was evidence of migration (i.e., 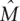≥ 0.1) in 17 out of 20 cases. Other parameter estimates were generally accurate and precise (see Table 2; Supplemental Fig. S4), although the estimates of θ_A were slightly underestimated in data sets generated with M = 0, and the estimates of T were slightly underestimated in data sets generated with M = 1 (for possible explanations, see Table 2).

Table 2.

Performance of MIMAR when detecting gene flow

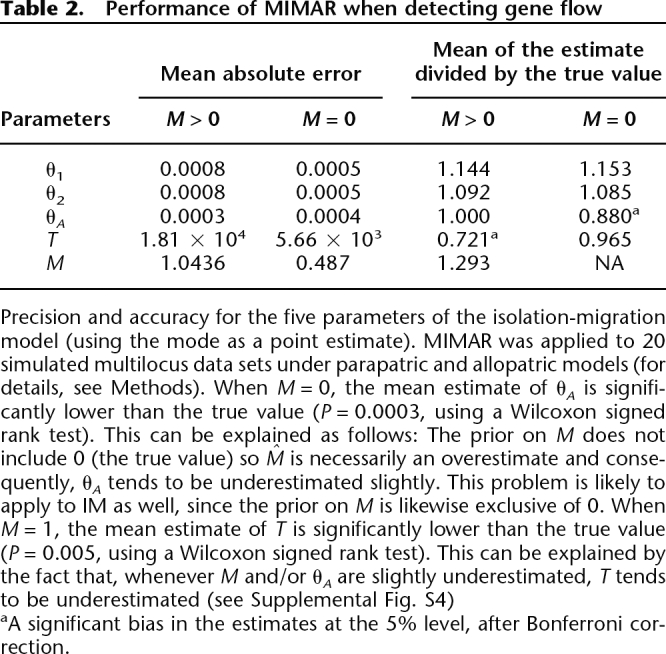
Precision and accuracy for the five parameters of the isolation-migration model (using the mode as a point estimate). MIMAR was applied to 20 simulated multilocus data sets under parapatric and allopatric models (for details, see Methods). When M = 0, the mean estimate of θ_A is significantly lower than the true value (P = 0.0003, using a Wilcoxon signed rank test). This can be explained as follows: The prior on M does not include 0 (the true value) so 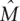is necessarily an overestimate and consequently, θ_A tends to be underestimated slightly. This problem is likely to apply to IM as well, since the prior on M is likewise exclusive of 0. When M = 1, the mean estimate of T is significantly lower than the true value (P = 0.005, using a Wilcoxon signed rank test). This can be explained by the fact that, whenever M and/or θ_A are slightly underestimated, T tends to be underestimated (see Supplemental Fig. S4)

^aA significant bias in the estimates at the 5% level, after Bonferroni correction.

When we applied either MIMAR and IM to smaller simulated data sets (i.e., 20 loci and no intralocus recombination), estimates of the split times and migration rates provided by both methods were much less reliable (data not shown).

Sensitivity to intralocus recombination rates

Intralocus recombination rates are often unknown or are estimated with substantial error. To assess how this might affect the reliability of MIMAR, we generated 16 data sets under an allopatric model, with parameter values applicable to Drosophila (see above). Each data set consisted of 10 recombining loci, with the locus-specific recombination rates chosen from an exponential distribution with mean c/μ = 10. These data sets were analyzed using MIMAR by fixing all the parameters but T to their true values, and (1) setting the locus-specific recombination rates to their true values, (2) sampling the recombination rates from the same prior as used when generating the simulated data, and (3) setting the intralocus recombination rates to 0 (for details, see Methods). The results from steps 1 and 2 were virtually identical, suggesting that error in the locus-specific recombination rates does not have much effect on the results so long as intralocus recombination is taken into account. In contrast, when we assumed no recombination in our analysis of recombining loci, the estimates of the split time were significantly less accurate and precise (see Supplemental Fig. S5). These results highlight the importance of allowing for intralocus recombination when estimating demographic parameters.

Application to ape data

We compiled a set of recently published resequencing data in bonobo and common chimpanzee, gorilla, and orangutan populations (Yu et al. 2003; Fischer et al. 2006; Thalmann et al. 2006). Won and Hey (2005) had previously reported evidence for intralocus recombination at some of the loci included in this study, and we found further evidence of recombination, in spite of low power to do so (given the small sample sizes). We therefore analyzed these data sets with MIMAR, allowing for intragenic recombination (see Methods). For these analyses, we assumed that the recombination rate is exponentially distributed across loci but constant within a locus. This model seems sensible for the short fragments (∼650 bp on average) that we considered but may not be appropriate for longer loci.

Chimpanzee species (P. paniscus and P. troglodytes) and subspecies (P. t. verus, P. t. troglodytes, and P. t. schweinfurthii)

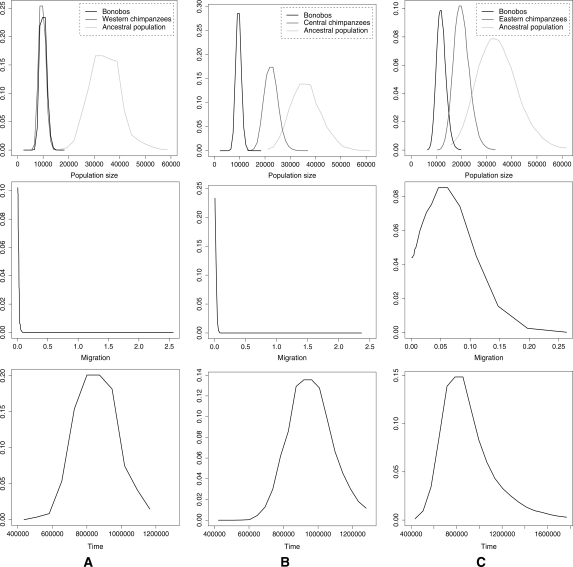
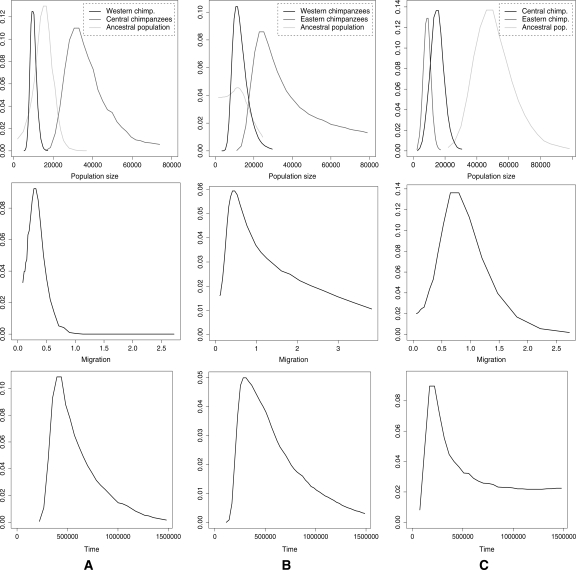
Figures 2 and 3 show the marginal posterior distributions for the parameters of the model, averaging the results for two independent runs (for details, see Methods). We considered each pair of populations in turn. Running MIMAR under a model that allows for gene flow strongly suggests that the bonobo and the common chimpanzee populations split without subsequent migration (Table 3). In contrast, there is evidence of gene flow since the split of Western, Central, and Eastern chimpanzee populations (Table 4; see also Won and Hey 2005). Figure 2 shows the posterior distribution estimates for the parameters of the model for bonobo and common chimpanzee populations and Figure 3, for Western, Central, and Eastern chimpanzee populations. We note slight support for gene flow between Eastern chimpanzees and bonobos (see Fig. 2C), whose ranges are closer together than those of bonobos and other chimpanzee subspecies. However, more data and more precise geographic information are needed to evaluate this possibility, especially in light of the relatively unreliable estimates of migration from small data sets (see simulation results above).

Figure 2.

Smoothed marginal posterior distributions estimated by MIMAR from bonobo and common chimpanzee polymorphism data (for details, see Methods). The range of the X-axis corresponds to the support of the prior. The distributions are for the analyses of bonobos and Western chimpanzees (A), bonobos and Central chimpanzees (B), and bonobos and Eastern chimpanzees (C).

Figure 3.

Smoothed marginal posterior distributions estimated by MIMAR from the common chimpanzee subpopulation polymorphism data (for details, see Methods and legend of Fig. 2). The distributions are for the analyses of Western and Central chimpanzees (A), Western and Eastern chimpanzees (B), and Central and Eastern chimpanzees (C).

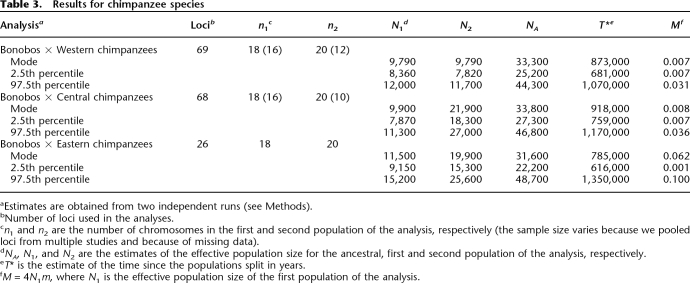
Table 3.

Results for chimpanzee species

^aEstimates are obtained from two independent runs (see Methods).

^bNumber of loci used in the analyses.

^cn₁ and n₂ are the number of chromosomes in the first and second population of the analysis, respectively (the sample size varies because we pooled loci from multiple studies and because of missing data).

^dN_A, N₁, and N₂ are the estimates of the effective population size for the ancestral, first and second population of the analysis, respectively.

^eT* is the estimate of the time since the populations split in years.

^fM = 4N₁m, where N₁ is the effective population size of the first population of the analysis.

Table 4.

Results for chimpanzee subspecies

^aFor details, see legend of Table 3.

Assuming 20 yr per generation and a mutation rate of 2 × 10⁻⁸ per base pair per generation (see Methods), the estimates of the effective population sizes of bonobos and Western chimpanzees are ∼10,000 in all analyses involving these populations. In turn, the estimates of split time for bonobos and common chimpanzee populations range from 790–920 Kya, and the estimates of the ancestral effective population size are ∼30,000. These estimates are consistent with those obtained by Won and Hey (2005), who applied IM to a smaller data set, which overlaps with ours. The only exception is that they estimated a smaller ancestral effective population size than we did, but the confidence intervals overlap slightly. These results confirm that polymorphism data from bonobos and common chimpanzees are consistent with an allopatric speciation model and that the divergence between the chimpanzee species occurred more recently than the estimated formation of the River Congo.

In the analyses of Western and Central chimpanzees and Western and Eastern chimpanzees, the time estimates range from 280–440 Kya, the ancestral effective population sizes from 11,000–15,000, and the migration rate, M = 4N₁m, from 0.32–0.43 (where N₁ is the effective population size of Western chimpanzees). These results are roughly consistent with those of Won and Hey (2005): Using a model that allowed for asymmetric migration rates, they estimated that M ∼ 0.28 from Western to Central chimpanzees but did not find evidence for gene flow in the opposite direction.

For the analyses of Central and Eastern chimpanzees, the split time estimate is ∼220 Kya, the ancestral effective population size is ∼46,000, and the migration rate, M = 4N₁m, is ∼0.80 (where N₁ is the effective population size of Central chimpanzees). Thus, it appears that the split time for Central and Eastern chimpanzees is about half that of Western and Central (or Eastern) chimpanzees.

While the estimates are generally consistent across pairwise analyses, the effective population size estimates for Central and Eastern chimpanzees are not. In both analyses of Central chimpanzees and bonobos and of Central and Eastern chimpanzees, the effective population size of Central chimpanzees is estimated to be 15,000–22,000 (consistent with the results of Won and Hey 2005). However, a larger population size estimate is obtained from the analysis of Western and Central chimpanzees. Similarly, in both analyses of bonobos and Eastern chimpanzees and of Western and Eastern chimpanzees, estimates of the effective population size of Eastern chimpanzees are 20,000–25,000, while in the analysis of Eastern and Central chimpanzees, the estimate is smaller. These discrepancies may reflect complex histories of chimpanzee populations not captured by the model (see the goodness-of-fit test below). For example, analyses of other data sets suggest that Central chimpanzees may have experienced a recent population expansion (Fischer et al. 2004; D. Reich, pers. comm.).

Gorilla subspecies, Western (G. gorilla) and Eastern gorillas (G. beringei)

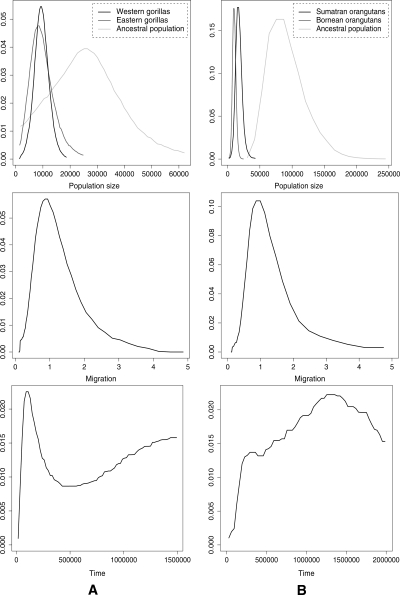
Figure 4A shows the posterior distributions of the five parameters of the parapatric model of speciation. Assuming 15 yr per generation and a mutation rate of 2 × 10⁻⁸ per base pair per generation (see Methods), the estimates of the effective population sizes for Western and Eastern gorillas and their ancestral population are ∼9000, ∼8000, and ∼27,000, respectively (see Table 5). The divergence time estimate between Western and Eastern gorilla subspecies is ∼92 Kya, and the migration rate, M = 4N₁m, is ∼0.87 (where N₁ is the effective population size of Western gorillas).

Figure 4.

Smoothed marginal posterior distributions estimated by MIMAR from the gorilla (A) and orangutan (B) subspecies polymorphism data (for details, see Methods and legend of Fig. 2). (A) Distributions for the analysis of Western and Eastern gorillas. The apparent multimodality of the marginal posterior distribution estimated for the split time was also noted by Thalmann et al. (2006). (B) Distributions for the analysis of Sumatran and Bornean orangutans. Note that the posterior distribution for the split time is rather flat, suggesting that the data do not carry much information about this parameter.

Table 5.

Results for gorilla and orangutan subspecies

^aFor details, see legend of Table 3.

To compare our estimates to those recently obtained by Thalmann et al. (2006) using IM, we considered their mutation rate estimate (1.44 × 10⁻⁸ per base pair per generation). Our estimates of the effective population sizes of Western gorillas and ancestral population and the split time are of the same order (∼13,000 vs. 17,500, ∼37,000 vs. 42,000, and 92 vs. 78 Kya), but our estimate of the effective population size of Eastern gorillas is larger (11,000 vs. 3000). Whether this discrepancy reflects differences in the use of summaries vs. the whole data or in the prior distributions is unclear.

Orangutan subspecies, Sumatran (P. p. abelii) and Bornean orangutans (P. p. pygmaeus)

The posterior distributions of the five parameters of the parapatric model of speciation are shown in Figure 4B. Assuming 20 yr per generation and a mutation rate of 2 × 10⁻⁸ per base pair per generation (see Methods), the estimates of the effective population sizes for Sumatran and Bornean orangutans and their ancestral population are ∼17,000, ∼10,000, and ∼87,000, respectively (see Table 5). The estimate of the symmetrical migration rate, M = 4N₁m, is ∼0.87 (where N₁ is the effective population size of Sumatran orangutans). The data further suggest that the split time for Sumatran and Borneon orangutan populations is likely to be older than 250 Kya. However, the data (19 loci) do not appear to carry much information about this parameter (see the posterior distribution estimate in Fig. 4B), and in particular, the mode of the posterior distribution, 1.4 Mya, is likely to be an unreliable estimate of the split time.

Since the islands of Borneo and Sumatra were connected during the two last glaciations ∼130–200 Kya and ∼10–100 Kya ago, it is not surprising to find evidence of gene flow between those two populations. Our results further suggest that the Sumatran and Bornean orangutan populations diverged before the second to last Ice Age. To our knowledge, this analysis provides the first estimates of population parameters for the two orangutan subspecies.

Goodness-of-fit test

To examine whether the isolation-migration model is an appropriate description of the history of the ape species and subspecies, we generated simulated data sets for parameters sampled from the posterior distributions estimated by MIMAR, and compared the simulated data to what is observed for a number of statistics. Encouragingly, the isolation-migration model appears to provide a reasonable fit to the four statistics used in the inferences of MIMAR as well as to the mean F_ST, π, and Tajima’s D across loci (Supplemental Fig. S6; for details, see Methods). The one exception is for Central and Eastern chimpanzees (Supplemental Fig. S6f): There is a poor fit to F_ST and to Tajima’s D for the Central chimpanzees (see also Supplemental Fig. S6b). This suggests either that an isolation-migration model is not appropriate for these subspecies or that a crucial demographic feature is missing from the model. Given the proximity of Central and Eastern chimpanzees and their low F_ST, one possibility is that, rather than a split model, a model of isolation by distance is more appropriate (Fischer et al. 2006). Interestingly, though, there does not appear to be substantial gene flow between the Eastern and Central ranges (see the estimates of the migration rate in this study and Becquet et al. 2007). We also find that, while the model fits most aspects of the bonobo data quite well, the observed Tajima’s D is lower than expected (Supplemental Fig. S6a–c), perhaps reflecting recent demographic events in bonobos not included in the model.

Discussion

Advantages and limitations of MIMAR

We have developed a new method to estimate parameters of simple allopatric and parapatric speciation models. It considers summaries of the polymorphism data from each locus, rather than the entire data set. Extensive simulations, and comparisons to IM for the case of no recombination, suggest that the use of these summaries provides accurate and precise estimates of parameters of interest from data sets comparable in size to those analyzed to date (see Table 1).

The method presents the important advantage of allowing for intralocus recombination. This feature makes the approach applicable to autosomal data, even in species where the ratio of recombination to mutation events is high (ρ/θ ≫ 1), such as in Drosophila (Andolfatto and Wall 2003) and Papilio (Putnam et al. 2007) and hence where any segment containing polymorphisms is likely to have experienced recombination in its genealogical history. In contrast, when applied to recombining regions, IM requires one to exclude loci that show evidence of recombination and assumes that no recombination occurred at the other loci, potentially biasing the estimates.

In other respects, the model of speciation that we consider is more restrictive than the one used in IM. Mutation rates for each locus are estimated from divergence data and then fixed, rather than coestimated along with other parameters (see Methods). We set the migration rate, m, to be symmetric between populations, which may be inappropriate. Finally, we assume that the distribution of coalescent times only varies across loci due to differences in the mode of inheritance and, therefore, that it can be specified a priori. In contrast, IM allows one to estimate inheritance scalars for each locus from the data, which may be important if a subset of loci have experienced recent selection (Hey and Nielsen 2004). Our model could readily be extended to allow for these features, notably for asymmetric migration rates (in fact, the MIMAR program that we make available already allows for this feature). However, the data from a given locus carry limited information, and it is unclear how many parameters can reliably be estimated, even using all the information. Indeed, our simulations suggested that IM and MIMAR estimates of the migration rate from a small data set can be unreliable even in the absence of these complications (see Results).

In its current implementation, our method is also limited in the type of data that it can consider, as it is not applicable to surveys of variation that suffer from ascertainment bias. Moreover, it assumes an infinite site model, so only two alleles can be present at a given site. As long as the ascertainment bias and mutation model are known, however, it should be reasonably straight-forward to extend the model to consider these cases (Nielsen and Signorovitch 2003). MIMAR is further intended for use on resequencing data from short, independently-evolving loci, in which there is little information about how genealogies change along the genome or, viewed another way, about linkage disequilibrium (McVean et al. 2004), and for which it is reasonable to assume that recombination rates are uniform. Applying MIMAR to longer stretches of sequence may require a change in the model of recombination to capture fine-scale heterogeneity in recombination rates. In that setting, it may also be helpful to consider summaries of linkage disequilibrium in addition to the four statistics used here. More generally, our approach could be extended to consider a number of other aspects of the data. For instance, one could consider the number of singletons in each population (in addition to the four current statistics) or the joint frequency spectrum in two population samples.

In addition to improving the inference method, it will also be important to consider more realistic models of speciation. For example, detailed studies of closely related species reveal that many apparent cases of parapatry may in fact reflect allopatric speciation followed by secondary contact (Coyne and Orr 2004b; Llopart et al. 2005). One approach to distinguishing between the two scenarios might be to allow migration between diverging populations to stop at different time points, and estimate which times are most likely given the polymorphism data. Similarly, for sets of species (or populations) that split over a short time period, it may be important to consider more than two species at a time (Wall 2000; Degnan and Rosenberg 2006; Pollard et al. 2006).

Another salient feature, ignored in existing methods, may be population structure in the ancestral population. Indeed, in many of our analyses of ape data, as well as in most analyses of the isolation-migration model published to date (e.g., Hey et al. 2004; Hey 2005; Won and Hey 2005; Thalmann et al. 2006), the estimate of the ancestral effective population size is larger than that of the descendant populations. Since it seems unlikely that so many populations have shrunk over time, this suggests that a salient and fairly common demographic feature is being ignored. One possibility is that the assumption of a panmictic ancestral population is inappropriate. If so, it may be relevant to consider a model of population structure in which a geographic barrier becomes stronger over time (e.g., Innan and Watanabe 2006). In this respect, an attractive feature of our method is that it is easy to generalize to other demographic settings (see Methods).

Finally, our approach could also be extended to scan the genome for regions that contribute to reproductive isolation (Won et al. 2005; Bull et al. 2006; Geraldes et al. 2006; Miller et al. 2006). Indeed, models of parapatric speciation predict that loci involved in the formation of species will experience no or little gene flow since the split and therefore have more fixed differences and fewer shared alleles than do background loci. Moreover, theoretical results suggest that, in this setting and unless selection in very strong, regions of marked differentiation should be relatively short (Barton and Bengtsson 1986). Thus, identifying regions with evidence for decreased gene flow should be an effective way to find the specific loci that contribute to reproductive isolation. This idea has been implemented by estimating gene flow for each locus separately (Won et al. 2005). However, this approach may have limited power to detect loci with reduced gene flow. An alternative may be to use the goodness-of-fit test results for individual loci to identify outliers that behave as expected if they contributed to reproductive isolation.

Analyses of ape polymorphism data

Analyses of genetic polymorphism data from apes can help to characterize the geographic distribution of variation (e.g., Becquet et al. 2007), shed light on their demographic history, and place the evolutionary history of humans in context (Stone and Verrelli 2006). Here, we considered the largest set of polymorphism data to date for all three species of nonhuman great apes, and estimated parameters of a simple isolation-migration model. Using a goodness-of-fit test, we find that this model provides a reasonable point of departure for analyzing ape data, other than for Eastern and Central common chimpanzees.

The use of the model suggests that the effective populations sizes of the ape populations range from 8000–33,000, on the same order as estimates for human populations (10,000–15,000; Frisse et al. 2001; Voight et al. 2005). In contrast, the subspecies split times appear to be older than those of human populations (Cavalli-Sforza and Feldman 2003; Goebel 2007), ranging from 92–440 Kya.

We find no evidence for gene flow since the split for chimpanzee species (with the possible exception of Eastern chimpanzees and bonobo), consistent with the results of Won and Hey (2005), but do detect limited migration (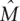 ≤ 1) for all ape subspecies. The split time estimate for chimpanzee species is 790–920 Kya, suggesting that speciation occurred after the formation of the River Congo, 1.5–3.5 Mya. These estimates do not take into account possible error in the mutation rate per year. But even if we consider a time to the most recent common ancestor between human and chimpanzee at the upper limit of what has been estimated so far, 8 Mya, and a generation time of only 15 yr, the central 95th percentile for the split time is 1–2.3 Mya. Moreover, the recent finding of a chimpanzee fossil in Kenya indicates that common chimpanzees may have occupied a much wider range than inferred on the basis of their current distribution (McBrearty and Jablonski 2005). Thus, existing data support a more recent speciation time for common chimpanzees and bonobos, which may have occurred outside of their current habitats.

More generally, this application illustrates how the increasing availability of multilocus polymorphism data sets, together with development of novel statistical approaches, can yield insights into speciation, both in apes and in other organisms.

Methods

Model

We consider a neutral model in which an ancestral population suddenly splits into two populations, which either diverge in isolation or continue to exchange migrants (Fig. 1). We further assume that n₁ and n₂ chromosomes have been sampled from two populations and fully resequenced at Y randomly chosen, independently-evolving loci.

The population model, often called “isolation-migration”, is described by the population split time in generations, T, and three population mutation rates, θ₁ = 4N₁μ, θ₂ = 4N₂μ, and θ_A = 4N_Aμ (Fig. 1). Throughout, the subscripts 1, 2, and A refer to parameters that describe populations 1 and 2 and the ancestral population, respectively. Following IM, we assume that there is an independent estimate of the average mutation rate across loci, μ, which can be used to estimate the effective population sizes from the population mutation rates (e.g., as N₁ = θ₁/4μ). In addition, there is a symmetric migration rate, m, which corresponds to the fraction of a population that is replaced by migrants from the other population each generation.

The parameters θ₁, θ₂, and θ_A are defined per base pair and are chosen from uniform distributions; the time in generations, T, is also chosen from a uniform distribution. The prior for the migration rate is on the expected number of individuals in population 1 replaced by migrants (backward in time), M = 4N₁m, where N₁ is obtained from θ₁ by dividing by 4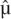 ( 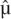is the estimate of μ). Specifically, ln(M) is chosen from a uniform distribution.

In addition to the five demographic parameters, there are a number of locus-specific parameters. We assume that each locus follows the infinite sites mutation model (Kimura 1969), then define an inheritance scalar, u, which, for example, is equal to 1 for autosomal, 3⁄4 for X-linked, and ¼ for Y-linked and mtDNA-linked loci. To allow for mutation rate variation among loci with the same mode of inheritance, we introduce an additional scalar, v, for each locus. Given this parameterization, the locus-specific mutation rate in population 1 is given by uvZθ₁, where Z is the length of the locus in base pairs; the locus-specific population mutation rates for other populations are defined analogously.

The population recombination rate per base pair is defined as ρ = 4N₁c, where c is the per base pair per generation recombination rate. We ignore gene conversion, treating all recombination as crossovers alone. We also define an inheritance scalar for recombination, w (w = 0 for the mtDNA and Y, 2/3 for X, and 1 for autosomes). We then consider three options to specify the locus-specific population recombination rate. We either fix ρ across loci, such that the population recombination rate at a locus is wZρ. Alternatively, if an estimate, 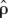, of the population recombination rate is available for each locus, we set the scalar w to the inheritance scalar for recombination multiplied by 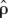to incorporate this knowledge in the estimation. The final option is to allow rates to vary for each locus, in which case the locus-specific population recombination rate is r ⋅ wZθ₁, and we draw the ratio r = ρ/θ₁ from an exponential distribution with mean λ for each locus. Thus, we allow for rate variation among loci but assume a constant rate within a locus. This model should be a sensible description of the rate variation if the loci are short (e.g., 1 kb), as in most data sets collected to date. The set of locus-specific population recombination rates, (ρ₁, ⋅ ⋅ ⋅ , ρ_Y), is referred to as P.

Data summaries

Our goal is to estimate the parameters of the isolation-migration model illustrated in Figure 1. We do so by estimating the posterior distribution π(Θ|D) ∝ p(D|Θ)p(Θ), where Θ= (θ₁,θ₂,θ_A,T,M,P),D is the data, and p(Θ) denotes the prior distribution. Unfortunately, whenD is the entire polymorphism data set under our model, estimating the likelihood of the data given the parameters, p( D|Θ), is computationally extremely intensive and becomes prohibitive when recombination is included (Nielsen and Wakeley 2001; Hey and Nielsen 2004). In their program IM, Hey and Nielsen (2004) address this problem by considering the full data set and using a MCMC approach but restricting themselves to a model with no intralocus recombination (i.e., P = 0). Instead, we focus on a model with intralocus recombination but summarize the polymorphism data from each locus with the summary statistics described below. To do so, we initially explored an importance sampling approach, which provided reliable estimates but was inefficient. We then implemented an MCMC algorithm, which is more efficient than our initial algorithm when the prior and posterior distributions differ substantially.

To summarize the data, we use the statistics introduced by Wakeley and Hey (1997) for this type of inference problem: For each locus, we consider the number of polymorphisms unique to the samples from populations 1 and 2 (S₁ and S₂, respectively), the number of shared alleles between the two samples (S₃), and the number of fixed alleles in either sample (S₄). Previous work has shown that these statistics contain considerable information about the demographic parameters of the isolation-migration model (e.g., Clark 1997; Wakeley and Hey 1997; Hudson and Coyne 2002; Leman et al. 2005). In what follows, we refer to the vector of summaries, S_k, k ∈ [1,4], for locus y asD_y. In turn, we refer to the set of statistics for the Y loci asD = (D₁, ⋅ ⋅ ⋅ ,D_Y).

In calculating these statistics, we assume that an outgroup sequence is available and can be used to determine which allele is derived without error. We note that, in practice, it may be advisable to use two outgroup sequences to minimize error in inferring the ancestral state. We assign each polymorphic site to one of the statistics depending of the frequency of the derived allele in the population i, f_i. Specifically, if 0 < f_i ≤ 1 in each population sample, the allele is shared, if f_i = 0, f_j = 1, i ≠ j, the allele is fixed in the sample j, and if f_i = 0 and f_j < 1, i ≠ j, the allele is specific to sample j. The statistics are easy to calculate and do not require determination of haplotypes.

Estimation method

Our goal is to sample from the posterior distribution,π(Θ| D) ∝ p (D|Θ)p(Θ), which is the likelihood of the data summaries given the parameters times the prior distributions of the parameters. The parameters are initially chosen from these prior distributions and subsequently updated using MCMC, which requires information about the likelihood of the data given the parameters. Very briefly, our strategy is to estimate the likelihood of the data summaries at all the loci for a chosen set of parameters by, for each of the Y loci, (1) generating a set of X ancestral recombination graphs (ARGs) (Hudson 1983) given the parameters and (2) calculating the probability of the data summaries given the set of ARGs. Specifically, we estimate the likelihood p( D|Θ) as

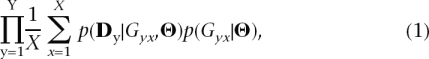where G_yx is the x^th ARG at locus y (Hudson 1983). In other words, we estimate p( D|Θ) by taking the average of p( D_y|G_yx,Θ) over X ARGs, then taking the product over loci (since they are assumed to be independent). The term p(G_yx|Θ) is given by the coalescent, using a modified version of the program ms (Hudson 2002).

We can readily calculate p( D_y|G_yx,Θ). Given a coalescent genealogy, G_yx, we compute the sum of the lengths of all the branches (in coalescent units), which would lead to unique polymorphisms in sample 1 and 2 (L₁ and L₂, respectively), alleles shared by both samples (L₃), and alleles fixed in either samples (L₄). Given the infinite site mutation model, the numbers of mutations, S_k, randomly placed along the branches of type k ∈ [1,4], is Poisson distributed with mean L_kuvZθ₁. Conditional on a genealogy, the probabilities of observing S₁, S₂, etc. . . are independent, so the probability of the dataD_y for the locus y is given by

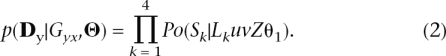Equation 2 also applies to a recombining locus, but in this case, G_yx is an ARG and L_k is computed as follows: With recombination, a locus of size Z has R segments of length Z_j, j ∈ [1, R], with different genealogical histories. The genealogy of a segment has branch length L_jk, such that L_k = 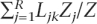for the ARG.

Our prior distributions for the parameters, p(Θ), are uniform over a bounded support (except for P and a uniform prior on ln(M)). For the MCMC, we use random walk Metropolis transition kernels to propose parameter values, so that the proposed value of a parameter is taken from a normal distribution with mean its previous value and variance defined to maximize the acceptance rate (after exploratory simulations) (Gilks et al. 1996). If a parameter value lies outside the support of the prior, the proposed set of parameters is rejected. In turn, P is a nuisance parameter and its values are either fixed (when ρ is fixed), or drawn from the distribution described above (see Model); in the MCMC, the values of P are sampled independently at each step from the prior.

Our approach follows a number of Bayesian methods based on summaries of the data, developed in other contexts (e.g., Tavaré et al. 1997; Pritchard et al. 1999; Beaumont et al. 2002; Przeworski 2003). It differs in that we update the parameters using MCMC rather than sampling them independently from the prior. This general approach was described by Beaumont (2003). As pointed out to us by Matthew Stephens (pers. comm.), our approach can also be viewed as a MCMC on the set of all genealogies, G = (G₁₁,...,G_1X,...,G_Y1,...,G_YX), and the parameters. In this case, the X ARGs are independent samples from the coalescent prior across the Y independent loci. Thus, for the MCMC, the set of ARGs is updated using the transition kernel q(G → G′) = p(G′|Θ), while the parameters of interest are updated using Metropolis transition kernels. We sample sets (G,Θ) from the following target distribution:

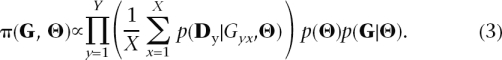The marginal distribution of sampled values of Θfrom the target distribution is π(Θ|D) (as shown in the Supplemental Materials; see also Beaumont 2003: appendix). A nice feature of viewing our approach in this way is that it demonstrates that the stationary distribution of the Markov chain is the correct distribution, i.e., that we are exploring the true posterior distribution rather than an approximation.

MIMAR—MCMC estimation of the isolation-migration model allowing for recombination

To sample from the target distribution π(G,Θ), we use an MCMC approach (MIMAR). In the initial step, Θis chosen from the prior, p(Θ), and G is sampled from the coalescent with those parameters. Subsequent sets (G,Θ) are updated following a Metropolis-Hastings algorithm (Metropolis et al. 1953; Hastings 1970). More specifically, we proceed as follows:

• I1. If now at (G,Θ), propose a move to (G′,Θ′) according to the transition kernels q(Θ → Θ′) and q(G → G′) (i.e., Generate X ARGs given the parametersΘ′ for each of the Y loci).

• I2. For the y^th locus:

  • a. Calculate p( D_y|G′_yx, Θ′) for each of the X ARGs using Equation 2.
  • b. If the average of p( D_y|G′_yx, Θ′) over the X ARGs is 0, record (G, Θ) and go to I1; else go to I2a for the locus y + 1.
• I3. Calculate

  

  where

  

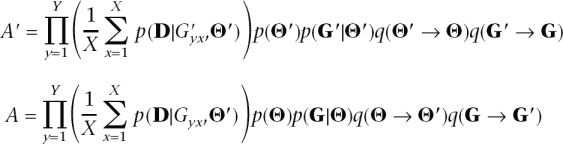
• I4. Move to (G′, Θ′) with probability h [i.e., record (G′, Θ′)] or else record (G, Θ). Return to I1.

  The choice of proposal distribution for G and P and normal kernel distributions and uniform prior distributions for the parameters of interest lead to the following simplification of Equation 4: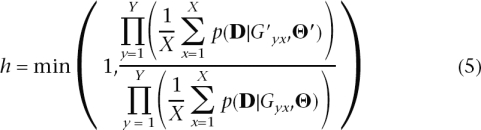

  

In practice, we consider X = 100 (or X = 50 or 5, see below), thus generating 100 (50 or 5) ARGs given the locus-specific parameters. Generating so many ARGs is computationally demanding, but we find that this approach has improved mixing over X = 1.

We note that our approach presents the advantage of being flexible, since it can easily be extended to consider any summaries for which p( D_y|G_yx,Θ) can be readily calculated, such as the allele frequency spectrum at each locus.

MIMAR and its documentation are available at http://mplab.bsd.uchicago.edu/dataNprograms.htm.

Assessing the performance of the estimator

To assess the performance of our method, we ran MIMAR on simulated data sets with two independent seeds (see below). We considered that MIMAR reached convergence when the posterior distributions from the two independent runs were highly similar (e.g., Supplemental Fig. S3). In the documentation provided with MIMAR, we describe a number of other criteria that can be used to assess convergence and proper mixing. We took the mode and the central 95th percentile of the marginal posterior distribution averaged over the two independent runs as the point estimate and measure of uncertainty, respectively.

Simulated data and performance analyses

We generated simulated data sets under the isolation-migration model using a modified version of the program ms (Hudson 2002). Unless otherwise indicated, we considered 20 loci of 1 kb each, and sampled 20 chromosomes from each of two populations.

Performance of MIMAR under allopatry

We generated 30 simulated data sets with no recombination and fixed parameter values relevant for Drosophila yakuba and D. santomea (Llopart et al. 2005), assuming a per base pair per generation mutation rate of μ = 2 × 10⁻⁹ and 20 generations per year (Andolfatto and Przeworski 2000). We analyzed the 30 simulated data sets for 60 h with 1 × 10⁵ burnin steps and prior distributions as indicated (see Supplemental Fig. S1).

Comparison to IM under allopatry

In order to compare our estimates with those generated by IM (Hey and Nielsen 2004), which does not allow for intralocus recombination, we set the population recombination rate, ρ, to 0. To be comparable to IM, we also chose uniform prior distributions with 0 as the lower limit. We generated 30 simulated data sets with parameters relevant for Drosophila species as above, setting M to 0 and drawing the other parameters from prior distributions: θ₁ and θ₂ from U (0, 0.01) and θ_A from U (0, 0.02) per base pair and T from U(0, 1.5 × 10⁷) generations. We analyzed those 30 simulated data sets with MIMAR and IM using the same prior distributions as used when simulating the data sets, 4 × 10⁶ recorded steps and 5 × 10⁵ burnin steps.

Assessing the evidence for gene flow

We generated 40 data sets, consisting of 40 recombining loci with parameter values relevant for apes (see below). We assumed that μ = 2 × 10⁻⁸ per base pair per generation to translate coalescent time units into generations (Nachman and Crowell 2000). This mutation rate estimate is also obtained assuming a most recent common ancestor of human and chimpanzee of 7 Mya and an average nucleotide divergence of 1.28% (The Chimpanzee Sequencing and Analysis Consortium 2005). The intralocus recombination rate was set for each locus by choosing r = c/μ from the prior exp(1/0.6) (assuming that the mean c is 1.2 × 10⁻⁸) (Kong et al. 2002). The other parameter values were sampled from the following prior distributions: θ₁, θ₂, and θ_A from U (0.0006, 0.006) per base pair and T from U(0, 1 × 10⁵) generations. M was either fixed to 0 (for 20 data sets simulated under the allopatric model) or to 1 (for 20 data sets simulated with parapatric divergence). We analyzed the 40 simulated data sets with MIMAR, choosing ln(M) from U (–5, 2) and the other parameters from the same prior distributions as used when simulating the data sets, the number of ARGs per locus set to X = 50, 4 × 10⁶ recorded steps, and 5 × 10⁵ burnin steps.

Effect of uncertainty in the intralocus recombination rates

We generated 16 simulated data sets, consisting of 10 recombining loci with parameter values relevant for Drosophila species. The intralocus recombination rate was set for each locus by choosing r = c/μ from the prior exp(1/10) (assuming that the mean c is 2 × 10⁻⁸; Andolfatto and Przeworski 2000). M was fixed to 0 and the other parameter values were sampled from the following prior distributions: θ₁, θ₂, and θ_A from U (0.001, 0.01) per base pair and T from U(0, 1 × 10⁶) generation. We then analyzed the data sets with MIMAR in three ways: (1) the locus-specific population recombination rates were fixed to their true values, (2) the locus-specific population recombination rates were sampled from the same prior as used when generating the simulated data, and (3) the locus-specific population recombination rates were set to 0. For the three sets of analysis, we fixed θ₁, θ₂, and θ_A to their true values and used the same prior distribution for T as when generating the simulated data. MIMAR was run with X = 5 (cases 1 and 2) or X = 100 (case 3), 4.5 × 10⁵ recorded steps, and 5 × 10⁴ burnin steps.

Analysis of ape polymorphism data

Polymorphism data

We analyzed the ape polymorphism data reported in Fischer et al. (2006), Thalmann et al. (2006), and Yu et al. (2003). The first set was kindly provided by A. Fischer (Max Planck Institute for Evolutionary Anthropology, Leipzig, Germany); we downloaded the two other data sets from GenBank (http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?CMD=search&DB=Nucleotide). The data from Fischer et al. (2006) (and Thalmann et al. 2006) and Yu et al. (2003), consisted of loci of median length ∼780 bp and ∼470 bp, respectively. The data sets were as follows (see Tables 3–5): 69 loci surveyed in nine unrelated bonobos (pigmy chimpanzee, P. paniscus), 26 loci in 10 and 43 loci in six Western chimpanzees (P. t. verus), 26 loci in 10 and 42 in five Central chimpanzees (P. t. troglodytes), 26 loci in 10 Eastern chimpanzees (P. t. schweinfurthii), 15 loci in 15 Western gorillas (G. gorilla) and three Eastern gorillas (G. beringei), and 19 loci in six Sumatran orangutans (P. p. abelii) and 10 Bornean orangutans (P. p. pygmaeus).

For each locus, we obtained two outgroup sequences. For the chimpanzee data sets, one orangutan sequence and one human sequence were available for 26 and 19 loci, respectively (Fischer et al. 2006); one human sequence (Yu et al. 2002) and one gorilla sequence (G. g. gorilla; Yu et al. 2004) were obtained for 43 loci. We blasted the seven remaining loci and downloaded a homologous human sequence for each of them (BLASTN, http://www.ncbi.nlm.nih.gov/BLAST) (Altschul et al. 1990). For the gorilla data set, one orangutan sequence and one human sequence were available for all loci; for the orangutan data set, one chimpanzee sequence and one human sequence were available for all loci (Fischer et al. 2006). We used CLUSTALW in MEGA3.1 (Thompson et al. 1994; Kumar et al. 2001) to align the resequencing data and the two outgroup sequences. We then wrote a Perl script that requires both outgroup sequences to be consistent to infer the ancestral state at each site, thus minimizing error in the reconstruction of the ancestral state. We ignored sites with gaps, missing data, and more than two variants. (There were only one site with three alleles in the entire gorilla data set, three in the orangutan data, and six in the chimpanzee/bonobo data.) We used a Perl script to calculate for each locus the four statistics S₁, S₂, S₃, and S₄ (see above) and F_ST (Hudson et al. 1992) for pairs of populations, as well as the mean pairwise differences, π (Nei and Li 1979) and Tajima’s D (Tajima 1989) in each population.

Estimates of mutation rate variation

To allow for variation in mutation rates, we used the scalars v described above. To do so, we calculated the mean pairwise divergence per site between a human sequence and an ape sequence (div), using a Perl script. We obtained the expected locus divergence given the number of base pairs, E(div) ⋅ Z, where E(div) is the mean divergence per base pair over the loci, and performed a goodness-of-fit test using Pearson’s χ² (Frisse et al. 2001). The gorilla and orangutan data did not deviate significantly from expectation (P-value = 0.24 and 0.85, respectively); therefore, we set v = 1 for all loci in the analysis of these two data sets. However, data from the three common chimpanzee populations and the bonobo rejected the null hypothesis of a homogeneous mutation rate across loci (at the 5% level). Thus, for a pair of chimpanzee populations or species, we set v at a locus to the observed divergences per base pair divided by E(div).

Recombination rates

Won and Hey (2005) found evidence of recombination in bonobos, Central and Western chimpanzees in 10 of the 43 short segments surveyed by Yu et al. (2003) used in this study. We estimated the locus-specific recombination rate in the data sets using MAXDIP (http://genapps.uchicago.edu/maxdip/index.html; Hudson 2001), setting 0.005 as the initial value and the gene conversion rate to 0. From each species, we chose the subspecies with the largest estimate of the mean recombination rate across loci, which were Central chimpanzees, Western gorillas, and Sumatran orangutans. Then, to assess whether the point estimates were significantly greater than 0, we simulated 1000 data sets using ms (Hudson 2002), setting the number of segregating sites to what was observed and ρ to 0. We ran MAXDIP on the simulated data sets and calculated how many times 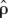(i.e., estimated by MAXDIP) was equal or larger than observed under the standard neutral model. By this approach, we rejected 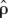= 0 for four out of 35 loci in Central chimpanzees, one out of seven loci in Western gorillas, and three out of 15 loci in Sumatran orangutans (at the 5% level). Given the small sample sizes, our power to detect recombination was limited. Nonetheless, our results suggest that ignoring recombination will result in a loss of data—even in species in which ρ/θ is relatively small. In the analyses of the ape data, we chose r = ρ/θ₁ for each locus from exp(1/0.6) (see above). We chose this distribution because it has been shown to be a good description of fine-scale recombination rate variation in humans and may also apply to a number of other organisms, notably to other apes (Coop and Przeworski 2007).

Analyses

We ran MIMAR for 2 × 10⁷ recording steps with 1 × 10⁶ burnin steps, X = 50, recording the parameters every 50 steps and using prior distributions chosen after preliminary analyses. We repeated our analyses for two independent seeds and considered that convergence was reached when the posterior distributions of both runs were very similar (data not shown). Results reported are for the average from the two independent runs. We obtained estimates of the effective population sizes and split times in years for all the ape species and subpopulations using μ = 2 × 10⁻⁸ per base pair per generation and assuming 20 yr per generation for chimpanzees and orangutans (Gage 1998; Fischer et al. 2004) and 15 yr per generation for gorillas (Thalmann et al. 2006).

Goodness-of-fit test

We investigated how well the data fit the estimated model by generating the posterior predictive distributions of the four statistics S₁, S₂, S₃, and S₄ summed over all loci, the mean F_ST (Hudson et al. 1992), and, in each population, the mean pairwise differences, π (Nei and Li 1979) and the mean Tajima’s D (Tajima 1989) across loci. To do so, we simulated data sets under the isolation-migration model, sampling the parameters from the posterior distribution estimated by MIMAR. We then compared the observed values of the statistics to the simulated distribution (see Supplemental Fig. S6), conservatively considering the model to be a poor fit if the observed value of a data summary fell in the 2.5th percentile tails of any statistic. We note that, since this goodness-of-fit test takes into account the uncertainties associated with the estimates, it is similar to the Bayesian posterior predictive P-value (e.g., Meng 1994).