Quasi-Steady Approximation for Ion Channel Currents

Abstract

Currents through ion channels are determined (among other parameters) by the concentration difference across the membrane containing the channel and the diffusive transport of the conducted ion toward the channel and away from it. Calculation of the current requires solving the diffusion equation around the channel. Here, we provide a quasi-steady approximation for the current and the local concentrations at the channel together with formulas linking the current and local concentrations at the channel to bulk concentrations and diffusion properties of the compartments.

INTRODUCTION

Transport of ions through membranes by channels or pores is one of the basic processes in cell physiology. Currents through ion channels determine plasma-membrane voltage dynamics. Channels on the membrane of intracellular storage compartments control the cytosolic Ca²⁺ concentration. These molecules represent sources and sinks, respectively, for the concentration of the ion that they transport.

The ions reach a sink or move away from a source by diffusion. Consequently, concentration gradients on both sides of the membrane are necessarily involved in the transport process and the concentrations at the channel are different from bulk concentrations. The concentration profiles during local release events of Ca²⁺ called puffs (with IP₃ receptor channels) and sparks (with ryanodine receptor channels) are a manifestation of large gradients inside cells that are due to conduction through ion channels. Currents of <0.1 pA may cause gradients of 2–3 orders of magnitude between concentrations at the channel and bulk concentrations on the relevant time and length scales (1,2). The reason is the strong localization of the ion source within a few nanometers, i.e., the large flux density. Since the current through a channel or transporter usually depends on the concentrations on both sides of the membrane, calculation of the current requires solving the complete diffusion problem.

Knowledge about the concentration gradients around transport molecules may be required for modeling purposes by the presence of regulatory binding sites for the conducted ion within the range of large gradients. That applies to all channels regulated by the ion they conduct and to communication with other compartments, channels, or chemical species. For example, it was observed that mitochondria taking up Ca²⁺ may be close to Ca²⁺ release sites of the endoplasmic reticulum (ER) and experience local concentrations much higher than bulk concentrations (3).

The occurrence of gradients has serious consequences for quantitative modeling. The above examples illustrate that models using spatially averaged bulk concentrations may be off by orders of magnitude in the concentrations at binding sites. However, taking gradients into account may turn a model from a system of ordinary differential equations into a system of partial differential equations (PDEs), which are much more difficult to solve. Moreover, since gradients are often steep and fast, the partial differential equations are typically computationally expensive to integrate.

Here we present a method that actually exploits the fast timescales. The concentration dynamics close to the channel are dominated by the channel flux. Concentrations reach very quickly a stationary state determined by the local fluxes and the diffusion and reactions in the bulk. However, the details of the bulk processes do not affect the local concentrations at the channel. That was shown numerically for Ca²⁺ release from the endoplasmic reticulum (1) and we show it here again. Binding of Ca²⁺ to buffer molecules in the cytosol does not affect the local concentration at the release channel as long as release currents are large enough. That “large enough” value is ∼0.05 pA for physiological buffer parameters already; i.e., it is met by realistic currents (1). On the basis of these observations, we calculate the current and local concentrations from a radically simplified set of partial differential equations. The results of the calculations in this report are simple expressions for the single channel current I

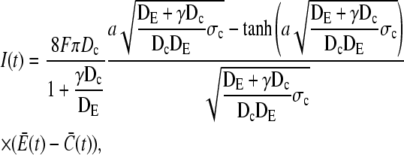(1)

and the concentration at the surface of the source volume modeling the channel

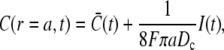(2a)

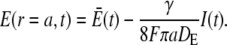(2b)

The values 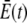and 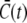are the average concentrations in ER and cytosol, respectively (at time t), or in the cytosol and extracellular space for a plasma membrane channel. E(r = a, t) and C(r = a, t) are the corresponding local concentrations. F is Faraday's constant, D_c is the diffusion coefficients of free Ca²⁺ in the cytosol, and D_E an effective diffusion coefficient in the ER taking its tubular shape into account (4), a is the radius of the channel vestibule (see Parameter Values), σ_c the channel flux constant and γ = 1 has to be used here (see Parameter Values). The quasi-stationary current and concentration values in Eqs. 1 and 2 are approached for times larger than τ = [(1 + γ)σ_c]⁻¹ upon channel opening and they are reached after typically 10⁻⁵ s (see Discussion of the Fast Transient). These results allow for substantial simplification of the integration of the complete partial differential equations (K. Bentele, A. Skupin, and M. Falcke, 2007, unpublished) or—if spatial information is not required—even for a reduction of the concentration dynamics to a system of ordinary differential equations as will be shown in this report.

The following two sections will introduce the processes determining currents and gradients, model equations, and the choice of parameter values. Subsequently, we derive a quasi-steady approximation for the channel current and compare it to the exact analytical solution of simplified linearized reaction diffusion equations and simulations of the complete nonlinear equations.

THE CONCENTRATION DYNAMICS

We model a single channel. The extension to many channels tightly packed into a cluster or with larger spacing is indicated in Discussion. The applicability of our results to plasma membrane channels will be also discussed there. We will consider the release of Ca²⁺ from the endoplasmic reticulum (ER) through a channel on its membrane and uptake by pumps. The concentration dynamics comprise:

1. Diffusion of free [Ca²⁺] in the cytosol D_c∇²[Ca²⁺] and the storage compartment D_E∇²[E];

2. Release from storage compartments by localized channels 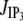= σ_c(r, t)([E] − [Ca²⁺]) and spatially homogeneous leak current J_leak = σ_l([E] − [Ca²⁺]);

3. Uptake into storage compartments by spatially homogeneously distributed pumps 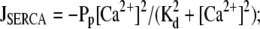and

4. Buffering of calcium by [Ca²⁺]-binding proteins [B_i] with the reaction rate 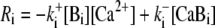in cytosol and ER and buffer diffusion D_B∇²[B_i] in the cytosol only.

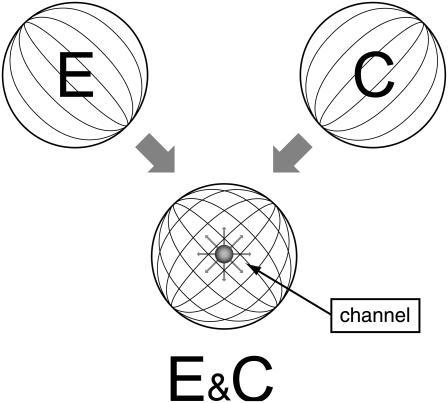
The ER is a large tubular network embedded into the cytosol (6). It was shown by Ölveczky and Verkman that diffusion in such a complicated structure can be mapped onto diffusion in unhindered space with a reduced effective diffusion coefficient (4). That spares modeling the tubular network. Similarly, we assume that all obstacles to diffusion in the cytosol also cause only a reduction of the diffusion coefficient. These simplifications turn a two-compartment model into the two-species model (also known as the bidomain model) with the species cytosolic Ca²⁺ and lumenal Ca²⁺ as shown in Fig. 1.

FIGURE 1.

The model has two compartments: the ER, a tubular network spanning the whole cell, and the cytosol. Calcium diffuses independently in both. Diffusion in the ER can be mapped onto diffusion in the unhindered space with an effective diffusion coefficient (Eq. 3). Ca²⁺ in the cytosol diffuses around many obstacles (including the ER) with an effective diffusion coefficient as given in Table 1. Hence we can describe the dynamics within the two compartments by defining two concentration fields in the same spatial domain: E for the free calcium in the ER and C for free calcium in the cytosol. These fields are coupled by fluxes through the ER membrane, i.e., the channel flux, leak flux, and Ca²⁺ pumps. The channel is in the center of the volume.

Conduction of an ion through a channel involves a complicated interaction between the channel molecule and the ion. Since we are interested in the dependence of currents on bulk concentrations, we take advantage of the fact that beyond the Donnan potential range (5–10 nm (7)) and in a distance larger than the Debye length from the molecule, the channel appears simply as a concentration sink or source, respectively. Consequently, an open channel is modeled by a small spherical volume with a nonzero Ca²⁺ source density proportional to the concentration difference between ER and cytosol. The channel parameter σ_c(r, t) is positive at the location r_c of an open channel of radius a and zero otherwise—i.e., it is σ_c(r, t) = Θ(a − |r − r_c|)σ_c if the channel is open with Θ being the Heaviside step function and σ_c(r, t) = 0 applies if the channel is closed.

In principle, there could be many different buffers in the cytosol or in the ER (denoted by [B_E]), but we restrict ourselves to only one mobile and one immobile () buffer species in the cytosol and one immobile buffer in the ER. The complete set of equations governing the concentration dynamics reads

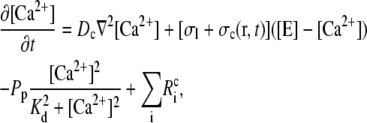(3a)

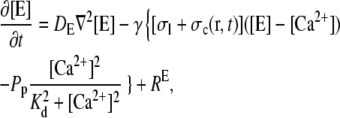(3b)

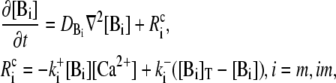(3c)

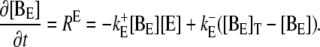(3d)

We assumed that binding of calcium does not affect the diffusion properties of buffers and that the total buffer concentration [B_i]_T = [B_i] + [CaB_i] is initially uniform in the cytosol and ER. Hence, only the free buffer has to be considered (8). The cell is modeled as a simple sphere with radius b. As will be seen below, that geometry is not important for the results since either local processes are considered or global processes are reduced to ordinary differential equations. The location of the channel r_c is neither important for current values as long as it is not too close (order of Ca²⁺ diffusion length) to the cell membrane. We choose r_c = 0.

The expressions in Eq. 3 are the complete problem, the solution of which would provide the current through the channel and the concentration fields. However, the expressions in Eq. 3 cannot be solved analytically to obtain expressions for the current and local concentrations at the channel. We will simplify them in several steps and will in the end compare the currents calculated with the simplifications with simulations of the expressions in Eq. 3.

Based on simulations in Thul and Falcke (1), we assume that the current through the channel does not depend on buffer concentrations. Hence, we drop the buffer dynamics for the purpose of calculating the current. To be able to apply analytical methods for the solution of the PDEs we linearize the remaining nonlinearity of the pump flux. For shorter notation, we substitute [Ca²⁺] and [E] by C and E and reach

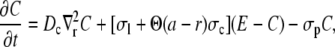(4a)

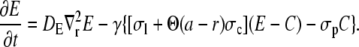(4b)

We apply Neumann boundary conditions in the ER and Dirichlet boundary conditions in the cytosol

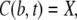(5a)

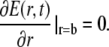(5b)

The initial condition in the cytosol was always set equal to the boundary condition value, i.e., C(r, 0) = X. The initial concentration in the lumen Y varies between different simulations. The analytical solution of that system of PDEs is given in the Appendix. We will need it to assess the quality of the current approximation. We solved the expressions in Eq. 4 analytically, but the complete expressions for the concentrations are several pages long. Hence, we will simplify the problem further in Quasi-Steady Approximation for the Channel Current.

It is worthwhile to introduce appropriate length- and timescales: We scale length by the radius of the channel a, time by σ_c, and the concentrations by the far-field concentration in the cytosol C_∞, i.e.,

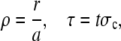(6)

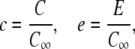(7)

and obtain

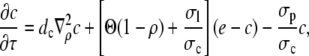(8a)

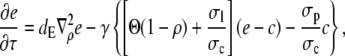(8b)

with

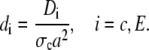PARAMETER VALUES

The diffusion coefficient of free calcium in the cytosol was measured by Allbritton et al. (15) to be ∼D_c = 220 μm² s⁻¹. Geometrical restrictions and the high viscosity of the lumenal medium lead to an estimate of the diffusion coefficient of free Ca²⁺ in the ER of D_E = 40–70 μm² s⁻¹ (1,4).

The nonlinear pumps in Eqs. 3a and 3b were linearized, such that the nonlinear and linear pump-rates agree exactly at the inflection point of the Hill curve, i.e.,

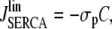(9)

with

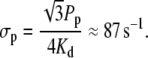(10)

The leak flux constant σ_l was fixed by the requirement that the uptake of calcium into the ER by the pumps equals the leak flux in the resting state. With typical resting concentrations of ∼C = 0.1 μM in the cytosol and E = 750 μM, σ_l is in the order of 0.01 s⁻¹ (6,10). The cytosolic resting concentration of free Ca²⁺ is determined by the plasma membrane fluxes.

Finally, we discuss how the channel flux parameter σ_c can be estimated. Its value depends on the channel radius a. The radius of a single channel vestibule was estimated by Mejía-Alvarez et al. (7) to be in the order of 5–10 nm. We chose 6 nm as channel radius on that basis. Thul et al. fitted the fluxes of a single channel measured in a lipid bilayer experiment (1,11). We approximated their nonlinear expression for the flux by a linear dependency

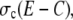(11)

and obtained σ_c ≈ 3.4 × 10⁶ s⁻¹.

A second estimate of σ_c is obtained by requiring a typical current of 0.1 pA with a typical concentration difference of 100 μM (1). That leads to σ_c ≈ 5.7 × 10⁶ s⁻¹. The value σ_c = 4.3 × 10⁶ s⁻¹ used in most of the calculations is between these two estimates.

If not stated otherwise, we will consider a cell radius b = 10 μm. The volume ratio γ = V_cyt/V_ER has to be set to 1 whenever local processes are considered and may assume different values in spatially averaged dynamics. In these cases, it was estimated to be ∼10 from geometrical considerations. The influence of immobile buffer in the ER can be taken into account by an increased effective lumenal volume V_ER, leading to the smaller value of γ = 1 (12), which we used throughout this report.

QUASI-STEADY APPROXIMATION FOR THE CHANNEL CURRENT

We simplify the expressions in Eq. 8 by using timescale separation and small parameters. The ratios 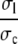and 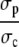in the expressions in Eq. 8 are much smaller than 1. Consequently, we neglect the pump and leak flux:

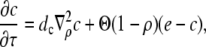(12a)

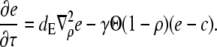(12b)

The boundary conditions are now both set by the far-field concentrations C_∞, and E_∞ as

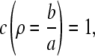(13a)

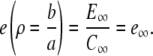(13b)

We solved the expressions in Eq. 12 with initial conditions equal to the boundary conditions in Eqs. 13a and 13b (c(ρ, 0) = 1, e(ρ, 0) = e_∞). Equation 12 is much simpler than the expressions in Eq. 8, since the expressions in Eq. 12 are uncoupled for ρ > 1.

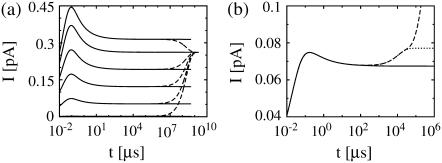
The currents of the complete expressions in Eq. 8 and the simplified problem in the expressions in Eq. 12 behave identically initially: very fast rise and multiexponential relaxation to a (quasi-)stationary value (see Fig. 2). The two solutions do not differ for short times and they relax to the same (quasi-) stationary level. The fast dynamics is completely captured by only taking into account the channel flux and diffusion. The same applies to the solutions with no-flux boundary conditions (Fig. 2 b). The solutions do not differ as the current rises and relaxes to the (quasi-)stationary level. After this relaxation the further time course is differential, and the dynamics of pumps, leak flux, and plasma membrane transport become important.

FIGURE 2.

Current calculated from the solution of the expressions in Eq. 12 taking only the channel current and diffusion into account (solid lines) compared to the current from the complete problem (see the expressions in Eq. 8) (dashed lines). Standard parameter values according to Table 1 were used, if not mentioned otherwise. (a) Dirichlet boundary condition for the expressions in Eq. 12 in the cytosol and ER keep the solution and the current constant for large t, while the solutions of the expressions in Eq. 8 approach all the same asymptotic state. The initial lumenal concentration varies from bottom to top: E = 5, 150, 350, 550, 750, and 900 μM. (b) The initial concentrations are 10 μM in the cytosol and 150 μM in the ER here. As the ER fills up, the current rises. The long timescale of pumping and leak flux does not appear in the solution of the expressions in Eq. 12. The case with no-flux boundary conditions for the expressions in Eq. 8 is additionally shown (dotted line). The current saturates since the ER fills less due to the lack of Ca²⁺ entry into the cell. Identical values for the diffusion coefficients (D_c = D_E = 220 μm² s⁻¹) are used.

The fluxes determining the slow timescale have a minor impact on concentrations and gradients close to the channel but act mainly on spatially averaged concentrations. We introduce that slow timescale into the simplified problem by taking the average concentrations as boundary conditions, i.e., 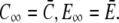To that end, we determine the time dependence of the spatially averaged concentrations by integrating the expressions in Eq. 4 over the cell volume V. With the definition of the average concentration

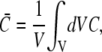(14)

we obtain

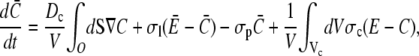(15a)

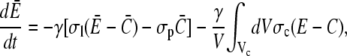(15b)

with channel volume V_c. The integral over the cell surface O arises from the boundary condition. The main contributions come from the leak and pump fluxes, since the channel current contribution has the small factor σ_cV_c/V ≈ 10⁻³ s⁻¹. Eq. 15b has no boundary integral since we apply no flux boundary conditions in the ER.

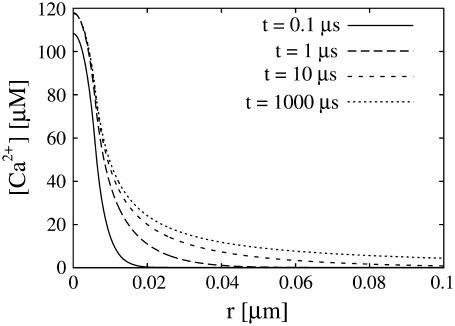
Another conclusion we can draw from the results in Fig. 2 is that the current reaches its stationary value for given boundary conditions very quickly. That applies also to the local concentrations (see Fig. 3). Therefore, we use a quasi-steady approximation. We solve for the stationary solution of the expressions in Eq. 12

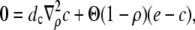(16a)

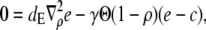(16b)

with the boundary conditions

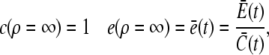(17)

and apply it within the channel range to calculate the current. As mentioned above, we set the spatially averaged concentrations as the boundary condition for the stationary solution of the expressions in Eq. 16 and obtain a self-contained set of equations as in Eqs. 15–17. The solution of the expressions in Eq. 16 for ρ < 1 then reads

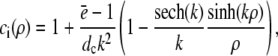(18a)

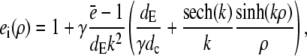(18b)

with k defined in Eq. 20 and for ρ > 1

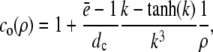(19a)

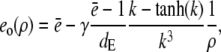(19b)

for which we required continuity of concentrations and fluxes at the channel boundary. We obtain rather simple expressions for the current and the concentration value at the surface of the channel ρ = 1,

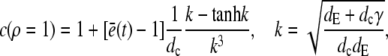(20)

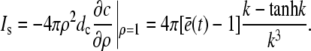(21)

Equation 21 is the scaled form of Eq. 1. We insert this approximation for the current into Eqs. 15a and 15b now as

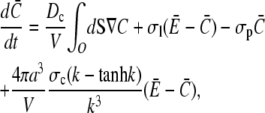(22a)

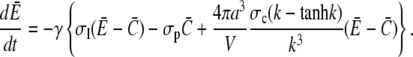(22b)

These equations can be solved in closed form for no-flux boundary conditions. For shorter notation, we introduce the new parameter

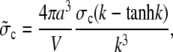(23)

which measures the contribution of one channel to the time course of the average concentrations. It is also convenient to define additionally

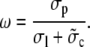(24)

The solution of the expressions in Eq. 22 in the case of vanishing surface integrals reads

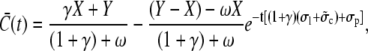(25a)

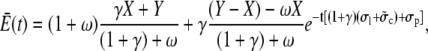(25b)

where X and Y denote the initial cytosolic and lumenal concentration, respectively. The average concentrations change on a timescale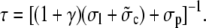

FIGURE 3.

Concentration profiles for different times in the cytosol. The steady state near the channel is quickly established. We used the standard parameter values of Table 1.

We cannot solve the equations in closed form with Dirichlet boundary conditions in the cytosol since we do not know the amount of calcium entering the cell through the plasma membrane from the expressions in Eq. 22. Therefore, with Dirichlet boundary conditions, the expressions in Eq. 22 were solved numerically and the surface integral was calculated using the explicit time- and space-dependent solution given by Eq. 54 (see Appendix).

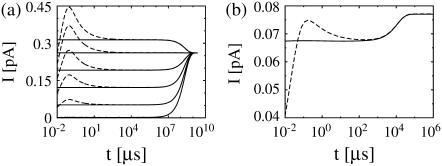
The approximation works very well in both cases. Fig. 4 b shows the exact current and the approximation for no-flux boundary conditions. The fast transient at the beginning is not reproduced by the approximation. However, the deviation is restricted to the initial transient and for times larger than ∼100 μs the approximation is excellent; it clearly reproduces the slower dynamics due to varying average concentrations. These observations all hold for the case with Dirichlet boundary conditions in the cytosol, too, as can be seen in Fig. 4 a. Here, we varied the initial concentration in the ER. Consequently, there is an influx or efflux of calcium through the cell membrane, which leads to an increase or decrease of the concentration within the ER.

FIGURE 4.

Approximation of the single channel current: dashed lines show the exact solution of the expressions in Eq. 8, solid lines the approximation (Eq. 1) with 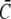and 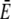from the solution of the expressions in Eq. 22. The approximation is excellent for t > 10² μs. Beside initial concentrations, all other parameter values are from Table 1. (a) The case with Dirichlet boundary conditions in the cytosol. The initial concentration within the ER varies from 5 μM to 900 μM from bottom to top as in Fig. 2 a, and we used always the same initial cytosolic concentration of 0.1 μM. (b) The approximation with no-flux boundary conditions can be calculated analytically (expressions in Eq. 25). The initial cytosolic concentration is 10 μM, the initial concentration in the ER is 150 μM, and identical diffusion coefficients as in Fig. 2 b were used. The approximation captures the slow dynamics due to varying average concentrations.

Discussion of the fast transient

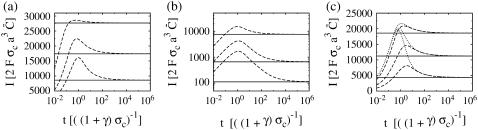
The most important parameters controlling the current are σ_c, a and the diffusion coefficients. σ_c is relevant for the fast buildup of the current due to release of the locally stored calcium on a timescale τ = [(1 + γ)σ_c]⁻¹. Fig. 5 shows that the maximum current is reached at ∼τ.

FIGURE 5.

Dependence of the scaled single channel current 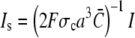on σ_c, channel radius a, and the diffusion coefficients D_c, D_E; solid lines show the approximation Eq. 21 with 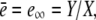and dashed and dotted lines show the time-dependent solution of the expressions in Eq. 12. Time is given in units of ((1 + γ)σ_c)⁻¹, which is the relevant timescale for the buildup of the current. Parameter values not mentioned are in Table 1. (a) Scaled single channel current for different σ_c, varied from bottom to top (σ_c, ((1 + γ)σ_c)⁻¹): (10⁷ s⁻¹, 0.05μs), (3 × 10⁶ s⁻¹, 0.17 μs), and (5 × 10⁵ s⁻¹, 1 μs). (b) Scaled single channel current for different channel radii a, varied from bottom to top: 100 nm, 40 nm, and 10 nm. (c) Scaled single channel current for different diffusion coefficients. The dotted lines show the current for D_c = 220 μm² s⁻¹ and D_E from bottom to top: 10 μm² s⁻¹, 40 μm² s⁻¹, and 150 μm² s⁻¹, whereas the dashed lines give the current for D_E = 220 μm² s⁻¹ and D_c from bottom to top: 10 μm² s⁻¹, 40 μm² s⁻¹, and 150 μm² s⁻¹.

We investigated the fast current transient with respect to its dependence on these parameters. The scaled current decreases with increasing σ_c (Fig. 5 a). Since the unscaled current is given by 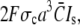it does not decrease for large σ_c but saturates (see also Eq. 29b).

In Fig. 5 c we vary the diffusion coefficients D_c and D_E. Calcium has to diffuse toward the channel inside the ER to maintain the current. Hence, it is not surprising that the smallest current has the smallest diffusion coefficient in the ER. Currents increase as well with increasing diffusion coefficient in the cytosol. The rise in diffusion decreases the local cytosolic Ca²⁺ concentration, and therefore increases the concentration difference across the channel, which causes larger current. The currents for parameter sets with the same d_eff (see below) relax to the same stationary current.

Calcium ion channels are grouped into tightly packed clusters. Therefore, several open channels within a single cluster can be lumped into one conducting volume equal to the sum of the conducting volumes of all open channels (1,13). Hence, the dependence on the radius of the channel area a is also examined (Fig. 5 b). The scaling of the current has to be taken into account in the interpretation of the results in Fig. 5 b. The channel radius varies from 100 nm to 10 nm from bottom to top. Again the scaled current decreases, whereas the unscaled stationary current grows linearly for large a (Eq. 29a). The relaxation time increases for larger radii since diffusion has to equilibrate on a larger length scale. For both σ_c and a, a larger value implies a larger, transient deviation of the time-dependent solution from the stationary current.

We introduce another dimensionless parameter d_eff = 1/k² = d_cd_E/(d_E + γd_c), which is ∼0.34 for a channel radius a = 6 nm and 1.2 × 10⁻³ for a = 100 nm. We can regard d_eff as an effective dimensionless diffusion parameter, taking into account the diffusion inside the cytosol and ER and additionally the channel parameters σ_c and a. The dimensionless current increases with the effective diffusion parameter d_eff. The larger the dimensionless current the faster it relaxes to the stationary value in all examples in Fig. 5. We conclude that the rate of relaxation to the stationary value grows with increasing d_eff. Besides uniquely determining the scaled stationary current, d_eff is also a measure for relaxation toward it.

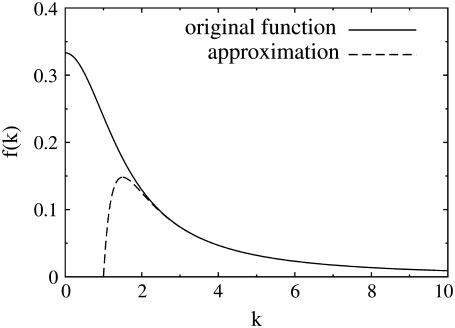
Asymptotic behavior of the single channel approximation

The quasi-stationary current after the fast transient is given by Eq. 21. Fig. 6 shows the function (k − tanh k)/k³ representing its k-dependency. It is equal to 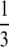for k = 0 and converges to zero for k → ∞. k → 0 holds for a → 0 or σ_c → 0. For k → 0, we obtain

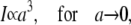(26a)

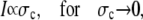(26b)

and for k → ∞,

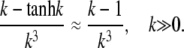(27)

The latter approximation is rather good for k ≥ 2 already, as Fig. 6 shows. We rewrite k as

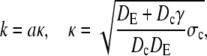(28a)

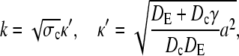(28b)

and reach

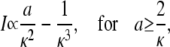(29a)

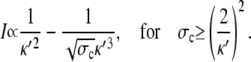(29b)

The asymptotic expressions are valid for a ≥ 7 nm and σ_c ≥ 6 × 10⁶ s⁻¹ with the standard parameters listed in Table 1. The linear dependence of the current on the channel radius a was found in Thul and Falcke (1), too. Simulations in that study described the channel as a hole in a plane membrane in difference to the spherical channel volume here. Nevertheless, the linear dependence on a holds for both cases.

FIGURE 6.

The solid line shows the function 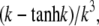which can be approximated by 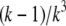for k ≥ 2 (dashed line).

TABLE 1.

Parameters

Parameter values
X	0.1 μM	Cytosolic resting level of free Ca2+, initial and boundary condition.
Y	750 μM	Lumenal resting level of free Ca2+, initial and boundary condition.
σc	4.3 × 106 s−1	Channel flux constant.
σp	86.6 s−1	Linear pump rate constant.
Pp	40 μM s−1	Nonlinear pump rate constant.
Kd	0.2 μM	Dissociation constant for nonlinear pumps.
σl	≈0.01 s−1	Leak flux constant.*
Dc	220 μm2 s−1	Diffusion coefficient of free Ca2+ in the cytosol.
DE	70 μm2 s−1	Diffusion coefficient of free Ca2+ in the ER.
a	6 nm	Channel radius.
b	10 μm	Cell radius.
γ	1	Volume ratio Vcyt/VER.
[Bm]T	100 μM	Total concentration of mobile cytosolic buffer.
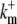	200 (μM s) −1	On-rate of mobile cytosolic buffer.
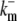	33.3 s−1	Off-rate of mobile cytosolic buffer.
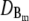	40 μm2 s−1	Diffusion coefficient of cytosolic buffer.
[Bim]T	100 μM	Total concentration of immobile cytosolic buffer.
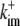	200 (μM s) −1	On-rate of immobile cytosolic buffer.
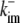	333 s−1	Off-rate of immobile cytosolic buffer.
[BE]T	5000 μM	Total concentration of immobile lumenal buffer.
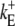	1 (μM s) −1	On-rate of immobile lumenal buffer.
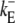	600 s−1	Off-rate of immobile lumenal buffer.
Parameter definitions
dc		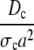Dimensionless diffusion coefficient within cytosol.
dE		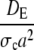Dimensionless diffusion coefficient within ER.
k		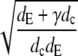Eigenvalue of the Laplace operator (∇2ψ = k2ψ).
V		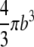Cell volume.
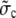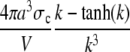		Channel flux constant for averaged concentrations.

^*The parameter σ_l is chosen such that the lumenal resting level equals 750 μM. Depending on whether we assume linear or nonlinear pumps, the value used differs by ∼8%.

The asymptotic limits upon varying the diffusion coefficients are

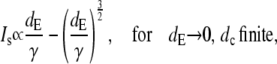(30a)

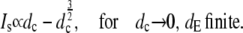(30b)

The values d_E → ∞ and d_c finite implies the vanishing of γ/d_E and therefore leads to a finite dimensionless current given by Eq. 21 with 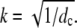For d_c → ∞ and d_E finite, we obtain the dimensionless current with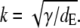

The current is controlled by three processes: diffusion from the bulk toward the channel inside the ER, the channel conductivity σ_c, and diffusion away from the channel into the bulk of the cytosol. If one of these processes becomes very fast, the other two still limit the current.

Validity of the quasi-steady approximation

In this section we go through the most important assumptions underlying the approximations we applied. We assumed that processes at the cell membrane do not have any direct effect on the channel current and solved the expressions in Eq. 16 in an infinite domain. We assess this assumption by calculating the current from the solution of the expressions in Eq. 16 in a finite domain with radius ρ_f and expand it with respect to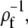

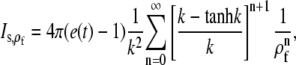(31)

where the first term just reproduces I_s. The relative deviation is

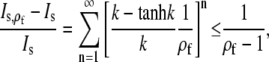(32)

where we used 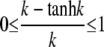and ρ_f > 1, as the cell boundary is clearly outside the channel. For the very unfavorable case with an effective channel radius a = 100 nm and a cell radius b = 5 μm, i.e., ρ_f = 50, the maximum relative deviation is only ∼2%.

Further, we assumed timescale separation between local concentrations at channels and the average concentration. Does this still hold with many open channels or does the average dynamics become fast then, too? Since several open channels within one cluster can be modeled like a single channel with an effective radius, the approximation will be checked for channel radii from a = 6 nm to a = 100 nm. For a = 6 nm, the timescale separation clearly holds. For the maximum radius a = 100 nm we obtain a value of 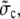defined in Eq. 23, of ∼1.5 × 10⁻² s⁻¹ (all other parameters like in Table 1). Multiplying the channel source term in the expressions in Eq. 22 with a rather large number of 10⁴ open clusters, we obtain as an estimate for the rate of spatially averaged concentrations. Thus timescale separation still holds.

Additionally, timescale separation has to hold for all other processes like buffering and the opening and closing of channels. Opening rates of a channel reach from 2 to 40 s⁻¹ and closing rates from 150 to 1000 s⁻¹ (14). These processes have to be at least slower than the relaxation of the current to a quasi-stationary level. This timescale is determined by τ = [(1 + γ)σ_c] and 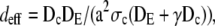but unfortunately cannot be estimated better since it involves the relaxation of many modes. We only can give numerical values for a given parameter set. For our standard parameters and a large radius a = 100 nm it is ∼1 ms. That can be considered as a maximum value.

Finally, we address the validity of the approximation in a nonlinear context. We did a set of comparisons of the quasi-steady approximation for the current and local concentrations embedded into the spatially averaged dynamics of the nonlinear problem (the expressions in Eq. 3) with simulations of the complete nonlinear partial differential system for the expressions in Eq. 3. The averaged equations are

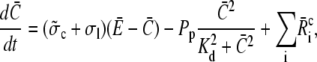(33a)

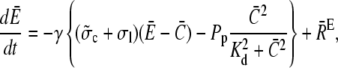(33b)

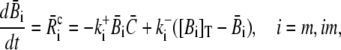(33c)

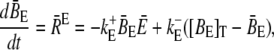(33d)

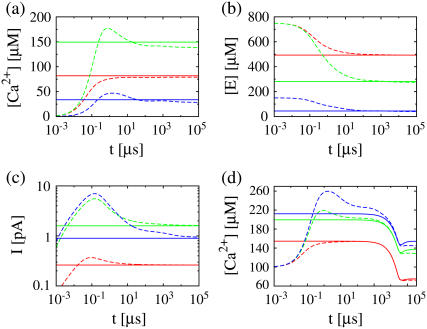
where we replaced the average of nonlinear functions of concentrations with the functions of the average. A surface integral does not appear since we applied no-flux boundary conditions in the ER and cytosol. The parameter 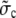is defined in Eq. 23. The results of some simulations are shown in Fig. 7. They illustrate that the approximations are applicable with different sets of parameter values. The quasi-steady approximation works very well for the complete nonlinear problem and for a wide range of parameters covering physiological ranges of ion channel currents.

FIGURE 7.

Comparison of simulations of the expressions in Eq. 3 (dashed lines) and the quasi-steady approximation of the expressions in Eqs. 1 and 2 (solid lines). 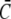and 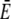required for the evaluation of the expressions in Eqs. 1 and 2 were obtained by numerical integration of the expressions in Eq. 33. In panels a–c, the colors indicate the following parameter sets: red, a = 6 nm; green, a = 20 nm and mobile buffer diffusion coefficient 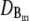= 70 μm² s⁻¹; blue, a = 50 nm; and σ_l is such that 150 μM is the stationary lumenal concentration with channels closed. These stationary concentrations were also the initial conditions in panels a–c. All other parameter values are as in Table 1. (a) Cytosolic concentration at the surface of the channel, (b) the corresponding lumenal concentration and (c) the channel current. (d) The cytosolic concentration at the surface of the channel is plotted. The initial concentrations were C = 100 μM in the cytosol and 600 μM in the ER, which is not the stationary state with closed channels. The colors again indicate different channel radii: red, a = 6 nm; green, a = 20 nm; and blue, a = 50 nm. To reach an asymptotic state within a reasonable computation time, the maximal pump-rate was set to P_p = 4000 μM s⁻¹ and a corresponding σ_l ≈ 1 s⁻¹. All other parameter values are as in Table 1.

DISCUSSION

We have presented a quasi-steady approximation for the current through ion channels. The approximation provides excellent agreement with exact simulations for times larger than τ = [(1 + γ)σ_c]⁻¹, which amounts to 10⁻⁵ s for typical parameters. That quick approach of the current to the quasi-stationary value guarantees as well that values calculated with the approximated current like, e.g., signal mass or distant concentrations, will be close to exact, too.

The quasi-steady approximation sets currents in relation to bulk concentrations (Eq. 1) and provides formulas for local concentrations (the expressions in Eq. 2). It is thus another tool for the experimental analysis of in vivo currents and concentrations if we know the values of the parameters in these formulas. We estimated σ_c of the IP₃ receptor channel for a = 6 nm to be 3.4–5.7 10⁶ s⁻¹. The parameters afflicted with the largest uncertainty are the lumenal parameters 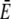and D_E. The cytosolic parameter 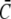has little influence on the current since it is much smaller than 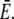D_c is known with an acceptable uncertainty to be ∼220 μm² s⁻¹ (15).

Local concentrations can be obtained from parameter values or alternatively by using current values suggested by experiments and detailed simulation studies (1). With the parameter values for a and D_c of Table 1 and I = 0.1 pA we obtain for the local cytosolic concentration at r = a ∼31 μM (which is 2–3 orders-of-magnitude larger than cytosolic resting levels). The local concentration dip in the ER is (31 μM) × γD_c/D_E. That illustrates again that gradients are not negligible in quantitative modeling. Even qualitative modeling has to take them into account since they determine the regime of channel state dynamics (16).

There are several studies using steady-state approximations for the complete diffusion problem (8,17,18). However, we noticed that this can be a rather poor approximation for different reasons. The timescale to reach the steady solution across the whole cell is in the range of 1 s or more. That is longer than typical release events. Furthermore, if no flux boundary conditions in the lumen are used, the stationary solution for the whole cell has a partially depleted endoplasmic reticulum and consequently underestimates currents (18). The quasi-steady approximation avoids these problems.

G. D. Smith suggested a matching procedure to obtain the current from bulk concentrations (17). The matching procedure relies on the stationary solution of the fast buffer approximation, which is given as an implicit equation. That does not lead to an explicit formula for the current like Eq. 1 and the relation between current and bulk concentration depends on buffer parameters. Here we showed that in good approximation the current depends on the bulk concentrations of free Ca²⁺ only and not on buffer parameters. Buffer parameters determine the current only indirectly via the free Ca²⁺ concentrations.

The quasi-steady approximation opens up two different routes of modeling of problems with many channels. If we neglect information on spatial interactions of individual channels and assume that they are coupled by the average concentration only, the expressions in Eqs. 22 or 33 apply. If we would like to include spatial concentration profiles in the cytosol into a model, we can use the quasi-steady approximation to turn the channel source terms in Eq. 3a into δ-functions with a strength given by Eq. 1. That simplifies the solution of the PDEs substantially since the value of the average lumenal concentration can still be obtained from spatially averaged equations. It allows for application of Green's function to solve the linearized cytosolic problem (K. Bentele, A. Skupin, and M. Falcke, 2007, unpublished). Since the clusters form an inhomogeneity in the cytosolic PDE consisting of a sum of δ-functions, the solution by Green's function illustrates that the cluster current contributions simply superpose linearly in that approximation. Therefore, the quasi-steady approximation neglects local interaction between channels by the concentration profiles in the calculation of these profiles. However, interaction will be negligible for channels more than a diffusion length of free Ca²⁺ apart and channels close to each other—like in a cluster—can be subsumed into a single source with a volume equal to the sum of the volumes of the subsumed open channels (19). Furthermore, note that the expressions for the quasi-steady current and local concentrations do not contain any reference to a specific geometry. They apply to any volume which is large enough (see Validity of the Quasi-Steady Approximation) and consequently also to plasma membrane channels.

In summary, the quasi-steady approximation provides simple formulas for analysis of experimental results and will allow for simple models without losing the information about local concentrations at open channels.

APPENDIX: TIME-DEPENDENT SOLUTION OF THE EXPRESSIONS IN EQ. 4

Solving for the time-dependent solution of the expressions in Eq. 4 starts with Laplace-transforming them. This leads to the boundary value problem,

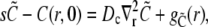(34a)

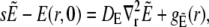(34b)

where 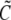and 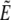denote the Laplace transformed functions and

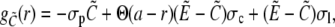(35a)

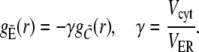(35b)

The initial conditions are

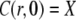(36a)

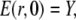(36b)

and the boundary conditions after Laplace transformation read

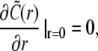(37a)

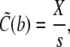(37b)

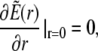(37c)

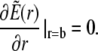(37d)

As the initial state is assumed to be homogeneous, the Dirichlet boundary conditions are chosen equal to the initial conditions to avoid any discontinuous jumps in the concentration profiles.

The solution of the problem will be obtained by solving the equations separately in- and outside the channel, i.e., for r < a and a < r. The corresponding solutions will be indexed with i and o. The proper matching conditions at r = a are continuity of concentrations and fluxes. They have to be fulfilled for each s:

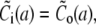(38a)

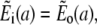(38b)

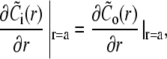(38c)

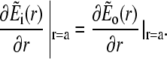(38d)

Two constants are chosen as particular solutions of the inhomogeneous equations. They are determined by the linear systems

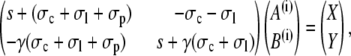(39a)

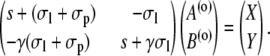(39b)

The solutions are

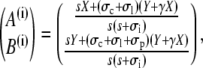(40a)

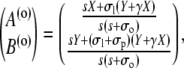(40b)

(40c)

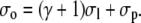(40d)

The homogeneous system is solved by the Ansatz

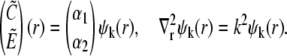(41)

That leads to the equations inside the channel

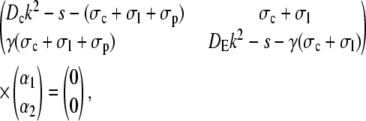(42)

and analogously outside the channel with σ_c = 0. The determinant of the coefficient matrix has to vanish for nontrivial solutions, which provides the equations to determine the eigenvalues k (Tr and Δ denote the trace and the determinant of the matrix, respectively),

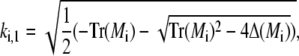(43a)

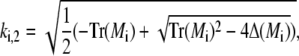(43b)

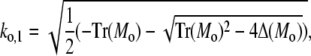(43c)

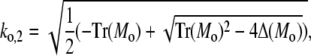(43d)

and eigenvectors

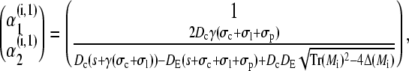(44a)

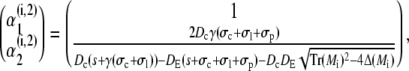(44b)

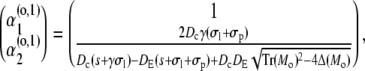(44c)

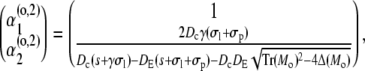(44d)

with M_i/o

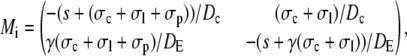(45a)

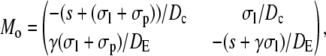(45b)

resulting in

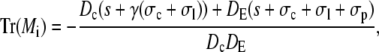(46a)

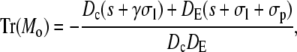(46b)

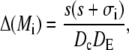(46c)

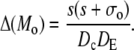(46d)

A necessary condition for the eigenvalue to vanish is that ΔM_(i/o) is zero. This is the case if s = 0, s = −σ_I, or s = −σ_o, respectively. It depends on the sign of Tr(M_(i/o)) as to which k will vanish, since we have for Δ(M_(i/o)) = 0. Thus we get zero eigenvalues according to

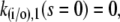(47a)

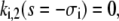(47b)

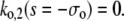(47c)

It should be further noted that the eigenvectors cannot become singular for any value of s. The denominators of the eigenvector components that could potentially become singular are of the form 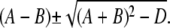This expression can only become zero if D = + 4AB, which is equivalent to γD_cD_E(σ_c + σ_l)(σ_c + σ_l + σ_p) = 0 and γD_cD_Eσ_l(σ_l + σ_p) = 0. However, all these parameters are positive and hence, this condition can never be met.With the eigenvalues and eigenvectors, we are able to construct the full solution. The solution has to be bounded at r = 0. That excludes cosh(kr)/r from the solution for r < a. We finally arrive at

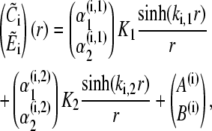(48a)

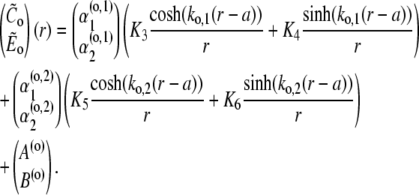(48b)

The boundary conditions (Eqs. 37a–d) and matching conditions (Eqs. 38a–d) lead to a linear system for the six constants K_i, given in matrix form by

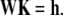(49)

For Dirichlet boundary conditions in the cytosol and Neumann boundary conditions in the ER, we obtain

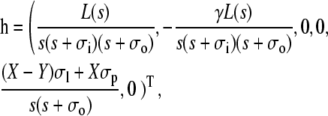(50)

where we have used the short-hand notation

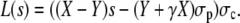(51)

The solution of Eq. 49 then reads

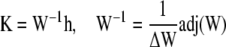(52)

with the adjoined matrix adj(W). The adjoined matrix cannot become singular for any value of s, since it is a combination of products and sums of the components of the eigenvectors, eigenvalues and the hyperbolic functions, which all cannot become singular as stated above. The constants K_i can only become singular due to the zeros of the determinant ΔW and the singularities of h.

We have to transform back the solution from Eq. 48. However, the constants K_i are very complicated expressions (several pages of Mathematica output). This is the reason why we are not able to calculate the series expansions around the potential branch points s = −σ_i, s = −σ_o, and s = 0, which would be necessary to exclude the functions to be multivalued. However, we solved the simpler problem with D_c = D_E and could show that it does not have any branch points. On these grounds we assume the solutions to be single-valued. The concentration profiles obtained from it seem to be physically meaningful, thus supporting this assumption. Furthermore, the singularities at s = −σ_i and s = −σ_o turned out to be removable. In the end, the residuum at the poles s = s′ can be calculated as

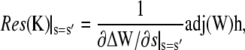(53)

with infinitely many of them along the negative real axis.

Now, we can use the theorem of residues to calculate the inverse Laplace transform. We have to consider the singularities of the constants K_i and of the particular solution 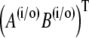in Eq. 48.

The time-dependent solution finally takes the form

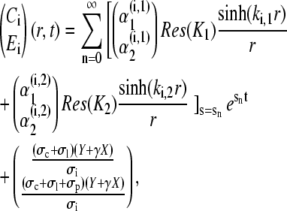(54a)

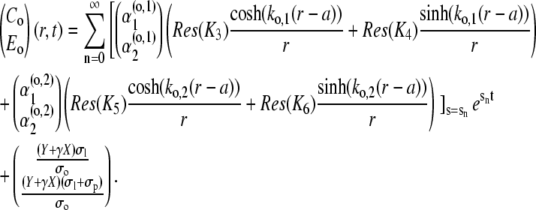(54b)

The first mode n = 0 refers to the stationary solution s₀ = 0. Since all s_n < 0, n ≠ 0, the contribution of the single spatial modes decay exponentially fast. Therefore, only a finite number of modes contribute to the concentration profiles for t > 0.