A Study of Collective Atomic Fluctuations and Cooperativity in a U1A-RNA Complex Based on Molecular Dynamics Simulations

Abstract

Cooperative interactions play an important role in recognition and binding in macromolecular systems. In this study, we find that cross-correlated fluctuations can be used to identify cooperative networks in a protein-RNA system. The dynamics of the RRM-containing protein U1A–stem loop 2 RNA complex have been calculated theoretically from a 10 ns molecular dynamics (MD) simulation. The simulation was analyzed by calculating the covariance matrix of all atomic fluctuations. These matrix elements are then presented in the form of a two-dimensional grid, which displays fluctuations on a per-residue basis. The results indicate the presence of strong, selective cross-correlated fluctuations throughout the RRM in U1A-RNA, which correspond well with the results from a statistical covariance analysis of 330 aligned RRM sequences and previous biophysical studies in which a multiplicity of cooperative networks have been reported. Moreover, the MD results indicate that the various networks identified in separate individual experiments are fluctuationally correlated into a hyper-network encompassing most of the RRM. This method has significant implications as a predictive tool regarding cooperativity in the protein-nucleic acid recognition process.

1. Introduction

Protein-RNA complexes are involved in most steps of gene expression, including the editing, transportation, translation, modification and degradation of RNA (Varani and Nagai, 1998; Chen and Varani, 2005). As such, insight into the protein-RNA recognition process is necessary for a complete understanding of gene expression. However, the high affinity and specificity with which proteins are able to recognize RNAs is a complicated issue to probe. Factors that contribute to protein-RNA recognition include the structures, thermodynamics, cooperative effects and dynamical motions of the macromolecules involved, all of which are highly interdependent. To probe this issue, we investigate the U1A-RNA complex by calculating the cross-correlations of atomic fluctuations derived from the analysis of a molecular dynamics (MD) simulation. We then suggest a link between the fluctuational cross-correlations and cooperative networks of interactions between residues in the U1A-RNA complex. This method enables one to link functional dynamics to cooperativity in the pursuit of a better understanding of protein-RNA recognition.

2. Background

The U1A-RNA complex has been well-characterized by numerous structural and chemical studies, making it a paradigm for the study of protein-RNA recognition, interaction and binding. The protein U1A recognizes its cognate RNA through one of the most common eukaryotic protein domains, the RNA recognition motif (RRM), also known as the RNA binding domain (RBD) or the ribonucleoprotein (RNP) domain. The general structure of the RRM is an antiparallel β-sheet flanked by two α-helices forming a βαββαβ motif (Maris et al., 2005).

U1A binds stem loop 2 (SL2) of U1 snRNA with high affinity and specificity (K_D < 10⁻⁹ M) (Green, 1991; Tsai et al., 1991; Hall, 1994; Stark et al., 2001). The complex of the N-terminal RRM of U1A with SL2 of U1 snRNA (hereafter referred to as U1A-RNA) has been solved by X-ray crystallography (Oubridge et al., 1994). The primary sequence and secondary structure of U1A are presented in Fig. 1. The tertiary structure of the U1A-RNA complex and the secondary structure of SL2 RNA are shown in Fig. 2. Upon complex formation, two highly conserved aromatic amino acids on the β-sheet stack with bases in the single-stranded loop region of the RNA: Tyr13 stacks with C5 and Phe56 stacks with A6, which stacks with C7 (Oubridge et al., 1994). A C-terminal α-helix, labeled α C in Fig. 2, is not part of the RRM, but has been shown to be important for the binding of RNA by U1A (Avis et al., 1996; Zeng and Hall, 1997; Kranz and Hall, 1998; Mittermaier et al., 1999). Loop 3 protrudes through the SL2 RNA loop upon binding (Oubridge et al., 1994) and loop 1, loop 3 and residues Thr89-Asp90-Ser91 (‘the TDS linker’) have been shown to be important for specificity in the binding of SL2 RNA by U1A (Scherly et al., 1990; Bentley and Keene, 1991; Boelens et al., 1991; Jessen et al., 1991; Laird-Offringa and Belasco, 1995; Allain et al., 1997). We have previously reported both experimental and molecular dynamics (MD) simulations to probe structural adaptations and the energetic origins of affinity and specificity in the U1A-stem loop 2 RNA complex (Nolan et al., 1999; Luchansky et al., 2000; Blakaj et al., 2001; Pitici et al., 2002; Shiels et al., 2002; Tuite et al., 2002; Gayle and Baranger, 2002; Zhao and Baranger, 2003; Zhao et al.).

Figure 1.

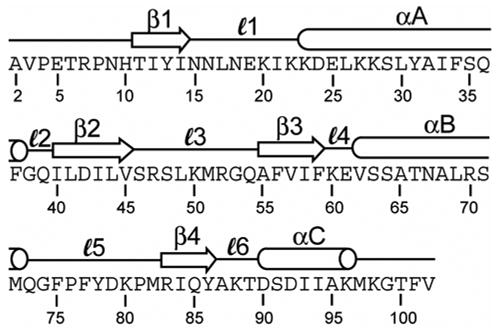
Amino acid sequence of the N-terminal RRM of the protein U1A. Residue numbers are labeled and the secondary structure is indicated above the sequence.

Figure 2.

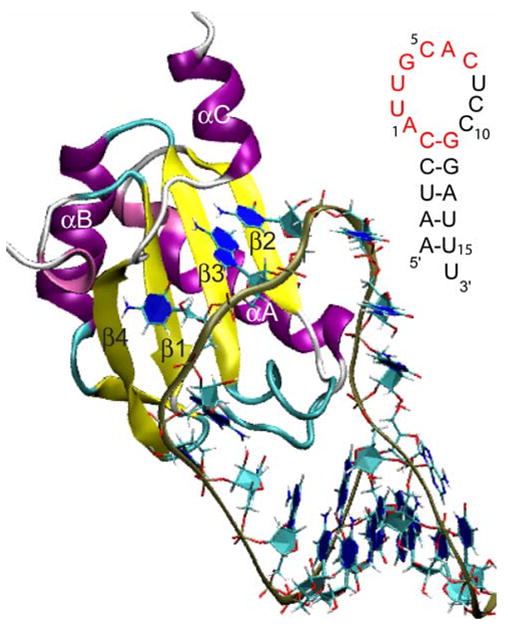
Tertiary structure of the N-terminal RRM of U1A bound to stem-loop 2 RNA (Oubridge et al., 1994). Inset: Nucleic acid sequence of stem-loop 2 RNA with nucleotides recognized by U1A for binding highlighted in red.

Recent studies have indicated that U1A-RNA recognition and binding occur not only as a result of direct interactions, but are also due to long-range effects that are not identifiable merely by inspection of the tertiary structure. One such effect is cooperativity, which plays a functional role in a number of macromolecular activities, including recognition and binding (Di Cera, 1998b). First introduced by Wyman (Wyman, 1948; Wyman and Gill, 1990), the concept of cooperativity represents an interdependence of two or more different groups in a system causing a higher binding affinity than would be expected from summing the association energies of the individual parts (nonadditivity). Common ways to determine cooperativity in a macromolecular system are through the use of site directed mutagenesis, alanine scanning, and double mutant cycles to determine the presence of energetic coupling between residues of interest (Ackers and Smith, 1985; Horovitz and Fersht, 1990; Di Cera, 1998a). A computational theory aimed at the elucidation of cooperative effects in proteins has been set forth in an extensive series of papers by Freire and coworkers (Murphy and Freire, 1992; Hilser et al., 1998; Freire, 1999; Luque et al., 2002). In these calculations, an ensemble of partially unfolded structures is generated using a crystal or NMR structure as a template. Configurational energies and related quantities of the structures are calculated from empirical energy functions fitted to solvent accessible surface areas. The configurational energies obtained in this manner are pairwise additive, and cooperative effects are elucidated by sensitivity analysis on a per residue basis. This approach goes directly from an enumeration of partially folded states to thermodynamic properties without explicitly generating structures, whereas the study described in this article is structure-based.

A series of recent studies have provided biophysical evidence for three cooperative networks of interactions throughout U1A that play a role in binding and specificity (Fig. 5). The first network was hypothesized by Kranz and Hall (1999) and involves interactions from Tyr13 through the RNA to the C-term residues (Fig. 5A). This hypothesis is based on a study in which double mutant cycles were used to reveal energetic coupling between Tyr13 and the C-terminal tail of U1A when bound to RNA (Kranz and Hall, 1998). The contribution of Phe56 has also been added to the cooperative network detailed in Fig. 5A. This is justified based on several studies. Kranz and Hall (1999) found energetic coupling found between Tyr13 and Phe56 based on double mutant cycles. In addition, studies by Baranger and coworkers showed that mutation of Phe56 to Ala altered the U1A-RNA binding affinity by more than would be anticipated from a loss in stacking interactions (Nolan et al., 1999; Tuite et al., 2002) and that A6 of RNA is energetically coupled to Phe56 (Shiels et al., 2002). The second network, also hypothesized by Kranz and Hall (1999), involves interactions from Tyr13 through Gln54 and the loop 3 residues through the RNA (Fig. 5B). This hypothesis is based on a study in which double mutant cycles were used to show energetic coupling between Tyr13 and Gln54, and NMR relaxation experiments showed that mutations in Tyr13, Gln54 and Phe56 affected the dynamics of loop 3 (Kranz and Hall, 1999). Laird-Offringa and coworkers have also performed studies reinforcing the role of Gln54 in the U1A-RNA cooperative networks (Katsamba et al., 2002; Law et al., 2005). The third cooperative network in U1A-RNA involves interactions from Gly53 through loop 1 and loop 3 to the TDS linker (Fig. 5C). This network is hypothesized due to a study in which Showalter and Hall (2002) used NMR, MD and reorientational eigenmode dynamics (RED) techniques to show that the motions of loop 1, loop 3 and loop 6 residues (the TDS linker) are correlated and that mutations in Gly53 affected those correlations. Using the same techniques, they showed that Gly53 has a specific role in RNA binding and that mutations of this residue weaken RNA binding, indicating decoupling of intradomain motions (Showalter and Hall, 2004). While this work was in progress, Showalter and Hall (2005) used MD and RED to identify correlated motions in the U1A-RNA complex and suggested the motions are a reflection of an extensive cooperative network of interactions in this system.

Figure 5.

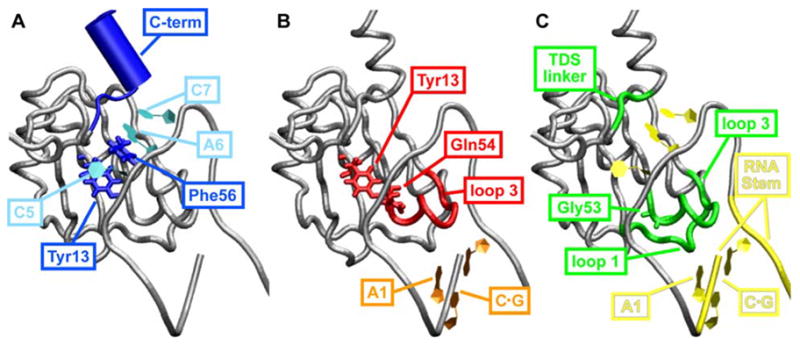
Cooperative networks of interactions between residues contributing to binding and specificity in U1A-RNA. (A) Network 1: Interactions from Tyr13 through C5 and Phe56 through A6 and C7, RNA to the C-terminal residues Lys96 – Phe101. (B) Network 2: Interactions from Tyr13 to Gln54 and the loop 3 residues through the RNA closing C·G base pair and A1. (C) Network 3: Interactions from Gly53 through loop 3 through loop 1, loops 1 and 3 through RNA to the TDS linker.

Generalizing the role of networks in protein-RNA binding, Crowder et al. (2001) performed a statistical covariance analysis (Lockless and Ranganathan, 1999) of 330 RRMs (including U1A) to probe the RNA-binding specificity of proteins that contain these binding motifs. They identified pairs of positions that are functionally coupled, revealing a network of covariant residue pairs beyond those determined in U1A cooperativity studies (vide supra). The Crowder et al. study implicates residues not only on the RNA-binding surface of the RRMs, but also those in the hydrophobic cores of the proteins, indicating extensive networks between residues in the interior of the protein and those in contact with RNA. These results expand upon the important role of functionally linked networks of residues in the binding of RNA by RRMs and specify positions present throughout 330 RRMs that are particularly important for this process.

In this study, we pursue the relationship of fluctuational cross-correlations and cooperativity. Functional dynamics in macromolecular systems are not easy to probe experimentally, and are impossible to determine from a visual inspection of crystal or NMR structures. Thus, computational theory and methodologies have a unique vantage point on this problem. MD simulations serve as a link between structure and dynamics by providing detailed atomic motions as a function of time (Karplus and Petsko, 1990; Doniach and Eastman, 1999; Karplus and McCammon, 2002; Karplus and Kuriyan, 2005). The extent to which atomic fluctuations are correlated with one another can then be extracted from an MD simulation by calculation of the covariance matrix of all atomic fluctuations (McCammon and Harvey, 1986; Brooks III et al., 1988). The matrix elements may then be presented graphically in a dynamical cross-correlation map (DCCM, perhaps better described as a fluctuational cross-correlation map), giving a picture of the correlated fluctuations throughout the course of the MD trajectory. The first studies utilizing this technique involved analysis of correlated motions in cytochrome c (McCammon, 1984), ribonuclease A with two different substrates (Brünger et al., 1985), HIV-1 protease (Harte et al., 1990; Harte et al., 1992; Swaminathan et al., 1991), and BPTI (Ichiye and Karplus, 1991). Since these pioneering studies, cross-correlations and DCCMs have been used to analyze the fluctuations of many diverse systems, including proteins (Arcangeli et al., 1999; Parchment and Essex, 2000; Arcangeli et al., 2001; Rizzuti et al., 2001; Young et al., 2001; Luo and Bruice, 2002; Zoete et al., 2002), protein-nucleic acid complexes (Suenaga et al., 2000; Trylska et al., 2005), and enzymes (Bahar et al., 1997; Radkiewicz and Brooks III, 2000; Rod et al., 2003; Sulpizi et al., 2003; Agarwal, 2004; Gunasekaran and Nussinov, 2004; Schiøtt, 2004; Wong et al., 2004; Fuxreiter et al., 2005; Gorfe and Caflisch, 2005; Ma et al., 2005). A recent study analyzing both the B1 domain of protein G and ubiquitin suggests the correlated motions obtained from MD simulations agree well with measured NMR data (Lange et al., 2005).

3. Methods and Calculations

3.1. MD Methods

The starting structure for the MD simulation of U1A-RNA was based on the x-ray cocrystal structure of the N-terminal RRM of U1A bound to SL2 of U1 snRNA solved at 1.92 Å resolution (Oubridge et al., 1994), PDB ID (Berman et al., 2000): 1URN. Biological unit 2 was chosen for the initial structure as it contains the most complete structural information for SL2 RNA. The U1A protein was extended from the crystal structure construct to obtain a structure containing residues 2 – 102, and two point mutations (H31Y and R36Q) were introduced to revert the protein to the wild type sequence. Details of these procedures are described in Pitici et al. (2002).

Trajectories were computed using the AMBER (Pearlman et al., 1995; Case et al., 2004) suite of programs with the parm96 (Kollman et al., 1997) force field. The U1A-RNA system was solvated in a box of explicit TIP3P (Jorgensen et al., 1983) water molecules that extended a minimum distance of 12 Å from the solute atoms. 13 Na⁺ ions were initially added to neutralize the system. A salt concentration of 250 mM was then obtained by adding 45 Na⁺ ions and 45 Cl⁻ ions to the system. The ions were randomized around the solute using the randomizeions command such that the ions could be no closer than 5 Å to the solute and no closer than 3 Å to each other. Minimization and MD simulation of the U1A-RNA complex followed the protocol described by Pitici et al. (2002). The results presented here are based on a production run of 10 ns.

3.2. Cross-Correlation Computation and DCCM Details

The extent to which the fluctuations of a system are correlated is dependent on the magnitude of the cross-correlation coefficient (Brooks III et al., 1988; McCammon and Harvey, 1986), C_ij, given by Eq. 1:

$$C_{ij}=\frac{\langle \mathrm{\Delta }{\mathbf{r}}_i·\mathrm{\Delta }{\mathbf{r}}_j\rangle }{{\left({\langle \mathrm{\Delta }{\mathbf{r}}_i\rangle }^2{\langle \mathrm{\Delta }{\mathbf{r}}_j\rangle }^2\right)}^{1/2}}$$ (1)

where i and j may be any two atoms, residues or domains, Δr_i and Δr_j are displacement vectors of i and j, and the angle brackets denote an ensemble average. This involves calculation of all inter-atomic cross-correlations of atomic fluctuations, forming a matrix whose elements C_ij may be displayed in a graphical representation as a dynamical (fluctuational) cross-correlation map, or DCCM. If C_ij = 1 the fluctuations of i and j are completely correlated (same period and same phase), if C_ij = −1 the fluctuations of i and j are completely anticorrelated (same period and opposite phase), and if C_ij = 0 the fluctuations of i and j are not correlated.

In the DCCMs reported in this paper, the average equilibrated structure from MD has been used as the reference. Only cross-correlation coefficients greater than 0.25 and less than −0.25 are plotted, with black indicating C_ij values of ±0.75 – 1.00, slate gray indicating C_ij values of ±0.50 – 0.75 and light gray indicating C_ij values of ±0.25 – 0.50. Typical characteristics of DCCMs include a line of strong cross-correlations along the diagonal, cross-correlations emanating from the diagonal, and off-diagonal cross-correlations. The strong correlated fluctuations along the diagonal occur for i = j, where C_ij is always equal to 1.00. Positive correlations emanating from the diagonal indicate fluctuational correlations between contiguous residues, typically within a secondary structure domain. Signature secondary structure patterns include a triangular pattern for an α-helix and a plume for a β-strand. Off-diagonal positive and negative correlations indicate fluctuational correlations between domains of non-contiguous residues. These correlations provide dynamical information about the structure that may not necessarily be apparent from inspection of an average or experimentally derived tertiary structure.

3.3. Technical Details

The choice of fitting procedure used to remove overall rotation from the coordinate sets derived from a MD trajectory has been a point of discussion in the literature. Karplus and coworkers (Ichiye and Karplus, 1991; Karplus and Ichiye, 1996; Zhou et al., 2000) have shown that minimization of the root mean square deviation (RMSD) of all C^α is the most appropriate choice to obtain a complete picture of the fluctuational correlations present within the system. Comparison of their results to those from normal mode analysis (Ichiye and Karplus, 1991) as well as an additional study using MD at zero-angular momentum (Zhou et al., 2000) revealed no spurious correlations when the structures are superimposed over all C^α. Prompers and Brüschweiler (2002) used an isotropically distributed ensemble analysis method which separates internal motion from overall motion and obtained results similar to those obtained by superposition over all C^α atoms. However, Hünenberger et al. (1995) suggest superposition of structures over the least mobile (secondary structure) C^α atoms is a more appropriate choice for fitting as it eliminates ‘artifactual’ correlations observed at long distances in the system. Schieborr and Rüterjans (2001) observe a similar result by comparing to a bias-free method of removing internal and overall motions. Abseher and Nilges (1998) showed that superposition of structures over the least mobile C^α atoms gives results more similar to those obtained from distance space results. Additionally, they showed that superposition over one rigid part of a molecule (for example, one of the monomers in a dimer) causes the misleading appearance of increased motional correlations in the other portions of the molecule. With this knowledge, the cross-correlation coefficients for the U1A-RNA complex were computed after superposition of structures over all C^α atoms and the resultant DCCM was compared to the DCCM computed after superposition over the C^α atoms of only the βαββαβ RRM residues. The resultant DCCMs were virtually identical (data not shown). As such, the results presented herein are those derived from superposition over all C^α atoms to avoid overemphasizing the motion of other structural elements (e.g., helix C).

Additional discussion is warranted regarding several other issues that must be considered when computing the cross-correlation coefficients for a molecule. One issue involves the choice of atoms for this type of analysis. An all-atom cross-correlation matrix is significantly memory- and data-intensive for any system on the scale of a macromolecule, so analysis is typically done by grouping atoms. Grouping for a protein may be done all-atom by residue, but is typically done for backbone atoms by residue. Sensitivity of this analysis to the choice of atom grouping for the protein was tested using the U1A protein. Grouping choices included all atoms by residue, backbone N-C^α-C-O atoms by residue, backbone N-C^α-C atoms by residue, and backbone C^α atoms by residue. All of the DCCMs that involved only backbone atoms looked very similar (data not shown). The cross-correlation coefficients for all atoms by residue showed the same patterns seen for the others, however the patterns were rougher and less correlated due to the increase in motion from inclusion of the more dynamic side chains in the analysis. As such, the DCCMs presented in this study have been grouped using the backbone N-C^α-C atoms by residue for U1A. Sensitivity of this analysis to the choice of atom grouping for the RNA was tested using SL2 RNA. Grouping choices included all-atom by nucleotide and the sugar-phosphate backbone P-O5′-C5′-C4′-C3′-O3′ atoms. Resultant cross-correlation coefficients for these two different grouping choices were similar (data not shown). For the DCCMs presented in this study, grouping for SL2 RNA has been done all-atom by nucleotide because the base-paired stem portion of the RNA revealed stronger correlations than for the results computed over the sugar-phosphate backbone.

The time scale over which correlation data are collected is another important issue to consider when computing cross-correlation coefficients. Fluctuational correlations will depend on the time scale over which the data is analyzed and different correlations may arise on different time scales. The DCCMs presented in this study are based on an ensemble average of one structure per picosecond compared to the equilibrated MD structure. This ensures that only the most important and/or consistent correlated fluctuations that are longer than 1 ps and shorter than 10 ns (or the length of the trajectory) will be observed in the results. As a test, block averages were computed for U1A over intervals of time for 5, 10, 25, 50, 100, 500 and 1000ps. The cross-correlation coefficients all looked very similar to those computed for the 1 ps time scale up to 100 ps (data not shown). At this point and for the larger time scales, the DCCMs become rougher and exhibit stronger correlations between much of the protein, a result of less sampling of the trajectory.

The final consideration of interest in this type of analysis is reproducibility of the results with other force fields. There have been several revision of the AMBER force field since this project was initiated (Wang et al., 2000; Okur et al., 2002). This issue was tested by running a simulation on U1A using the “Stony Brook” modification to the ff99 backbone torsions (Hornak et al., 2006) in AMBER (Case et al., 2006), f99SB, and comparing the cross-correlation coefficients computed from this analysis to those from the parm96 force field. A few residues exhibited slightly stronger correlated fluctuations in the DCCM from the ff99SB force field, but overall, the DCCMs were very similar. This indicates the dynamics of U1A are very similar and can be reproduced using these two different force fields.

3.4. Images

All molecular images were created using VMD (Humphrey et al., 1996) and rendered using POV-Ray (2004). All DCCM images were created using Molecular Dynamics (MD) Toolchest (Ravishanker et al., 1998) and WesGraph (Ehresman et al., 1995).

4. Results

4.1. MD results

A molecular dynamics trajectory was computed for the U1A-RNA complex for 10 ns. The root-mean-square deviation (RMSD) of the protein backbone and all RNA atoms from the equilibrated structure was calculated over the course of the trajectory and is plotted in Fig. 3. The RMSD stabilized after 0.6 ns and remained stable throughout the remainder of the simulation. Verification of the trajectory was provided by comparison to previous MD studies on the U1A-RNA system (Blakaj et al., 2001; Hermann and Westhof, 1999; Reyes and Kollman, 1999; Showalter and Hall, 2005; Tang and Nilsson, 1999). The average RMSD of 1.4 Å (computed for the protein backbone and over all RNA atoms) is consistent with the prior studies. The root-mean-square fluctuations (RMSF) over the course of the trajectory were computed on a residue or nucleotide basis with reference to the average structure and are plotted in Fig. 4. The largest fluctuations occur in the flexible N- and C-terminal regions of the U1A protein, and in the flexible stem and U8/C9/C10 nucleotides of SL2 RNA, nucleotides that do not interact with the protein. Additional analyses of this trajectory are currently in progress, including a complete analysis of the ion and hydration atmospheres.

Figure 3.

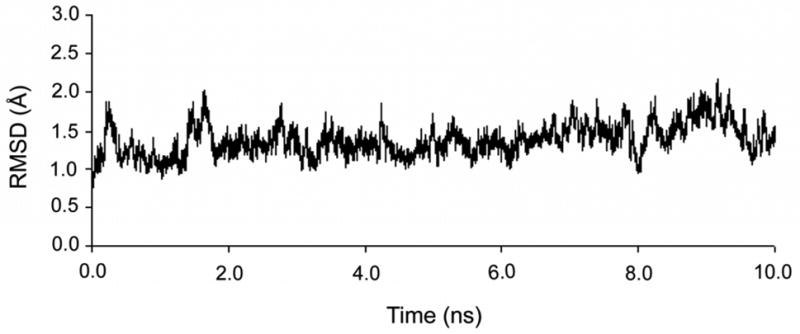
Root-mean-square deviation (RMSD) of the protein backbone and all RNA atoms from the equilibrated structure calculated over the 10 ns simulation of the U1A-SL2 RNA complex.

Figure 4.

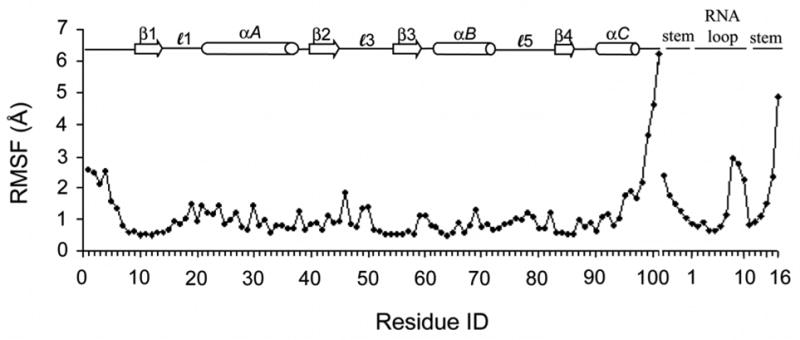
Root-mean-square fluctuations (RMSF) computed on a residue or nucleotide basis with reference to the average structure calculated over the 10 ns simulation of the U1A-SL2 RNA complex.

4.2. DCCM of U1A-RNA

Cross-correlation coefficients were computed from the MD trajectory of the U1A-RNA complex using Eq. 1 and are presented in the DCCM shown in Fig. 6. For the DCCM results presented in this study, cross-correlation coefficients have been computed by residue over the center of mass of N, C^α and C backbone atoms in U1A and by nucleotide over the center of mass of all atoms in SL2 RNA, using the equilibrated structure as the reference structure. The analysis is based on an ensemble average of one structure per picosecond over the entire 10 ns trajectory. Structures for this analysis were superimposed by minimizing the RMSD over all C^α to the equilibrated structure. Positive correlations are collected in the upper triangle of the DCCM and negative correlations are collected in the lower triangle. Only correlations stronger than 0.25 are shown and darker colors indicate stronger correlated fluctuations where black indicates C_ij values of ±0.75 – 1.00, slate gray indicates C_ij values of ±0.50 – 0.75 and light gray indicates C_ij values of ±0.25 – 0.50. Note that not only are protein-protein correlated fluctuations obtained, but protein-RNA and RNA-RNA correlations are obtained, as well. Red (positive correlated fluctuations) and blue (negative correlated fluctuations) boxes have been drawn on the plot in Fig. 6 to indicate locations of intramolecular U1A secondary structure intersections. Orange (positive correlated fluctuations) and green (negative correlated fluctuations) lines have been drawn on the plot to distinguish between SL2 stem and loop nucleotides. This DCCM provides a picture of the correlated fluctuations within the U1A-RNA system that occur throughout the 10 ns MD trajectory.

Figure 6.

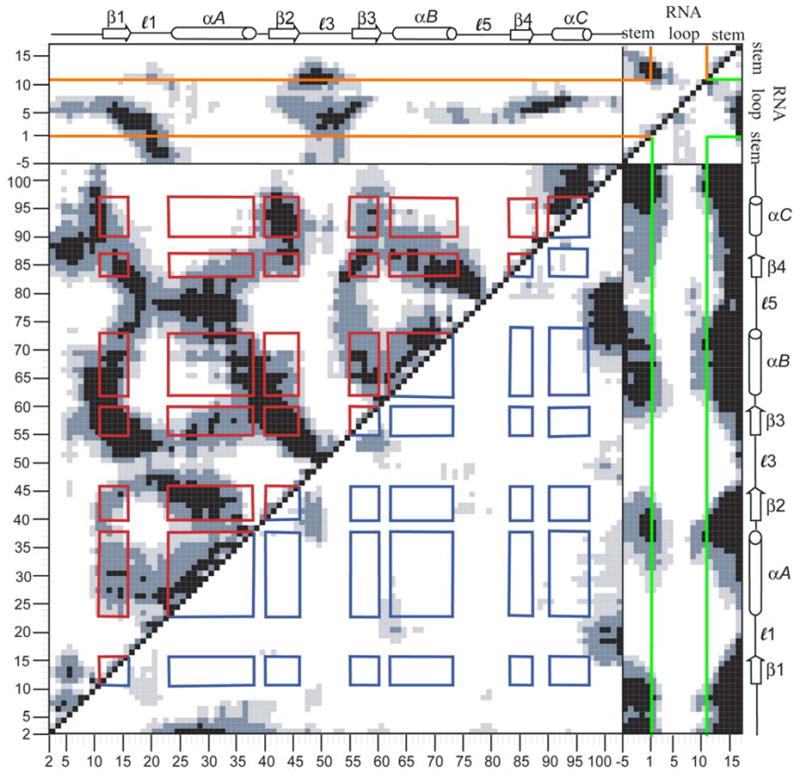
Calculated dynamical cross-correlation map (DCCM) for U1A-RNA. Magnitudes of calculated cross-correlations are indicated via a grey scale with black, slate gray and light gray regions corresponding to strong (C_ij = ± 0.75–1.00), moderate (C_ij = ± 0.50–0.75), and weak (C_ij = ± 0.25–0.50) correlated fluctuations, respectively. Red and blue squares have been drawn to illustrate positive and negative protein-protein secondary structure intersections, respectively. Orange (positive correlations) and green (negative correlations) lines have been drawn to distinguish between RNA stem and loop nucleotides. Additional details can be found in the text.

4.2.1. Protein – protein correlations

U1A intramolecular correlated fluctuations are shown in the large box in the lower left of Fig. 6 with residues labeled from 2 to 102. Signature triangle patterns emanating from diagonal are evident for the three α-helices in U1A; helix A includes residues Lys23 – Phe37, helix B includes Val62 – Met72, and helix C includes residues Asp90 – Lys98. The single pair of contiguous β-strands, β2 – β3, exhibits the signature plume of an antiparallel β-sheet emanating from the diagonal. The remainder of the β-strands comprising the β-sheet are seen in signature plumes that occur off-diagonal as they occur in non-contiguous residues; the direction of the plume depends on whether the β-strands in question run parallel or antiparallel. β1 includes residues Thr11 – Asn 15, β2 includes residues Ile40 – Val45, β3 includes residues Ala55 – Phe59, and β4 includes residues Arg83 – Tyr86. Note there is a significant amount of correlation off of the diagonal, indicating a large amount of fluctuational correlation between non-contiguous residues in the U1A protein. There is not a great deal of anticorrelated protein – protein fluctuation. The most significant is seen between the N- terminal residues with helix A, the C-terminal residues with loops 1 and 5, and the N- and C-terminal ends of loop 3 with β2 and β3.

4.2.2 Protein – RNA correlations

U1A positive and negative correlated fluctuations with SL2 RNA are shown in the rectangles at the top and on the right of Fig. 6, respectively, where U1A is labeled 2 to 102, the 5′ RNA stem is labeled −5 to −1, the single-stranded RNA loop is labeled 1 to 10, and the 3′ RNA stem is labeled 11 to 16. The fluctuations of the loop nucleotides of SL2 RNA are strongly correlated with those of the U1A β-sheet, especially β1 and β3, in which stacking interactions are taking place with the conserved aromatic residues: Tyr13/C5 and Phe56/A6/C7. Loop 1 reveals positive cross-correlations with nucleotides in the RNA loop preceding those involved in stacking with the protein, A1, U2, U3, and G4. Many of these correlations correspond with RNA-protein interactions observed in the X-ray crystal structure (Oubridge et al., 1994): U2 hydrogen bonds Glu19, U3 hydrogen bonds Asn16, and G4 hydrogen bonds Asn15 and Asn16, and interacts with Leu17 through a water-mediated hydrogen bond. However, the strongly correlated fluctuations between loop 1 and the RNA loop extend beyond that predicted by the contacts. Loop 3 reveals positive cross-correlations with the single-stranded nucleotides and the C-G base pair of the SL2 sequence that is recognized by U1A. As with loop 1, some of the U1A loop 3 – RNA cross-correlated fluctuations correspond to interactions shown in the crystal structure, while others extend beyond the contacts. Crystal structure contacts in this region include: Arg52 hydrogen bonds A1, G4 interacts with Leu49 through a water-mediated hydrogen bond and stacks with Gln54, and C5 hydrogen bonds Gln54. Single-stranded loop nucleotides also reveal some strong fluctuational correlations with loop 5 and helix C. Crystal contacts in this region include: C5 hydrogen bonds Lys88, A6 hydrogen bonds Thr89 and Ser90 and interacts with Lys88 through a water-mediated hydrogen bond, and C7 hydrogen bonds Ser91 and Asp92. Again, the positive fluctuational correlations in this region extend beyond the specific protein-RNA interactions. Loops 1 and 3 additionally have positive cross-correlations with stem. Crystal structure interactions in this region include: Lys20 and Lys22 interact with the sugar-phosphate backbone of the 5′ stem and Arg52 hydrogen bonds the closing C-G base pair. Again, cross-correlated fluctuations extend beyond the contacts. The fluctuations of the remainder of the stem are generally anticorrelated with those of the protein, except for loops 1 and 3.

4.2.3. RNA – RNA correlations

The SL2 RNA fluctuational cross-correlations with itself are shown in the small box in the top right of Fig. 6, and nucleotides are labeled from −5 to 16. The 5′ and 3′ stem nucleotides are strongly correlated, as is expected between Watson-Crick base-paired nucleotides. There are also positive cross-correlations seen within each 5′ and 3′ stem region which may be expected with intrastrand stacking. The single stranded loop nucleotides show anticorrelated fluctuations with stem, most noticeably with the dangling U16 nucleotide.

4.3. Correlated fluctuations and cooperativity

This analysis has demonstrated that using a DCCM to analyze a molecular dynamics trajectory can provide a useful picture of the collective atomic fluctuations taking place in the simulation. Next, we address the hypothesis that collective atomic fluctuations are indicative of cooperative effects by comparing the computed cross-correlation coefficients to observed cooperativity data in U1A-RNA. The issue of a cooperative network of interactions between residues in the U1A-SL2 RNA system that contributes to both binding and maintaining the complex has been primarily addressed by the work of Hall and coworkers (Kranz and Hall, 1998, 1999; Showalter and Hall, 2002, 2004; Showalter and Hall, 2005), Baranger and coworkers (Nolan et al., 1999; Shiels et al., 2002; Tuite et al., 2002; Zhao and Baranger, 2003), and Laird-Offringa and coworkers (Katsamba et al., 2002; Law et al., 2005). We have observed that the residues involved in strong fluctuational correlations in the U1A-RNA complex correspond well to those observed to be a part of the cooperative networks of interactions. (The cooperative interactions that contribute to binding and the extent to which these correlations change in U1A and RNA upon binding will be explored in a forthcoming study.)

The cooperative networks of interactions that emerge from the previous studies on U1A-RNA and the residues involved are summarized in Fig. 5. The first network (Fig. 5A) involves conserved residues Tyr13 and Phe56, through the RNA nucleotides C5, A6 and C7, to the C-terminal U1A residues, Lys96 – Phe101 (Kranz and Hall, 1998, 1999; Nolan et al., 1999; Shiels et al., 2002; Tuite et al., 2002; Zhao and Baranger, 2003; Law et al., 2005). The second network (Fig. 5B) involves Tyr13 to Gln54 to loop 3 to the RNA closing C-G base pair and A1 (Kranz and Hall, 1999; Katsamba et al., 2002; Law et al., 2005). The third network (Fig. 5C) involves Gly53, loop 1 and loop 3 through the RNA to Thr89-Asp90-Ser91 (the ‘TDS linker’) (Showalter and Hall, 2002, 2004).

The fluctuational correlations of the specific residues implicated in the cooperative networks are highlighted in the DCCM in Fig. 7A. The residues in the first network are outlined in red. Tyr13 is strongly correlated with C5, Phe56 is strongly correlated with A6, A6 is moderately correlated with C7, and C5, A6, and C7 are correlated with the C-terminal U1A residues. The residues in the second network are outlined in orange. Tyr13 is strongly correlated with Gln54, Gln54 is correlated to loop 3, especially the N-terminal residues, and the loop 3 residues are strongly to moderately correlated to A1 and the closing C-G base pair of the RNA. Residues in the third network are outlined in yellow. Gly53 is strongly correlated to loop 3, especially the N-terminal residues, loop 3 and loop 1 are strongly correlated, loop 1 is strongly correlated with the 5′ stem and loop nucleotides of RNA, loop 3 is strongly to moderately correlated to A1 and the closing C-G base pair of the RNA, and C5, A6 and C7 are strongly correlated to T89-D90-S91. These results show that residues found to be energetically coupled are fluctuationally correlated, and that every residue involved in each of the three networks is fluctuationally correlated with the subsequent residue(s) in the network. In addition, Fig. 7A shows that the residues involved in these three networks are also fluctuationally correlated with one another, revealing connections between the three individual networks. For example, Tyr13 is correlated with Gln54, (orange box) which is correlated with loop 1 (yellow box). The overall picture emerging from this analysis is that a network of fluctuational correlations can be mapped out connecting all three networks, indicating that these residues are a part of one larger cooperative hypernetwork.

Figure 7.

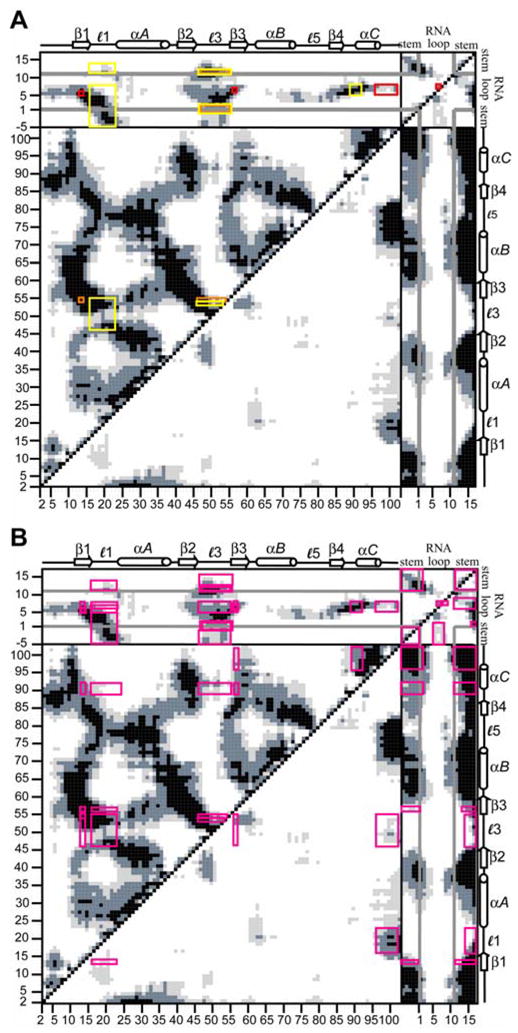
Calculated DCCMs for U1A-RNA indicating residues implicated in cooperativity studies. (A) Red, orange and yellow boxes drawn indicate correlated fluctuations of the residues implicated in networks 1, 2 and 3, respectively. (B) Boxes drawn indicate correlated fluctuations of all residues implicated in the three cooperative networks with each other.

To further explore this idea, Fig. 7B outlines all of the residues implicated in the three cooperative networks and their cross-correlated fluctuations with each other. This analysis indicates that the majority of the residues implicated in the three cooperative networks are fluctuationally correlated with each other with cross-correlation coefficients greater than 0.25 or less than −0.25, supporting the idea that the cooperative networks are all part of a larger hypernetwork of cooperativity. The residues that reveal cross-correlation coefficients between −0.25 – 0.25, indicated by white space, are important for further clarifying the intricacies of the cooperative network. For instance, loop 3 has been implicated in the networks; however all of the residues in loop 3 are not fluctuationally correlated with all of the other residues. Tyr13 is correlated with the Lys50 – Gln54 residues of loop 3, while Thr89 – Ser91 are correlated with the Ser46 – Met51 and Gln 54 residues of loop 3. This DCCM analysis helps to clarify the cooperative network in U1A-RNA through fluctuational correlations. These results, along with those reported by Showalter and Hall (2005) from the analysis of MD using RED, provide encouraging evidence for the use of calculated fluctuational cross-correlations to map out cooperativity in protein-nucleic acid systems.

4.4. Correlated fluctuations and statistical covariance analysis

Independent validation of the link between fluctuational correlations and cooperativity is provided by comparison of our results to an RRM statistical covariance study. Crowder et al. (2001) analyzed the statistical covariance of 330 RRM-containing proteins, including U1A, and were able to subsequently identify a network of covariant amino acid residues present within those RRMs. The results from Crowder et al. compared with the present study are shown in Fig. 8. Positions of residues exhibiting high covariance (> 3.5 σ) are indicated on the DCCM in Fig. 8 by yellow rectangles. The covariant pairs reveal strongly correlated fluctuations from the calculated cross-correlation coefficients. The majority (76%) of the residues shown to covary exhibit fluctuational correlations stronger than 0.50 in the MD simulation. Only one of the covariant pairs exhibited anticorrelated fluctuations, Arg52 – Phe56. This result provides further evidence that a significant amount of information regarding networks of interactions between residues may be extracted from calculation of the cross-correlation coefficients from a MD simulation.

Figure 8.

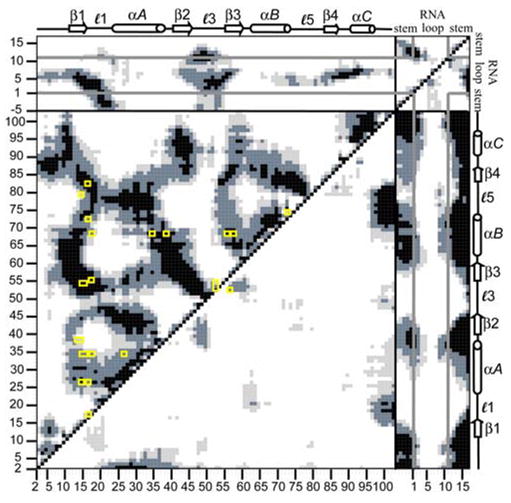
Calculated DCCM for U1A-RNA. Yellow boxes indicate residues revealed to exhibit high covariance from Crowder et al. (2001) statistical covariance analysis of 330 RRM-containing proteins.

5. Discussion

We have investigated the collective atomic fluctuations of an RRM by calculating the cross-correlation coefficients from a 10 ns MD simulation on the U1A-RNA complex. Analysis was facilitated by displaying the results in the form of a DCCM, which provides a picture of the cross-correlations of atomic fluctuations of U1A-RNA over the entire simulation. Highly correlated fluctuations were found, as expected, between residues and nucleotides involved in contact interactions. More important to this study is that the calculated cross-correlations are indicative of considerable through-space correlation as well, which is not obvious from simply examining the structure per se.

These calculations provide a definition of “dynamical contact” which may carry different information than spatial contacts. Within the protein-protein intramolecular section of the DCCM, well differentiated patterns of positive correlated fluctuations are exhibited that interconnect the entire RRM. This indicates that the RRM of U1A moves in concert as one unit. This observation is consistent with other studies that have shown that U1A has a rigid binding surface (Reyes and Kollman, 1999; Kranz and Hall, 1999; Showalter and Hall, 2005) and that U1A unfolds in a manner consistent with a two state model (Silow and Oliveberg, 1997), however it also shows that concerted fluctuations are exhibited beyond the binding surface and throughout the RRM. The majority of protein-protein anticorrelated cross-correlations seen in the DCCM occur in the N- and C-terminal residues, indicating fluctuations of the flexible N- and C-terminal tails in response to the global motion of the rest of the molecule. The intermolecular fluctuations between protein and RNA that appear from the DCCM analysis indicate correlated motions between the RNA loop nucleotides and the U1A protein due to the stacking interactions with the RRM, and anticorrelated motions between the RNA stem nucleotides and the U1A protein. The anticorrelated fluctuations between U1A and the RNA stem nucleotides indicate a global motion between U1A and RNA, in which the RNA stem and protein move toward each other and then away from each other throughout the MD simulation.

The results of our calculated cross–correlations from MD simulations agree very well with experimentally observed cooperativities in U1A. Moreover, the MD results show cross-correlations predicting that the observed networks are all components of one larger hyper-network. It can be seen from Fig. 7B that this network is quite extensive. However, these residues that have been studied to date by experimental methods only encompass a fraction of the total number of residues in the U1A-RNA, and there are a significant amount of correlated fluctuations in the U1A-RNA system outside of these residues. This indicates the potential for the discovery of additional residues that contribute to cooperativity in this system.

The agreement between our cross-correlation results and cooperativity studies suggests the possibility of using the cross-correlation data to predict additional residues involved in cooperative networks in U1A-RNA. For example, the residues that have cross-correlation values greater than 0.75 with residues that are hydrogen bonded or in VDW contact with RNA nucleotides could be investigated. From such an analysis, several residues have a greater occurrence than the others (Data not shown). These residues include Asp42, Ile43, Leu44, Ala55 and Val57, all of which may contribute to the cooperative network of interactions in U1A-RNA. Of these residues, only Leu44 has been previously studied, the results showing that it is crucial for specificity(Scherly et al., 1990) and that mutation of Leu44 to Val causes a 3.3-fold loss in binding affinity (Rimmele and Belasco, 1998). These findings support the utility of DCCMs for predicting residues important in the network of interactions in U1A-RNA.

It is particularly significant that our calculated cross–correlations are in agreement with results of the statistical covariance analysis of 330 RRMs, which is validation for making additional predictions based on covariance information. For example, several of the covariant residues from this study contact SL2 RNA in the U1A-RNA complex, including Tyr13, Asn15, Asn16, Arg52, Gly53, Gln54 and Phe56. The residues with which each of these residues covary may also be important in the network of interactions in U1A-RNA. The positions of these residues can be seen in Fig. 9. Of these residues, the strongest correlated fluctuations involve Ile14 (with Gln54) and Met82 (with Asn16), moderate correlated fluctuations involve Leu17 (with Asn16), Leu26 (with Asn16), Phe34 (with Asn15), and Met72 (with Asn16), and weaker correlated fluctuations involve Gly38 (with Tyr13). None of these residues have been subjected to mutational analysis to date; however, they show potential to be interesting candidates for the study of cooperative networks in the U1A-RNA system.

Figure 9.

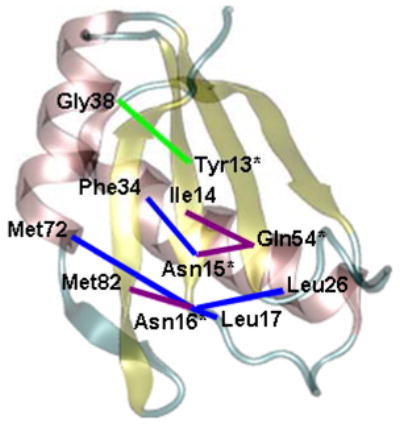
Cooperative interactions related to the U1A-RNA binding interface predicted from both MD calculated fluctuations and statistical covariance analysis for U1A. Residues directly in contact with RNA are indicated by an asterisk. The magnitude of fluctuational covariance between residues corresponds to the line coloring: purple: C_ij = ± 0.75–1.00, blue: C_ij = ± 0.50–0.75, green: C_ij = ± 0.25–0.50.

Of course, many factors are involved in the binding of any macromolecules, and it is important when investigating binding and recognition to study not only the bound form, but the free constituents as well. Cooperative interactions important for recognition in the unbound macromolecules may change significantly upon binding in order to maintain the complex. As such, dynamical cross-correlation studies on the free constituents and mutants are forthcoming to address issues of affinity and specificity within the U1A-RNA system.

Although a direct connection between fluctuational correlations and cooperativity has not necessarily been proven with this study, the analysis reveals a significant link that should continue to be explored. We plan on further probing this connection between collective atomic fluctuations and cooperativity on small test systems in which cooperativity has been observed. Other potential applications of this method include the study of evolutionarily conserved cooperative networks in RRMs as done for the DNA cytosine methyltransferase family (Estabrook et al., 2005).

6. Summary and Conclusions

We have presented here a dynamical picture of an RRM obtained by calculating the cross-correlations of atomic fluctuations from a MD simulation of the U1A-RNA complex. We have found that cross-correlated fluctuations in the U1A-RNA complex can account for the observed cooperative effects from biophysical experiments and the results of a statistical covariance analysis on 330 examples of biological RRMs. Our calculations suggest that the various observed cooperative networks are correlated with each other, which is consistent with the observed rigidity of the U1A binding surface and the two state folding pathway of U1A. Finally, based on this analysis, we have presented additional residues in U1A that may be important for recognition and binding in this system. The results support the hypothesis that collective fluctuations are indicative of cooperativity. The combination of MD and DCCM analysis is thus a powerful and unique method for understanding and predicting cooperativity at the molecular level in protein-RNA binding, and for elucidating long range, through-space communication in a protein-nucleic acid complex. This approach can be adapted to the study of cooperativity in many systems, including other protein-nucleic acid or protein-protein systems.