Modeling backbone flexibility to achieve sequence diversity: The design of novel alpha-helical ligands for Bcl-x_L

Abstract

Computational protein design can be used to select sequences that are compatible with a fixed-backbone template. This strategy has been used in numerous instances to engineer novel proteins. However, the fixed-backbone assumption severely restricts the sequence space that is accessible via design. For challenging problems, such as the design of functional proteins, this may not be acceptable. In this paper, we present a method for introducing backbone flexibility into protein design calculations and apply it to the design of diverse helical BH3 ligands that bind to the anti-apoptotic protein Bcl-x_L, a member of the Bcl-2 protein family. We demonstrate how normal mode analysis can be used to sample different BH3 backbones, and show that this leads to a larger and more diverse set of low-energy solutions than can be achieved using a native high-resolution Bcl-x_L complex crystal structure as a template. We tested several of the designed solutions experimentally and found that this approach worked well when normal mode calculations were used to deform a native BH3 helix structure, but less well when they were used to deform an idealized helix. A subsequent round of design and testing identified a likely source of the problem as inadequate sampling of the helix pitch. In all, we tested seventeen designed BH3 peptide sequences, including several point mutants. Of these, eight bound well to Bcl-x_L and four others showed weak but detectable binding. The successful designs showed a diversity of sequences that would have been difficult or impossible to achieve using only a fixed backbone. Thus, introducing backbone flexibility via normal mode analysis effectively broadened the set of sequences identified by computational design, and provided insight into positions important for binding Bcl-x_L.

Introduction

Computational protein design holds great promise for guiding the discovery of useful biomolecules. In particular, the design of proteins that form specific interactions could facilitate the development of therapeutic inhibitors or agonists. There have been many experimentally validated examples of protein design, including the design of stable folds, active enzymes and specific receptors.^1–18 Most successful protein design calculations so far have sought to identify a sequence that stabilizes a fixed backbone geometry, as defined by a high-resolution structure. Fixed-backbone design is used to limit the potentially infinite search space and make design problems more tractable. However, the fixed-backbone approximation is an artificial limitation that severely restricts the space of possible design solutions. For example, it has frequently been observed that sequences designed using a fixed backbone are very native-like.^19–21 As the demands placed on protein design problems increase, e.g. as designed proteins are required to be more specific, more highly functional, less aggregation prone or easier to encode in DNA libraries, artificial restrictions such as those imposed by using a fixed backbone become less tolerable. In this paper, we propose a new method for introducing backbone structural variation using normal mode (NM) analysis and explore it in the context of a protein-protein interaction that is of critical importance for cancer and other diseases – the interaction of pro-apoptotic peptides with anti-apoptotic members of the Bcl-2 family.

The Bcl-2 family comprises both pro- and anti-apoptotic proteins.^22,23 Five mammalian anti-apoptotic family members, Bcl-2, Bcl-x_L, Bcl-w, Mcl-1 and (presumably) A1, have a conserved globular structure, and all known family members, both pro- and anti-apoptotic, share a weakly conserved short BH3 (Bcl-2 homology 3) sequence. Peptides corresponding to the BH3 region have been shown in several instances to adopt an α-helical structure when bound into a hydrophobic groove on the surface of anti-apoptotic proteins.^24–27 This interaction mode is assumed to be conserved for a larger group of BH3 peptides and anti-apoptotic receptors that have been observed to interact.²⁸ Recent studies have begun to map the interaction preferences of the Bcl-2 family of proteins and have shown that BH3 peptides have distinct binding profiles, with some binding only a subset of anti-apoptotic receptors and others interacting promiscuously.^29–32 Several models have been proposed to explain how the selectivity of this interaction is important for regulating apoptosis via mitochondrial pathways.^29–31 All of these models support the idea that selective disruption of specific interactions could be a valuable strategy for treating cancers.

Both peptide and small-molecule inhibitors that disrupt Bcl-2 interactions have been identified. In a protein engineering approach, the Schepartz group grafted BH3 sequences onto a mini-protein scaffold derived from an avian pancreatic polypeptide.^33,34 By screening a combinatorial library at selected positions in the BH3 part of the sequence, several peptides were identified that bound to Bcl-2 and Bcl-x_L. Sadowsky et al.³⁵ designed a novel α/β α–amino acid backbone scaffold and identified a sequence that bound to Bcl-x_L with sub-nanomolar affinity. Small-molecule inhibitors that interrupt the interactions between BH3 and Bcl-x_L in the low micromolar range were identified in 2001.³⁶ More recently, Olterstorf et al.³⁷ screened hundreds of small molecule fragments using NMR to identify those that bound tightly to Bcl-x_L. A promising compound constructed from these fragments has nanomolar affinity and is now in pre-clinical trials for suppressing certain tumors. Although these inhibitors span a wide range of physical and chemical properties, a common theme in their development was the use of extensive screening and selection to identify compounds with high binding affinity.

BH3 peptides have very diverse sequences and show varying levels of binding to anti-apoptotic Bcl-2 proteins.³⁰ It would be useful to generate artificial peptides that exhibit diverse binding profiles, distinct from those of native peptides, with respect to Bcl-2 family receptors. Such peptides could serve as reagents to help dissect the biological consequences of different interactions in apoptosis and could lead to the development of more specific inhibitors with better therapeutic properties. Until very recently, however, only one high-resolution crystal structure of a Bcl-2 family receptor/BH3 complex has been solved - a complex of Bcl-x_L with a BH3 peptide derived from Bim.^26,38,39 Ligands designed based on this fixed-backbone structure are likely to sample only a small portion of the sequence space that holds interesting, diverse binding peptides. Introducing backbone flexibility to the design protocol may provide a way to overcome this limitation (see Figure 1).

Figure 1.

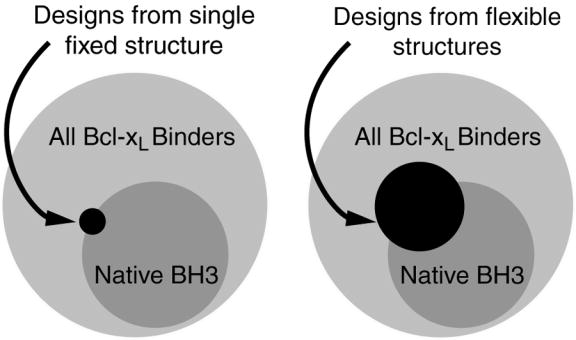
Cartoon illustrating the idea of using flexible backbones to expand the accessible BH3 peptide sequence space. Circles encompassing varying areas indicate the sequence diversity of 26mers meeting different criteria.

Protein backbones have many degrees of freedom, and sampling these efficiently in protein design is quite challenging, as reviewed by Butterfoss and Kulman.⁴⁰ One approach has been to use small sets of parameters to describe variation using a simplified geometry. This technique has been applied to coiled coils and helical bundles,^41,42 and a related approach has been used to vary the orientation of secondary structure elements in the α/β fold of the β1 immunoglobulin-binding domain of streptococcal protein G.¹⁵ The Baker group has had tremendous success modeling backbones in structure prediction by sampling from peptide fragments in the PDB. They have also demonstrated that this approach is effective in protein design.^16,43 Kono and Saven used NMR structure ensembles to represent possible backbone conformations,⁴⁴ and Larson et al. used a Monte Carlo procedure to sample backbone φ and ϕ angles and generate ‘native-like’ structure ensembles.⁴⁵ In this paper, we use normal mode (NM) analysis to introduce backbone flexibility. This method has proven useful for modeling variations of secondary structure elements.^46,47 It shares the advantages of parameterized sampling but can potentially be applied more broadly.

Any protein motion can be described as a sum of NM distortions, but such a description is most useful if the number of modes making significant contributions to structural variation is small, and if these can be identified. As described in a recent review by Ma,⁴⁸ a small number of low-frequency normal modes can be used to model functionally important conformational transitions in several biomolecules that agree with motions observed in molecular dynamics simulations. It has also been noted that a significant amount of the variation seen among different crystal structures of the same, or closely related, proteins can be described by a small set of NM values.^49,50 Specifically for helical regions, Emberly et al. have shown that most of the deformation of the C_α trace can be captured by three low-energy modes.⁴⁶ These modes are two perpendicular bends and a helical twist.

We have used NM calculations to generate deformations associated with the C_α, C and N- atom backbone of helical peptides for protein design. We started with the crystal structure of a Bcl-x_L/Bim-BH3^* complex²⁶ and used NM analysis to construct diverse sets of backbones by fixing the receptor structure and varying the conformation of the binding helix. We then ran computational design calculations on both the crystal structure and on structures in the flexible backbone sets. A larger sequence space could be accessed when flexible backbones were considered. The binding of seventeen designed peptides spanning a range of backbone geometries was tested against three receptor proteins. Eight peptides bound well to Bcl-x_L, as intended, and four more showed weak but detectable binding. Several peptides showed altered binding profiles compared to the wild-type Bim peptide on which the designs were based.

Results

The following sections describe how NM analysis can be used to generate structural variation in helical backbones for protein design, and how we have used such a strategy to design novel Bcl-x_L ligands.

Flexible backbones generated using normal mode analysis

NM analysis has been widely recognized as a way to model functionally important conformational changes in biomolecules.⁴⁸ We speculated that it might also provide an effective strategy for modeling the backbone variation seen among instances of a protein fold as the sequence changes. NM analysis can generate basis vectors that allow for sampling all 3N-6 internal degrees of freedom of any structure with N atoms. But the mode space required to accomplish this is prohibitively large. If the number of modes that contribute to significant structural deviations is small, however, NM analysis could provide a highly efficient way of sampling non-local conformational change. As discussed in the Introduction, Emberly et al.⁴⁶ have shown that this is the case for α-helices. Their results suggest NM analysis as a promising way to sample the structural deformations associated with sequence changes for α-helical segments, and possibly other structures, in protein design calculations. Previously, Emberly et al. used the C_α backbone trace to generate normal modes and fit these to existing protein structures. Here we report the use of NM analysis to generate deformations associated with the C_α, C and N- backbone atoms of helical peptides. The 3-atom method has an advantage because the C_α, C and N atoms are positioned explicitly, leaving no ambiguity in the construction of the backbone.

To probe the structural variation of helices in the PDB, we extracted over 45,000 protein fragments of at least 15 consecutive residues with φ and ϕ angles in the range of −50° +/− 30° from x-ray crystal structures with resolution of 2.5 Å or better. Among these structures, the two normal modes with the lowest frequencies (modes 1 and 2), along with one other mode, can on average capture ~70% of the total deformation (Figure 2a and b). In addition, when looking at the three modes with the largest contribution, modes 1 or 2 occur in the top 3 40–50% of the time. Most importantly, for helices of a given length, modes 1 and 2 have the largest standard deviation over structures (Figure 2c), illustrating that these modes encompass most of the variability and are good candidates to sample structure space.

Figure 2.

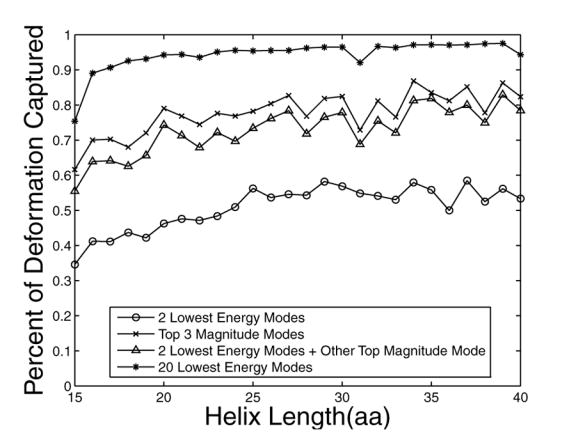
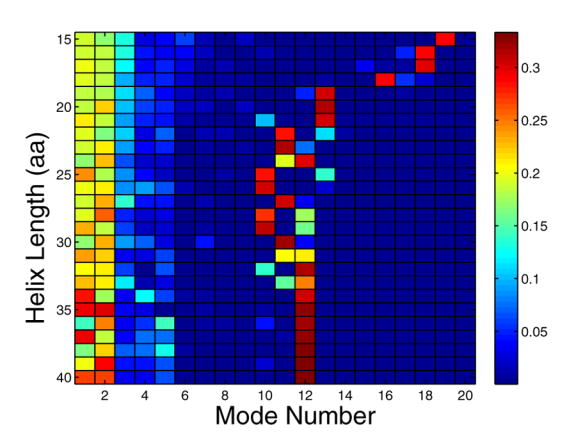
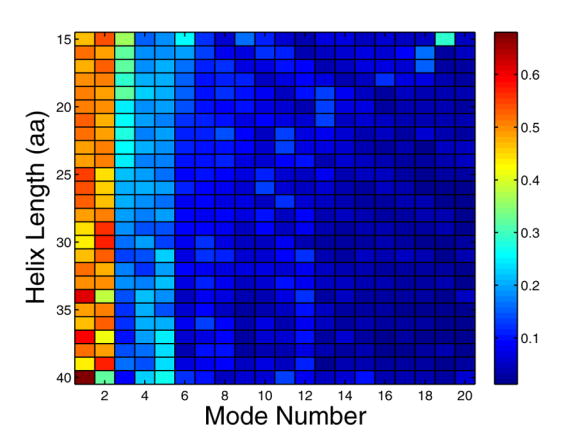
Capturing the structural variation of α-helices using normal modes. A large number of helices with lengths between 15 and 40 residues were extracted from the PDB and analyzed to generate panels a–c (see Methods). (a) shows the fractional deviation from an ideal-helix geometry that can be described with the indicated normal modes, as a function of the length of the helices being modeled. Circles indicate the two lowest energy modes, crosses the top three magnitude modes, triangles the two lowest energy modes plus the next largest magnitude mode, and asterisks the top 20 modes. (b) indicates the fractional contribution of modes 1–20 and (c) shows the normalized standard deviation of this contribution. In (b), the color indicates the fraction of occurrences in which a mode is among the top 3 magnitude modes. In (c), the color indicates the standard deviation of normal mode magnitudes across all helices of a given length. Standard deviations are normalized so that the total sum of standard deviations for a given length helix sums to 1.

Given the observations above, we used NM analysis to generate two sets of variable templates for protein design. Two hundred I-set (ideal-helix set) and 200 N-set (native-helix set) backbones were generated as described in the Methods. The primary difference between these two sets is in the local deformations. The N-set retains small relaxations associated with the match of the native ligand to the receptor, whereas these have all been removed in the I-set. The purpose of generating two sets of backbones was to reflect different design scenarios that may be encountered. The N-set backbones may be a good choice in cases where a crystal structure complex of the target helix is available. The I-set could be used in the more general case in which a helix must be constructed de novo. Here we use information from the complex structure to position the deformed helices with respect to the receptor, but with docking methods this helix could be placed without this prior knowledge.

Before using the flexible backbone templates for design, we characterized them by repacking the native sequence of Bcl-x_L/Bim on each structure, as described in the Methods. The N-set backbones included solutions that were very close to the native structure in both rmsd and energy, and extended to ~3 Å rmsd (Figure 3). Our energy function effectively recognized the native structure, assigning higher energies to structures with higher deviations. Energy minimization of the Bim helix led to minimal structural changes and little change in energy for the best N-set templates, whereas small steric clashes were relieved in the higher-energy structures. The I-set gave structures with larger backbone rmsd from the native structure (up to ~6 Å) and considerably higher energies. Minimization of the I-set Bim helix backbones gave little structural change. However, the energies of the best of these solutions became comparable to those of the minimized N-set, with rmsd values ranging from ~1.5 – 4.3 Å. This analysis suggested that both sets might be reasonable design templates, provided the helix backbone structures were relaxed, with the N-set sampling more native-like structures and the I-set including greater variability.

Figure 3.

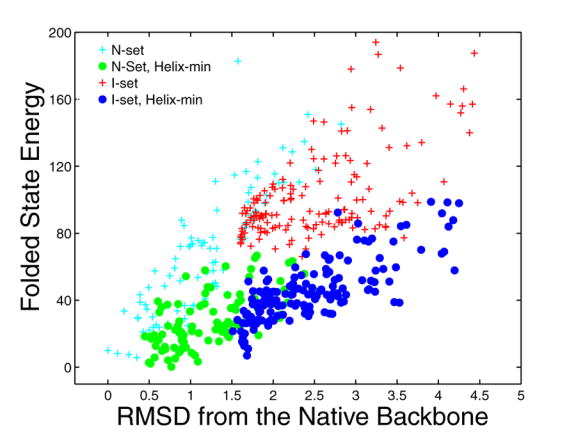
Modeling the complex of Bcl-x_L with Bim using different backbone sets. The folded-state energy relative to the crystal-structure energy is plotted against the backbone rmsd from the crystal structure (in Å). Energies were evaluated without (crosses) or with (circles) minimization to relax the structure (see Methods). N-set structures prior to minimization are shown in cyan and those after are shown in green. Energies of I-set structures prior to minimization are shown in red and those after are shown in blue.

The sequence landscape over multiple backbones

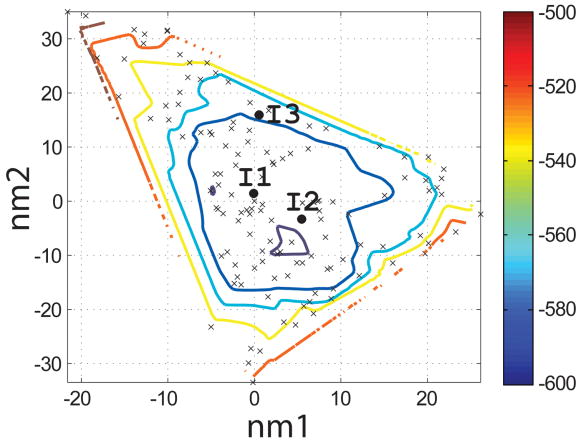
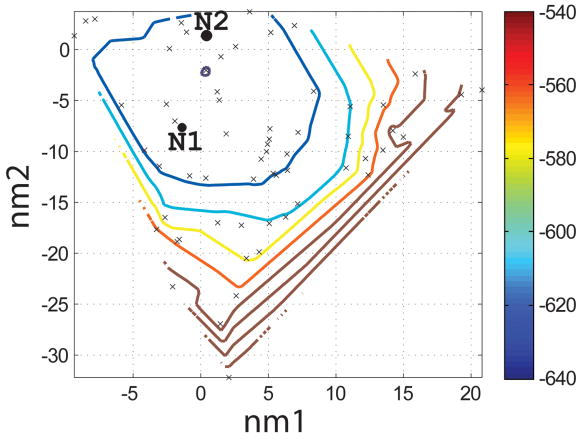
To evaluate which of the 400 backbones in the N- and I-sets were appropriate for designing helical ligands for Bcl-x_L, we used the SCADS program. SCADS is a statistical protein design method that can rapidly generate sequence profiles that are consistent, in a mean-field sense, with a fixed backbone geometry. We used it to determine which N- and I-set backbones were compatible with low-energy sequences by redesigning all 26 residues of Bim on each template. The conformational energies of designed sequence profiles (E_conf, see Methods) are plotted as a function of the values of normal mode 1 and normal mode 2 (nm1 and nm2) for each backbone in Figure 4c and d. A smooth energy surface with a relatively flat well is observed for both structure sets. As shown in a similar plot of the rmsd from the native backbone (Figure 4a and b), we found that the lowest energy region is in the vicinity of the wild-type structure.

Figure 4.

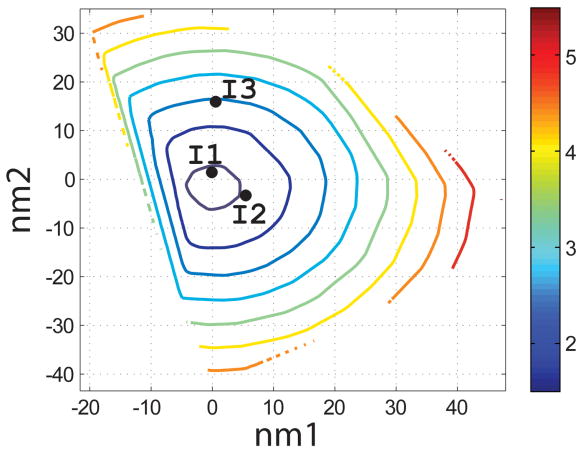
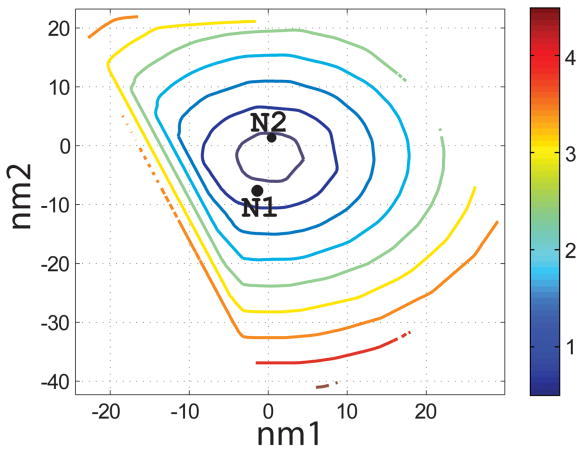
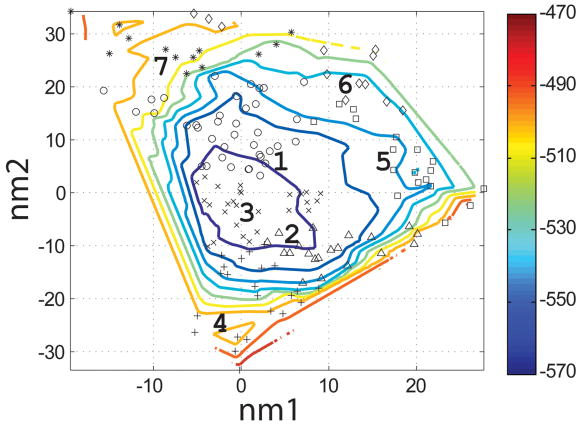
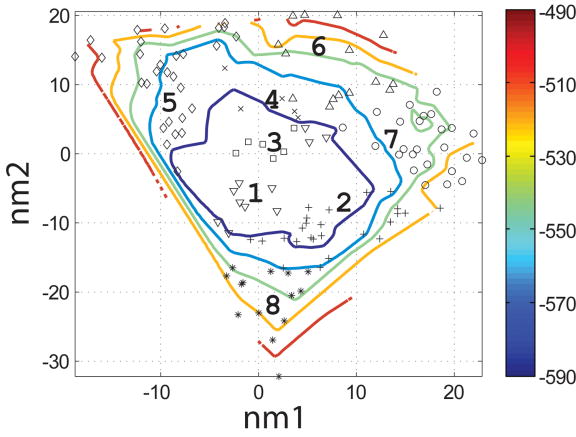
Characterization of the I- and N- sets using SCADS protein design. (a) and (b) Contour diagrams of the root-mean square deviation (rmsd) between the native backbone and (A) I-set backbones or (b) N-set backbones. (c) and (d) The E_conf energy landscape of the full-sequence design of (c) I-set or (D) N-set backbones. (e) and (f) The E_conf energy landscape of the design of the binding interface of (e) I-set or (f) N-set backbones. In figures (c) – (f), each symbol represents a structure for which a sequence profile was computed. In (c) and (d), structures were grouped into clusters based on the similarity of their sequence profiles from SCADS. Clusters are indicated by distinct symbols and are numbered in order of increasing energy. Color in (a) and (b) represents rmsd (Å) from the native backbone, and that in (c) – (f) represents the E_conf energy (kcal/mol) interpolated from the points shown in the figures using Matlab.⁸³ The labeled black dots in (a), (b), (e) and (f) are structures that were selected for experimental testing.

To probe the extent to which structural variation can provide diversity in designed sequences, we compared sequence profiles generated from the crystal structure backbone and from both sets of distorted backbones. Backbones were clustered according to sequence profiles derived from them, using a pairwise sequence profile similarity score (ΔSS) and the Xcluster program.⁵¹ Seven clusters were defined in the I-set and eight in the N-set. Structures from the same sequence-profile cluster are indicated with the same symbol in Figure 4c and d, showing that the clusters defined in sequence space are also clustered in structure space. The clusters are numbered in order of increasing E_conf of the lowest energy profile in each cluster. Thus, structures in clusters with low energies, such as clusters 1 to 3 in the I-set and 1 to 4 in the N-set, are potentially good design templates.

Conserved residues may not be conserved for binding

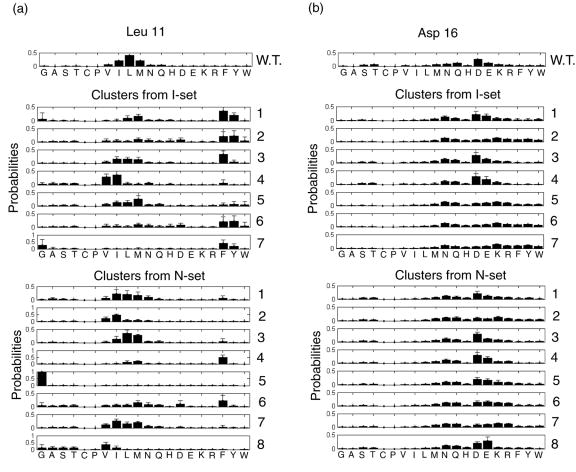
Figure 5 shows SCADS design profiles for positions 11 and 16 on the native backbone and on backbones from the I- and N-sets. For the flexible backbones (I- and N- sets), the profiles were averaged within each cluster shown in Figure 4c and d. These two residues are highly conserved in native BH3 sequences as Leu and Asp, respectively, and previous alanine-scanning studies by Sattler et al.²⁴ have shown that they are important for binding. SCADS calculations on the native backbone also indicated that the native residues are strongly preferred at both positions, as shown in the top panels of Figure 5a and b. However, when we included backbone flexibility in the re-design of these positions, phenylalanine, a much larger residue than leucine, was preferred in low-energy clusters at position 11 (clusters 1–3 in the I-set and cluster 4 in the N-set). At position 16, the native residue aspartic acid was preferred on the native backbone and for the lowest energy clusters, but lysine was found to be highly probable in cluster 2 in both backbone sets. Alanine is predicted to be unfavorable at both positions on all backbones, consistent with the alanine-scanning experiments.²⁴

Figure 5.

Sequence profiles computed with SCADS for positions (a) Leu 11 and (b) Asp 16. “W.T.” indicates the native structure whereas numbers indicate clusters of backbones that give rise to similar sequence profiles, as indicated in Figure 4. Clusters are numbered by increasing E_conf. Profiles for clusters are the average over all structures in that cluster. Error bars show standard deviations.

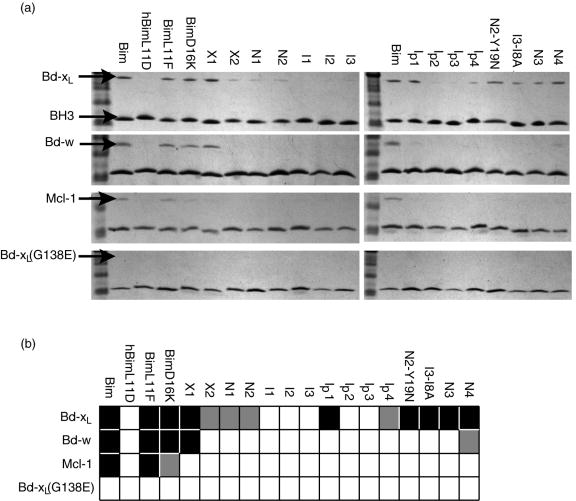
These results suggest that the conservation of Leu 11 and Asp 16 may not be due to a strict requirement for binding. To test whether residues predicted to be stable using the flexible-helix backbones are indeed competent for binding, two single mutants, Bim-L11F and Bim-D16K were made and their binding to Bcl-x_L was tested using a solution pull-down assay. Wild-type Bim and human Bim with Leu 11 mutated to Asp (hBim-L11D) were used as positive and negative controls, respectively. The results are shown in Figure 6. Both single mutants bind to Bcl-x_L approximately as tightly as the native Bim helix.

Figure 6.

(a) Solution pull-down assay for interaction of BH3-like peptides, listed at the top of each lane, with Bcl-x_L, Bcl-w, Mcl-1 and negative control Bcl-x_L G138E, as indicated at left. (b) Summary of (a). Color code: black – strong interaction (similar to the native); grey – weak interaction; white – no discernable interaction.

Design of novel Bcl-x_L binding peptides

As discussed in the Introduction, relieving the fixed-backbone approximation can potentially provide more diverse sequences from protein design calculations than are otherwise available. This is supported by the fact that we could identify point mutations, particularly L11F, that are tolerated at highly conserved positions using flexible backbones, but not the native backbone. To explore this idea further, we redesigned the binding interface of the Bim peptide using the flexible backbone templates. Eleven core and boundary positions were selected for redesign (see Table 1). Hydrophobic residues A, F, G, I, L, M, and V were allowed at the core positions, and all amino acids except Cys and Trp were allowed at the boundary positions. Cys was excluded to avoid disulfide bond formation. Trp was excluded to maintain peptide solubility. Bim residues not in the binding interface were retained with their wild-type identities, but the side-chain conformations were allowed to change.

Table 1.

Redesigned positions of Bim. Numbering starts from “1” for residue 2 of Bim chain B in structure 1PQ1.

Subgroup	SASA range	Positions	Allowed residues
Core	<10%	I7, A8, L11, I14, G15, F18 E4, R12, D16*, N19*, Y22*	A, F, G, I, L, M, V
Boundary	10%~20%		A, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, Y
Exposed	>20%	L1, R2, P3, I5, R6, Q9, E10, R13, E17, E20, T21*, T23, R24, R25, V26	Native residues

^*These positions were categorized manually based on visual inspection.

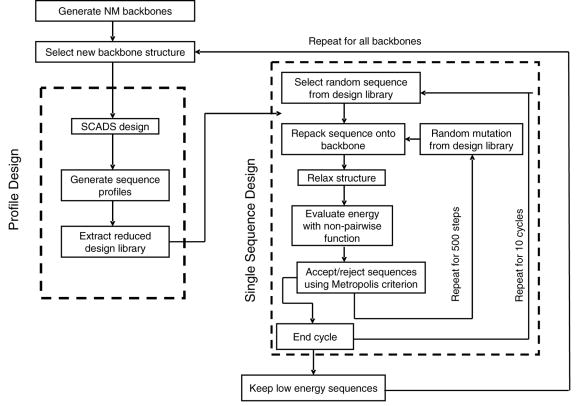
The I- and N-set backbones were used in this study, along with the crystal structure backbone. Sequences designed using the x-ray structure as a template are referred to as the X-set. We adopted a two-tier design strategy to explore the large sequence-structure space (Figure 7). First, SCADS was used to eliminate non-designable backbones and generate profiles of amino acids compatible with each designable backbone. Subsequently, specific sequences were selected using a Monte Carlo (MC) procedure and a different energy function. The two-tier strategy was designed to take advantage of the strengths, and minimize the disadvantages, of these two approaches. SCADS is a method based on the maximization of entropy, and it is ideally suited to identifying the broadest possible set of sequences compatible with a given backbone template at a given design temperature.⁵² It is very fast. It can rapidly identify backbone structures that lead to irresolvable clashes or that cannot support good packing interactions. Finally, it has been developed to reproduce patterns of hydrophobic and polar residues that are typical of native structures. Although SCADS has been used alone for many design problems,^2–4 we have found that the results are sensitive to the environmental energy score used (this parameter is constrained to a pre-defined value in these calculations). This can make it difficult to use SCADS to select specific sequences for experimental testing. Thus, we used SCADS to generate restricted amino-acid libraries and analyzed individual sequences selected from these libraries using a Monte Carlo procedure and a different, more physically interpretable, energy function. At each step of the MC search, a structure was generated using side-chain repacking and then relaxed by briefly minimizing all side chains and the helix backbone. This was previously shown to be necessary to give reasonable energies (Figure 3). Energies of the relaxed structures were evaluated using the function described in the Methods. The use of two different energy functions with different molecular mechanics parameters for protein design has been suggested to help minimize the error due to biases in either of them individually.¹⁸

Figure 7.

Schematic of the two-tiered design method.

Energies of all sequences visited by the MC search on their respective X-, N- and I-set structures were compared to the energy of the wild-type sequence evaluated in the context of the crystal structure. Sequences with binding energies lower than the wild-type sequence were considered as possible design candidates and screened further. One hundred and nine sequences were identified using the I-set, and 494 sequences were found from the N-set. Only 35 sequences were found on the crystal-structure backbone. Petros et al. have shown that higher helix propensities for BH3 peptides favor binding.²⁵ Therefore, we eliminated peptides with helix propensities⁵³ lower than wild-type Bim from the N-set and I-set. This included 341 sequences from the N-set and 28 sequences from the I-set.

In Figure 4e and f, the symbols on the energy landscape indicate I- and N-set backbones on which good design candidates were selected by SCADS. Each symbol represents a backbone. After Monte-Carlo selection, only a few of these backbones, 24 out of 200 in the I-set and 17 out of 200 in the N-set, had one or more sequences that met the two requirements of having lower energy and higher helix propensity than the wild-type structure. Of these, backbones from the N-set had lower SCADS E_conf (−640 ~ −620 kcal/mol) than those from the I-set (−600 ~ −560 kcal/mol). The same trend was apparent in energies used for evaluation of single sequences in the Monte Carlo search.

To assess the diversity of sequences generated by this design protocol, all three sets of sequences, N-, I- and X-, were clustered with selected native BH3 sequences using Clustal-X.⁵⁴ Only the eleven designed positions were used for clustering. To more clearly visualize the results, we restricted the clustering to the 10 lowest-energy sequences per backbone and up to 50 sequences total for each of the I-, and N- sets (Figure 8). Clustering including the entire I- and N-sets gave similar results (data not shown). The 35 sequences in the X-set (blue lines in Figure 8) comprise a subfamily of limited diversity. The N-set (green lines) and I-set (red lines) both span a larger space than the X-set, because they contain more backbone structures and provide access to greater sequence diversity.

Figure 8.

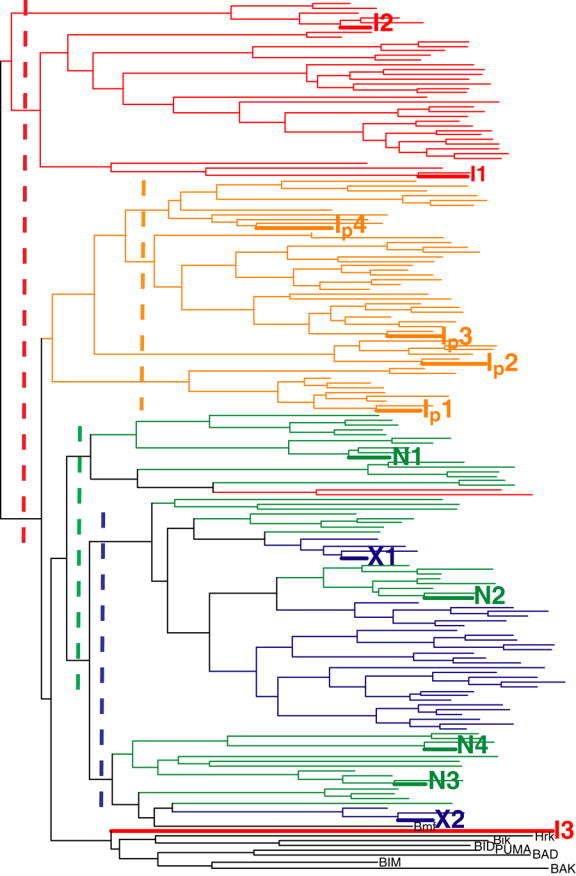
Clustering of sequences designed on I-set (red), N-set (green), X-set (blue), and I_p-set (orange) backbones, along with sequences of native BH3 peptides (black) that have been observed to bind Bcl-x_L. The vertical dashed lines show the thresholds used for picking clusters to be tested experimentally.

The results above show that relieving the rigid backbone approximation can lead to a significantly larger number of sequences that are predicted to have good complementarity with Bcl-x_L and favorable helix propensity. As shown in Figure 4a–d, the differences in the backbone can be small but still allow for sequences that would not be designed without the use of an expanded backbone set. There are additional requirements for a sequence to make a good ligand in solution, however. The designed peptide must be soluble, it must not adopt alternative structures not considered in the design procedure, and the energy function used must model not only the bound state but also the unbound state with sufficient accuracy to give high-affinity designs. To test whether our designed peptides met these criteria, the lowest-energy sequences from several clusters in Figure 8 were chosen for experimental testing. Thresholds defining clusters for the X-, N- and I-sets, shown as dashed lines in Figure 8, were chosen manually to sample the space. The cutoffs give three and two sub-trees for the I- and the N- set, respectively.

Seven sequences were selected for experimental testing: two from the X-set (X1 and X2), three from the I-set (I1, I2 and I3) and two from the N-set (N1 and N2). The sequences selected from the flexible backbones (I- and N- sequences) are shown as the black dots in Figure 4e and f. To demonstrate that the I- and N- sequences would not have been identified using the rigid crystal structure, the energies of all sequences evaluated on the crystal-structure backbone and on their respective normal mode design backbones are shown in Table 2. When modeled on the crystal structure, the designed sequences are predicted to be at least 8 kcal/mol less stable than the wild-type sequence, with more than 4800 sequences in the combined N-, I- and X-sets predicted to have better binding affinity. Thus, the selected sequences cover a sequence space that cannot be accessed by fixed backbone design.

Table 2.

Sequences designed on flexible backbones that were chosen for experimental characterization.

	Sequences*	energy on NM bb (kcal/mol)	energy on x-ray bb (kcal/mol)
Bim	LRPEIRIAQELRRIGDEFNETYTRRV		0
BimL11F	---E--IA--FR-IGD-FN--Y----	−4.4†	6.6
BimD16K	---E--IA--LR-IGK-FN--Y----	2.2†	6.7
X1	---N--IA--MV-IAR-FH--H----		−2.9
X2	---V--VG--MM-IGR-FF--H----		−2.1
N1	---F--VA--LM-FAH-FD--H----	−14.3	8.3
N2	---V--VA--LM-MGK-FY--M----	−6.7	23.0
I1	---H--IV--FK-FGN-IQ--K----	−10.4	30.8
I2	---F--IA--FM-FAQ-MY--I----	−4.5	26.0
I3	---L--LI--LQ-LGY-FN--A----	−2.6	29.1
Ip1	---A--LA--MR-FAR-FE--A----	−10.7	2.2
Ip2	---R--VA--LE-MAN-LR--N----	−10.3	15.1
Ip3	---I--AA--LQ-FAM-FR--D----	−10.1	13.7
Ip4	---M--IA--LR-FAR-FR--D----	−9.8	7.3
N2-Y19N	---V--VA--LM-MGK-FN--M----	−0.1†	9.5
I3-I8A	---L--LA--LQ-LGY-FN--A----	3.3†	3.3
N3	---V--VG--LM-IAR-FD--T----	−7.8	7.6
N4	---F--VA--LN-IAK-FH--F----	−2.7	4.1

All energies are relative to the energy of the x-ray structure of Bcl-x_L/Bim. Dashes indicate the native Bim residue at that position

^*The first Leu was mutated to Glu in experimental tests for all sequences except Bim, BimL11F and BimD16K, see text.

^†Sequences for point mutants were evaluated on all backbones. The lowest energy is reported.

The designed peptides were tested in a solution pull-down assay. Because previous experiments suggested that designed BH3 peptides can be poorly soluble in aqueous buffers (data not shown), a leucine at the first position of the peptide was mutated to glutamic acid. This site is a surface position and as a result is not expected to influence the binding interaction significantly. Wild-type Bim was used as a positive control and hBim-L11D as a negative control. As a negative control of the receptor protein, we used a Bcl-x_L mutant in which Gly 138, a residue in the hydrophobic binding cleft, was mutated to glutamic acid. The results are shown in Figure 6. For the two X-set designs, X1 bound well to Bcl-x_L with X2 binding more weakly. Designed peptides N1 and N2 bound, but more weakly than the positive control. The other three peptides I1, I2, and I3 did not bind. As expected, none of the peptides, including the native Bim positive control, bound to the Bcl-x_L negative control. We also tested all peptides for binding to anti-apoptotic proteins Mcl-1 and Bcl-w. Pull-down results showed that, except for the X1 design and the two point mutants Bim-L11F and Bim-D16K, none of the designed peptides bound to either protein.

To explore why several peptides from the first round of design did not bind well, we manually designed and tested several point mutants. In most of the native BH3 peptides, position 8 is an alanine or glycine. However two of the I-set designs have a larger side chain at this site. To test whether this could be causing a steric problem, we made an Ile to Ala mutation in design I3. The resulting peptide, I3-I8A, showed improved binding to Bcl-x_L (Figure 6). In another case, for design N2, the Tyr residue at position 19 is larger and more hydrophobic than the native asparagine. Gel filtration analysis showed that this peptide eluted somewhat later than native Bim, with a peak that had a long tail, suggesting that it may be sticky and potentially self-associating or aggregating (data not shown). To address this we restored the native Asn at position 19. Again, this peptide bound Bcl-x_L better than the original design (N2-Y19N in Figure 6).

All three sequences designed on the I-set backbones performed poorly, suggesting these structures may not be good templates. In our statistical analysis of helices in the PDB we saw that for helices of length 26, the first two normal modes encompass most of the standard deviation (Figure 2c) but mode 10 also contributes to the overall difference from the “idealized” helix that we used as a reference (Figure 2b). Mode 10 represents a twisting deformation around the helix axis. To test if adjusting the helical pitch would improve the I-set designs, we constructed a new backbone set, the I_p-set, for which the coefficient for mode 10 was set to the native value of the Bim helix, −6.13. Using this new set, we repeated the design calculations and selected sequences with energy lower than wild-type, giving a total of 249 designed peptides. These sequences were filtered by removing those with helix propensity less favorable than wild type (6 sequences removed), and the 50 lowest-energy sequences remaining were clustered along with the other backbone sets, as shown in Figure 8. As with the I-set, the I_p-set designs clustered together, although they were somewhat more similar to the N-set and X-set sequences. Four sequences were chosen for testing by dividing the I_p-set cluster using the dashed yellow line shown in Figure 8. Figure 6 shows that I_p1 bound Bcl-x_L quite well, I_p4 more weakly, and I_p2 and I_p3 not very much at all. These peptides were also tested against Mcl-1 and Bcl-w; none showed any binding.

Because the N-set designs bound better than the I-set designs, we considered more of these sequences in our next round of experimental tests. We originally chose N1 and N2 from separate clusters, as seen in Figure 8, but ignored a third clustering of N-set peptides, because it contained slightly higher energy sequences. We selected two sequences from this cluster, N3 and N4 as shown in Figure 8, and found that both bound well to the Bcl-x_L receptor. The binding affinity of these two sequences was also tested against the three other Bcl-2 receptors. N4 showed very weak binding, whereas N3 showed no binding to Bcl-w. Neither of them showed binding to Mcl-1 or Bcl-x_L-G138E. Overall, 12 out of 17 designs considered in this study, which contained from one to eight mutations relative to Bim, showed some level of binding to the Bcl-x_L receptor.

Competition binding experiments

To further characterize the binding of several designed peptides, we tested them in a fluorescence polarization competition assay. Bad-BH3 is a native BH3 peptide that binds in the hydrophobic groove of Bcl-x_L, as determined by previous binding studies and by a solution structure of the complex.²⁵ In our assay, fluoresceinated Bad-BH3 (FITC-Bad) with a reported K_d of 21.48 nM⁵⁵ was competed off of Bcl-x_L by increasing concentrations of Bim, X1, N4 or Ip1. The Bcl-x_L construct used in our assay was slightly different from what was reported, and we measured the K_d of FITC-Bad as 16.7 nM (inset in Figure 9). This values was used to fit the competition binding curves, shown in Figure 9. The K_d values obtained from duplicate experiments were: K_d(Bim)=0.1–0.8 nM, K_d(X1)=9.4–22.4 nM, K_d(N4)=233.1–239.7 nM and K_d(I_p1)=47.7–73.8 nM.

Figure 9.

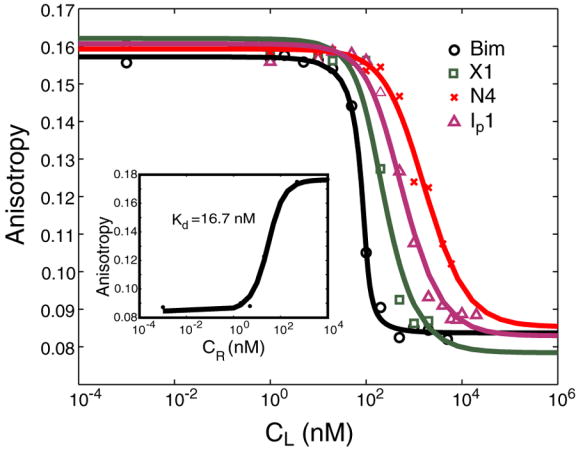
Competition binding curves from fluorescence polarization assay. The assay was done at room temperature with murine Bcl-x_L at 100 nM and FITC-Bad at 25 nM. Competing peptides MBM, X1, N4 and Ip1 are shown in black, green, red and purple, respectively. The lines are binding curves fit to the data points. C_L is the initial concentration of the competitor peptide. The inset shows the direct binding of FITC-Bad to murine Bcl-x_L (K_d = 16.7 nM). Here C_R is the initial concentration of Bcl-x_L. The K_d values of the competing peptides (MBM, X1, N4, and Ip1) were derived using our measured K_d (Bad/Bcl-x_L). Competition binding measurements were done in duplicate and gave the following ranges of K_d values: K_d(Bim)=0.1–0.8 nM, K_d(X1)=9.4–22.4 nM, K_d(N4)=233.1–239.7 nM, K_d(I_p1)=47.7–73.8 nM.

Discussion

Previous studies aimed at designing protein-protein interactions have focused primarily on identifying one or a few high-affinity, specific complexes, usually by re-engineering the sequence of both binding partners.^5–7,17,18 There are only a small number of examples in which a protein or peptide has successfully been designed to bind a native target.^8–10 Here, we report the successful design of several new 26-residue peptides that bind to Bcl-x_L. The designs exploited a new method for sampling backbone flexibility using NM analysis. In three rounds of computation and experimental testing, we gained insights into features of the BH3 sequences that are and are not important for binding. We also uncovered important considerations for sampling helical backbone structures. In this section we discuss these issues, as well as the general importance of including backbone flexibility in protein design and some possible areas for future improvements.

Backbone Templates

Carefully selected backbone structures are key for structure-based computational design.¹⁶ Although native backbone structures determined by x-ray crystallography have been successfully used in many cases, they have obvious limitations. One is that sequences designed on a fixed native backbone are strongly biased by the exact atomic coordinates of the selected structure, as shown in Figure 5 and Figure 8. However, fixed backbone design has been successful partly because starting with an x-ray crystal structure guarantees that the template is designable. When flexible or de novo backbones are used, additional criteria are needed to select a designable scaffold. Our goal in this study was to increase the sequence space that could be accessed in protein design by introducing backbone flexibility in a way that sampled realistic structures. NM analysis has been shown to be effective for describing structural deformations of helices,⁴⁶ and we found that this was also a convenient way to generate structural variants for design. We used this approach to identify a wide range of candidate BH3 ligands for Bcl-x_L.

From our initial round of design, only two of the five peptides that we tested bound to Bcl-x_L. The two that bound were designed from the native-like N-set, and those that did not bind were from the I-set. Additionally, we were able to design binding peptides using the crystal structure as a template. This suggested that the I-set did not provide good templates. The I-set structures were derived de novo from an idealized helix backbone using only the two lowest-frequency normal modes to generate structural variation. However, these two modes capture less than half of the deviation between our reference helix and α-helices in the PDB. For helices of length 26, ~70% of the deformation from the ideal helix can be captured by modes 1, 2 and 10, with mode 10 corresponding to changing the pitch of the helix. The contribution of mode 10 to helices of length 26 is approximately constant (Figure 2b and c) and indicates that the pitch of our “ideal” helix is larger than what is found in the PDB. Consistent with this, we found that when we minimized the I-set helices as part of the design procedure, the value of mode 10 changed to be closer to the average value in the PDB. We postulated that modifying the I-set structures to reflect the native value of mode 10 in the Bcl-x_L/Bim structure could improve the quality of the templates. A new I_p-set was used to design four peptides and resulted in two that did bind Bcl-x_L. This suggests that using an ‘ideal’ helix to construct a new backbone set can be an effective strategy, as long as the pitch is set appropriately.

The I-set sequences that we chose for experimental characterization were scored as low in energy by our design procedure, yet they failed to bind Bcl-x_L. This occurred despite the fact that for the native sequence we were able to distinguish I-set backbone models as higher in energy than N-set models (Figure 3). We were also able to relax the I-set backbones towards more native-like structures in the Monte Carlo design procedure. That our energy function was reasonably effective for prediction but showed deficiencies in design is not necessarily surprising. For example, if van der Waals, electrostatic interactions and φ and ϕ dihedral strain are not balanced, it is possible that the design procedure could systematically exploit this to introduce unrealistic interactions that compensate for poor backbone geometry (e.g. see below). Choosing a backbone set, such as the N-set, that samples more realistic structures can help to address this. It is interesting to note that the choice of energy function and the method for varying backbone structure may be linked; shortcomings in one can be partially compensated for by adjustments in the other.

Although we successfully introduced flexibility in the binding BH3 helix, the Bcl-x_L receptor was held fixed. It is clear from available NMR and X-ray structures of Bcl-x_L bound to BH3 peptides ^{24–26,38,56}, as well as to small molecules ^37,57, that there is some variability in the structure of α-helices 3 and 4, which form part of the binding site. This is another degree of freedom that could be sampled to further increase the design diversity. Although normal mode analysis may not be an efficient way to sample the irregular structural changes involved in this region, one strategy could be to use existing experimental structures as a guide. Qian et. al. have shown that principle component analysis can be used to efficiently sample natural variation, when this is represented by a set of existing structures.⁵⁸ With several Bcl-x_L complex structures available,^26,38 and more likely to be solved in the future, this represents a possible route towards designing yet more diverse BH3 peptide ligands.

Analysis of designed BH3 sequences

Native BH3 peptides are quite diverse and have only a weak consensus: ------h{A/G}--L--h{G/A}D-h----------, where “h” represents a hydrophobic residue, {x/y} indicates that residues x and y are commonly found at a given site, and “-“ indicates no strong consensus. Leu 11 and Asp 16 are the most strongly conserved residues and are present in all native BH3 peptides that are known to bind Bcl-x_L. Our first round of design calculations (using SCADS only) indicated that despite being strongly conserved, Leu 11 and Asp 16 are not strongly favored at their respective positions once backbone flexibility is considered. Slight backbone motions can accommodate the larger Phe residue at position 11 (see Figure 10), and several backbones favor Lys over Asp at position 16. Experiments confirmed that the dramatic sequence changes of Leu to Phe at position 11 and Asp to Lys at position 16, do not disrupt binding of Bim to Bcl-x_L. Thus, these residues are probably conserved for some reason other than maintaining binding affinity to this target.

Figure 10.

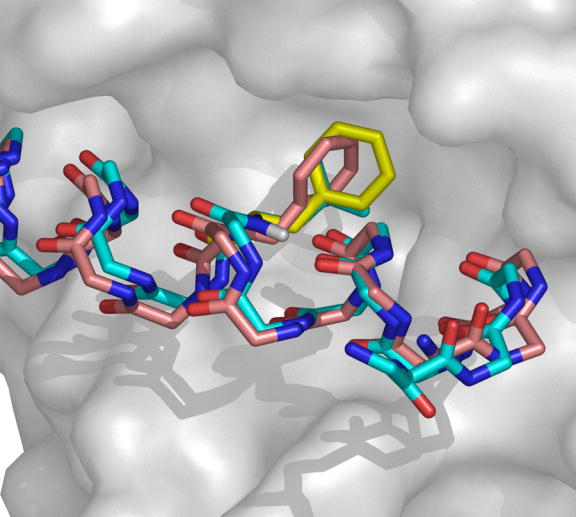
Slight backbone changes are sufficient to accommodate the Leu to Phe mutation at position 11 of Bim. Bcl-x_L is shown as a surface representation colored in gray. BH3 backbones and the side chains at position 11 are shown using sticks. The native BH3 backbone and Leu 11 side chain are shown in cyan. The L11F mutant side chain modeled on the native backbone is shown in yellow. The L11F backbone and side chain designed on an N-set normal mode-generated backbone are shown in pink. Figure generated using Pymol.

Two other sequence changes suggested by the designs also contradicted the consensus sequence. These were the designs of a Val or Ile residue at position 8, a site normally occupied by Ala or Gly. Peptides I1 and I3 with these substitutions were designed using the I-set backbones and, when tested experimentally, failed to bind Bcl-x_L. A point mutation of Ile 8 to Ala in design I3 restored binding. Thus, it seems that a small residue at position 8 is probably a requirement for binding Bcl-x_L. Our energy function indicated that Ile or Val at this site could form favorable interactions with the receptor, but only in the context of the I-set backbones. Such β-branched residues could not be accommodated at this site using the N- or X-sets, and only four of the top 50 I_p-sets sequences have valine. Our energy function did not correctly balance the reward of a favorable van der Waals interaction with a suitable penalty for the I-set backbones having an inappropriate pitch. We addressed this by introducing the I_p set, restricting our backbone search to more realistic structures.

In total, our 12 BH3 designs spanned a significant sequence space. All designs (other than the point mutants) had 6–8 sequence changes from native Bim, out of 11 interface positions. All of the designed sequences maintained the four conserved hydrophobic residues that pack into Bcl-x_L, but the identities of these varied according to the backbone structures on which the sequences were designed. Boundary residues varied more significantly, with charged residues such as Glu 4 and Asp 16 in Bim sometimes being replaced by hydrophobic or oppositely charged residues. Such changes of residue type may be particularly important for designing BH3 ligands with altered binding specificity (see below).

Backbone flexibility for specificity design

In signaling pathways leading to apoptosis, the binding specificity of native BH3 peptides for multi-domain anti-apoptotic Bcl-2 family members is a key factor in triggering cell death.^29–31 In particular, it is important whether BH3 peptides bind to all or to only a subset of the anti-apoptotic proteins. It would be useful to design synthetic peptides with desired binding specificity profiles, e.g. peptides that bind to Bcl-x_L but not Bcl-w or Mcl-1, in order to understand and manipulate the interactions of these proteins. If crystal structures of multiple Bcl-2 family complexes were available, it might be possible to engineer specificity profiles directly, using a multi-state design procedure (however, see below). But structural data for Bcl-2 family complexes is scant, and such an approach is currently not an option. With only the x-ray structure of Bcl-x_L/Bim to use as a template (we have found that available NMR structures do not give good results in repacking calculations), our ability to design novel specificity profiles is hindered by a strong bias that causes designed sequences to resemble native Bim in core positions, and have low sequence diversity in all design sites. Including multiple backbones can counteract this structural bias and provide access to a larger sequence space, a space that potentially includes sequences with novel specificity profiles, as illustrated in Figure 6.

Our results support this idea. Native Bim is promiscuous and binds to all anti-apoptotic Bcl-2 family members, including Bcl-x_L, Mcl-1 and Bcl-w (Figure 6). The two designed point mutants, BimL11F and BimD16K, which are similar in sequence to native Bim, both bound Bcl-w. BimL11F also bound Mcl-1, whereas BimD16K bound Mcl-1 very weakly. In contrast, when 11 positions were redesigned on a range of backbones, only one sequence designed from the crystal backbone (X1) bound Bcl-w, and one from a native-like backbone (N4) bound Bcl-w very weakly. None of the designed sequences show detectable binding with Mcl-1.

In the future, it may be possible to use additional crystal structures to select directly for sequences that bind to certain anti-apoptotic Bcl-2 family members but not others. In such an application, the ability to model backbone flexibility will remain very important. First, with increasing demands on the designed sequences, artificial constraints on the space of possible solutions become less acceptable. Furthermore, backbone flexibility is a critical element of negative design against undesired “decoy” targets. A common problem in negative design is that decoy states must be modeled and their energies accurately evaluated. With fixed backbone design, this is problematic because structures may have high energies based on slight steric clashes that are easy to resolve with backbone relaxation or flexibility. The BimL11F mutant provides a good example of this (see Figure 10). If the complex of Bcl-x_L with Bim was a negative design target, then fixed backbone design would predict that Phe at position 11 would disfavor this structure. In contrast, we find that BimL11F binds well to Bcl-x_L.

Possible directions for future improvements

In this work, we used a range of starting structures as templates for design, with the goal of generating a set of peptides with diverse properties that bind to Bcl-x_L. Practical considerations led us to constrain our search to a sequence space identified as favorable by SCADS, and to use a fairly slow non-pairwise energy function for evaluation. Thus, in an attempt to sample broadly, we have sacrificed local optimization. Although we found many good sequences, we may not have identified minima in either structure or sequence space. A possible strategy for the future is to use sequences from experimentally validated clusters as starting points for further rounds of design. Additionally, Baker and colleagues have demonstrated the power of iteratively optimizing sequence and structure.^16,43 A similar approach could help to identify tighter binding sequences in the space of NM-sampled backbones. Finally, energy functions that are suitable for fixed-backbone design may not be optimal for flexible-backbone design. Further work may be needed to determine how best to balance the internal energy of the template with the interaction energy of the designed side chains. Sampling normal modes in dihedral space rather than Cartesian space may generate backbones that better maintain ideal bond lengths and angles, while retaining suitable dihedral values. Nevertheless, the use of NM analysis focuses backbone sampling to a realistic parts of structure space very efficiently, using only 2–3 parameters. A set of realistic templates reduces the burden placed on the search and evaluation functions in design. The NM strategy can be used to sample variation of any α-helices present in a design template. Further, the use of NM analysis, which has a very general formulation, may extend well to other secondary or super-secondary structural elements.

Methods

Construction of flexible backbone structures

Starting templates

The 1.65 Å resolution structure of Bcl-x_L/Bim was used as a template (PDB code: 1PQ1).²⁶ The backbone of Bcl-x_L, chain A, was held fixed. The backbone of chain B, corresponding to Bim, was varied. An ideal α-helical backbone (φ = −57.0°, ψ = −47.0°, and Ω = 180.0°)⁵⁹ was generated using default bond lengths and bond angles from CHARMM param19.^60,61 The C, C_α and N backbone atoms of the ideal helix were aligned to chain B in the crystal structure using ProFit 2.2.⁶² The side chains were generated using param19 values for bond angles and bond lengths and the crystal-structure dihedral angles. The original x-ray structure and the structure with chain B replaced by an aligned ideal helix were both used as starting templates.

Backbone variations in normal mode space

To construct helical backbones, we used a set of NM vectors similar to those described by Emberly et al.,^46,47 with slight modifications. The C, C_α and N backbone atoms, rather than only C_α atoms, were used to compute the NM potential. In Cartesian space, the harmonic potential of a structure can be calculated using the following function described by Tirion⁶³ and later used by Tama et al.⁵⁰:

$$V=\sum _{d_{ij}^o\le R_c}k{(d_{ij}-d_{ij}^o)}^2$$ (1)

Here k is a force constant that was set to 10 for all pairs of atoms, d_ij is the distance between atoms i and j of a structure, and $d_{ij}^o$ is the reference distance between these two atoms in the ideal-helix structure. This potential does not contain values for pairs of atoms with distances larger than the cutoff of R_c. This value was set to 8 Å as suggested by Tama et al.⁵⁰ and Bahar et al.⁶⁴ From this potential the Hessian (H) can be calculated:

$$H_{i,m,j,n}=\frac{{\partial }^{2}V}{{\partial x}_{i,m}{\partial x}_{i,n}}$$ (2)

Here x_i,m is m^th Cartesian coordinate of atom i. The eigenvectors $\left\{\stackrel{\rightharpoonup }{X_i}\right\}$ of this matrix are the normal modes, and the eigenvalues are the corresponding frequencies. Modes corresponding to the six rotational and translational degrees of freedom were discarded and the remaining modes were used to sample distortions of a helix about a fixed Cartesian center. A separate set of NM vectors must be calculated for each helix of length L (number of residues). To generate a variable helix F, a set of 9L-6 NM amplitudes {a_i} was multiplied by the NM vectors and added to the ideal helix I:

$$\text{F}=\text{I}+\sum _{i=1}^{9L-6}{a}_i{\stackrel{\rightharpoonup }{X}}_i$$ (3)

Three choices of {a_i} values were used to construct backbone sets in this study. Abbreviations for, and descriptions of, these sets are summarized in Table 3. For the I-set (ideal-helix set), all values of a_i except for the two lowest frequency ones were fixed as zero, corresponding to the NM values of an ideal helix. Helices in the I_p set (ideal-helix with native pitch) were constructed in the same manner as the I-set, except that the 10^th lowest frequency normal mode, a mode corresponding to the change of the helical pitch, was set to the crystal structure value of −6.13. Finally, for the N-set (native-helix set), all a_i’s with i greater than 2 were fixed as those of the native helix. To determine the NM values of the native helix, a difference vector between the native helix and the aligned ideal helix was calculated. This vector was fit to a linear combination of NM vectors using linear regression. The fitted linear coefficients gave the {a_i} of the native helix.

Table 3.

Abbreviations and descriptions for backbone sets used in design calculations.

Set Name	Starting Structure	Modes fixed to 0	Modes fixed to Native
X-set	Native helix	None	All
I-set	Ideal helix	All except 1 and 2	none
N-set	Native helix	None	All except 1 and 2
Ip-set	Ideal helix	All except 1, 2 and 10	10

To generate a new NM structure, all atoms of the helix were removed except for the backbone C, C_α, and N. The backbone was deformed by applying a linear combination of NM vectors to the ideal helix, as described above. We chose random values for the two lowest frequency NM parameters from a Gaussian distribution approximating the mode values seen in helices in the PDB, centered on the starting values for the set. The backbone was reconstructed by regenerating H and O atoms with CHARMM param19 default parameters. The side chains were assigned CHARMM default values for bond lengths and bond angles, but crystal-structure dihedral values. Structures with backbone atoms on different chains within 3 Å were discarded. The remaining NM structures were used for design.

Design Calculation

Two types of design calculations were preformed. In the first, Statistical Computationally Assisted Design Strategy (SCADS), developed by the Saven group,^2,44,65 was used to rapidly characterize the sequence and structure space of α-helical ligands of Bcl-x_L. In the second, a two-tiered strategy was implemented to select single sequences for experimental testing. The two tier-procedure included a SCADS profile design, used to narrow the library of amino acids, followed by a single-sequence Monte Carlo design (Figure 7). In SCADS, the AMBER force field,⁶⁶ with a united atom representation, was used to calculate non-bonded interactions. A statistical environmental score (E_env) was included as a constraint to enforce the hydrophobic patterning of native proteins.⁴⁴ A tri-peptide model was used to approximate the unfolded/unbound state of the BH3 peptide.² The Richardson-Richardson rotamer library⁶⁷ was used with the χ₁ angles of Phe, Trp and Tyr expanded by ± 5° and ± 10°, increasing the total number of rotamers to 254. Bcl-x_L residues with at least one atom located within 10 Å of any atoms of the helix were allowed conformational flexibility. All other residues were held fixed with the crystal-structure coordinates. Sequence profiles, in the form of a set of amino-acid probabilities at each site, were obtained for each backbone structure. A conformational energy (E_conf) for each profile was evaluated by averaging non-bonded mean-field energies at each position, weighted by the appropriate amino-acid probabilities. E_conf consists of side chain – side chain and side chain - backbone terms and was evaluated at β=0.3 (kcal/mol)⁻¹, where β is an effective inverse temperature.

The second tier of design utilized a Monte Carlo strategy. Here a subset of amino acids was chosen based upon SCADS sequence profiles. For each site, the number of amino acids included in the design was determined by the site-specific sequence entropy S_i.

$$S_i=\sum _{{\alpha }_i}{p}_{i,{\alpha }_i}ln{p}_{i,{\alpha }_i}$$ (4)

Here p_i,_αii is the probability of a particular amino acid α_i at site i derived from the SCADS calculation. The probabilities were rescaled from the original β=0.3 calculation to β=1.0 to limit the sequence search to high probability amino acids. The top n_i ( n_i = exp(S_i ) ) most probable amino acids were included in the design at each site (n_i was rounded up to the nearest integer). Using this limited amino-acid library, 10 independent runs of 500 steps of Monte Carlo design were performed for each structure. For each Monte Carlo design step in sequence space, we performed a repacking calculation to model the side-chain conformations, followed by an energy evaluation step to guide the Metropolis sampling. Structures were repacked as described by Ali et al.,¹⁷ with a few modifications. The energy function included CHARMM van der Waals energy with the atomic radii scaled to 90%, EEF1⁶⁸ for solvation, distance dependent dielectric electrostatics with ε=4r, and CHARMM torsional energies. The same rotamer library as for the SCADS calculation was used. All helix residues and all receptor residues within 8 Å of the helix were allowed conformational flexibility. All other residues were held fixed with the crystal structure coordinates. Sequence repacking was performed using Dead-End Elimination (DEE) and the A* algorithm.^69–74 Following repacking, we minimized the structure using CHARMM with 1000 steps of steepest-decent minimization and 1000 steps of adapted bases Newton-Raphson. The energy function for minimization included the van der Waals energy with 100% van der Waals radii, bond angle, bond length, dihedral angle and improper dihedral angle molecular mechanics energies, and ε=r distance dependent dielectric electrostatic interaction energy. The receptor backbone atoms were fixed during minimization. Finally, a non-pairwise decomposable energy function was used to evaluate the energy of the minimized structures. This energy was used to guide the Monte Carlo search. It included terms for van der Waals interactions with 100% van der Waals radii, finite-difference Poisson-Boltzmann (FDPB) solvation energy, Coulombic electrostatic interactions with external and internal dielectric of 4, and a solvent-accessible surface area cavitation energy with a proportionality constant of 10 cal/mol·Å². The van der Waals and Columbic energy terms were evaluated using CHARMM and the FDPB calculations using DelPhi V.4;^75,76 the surface area was calculated using NACCESS.⁷⁷

In accord with experimental observation,²⁵ we modeled the unfolding pathway as a transition from the bound complex (R-H) to an isolated receptor (R) and a random coil (RC). The energy of this transition can be described as follows.

$$\mathrm{\Delta }{E}_{\mathit{total}}=E_{R-H}-(E_{RC}+E_R)$$ (5)

The energy of the isolated receptor is the same for all design calculations and can be ignored. It is difficult to evaluate the energy of a random coil, but the contribution of an amino acid to the transition from a random coil to a folded helix can be captured using experimentally determined helix propensities. Helix propensities are reasonably context independent, with good agreement found between measurements made in different environments.^78,79 Consequently we define $E_{H_i^{\ast }}$ as the self energy of a single amino-acid side chain i in the context of a poly-alanine peptide, and write:

$$\sum _i{HP}_i\approx \sum _i{E}_{H_i^{\ast }}-E_{RC}$$ (6)

HP_i are helix propensities as measured by O’Neil and Degrado⁵³ and $E_{H_i^{\ast }}$ was calculated using the same repacking, minimization and energy evaluation described above. Given our original folding equation, we can add and subtract $\sum _i{E}_{H_i^{\ast }}$ giving

$$\mathrm{\Delta }{E}_{\mathit{Tot}}=(E_{R-H}-{\sum }_i{E}_{H_i^{\ast }})+({\sum }_i{E}_{H_i^{\ast }}-E_{RC})$$ (7)

or

$$\mathrm{\Delta }{E}_{\mathit{Tot}}=(E_{R-H}-\sum _i{E}_{H_i^{\ast }})+{\sum }_i{HP}_i$$ (8)

E_R-H was calculated explicitly as the energy of the complex. ΔE_tot is the energy used in the MC design procedure.

Selection of the design positions

Although there are 33 residues in the B chain of Bcl-x_L/Bim structure 1PQ1,²⁶ some residues at the N- and C- termini do not make direct contact with the receptor protein. In the design calculations, we considered residues 2 to 27, and re-numbered these as 1 to 26. In an initial set of SCADS calculations, all twenty-six residues from chain B were designed and allowed to be any amino acid. When designing individual sequences with our two-tier procedure, only residues at the binding interface were re-designed. The binding interface was defined based on solvent-accessible surface area (SASA) calculated by NACCESS,⁷⁷ followed by manual inspection. Design positions for these calculations, and residues allowed at each position, are given in Table 1.

Characterization of sequence space

Comparing sequence profiles

A sequence profile can be either a set of site-specific probabilities, such as those obtained from multiple sequence alignment, a SCADS design calculation, or a single sequence, which is equivalent to a profile with all site-specific probabilities either 1 or 0. The sequence similarity score defined by Panchenko et al.⁸⁰ (ΔSS) was used to compare pairs of sequence profiles (p1 and p2):

$$\mathrm{\Delta }SS=SS-\overline{SS}$$ (9)

where SS is a raw pair-wise similarity score, and $\overline{SS}$ is a reference sequence score.⁸⁰ Only sequences with the same chain length (L) were studied in this work. SS and $\overline{SS}$ were calculated with the following equations:

$$SS=\frac{1}{L}\sum _{i=1}^L\mathit{score}(p_{1,i},p_{2,i})$$ (10)

$$\overline{SS}=\frac{1}{L^2}\sum _{i=1}^L\sum _{j=1}^L\mathit{score}(p_{1,i},p_{2,j})$$ (11)

with score( p_1,i, p_{2, j} ) characterizing the sequence similarity between profile 1 (p1) at position i and profile 2 (p2) at position j. The BLOSUM62 substitution matrix (M) was used to evaluate the similarity of any pair of amino-acid residues (α_p1,i and α_p2,j):

$$\mathit{score}(p_{1,i},p_{2,j})=\sum _{{\alpha }_{p1,j}=1}^{20}\sum _{{\alpha }_{p2,j}=1}^{20}P({\alpha }_{p1,i})P({\alpha }_{p2,j})M({\alpha }_{p1,i},{\alpha }_{p2,j})$$ (12)

Sequence clusters

X-cluster⁵¹ was used to cluster sequence profiles by their sequence similarity scores. The k-mean algorithm was used to find the clusters. Up to ten clusters were defined for all pairs of profiles. Clustal-X⁵⁴ was used to cluster single sequences. Only the eleven interface residues listed in Table 1 were used in the clustering calculations.

Experimental methods

Sample preparation

Twenty-six-residue peptide ligands (BH3 peptides) were constructed using gene synthesis. Oligonucleotides were designed using DNAWorks 3.0⁸¹, with 5′ BamHI and 3′ NotI restriction sites and ordered from IDT. Standard PCR conditions were used to synthesize genes, using temperatures suggested by DNAWorks. The PCR reaction products were cloned into a modified pDEST17 vector, containing an N-terminal His₆ tag, a tobacco etch virus (TEV) cleavage site and a C-terminal flag tag, giving the sequence: SYY-HHHHHH-LESTSLYKKAGSGS-ENLYFQ-GGS-BH3-GGR-DYKDDDDK. Peptides were expressed in E. coli RP3098 or BL21 cell. The expressed peptides were purified by Ni-NTA affinity chromatography followed by HPLC to greater than 99% purity. The molecular weights of the purified peptides were confirmed by mass spectrometry and were accurate to within 1% of the expected molecular weight.

Murine Bcl-x_L (provided by G. Nunez, University of Michigan), residues 1–209, which excludes the C-terminal transmembrane domain, was sub-cloned by PCR with 5′ BglII and 3′ XhoI sites. The fragment was ligated into a modified pDEST17 vector, containing an N-terminal His₆ tag followed by a TEV protease cleavage site, using BamHI and XhoI sites. The protein was expressed in BL21-pLysS cells. The protein was purified by Ni-affinity chromatography (Ni-NTA agarose) under native conditions, followed by ion-exchange chromatography using Q sepharose.

The human Bcl-x_L negative control construct was generated by PCR amplification of two halves of the Bcl-x_L gene, 1–138 and 138–209, mutating residue 138 from Gly (5′-GGT-3′) to Glu (5′-GAG-3′). The two halves were combined by overlapping extension with end primers containing 5′ BglII and 3′ XhoI sites. The Bcl-x_L G138E mutant DNA was ligated into pSV282 (using 5′ BamHI and 3′ Xho), a vector containing an N-terminal His-tagged MBP (maltose binding protein) followed by a TEV protease cleavage site. Human Mcl-1 was subcloned, removing the N-terminal PEST domain and C-terminal transmembrane domain. Residues 166–327 were PCR amplified with 5′ BamHI and 3′ XhoI sites and ligated into pSV282. Human Bcl-w, residues 1–176, was cloned into pSV282 following the same protocol as for Mcl-1. The human clones of Bcl-x_L and Mcl-1 were obtained from J. Kramer, Harvard Institute of Proteomics. The cDNA of human Bcl-w was provided by D. Huang at WEHI in Australia. The pSV282 vector was provided by L. Mizoue at Vanderbilt University, Center for Structural Biology.

The human Bcl-x_L negative control, Mcl-1 and Bcl-w were expressed in BL21 pLysS and purified by Ni-affinity chromatography under native conditions. Ni-purified proteins were cleaved with TEV protease (~1 μM) in a buffer containing 50 mM Tris, 50 mM NaCl, 0.5 mM EDTA at pH 8.0 for 2.5 hours at room temperature. The untagged TEV cleavage product was purified by Ni-affinity chromatography, separating it from His-tagged MBP and TEV. The Bcl-x_L and Mcl-1 proteins were further purified by gel filtration chromatography with an S75 column. The Bcl-w protein was purified on a Q sepharose column.

Solution pull-down assay

All pull-down experiments were conducted in TBS buffer (150 mM NaCl, 50 mM Tris, pH=7.4) containing 0.1% Triton X-100 using 200 μM of the receptor proteins and 12 μg/ml of the peptides. Mixtures of the receptor proteins and BH3 peptides were incubated at 4 °C on a rocker for one hour before a fixed amount of α-flag beads (Sigma) was added. The protein and bead solutions were incubated at 4 °C on a rocker for another 30 minutes. Washes and elutions were done following the manufacturer’s protocol. Elution fractions were analyzed on polyacrylamide gels stained with Coomassie dye.

Fluorescence polarization assay

Fluoreseinated-Bad (FITC-Bad, Abbott) ⁵⁵ was dissolved in DMSO at 500 nM. Bcl-x_L and the competing peptides are the same as described above. Both Bcl-x_L and the peptides were dissolved in binding buffer (20 mM phosphate buffer, pH 7.5, 50 mM NaCl, 1mM EDTA, and 0.001% triton X100). The concentration of the Bcl-x_L stock was measured at 280 nM in Edelhoch buffer.⁸² Peptide concentrations were measured directly in the binding buffer due to limited solubility.

Direct and competition binding assays were conducted at 25°C in the binding buffer as described.⁵⁵ In all samples, FITC-Bad was present at 25 nM, with 5% DMSO. In the competition binding assays, the concentration of Bcl-x_L was fixed at 100 nM. For direct binding, the samples were equilibrated for at least 30 minutes. For the competition binding, the samples were equilibrated for at least three hours. Fluorescence polarization measurements were done using a PTI QM-2000-4SE spectrofluorometer (Lawrenceville, New Jersey) with excitation wavelength of 485 nm, and emission wavelength of 517 nm. A model considering depletion of the labeled peptides was used to fit the direct binding data, and a model considering depletion of both the labeled and unlabeled peptides was used to fit the competition binding data (see supplemental material for the fitting models). The ability to determine the saturated baselines was limited by the solubility of the peptides. A single additional data point at [competition peptide] = 1 mM was added with an anisotropy value determined by averaging the values of Bim at 1000 and 2000 nM before fitting the competition curves. Experiments were done in duplicate, with one replicate shown in Figure 9 and the range of measured K_d’s given in the figure.