Artifacts in T1ρ-Weighted Imaging: Compensation for B₁ and B₀ Field Imperfections

Abstract

The origin of spin locking image artifacts in the presence of B₀ and B₁ magnetic field imperfections is shown theoretically using the Bloch equations and experimentally at low (ω₁ ≪ Δω₀), intermediate (ω₁ ~ Δω₀) and high (ω₁ ≫ Δω₀) spin locking field strengths. At low spin locking fields, the magnetization is shown to oscillate about an effective field in the rotating frame causing signature banding artifacts in the image. At high spin lock fields, the effect of the resonance offset Δω₀ is quenched, but imperfections in the flip angle cause oscillations about the ω₁ field. A new pulse sequence is presented that consists of an integrated spin echo and spin lock experiment followed by magnetization storage along the -z-axis. It is shown that this sequence almost entirely eliminates banding artifacts from both types of field inhomogeneities at all spin locking field strengths. The sequence was used to obtain artifact free images of agarose in inhomogeneous B₀ and B₁ fields, off-resonance spins in fat and in vivo human brain images at 3T. The new pulse sequence can be used to probe very low frequency (0–400 Hz) dynamic and static interactions in tissues without contaminating B₀ and B₁ field artifacts.

1. Introduction

Magnetic resonance (MR) tissue contrast depends on differences in tissue relaxation times T1 and T2, diffusion-weighting, magnetization transfer (MT) or perfusion effects to distinguish healthy and diseased tissues. In addition to these conventional contrast techniques, a powerful method to create tissue contrast is the spin-lattice relaxation time in the rotating frame (T1ρ) characterized first in spectroscopic experiments by Redfield [1].

T1ρ-weighted contrast is obtained by allowing magnetization to relax under the influence of an on-resonance, continuous wave (cw) radiofrequency (RF) pulse. T1ρ-weighted contrast is sensitive to both low frequency motional processes and static processes. Low frequency motional processes in tissues include proton exchange with hydroxyl or amide groups in proteins [2–4] while static processes include static dipolar interactions [5]. In particular, T1ρ-weighted contrast has distinguished early acute cerebral ischemia in rats [6–8], human gliomas [9] and tumor in breast tissues [10], tracked the early degeneration of cartilage in osteoarthritis [11] and the nucleus pulposus of lumbar intervertebral discs [12] and indirectly detected metabolic H₂¹⁷O in vivo [13–16].

Variations of the preparatory pulse cluster used for T1ρ-weighted imaging are listed in Table 1. Two popular implementations involve either a rotary echo [17; 18] or adiabatic excitation [10] to compensate for B₁ inhomogeneities. A degree of ΔB₀ insensitivity is achieved using offset-independent adiabatic pulses, particularly those of the HSn family, however, there are restrictions on the minimum ω_1max needed for a uniform flip angle across the sample [19]. Variations of the spin lock may also be used for low SAR acquisition by manipulating the T1ρ-weighting in k-space [20] or by spin-locking off-resonance [21; 22]. In addition, the spin locking pulse may be substituted with an adiabatic full passage pulse train to modulate T1ρ-weighted contrast dynamically during the preparation period [23].

Table 1.

Sources of artifacts in T1ρ-weighted imaging and their pulse sequence correction schemes. T1ρ clusters with adiabatic excitation and storage pulses are complementary to the four pulse sequences analyzed in this paper.

Spin Lock Sequence	Reference	B1 Insensitivity	Flip Angle (α = 90°)	ΔB0 Insensitivity	Off-resonance
Conventional
Adiabatic (ω1max ≫ Δω0)	[8]	X
Rotary Echo (B1 Insensitive)	[17]	X	X
Off-Resonance	[21, 22]	X	X		X
ΔB0 Insensitive	[25]	X		X
B1 & ΔB0 Insensitive	[this manuscript]	X	X	X

Ideally, to achieve maximum T1ρ-weighted contrast, the spin locking amplitude (ω₁ = γB₁) should coincide with the T1ρ dispersion corresponding to the physical process involved, although, in practice, possible spin lock amplitudes are compromised by B₀ field gradient artifacts and the high specific absorption rate (SAR) of radiation delivered to tissues. Rotary echoes or adiabatic excitation combined with a high amplitude spin lock (ω₁ ≫ Δω₀) remove artifacts from gradients in the B₁ and B₀ field [24], however, increasing ω₁ to reduce artifacts and decreasing ω₁ to reduce SAR is a vice, limiting the acceptable spin lock amplitude on 1.5 and 3 T clinical scanners to ω₁ = 400–600 Hz to obtain a T1ρ-weighted image. Also scanners continue to increase in field strength to 7 T, there may be no range over which ω₁ is acceptable. A technique to widen the acceptable spin lock range is necessary, particularly in the low-frequency regime where useful clinical contrast is generated by the scalar coupling between ¹H and ¹⁷O in studies of brain metabolism or static dipole-dipole or ¹H exchange dynamics in human cartilage.

Here, we examine the origin of ΔB₀ and B₁ spin locking artifacts using the Bloch equations and analyze a new pulse sequence which significantly corrects for these artifacts. This sequence allows spin lock amplitudes in the ω₁ = 0–600 Hz range and is demonstrated on an agarose phantom, a water and fat phantom and in vivo in the human brain.

2. Theory

2.1 General Spin Lock

A general pulse sequence for spin locking is shown in Figure 1. In the following sections, we will analyze how the choice of phase or pulse composition in the above sequence can be used to eliminate artifacts from variations in the B₀ or B₁ fields.

Figure 1.

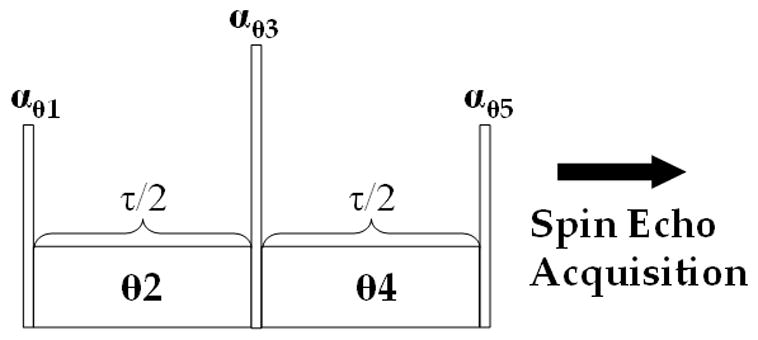
A generalized pulse sequence for T1ρ-weighted imaging. Each pulse is characterized by a flip angle α and phase θ. Spin locking pulses have both an amplitude ω₁ and phase θ. Each of the four fixed amplitude spin lock pulse sequences in Sections 2.2–2.5 are special cases of this generalized sequence.

Using the Bloch equations, we can trace the path of the magnetization vector M(r; t) = [M_x (r; t), M_y (r; t), M_z (r; t)]^T at the spatial location r = [x, y, z] and time t during the conventional spin locking pulse sequence (Fig. 1). Prior to excitation, the magnetization vector in the rotating frame is

$$\mathbf{M}(\mathbf{r};0^{-})={\left[0,0,{\mathbf{M}}_0(\mathbf{r};0^{-})\right]}^{\text{T}}$$ [1]

where M₀ denotes the equilibrium magnetization and t = 0⁻ is the time prior to excitation and ^T denotes the transpose operation. An instantaneous RF pulse may be represented compactly in matrix notation by terms like R_θ(α), where R denotes a matrix rotation, θ the pulse phase and α the pulse flip angle. Ideally, magnetization is excited by an instantaneous R_θ1(90°) (phase = θ₁) pulse in the conventional spin locking sequence, however, variations in the B₁ field may cause imperfect 90° flip angles across the sample, such that the flip angle α is instead

$$\alpha (\mathbf{r})=\gamma {\mathbf{B}}_1(\mathbf{r})\tau$$ [2]

where B₁ is the actual RF field strength. While an ideal B₁ field is uniform across the sample, e.g. B₁ (r) = B₁, the field may vary significantly in commercial systems with volume head coils.

After excitation, the magnetization is

$$\mathbf{M}(0^{+})={\mathbf{R}}_{{\theta }_1}(\alpha )\mathbf{M}(0^{-})$$ [3]

where the spatial coordinate r is dropped for simplicity. Magnetization is now spin locked by a long duration RF pulse for a time τ. Ideally, nuclear spins are on-resonance during the spin lock, but B₀ field gradients give a distribution of spins about resonance. Off-resonance magnetization is incorporated into the Bloch equations, neglecting relaxation

$$\frac{\text{d}\mathbf{M}(\text{t})}{\text{dt}}=\gamma \mathbf{M}(\text{t})\hspace{0.17em}\text{x\hspace{0.17em}}\mathbf{B}(\text{t})$$ [4]

where the effective magnetic field in the rotating frame is

$$\mathbf{B}(\text{t})={\left[{\text{B}}_{1}cos{\theta }_2,{\text{B}}_{1}sin{\theta }_2,{\text{B}}_0-\frac{\omega }{\gamma }\right]}^{\text{T}}$$ [5]

Here, ωis frequency of the rotating frame coordinate system chosen to coincide with the RF pulse carrier frequency ω_RF, ω₀ = γB₀ is the spin Larmor frequency, θ₂ is the phase of the spin locking pulse and we assume ω₁ ≪ ω₀. Of course, on-resonance ω_RF = ω₀, but we relax this assumption in Eq. [5] because of inhomogeneity in the B₀ field. The solutions to Eq. [4] cause the net magnetization to nutate about the axis of the effective field z′, which makes an angle with the z-axis

$$\varphi ={tan}^{-1}(\frac{{\omega }_1}{\mathrm{\Delta }{\omega }_0})$$ [6]

where Δω₀ = ω₀ −ω_RF. In matrix notation M(t + τ) = R_z′(ω_eff τ)M(t), magnetization evolves during the spin locking pulse under the influence of the effective field

$$\mid {\omega }_{\text{eff}}\mid =\sqrt{{\omega }_1^2+\mathrm{\Delta }{\omega }_0^2}$$ [7]

by the off-resonance pulse propagator R_z′ (ω_eff τ). The nutation of the magnetization vector around the effective field is described by transformation to the tilted rotating frame

$${\mathbf{R}}_{{\text{z}}^{″}}({\omega }_{\text{eff}}\tau )={\mathbf{R}}_{{\theta }_2}(\varphi ){\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau ){\mathbf{R}}_{{\theta }_2}(-\varphi )$$ [8]

Magnetization is now flipped by another instantaneous pulse R_θ3 (α₂) after which it is spin locked by another cw pulse with phase θ₄ and instantaneously flipped one last time. The final magnetization after this series of rotations and spin locks is

$$\begin{array}{l}\mathbf{M}({\tau }^{+})={\mathbf{R}}_{{\theta }_5}({\alpha }_3){\mathbf{R}}_{{\theta }_4}(\varphi ){\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{{\theta }_4}(-\varphi ){\mathbf{R}}_{{\theta }_3}({\alpha }_2)\dots \\ {\mathbf{R}}_{{\theta }_2}(\varphi ){\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{{\theta }_2}(-\varphi ){\mathbf{R}}_{{\theta }_1}({\alpha }_1)\mathbf{M}(0^{-})\end{array}$$ [9]

It is possible to further generalize Eq. [9] by making the first and second cw durations and amplitudes inequivalent, however, we will instead simplify to examine special cases of Eq. [9].

2.2 Conventional Spin Lock: 90_x-τ_y-90_−x

The conventional spin lock pulse cluster is sensitive to variations in both the B₀ and B₁ magnetic fields. While the conventional spin lock is in regular use in spectroscopy, it is replaced by adiabatic and rotary echo methods at spin lock amplitudes ω₁ ≫ Δω₀ in MR imaging.

For conventional spin locking, Eq.[9] reduces to

$$\mathbf{M}({\tau }^{+})={\mathbf{R}}_{-\text{x}}(\alpha ){\mathbf{R}}_{\text{y}}(\varphi ){\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{y}}(-\varphi ){\mathbf{R}}_{\text{x}}(\alpha )\mathbf{M}(0^{-})$$ [10]

After excitation, the magnetization is

$$\mathbf{M}(0^{-})=\left[\begin{array}{c}0\\ {\text{M}}_{0}sin\alpha \\ {\text{M}}_{0}cos\alpha \end{array}\right]$$ [11]

After the full spin locking duration τ, the magnetization is

$$\begin{array}{l}\mathbf{M}({\tau }^{-})=\left[\begin{array}{ccc}1& \hspace{0.17em}& \hspace{0.17em}\\ \hspace{0.17em}& cos(\varphi )& sin(\varphi )\\ \hspace{0.17em}& -sin(\varphi )& cos(\varphi )\end{array}\right]\left[\begin{array}{ccc}cos({\omega }_{\text{eff}}\tau )& sin({\omega }_{\text{eff}}\tau )& \hspace{0.17em}\\ -sin({\omega }_{\text{eff}}\tau )& cos({\omega }_{\text{eff}}\tau )& \hspace{0.17em}\\ \hspace{0.17em}& \hspace{0.17em}& 1\end{array}\right]\\ \left[\begin{array}{ccc}1& \hspace{0.17em}& \hspace{0.17em}\\ \hspace{0.17em}& cos(\varphi )& -sin(\varphi )\\ \hspace{0.17em}& sin(\varphi )& cos(\varphi )\end{array}\right]\left[\begin{array}{c}0\\ {\text{M}}_{0}sin\alpha \\ {\text{M}}_{0}cos\alpha \end{array}\right]\end{array}$$ [12]

Finally, the T1ρ-weighted magnetization is stored longitudinally with a final α_−x pulse, where, including inhomogeneity in the RF field

$$\mathbf{M}({\tau }^{+})=\left[\begin{array}{c}{\mathbf{M}}_{\text{x}}({\tau }^{-})\\ -{\mathbf{M}}_{\text{y}}({\tau }^{-})sin\alpha \\ {\mathbf{M}}_{\text{z}}({\tau }^{-})cos\alpha \end{array}\right]$$ [13]

A spoiler gradient eliminates the residual transverse magnetization, so the final longitudinal magnetization

$${\mathbf{M}}_{\text{z}}({\tau }^{+})={\text{M}}_0[cos({\omega }_{\text{eff}}\tau )sin(-\alpha +\varphi )sin(\alpha +\varphi )+cos(-\alpha +\varphi )(cos\alpha +\varphi )]$$ [14]

whereα, ω_eff and ϕ are functions of r. If the B₁ field strength is much greater than the resonance offset (ω₁ ≫ Δω), then the angle ϕ between z′ and z is nearly 90°. This amounts to a 90° phase shift of angular terms in Eq. [14], so

$$({\omega }_1\gg \mathrm{\Delta }{\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{M}}_{\text{z}}(\mathbf{r};{\tau }^{+})={\text{M}}_0[cos({\omega }_1\tau ){cos}^2(\alpha )-{sin}^2(\alpha )]$$ [15]

When α is not 90°, there is a cosinusoidal ω₁ τ dependence to the magnetization. These artifacts appear as oscillating regions of signal intensity arranged along the gradients of the B₁ field. We show this special case in Figure 2A.

Figure 2.

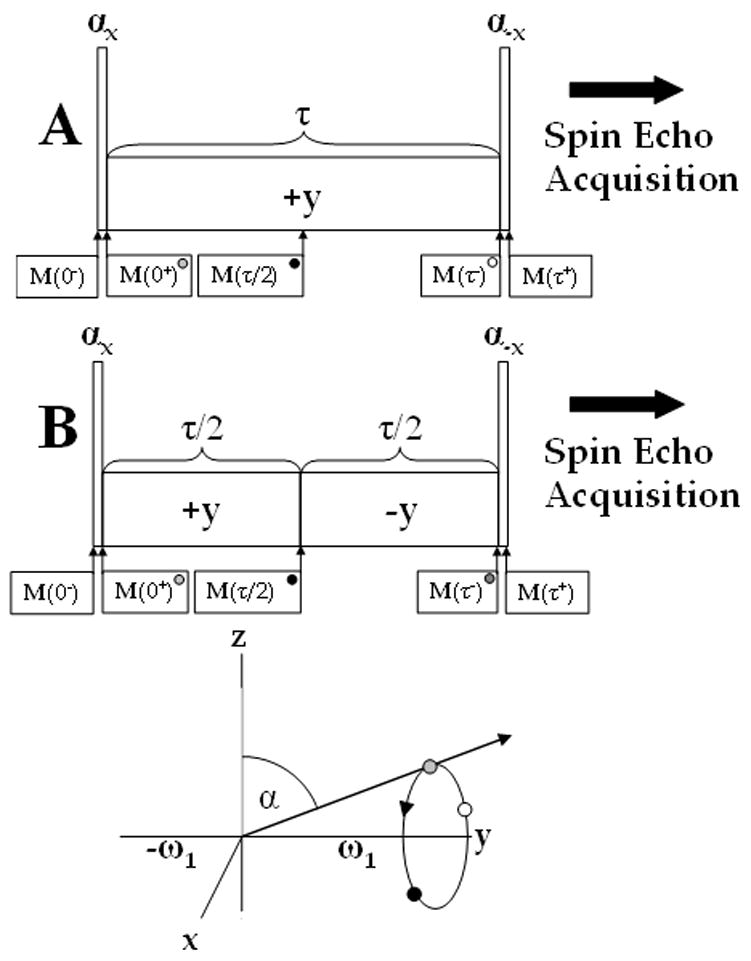
Conventional (A) and rotary echo (B) composite pulses for T1ρ relaxation measurements and the magnetization path during on-resonance spin locking pulse. Magnetization flipped at an angle α with the y-axis (grey) nutates about the ω₁ or y-axis and at τ/2 accumulates a phase ω_eff τ/2 (black). While the traditional pulse sequence continues accumulating phase in the same direction (white), the rotary echo returns the magnetization back to its initial position (grey).

Conversely, if ω₁ ≪ Δω₀, then the angle ϕ between z′ and z is nearly 0° and

$$({\omega }_1\ll \mathrm{\Delta }{\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{M}}_{\text{z}}(\mathbf{r};{\tau }^{+})={\text{M}}_0[-cos(\mathrm{\Delta }\omega \tau ){sin}^2(\alpha )+{cos}^2(\alpha )]$$ [16]

When α is 90°, T1ρ-weighted images are contaminated with artifacts due to gradients in the B₀ field because of the first term in Eq. [16].

2.3 B₁ Insensitive Spin Lock: 90_x-τ/2_y-τ/2_−y-90_−x

The B₁ insensitive spin lock applies Solomon’s rotary echo to imaging pulse sequences [24]. Charagundla, et al. implemented the rotary echo to remove the signal dependence of the variation in the B₁ field [17]. Instead of a single, long duration spin lock, the pulse is separated into two equal duration pulses with opposite phase ±y and Eq. [9] is reduced to

$$\mathbf{M}({\tau }^{+})={\mathbf{R}}_{-\text{x}}(\alpha ){\mathbf{R}}_{\text{x}}(\varphi ){\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{x}}(-\varphi ){\mathbf{R}}_{\text{x}}(\varphi ){\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{x}}(-\varphi ){\mathbf{R}}_{\text{x}}(\alpha )\mathbf{M}(0^{-})$$ [17]

During the second τ/2 spin locking pulse, the effective field angle

$$-\varphi ={tan}^{-1}(\frac{-{\omega }_1}{\mathrm{\Delta }\omega })$$ [18]

is rotated in the opposite sense about the z-axis.

The full expression for the longitudinal magnetization is extensive and is more easily implemented in matrix form as Eq. [17], however, in the limit ω₁ ≫ Δω₀, ϕ = 90° and Eq. [17] becomes

$$({\omega }_1\gg \mathrm{\Delta }{\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{M}({\tau }^{+})={\mathbf{R}}_{-\text{x}}(\alpha ){\mathbf{R}}_{-\text{y}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{y}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{x}}(\alpha )\mathbf{M}(0^{-})$$ [19]

Which, because R_−yR_y = and R_x(α)R_x(−α) = may be simplified to

$$({\omega }_1\gg {\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{M}({\tau }^{+})=\mathbf{M}(0^{-})$$ [20]

where the direction of the effective field is entirely along +y for the first τ period and along −y for the second. The signal at M(τ⁺) no longer depends on cos(ω₁τ) or α and so the image is free of banding artifacts inherent to the conventional spin lock. The B₁ insensitive pulse cluster is ideal for situations where the B₁ field greatly exceeds the resonance offset (see Figure 2B).

On the other hand, if ω₁ ≪ Δω₀, Eq. [17] may be reduced to

$$\mathbf{M}({\tau }^{+})={\mathbf{R}}_{\text{x}}(\alpha ){\mathbf{R}}_{\text{z}}(\mathrm{\Delta }\omega \tau ){\mathbf{R}}_{\text{x}}(-\alpha )\text{M}(0^{-})$$ [21]

and the T1ρ-weighted longitudinal component is the same as the conventional spin lock (Eq. [16]).

2.4 ΔB₀ Insensitive Spin Lock: 90_x-τ/2_y-180_y-τ/2_−y-90_−x

Avison, et al. introduced a spin locking pulse cluster which compensates for gradients in the B₀ field, but does not eliminate artifacts from imperfect flip angles α ≠ 90° (Figure 2A) [25]. With a 2α (ideally, 2α = 180°) pulse between the spin locking pulse clusters Eq. [9] reduces to

$$\begin{array}{l}\mathbf{M}({\tau }^{+})={\mathbf{R}}_{\text{x}}(\alpha ){\mathbf{R}}_{\text{x}}(\varphi ){\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{x}}(-\varphi ){\mathbf{R}}_{\text{y}}(2\alpha ){\mathbf{R}}_{\text{x}}(-\varphi )\dots \\ {\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{x}}(\varphi ){\mathbf{R}}_{\text{x}}(-\alpha )\mathbf{M}(0^{-})\end{array}$$ [22]

If ω₁ ≫ Δω₀, ϕ = 90°, and Eq. [22] becomes

$$({\omega }_1\gg {\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{M}({\tau }^{+})={\mathbf{R}}_{-\text{x}}(\alpha ){\mathbf{R}}_{-\text{y}}({\omega }_1\tau /2){\mathbf{R}}_{\text{y}}({\omega }_1\tau /2){\mathbf{R}}_{\text{x}}(\alpha )\mathbf{M}(0^{-})$$ [23]

If the initial flip angle α = 90°, then the magnetization is entirely along +y during both spin lock periods, R_y(2α) has no effect on the magnetization directed along +y and the result is Eq. [20]. Allowing for B₁ imperfections, α ≠ 90° and the final longitudinal magnetization

$$({\omega }_1\gg \mathrm{\Delta }{\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{M}}_{\text{z}}({\tau }^{+})={\text{M}}_0[{sin}^2(\alpha )+{cos}^2(\alpha )cos(2\alpha )]$$ [24]

does not depend on the nutation frequency cos(ω₁τ). Conversely, if ω₁ ≪ Δω₀, then ϕ = 0° and we rewrite Eq. [23] as

$$({\omega }_1\ll \mathrm{\Delta }{\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{M}({\tau }^{+})={\mathbf{R}}_{-\text{x}}(\alpha ){\mathbf{R}}_{\text{z}}(\mathrm{\Delta }{\omega }_0\tau /2){\mathbf{R}}_{\text{y}}(2\alpha ){\mathbf{R}}_{\text{z}}(\mathrm{\Delta }{\omega }_0\tau /2){\mathbf{R}}_{\text{x}}(\alpha )\mathbf{M}(0^{-})$$ [25]

Specifically, if R_y(2α) = R_y(180°), then Eq. [25] reduces to Eq. [20] and is independent of off-resonance effects Δω₀. At intermediate field strengths (ω₁ ~ Δω₀), however, Eq. [22] requires both R_x(α) = R_x(90°) and R_y(2α) = R_y(180°) to remove terms like cos(ω_effτ) and this requirement is almost never satisfied across the sample.

2.5 ΔB₀ and B₁ Insensitive Spin Lock: 90_x-τ/2_y-180_y-τ/2_−y-90_x

Alternating the phase of the last 90° pulse in the spin lock pulse cluster aligns the final magnetization along the −z-axis rather than along the +z-axis (Figure 2B). The alternation of the phase of the final 90° pulse from −x to +x in the cluster compensates for imperfect flip angles α ≠ 90° in an inhomogeneous B₁ field. The expression for the full pulse propagator is the same as Eq. [22] except for the final phase shift

$$\begin{array}{l}\mathbf{M}({\tau }^{+})={\mathbf{R}}_{\text{x}}(-\alpha ){\mathbf{R}}_{\text{x}}(\varphi ){\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{x}}(-\varphi ){\mathbf{R}}_{\text{y}}(2\alpha ){\mathbf{R}}_{\text{x}}(-\varphi )\dots \\ {\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau /2){\mathbf{R}}_{\text{x}}(\varphi ){\mathbf{R}}_{\text{x}}(-\alpha )\mathbf{M}(0^{-})\end{array}$$ [26]

If ω₁ ≫ Δω₀, then ϕ = 90° and Eq. [26] reduces to

$$({\omega }_1\gg \mathrm{\Delta }{\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{M}({\tau }^{+})={\mathbf{R}}_{\text{x}}(\alpha ){\mathbf{R}}_{-\text{y}}({\omega }_1\tau /2){\mathbf{R}}_{\text{y}}(2\alpha ){\mathbf{R}}_{\text{y}}({\omega }_1\tau /2){\mathbf{R}}_{\text{x}}(\alpha )\mathbf{M}(0^{-})$$ [27]

and the final longitudinal magnetization is

$$({\omega }_1\gg \mathrm{\Delta }{\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{M}}_{\text{z}}({\tau }^{+})={\text{M}}_0[-{sin}^2(\alpha )+{cos}^2(\alpha )cos(2\alpha )]$$ [28]

and is identical to Eq. [24] but with the first term inverted. The implication is that if α = 90°, the absolute magnetization in unaffected by the pulse phase shift. Instead, if ω₁ ≪ Δω₀ then magnetization is

$$({\omega }_1\ll \mathrm{\Delta }{\omega }_0)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{M}({\tau }^{+})={\mathbf{R}}_{\text{x}}(\alpha ){\mathbf{R}}_{\text{z}}(\mathrm{\Delta }{\omega }_0\tau /2){\mathbf{R}}_{\text{y}}(2\alpha ){\mathbf{R}}_{\text{z}}(\mathrm{\Delta }{\omega }_0\tau /2){\mathbf{R}}_{\text{x}}(\alpha )\mathbf{M}(0^{-})$$ [29]

The key feature of Eq. [26] and [29] is that the final phase shift −x to +x no longer requires that R_x(α) = R_x(90°), however, to completely reduce Eq. [29] to Eq. [20] we still require R_y(2α) = R_y(180°). In this case Eq. [29] becomes

$$({\omega }_1\ll \mathrm{\Delta }{\omega }_0)\hspace{0.17em}{\text{R}}_{\text{y}}(2\alpha )={\text{R}}_{\text{y}}(180°)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{M}({\tau }^{+})=-\mathbf{M}(0^{-})$$ [30]

Despite the inability to achieve a perfect 180° flip in practice, artifacts are less severe than in the ΔB₀ insensitive spin lock. In addition, the rectangular 180° may be substituted with a composite 180° RF pulse to further reduce these artifacts [26].

3. Methods

Imaging was performed on a Siemens Trio 3T clinical imaging system equipped with a Bruker birdcage head coil. To maintain consistent B₀ and B₁ field maps throughout the experiment, automated single slice shim and pulse calibration was performed once and without any further adjustments. Volunteers were recruited to the study and scanned following a pre-approved protocol, described below, by the Institutional Review Board of the University of Pennsylvania. Agarose (3% w/v, 200 mM ²³Na) or water/fat phantom (150 mL mineral oil/200 mL doped H₂O) imaging was performed using a similar protocol (FOV = 15 cm²).

A B₀ field map (Fig. 4, 6–8) was obtained from four complex gradient echo images with TE = 5, 10, 15 and 20 ms, TR = 700 ms, FOV = 23 cm², slice thickness = 4 mm and BW = 130 Hz/pixel. Following phase unwrap, the accumulated pixel phase Δθ₀ was related to the frequency offset by

Figure 4.

Simulated and actual spin lock artifacts at TSL = 30 ms in 3 different ω₁ regimes: (1) Δω≫ ω₁ (ω₁ = 0 Hz) (2) Δω~ ω₁ (ω₁ = 25 Hz) and (3) Δω≪ ω₁ (ω₁ = 400 Hz). B₁ and B₀ field maps were obtained after automatic pulse calibration and shimming protocols on a Siemens Trio 3T clinical imaging system. The B₁ field map was scaled to an ideal π/2 flip angle with a 200 μs rectangular pulse (ω₁ = 1250 Hz). The actual ω₁ amplitude varies throughout the sample. To amplify image artifacts, the excitation and storage pulses were 80° instead of the nominal 90°.

Figure 6.

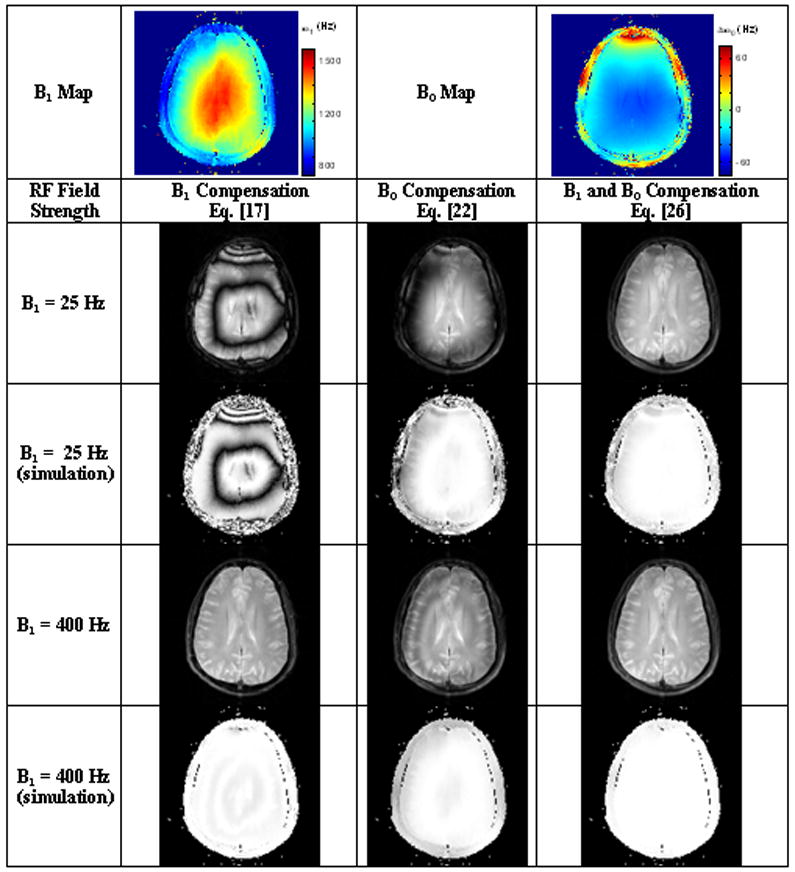
T1ρ-weighted images of the brain at 3T. Low spin lock amplitudes (ω₁ = 25 Hz) induce Δω₀ banding artifacts in both B₁ compensation and B₀ compensation sequence variants. These artifacts are greatly reduced at higher spin lock amplitudes or with both B₁ and B₀ compensation.

Figure 8.

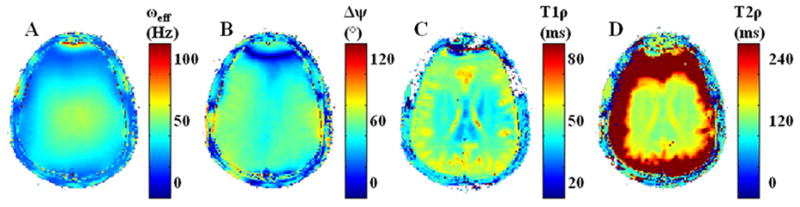
The origin of relaxation-dependent artifacts in Fig. 6 and 7 is detailed. (A) The effective field ( ${\omega }_{\text{eff}}=\sqrt{{\omega }_1+\mathrm{\Delta }{\omega }_0}$) varies spatially at ω₁ = 25 Hz primarily because of variations in ΔB₀ at 3T. (B) The angular difference between initial excitation and the orientation of the effective field (Δψ = α – ϕ). (C, D) T1ρ and T2ρ relaxation maps obtained from Eq. [9] using the transient solutions to the Bloch equations.

$$\mathrm{\Delta }{\omega }_0\mathrm{\Delta }\text{TE}=\mathrm{\Delta }{\theta }_0$$ [31]

The final B₀ field map was obtained by minimizing pixel by pixel the chi-square error statistic to Eq. [31] given the image echo times (TE) and pixel phases (Δθ₀) using a linear least squares fitting algorithm in IDL (ITT Visual Information Solutions, Boulder, CO).

A B₁ field map (Fig. 4, 6–8) was obtained using the following protocol. 4 images were obtained with varied rectangular pulse duration τ = 150, 200, 250 and 300 μs using a single rectangular pulse θ°_x followed by a spoiler gradient and 2D single slice fast spin echo frequency and phase encoding sequence with the following imaging parameters: TE_eff/TR = 13/2500 ms, 128×128 image matrix, FOV = 23 cm², slice thickness = 4 mm, echo train length = 7, BW = 130 Hz/pixel. B₁ field maps were generated using a function in IDL based on the Levenberg-Marquardt algorithm [27] to compute a non-linear least squares fit to the function

$$\text{S}(\tau )=\text{S}(0)cos({\omega }_1\tau )$$ [32]

where S(τ) denotes pixel signal in an image with rectangular pulse duration τ and ω₁ is the B₁ field amplitude.

Post-processing of both the ΔB₀ and B₁ field maps involved zeroing non-finite pixel values, 3×3 boxcar smoothing filter and a binary mask of linear fits with R² < 0.995.

Four variations of a pulse cluster used for T1ρ-weighting (described each in Sections 2.2–2.5) were followed by a gradient to spoil residual transverse magnetization and a 2D single slice fast spin echo frequency and phase encoding sequence with spin lock duration (τ = TSL) = 40 ms, ω₁ = 0, 25 or 400 Hz, echo train length = 7, BW = 130 Hz/pixel.

To verify the experimentally acquired T1ρ-weighted images (Fig. 4, 6–8), simulated images were created from experimental ΔB₀ and B₁ field maps using the Bloch equations with identical T1ρ-weighted imaging parameters: spin lock duration (τ = TSL) = 40 ms, ω₁ = 0, 25 or 400 Hz. Rather than use explicit solutions to the Bloch equations for each pulse sequence (Eq.’s [14, 17, 22 and 26), it was fortuitous to use the generalized matrix notation of Eq. [9], however, Fig. 4 and 6 do not incorporate artifacts from relaxation processes.

The contribution to image artifacts from tissue relaxation and an imperfect refocusing pulse is examined in Fig. 7 and 8. Relaxation was modeled during the spin locking pulses using the transient solutions to the Bloch equations [28]. In the tilted rotating frame, the matrix formulation for both precession about the effective field and relaxation is

Figure 7.

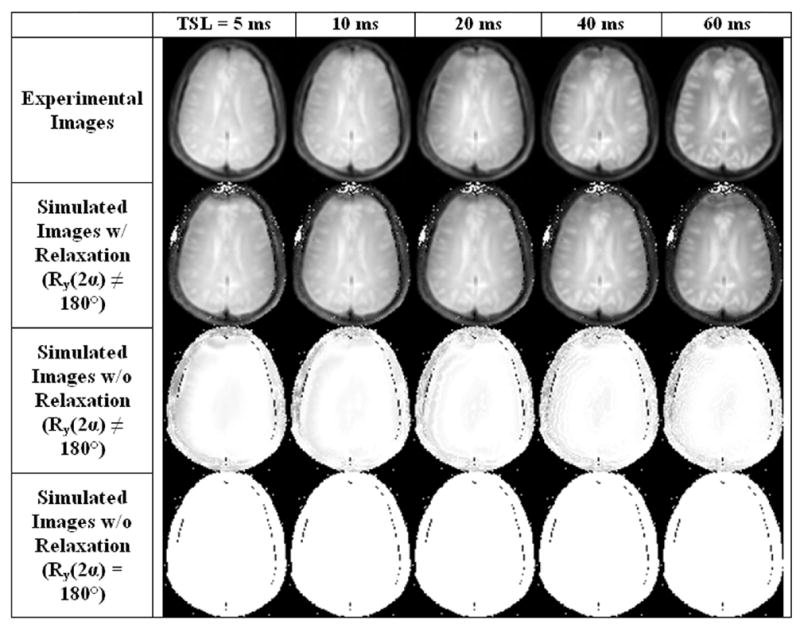
Experimental and simulated T1ρ-weighted images of the brain using the pulse sequence described in Section 2.5 at a spin locking field strength ω₁ = 25 Hz. Row 1: Experimental T1ρ-weighted images obtained for 5 spin lock durations 5–60 ms. Row 2: Simulated T1ρ-weighted images from B₁ and ΔB₀ field maps using transient solutions to the Bloch equations and a parametric fit of the unknown relaxation times T1ρ and T2ρ to the experimental images in Row 1. Row 3: Simulated T1ρ-weighted images from B₁ and ΔB₀ field maps to the Bloch equations, neglecting relaxation, but using the actual refocusing pulse R_y(2α ≠ 180°). Row 4: Simulated T1ρ-weighted images from B₁ and ΔB₀ field maps to the Bloch equations, neglecting relaxation and assuming a perfect refocusing pulse R_y(2α = 180°). Without modeling relaxation, there is consequently no relaxation-dependent contrast in Rows 3 and 4. Artifacts from relaxation effects are predominantly localized to the frontal cortex, suggesting relaxation artifacts are primarily dependent on regions of poor B₀ field homogeneity, such as near nasal cavities. Artifacts from imperfect refocusing pulses localized to the brain periphery where B₁ field inhomogeneity is poor.

$${\text{R}}_{{\text{z}}^{″}}({\omega }_{\text{eff}}\tau )=\left[\begin{array}{ccc}cos({\omega }_{\text{eff}}\tau ){\text{e}}^{-\tau /\text{T}2\rho }& sin({\omega }_{\text{eff}}\tau ){\text{e}}^{-\tau /\text{T}2\rho }& \hspace{0.17em}\\ -sin({\omega }_{\text{eff}}\tau ){\text{e}}^{-\tau /\text{T}2\rho }& cos({\omega }_{\text{eff}}\tau ){\text{e}}^{-\tau /\text{T}2\rho }& \hspace{0.17em}\\ \hspace{0.17em}& \hspace{0.17em}& {\text{e}}^{-\tau /\text{T}1\rho }\end{array}\right]$$ [33]

In general, both T1ρ and T2ρ are dependent on the B₀ and B₁ fields and may be written as T1ρ(Δω₀ = 0, ω₁) and T2ρ(Δω₀ = 0, ω₁) or, for arbitrary Δω₀, T1ρ_off(Δω₀, ω₁) and T2ρ _off(Δω₀, ω₁). In addition, the steady-state solution to the Bloch equations requires an additional term

$$\mathbf{M}({\tau }^{+})={\mathbf{R}}_{\text{z}}({\omega }_{\text{eff}}\tau )\mathbf{M}({\tau }^{-})+{\text{M}}_{\text{ss}}(1-{\text{e}}^{-\tau /\text{T}1\rho }){\mathbf{z}}^{″}$$ [34]

Where z″ denotes the unit vector in the direction of the effective field and M_ss is the steady-state magnetization. The rotary echo further complicates an analysis of relaxation, since the magnetization approaches two distinct steady-states during each period.

Relaxation-dependent artifacts were examined by substituting Eq. [33] and [34] into Eq. [8] with T1ρ and T2ρ as unknowns. The steady-state magnetization was fixed (M_ss = 0) for the simulation. T1ρ and T2ρ relaxation maps were calculated from Eq. [9] using a Levenberg-Marquardt algorithm [27] in IDL using initial estimates T1ρ = 50 ms and T2ρ = 140 ms.

The specific absorption rate (SAR) delivered during the T1ρ-weighted sequences was determined by estimating the SAR during an arbitrary RF pulse [29]:

$${\text{SAR}}_{\tau /\alpha }=\text{f}{\left(\frac{3\hspace{0.17em}\text{ms}}{\tau }\right)}^2{\left(\frac{\alpha }{90°}\right)}^2{\text{SAR}}_{3\text{ms}/90°}$$ [35]

where SAR_3ms/90° is the average SAR delivered to the head during a 3 ms rectangular pulse with flip angle α = 90° using a quadrature birdcage coil, f is the pulse shape factor (rectangular pulse = 1.0, sinc pulse = 2.0), τ is the RF pulse duration and α is the RF pulse flip angle. For example, the average SAR_3ms/90° in the brain (W/kg) at 3 T for a quadrature birdcage coil is between 0.242 W/kg (1.5 T) and 2.16 W/kg (4.1 T). For a generalized pulse sequence, the average SAR delivered is the sum of the energy absorbed by each RF pulse divided by the total time to acquire the image

$$\text{SAR}=\frac{\underset{\text{n}=1}{\overset{\text{N}}{\Sigma }}{\text{SAR}}_{{\tau }_{\text{n}}/{\alpha }_{\text{n}}}{\tau }_{\text{n}}}{\text{TT}}$$ [36]

where SAR denotes the average delivered SAR over a total time period TT and τ_n is the n^th RF pulse duration and α_n the n^th RF pulse flip angle. The FDA limits the delivered SAR to 3 W/kg averaged over the head during a 10 minute period and assuming continuous scanning during this period, 3 W/kg per TR. Eq. [36] estimates the average SAR delivered to the brain (Fig. 6) during the T1ρ-weighted sequences is approximately 0.5 W/kg/TR at ω₁ = 400 Hz and 0.08 W/kg/TR at ω₁ = 25 Hz. By comparison, the SAR delivered during a T1ρ-weighted sequence with TSL = 100 ms at ω₁ = 800 Hz is 3.8 W/kg/TR, surpassing FDA regulations. The actual SAR may differ from this estimate because of coil and head geometry.

4. Results

We confirmed the theory in 3% agarose phantoms to demonstrate the effectiveness of the four different T1ρ pulse clusters to ΔB₀ and B₁ field gradients. While none of the four pulse clusters completely eliminated artifacts at all spin locking field strengths (ω₁ = 0 Hz, 25 Hz and 400 Hz), we found the ΔB₀ and B₁ insensitive pulse cluster was the most robust. The remaining artifacts are attributed to an imperfect 180° pulses, but may be removed using either composite 180° or an adiabatic refocusing pulse.

T1ρ-weighted images were simulated from B₁ and ΔB₀ maps to verify that spin locking artifacts could be modeled using the Bloch equations. The simulated images were obtained using Eq.s [14], [17], [22] and [26] and are displayed alongside the actual T1ρ-weighted images in Figure 4. Actual images were collected using four spin locking composite pulse clusters and three different spin locking field strengths ω₁: (1) Δω₀ ≫ ω₁ (ω₁ = 0 Hz) (2) Δω₀ ~ ω₁ (ω₁ = 25 Hz) and (3) Δω₀ ≪ ω₁ (ω₁ = 400 Hz).

At ω₁ = 400 Hz and Δω₀ ≪ ω₁, conventional spin locking artifacts described by Eq. [15] are arranged along the gradients of the ω₁ field. Banding artifacts form every ω₁τ = 2π and while the B₁ insensitive spin lock removes these artifacts, they reemerge in the ΔB₀ insensitive sequence. Inverting the phase of the final 90° pulse +x removes these artifacts.

At ω₁ = 0 Hz and Δω ≫ ω₁, B₀ field gradients create banding artifacts described by Eq. [16]. These artifacts are best known among fatty tissues or nasal cavities where the corresponding chemical shift or tissue susceptibility difference gives a large resonance offset. A sample in a Gaussian-like B₀ field gradient forms bands for every Δω₀τ = 2π and increasing either the resonance offset Δω₀ or the spin lock duration τ increases the total number of bands in the image. The banding artifacts are identical in both the conventional and B₁ insensitive spin locking sequences since, in the limit ω₁ → 0, the two sequences are identical. Inserting a 180° pulse theoretically removes the dependence on the resonance offset (from Eq. 25), but banding artifacts remain from a combination of imperfect 180° (ΔB₀ and B₁ insensitive) and imperfect 90° pulses (ΔB₀ insensitive).

To illustrate full ΔB₀ insensitivity during spin locking, a series of images were collected in a fat and water phantom at varying spin lock durations τ (Fig. 5). At 3T and ω₁ = 500 Hz, the effective field makes an angle ϕ ≈ 51° to the z-axis and produces severe banding artifacts in both conventional and B₁ insensitive T1ρ-weighted imaging. The artifact is removed in ΔB₀ or ΔB₀ and B₁ insensitive pulse clusters provided the hard pulse flip angles (90° or 180°) are conserved.

Figure 5.

T1ρ-weighted images of a water (bottom) and fat (top) phantom. Off-resonance fat protons produce artifacts in conventional and B₁ insensitive T1ρ-weighted images, but are absent in ΔB₀ insensitive methods. Contrast between water and fat varies in each of the four pulse sequences and is attributed to the off-resonance relaxation of fat spins.

T1ρ-weighted images were obtained of the human brain in vivo and show significant Δω₀ banding artifacts at low spin lock amplitudes (ω₁ ~ Δω₀) in Figure 6. At higher spin lock amplitudes (ω₁ ≫ Δω₀), the magnetization for each of the pulse sequences is described by Eq.’s [20], [24] and [28], respectively, and the magnetization is independent of nutation about the effective field. By compensating for both B₁ and B₀ imperfections, artifacts are significantly reduced at ω₁ = 25 Hz as well.

The high artifact suppression in the ΔB₀ and B₁ insensitive pulse sequence shows remarkable robustness to field inhomogeneities despite possible artifacts from relaxation processes. The pulse sequence used for ΔB₀ and B₁ correction, 90_x-τ/2_y-180_y-τ/2_−y-90_x, is not a unique solution and an alternative such as 90_x-τ/2_y-180_−x-τ/2_y-90_−x is equally robust (data not shown). Also, there exist 2 additional solutions for each excitation phase 90_y, 90_−x or 90_−y

Additional artifacts emerge because of both tissue relaxation and an imperfect refocusing pulse; these additional artifacts are considered in Figure 7. Row 1 shows experimental images using the ΔB₀ and B₁ insensitive pulse sequence for 5 different spin locking durations (TSL = 5, 10, 20, 40, and 60 ms) at ω₁ = 25 Hz. Except for the frontal cortex, a region of significant B₀ field inhomogeneity, the experimental images are free of low ω₁ band artifacts. The location of the artifacts can be reproduced in simulated images that model T1ρ and T2ρ relaxation (Row 2), but are not observed in simulations that do not model relaxation (Row 4). To some extent, an imperfect refocusing pulse produces artifacts around the periphery in regions of significant B₁ field inhomogeneity (Row 3) and also in the frontal cortex.

The relationship between tissue relaxation, field inhomogeneity and the residual artifacts may be considered as follows: As magnetization nutates around the effective field, the component parallel to the effective field M_|| will decay to the steady state magnetization at a rate 1/T1ρ and the component perpendicular to the effective field M_T will decay at a rate 1/T2ρ. As the ratio M_T/M_|| changes during the spin lock, so does the nutation angle between the effective field and magnetization. If the nutation angle changes, the final spin locked magnetization (Eq. [30]) will not be stored parallel to the −z-axis and field dependent artifacts may emerge. Therefore, field inhomogeneity has two primary effects, to nutate the magnetization different angles because of variations in ω_eff and also to cause relaxation-dependent artifacts. As Figures 6 and 7 demonstrate, small field inhomogeneities have a substantial effect on nutation angle banding artifacts, but don’t affect relaxation dependent artifacts nearly as much.

There is a threshold for field inhomogeneity beyond which low ω₁ imaging becomes unacceptable. Relaxation-dependent artifacts are worse for larger spin lock durations and higher B₀ field inhomogeneities and so the threshold is quantified in terms of τ and ΔB₀. As stated previously, T2ρ relaxation will change the angle between the effective field and the initially excited magnetization, so artifacts are significant for when times τ ~ T2ρ and the difference angle between the initial excitation and the effective field

$$\mathrm{\Delta }\psi =\alpha -\varphi$$ [37]

is appreciable. There are three regimes for relaxation-dependent artifacts. For large Δψ, there is a significant amount of T2ρ relaxation at long τ durations. T2ρ relaxation can be easily quantified because a large component of the magnetization is perpendicular to the effective field. Conversely, for small Δψ, T1ρ relaxation can be easily quantified, because a large component of the magnetization is parallel to the effective field. Only gradients in Δψ will cause artifacts, because of significant differences in the relaxation times T1ρ and T2ρ. In the third regime, when Δψ ~ 45°, T1ρ and T2ρ can be quantified, but a convergent solution is less likely. Figure 8 demonstrates how Δψ affects quantification of T1ρ and T2ρ. While both T1ρ and T2ρ depend on ω_eff (Fig. 8A), there is a clear spatial dependence of the relaxation times on Δψ (Fig 8B). For example, where Δψ is large, T2ρ takes on usual brain tissue values (T2ρ = 140 ms, Fig. 8D), but when Δψ is small, the magnetization lies parallel to the effective field and T2ρ quantification is not possible. Conversely, T1ρ is quantified when Δψ is small (Fig. 8C), but more difficult when Δψ is large, such as in the frontal cortex. T1ρ is nearly 5 ms lower in the midbrain white matter regions (Δψ = 45°) than in the white matter regions of the periphery (Δψ < 45°),

5. Discussion

Section 2.5 and Figure 4 suggest that the ΔB₀ and B₁ insensitive pulse sequence is the most robust against variations in B₀ and B₁ field gradients. Furthermore, the insensitivity of the sequence may be further improved by decomposing the central R_y(180°) into a composite 180° pulse or substitution with an adiabatic refocusing pulse.

While the foregoing theory entirely corrects for nutations about the effective magnetic field, magnetization dynamics are complicated by relaxation processes. Tissue relaxation during a cw pulse is a complex process that depends on ω₁, Δω₀ and the component of magnetization parallel (T1ρ) or perpendicular (T2ρ) to the applied RF field. In general, the system is driven by ω₁ and damped by both T1 and T2 relaxation until it approaches a steady-state magnetization parallel to the effective field [28]. True monoexponential T1ρ relaxation is observed by flipping the magnetization parallel to ω₁ on-resonance and is distorted by Δω₀ and T2ρ. When ω₁ ≪ Δω₀, α ≠ 90° or both, these Δ effects compound to cause the magnetization to deviate from monoexponential T1ρ relaxation and cause additional image artifacts.

T1ρ relaxation measurements are a useful diagnostic tool in clinical imaging and any off-resonance spins interfere with T1ρ quantification. In particular, a T1ρ map displays the spatial variation in T1ρ across the sample. Often the T1ρ map contains artifacts, even if a single T1ρ-weighted image is artifact free, because the decay of spin magnetization is no longer monoexponential. The T1ρ map is improved by the ΔB₀ and B₁ insensitive pulse sequence and the possibility is now available for tissue studies of very low frequency T1ρ dispersion. Several T1ρ-weighted images collected at low frequency ω₁ may be more sensitive to residual dipolar interactions (ω_D ~ 200 Hz) in tissues and provide a useful form of dipolar contrast among tissues composed of oriented collagen, muscle fibers or myelinated axons. As in Figure 8, combined quantification of T1ρ and T2ρ is also possible, but must be interpreted in the context of a spatially varying effective field and usually both relaxation times will not be quantifiable simultaneously in a pixel.

Very low amplitude spin locking offers several interesting imaging capabilities. As Santyr, et al. initially suggested, it is possible to estimate the contribution of the local static field B_loc by measuring T1ρ dispersion in tissues [30]. In practice, at spin lock amplitudes ω₁ ~ γB_loc the contribution of the local static fields confounds a measurement of T1ρ because they induce oscillations of the magnetization about an effective field in the case of either off-resonance spins, chemical shift and secular J-coupling. And while this manuscript makes use of the Bloch equations, it can be shown using product operator theory that any static interaction that commutes with the spin operator I_z will be refocused. In this way, a low amplitude spin lock dispersion measurement can be used to probe dynamical interactions or spin diffusion independent of spin nutation about the effective field.

Low frequency T1ρ-weighted imaging has two potential applications in medicine where ω₁ ~ γB_loc. We suspect that it will generate useful contrast in indirectly detected H₂¹⁷O for studies of brain metabolism because of the low-frequency scalar coupling between ¹H and ¹⁷O [13]. A bolus of enriched ¹⁷O₂ may be given to a human subject and converted to metabolically produced H₂O¹⁷. The magnetically active ¹⁷O nucleus interacts with water protons through scalar coupling and differences between low frequency (ω₁ ~ J_H–O) and high frequency (ω₁ ≫ J_H–O) T1ρ-weighted images are sensitive to ¹⁷O. This phenomenon has been observed in rat models, but is limited by B₀ field inhomogeneities in the low frequency regime (ω₁ ~ J_H–O) [16]. In addition, static dipole-dipole interactions are known to exist in oriented tissues such as collagen layers of human cartilage[5; 31]. In the anisotropic environment of collagen tissues, ¹H-¹H static dipole-dipole interactions are partially averaged, such that ω_D ~ 200 Hz. Low frequency T1ρ-weighted imaging may be sensitive to changes in this interaction, especially during diseases of the cartilage like osteoarthritis.

6. Conclusion

The origin of inhomogeneous Δω₀ and ω₁ field artifacts in T1ρ-weighted images are oscillations about the effective field at low ω₁ and imperfect flip angles α ≠ 90° at all field strengths. We introduced a spin locking pulse sequence that almost entirely compensates for both types of artifacts at all field strengths. The sequence combines the familiar spin echo with a final pulse phase inversion to flip magnetization along the −z-axis. Consequently, several experimental images were shown on agarose gel and water fat phantoms confirming both Δω₀ and ω₁ insensitivity. These results were confirmed with the derived theory and simulation. The foregoing theory and sequence should be useful for spin locking in the low frequency (ω₁ = 0–600 Hz) regime and generate useful contrast for T1ρ-weighted imaging applications.

Figure 3.

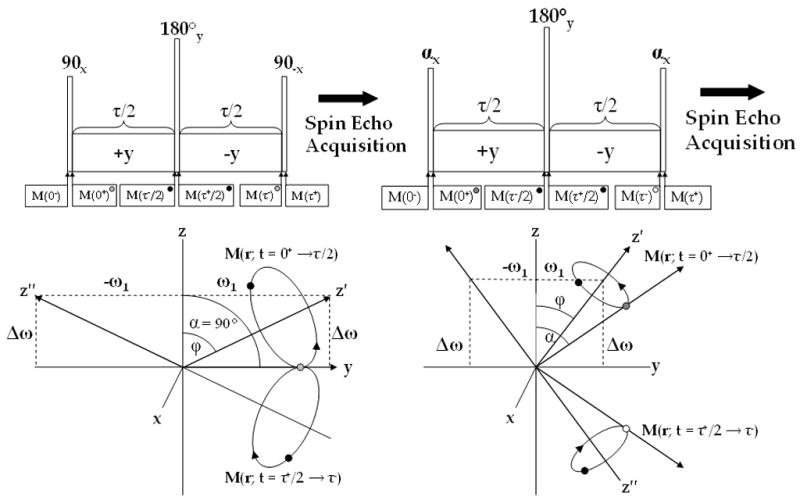
ΔB₀ insensitive (A) and B₁ and ΔB₀ insensitive (B) composite pulses for T1ρ weighted imaging and the magnetization path during each sequence. In (A) magnetization is flipped along the y-axis (grey), where it nutates about the effective field (z′-axis) and at time τ/2 (black) is flipped 180° about the y-axis where it nutates around the effective field (z″-axis) back along the y-axis (grey). In (B) the magnetization follows a similar path, but with two differences: (1) the excitation flip angle does not need to be 90° and (2) B₁ insensitivity is maintained by flipping the magnetization along the −z-axis. While (B) is more robust than (A), an imperfect 180° flip can still produce artifacts.