Submillisecond protein folding kinetics studied by ultrarapid mixing

Abstract

An ultrarapid-mixing continuous-flow method has been developed to study submillisecond folding of chemically denatured proteins. Turbulent flow created by pumping solutions through a small gap dilutes the denaturant in tens of microseconds. We have used this method to study cytochrome c folding kinetics in the previously inaccessible time range 80 μs to 3 ms. To eliminate the heme–ligand exchange chemistry that complicates and slows the folding kinetics by trapping misfolded structures, measurements were made with the imidazole complex. Fluorescence quenching due to excitation energy transfer from the tryptophan to the heme was used to monitor the distance between these groups. The fluorescence decrease is biphasic. There is an unresolved process with τ < 50 μs, followed by a slower, exponential process with τ = 600 μs at the lowest denaturant concentration (0.2 M guanidine hydrochloride). These kinetics are interpreted as a barrier-free, partial collapse to the new equilibrium unfolded state at the lower denaturant concentration, followed by slower crossing of a free energy barrier separating the unfolded and folded states. The results raise several fundamental issues concerning the dynamics of collapse and barrier crossings in protein folding.

Under suitable conditions it would appear that most proteins refold from the chemically denatured state (1, 2). As a consequence, rapid dilution of a denaturant using the stopped-flow method has been the most useful and common experimental technique for studying protein folding kinetics (3–5). A major limitation in this method, however, is that kinetic studies are restricted to times longer than a few milliseconds. Collapse of the polypeptide chain and secondary structure formation therefore often occur before any observations can be made (6). It has been suggested, moreover, that much of the folding kinetics observed up to now correspond to the escape of partially folded or misfolded structures from traps in the energy landscape, revealing little about the fast direct pathways to the native state (7, 8).

Observation of submillisecond processes in protein folding has presented a challenge that has stimulated considerable interest in developing new experimental methods. Dramatic improvement in time resolution has been obtained by using short laser pulses to initiate folding, either by photochemical triggering (9–13) or by temperature-jump (14–17). The results of these studies are discussed in two recent reviews (18, 19) in terms of new theoretical developments in understanding how proteins fold (8, 20–23). To observe submillisecond folding kinetics we have developed an ultrarapid continuous-flow mixing method. The method has previously been used to study very fast bimolecular reactions (24–26). The critical feature for achieving rapid mixing is that the solutions are pumped through a very narrow gap, resulting in high shear that creates turbulence (24). Turbulence “breaks” the liquids into very small volume elements (27). Mixing is rapid because diffusion now occurs over short distances (∼0.1 μm). Here we report our initial results with this method, where folding of cytochrome c is monitored by excitation energy transfer from tryptophan to the heme.

We chose cytochrome c for our initial studies with this new technique because there is a very large submillisecond fluorescence change upon folding (7, 28–31) and the physics of this spectroscopic change can be reasonably well understood. There is a single tryptophan in horse cytochrome c, ∼40 residues distant along the 104 amino acid sequence from the covalently connected heme group. In the chemically denatured state, there is partial quenching of tryptophan fluorescence from excitation energy transfer to the heme. In the native structure the heme-to-tryptophan distance is so short (∼1 nm) that the tryptophan fluorescence is almost completely quenched. This fluorescence is therefore a sensitive probe for measuring the decrease in heme–tryptophan distance, which is presumed to reflect the overall collapse of the unfolded protein (7, 28–31).

To eliminate the heme ligand-exchange chemistry that complicates and slows the kinetics by trapping misfolded structures (7, 29–31), even at acid pH (32), we have studied folding with the extrinsic ligand imidazole bound to the heme (29, 33). Imidazole binding prevents intramolecular ligation of the heme by histidines in positions 26 and 33 in the unfolded state (34); it dissociates much more slowly than folding (29), and it remains bound in place of methionine in the folded structure (35, 36). In this way folding of cytochrome c more nearly resembles that of a protein that has no prosthetic group.

MATERIALS AND METHODS

Horse heart cytochrome c (Sigma catalog no. C7752) was used without further purification. Equilibrium unfolding curves were measured by fluorescence, using an SLM8000 spectrofluorimeter (SLM–Aminco, Rochester, NY), and by far-ultraviolet circular dichroism, using a Jasco 710 spectropolarimeter. Stopped-flow kinetic measurements were performed with a mixer (SFM-3 from Bio-Logic, Grenoble, France) which was mounted onto the back of the sample housing of the Jasco spectropolarimeter. The xenon source and monochromator of the Jasco, focused on the stopped-flow cuvette by a fused silica lens, provided excitation at 266 nm; fluorescence at 90° was detected with a lens, bandpass filter, and photomultiplier mounted on the frame of the SFM-3. Data were digitized by a Nicolet 440 oscilliscope and stored in a personal computer.

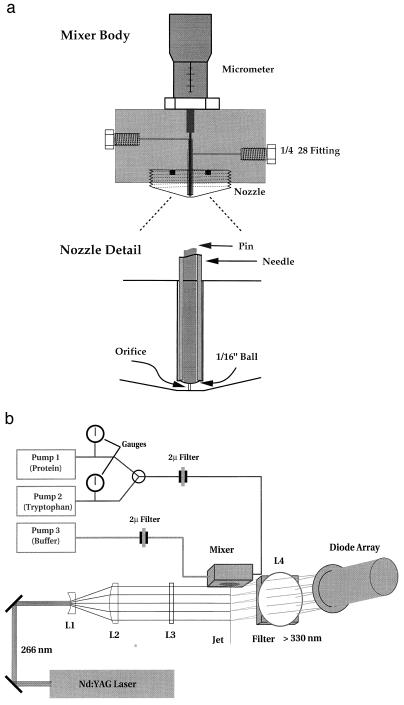
Fig. 1a is a schematic of the mixer used in the kinetic studies. The two solutions to be mixed are pumped on either side of a stainless steel needle by two medium-pressure liquid chromatography pumps (P500, Pharmacia). Mixing takes place in the narrow gap (∼5 μm) between the tip of the pin and a mated surface machined into the nozzle. The mixed solutions form a jet with a linear velocity that varies from about 5 to 50 μm/μs, depending on the pumping rate and the diameter of the orifice, which was either 50 μm or 100 μm. Reactions were monitored by the fluorescence in the output jet of the mixer, the time at each position along the jet being determined by the flow velocity and the distance (Fig. 1b). The fourth harmonic (266 nm) of a SureLite I Q-switched Nd:YAG laser (Continuum; Santa Clara, CA) was used as the excitation source for fluorescence measurements.** The laser beam was expanded to a diameter of about 5 cm (L1, L2), then focused to a line along the jet using a cylindrical lens (L3). The fluorescence emitted from the jet was imaged onto a diode array detector (model 1412 from EG & G; Princeton) by a 5-cm-diameter lens. A pair of 330-nm sharp-cut filters were used to block scattered light and tyrosine emission. The detector controller (EG & G model 1461) was triggered to read the array ∼100 μs after the laser output pulse. Data from 200 laser shots were summed in the detector controller and transferred to a personal computer for storage. Data analysis was carried out in Matlab (The MathWorks, Natick, MA).

Figure 1.

Schematic of ultrarapid-mixing continuous-flow mixer.

We demonstrated that mixing is nearly complete as the jet leaves the nozzle by measuring the diffusion-limited quenching of tryptophan fluorescence by iodide (Fig. 2a). Regenfuss et al. (24) derived an approximate lower limit for the mixing time:

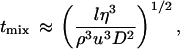1

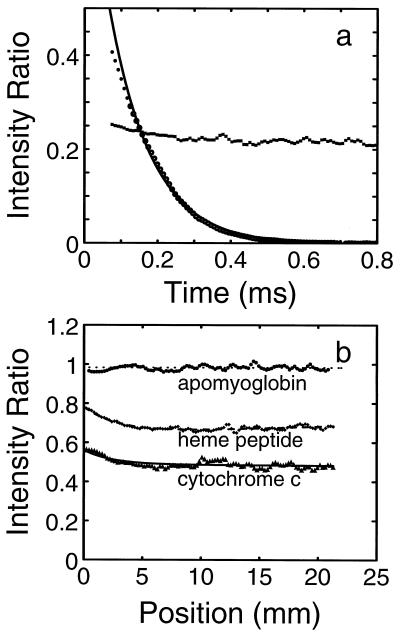
where l is the size of the largest turbulent eddies, u is the maximum velocity of the liquids in the gap, D is the diffusion coefficient of the most rapidly diffusing solute, and η and ρ are the viscosity and density of the liquids (27). Under the conditions of our experiments l ≈ 10⁻³ cm, u ≈ 10⁴ cm/s, η = 10⁻² poise, ρ = 1 g/cm³, and D = 10⁻⁵ cm²/s, resulting in a t_mix ≈ 1–10 μs, consistent with our experiments. The time between mixing and exiting the 50-μm and 100-μm nozzles (the “dead time”) was established to be 80 μs and 200 μs, respectively, by measuring the fluorescence decay resulting from the reaction of N-acetyltryptophanamide (NATA) with N-bromosuccinimide (NBS) (37) (Fig. 2a).

Figure 2.

Control experiments. (a) Determination of mixing efficiency and apparent dead time. The characteristics of the mixer were probed by measuring the quenching of tryptophan fluorescence by iodide under conditions identical to those used in the folding experiments (▪). The relative fluorescence intensity observed after mixing (0.2) is close to that determined from a Stern–Volmer plot at the same NaI concentration, and the time independence of the measured value indicates that the solutions are well mixed. The time delay between mixing and the first observation point (dead time of the mixer) was determined from measurement of the disappearance of N-acetyltryptophanamide (NATA) fluorescence (•) due to the reaction with N-bromosuccinimide (NBS) (37). Under the conditions of the experiment ([NATA] = 40 μM; [NBS] = 4 mM), this reaction is pseudo-first-order and the dead time of the mixer can then be calculated by back-extrapolating the exponential fit of the observed amplitudes (continuous curve) to the initial fluorescence amplitude. Dead times of 80 μs and 200 μs were determined for the 50-μm- and 100-μm-diameter nozzles, respectively. (b) Control experiments on scattering and self-absorption in the jet. Measured data are shown for apomyoglobin, an equimolar mixture of the heme peptide of cytochrome c (residues 11–21 attached to the heme), and cytochrome c after 5:1 dilution in 4.4 M guanidine hydrochloride (Gdn·HCl).

In a typical folding experiment 0.6 mM cytochrome c in 4.4 M Gdn·HCl and 0.2 M imidazole was diluted with buffer also containing 0.2 M imidazole. To vary the final Gdn·HCl concentration, mixing ratios were varied from 2:1 to 12:1. Obtaining quantum yields relative to tryptophan was a two-step procedure. First, the intensity at each position along the jet was divided by the reference intensity obtained by diluting tryptophan at roughly half the molar concentration with the same buffer containing 0.2 M imidazole. This ratio eliminated fluorescence intensity changes along the jet due to variation of laser excitation intensity and some of the effects that result from scattering by the spraying jet. A second step was required to account for unanticipated inner filter effects. For a homogeneous jet of 100-μm diameter the average absorbance (due to absorption by the heme) that overlaps the tryptophan fluorescence, weighted by the fluorescence intensity at each wavelength, is only about 0.03. The inner filter effect from this amount of absorption of the fluorescent light would reduce the measured intensity by only about 7%. Absorption of the excitation light by the heme is comparable. However, the filter effects are apparently significantly larger in the jet because it breaks into small droplets, which produce multiple reflections of both the incident and emitted light. These effects were demonstrated by an experiment in which the heme undecapeptide of cytochrome c and an equimolar concentration of tryptophan were mixed (Fig. 2b). At a final cytochrome c concentration of 132 μM fluorescence is reduced by ∼20% at the exit of the 100-μm nozzle and by ∼30% at points beyond 5 mm from the nozzle. At concentrations that are sufficiently low to eliminate these absorption effects, the signal-to-noise ratio is too poor to obtain meaningful data. We therefore chose to use an empirical correction to eliminate the self-absorption effect by dividing by the intensity obtained in an experiment in which cytochrome c in 4.4 M Gdn·HCl (where unfolding is complete, Fig. 3) was diluted in the same buffer. Under these conditions, the intensity profile for denatured cytochrome c is indistinguishable from that of the mixture of tryptophan and the heme-peptide (Fig. 2b).

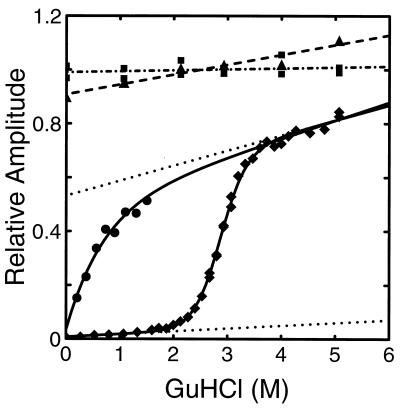
Figure 3.

Equilibrium unfolding curve and initial amplitudes from folding experiments. The fluorescence intensity resulting from 266-nm excitation of cytochrome c (♦, solid curve), tryptophan (▪, dot–dash line), and the 55–63 nonapeptide (▴, dashed line) are plotted versus Gdn·HCl concentration. The solutions contained 0.2 M imidazole, 0.1 M potassium phosphate at pH 7, and various concentrations of Gdn·HCl at 20°C. The dotted lines describe the (assumed) Gdn·HCl-dependent fluorescence of the folded and unfolded states obtained from a two-state fit to both the equilibrium (♦) and kinetic data (Fig. 5). This fit produced C_m = 2.85, m = 2.43 for the midpoint and slope of the folding curve, respectively; the {slope, intercept} of the native and unfolded baselines are {0.010, 0.008} and {0.056, 0.532}, respectively. The equilibrium constant was scaled by a factor of 1.28 in the best fit. (See ‡‡ footnote on later page.) The corresponding values obtained from a fit to the equilibrium data alone were C_m = 2.86, m = 2.85; with native and unfolded baseline parameters {0.23, 0.001} and {0.069, 0.472}. Also shown are the initial (∼100-μs) amplitudes of the kinetic data obtained from continuous-flow experiments (Figs. 4 and 5) (•). The solid curve through these data is a fit to the empirical equation Amplitude = 0.49 + 0.388[Gdn·HCl] − 0.443 exp(−1.45[Gdn·HCl]).

RESULTS

Equilibrium Unfolding Curve.

Fig. 3 shows the equilibrium unfolding curve, obtained by measuring the steady-state fluorescence intensity as a function of Gdn·HCl at pH 7 in the presence of imidazole. Also shown is the guanidine dependence of the fluorescence of tryptophan alone and the tryptophan (W59)-containing nonapeptide from cytochrome c (KGITWKEET). The peptide is a more suitable reference for calculating the quenching efficiency of the heme, while the tryptophan is more practical as a reference in the flow experiments, which consume significant amounts of material. The unfolding curve is readily fit with a two-state model, assuming a linear relation between the free energy of folding and the concentration of Gdn·HCl.

The average quantum yield of fluorescence 〈Φ(r)〉 relative to the quantum yield in the absence of heme is given by

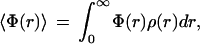2

where ρ(r) is the normalized distribution of heme–tryptophan distances r, and Φ(r) is given by Forster’s theory for the rate of excitation energy transfer as

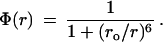3

The value of r_o can be calculated from the overlap integral of the normalized fluorescence spectrum of tryptophan and the absorption spectrum of the heme, and it is found to be 3.4 nm for the imidazole complex of cytochrome c. The fluorescence is almost completely quenched (<2%) in the absence of Gdn·HCl because the center of the tryptophan is only 1 nm from the center of the heme. If we assume a random-coil distribution for ρ(r) and a value of 8 for the Flory characteristic ratio (38, 39), we calculate 〈Φ(r)〉 ≈ 0.8. At 4.4 M Gdn·HCl the measured quantum yield relative to the tryptophan-59-containing nonapeptide of cytochrome c is 0.7 (Fig. 3) suggesting that the unfolded state is nearly a random coil under the initial conditions for our kinetic studies. At higher Gdn·HCl concentrations, the quantum yield continues to increase, suggesting expansion of the unfolded state (increase in the average heme–tryptophan distance) as the quality of the solvent improves (39).

Folding kinetics.

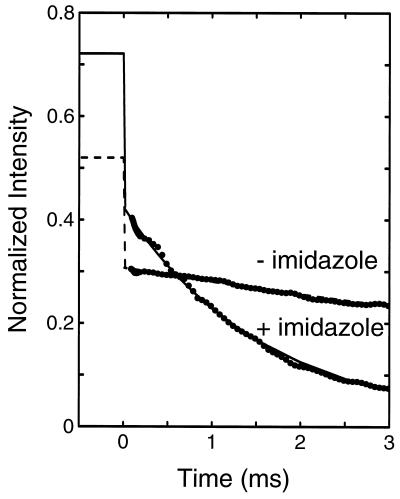
The kinetics of folding were studied by diluting a cytochrome c solution in 4.4 M Gdn·HCl with buffer. At 4.4 M Gdn·HCl the protein is completely unfolded both in the presence and in the absence (data not shown) of imidazole (Fig. 3). Fig. 4 shows the kinetics of the fluorescence decay after dilution from 4.4 M to 0.7 M Gdn·HCl. In the absence of imidazole, there is only a small decrease in fluorescence intensity, which corresponds to the beginning of an exponential process with an apparent relaxation time of ∼10 ms. Addition of imidazole dramatically changes the kinetics. At 3 ms, a typical dead time for stopped-flow experiments, the fluorescence is already 90% quenched. The data can be well fit by a single-exponential function with a time constant of 1.6 ms. The relative quantum yield at zero time, however, is only about 0.4 (after correction for the filter effects), compared with the expected value (∼0.72). The overall fluorescence decay must therefore contain an additional faster phase. A faster phase also exists in the absence of imidazole. Because this phase is unresolved in our experiments, its relaxation time must be less than ∼50 μs.

Figure 4.

Kinetics of cytochrome c folding in the presence and absence of imidazole following dilution of chemical denaturant. Cytochrome c in 4.4 M Gdn·HCl (0.2 M imidazole/0.1 M potassium phosphate buffer, pH 7) was diluted 6-fold with buffer (0.2 M imidazole/0.1 M potassium phosphate, pH 7) to a final Gdn·HCl concentration of 0.7 M at 20°C. The total fluorescence intensity at wavelengths longer than 320 nm was measured relative to tryptophan, and has been scaled as described in the text. The values at negative times indicate the expected intensity at zero time, calculated by correcting the intensity at 4.4 M Gdn·HCl for the influence of Gdn·HCl as determined from the nonapeptide. The intensity at 0.7 M Gdn·HCl for the 1–65 fragment is 0.4 (7). The lines show exponential fits to the data, with relaxation times of 1.6 ms (solid line) and 10.9 ms (broken line).

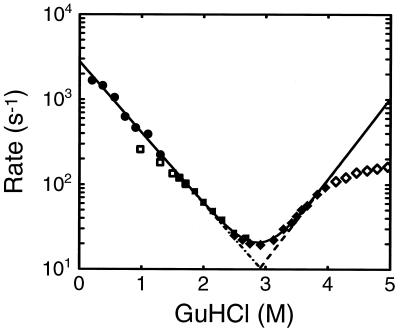
The kinetics observed in stopped-flow experiments at higher final Gdn·HCl concentrations are also well described by single exponentials. The rates and amplitudes obtained from folding and unfolding experiments are shown in Fig. 5, together with those obtained from the continuous-flow experiments. The folding rates measured by continuous flow at low Gdn·HCl concentrations extrapolate linearly to those measured by stopped flow at final Gdn·HCl concentrations between 1.4 M and 2.4 M. The apparent rates observed in unfolding experiments near the midpoint of the folding transition (2.9 M Gdn·HCl) are identical to those observed in folding experiments.

Figure 5.

Folding and unfolding rates as a function of Gdn·HCl concentration. •, Rates obtained from exponential fits to data from continuous-flow experiments (e.g., Fig. 4). ▪ and □, Rates obtained from stopped-flow folding experiments in which solutions were mixed from 4.4 M Gdn·HCl to the indicated final concentration. ♦ and ⋄ Rates obtained from stopped-flow experiments in which solutions of native protein in aqueous buffer were mixed to the indicated final Gdn·HCl concentration. Reciprocal relaxation times (solid line), folding rates (dot–dash line]), and unfolding rates (dashed line) obtained from simultaneous fit to kinetic and equilibrium data using the two-state model. Only the filled data points were included in the fit. The unfilled points from the stopped-flow experiments at low Gdn·HCl concentration were not included in the fits because most of the decay cannot be observed. The origin of the curvature in the stopped-flow data at high Gdn·HCl concentration remains unknown (30, 31).

DISCUSSION

We have shown that it is possible to increase the time resolution in folding experiments from the chemically denatured state by almost two orders of magnitude by using a new mixing continuous-flow kinetic method. At the lowest final denaturant concentrations studied (0.2–0.4 M Gdn·HCl), the kinetics are essentially complete before any observations can be made by stopped flow. Several results show that accurate kinetics can be measured with this method. These include the nearly perfect exponential time course observed for a very fast bimolecular reaction under pseudo-first-order conditions (Fig. 2a) and the consistency of the relaxation rates measured by our new method and conventional stopped flow (Fig. 5).

By paying close attention to quantum yields, we have found that, in the previously unobservable submillisecond time regime, the kinetics are clearly biphasic. They consist of a very fast decrease in fluorescence, occurring in less than 50 μs, followed by a slower exponential decrease. In the absence of imidazole the slower process has previously been interpreted as being rate-limited by the dissociation of histidines (7, 29–32). Addition of imidazole prevents histidine ligation and dramatically speeds up folding. More than 90% of the fluorescence remaining after the sub-50-μs phase disappears in a single exponential process.

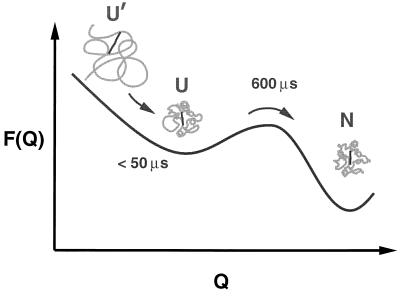
There is a straightforward interpretation for the two processes (Fig. 6). Upon dilution of the denaturant, the polypeptide partially collapses from a near random coil distribution of structures to a distribution where the structures are more compact. We interpret this process as simply the response of the unfolded state to the change in denaturant concentration. Fast partial collapse has previously been suggested to explain part of the nonresolvable fluorescence change in stopped-flow studies (the so-called “burst phase amplitude”) (29, 31, 40). Collapse prior to a barrier crossing has also been observed in computer simulations of protein folding using simplified lattice representations (41–44). This process is followed by crossing an effective free energy barrier that separates the partially collapsed, unfolded structures from the folded conformation. If this short-lived compact state remains highly random, its size can be estimated from the fluorescence intensity remaining after the sub-50-μs relaxation, using Eqs. 2 and 3 and a random-coil distribution for Φ(r) (38). These amplitudes are plotted in Fig. 3. At 1.5 M Gdn·HCl, the quantum yield is about 0.5 relative to the peptide, consistent with 〈r²〉 = (4.0 nm)², while at 0.2 M Gdn·HCl, the relative yield is only 0.15, consistent with 〈r²〉 = (2.3 nm)². The guanidine dependence of the amplitude is similar to that observed for the equilibrium fluorescence of the 1–65 and 1–80 heme-containing fragments of cytochrome c, in which no folding occurs (31).

Figure 6.

Schematic diagram of partial collapse followed by barrier crossing. The free energy is shown as a function of the effective reaction coordinate, Q, which measures the similarity to the native structure (N). One choice for Q, for example, is the fraction of the contacts between residues that are found in the native structure (8). At 4.4 M Gdn·HCl the protein is nearly a random coil (U′). Upon dilution of the denaturant the increased intrachain interactions produce a partial collapse in less than ∼50 μs, which is followed by crossing the free energy barrier separating the equilibrium unfolded (U) and folded states with a relaxation time of 600 μs at the lowest denaturant concentration studied.

Is it surprising that partial collapse occurs in less than 50 μs? A naive but simple model for the polypeptide dynamics is to consider the motion of tryptophan-59 relative to the heme as occurring on a harmonic potential. This approach was used by Szabo et al. (45) in their analytical theory for end-to-end motion of a gaussian chain and by Hagen et al. (10) in their study of the kinetics of intramolecular contact formation in unfolded cytochrome c. Using this model, we can estimate the time scale for the unresolved fluorescence decrease. To do so, we assume that the shift in the distribution of heme–tryptophan distances to smaller values can be represented by simply increasing the curvature of the harmonic potential. The relaxation time for 〈r²〉 is then given by 〈r²〉_eq/6D, where 〈r²〉_eq is the equilibrium, mean-squared heme–tryptophan distance at the final denaturant concentration, and D is the effective diffusion coefficient for the relative motion of the heme and tryptophan. Using D = 4 × 10⁻⁷ cm²/s from the work of Hagen et al. (10) and the above values of 〈r²〉_eq, we obtain a relaxation time of ∼0.1 μs. Hagen et al. (10) determined D at 5.6 M Gdn·HCl (40°C). As the denaturant concentration decreases, diffusion is expected to be slowed because increased interresidue interactions produce a rougher energy landscape (8, 46). We would therefore expect collapse to be somewhat slower than estimated from this calculation. It is interesting in this regard that temperature-jump studies of cold-denatured apomyoglobin have suggested collapse of the unfolded protein to occur in ∼5 μs (16).

The observation of an exponential time course for the barrier crossing process in imidazole cytochrome c is not a trivial result. It suggests that the interconversion among the structures in the more compact distribution at the final denaturant concentration is fast compared with the barrier crossing rate (47). Both this result and the <50-μs partial collapse time argue that this distribution must be close to the equilibrium distribution of structures in the unfolded state (U) at the lower denaturant concentration, as depicted in Fig. 6. The state U should therefore not be regarded as a kinetic “intermediate.” That is, U′ → U is not the formation of an intermediate at the final denaturant concentration, but is simply the response of the unfolded state to the change in denaturant concentration in a downhill (i.e., barrier-free) process.

This work raises two other interesting issues concerning the position and height of the free energy barrier separating the folded and unfolded states. The linear dependence of the logarithm of both the equilibrium constant K and folding rate k_f on the Gdn·HCl concentration (Figs. 3 and 5) implies a linear free energy relation—i.e., dlnk_f/dlnK = constant. Such a relation occurs if the change in the free energy of the transition state produced by some perturbation (e.g., Gdn·HCl) can be expressed as a linear combination of the changes in the free energy of the initial and final states. The slope, dlnk_f/dlnK, then provides a measure of the response of the transition state to the perturbation, relative to that of the initial or final states. This slope has heuristically been taken as a measure of the distance of the transition state along the reaction coordinate from the initial to the final state (48). For protein folding it has been suggested that a relevant reaction coordinate is the fraction of native interresidue contacts (8), and recent simulations of the kinetics of folding in lattice models of proteins show that dlnk_f/dlnK is equal to the fractional distance along the reaction coordinate defined in this way (49).

The slope of the linear free energy plot for the folding of imidazole cytochrome c is between 0.4 and 0.5 (Figs. 3 and 5), indicating that the transition state is 40–50% of the distance along the reaction coordinate from the unfolded to the folded state. This slope is the same as the slopes reported for the fast-folding fraction of oxidized cytochrome c at pH 5 (0.45) (31) and for reduced cytochrome c (0.40) (11, 12), showing that changes in heme ligation and oxidation state per se do not influence the position of the transition state (indicated by ^‡).‡‡ If the fraction of native contacts scales linearly with the buried surface area (as it does in the lattice model), the ratio m^‡/m (∼0.45) corresponds to the average fraction of groups buried in the transition state ensemble which bind denaturant in the unfolded state but not in the native state. Even more interesting is the fact that, at similar denaturant concentrations, the rates of folding of reduced cytochrome c and oxidized imidazole-cytochrome c (as well as uncomplexed cytochrome c) are nearly identical despite the very large difference in stability (e.g., k_red/k_ox ≈ 3, K_red/K_ox ≈ 10⁶ at 2 M Gdn·HCl, (Fig. 5, refs. 9 and 12). Since the iron-methionine bond is believed to be a major contributor to the increased stability of reduced cytochrome c (A. Schejter, personal communication), this result argues that this bond is not present in the vast majority of structures that make up the transition-state ensemble (49).

What is the height of the free energy barrier separating the unfolded and folded states? The barrier height cannot be calculated from the experimental folding rate constant by using a formula of the type k = k_oexp(−ΔG^‡/RT), without knowing the pre-exponential factor [the gas-phase transition state pre-exponential factor k_BT/h = 6 × 10¹² s⁻¹ is of course inappropriate (8, 46)]. However, using the estimate for the maximum barrierless rate of protein folding, k_o^max ≈ 10⁶ s⁻¹ (10) and the maximum observed rate constant of 1.8 × 10³ s⁻¹, we can conclude that the barrier height must be smaller than ∼4 kcal/mol. This low value suggests that conditions may exist where folding occurs in the absence of a free energy barrier, the so-called “downhill scenario” in the classification of folding mechanisms by Bryngelson et al. (8). The importance of downhill folding is that the population of intermediate structures is significant at all values of the reaction coordinate. It might therefore be possible to monitor the complete evolution of the structure distribution from the unfolded to native states. Such results would be an important supplement to the structural information on the (unobservable) transition state ensemble obtained from the mutational perturbation approach of Fersht and co-workers (49–52).

Finally, although optical triggering techniques have much better time resolution, an important advantage of the continuous-flow method described in this work is that it is applicable to many more proteins. Most proteins can be chemically unfolded in a soluble state, and there is clearly much to be learned about both folding and aggregation of proteins that do not completely refold, particularly in disease states caused by misfolded/aggregated proteins (53). The continuous-flow method is also compatible with a number of other monitoring techniques. Takahashi et al. (32) have used resonance Raman spectroscopy and a continuous-flow mixer of somewhat different design to study the kinetics of ligand exchange during folding. It would be interesting to combine optical activity and small-angle x-ray scattering measurements (54) to study the relationship between secondary structure and compactness in the transient unfolded state under strong folding conditions where it is not significantly populated at equilibrium.

ABBREVIATION

Gdn·HCl

guanidine hydrochloride