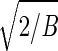An elementary mode coupling theory of random heteropolymer dynamics

Abstract

The Langevin dynamics of a random heteropolymer and its dynamic glass transition are studied using elementary mode coupling theory. Contrary to recent reports using a similar framework, a discontinuous ergodic–nonergodic phase transition is predicted for all Rouse modes at a finite temperature T_A. For sufficiently long chains, T_A is almost independent of chain length and is in good agreement with the value previously estimated by a static replica theory.

The self-organization of evolved biopolymers, such as foldable proteins, ultimately depends upon the chain dynamics of heteropolymers. The modern statistical mechanical view using energy landscape ideas focuses on the analogy of folding with phase transitions in finite size systems and exploits to a large extent our understanding of the quasi-thermodynamic and static features of both regular systems and frustrated disordered systems, such as spin glasses (1). The connection with detailed analytical theories of the time dependence of fluctuational motions of a randomly interacting chain has only recently received attention (2–5).

For completely random heteropolymers (RHP) the quasi-thermodynamic analyses (19, 20) using replica techniques give results parallel to those for other systems with random first order phase transitions such as the mean field Potts spin glasses (6). An important feature of theories of random first order transitions is the presence of two transitions; one is static, while the other is dynamic and generally occurs at a higher temperature. The dynamical transition signals a crossover to a motional mechanism involving activated motions (6–8) (We denote this dynamical transition temperature T_A). For RHPs, two different kinds of approximate quasi-static theories based on replicas (19) and on the generalized random energy model (9) that takes into account correlation in the energy landscape yield these two transitions. Replica-based techniques also yield estimates for the free energy barrier heights of activated motions between the two characteristic temperatures (19). Purely dynamical theories based on mode coupling ideas generally yield a transition in harmony with the quasi-static analysis of the dynamical transition, which is in some sense a spinodal. While mode coupling theory (MCT) is perturbatively well defined for spin systems with long-range random interactions (7, 8, 10), there are various versions developed in the theory of fluids (11) and polymers (12–14) that are forced to make uncontrolled approximations. On the basis of two such calculations, the validity of the emerging picture of the dynamics and the energy landscape of RHPs have been questioned (4).

Roan and Shakhnovich (4) derive a MCT of the RHP and explicitly solve it for a polymer in a good solvent. It is no surprise that an uncollapsed chain has no dynamical transition, but the authors further claim that this is actually a structural feature of the RHP mode coupling equations independent of the state of collapse. Thirumalai et al. (5) derive another set of mode coupling equations for a somewhat different model that exhibits no static replica symmetry breaking (15) and conclude there is a dynamical transition with a transition temperature that depends on the length scale of the motional mode considered (5). A numerical treatment of self-consistent equations for heteropolymer collapse, on the other hand, does show evidence for a dynamic freezing transition (3). The inconsistency of these results with each other and in the first two cases with replica calculations is disturbing. The technical intricacy of these mode coupling calculations is a barrier to understanding their inconsistencies. We have therefore derived mode coupling equations using “elementary” methods like those used decades ago in the theory of critical phenomena (11). The resulting equations differ in some respects from those of the earlier workers but clearly yield transitions in harmony with the quasi-static results. These equations also lead to an understanding of how the dynamical freezing depends on chain length and state of collapse, as well as how the dynamics varies for different modes of chain motion.

We consider a standard Hamiltonian for N interacting beads

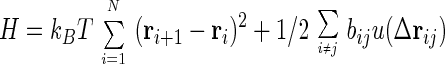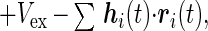1

where r_i are the bead locations, b_ij is chosen as Gaussian random with mean b₀ and variance b², Δr_ij = r_i − r_j, and u(r) is the two-body interaction chosen as a Gaussian exp −r²/σ². V_ex is the excluded volume term, which usually contains three body terms, but it is enough, at the level of the present analysis for phantom chain, to replace it with an effective Gaussian confinement term V_conf = k_BTB∑r_i², with the constant B chosen so that the radius of gyration R_g becomes the physically required value determined by the packing fraction, η.† h_i is the external force introduced for convenience in the derivation of the response function. For technical simplicity, we adopt a ring polymer model where r_N+1 = r₁. The Langevin equation for the beads is

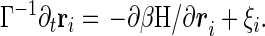2

Here ξ_i(t) is a Gaussian random force for which the first two moments are given by 〈ξ_i(t)〉 = 0 and 〈ξ_i(t)ξ_j(t′)〉 = 2Γ⁻¹ δ_ijδ(t − t′)1 (1 is the 3 by 3 unit matrix), Γ determines the microscopic time scale (it will be set to unity) and β = 1/k_BT as usual. Since our main interest is in collapsed states where hydrodynamic effects are less important, we ignore them for simplicity, although their inclusion is not very hard. A more essential simplification of our treatment is the neglect of entanglement effects. An uncrossable chain will possess more friction than the phantom chain treated here (12–14), modifying the dynamical transition temperature.

A standard tool for dealing with the average over the quenched randomness in the Langevin dynamics has been the dynamic functional integral (DFI) formalism (7, 8, 10). Although this approach is generally accepted for the infinite range spin model, direct application of the formalism to RHP models is questionable for two reasons: (i) The heteropolymer interaction is short range so that the mean field approximation is not exact; in such a situation, there exists some ambiguity with the DFI formalism in its use of steepest descents. (ii) In contrast to spin models, the Jacobian appearing in the DFI formalism of the heteropolymer model depends on the randomness. This point was neglected in previous treatments. The usual formal identity for averaging over randomness in the Hamiltonian for a spin-glass model is no longer precisely true. Thus, we take an alternative and simpler route here; we use a perturbation theory in the randomness b_ij along with a self-consistent prescription that corresponds to a particular resummation of higher order terms. In the case of the infinite range p-spin model (including the Sherrington–Kirkpatrick model), this procedure still leads to exactly the same results as the DFI formalism (7, 8).

We sketch the perturbation scheme briefly since details will be published elsewhere. The Langevin equation, Eq. 2, can be expressed as

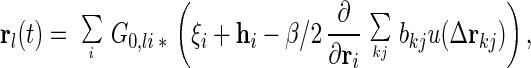3

where ∗ represents the time convolution and G_0,ij(t − t′) is the 0-th order response function ∂〈r_i⁽⁰⁾(t)〉/∂h_j(t′). Inserting the 0-th order solution r_l⁽⁰⁾ = ∑G_0,li ∗ ξ_i into the right-hand side of Eq. 3 gives the first order solution r_l⁽¹⁾ = r_l⁽⁰⁾ − β/2Σ_iG_0,li ∗ ∂/∂r_i⁽⁰⁾Σ_kjb_kju(Δr_kj⁽⁰⁾). We insert this once again into Eq. 3, yielding the second order solution. After taking an average over b_ij, we multiply the resulting equation by G₀⁻¹, which yields

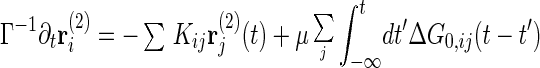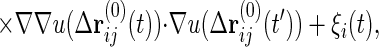4

where K_ij is the harmonic constant matrix including the confinement term, K_ij1 ≡ k_BT ∂²/∂r_i∂r_j [∑(r_i+1 − r_i)² + B∑r_i²], μ = (βb)², and ΔG_0,ij = G_0,ii − G_0,ij − G_0,ji + G_0,jj. The random noise correlation can also be calculated by perturbation theory. With the use of the relation C_lm = Σ_ijG_li ∗ 〈φ_iφ_j〉 ∗ G_mj, we can derive the expression for the correlations up to second order, C⁽²⁾, which includes 〈φ_i(t)φ_j(t′)〉⁽²⁾.

A part of higher order terms can be taken into account by employing a self-consistent prescription. To this end, we first expand the memory kernel of Eq. 4 in Δr_ij(t′). Then, in the spirit of Kawasaki’s derivation of MCT of critical dynamics (11), we replace r_i⁽⁰⁾ in the right-hand side by r_i and G₀ by the perturbed response function, G, giving a renormalized Langevin equation,

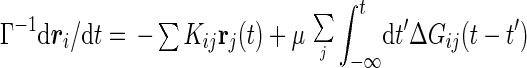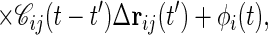5

where 𝒞_ij = 〈∂[∇∇u(Δr_ij(t))·∇u(Δr_ij(t′))]/∂Δr_ij(t′)〉. In deriving this equation, we used the isotropic symmetry of the model. The random force φ_i(t) is also renormalized in the same way. In the expression for 〈φ_i(t)φ_j(t′)〉⁽²⁾, replacement of r_i⁽⁰⁾ by r_i leads to the colored noise correlation function,

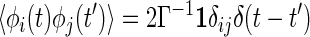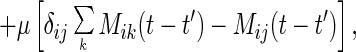6

where M_ij = 〈∇u(Δr_ij(t))∇u(Δr_ij(t′))〉 is the force–force correlation on different beads. In calculating 𝒞 and M we approximate the stochastic process as Gaussian. The explicit expression for M becomes M_ij(t) = [(1 + sΔC_ij(0))² − (sΔC_ij(t))²]^−5/2ΔC_ij(t), where ΔC_ij = C_ii − C_ij − C_ji + C_jj and s = 2/σ². For the ergodic phase, with the time-translational symmetry and the relation [∂_tΔC_ij(t − t′)]𝒞_ij(t − t′) = ∂_tM_ij(t − t′), we can verify that the fluctuation–dissipation theorem indeed holds.

From Eqs. 5 and 6, a straightforward generalization of refs. 7 and 8 scheme for the p-spin model leads to a closed set of integro-differential equations for the correlation functions. In this case, due to the sequence–translational symmetry of ring polymers, it is more transparent to write the equation in the Rouse mode representation. Namely, the Fourier transform of the correlation function with respect to the sequence satisfies the equation

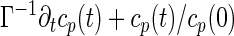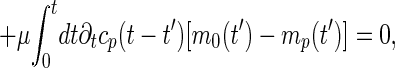7

where c_p(t) = FT_(i−j)→p[C_ij(t)] is the Rouse mode correlation function and m_p(t) = FT_(i−j)→p[M_ij(t)] is a nonlinear function of all of the correlations {c_p′}. The equal time correlation function c_p(0) obeys

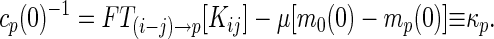8

If we introduce the normalized Edwards–Anderson (EA) Rouse–Zimm order parameters q̃_p = lim_t→∞c_p(t)/c_p(0), the self-consistent equation for q̃_p becomes

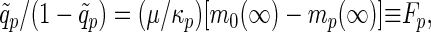9

which is isomorphous to the equations for the MCT of structural glasses (18). Notice that if F_p ≠ 0 the Rouse–Zimm modes have a static offset indicating the trapping in a local minimum, and that all p modes are coupled in evaluating m_p(∞). Thus, clearly, the dynamic glass transition, if any, should occur simultaneously for all modes in this analysis. In general, the dynamic glass transition can be obtained by two steps. We first solve Eq. 8 for c_p(0) and then look for a nontrivial solution of Eq. 9. Assuming c_p(0), a purely static quantity, does not exhibit any singular behavior (7, 8, 18), we use an unperturbed confined Rouse value (i.e., FT_(i−j)→p[K_ij]) for c_p(0) here avoiding the first step.

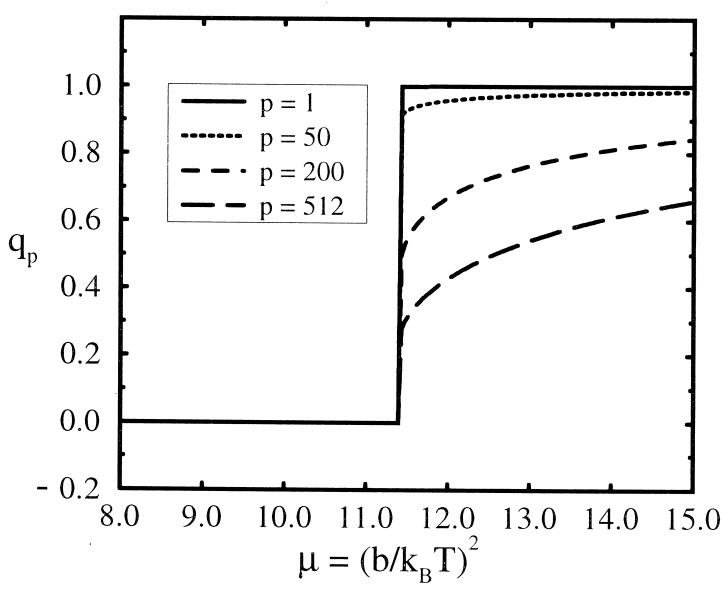
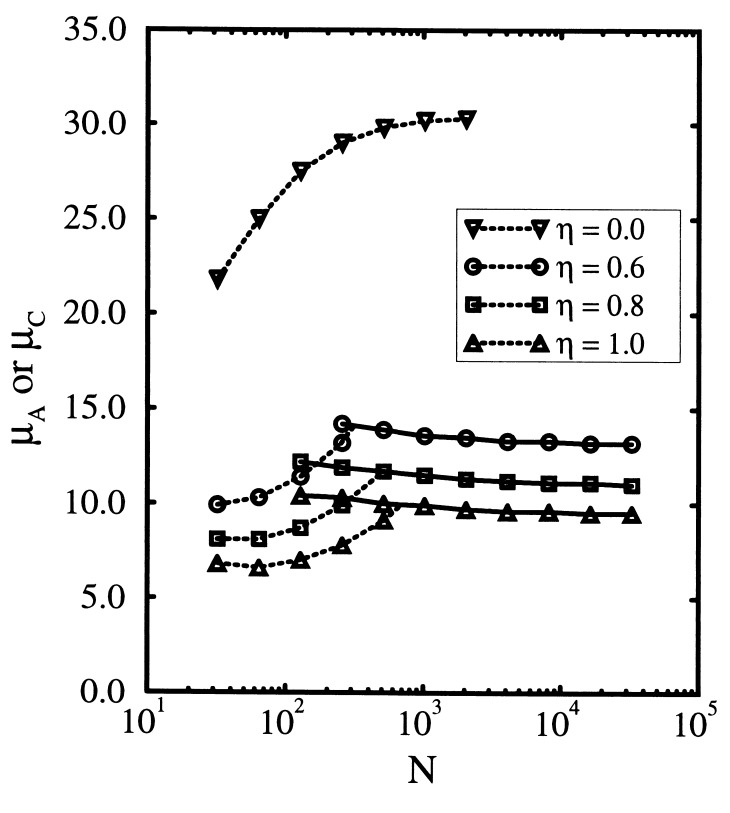
Fig. 1 shows EA parameters q̃_p as a function of μ with p = 1, 50, 200, and 512 for a 1024-mer with parameters σ = 1 and η = 0.8. The EA parameters indeed exhibit a discontinuous (first order) transition at a critical value denoted by μ_A for all p modes. Increasing the chain length up to 32,768, we numerically show that T_A, defined by μ_A = (b/k_BT_A)² , converges to a finite value T_A = 0.3b (Fig. 2), which is in good agreement with the value 0.292b estimated by the static replica theory for essentially the same model (20). This value depends little on the choice of η and thus the agreement with the replica result is quite robust; with η = 0.6 and η = 1.0 we found T_A = 0.28b and T_A = 0.32b, respectively.

Figure 1.

EA order parameters q_p for p = 1, 50, 200, and 512 as a function of μ = (βb)². Parameters used are n = 1024, Γ = 1, σ = 1, and η = 0.8.

Figure 2.

μ_A = (b/k_BT_A)² and μ_c as a function of chain length N. μ_A (solid curve) and μ_c (broken curve) are actually computed at chain length 2^p with p = 5, . . . , 15. η = 0 for Θ solvent and η = 0.6, 0.8, and 1.0 for the collapsed state. Parameters used are Γ = σ = 1 .

Scanning a wide range of chain lengths, N, the self-consistent equations yield two different transitions depending on chain length and state of collapse (Fig. 2). For collapsed phase (e.g., η = 0.8), with short chain length, the EA parameters first achieve a small nonzero value (of order 10⁻²) giving a weakly nonergodic phase at a parameter value μ_c (broken curve in Fig. 2). A stronger nonergodic phase, in which EA parameters become of order unity (μ_A), appears for collapsed states with chain length longer than 128 (solid curve in Fig. 2). μ_c and μ_A coalesce at N ∼ 512, above which no weakly nonergodic phase exists. Under Θ solvent conditions (i.e., η = 0 ), on the other hand, we do not find any second transition and μ_c continues to increase with N. Since the statistical dynamical theory presented here is inherently appropriate for sufficiently large systems, we interpret the transition at μ_A to correspond to the dynamical transition found by the replica approach (19, 20). The weak transition (μ_c) found here only for short chains is fragile and could be an artifact of the model and we postpone its detailed interpretation.

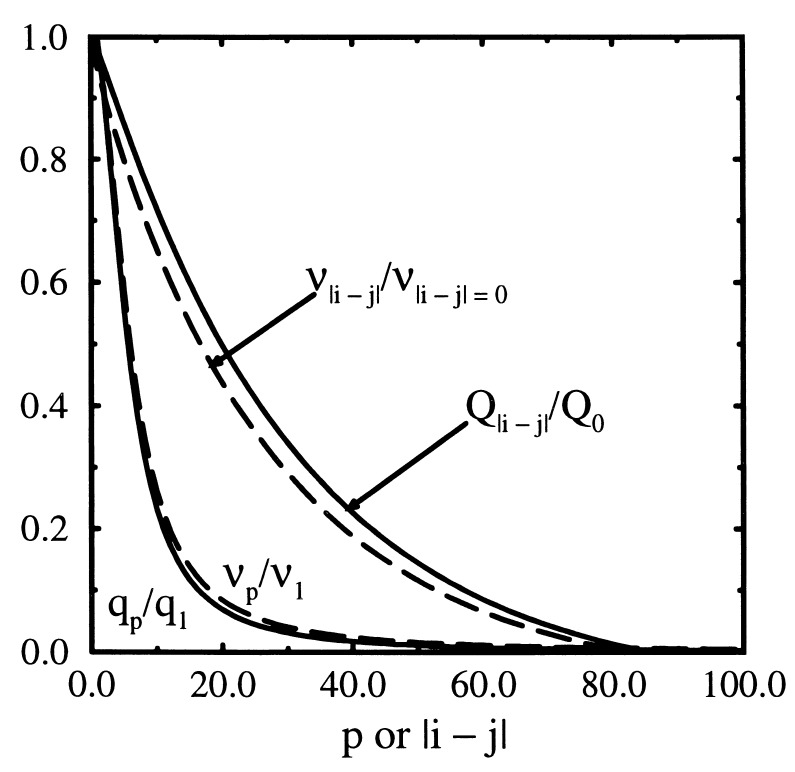
Fig. 3 plots q = lim_t→∞c_p(t) as a function of p as well as its inverse Fourier transformed frozen static displacement Q_i−j. Since the p = 0 mode is purely diffusive, we drop this component. Roughly, the frozen fluctuations q_p and Q_i−js vary with p and i − j in a manner quite similar to the equal time fluctuations c_p(0) and C_i−j, respectively. Although the frozen modes are quite localized in the bead representation, the long wavelength fluctuations corresponding to small p are considerable.

Figure 3.

EA order parameters q_p and Q_i−j as a function of p and i − j (solid curves) and vector components ν_p and ν_i−j of the dangerous mode in p and i − j representations (broken curves). Parameters used are the same as in Fig. 1 and μ is slightly above μ_A.

Which mode is dominantly responsible for the transition? The reduction theorem of Götze (18) suggests that within MCT only one particular mode causes the instability of the nonergodic glass phase and the eigenvector of the stability matrix S_pp′ = ∂F_p/∂q̃_p′ with the largest eigenvalue corresponds to the most dangerous mode. Dashed curves in Fig. 3 show the right-eigenvector of this dangerous mode in the Rouse and bead representation; ν_p and ν_i−j have similar behavior to c_p(0) and C_i−j, respectively.

Eq. 7 can directly be integrated to get the explicit time dependence of c_p(t). As in the MCT for structural glasses, critical slowing down is expected to be found as T_A is approached. Details will be given elsewhere.

As mentioned above, the analysis of Roan and Shakhnovich (4) yielded no singular behavior in the relaxation spectrum. There are several points in their analysis that differ from the present one but primarily their analysis is a lowest order perturbation with respect to b_ij. However, it is clear from our argument that the self-consistent nature of the MC calculation is essential for the dynamic glass transition and obviously this is included at a higher order in perturbation. This is a principal reason for their discordant result. The approach of Thirumalai et al. (5) is quite similar in spirit to ours, but they analyze an uncoupled mode equation analogous to Eq. 7, which yields a scale-dependent transition temperature. We believe that it is more accurate to include the coupling of different Rouse modes, forcing them to freeze simulutaneously. The consistency with the static replica calculation buttresses the belief.

We emphasize again that the dynamic glass transition studied here by elementary MCT is, in reality, a crossover being smeared out due to entropic droplets as discussed in refs. 6 and 20). Thus, T_A should not be viewed as a crisp phase transition, but a characteristic temperature at which the nature of chain dynamics changes qualitatively from renormalized free chain dynamics to activated escape from traps. Above T_A, the so-called cage effect due to the mode coupling addressed here renormalizes the Rouse relaxation through internal friction yielding slow dynamics analogous to the α relaxation of supercooled liquids, whereas below T_A (but still above the static glass transition temperature) escape from localized free energy minima by (local) thermal activations, i.e., entropic droplets, controls the dynamics.

In applying these results to protein folding we need to consider that proteins are not entirely random but have evolved to satisfy the minimal frustration principle (1), so as to avoid being trapped in nonnative local minima. The sequence is designed so that energetically favorable but structurally incorrect amino acid contacts are minimized. Thus, effects of the RHP’s interaction considered here are superimposed on the flow of configurations through a global funnel leading to the native structure (1). Qualitatively, the folding transition temperature T_F should be larger than the static glass transition T_K for fast folding and may perhaps be even larger than T_A. If this is the case, folding can be viewed as a diffusion process in an order parameter space, where slow dynamics renormalized by mode coupling controls the configurational diffusion rate.

ABBREVIATIONS

MCT

mode coupling theory

RHP

random heteropolymer

DFI

dynamic functional integral

EA

Edwards–Anderson