Signaling among relatives. III. Talk is cheap

Abstract

The Sir Philip Sidney game has been used by numerous authors to show how signal cost can facilitate honest signaling among relatives. Here, we demonstrate that, in this game, honest cost-free signals are possible as well, under very general conditions. Moreover, these cost-free signals are better for all participants than the previously explored alternatives. Recent empirical evidence suggests that begging is energetically inexpensive for nestling birds; this finding led some researchers to question the applicability of the costly signaling framework to nestling begging. Our results show that cost-free or inexpensive signals, as observed empirically, fall within the framework of signaling theory.

How can relatives communicate honestly despite interests that sometimes conflict? Several authors have addressed this question by extending the costly signaling framework of Zahavi (1, 2) and Grafen (3) to treat signaling of need among relatives (4–9). Broadly speaking, their results demonstrate that signal cost plays much the same role in signaling of need among relatives as it does in the examples of sexual selection signaling originally treated by Grafen (3, 10)—namely, cost serves to ensure honest signaling. These signaling games often allow multiple signaling equilibria [Lachmann and Bergstrom (11), referred to from here on as Signaling II]. A signaling equilibrium is defined as a pair of signaler and signal-receiver strategies that is an equilibrium in the game-theoretic Nash equilibrium sense, in which neither player will gain an advantage from unilaterally altering strategy. The equilibria may be separating equilibria, in which signalers in different states each send distinct signals, or they may be pooling or partially pooling equilibria, in which some signalers in different states share a common signal. (We borrow these definitions from economics; see, e.g., refs. 12–14.) Here, signals are taken to be distinct if they are distinguished by some signal receiver.

Both kinds of equilibria are plausible in biological signaling systems. Consider a situation akin to that described by Godfray (6, 9), in which a mother bird arrives at her nest and must decide how much to feed each of her nestlings. The nestlings signal their hunger level by begging. If the mother is able to distinguish the hunger levels of each nestling by observing the (continuously distributed) volume of each nestling’s vocalization, we may have a separating equilibrium. If instead she is unable or unwilling to distinguish among different degrees of begging and only observes whether or not each bird is begging, we will have a pooling equilibrium. From the perspective of the signal receiver (i.e., the mother), birds with different levels of hunger will all be sharing a common signal—“squawk,” or, alternatively, “don’t squawk.” We also could imagine a partially pooling equilibrium, in which nestlings send the same signal—not begging at all—below some threshold level of hunger but send a continuously intensifying signal as hunger increases above this threshold. The mother then would be able to distinguish among the hunger levels of each nestling above the threshold, while the nestlings below the threshold would all share a common signal despite some differences in hunger level.

Previous biological models of signaling among relatives have focused on only the separating equilibria; this omission is a consequence of the differential equation-based approach used in these models, as discussed in Signaling II. Maynard Smith’s model (8), treated in Section 1, is an exception—it is constrained to allow fewer available signals than there are different signaler states.

At these separating equilibria, communication is very costly. Bergstrom and Lachmann (15) (referred to from here on as Signaling I) examined the discrete and continuous Sir Philip Sidney (SPS) games of Maynard Smith and Johnstone and Grafen (5, 7) and prove that, although costly signaling among relatives can indeed be a stable equilibrium, it often leaves both participants worse off than if no signaling were to have occurred at all. Rodriguez-Girones et al. (16) demonstrate that similar results hold for Godfray’s (6) model of nestling begging. In these models, the separating signaling equilibrium takes the form of an inferior equilibrium of a coordination game. That is, the sender and receiver of the signal aim to coordinate either on the mutual assumption of signaling or on the mutual assumption that there will be no signaling. Signaling is too costly in these cases because when signaling equilibria take this separating form, the cost of signaling is independent of the distribution of signaler states, whereas the average value of signaling—the fitness gain made possible by the signal—depends on this distribution (see Signaling I). Consequently, rare signaler types can inflate greatly the signal cost without appreciably altering signal value, and thus signals can cost more than they are “worth” to either sender or receiver.

These results raise problems for the application of signaling theory to empirical systems. First, theoretical models predict relatively large signal costs, whereas empirical data suggest costs are generally small (see Section 3). Second, if separating signaling equilibria are too costly to be worthwhile for sender or receiver, then signaling systems only would arise among relatives when evolution became stuck at a “bad” equilibrium. This seems unlikely, given that no-signaling is most likely the ancestral condition (15, 16). As mentioned above, however, separating equilibria are not the only possible signaling equilibria. In Signaling II, we show that a large number of pooling and partially pooling equilibria can be stable in signaling games played among relatives. With the possibility of pooling equilibria comes the opportunity to use inexpensive or even zero-cost signals, with only a modest decline in signal value. In this paper, we explore these cheap signaling equilibria in detail.

Because multiple signaling equilibria exist, models of signal evolution are required to predict which equilibrium will be observed in a given signaling game (see Signaling II). Moreover, because signaler and receiver interests do not entirely coincide, the equilibrium that is best for the signaler may not also be the best for the signal receiver. As a result, there is no obvious way to define which signaling equilibrium is optimal in a particular signaling system. For this reason, we do not concern ourselves here with finding the optimal equilibria.

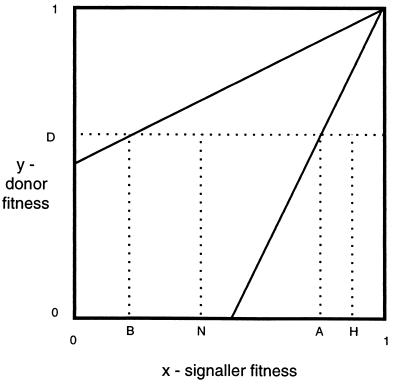
Instead, in Section 1, we demonstrate mathematically that cost-free signaling equilibria are far more common than previously believed in systems of signaling among relatives. We show that, in the SPS game, these cost-free equilibria are better for both sender and receiver than either the no-signaling equilibrium, for which all signalers share the cheapest signal, or the separating equilibrium considered in previous analyses. We consider two different reasons why signaling may be cost-free. First, as depicted in Fig. 1 and treated in detail by Maynard Smith (8), signaling can be cost-free when there is no gain in misrepresenting one’s condition to anyone. Second, as depicted in Fig. 4, we demonstrate that signaling can be cost-free when there is a gain to misrepresenting one’s condition to some, as long as there is on average no gain in misrepresenting one’s condition to everyone.

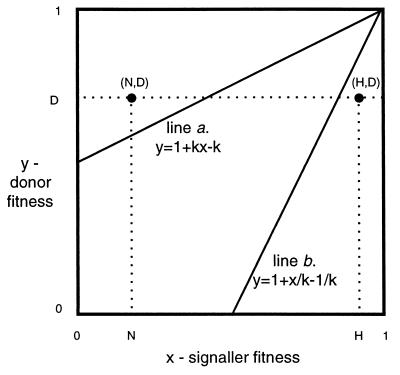
Figure 1.

A trivial example of cost-free signaling, in which there is no gain to any signaler in deceiving any donor.

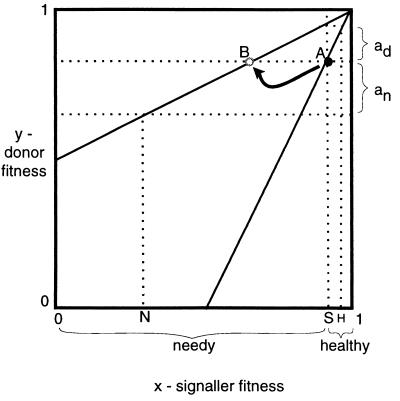
Figure 4.

Stable cost-free signaling despite conflict of interest between some signaler–donor pairs. Axes are as in Fig. 1. Consider a signaling system with a stable two-pool cost-free signaling equilibrium, with the boundary between the two pools at S. A signaler at this boundary—represented by point A—would like to receive the resource from the donors in the region a_d but not from those in the region a_n. Therefore, this signaler ideally would choose to be seen by donors as being at point B. However, in this signaling system, there is no signal available that would be understood as indicating quality B; the signalers can either signal that they are needy and be treated as if they have the mean fitness of signalers in the needy pool, N, or they can signal that they are healthy and thus be treated as if they have the mean fitness of those in the healthy pool, H. Although the signalers could deceive the donors in a_dby signaling needy, by doing so they also would deceive the donors in a_n into transferring. This action runs counter to the signalers’ interest because they do not benefit from receiving the resource from these donors. The benefit of deceiving a_d is offset by the cost of deceiving a_n; the signaler at A has no incentive to signal needy. All of the signalers to the right of A will have even more to lose and less to gain by signaling “needy” and therefore will also signal “healthy.” Hence this cost-free signaling equilibrium is stable despite some conflict of interest.

In Section 2, we show that, in some cases, no cost-free signaling equilibria exist. In such cases, pooling equilibria that use costly signals can be better for both sender and receiver than either the no-signaling or the completely separating equilibrium.

In Section 3, we address recent empirical data that have led some to question the applicability of costly signaling theory to systems such as nestling begging, on the grounds that the high signal costs generally predicted by the theory are not observed in the field. Our results demonstrate that the costly signaling framework is indeed consistent with these results, in that it reveals the potential for inexpensive or cost-free signaling to be used among relatives, even when there is some conflict of interest.

1. Cost-Free Signaling in the SPS Game

Defining Signal Cost.

In this paper, we are interested in the strategic role of signal cost: When is signal cost necessary for signaling to be stable? Here, we present a working definition of signal cost, in accord with Grafen’s (3) formulation, which will allow us to address these issues. For discussion of the additional complexities that arise in defining signal cost, see Hasson (17) and Maynard Smith and Harper (18).

First of all, we will treat signal cost as a relative quantity. We always will look at the difference between the cost of sending a signal and the cost of taking some other action—for example, sending a different signal or even doing nothing. (Notice that doing nothing can itself be a signal and therefore usually will be considered as one of the possible alternative signals, as discussed in Signaling I). Computing signal costs as a relative measure makes intuitive sense—costs generally are computed relative only to the set of feasible alternatives. Moreover, this treatment of cost is in accordance with the theoretical basis for stable signaling. In Signaling II, we showed (Section 3, expressions 4, 6, and 8) that the conditions for signal stability involve only the differences in signal costs and not the absolute signal costs.

This said, we define the difference in signal cost between signal A and signal B as the change in fitness that results from sending signal B instead of signal A, with the response of the signal receiver held constant. (In the present model, signal cost is independent of the receiver response; in other models the two may co-vary. In that case, signal cost can be defined only with respect to a particular receiver response.) Notice that, because receiver response is held constant under this definition, signal cost refers only to the fitness consequences that do not result from the actions of the intended receiver, i.e., to what Hasson (17) labels the basal fitness or F-component of the signal. For example, if we are interested in nestling begging, signal costs include the energetic costs of production and the costs of predation by unintended receivers of the signal but not the costs or the benefits arising from the responses of the intended receivers, the parents. We now also can define “cost-free”: we say that signaling can be cost-free when it remains stable even as differences in the signal costs go to zero. In this paper, we demonstrate that signaling among relatives can be cost-free, even when the interests of the signaler and signal-receiver sometimes conflict. We do not argue that, in practice, signals can be produced physically at zero cost (although this is not an unreasonable possibility). We only argue that cost is not necessary for signal stability, i.e., that signals can be stable even if their costs (relative to no-signaling) are zero. We show that empirical evidence of low signal cost is not in conflict with theoretical models of honest signaling.

The SPS Game.

In this paper, we use a general form of the continuous SPS game described in Johnstone and Grafen (7) and in Signaling I as a model of signaling of need among relatives. In the discussion that follows, we assume that each player tries to maximize inclusive fitness and that the shared interest between the two players arises from kin selection; similar conclusions would follow from other forms of shared interest as well (8). In the two-player SPS game, an individual called the donor is in command of a single indivisible resource, which the individual either can keep for individual use or transfer to the second player, a relative. This second player, the signaler, can influence the donor’s decision by signaling a need for the resource. Here, we formulate the game as in Section 4 of Signaling I. Signaler and donor, related by coefficient of relatedness k, have fitnesses of x and y, respectively, in the absence of the resource. Signaler and donor fitnesses are drawn from probability distributions P and Q, with probability densities p(x) and q(y), both on [0, 1]. If the donor retains the resource, the donor’s (personal) fitness will be 1 and the signaler’s (personal) fitness will be x. If the donor donates the resource, the donor’s fitness will be y and the signaler’s fitness will be 1 minus the cost of any signal sent. The signaler can choose to send a signal of need with cost c ≥ 0.

As mentioned in the introduction, a signaling equilibrium is a Nash equilibrium pair of signaler and donor strategies. In the SPS game, the signaler’s strategy specifies what to signal for each possible condition, and the donor’s strategy specifies whether to give the resource to the signaler, conditional on the received signal and the donor’s condition. As derived in Signaling II, the only possible equilibrium strategies for the signalers associate each signal with a contiguous pool of fitnesses. That is, only signalers between a certain minimum fitness and a certain maximum fitness will send a given signal, and no signaler in this range will send any other signal. At equilibrium, donors will respond to each signal as they would to a signaler whose fitness was known to be the average fitness of individuals sending that particular signal.

A Trivial Example of Cost-Free Signaling.

In analyzing the SPS game, it is helpful to consider a diagram such as Fig. 1. Each point on the graph represents a signaler–donor pair. The signaler’s condition without the resource is given by the x axis, and the donor’s condition is given by the y axis. At any point below line a, the donor has a higher inclusive fitness if the donor keeps the resource; above line a, the donor has a higher inclusive fitness if the donor donates it. Below line b, the signaler has a higher inclusive fitness if the donor keeps the resource; above line b, the signaler has a higher inclusive fitness if the donor transfers it.

Fig. 1 illustrates a situation in which signaling can be cost-free, very similar to the case described by Maynard Smith (8). In this system, there is only one type of donor, with fitness D, and two types of signalers. One signaler type has a high fitness H even without the resource. Such a signaler actually would suffer a reduction in inclusive fitness were the donor to transfer the resource because the point (H, D) lies below line b. The other type of signaler has a low fitness N. A donor benefits from transferring to such a signaler because (N, D) lies above line a. If each signaler type were to signal her or his condition, the donors would give the resource only to the signalers with fitness N. No signaler would benefit from sending the signal of the other type, so signaling can be cost-free.

Cost-Free Signaling in the Continuous SPS Game.

Cost-free signaling also can be stable when signaler and donor fitnesses are distributed continuously over the interval 0 to 1. For example, when donors as well as signalers are uniformly distributed, there exists a partition into two pools, each sending a cost-free signal: [0, a] and (a, 1], where a = (4 − 3k²)/(4 − 2k²) and k is the coefficient of relatedness (Appendix A). In fact, for any continuous distribution of donors and signalers, if both the best and worst signalers rather would reveal their exact quality than be thought of as having the average quality of the population, then there exists a signaling equilibrium in which the signalers divide themselves into two or more pools, with no signal cost (Appendix B).

Cost-free signaling equilibria need not have exactly two pools. The completely pooling (or “no-signaling”) equilibrium, in which all signalers send the same zero-cost signal, is a cost-free signaling equilibrium with one pool. In the system with a uniform distribution of signalers and donor fitnesses on [0, 1] [as in Johnstone and Grafen (7)], there are also equilibria with 2, 3, 4, or any number of signals, all without cost. In the three-signal equilibrium, the signals can be interpreted as follows: The first indicates need, the second indicates that the signaler does not want the resource, and the third indicates that the signaler does not want the resource even from the donors who willingly would transfer the resource in response to the second signal. There also is an equilibrium with an infinite number of signals, each with zero cost. Table 1 shows the locations of the pool boundaries in the cost-free partitions with 2 through 5 separate pools, for this system. Fig. 2 shows the average fitness of the signaler for several cost-free signaling partitions, compared with the no-signaling and separating equilibria. Fig. 3 shows the average fitness of the donor for the same partitions.

Table 1.

Locations of the boundaries between pools for partitions with 2, 3, 4, and 5 cost-free signals in the SPS game with signalers distributed uniformly on [0, 1] and k = 0.75

	Pool boundaries
Two pools	0.804	–	–	–
Three pools	0.797	0.960	–	–
Four pools	0.796	0.959	0.992	–
Five pools	0.796	0.958	0.992	0.998

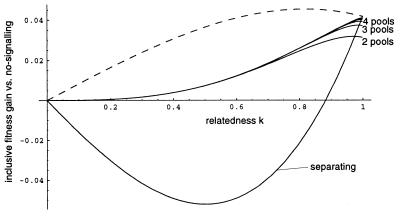
Figure 2.

Fitness advantage of the signaler relative to the no-signaling equilibrium, as a function of the coefficient of relatedness k in the SPS game with signalers distributed uniformly on [0, 1]. The dotted curve is for complete information transfer at no cost, which we have included to illustrate the efficiency of the cost-free equilibria. The lowest curve is for complete information transfer, at the cost necessary to enforce the separating equilibrium. Intermediate curves are for partitions with 2, 3, 4, etc., cost-free signals.

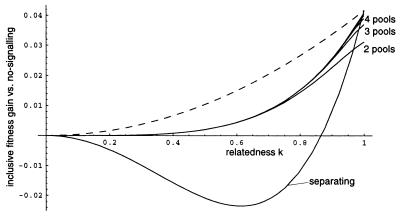
Figure 3.

Fitness advantage of the donor relative to the no-signaling equilibrium, as a function of the coefficient of relatedness k. As in Fig. 2, the dotted curve is for complete information transfer at no cost, and the lowest curve is for complete information transfer at the cost necessary to enforce the separating equilibrium. Intermediate curves are for partitions with 2, 3, 4, etc., cost-free signals.

These figures show that, in this system, cost-free signaling with two or more pools is actually better for both signaler and donor than is the completely pooling equilibrium. Moreover, the completely pooling equilibrium is better than the separating equilibrium—as demonstrated in Signaling I, where we considered only the lowest (completely separating equilibrium) curve of Figs. 2 and 3. This result illustrates the potential utility of cost-free signaling among relatives and, additionally, highlights a major corollary of the results from Signaling II: Pooling equilibria can be better for both signaler and donor than are either separating or no-signaling equilibria. For biologically reasonable k values (k ≤ 0.75), there is little or nothing to be gained from having more than two pools if only cost-free signals are used. This reinforces Johnstone’s argument (19) in favor of “all-or-nothing” signals—signals that are binary, rather than graded. In the present model, however, perceptual error is not necessary to ensure the stability of these all-or-nothing signaling equilibria. In the example of Fig. 1, there is no conflict of interest between signaler and donor; both benefit directly from honest communication. As noted by Maynard Smith, however, signals can be cost-free even when signalers have a conflict of interest with some of the donors (8). Fig. 4 illustrates this point. Notice that bimodality of the signaler distribution is not required.

Additionally, we should clarify the discrepancy between our results and those of Maynard Smith (8, 18). Although we find cost-free signaling to be possible with very liberal conditions on signaler and donor distributions, Maynard Smith argues that, barring extreme cases, cost-free signaling is only possible when distributions of signaler quality are not unimodal. Maynard Smith’s claim is correct given an assumption made in his model—that all donors respond uniformly to a given signal. This need not be the case in nature, however, because the donor’s internal state as well as the signal received may play a role in determining the donor’s response. We therefore abandon this assumption in our formulation and find that as a consequence, cost-free signaling is obtained readily even for uniform and unimodal distributions of signaler quality.

2. Costly Signaling in the SPS Game

In the previous section, we have shown that under very liberal conditions on signaler and donor distribution, cost-free signaling equilibria exist in the SPS game. However, we do not want to imply that there will never be costly signals in this game. As discussed in Signaling II, many different signaling equilibria are possible, and, without modeling the dynamics of signal evolution, there is no way to predict which of these equilibria will be selected by the evolutionary process. We emphasize that cost-free signaling (or no-signaling) will not always be optimal; in some cases, costly signaling will be better than cost-free signaling for both signaler and donor. We present such a case below.

Consider the example illustrated in Fig. 5. There is a single type of donor, with fitness D. Signalers are continuously distributed on [0, 1] with probability density p(x). D is sufficiently low that, in the no-signaling equilibrium, the donor will keep the resource. Notice that, because there is only one donor type, there will never need to be, in practice, more than two pools of signalers—one that receives the resource from this donor, and one that does not. If there are two cost-free pools, the boundary between them must lie at point A (otherwise there will be incentive for some signalers to change strategy). Given a split at A, the mean fitness of signalers the “needy” pool covering [0, A] is given by N, and the mean fitness of signalers in the healthy pool covering (A, 1] is given by H.

Figure 5.

A system in which costly signaling is better for signaler and donor than is cost-free signaling. Axes are as in Fig. 1. Signalers have fitnesses on [0, 1] with probability density function p(x), and all donors have fitness D. There can be no cost-free signaling equilibrium other than the no-signaling equilibrium; the costly signaling equilibrium with two pools, divided at B, is better for both players.

Donors, with fitness D, will not transfer to signalers at N or H, and hence if the pool boundary is at A, neither pool will receive the resource from the donors. We then have, in effect, the completely pooling (no-signaling) equilibrium; there can be no cost-free signaling equilibrium in this system other than this single-pool equilibrium.

Therefore, we have only costly signaling equilibria and the single-pool (no-signaling) equilibrium as possible equilibria in this system. To see that the costly signaling is optimal, we now need only demonstrate that there exists a costly signaling equilibrium that is better for both signaler and donor than this completely pooling equilibrium. Again, we examine partitions with two pools, one that receives the resource from the donors and one that does not.

Consider two pools, with their boundary at signaler fitness B = 1 + (D − 1)/k as shown in Fig. 5. This partition essentially gives the donors complete information because the signalers are partitioned precisely into those whom the donors wish to aid and those whom the donors wish to ignore. This partition is obviously better for the signalers than the no-signaling equilibrium because each signaler could choose not to signal and then would fare exactly as at the no-signaling equilibrium. It is also better for the donors. They gain essentially complete information, and the cost—if less than the benefit for the signalers—is certainly likewise for the donors. This result is not dependent on there being only a single donor quality level, as can be demonstrated by considering a band of donor fitnesses around fitness D.

3. Implications

Above, we have shown that reliable cost-free signaling among relatives is obtained easily in the SPS game and that signaling, even when costly, may not be as costly as predicted by separating equilibrium models. This analysis may explain recent results from empirical tests of costly signaling theory. Many of these studies have focused on the begging calls of nestlings, which have been suggested to be costly signals of need, in the vein of the SPS model (4, 6, 9, 20). Empirical studies confirm that many of the assumptions of the costly signaling model are met by nestling begging [reviewed by Kilner and Johnstone (21)]. Nestlings that beg are more likely to be fed than those that do not (22, 23). Begging level correlates with hunger level (refs. 23 and 24 and references therein). Moreover, provisioning the offspring is costly to the parents, in terms of mortality risk (25), status in subsequent years (26), reduction of further mating opportunities (27), and reduced immune system function (28). Harper (4) and Godfray (9) summarize additional supporting evidence.

Although measuring the cost of signaling in the field is extremely difficult (29, 30), recent evidence suggests that begging signals may not be as costly as would be expected from the theoretical models. Leech and Leonard (31) and McCarty (32) measured the oxygen consumption rates of resting and actively begging nestling passerines (paying particular attention to tree swallows Tachycineta bicolor and European starlings Sturnum vulgaris). They found that, although there was a slight cost of begging (≈28% and 5% above resting metabolic rate for tree swallows and starlings, respectively), begging behavior was not nearly as expensive as might be expected to be necessary in maintaining honest signaling. Weathers et al. (29) report similar results in zebra finches. Horn et al. (33) and Chappell et al. (34) found low energetic costs for crowing behavior in roosters and jungle fowl; other authors (ref. 35 but see refs. 36 and 37) argue that singing in adult passerines is also relatively inexpensive. On the other hand, because singing requires time free from foraging activity (35), it could be a costly signal of leisure sensu Veblen (38) featuring opportunity cost rather than energetic cost. Although increased predation risk may account for some of the signal cost, evidence suggests that this risk plays an important role only in ground-nesting birds (ref. 39 but see ref. 40).

Such results lead McCarty (32) to suggest that the application of signaling theory to begging behavior must be viewed with caution. We argue otherwise. Our results from the previous sections demonstrate that the basic framework used to model costly signaling can generate predictions in accord with these empirical results, namely, that signaling in such situations can be cost-free or relatively inexpensive. Because cost-free and inexpensive pooling equilibria are prevalent and relatively efficient solutions to the SPS problem, we should not be surprised to find that measured signal costs for this type of communication are low.

4. Discussion

Costly signaling systems allow two types of equilibria: separating equilibria, in which distinct signalers send distinct signals, and pooling equilibria, in which some distinct signalers share common signals. With one exception, previous models of signaling among relatives have considered only separating equilibria. Maynard Smith’s model (8) is effectively a model of pooling equilibria and consequently reveals—for the special case of bimodally distributed signaler fitness—the possibility of free signals. Here, we demonstrate more generally that, when pooling equilibria are considered, reliable cost-free signaling is possible, and in fact quite efficient, in systems of signaling among relatives.

Recent empirical studies have revealed low signal costs in signaling among relatives and have led some researchers to question the applicability of signaling theory to behaviors such as nestling begging. Our results demonstrate that these low signal costs are indeed predicted by the signaling theory; we argue therefore that signaling theory is indeed an appropriate framework for modeling nestling begging behavior.

Previous authors also have attempted to provide a theoretical basis for cost-free signaling among relatives. Maynard Smith’s model (8) has been discussed above. The other models generally rely on special features of the signaling system. Hurd (41) considers models in which signal cost depends on the quality of the signaler and points out that high signal costs need not actually be expressed to maintain signal reliability. Some signals may be cost-free to desirable signalers but very costly to less desirable signalers. This cost structure can produce an equilibrium in which only those who can signal at no cost choose to signal. Krakauer and Pagel show that, in a spatially structured model, population viscosity allows for stable cost-free honest signaling (42). Viljugrein shows that cost-free signaling can be stable when “lies” can be detected and subsequently punished (43).

Our results serve to answer two theoretical criticisms of signaling theory, as well. Dawkins and Guilford (44) argue that, to be effective, signaling must involve stern viability costs, and consequently natural selection will often oppose signal reliability. Our results, and those of the authors mentioned immediately above, demonstrate that strong viability cost is not the factor that makes signals reliable and that high cost is not necessary for honest communication. Indeed, we demonstrate that, despite some conflicting interests, a great deal of information can be sent cheaply or even for free. Having established this, we predict that signaling will be even more prevalent than previously expected precisely because it does not need to clash so strongly with direct viability selection.

Another valid concern is pointed out by Godfray (9): Costly signaling equilibria are unstable to mutations that reduce signal cost without altering signal form. If evolutionary innovations that reduce signal cost are possible, costly signaling equilibria will not be stable in the long term and we might expect reliable signaling to be relatively uncommon. The existence of cost-free signaling equilibria alleviates this concern; even as signal costs decline to zero, reliable information transfer remains possible. Cost-reducing innovations should cause signaling systems to approach the cost-free equilibria rather than to decay entirely.

Given the results of our analysis, how should we expect pooling equilibria to be expressed in nature? We suggest that often the least needy signalers pool together, sending the least costly signal (usually, that which we call no-signaling). In a nest of begging baby birds, for example, several birds may exhibit no pronounced begging behavior when the mother arrives at the nest, despite varying hunger levels. These birds form a pool sharing a common signal. An additional, testable prediction of this theory is that signaling systems may feature fewer signals, and subsequently less costly signals, than is suggested by models exhibiting only the separating equilibrium. We predict that the amount of information transferred in signaling interactions will be less than that suggested by separating equilibrium models.

Finally, we emphasize that our results are not in conflict with the Zahavi/Grafen signaling honest signaling framework. Rather, this framework is demonstrated to be more broadly applicable than previously realized, in that it predicts the existence of numerous cost-free signaling equilibria, as well as the costly signaling equilibria that it was designed to treat.

Appendix

A. We demonstrated in Appendix 1 of Signalling II that, when the distribution of signaler and donor qualities is uniform on [0, 1], a stable pooling equilibrium exists with two pools, X₁ = (a, 1] and X₂ = [0, a]. The difference in signal costs for partitions X₂ and X₁ is then c₂ − c₁ = k/2(1 − a + k²(a/2 − 3/4)). Cost-free signaling is possible when c₂ − c₁ = 0, i.e., when the boundary between the two pools is located at a = (4 − 3k²)/(4 − 2k²).

B. Consider any continuous distribution of signallers with range [m, n] where 0 ≤ m < n ≤ 1. Split this range at x to form two pools, X₂ = [m, x] and X₁ = (x, n]. Define the function f(x) = c₂(x) − c₁(x) as the difference in signal costs when the boundary between these pools lies at x. Because a signaler with condition m rather would be judged to be at m than as the mean for the whole [m, n] interval, f(m) > 0. Similarly, because a signaller at n rather would be judged to be at n than at the mean for the whole interval, f(n) < 0. It follows from the intermediate value theorem and the continuity of f that there exists a point a with f(a) = 0, i.e., with c₂(a) = c₁(a). Here, cost-free signaling is stable. A parallel argument can be used to show that, whenever there is a stable cost-free partition with n pools, there also exists a stable cost-free partition with two pools.