Evaluation of Ion Binding to DNA Duplexes Using a Size-Modified Poisson-Boltzmann Theory

Abstract

Poisson-Boltzmann (PB) theory is among the most widely applied electrostatic theories in biological and chemical science. Despite its reasonable success in explaining a wide variety of phenomena, it fails to incorporate two basic physical effects, ion size and ion-ion correlations, into its theoretical treatment. Recent experimental work has shown significant deviations from PB theory in competitive monovalent and divalent ion binding to a DNA duplex. The experimental data for monovalent binding are consistent with a hypothesis that attributes these deviations to counterion size. To model the observed differences, we have generalized an existing size-modified Poisson-Boltzmann (SMPB) theory and developed a new numerical implementation that solves the generalized theory around complex, atomistic representations of biological molecules. The results of our analysis show that good agreement to data at monovalent ion concentrations up to ∼150 mM can be attained by adjusting the ion-size parameters in the new size-modified theory. SMPB calculations employing calibrated ion-size parameters predict experimental observations for other nucleic acid structures and salt conditions, demonstrating that the theory is predictive. We are, however, unable to model the observed deviations in the divalent competition data with a theory that only accounts for size but neglects ion-ion correlations, highlighting the need for theoretical descriptions that further incorporate ion-ion correlations. The accompanying numerical solver has been released publicly, providing the general scientific community the ability to compute SMPB solutions around a variety of different biological structures with only modest computational resources.

INTRODUCTION

The electrostatic interactions between biological macromolecules such as proteins and nucleic acids and their associated ion atmospheres play important roles in a variety of cellular processes. Quantitative understanding of these electrostatic effects is a necessary part of any theoretical treatment of biological processes at the molecular level. Poisson-Boltzmann (PB) theory has become a standard tool in biology for elucidating the role of electrostatics in biomolecular interactions. Its mean-field approach to electrolyte interactions and continuum solvent model is simple and computationally tractable.

The increasingly diverse application of PB theory is partially the result of the growing availability of software routines designed to solve PB for complex biological systems (1,2). PB theory has been used, among other things, to analyze fundamental nucleic acid processes (3,4), RNA folding (5,6), ligand binding and protein association to nucleic acids (7), the role of histone tails in chromatin and nucleosomes (8,9), and other applications (10).

Despite its wide applicability, PB theory suffers from two limitations: it does not include ion size or ion-ion correlations in its treatment. In the PB framework, solvated ions are characterized only by their valences as point charges that interact with an averaged electrostatic potential. The simplistic treatment greatly facilitates computation but precludes an accurate treatment of ion behavior. In particular, ions of different sizes but equal valences are treated identically in PB theory, even though differences in diffuse ion binding to polyelectrolytes and nucleic acids have been observed experimentally (11–13).

Many efforts have been made to model size effects in electrolyte solutions. These theories use a variety of different strategies, including exclusion layer models (where ions are forbidden from approaching within a certain distance), Monte Carlo, and mean-field approaches (14–18). These strategies suffer from several different drawbacks. Simple exclusion layer models cannot be applied to a complex mixture of ions with different sizes and do not account for excluded volume effects among the ions. In principle, Monte Carlo approaches can be very accurate, but at a high computational cost, making the approach impractical for high-throughput computation on ensembles of structures or salt conditions. Other theoretical approaches require simplification of the molecular geometry or lack a general implementation that is available to the scientific community.

In solution, ions interact via long-ranged Coulomb interactions and a short-ranged, hard-core repulsion, characterized by the size of the ions (14). To address the lack of size in PB theory, we extend the lattice gas approach of Borukhov et al. (16) by generalizing their result for a single ion size to the case of two ion sizes, a necessary development of the theory if we are to model the competition between two ions of different size as is typically the situation in experiments and in vivo. In our theoretical approach, the hard-core repulsion between solvated ions is approximated with an excluded volume term in the free energy density of a lattice gas model of the ionic solution. We have implemented this size-modified Poisson-Boltzmann (SMPB) theory in a numerical solver by modifying the widely available Adaptive Poisson-Boltzmann Solver (APBS) (19). This implementation has been made publicly available to the scientific community.

In the following sections, we apply SMPB to analyze competitive nonspecific binding of two ion species to a DNA duplex where size effects cause significant departures from PB theory (12) and show that it can be used to account for differences in monovalent association for ions of different sizes and monovalent ion concentrations ≤150 mM. Furthermore, we show in some relatively simple cases that SMPB theory can be generalized to analyze other nucleic-acid structures, especially in situations where an accurate treatment of ion size is necessary. Accurate treatment of divalent cations remains elusive in a mean-field framework, due to the neglect of ion-ion correlation, necessitating further advances in theory.

METHODS

Derivation of the SMPB equation

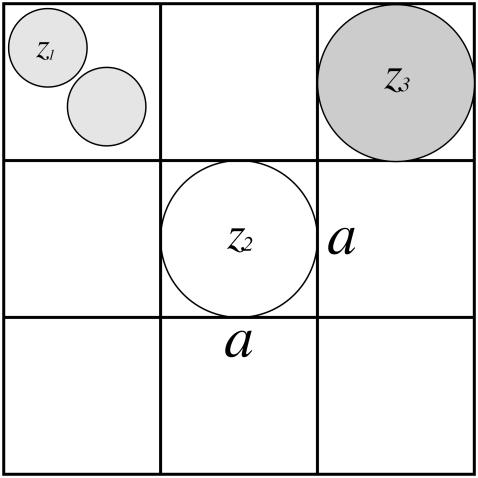
Following Borukhov et al., we treat the ionic solution as a simple lattice gas to approximate the excluded-volume effects of the ions in solution (16). However, we extend their work by generalizing their result to treat asymmetric ion sizes and writing a numerical implementation that deals with arbitrary geometries. In the lattice gas formalism, the domain around the charged biomolecule is treated as a three-dimensional lattice with N evenly spaced points a apart. This characteristic lattice spacing a sets the volume of the larger ions at a³ while a dimensionless parameter k sets the volume of the smaller ions at a³/k. For concreteness, assume that ion species 1 is the smaller ion species with volume a³/k and that ion species 2 and 3 are the larger ion species, both with volume a³ (Fig. 1).

FIGURE 1.

Schematic illustration of the lattice gas model. The lattice size a sets the size of the species with valences z₂ and z₃ while the k parameter (in this case, k = 2) sets the relative size of the smaller ion with valence z₁.

The size parameters a and ak^−1/3 are the cell-size parameters of the larger and smaller ion species and can be adjusted to fit experiments. The ion-size parameters must be understood as adjustable parameters and do not correspond to formal notions of hydrated ion structure (e.g., hydration shells). Instead, the ion-size parameters act as effective ion sizes, reflecting how ions behave in solution. Once calibrated against experiments, the ion-size parameters have predictive power for monovalent ion concentrations ≤150 mM, as demonstrated later in the article.

Consider a charged biomolecule in an ionic solution with three species with valences z₁, z₂, and z₃, and bulk concentrations 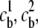and 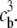The biomolecule is described by a fixed charge density ρ_f and a solvent accessibility function 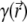that is zero for points 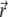inaccessible to the solvent and unity for solvent-accessible points.

For integral k, each lattice site can contain at most a single ion of volume a³ or k ions of volume a³/k. Proceeding from this assumption, the grand partition function for each lattice site (enumerating all possible occupancies of the lattice site) is given by

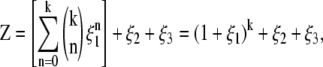(1)

where ξ_i = exp ((μ_i – z_ieψ)/k_BT), μ_i is the chemical potential of species i, e is the fundamental charge, ψ is the electrostatic potential at a lattice site, k_B is Boltzmann's constant, and T is the absolute temperature. Note that SMPB, like PB, treats the ion-ion interaction with a mean-field approximation, neglecting ion-ion correlations.

The relationship between the bulk concentration 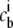and the chemical potential of each species μ_i is obtained by deriving the grand partition function with respect to the chemical potential:

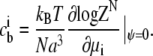(2)

The chemical potentials μ_i as a function of the bulk concentrations 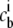can be obtained by inverting Eq. 2. The average concentration at each lattice site with electrostatic potential ψ is obtained similarly:

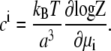(3)

The average concentration at each lattice site can then be substituted into Poisson's Equation:

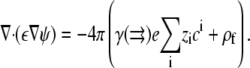(4)

Combining Eqs. 2–4 and rewriting the electrostatic potential in dimensionless units u = eψ/k_BT yields the SMPB equation,

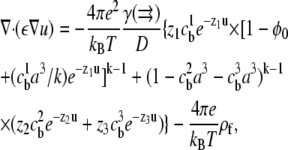(5)

where 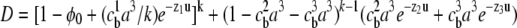and 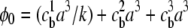is the fractional occupancy of each lattice site in the bulk. In the limit of k → 1 (equal-sized ions), Borukhov's result is obtained (16). Although Eq. 5 was derived for integral k, the continuity of the grand partition function for nonintegral k allows us to choose any real value of k and therefore any two arbitrary ion sizes. An expression for the free energy density of the lattice gas, with an explicit treatment of excluded volume effects, is presented in Eq. 7 of the Supplementary Material and can be employed to compute the free energy due to the electrostatics of the ion atmosphere.

Numerical implementation

Several numerical solvers have been developed to solve the PB equation (19,20). We chose to implement the SMPB equation by modifying the Adaptive Poisson-Boltzmann Solver (APBS), an open source software package developed by Baker et al. to solve the PB equation numerically around complex all-atom representations of biological macromolecules (19). An implementation of the SMPB theory is available on the APBS web site (http://apbs.sourceforge.net/).

All simulations employed all-atom PDB models of the nucleic acid structure with atomic partial charges and radii assigned by the CHARMM force field (21,22) with the PDB2PQR utility (23), a standard part of the APBS package. The 24- and 44-bp DNA duplex models were created with the Nucleic Acid Builder software package in the standard B-form geometry (24). The 24-bp triplex model was created by axially stacking the solution structure of an 8-bp DNA triplex (PDB ID code 1D3X) three times using the average rise/base and twist/base of the triplex to translate and rotate the stacked triplexes to achieve correct alignment (25).

We solved the SMPB equation on a 192 × 192 × 225 Å grid with 128 × 128 × 225 points (1.5 Å grid spacing). Solvent points were assigned a dielectric value of ε = 78.54 and ε = 2.00 to DNA duplex points. Boundary condition values were determined using the Debye-Hückel approximation. In all calculations, the box size was large enough so that charge neutrality did not vary by >1.3%. Control calculations that varied force field (AMBER instead of CHARMM), internal dielectric, grid spacing (0.5, 1.00, 1.50, and 2 Å), and box size (multiplying box dimensions by a factor between 0.66 and 1.3) varied the computed ions counts insignificantly. The interior of the molecule was defined as the union of spheres centered on the atomic positions with radii equal to the van der Waals radius of the atom, plus a solvent probe radius of 1.4 Å. The ion accessible region was defined similarly as the Van der Waals radius plus a Stern layer of 2.0 Å. Further details regarding the calculation may be found in the Supplementary Material. The modified and unmodified versions of APBS have similar processor and memory demands, requiring ∼10 min on an Intel Xeon 3.06 GHz processor to calculate the ion binding at one salt and size condition, well within the reach of many researchers. On highly optimized systems such as the Jacquard cluster at the National Energy Research Scientific Computing Center, each calculation only required 3 min on a single processor, opening the possibility of high-throughput calculation on a large number of structures, salt, and size conditions.

Size parameter calibration

To calibrate the size parameters in SMPB, we analyzed the results of experiments conducted by Bai et al. on the competition between two cation species around a 24-bp DNA duplex (12). In their experiments, a positively-charged competing counterion (CC) species was titrated against a background counterion (BC) species held at fixed concentration. In the experiments, both BC and CC shared the same anion. As the concentration of CC was increased, it gradually replaced the BC in the mobile ion atmosphere around the duplex. The number of each cation species accumulated around each duplex was determined by atomic emission spectroscopy and a competition constant for each CC was computed from the results. (Note that, following the convention established in (12), we define the competition constant as the [M]_1/2 obtained from fitting the BC titration curve to an empirical two-state model: 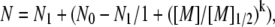where N₀ and N₁ are the number of BC at start and end states.) Bai et al. have quantitated the number of monovalent CC (5–500 mM Li⁺, K⁺, or Rb⁺) titrated against a monovalent BC (50 mM of Na⁺). Ion counts were also obtained for a divalent CC (0.1–50 mM of Mg²⁺, Ca²⁺, Sr²⁺, or Ba²⁺) against monovalent BC (20 mM of Na⁺), as well as divalent CC (0.2–10 mM of Ca²⁺, Sr²⁺, or Ba²⁺) against divalent BC (2 mM Mg²⁺) (12).

The size parameters were calibrated by fitting the theoretical predictions for the monovalent cation accumulation against the experimental results with a minimum-χ² search. Size parameters for Li⁺, Na⁺, K⁺, and Rb⁺ were allowed to vary independently in 0.5 Å steps between 1 and 10 Å. The hypothetical ion-binding curves for each combination of sizes was compared to experiment until the global deviation from experiment—defined as the sum of the squared differences of the number of CC and BC accumulated between experiment and theory—was minimized. It is important to note that no prior assumptions were made on the ordering of ion size parameters (e.g. we did not assume that Li⁺ was smaller than Na⁺). In total, ∼60,000 individual SMPB calculations were computed in the course of the study, covering the different combinations of size, ion concentration, and structure.

The number of an ion species i associated with the DNA duplex at each size and concentration condition was computed from SMPB theory using the following integral over the solution domain Γ (numerically approximated by a sum over grid points):

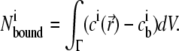(6)

In the case where the size of the CC was less (greater) than the size of the BC, the ion counts were calculated with the CC as species 1 (2) and the BC as species 2 (1) in Eq. 5. In all cases, the co-ion was treated as species 3. Although the size of the co-ion in the model varies, control experiments performed by Bai et al. show that the size of the co-ion does not significantly affect its preferential exclusion (12).

Due to the unknown dependence of the χ² on the fitted ion size parameters, we chose not to use the general least-squares fitting procedure to establish confidence bands on the fitted size parameters. Instead, as a more robust test of our confidence bands, we used a bootstrapping strategy (26). From the original experimental monovalent dataset, we generated 2000 simulated experimental datasets by randomly selecting data points with repeats. Subjecting these 2000 datasets to the same fitting procedure allowed us to probe the distribution of the fitted parameters and establish confidence bands on them, which we defined to be one standard deviation from the average value.

RESULTS AND DISCUSSION

Analysis of monovalent competition

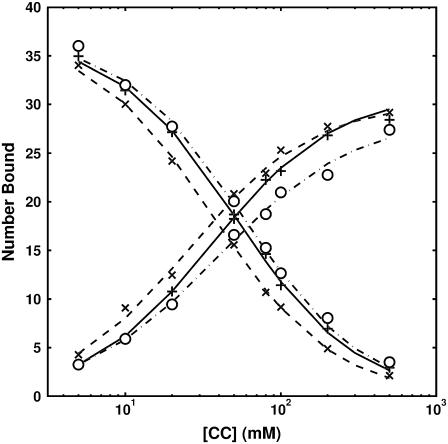
Fig. 2 displays experimentally observed ion binding curves for Li⁺, K⁺, and Rb⁺ against a fixed background of 50 mM Na⁺. In the PB treatment, all monovalent ions are treated identically and therefore no difference in titration curves or competition constants between different ion species is predicted; however, the experimental results (Fig. 2) display deviations from this theoretical prediction. Although the deviations are not large, they are not explained by random experimental error and represent statistically significant departures from idealized PB behavior. Furthermore, the order of competition constants (Li⁺ < K⁺ < Rb⁺) suggests a size-mediated effect (12).

FIGURE 2.

Experimental competitive ion binding curves between monovalent cations and 50 mM Na⁺ (12). Monovalent cations tested: Li⁺ (×, dashed), K⁺ (+, solid), Rb⁺ (○, dash-dot). Plotted curves are the best-fits of the data to an empirical two-state model. (Note that, following the convention established in (12), we define the competition constant as the [M]_1/2 obtained from fitting the BC titration curve to an empirical two-state model: 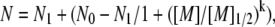where N₀ and N₁ are the number of BC at start and end states.) For all curves, as the bulk concentration of CC is increased, the CC is bound preferentially over the BC. Therefore, all of the CC curves increase while the BC ones decrease. The competition constants for each species are not identical for monovalent ions, in disagreement with the PB prediction. The order of the competition constants suggests a size-mediated effect.

The difference in affinity between ion species (determined by comparing competition constants) can be intuitively explained by considering a simple size-modified picture: larger CC have a harder time packing around the DNA duplex and neutralizing the negatively charged phosphate backbone than smaller CC, increasing their competition constants relative to smaller CC.

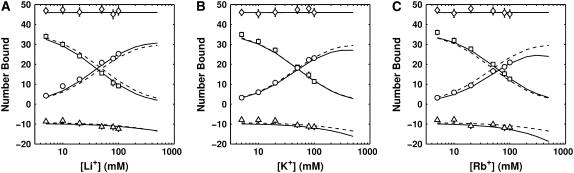
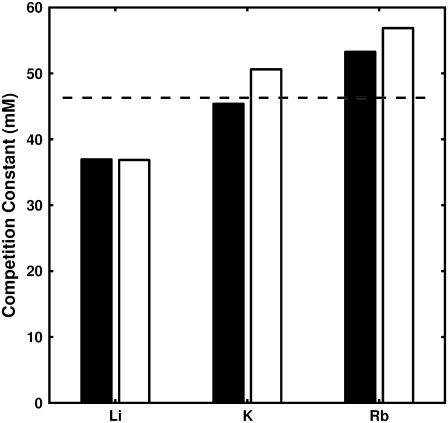
To calibrate the SMPB size parameters, simulated titration curves were generated for the Li⁺, K⁺, and Rb⁺ (competing against fixed 50 mM Na⁺) monovalent datasets. The simulated binding curves were then subjected to the calibration procedure described in Methods; the best fits are plotted in Fig. 3. Competition constants (see Size Parameter Calibration, above), derived by fitting the best-fit BC titration curve to an empirical two-state model, are plotted in Fig. 4.

FIGURE 3.

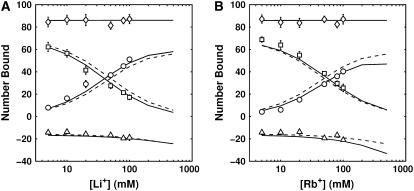
Best-fit ion binding curves for BC = 50 mM Na⁺, CC = Li⁺ (A), K⁺ (B), or Rb⁺ (C), competing around a 24 bp DNA duplex. Net charge (⋄), CC (□), fixed BC (○), and co-ion (▵). SMPB, computed with best-fit ion-size parameters (Table 1) is plotted with solid lines while unmodified PB theory is plotted with dashed lines.

FIGURE 4.

Comparison of competition-constants obtained by fitting experimental data (solid) and SMPB-predictions (open) to an empirical two-state model. The single PB prediction for the monovalent competition constant is denoted by the dashed line.

SMPB theory predicts both the total number of CC and BC bound as well as the competition constants far better than PB. Using reduced χ² as a statistical measure of goodness-of-fit with ν as the number of degrees of freedom, SMPB yields significantly improved fits over PB (χ²/ν = 1.13 for SMPB versus χ²/ν = 2.45 for PB). In this case, the χ² statistic reflects discrepancies arising from experimental error and the approximations made in the theoretical model. If P is the probability that random fluctuations explain the observed deviations between model and experiment, from the standard χ² distribution, this corresponds to P = 0.28 for SMPB and P = 2.8 × 10⁻⁶ for PB theory.

We employed the bootstrapping analysis described in Methods to establish confidence bands on calibrated size parameters. The results of the bootstrapping analysis are presented in Fig. 7 and in the Supplementary Material. The bootstrapping analysis shows that the distribution of each calibrated size parameter is tightly clustered around an average size which differs from the calibrated size parameters by, at most, 5%. The calibrated size parameters from fitting and confidence bands from bootstrapping are presented in Table 1.

FIGURE 7.

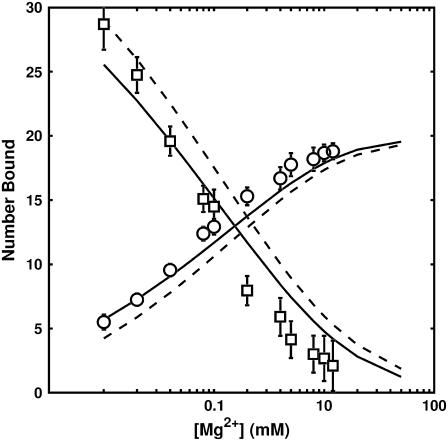
Global best-fit ion-binding curves for Mg²⁺. Mg²⁺ (○), Na⁺ (□). SMPB is plotted with solid lines while PB theory is plotted with dashed lines.

TABLE 1.

Summary of size parameters obtained from fitting and bootstrapping for Li⁺, Na⁺, K⁺, and Rb⁺

	Best-fit (Å)	Bootstrap (Å)
Li+	1.00	1.00 ± 0.03
Na+	7.16	7.00 ± 0.36
K+	7.42	7.30 ± 0.53
Rb+	9.47	9.39 ± 0.22

It is important to note that these ion-size parameters do not correspond to physical ion sizes; rather, they describe how ions behave in solution. Therefore, direct comparisons with published data on hydrated size cannot be made; however, the order of fitted ion-size parameters is consistent with the order of the radii of the first hydration shell (i.e., Li⁺ behaves smaller than Rb⁺) (27).

We have tentatively tested SMPB's predictive ability in alternate nucleic acid structures and salt conditions by using the calibrated ion-size parameters to predict ion-binding curves for a limited set of other preliminary experimental data. Using size parameters obtained from the training data set (24-bp duplex in 50 mM Na⁺), we made predictions for Li⁺ and Rb⁺ (competing against fixed 50 mM Na⁺) around a 44-bp duplex and a 24-bp triplex to test different structures and for Li⁺ and Rb⁺ (competing against fixed 10 mM Na⁺) around a 24-bp duplex to test an alternate salt condition. Table 2 compares the reduced χ² statistic for SMPB and PB predictions.

TABLE 2.

Comparison of reduced χ² values for SMPB and PB predictions for Li⁺ and Rb⁺ titrations for different nucleic acid structures and salt conditions

	SMPB*	PB
44-bp Duplex (50 mM Na+)	1.40	5.62
24-bp Triplex (50 mM Na+)	1.30	7.28
24-bp Duplex (10 mM Na+)	2.94	2.98

^*Computed using calibrated size parameters obtained from fitting the 24-bp duplex (50 mM Na⁺) dataset (Table 1).

SMPB is able to predict the observed titration curves obtained for different nucleic acid structures far better than PB, judged by comparing the reduced χ² statistic and by examining the predicted concentration dependence of binding (Fig. 5, and Fig. 8 in the Supplementary Material). At the alternate 10 mM fixed Na⁺ salt condition, SMPB yields a slightly better fit than PB (Fig. 9 in the Supplementary Material). However, the discrepancy between PB and experiment is not very large to begin with, probably due to the fact that excluded volume effects become less important at lower ion concentrations. It is important to emphasize that the data used to calibrate the ion-size parameters and the data for which predictions were made are entirely disjoint, demonstrating the generality of the calibrated theory across a limited range of different structures and salt conditions. Future work should test the predictive power of SMPB on a wider range of structures and monovalent salt conditions.

FIGURE 5.

SMPB (solid) and PB (dashed) prediction for CC = Li⁺ (A) or Rb⁺ (B) competing against BC = 50 mM Na⁺ around a 44-bp DNA duplex. Net charge (⋄), CC (□), fixed BC (○), and co-ion (▵). SMPB curves were computed using size parameters obtained from fitting against 50 mM Na⁺ 24-bp duplex competition data.

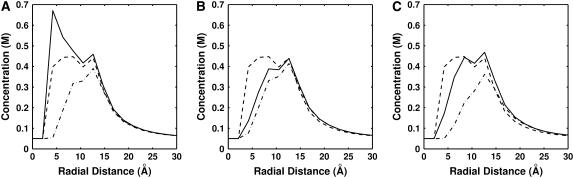
Examination of the radial density function (RDF) for each ion species elucidates the effect of size on the ion distribution around the DNA duplex. RDFs were obtained by axially and radially averaging the concentration of each cation species (both in competition at 50 mM concentration) in a slice 3 Å thick at the center of the duplex to avoid end effects and to probe the distribution over a 1-bp section of the duplex. RDFs are plotted in Fig. 6. PB theory does not account for size, so both ion species have the same distribution around the duplex (dashed line). This is in contrast with SMPB, where the inclusion of size has a marked effect on ion distribution. Fig. 6 A is the RDF computed using the best-fit size parameters for Li⁺ and Na⁺; in this plot, the smaller Li⁺ ions are able to penetrate into the minor groove of the helix, indicated by the peak in concentration around r = 5 Å. As the size of the CC is made larger (Fig. 6, B and C), we see that it is increasingly excluded from the immediate vicinity of the duplex, in accordance with our expectation that larger CC have a harder time approaching closely to the duplex than smaller CC.

FIGURE 6.

Radial distribution functions (RDF) for two monovalent ion species at 50 mM concentration around a DNA duplex. RDFs were averaged over the middle 3 Å of the duplex. Dashed line denotes concentration profile obtained from PB. SMPB theory is plotted with solid lines (smaller ion) and dash-dot lines (larger ion). Three different size combinations are plotted (representing 50 mM Li⁺, K⁺, and Rb⁺ in competition against 50 mM Na⁺): (A) 1.00 and 7.16 Å, (B) 7.16 and 7.41 Å, and (C) 7.16 and 9.47 Å.

The analysis of monovalent competition shows that SMPB can model the departures from PB theory in a simple mean-field framework that takes into account the excluded volume of the diffusely bound ions. Although SMPB, as a mean-field theory, does not take ion-ion correlations into account, its success in interpreting nonspecific monovalent binding is most likely due to the fact that ion-ion correlations are not very important in solutions of low to moderate monovalent ion concentrations (28,29).

Analysis of divalent competition

Departures from PB have also been observed in divalent versus monovalent and divalent versus divalent competition. In particular, PB underestimates the competitive ability of divalent ions competing against a fixed concentration of monovalent ions; additionally, PB does not predict the observed size deviations in divalent versus divalent competition (12).

Subjecting the divalent versus monovalent dataset to a fitting routine similar to the one performed on the monovalent dataset yields best-fit size parameters that fit the data better than PB (χ²/ν = 3.27 for SMPB versus χ²/ν = 7.95 for PB); in this sense, there is statistical improvement over PB alone (Fig. 7, and Fig. 10 in the Supplementary Material). The fitting procedure returned results that suggested that, in the SMPB framework, divalent metal ions have a smaller apparent size than the background sodium ions. In future calculations, these apparent sizes may be used to obtain better fits than unmodified PB alone. We do not, however, believe that SMPB was able to satisfactorily model the enhanced accumulation of divalent CC over the tested parameter space of ion-size parameters. Furthermore, size parameters obtained from fitting divalent versus monovalent datasets are not consistent with the best-fit parameters from the divalent versus divalent datasets.

The inconsistency of best-fit size parameters between datasets shows that a mean-field theory—even one that accounts for ion size—cannot explain all of the observed deviations from PB theory. Although some of these discrepancies are probably attributable to the finite size of the solution ions, ion-ion correlations presumably play a larger role due to the higher valence of the ions (28,29). The failure of SMPB highlights the need for an adequate theoretical treatment for divalent ions, especially since divalent ions play important roles in many biological processes.

Range of validity

SMPB is valid for monovalent ion concentrations up to ∼150 mM; in this concentration range, SMPB gives a good visual fit to the experimental data. Above this concentration, the SMPB prediction for the number of bound co-ions shows increasing deviation (≥10%) from experimental observations. As the CC concentration in solution is increased, SMPB predicts increasing depletion of co-ions in the vicinity of the duplex, reflected in the downward slope of the co-ion curve (Fig. 3 C, for instance). Similar depletion has also been observed in PB calculations by Misra and Draper (30), Ni et al. (31), and Shkel et al. (32).

The charge of the duplex is neutralized by a combination of counterion association and co-ion exclusion; the former becomes entropically unfavorable with increasing CC concentration (30). As the co-ions are depleted from the vicinity of the duplex, the number of CC bound necessarily falls because fewer CC are required to neutralize the charge of the duplex. This depletion effect is not observed experimentally at the magnitude suggested by SMPB, suggesting its accuracy is limited at higher ionic concentrations, perhaps due to neglect of ion-ion correlations or an inaccurate treatment of the hard-core repulsion, both of which become more important at higher ion concentrations. Co-ion exclusion occurs more strongly and at lower concentrations for SMPB theory than for PB due to the inclusion of the excluded volume effects in the free energy density. This is not at all surprising; the addition of excluded-volume effects makes the depletion of co-ion from the duplex energetically more favorable since the finite size of the co-ions makes them easier to exclude.

Application to modeling

Due to its mean-field treatment and continuum solvent model, numerical implementation of SMPB theory (Eq. 5) requires computing resources comparable to PB, well within the reach of many researchers. This approach, while a considerable improvement over PB, is at the cost of some accuracy due to the limitations of the mean-field approach and continuum solvent model (31), especially at higher ion concentrations. As an added advantage, the electrostatic free energy for a given salt condition is easily computed from an SMPB calculation, extending its usefulness to energetic calculations, an area of ongoing development.

Because of its improvement in predicting competitive effects between different ions, we believe that SMPB can play an important role in the development of continuum models, especially in systems where steric and competitive effects are important. Possible examples of such systems involve binding to the minor groove of DNA (33) and membrane channel transport (34,35). The similarities between RNA and DNA also suggest that SMPB may also be applicable more broadly to other nucleic acid systems.

Beyond its use in biology, electrostatics and PB theory have been used widely in colloid science and electrochemistry. For instance, PB theory has been used to model ion transport across membranes (36), which has implications for battery design and to control microfluidic flows (10). Advancements in PB theory have the potential to advance crucial technologies, especially in systems of high charge density in environments with asymmetric ion size (37).

CONCLUSIONS AND IMPLICATIONS

Proper theoretical descriptions of electrostatic effects are essential in building models of interactions between highly-charged biological macromolecules. Traditionally, PB theory has been applied to analyze these interactions. However, its mean-field treatment of the electrostatic field and point-charge treatment for ions limits its accuracy in systems where ion correlations and size are important. Recent experimental work on nonspecific ion binding has shown significant deviations from idealized PB ion behavior; in monovalent salts, these deviations appear to be due primarily to size, motivating further developments in theory. In this article, we have presented a SMPB theory which incorporates the finite-size of the solution ions and a numerical implementation that solves SMPB numerically around arbitrary molecular structures. Our results show that this SMPB theory accurately describes the size-mediated departures from PB in competitive monovalent ion binding for a limited range of nucleic acid structures and salt conditions. Effective size parameters for Li⁺, Na⁺, K⁺, and Rb⁺, which can be used in future SMPB calculations, are obtained by fitting theory against experimental results. The numerical implementation is available from the APBS web site (http://apbs.sourceforge.net/).

Unfortunately, despite fitting the corresponding data better than PB, SMPB cannot model all of the deviations in the divalent data. This result is not surprising as the effects of ion-ion correlations cannot be ignored for divalent ions. As divalent ions are of great importance in a variety of nucleic acid systems, we are planning further improvements in theory which will be needed to explain these deviations in a satisfactory fashion.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.