Abstract
Hydrated divalent magnesium and calcium clusters are used as nanocalorimeters to measure the internal energy deposited into size-selected clusters upon capture of a thermally generated electron. The infrared radiation emitted from the cell and vacuum chamber surfaces as well as from the heated cathode results in some activation of these clusters, but this activation is minimal. No measurable excitation due to inelastic collisions occurs with the low-energy electrons used under these conditions. Two different dissociation pathways are observed for the divalent clusters that capture an electron: loss of water molecules (pathway I) and loss of a H atom and water molecules (pathway II). For , pathway I occurs exclusively for n ≥ 30 whereas pathway II occurs exclusively for n ≤ 22 with a sharp transition in the branching ratio for these two processes that occurs for n ≈ 24. The number of water molecules lost by both pathways increases with increasing cluster size reaching a broad maximum between n = 23 and 32, and then decreases for larger clusters. From the number of water molecules that are lost from the reduced cluster, the average and maximum possible internal energy is determined to be ~4.4 and 5.2 eV, respectively, for . This value is approximately the same as the calculated ionization energies of , M = Mg and Ca, for large n indicating that the vast majority of the recombination energy is partitioned into internal modes of the ion and that the dissociation of these ions is statistical. For smaller clusters, estimates of the dissociation energies for the loss of H and of water molecules are obtained from theory. For , n = 4 – 6, the average internal energy deposition is estimated to be 4.2 – 4.6 eV. The maximum possible energy deposited into the n = 5 cluster is < 7.1 eV, which is significantly less than the calculated recombination energy for this cluster. There does not appear to be a significant trend in the internal energy deposition with cluster size whereas the recombination energy is calculated to increase significantly for clusters with fewer than 10 water molecules. These, and other results, indicate that the dissociation of these smaller clusters is nonergodic.
Introduction
Advances in protein characterization by mass spectrometry (MS) have been accelerated by new instrumentation and methods of analysis that have blossomed over the last decade. The “bottom-up” approach to protein characterization has been used to identify as many as 7,800 proteins from whole cell lysis of the mouse brain [1]. The effectiveness of the bottom-up method for complex samples can be enhanced by using multidimensional separations. Clemmer and coworkers elegantly demonstrated that combining on-line liquid chromatography (LC) with ion mobility spectrometry and MS can greatly improve separations without increasing analysis times over LC/MS alone [2-4]. In contrast, the “top-down” approach to protein characterization has the advantage that de novo sequencing, including the identification and structural localization of labile posttranslational modifications, can be done directly on protein mixtures without proteolysis [5, 6]. This top-down approach has greatly benefited from the development of electron capture dissociation (ECD), a method pioneered by McLafferty and coworkers [6-9]. In a typical ECD experiment, multiply protonated or cationized ions are reduced by the capture of thermally generated electrons to produce odd electron ions. For multiply protonated proteins, electron capture (EC) typically results in generation of “c” and “z” ions corresponding to cleavage of the protein backbone N-Cα bond. For small proteins, ECD can result in over 90% sequence coverage [9]. Analogous methods that use collisions with anions (ETD) [10, 11] or neutral atoms (ECID) [12, 13] to reduce precursor ions result in similar fragmentation products for proteins.
Although ECD was first demonstrated nearly 10 years ago [7] and has been the subject of extensive reviews [14-17], the mechanism by which fragment ions are formed is still hotly debated. McLafferty and coworkers proposed that capture of an electron by a multiply charged protein results in nonergodic dissociation through high-n Rydberg states [18]. In contrast, Turěek and coworkers have argued that the odd electron ions formed by electron capture have very low bond dissociation energies and that dissociation of these ions is rapid even at thermal energies [19-25]. Experimental and computational evidence supporting both of these mechanisms have been reported [26-37], including evidence for some long-lived intermediates from elegant double resonance and H/D scrambling experiments by O’Connor and coworkers [35-37].
Electron capture by a multiply charged ion is the reverse process of ionization of the corresponding ion with one additional electron. For multiply protonated proteins, this recombination energy resulting from EC has been estimated to be 4 – 7 eV [7, 15]. The recombination energy for protonated, lithiated, and cesiated glycine decreases with increasing cation size [38]. The fragment ions formed by ECD of peptides that are cationized with two different cations are consistent with the preferred neutralization of the cation of highest recombination energy [38]. Similar results have been reported by Liu and Hakansson for metalated peptides [33, 34].
A useful parameter to determine the extent to which a dissociation process is ergodic or nonergodic is what fraction of the recombination energy is converted into internal modes of the reduced ion. In principle, it is possible to obtain a measure of the internal energy deposition of an ion activation method by using “chemical thermometers” [39-46]. Several different approaches for this have been demonstrated. In one method, a measure of the internal energy is obtained from the branching ratio for two or more product ions formed by competing pathways with different and known dissociation enthalpies and entropies [39-41]. For example, the molecular ion of n-butyl benzene can dissociate via a direct bond cleavage to form (m/z 91) or via a McLafferty rearrangement to form (m/z 92). The latter process has a lower activation energy but higher entropy; formation of m/z 92 ion is favored at low internal energies, whereas m/z 91 is favored at higher internal energies. Thus, the ratio of these two ions serve as a measure of the internal energy deposited into this ion [39-41]. A measure of the internal energy can also be obtained from the abundances of fragment ions formed via consecutive reaction pathways with known critical formation energies [42-45]. For example, activation of can result in sequential loss of CO molecules with critical energies ranging from 1.15 eV for the loss of the first CO molecule to 7.58 eV for the loss of all five CO molecules; formation of FeC+ requires 15.7 eV [43]. The abundances of the fragment ions formed by activation of or analogous ions provide a measure of the range and magnitude of the internal energy that is deposited into this ion. This method, first demonstrated by Kenttämaa and Cooks [42], has been used to characterize the internal energy distribution resulting from ion-surface and ion-gas collisions [43] as well as other activation methods [44, 45]. The effective internal temperature of an ion can also be obtained from measurements of dissociation kinetics if Arrhenius parameters in the rapid energy exchange limit for the dissociation process are known. For large ions, these parameters can be obtained directly from blackbody infrared radiative dissociation (BIRD) experiments [47] and used to obtain the effective temperature of ions activated by other methods. This method has been used to measure effective temperatures of peptide ions activated by multiple gas-phase collisions [46].
Here, ECD spectra of hydrated clusters of divalent calcium and magnesium clusters are reported as a function of cluster size. Two different dissociation pathways are observed and the branching ratio for these pathways depends on cluster size. We demonstrate that these nanometer-size clusters can be used as calorimeters to measure the energy that is deposited into these ions upon EC. Using this “nanocalorimetry” method, we show that the vast majority of the recombination energy is transferred into internal modes of large clusters and that the dissociation process is ergodic. For smaller clusters, we show that significantly less energy than the potentially available recombination energy is transferred into internal modes of the reduced species and that ECD is nonergodic for these clusters.
Experimental
Instrument and Methods
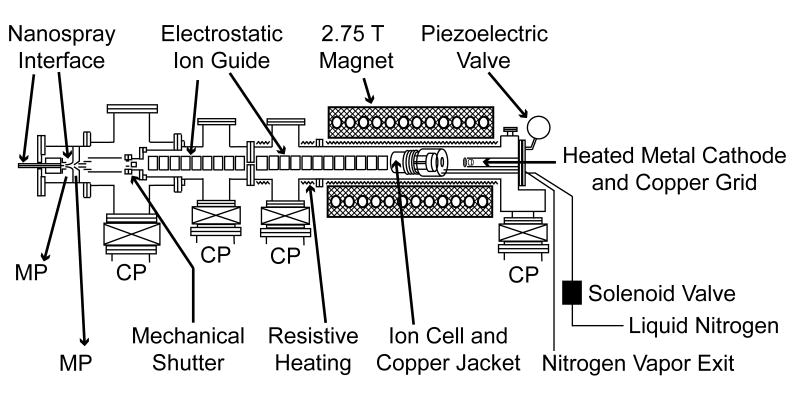
Experiments were performed on a 2.75 Tesla Fourier-transform ion cyclotron resonance (FT/ICR) mass spectrometer with an external electrospray ionization source (Figure 1). This instrument, which has a temperature controlled ion cell that can be cooled using a regulated flow of liquid N2 [48] and an electrospray ionization source that is used to produce extensively hydrated ions [49] is described in detail elsewhere. Hydrated divalent calcium and magnesium ions were formed by nanospray from aqueous solutions that are 2 mM in metal ion (from CaCl2 and MgSO4). Tips used for nanospray are produced from pulled borosilicate capillaries that have an inner tip diameter of ~1 μm. A ~550 V potential (relative to the ~115 °C heated metal capillary) is applied to a platinum wire in direct contact with the solution. Hydrated ions are introduced into the ion cell through five stages of differential pumping and accumulated for 4 s during which time N2 gas is introduced at a pressure of ~10-6 Torr using a piezoelectric valve to enhance trapping and thermalization of the ions. A mechanical shutter is subsequently closed so that no additional ions are introduced into the cell. The ions then are stored for 6 s to ensure that a steady state internal energy distribution is established and to allow pressure in the instrument to return to < 10-8 Torr prior to ECD. The temperature of the copper jacket surrounding the ion cell is kept at -140 °C.
Figure 1.
Schematic diagram of the 2.75 T Fourier-transform ion cyclotron resonance mass spectrometer used in these experiments. This instrument has an external electrospray ionization source, a temperature controlled ion cell that is cooled to 130 K with a regulated flow of liquid N2 and a heated metal dispenser cathode mounted on the central axis of the vacuum chamber and positioned 20 cm from the cell center for generation of thermal electrons for ECD. MP and CP indicate mechanical pumps and cryopumps, respectively.
For ECD, a 1.0 cm diameter heated dispenser cathode impregnated with barium scandate (Heatwave Labs, Watsonville, CA) was mounted axially with respect to the vacuum chamber 20 cm away from the cell center. A direct current of 3 A is used to heat the dispenser cathode to a temperature of 950 °C. Ion isolation with SWIFT waveforms is followed by a 50 ms delay prior to ECD. To introduce electrons into the cell for ECD, the potential of the cathode housing is pulsed from +10 to -1.4 V for 40 ms. A cathode potential of -1.4 V was found to be optimal for the production of ECD product ions in these experiments. A potential of +9 V was applied to a copper wire mesh mounted 0.5 cm in front of the cathode for all experiments. All potentials are referenced to instrumental ground.
A MIDAS data system was used to acquire 64 K data point transients. The average number of water molecules lost from these ions is determined from a weighted average of the product ion intensities observed. By subtracting the value attributable to BIRD from the weighted average of product ion intensities, the corrected average loss due to EC is obtained.
Computational chemistry
Candidate low-energy structures were determined using conformational searching and chemical intuition. Initial structures of [MOH(H2O)n]+, M = Mg and Ca, were generated using Monte Carlo conformation searching with the MMFF94 force field using Macromodel 8.1 (Schrödinger, Inc. Portland, OR). Initial structures of [M(H2O)n]+ were generated from low-energy structures of [Ca(H2O)n]2+, with smaller clusters identified by removing selected water molecules from those structures and substituting Ca with Mg. Additional structures were generated from MP2/6-31G** energy minimized structures reported by Siu and Liu [50].
Candidate structures were energy minimized with hybrid method density functional calculations (B3LYP) using the 6-311++G** basis set. Even electron species were evaluated using restricted spin methods, whereas odd electron species were evaluated using unrestricted spin methods. Vibrational frequencies were calculated to determine zero-point energies. These structures yielded all positive frequency vibrational modes, indicative of local-minima structures. Calculations were performed in Jaguar v6.5 (Schrödinger, Inc. Portland, OR) and Gaussian 03 (Gaussian, Inc. Wallingford, CT) [51] for structures containing Mg and Ca, respectively.
Results and Discussion
Precursor Activation
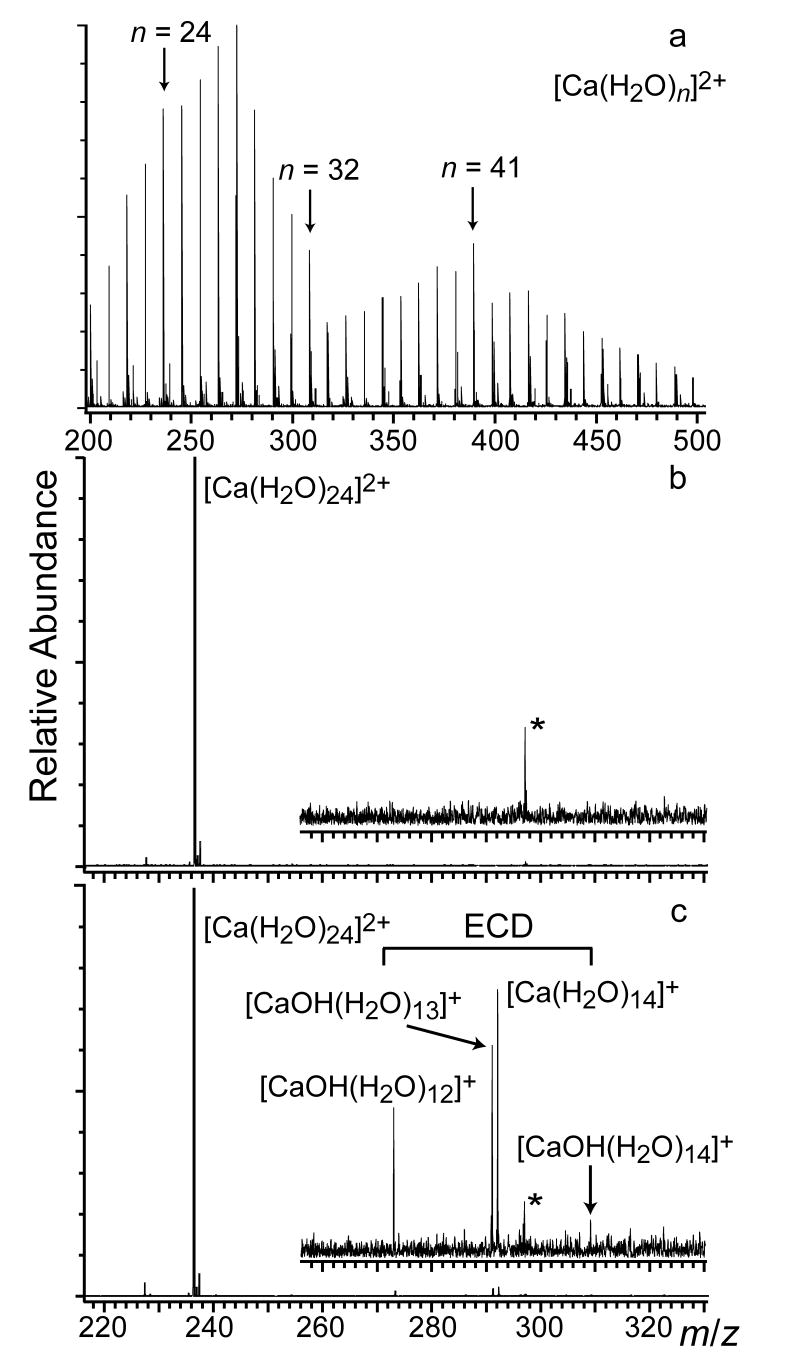
Hydrated divalent calcium ions, , were produced using nano ESI of a 2 mM aqueous CaCl2 solution. The resulting cluster distributions are typically broad (Figure 2a) and can be shifted to either larger or smaller cluster size by changing instrumental parameters [49]. Low abundances of and are also observed under these conditions. Ions from n = 4 – 47 were formed with sufficient abundance to isolate and measure their ECD spectra. Figure 2b shows an isolation spectrum for ; a fragment ion at m/z 227 corresponding to the loss of a single water molecule from the isolated precursor ion is observed. This ion is predominantly formed by BIRD as a result of infrared (IR) photons emitted from the cell and vacuum chamber surfaces as well as from the heated cathode (950 °C) that is located 20 cm away from the cell center.
Figure 2.
Mass spectra from a) ESI of a 2 mM aqueous CaCl2 showing a broad distribution of clusters (selected n are labeled); b) SWIFT isolation of and c) ECD of with product ions indicated in the spectrum. A noise peak at ~297 m/z is labeled with an asterisk.
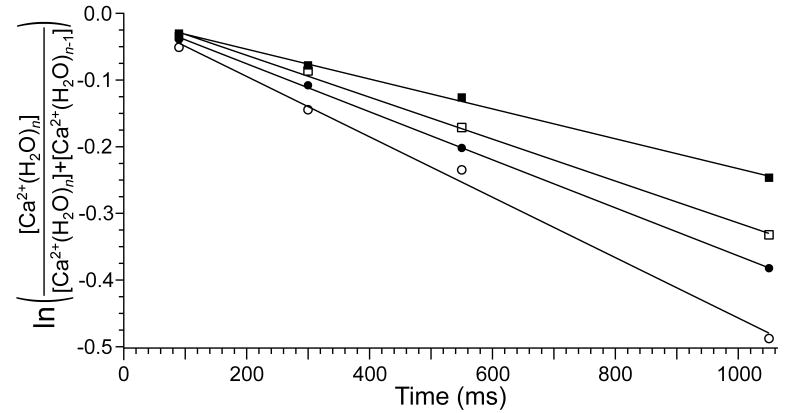
To determine the effects of these IR photons on the ion population, , n = 24 and 32, were stored in the ion cell for times ranging from 90 ms to 1090 ms both with and without the cathode heated. In both cases, the potential of the cathode was +10 V so that no electrons were introduced into the cell and no ECD occurs. The kinetic data obtained from these experiments are shown in Figure 3. Substantial dissociation occurs for both of these ions even without the cathode heated due to blackbody radiation from the cell and surroundings. The dissociation kinetics are first order. Without the cathode heated, the dissociation rate constant is about 60% greater than that for . Faster dissociation with increasing cluster size is primarily due to the higher internal energies and faster radiative absorption rates of larger clusters [47], although slightly decreasing binding energies with increasing cluster size may also contribute to this effect. When the cathode is heated to 950 °C, the dissociation rates of these clusters increases by 26% and 40% for the and clusters, respectively. This indicates that substantial activation of the precursor occurs due to absorption of radiation generated from the heated cathode. However, the extent of this activation is minimal for the 90 ms between ion isolation and detection in these ECD experiments. The abundance of the fragment ion corresponding to the loss of a water molecule from is ~2% of the precursor abundance in the isolation mass spectra when the cathode is heated. Loss of a water molecule directly attributable to the heated cathode comprises 1.6% and 1.3% abundance relative to the precursor intensities for the and clusters, respectively. The abundance of this fragment ion increases with increasing cluster size; 9% of the precursor dissociates under these conditions. Thus, the effects of IR emission from the heated cathode are observable, but have minimal impact on these ECD experiments. These effects could be reduced by placing the cathode a greater distance from the ion cell.
Figure 3.
BIRD dissociation kinetics for the loss of a water molecule from , n = 24 and 32, both with the ECD cathode at room temperature and with the cathode heated to 950 °C but with no electrons introduced into the cell: cathode at room temperature (■) and at 950 °C (□); cathode at room temperature (●) and at 950 °C (○).
In addition to activation by absorption of blackbody radiation, the precursor ions could also potentially be activated by inelastic collisions with electrons. Ion dissociation using low-energy electrons was first demonstrated by Cody and Freiser who termed this method electron impact excitation of ions from organics (EIEIO) [52]. To determine if any EIEIO occurs under the conditions of these ECD experiments, the loss of a water molecule from the isolated precursor ion was compared between experiments with and without electrons injected into the cell. Electrons are introduced into the cell for 40 ms by lowering the potential on the heated cathode from +10 V to -1.4 V. There was no significant difference in the abundance of the product ion corresponding to the loss of a water molecule from the precursor ion under the conditions of this experiment indicating that ion excitation due to EIEIO is negligible. An increase in water loss is observed when the electron kinetic energy is increased to 9 eV. However, no reduced product ions formed by ECD were detected with these conditions.
Electron Capture Fragmentation Pathways
As has been noted by others [53, 54], the efficiency of the ECD process is very sensitive to the electron energy, with the filament or cathode producing the most efficient capture conditions for polypeptides at potentials near 0 V. Another broad maximum in polypeptide capture efficiency has been noted at higher voltages, between -3 V to -13 V, and due to the appearance of additional fragmentation products, has been referred to as ‘hot’ electron capture dissociation [14]. The cathode potential of -1.4 V used in these experiments was selected by maximizing the efficiency for formation of ECD product ions of ; this potential also produced optimum ECD fragment abundances for the polypeptide Substance P under similar experimental conditions.
Capture of an electron by , M = Ca or Mg, can result in dissociation by two competing pathways (Scheme 1): losses of multiple water molecules (pathway I), or ejection of a hydrogen atom forming a hydrated metal hydroxide with a single net charge and loss of multiple water molecules (pathway II). The branching ratio for these two processes depends on cluster size and these data are shown in Figure 4. Pathway I exclusively occurs for clusters with n ≥ 30, whereas pathway II is the exclusive process observed for n ≤ 22. Between n = 23 to 28, both processes are observed and there is a relatively sharp transition in the branching ratio around n = 24.
Scheme 1.
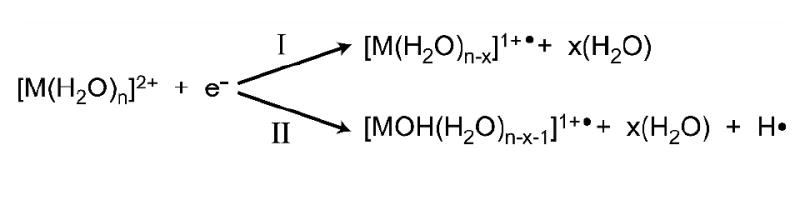
Figure 4.
Plot of the normalized product ion intensities from dissociation by pathways I and II (Scheme 1) resulting from electron capture by , n = 4 – 47, as a function of cluster size. A rapid transition from the loss of a single H atom and loss of water molecules (■; pathway II) to exclusively loss of water molecules (▲; pathway I) occurs between n = 22 and n = 30. Sigmoidal trend lines were fit to these data as a guide.
The ECD spectrum of , which has products from both dissociation pathways, is shown in Figure 2c. In this spectrum, a single product ion that has lost 10 water molecules upon reduction, , is formed by pathway I. Three product ions, , n = 12 – 14, are formed by pathway II indicating that on average, 10.2 water molecules in addition to the hydrogen atom are lost from the reduced precursor as a result of this process. It should be noted that the natural isotope distribution of calcium does not interfere with distinguishing product ions from these two dissociation pathways. The narrow width of the product ion distributions resulting from electron capture is particularly interesting. For pathway I, the appearance of just a single product ion indicates that a very narrow range of internal energies resulting from EC contributes to the formation of this ion. For pathway II, the formation of three product ions suggests that that the overall internal energy distribution resulting from EC is somewhat broader but still relatively narrow compared to other activation methods [43].
Reactions of hydrated magnesium monocations have been investigated previously [55-57]. Using an expansion source, it was demonstrated that clusters were formed for n = 1 – 5 and n ≥ 15 whereas was observed for n = 6 – 14 [56]. In elegant BIRD experiments by Bondybey and coworkers who investigated solvent evaporation from singly charged hydrated magnesium cations, loss of water molecules rapidly occurred at room temperature for large clusters, but below about 21 water molecules, was formed [57]. Another transition was noted for clusters with n ≤ 6, where water loss was again the only dissociation pathway observed [57].
Effects of Cluster Size
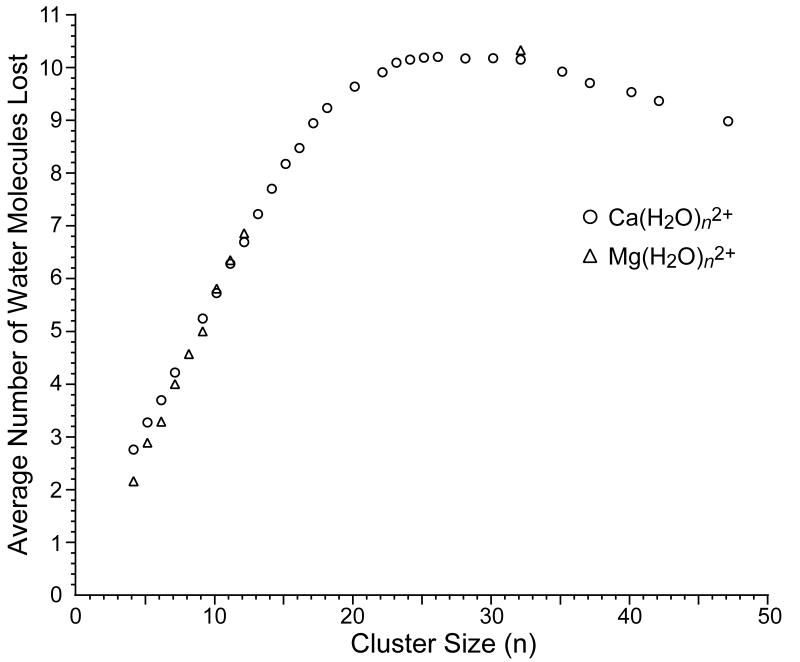
The average number of water molecules lost from the reduced precursor upon EC (from both dissociation channels) as a function of cluster size from n = 4 – 47 are summarized in Figure 5. This value increases nearly linearly with cluster size and reaches a broad plateau around n = 23 – 32 from which an average loss of ~10.2 water molecules is observed. The average number of water molecules lost decreases slightly for cluster sizes larger than n = 35. Also shown on this plot are several values obtained for divalent magnesium clusters which closely track the corresponding values for calcium.
Figure 5.
The average number of water molecules lost from the reduced precursor ion due to electron capture by , M = Ca (○) and M = Mg (△), as a function of cluster size. The average number of water molecules lost is determined from both dissociation pathways (Scheme 1).
The trends in the extent of water loss with cluster size can be qualitatively explained by two competing factors. For smaller clusters, the binding energy of water increases with decreasing cluster size [58-60]. Thus, for the smaller clusters, a fixed internal energy deposition will result in the evaporation of fewer water molecules. This appears to dominate over any increased internal energy deposition that may be expected for smaller clusters (vide infra). For larger clusters, the binding energy of water is not expected to change significantly with cluster size [59]. The most labile water molecules in larger clusters are largely shielded from the cation by other water molecules; thus, the binding energy of the outer shell molecules is predominantly determined by inter-water hydrogen bonds. The decrease in the number of water molecules lost from the larger clusters is likely due to the increased degrees of freedom of the precursor [61]. For a given deposited internal energy, the kinetic rate for ion dissociation will decrease with increasing cluster size because the energy can be spread over more internal modes. This will make it possible for competing energy loss mechanisms, such as collisions or radiative emission, to reduce the energy of the cluster. Under the conditions of these experiments (< 10-8 Torr, ~130 K), it is expected that radiative emission plays a greater role [47].
Internal Energy Deposition
In principle, it should be possible to determine the extent to which internal energy is deposited into internal modes of the reduced precursor ions upon electron capture from the distribution of the observed product ions. Specifically, if the threshold dissociation energies for a series of consecutive reactions are known, information about the internal energy deposition can be obtained from the distribution of product ions formed. This method, pioneered by Cooks and coworkers [42, 43], has been used to characterize the internal energy deposition of several activation methods [43-45]. For large clusters, where loss of water molecules is the only process observed, we have shown that the number of water molecules lost from the reduced precursor can be used as a measure of the internal energy deposition in these clusters [62]. Thus, these nanometer-size clusters can be used as nanocalorimeters to measure energy conversion in ECD or any other process [62].
The binding energies of water to protonated water clusters have been measured using different methods. The sequential binding energies rapidly decrease with cluster size; the proton affinity of water is 165.2 kcal/mol, but loss of a water molecule from a proton-bound dimer requires only 36 kcal/mol [63]. The 6th, 7th, and 8th water molecule binding enthalpies in protonated water clusters are 13.0, 11.7, and 10.3 kcal/mol, respectively [63]. Castleman and coworkers reported that the sequential binding energies for protonated water clusters with 8 – 28 water molecules range between 9 – 11 kcal/mol [59].
Effects of cation identity on water binding energies are significant for very small clusters, but become negligible for larger clusters. The sixth water binding energies of , M = Li, Na, and K, are 12.1, 10.7, and 10.0 kcal/mol, respectively [58]. Interestingly, the fourth water binding energies of for M = Na, Mg, and Al, are 13.1, 11.5, and 12.5 kcal/mol [60]. This suggests that the binding energy of water does not depend strongly on metal ion identity when the clusters approach a large size. Unfortunately, values for significantly larger clusters, such as those formed here, have not been reported.
An estimate of the binding energy to infinitely large clusters can be obtained from the heat of vaporization of water. This value ranges from 10.8 to 9.7 kcal/mol for temperatures between 0 to 100 °C [64]. The heat of sublimation for hexagonal ice has been reported using a low temperature equation of state developed from thermodynamic equilibrium properties at temperatures ranging from 273.16 to 130 K. The enthalpy of sublimation is relatively constant across these temperatures, ranging from 12.2 to 12.0 kcal/mol [65]. For droplets, the surface energy reduces the vaporization enthalpy from that of the bulk. For neutral water clusters, the evaporation enthalpy of a single water molecule from a cluster of size n can be estimated from the bulk enthalpy of vaporization less a surface energy term which scales as n-1/3 [66]. Using a value for the bulk enthalpy of vaporization of hexagonal ice of 11.2 kcal/mol at zero K, the energy required to evaporate a single water molecule from water clusters from n = 20 – 50 is estimated to vary from 9.2 - 9.7 kcal/mol. This suggests that the effects of surface energy are small for clusters in this size range.
Extrapolating bulk physical properties from cluster data can have significant uncertainties. However, these data all suggest that the binding energy of water to the reduced precursors investigated here should be approximately 10 kcal/mol. This value depends on the cluster temperature, size and to a limited extent on shell structures or “magic” numbers observed for some clusters. However, we anticipate that any variations that may be present will be small compared to other uncertainties in our method. Although it is difficult to fully access the uncertainty in the water binding enthalpies, we estimate this uncertainty to be about ± 10%. For the smaller clusters, where the degrees of freedom are low, the initial effective temperature of the reduced cluster is very high and the effects of temperature on the vaporization energy of water will be more substantial. The energy resolution of this method is also limited by the sequential binding energies of the ligands.
Using this estimated value of roughly 10 kcal/mol per water molecule lost from large clusters, we can determine an average (Eavg) and an upper limit (EUL) to the internal energy deposited into the clusters upon electron capture. For , which is in the plateau region of maximum water loss (Figure 5), reduction by electron capture results in formation of and with normalized relative abundances of 0.3 and 1.0, respectively, corresponding to an average of 10.2 water molecules lost. This value must be corrected for residual background dissociation that is due to blackbody radiation (vide supra). To do this, we assume that activation of the precursor and the reduced precursor by BIRD is the same; capture of an electron to form the reduced precursor can occur any time during the 40 ms electron irradiation time so that some fraction of the reduced species will be from the precursor that has lost a single water molecule. To the extent that the fragmentation of precursor and the reduced precursor are the same, it is possible to account for dissociation by BIRD. For , this correction corresponds to an average water molecule loss of 5%. This value is comparable to the values for other clusters, and varies with cluster size from 1% to 9% for the and clusters, respectively. Thus, the average water loss from due only to electron capture is 10.23 − 0.05 ≈ 10.2 water molecules. This water loss corresponds to an average internal energy deposition of 10.2 × 10 kcal/mol = 102 kcal/mol (4.4 eV). Formation of the product ion corresponding to the reduced precursor that has lost 11 water molecules requires 110 kcal/mol (4.8 eV). The absence of a product ion corresponding to the loss of 12 water molecules indicates that the maximum possible internal energy that is deposited into upon EC is between 110 and 120 kcal/mol (4.8 – 5.2 eV). It should be emphasized that the uncertainty in the energy values obtained with this method is attributable to the uncertainty in the binding enthalpy of water used to obtain these values from the number of water molecules lost, which we estimate to be about ± 10%. These values are close to 4.5 eV, the value calculated for the vertical ionization energy of [62] which is a rough estimate of the recombination energy in this EC experiment. Because the internal energy deposition we obtain from this method is comparable to the estimated recombination energy, we conclude that the vast majority of the recombination energy is deposited into internal modes of the ions, i.e., ECD is ergodic for these larger cluster ions. Additional evidence for ergodic dissociation for the larger clusters is the decreasing number of water molecules lost from the cluster with increasing cluster size (Figure 5), consistent with a degree of freedom effect (vide supra).
ECD Energetics for Small Clusters
In order to estimate the internal energy that is deposited into the smaller clusters where the loss of a H atom in addition to water loss occurs, dissociation energies for the loss of the H atom and for losses of water must be known. The lowest-energy structures and the barriers for H loss for , n = 1 – 6, have been calculated by Siu and Liu [50] using MP2/6-31G**. From the reported zero-point corrected energies of these structures, the binding energies of water are determined. The binding energy of water should be approximately equal to the activation energy for dissociation, because any reverse activation barrier should be small. These values are given in Table 1. For comparison, experimentally determined bond dissociation energies for loss of water from , n = 1 – 4 [60], are also presented. The activation energy barrier for loss of H is higher than that for the loss of water from , n = 1 – 5, but loss of a H atom is more energetically favorable for n = 6 and 7. This result is reasonably consistent with the results of BIRD experiments of Bondybey and coworkers [57] where the loss of water was the exclusive loss channel observed for clusters with n < 7, but H atom loss occurred for n = 7 – 21. For smaller clusters, only the loss of water was observed indicating that the activation barrier for loss of a H atom is higher than that for loss of a water molecule for clusters with six or fewer water molecules.
Table 1.
Zero-point energy corrected water and hydrogen binding energies (in kcal/mol) from B3LYP/6-311++G** calculations for [X(H2O)n]+, X = Mg, Ca, MgOH, and CaOH. MP2/6-31G** water binding energies to [Mg(H2O)n]+ and hydrogen loss barrier energies from [50], and experimental CID results from [60], are included for comparison.
| CIDa | MP2/6-31G* | B3LYP/6-311++G** | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Mg | Mg | Mg | MgOH | Ca | CaOH | |||||
| H2O | H2Ob | H | H2O | H | H2O | H2O | H | H2O | |||
| 1 | 28.4 ± 3.0 | 36.8 | 71.9c | 31.0 | 78.1 | 50.4 | 28.1 | 36.8 | 29.9 | ||
| 2 | 22.4 ± 1.6 | 30.4 | 49.0c | 24.0 | 51.7 | 37.3 | 25.3 | 32.2 | 27.0 | ||
| 3 | 17.3 ± 2.1 | 26.2 | 33.9c | 21.1 | 35.5 | 29.2 | 19.2 | 24.5 | 23.7 | ||
| 4 | 11.5 ± 2.1 | 19.1 | 31.5c (22.0d) | 15.0 | 21.3 | 20.6 | 17.5 | 18.2 | 19.6 | ||
| 5 | --- | 16.5 | 17.9c (14.2d) | 8.7 | 9.4 | 16.6 | 16.1 | 14.7 | 17.3 | ||
| 6 | --- | 14.8 | 12.4e (6.9d) | 24.1 | 17.0 | --- | 17.8 | 15.3 | --- | ||
Zero K experimental bond dissociation energies from [60] upon collision of , n = 1 – 4, with xenon gas.
We calculated MP2/6-31G** energies for Mg+ and H2O. These values and those determined in [50] were used to determine zero-point energy corrected adiabatic water binding energies for these ions.
Dissociation barrier for direct hydrogen loss from the lowest-energy [Mg(H2O)n]+ structure determined in [50].
Dissociation barrier for hydrogen loss from [Mg(H2O)n]+ allowing structural isomerization barrier prior to hydrogen loss. For selected structures studied, the isomerization barriers were less than the hydrogen loss dissociation barriers [50].
The dissociation barrier for direct hydrogen loss from the lowest energy [Mg(H2O)6]+ structure (4+2a) was not reported; the value for a very similar, albeit slightly higher energy, structure (4+2b) is reported instead [50]. Based on the similarities between the two structures, we would expect them to have similar dissociation barriers for direct hydrogen loss.
From these calculated dissociation energies, several measures of the internal energy that is deposited into the smaller divalent ion clusters upon EC can be determined. The average value (Eavg) is determined from the sum of dissociation energies for the loss of H and water weighted by the product ion abundances. The maximum observed energy (EMO) is the sum of dissociation energies observed for the smallest product cluster that is observed in these experiments. This cluster is the ion that has lost the maximum number of water molecules from the reduced precursor. An upper limit to the internal energy deposition (EUL) can be obtained from the energy required to form the product ion with one less water molecule relative to the smallest product cluster observed. These energies for , n = 4 – 6, are given in Table 2.
Table 2.
Normalized relative abundances of , M = Mg,Ca, x = 0 – 2, formed by ECD of , n = 4 – 6, with estimated average (Eavg), maximum observed (EMO), and maximum possible (EUL) internal energy depositions (eV) obtained from ligand dissociation energies from A) B3LYP/6-311++G** and B) MP2/6-31G** [50] calculations (Table 1)
| Internal Energy Deposition (eV) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | ||||||||||
| M | n | x = 2 | x = 1 | x = 0 | Eavg | EMO | EUL | Eavg | EMO | EUL | |
| Mg | 4 | --- | 0.84 | 0.16 | 4.16 | 5.99 | --- | 4.46 | 6.40 | --- | |
| 5 | 0.11 | 0.89 | --- | 4.01 | 4.19 | 6.37 | 4.61 | 4.80 | 7.12 | ||
| 6 | 0.71 | 0.29 | --- | 4.08 | 5.23 | 7.41 | 4.17 | 5.45 | 7.76 | ||
|
| |||||||||||
| Ca | 4 | --- | 0.24 | 0.76 | 3.98 | 4.29 | --- | --- | --- | --- | |
| 5 | --- | 0.73 | 0.27 | 4.04 | 4.98 | --- | --- | --- | --- | ||
| 6 | 0.31 | 0.69 | --- | 4.10 | 4.46 | 5.76 | --- | --- | --- | ||
An EUL is not reported for because the smallest product ion that is formed is MgOH+. The dissociation energy of the metal hydroxide is much higher than that for water to the reduced clusters, so MgOH+ could be “hot” and no further dissociation will occur. For , the average values for internal energy deposition of 4.5 eV is not likely to be skewed significantly because the product ion that has a single water molecule attached is the most abundant fragment formed (84%). For and , no MgOH+ is formed making these ions the best candidates for chemical thermometers of the smaller clusters.
With these caveats, it is interesting to note that there appears to be very little effect of cluster size on the average internal energy deposition resulting from EC. For , this value for n = 32 (~4.5 eV) is essentially the same as the values obtained for n = 4 – 6 (4.2 – 4.6 eV).
ECD Energetics for Small Clusters
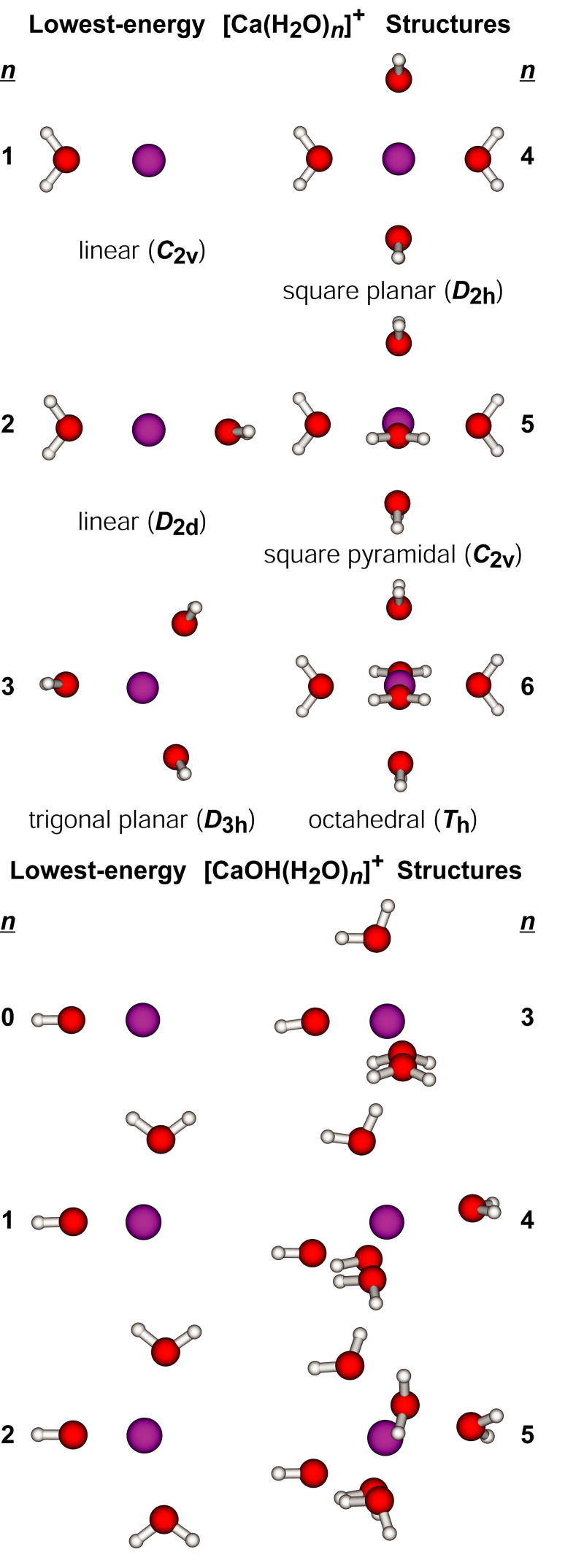
Calculated dissociation energies for the loss of H from have not been previously reported, but values for H atom and water molecule binding energies to these clusters have [67]. Surprisingly, self-consistent field calculations indicate that loss of a H atom from the clusters is exothermic for n > 4 [67]. We evaluated low-energy structures and binding energies for these ions at the B3LYP/6-311++G** level of theory. Lowest-energy structures for both and are shown in Figure 6. The structures of , n = 1 – 3, and , n = 1 – 5, are the same as those reported by Watanabe et al. [67]. For , both levels of theory indicate that Ca+ is solvated by four water molecules in plane with the metal ion, although we found a D2h symmetry to be slightly lower in energy than the Cs-symmetry structure with distorted O-Ca-O bond angles identified previously. For and , our calculations indicate that all water molecules in the lowest-energy structure coordinate directly to the metal ion, whereas the previous calculations indicate that structures with four inner-shell water molecules are lowest in energy. Because Watanabe et al. [67] reported relative free energies for structures, it is difficult to directly compare these results.
Figure 6.
Lowest-energy structures of , n = 1 – 6, and , n = 1 – 5, at the B3LYP/6-311++G** level of theory. Point groups and inner-shell coordination geometries are included.
From these structures, the binding energies of H and a water molecule to and of a water molecule to were determined and these values are given in Table 1. These water binding energies are similar to those reported previously, although our values for are generally slightly higher, whereas our values for are generally slightly lower. Our calculated hydrogen atom binding energies for , n ≥ 4 are substantially higher than those reported by Watanabe et al. [67], whereas our values for n < 4 are very similar. Our calculations show that the loss of a H atom from , n = 1 – 6, is endothermic although these values are lower than the corresponding water molecule binding energies for n = 5 and 6.
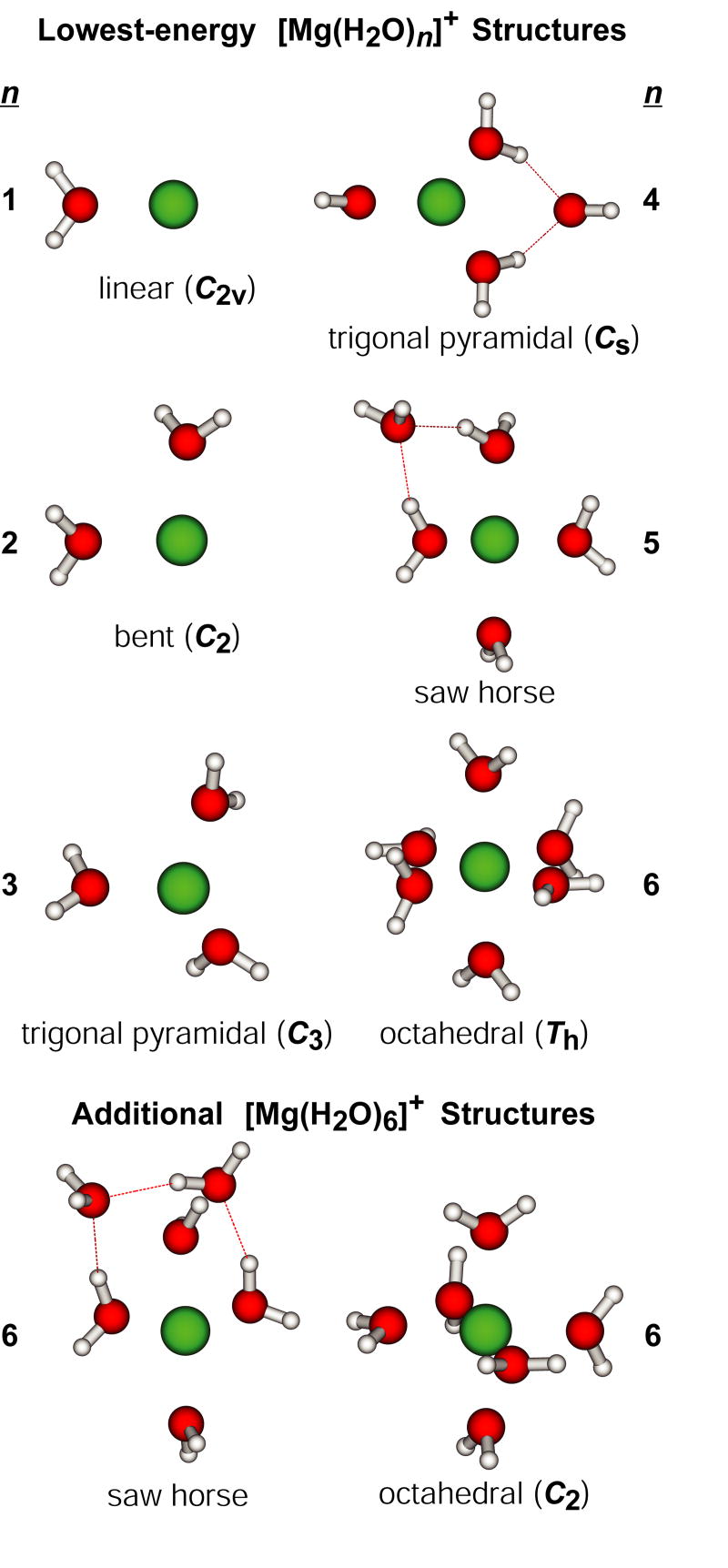
The values we calculate are binding energies, not activation energies for dissociation. Although these values for the loss of a water molecule should be similar, these values for the loss of a H atom may not. To obtain a rough estimate of the extent to which these values differ, calculations were also done on and at the B3LYP/6-311++G** level of theory. The lowest-energy structures of are shown in Figure 7 and binding energies for H and for water are given in Table 1. The lowest-energy structures of generally resemble those of , shown in Figure 6, with the notable difference that MgOH(H2O)+ is linear. It is interesting to compare these results with those from MP2/6-31G** calculations reported previously [50]. Both levels of theory support identical lowest-energy structures for , n = 1 – 5, and these structures are consistent with IR photodissociation spectra of [Mg(H2O)n]+, n = 1 – 4, reported by Inokuch et al. [68]. For n = 6, the MP2/6-31G** calculations indicate that the lowest-energy structure has a saw horse inner shell, like that in the lowest-energy structure of [Mg(H2O)5]+, with two water molecules in the second solvation shell.
Figure 7.
Lowest-energy structure of , n = 1 – 6, at the B3LYP/6-311++G** level of theory. Two higher-energy structures of are included for comparison. Point groups and inner-shell coordination geometries are included.
The lowest-energy structure of [Mg(H2O)6]+ identified with B3LYP/6-311++G** was not considered in the previous report, although another six coordinate structure with reduced symmetry (C2) was calculated to be 5.6 kcal/mol higher in energy than the saw horse structure. The C2-symmetry and saw horse structures (Figure 7) are 2.7 and 8.9 kcal/mol higher in energy than the Th-symmetry structure at B3LYP/6-311++G** level of theory. To help determine why these two levels of theory yield such different relative energies, selected structures were also evaluated using the smaller basis set employed in the previous MP2 calculations. At the B3LYP/6-31G** level of theory, the C2-symmetry structure is 0.4 kcal/mol higher in the energy than the saw horse structure, whereas the C2-symmetry structure is 6.2 kcal/mol lower in energy than the saw horse structure when the 6-311++G** basis set is used. This indicates that the more complete basis set, which includes diffuse functions and two basis functions per molecular orbital, preferentially stabilizes the C2-symmetry structure by 6.4 kcal/mol. Additionally, the Th-symmetry structure was not stable at the B3LYP/6-31G** level of theory. Upon energy minimization, the water molecules changed orientation relative to the metal ion and more closely resembled those in the C2-symmetry structure. These results indicate that more complete basis sets that include diffuse functions are important for determining the relative stabilities of these ions.
Despite the differences in these calculations, the B3LYP/6-311++G** binding energies of water molecules and hydrogen atoms to are similar to values reported by Siu and Liu [50]. Our values for are anomalously low, indicating that the lowest-energy structure of this ion may not have been identified. Note that if a lower-energy structure of [Mg(H2O)5]+ were identified, this would increase the water and hydrogen binding energies of [Mg(H2O)5]+, decrease the water binding energy of [Mg(H2O)6]+, but not change the energy difference between the water and hydrogen binding energies of [Mg(H2O)5]+. The adiabatic hydrogen binding energies calculated here are within ~10 kcal/mol of the activation barriers for hydrogen loss calculated by Siu and Liu [50] and there is no systematic deviation. This suggests that any reverse activation barrier for H loss is small and that the hydrogen binding energies calculated for are likely very good approximations for the activation energies for dissociation.
The relative binding energies we calculate for the two competing dissociation processes for are in excellent agreement with experimental results of Sanekata et al. [56]. When Ca+ is reacted with water vapor, the hydrogen loss product [CaOH(H2O)n]+ is predominant for 4 < n < 13 and [Ca(H2O)n]+ is primarily observed for the remaining cluster sizes. The switch between mostly [Ca(H2O)n]+, n ≤ 4, to predominantly [CaOH(H2O)4]+, n > 4, occurs at the same cluster size expected from the calculated binding energies.
With the caveats stated above, the average (Eavg), maximum observed (EMO), and maximum possible (EUL) internal energy deposition from EC by Ca(H2On)+ can be determined. These values as well as values for determined from binding energies calculated at this same level of theory are given in Table 2. The values for are slightly lower than those calculated using the corresponding values from Siu and Liu [50] although this difference is less than 0.5 eV in most cases. As was noted previously for , there is no significant trend in the average internal energy deposition with cluster size for . It is also interesting to note that the average internal energy deposition for clusters with Mg and Ca are essentially the same.
Evidence for Nonergodic Dissociation
Although dissociation via pathway I appears to be ergodic for the larger clusters, three pieces of evidence suggest that pathway II is nonergodic, at least for the smaller clusters. First, the internal energy deposited into the clusters does not depend on cluster size and is significantly less than the calculated ionization energy of the corresponding reduced species for the smaller clusters. Second, the fragmentation pathway for the reduced ions of the smaller clusters is not the same as when these ions are thermally activated. Third, the distribution of product ions observed via pathway II is broader than that for pathway I indicating that the ejected hydrogen atom takes away a broad range of kinetic energies. Each of these pieces of evidence is discussed in more detail below.
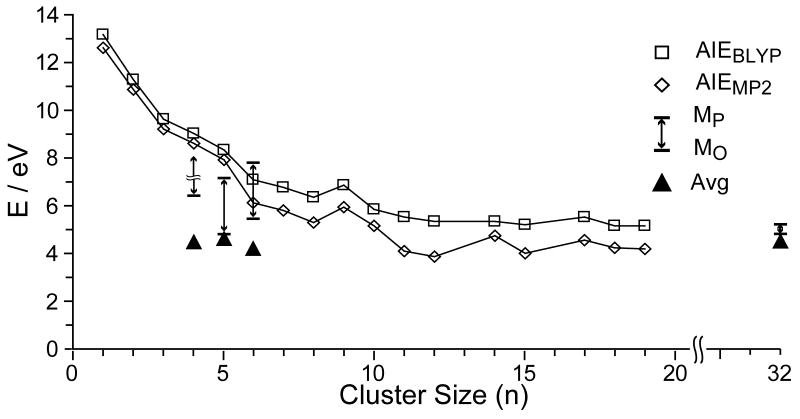
The adiabatic ionization energies of hydrated clusters of have been calculated by Niedner-Schatteburg and coworkers [69]. Results of these calculations as a function of cation size are plotted in Figure 8 along with values for the internal energy deposition from EC for selected clusters measured here. It should be noted that the recombination energy that we obtain with this method in the limit of complete energy randomization should be approximately the same as the adiabatic ionization energy of the reduced cluster. A 50 ms delay after ECD of but before ion detection resulted in no additional water loss. This is sufficient time for solvent reorganization to occur and any energy released from this process results in heating of the cluster. Thus, the recombination energy values we obtain should be comparable to the adiabatic ionization energies calculated by Niedner-Schatteburg and coworkers if all the energy is randomized. The calculated values rapidly decrease with increasing cluster size approaching an asymptotic limit of 3.9 – 4.8 and 5.1 – 5.5 eV for clusters with n = 11 – 19 at the MP2 and BLYP levels of theory, respectively [69]. For , we find an average internal energy deposition (Eavg) of about 4.5 eV and a maximum value of 4.8 –5.2 eV. These measured values are slightly higher than the recombination energies calculated at the MP2 level, but are comparable to BLYP values for large n [69].
Figure 8.
Comparison of the internal energy deposition from electron capture by , n = 4 – 6, 32, with adiabatic ionization energies of from BLYP (□) and MP2 (◊) calculations from [69] as a function of cluster size. The average energy deposition (Eavg; ▲), as well as the range of energies from the maximum observed (EMO) to the maximum possible (EUL), are indicated. For , no upper limit (EUL) is indicated because MgOH+ is formed. (see text).
In contrast to the strong trends in calculated ionization energies with cluster size, the experimental data show no significant trend with respect to cluster size. Most striking are the results for for which our data should provide an accurate measure of the maximum possible internal energy deposition. For this ion, the Eavg, EMO and EUL deposited upon EC is 4.6, 4.8, and 7.1 eV, respectively (4.0, 4.2, and 6.4 eV using the B3LYP binding energies). If internal energy in excess of 7.1 eV was deposited into this ion, MgOH+ should have been formed; this ion is not observed. In contrast, the ionization energy of is calculated to be 7.92 eV [69]. Ionization energies obtained from CC2 and BLYP calculations for this ion are 7.94 and 8.34 eV, respectively [69], indicating that this result does not depend strongly on the type of theory used. The lower value obtained from this experiment suggests that less energy is deposited into than would be expected if the entire recombination energy that is potentially available in the EC process were converted to internal modes of the ion. Thus, the excess energy could be lost either in the form of kinetic energy of the departing ligands, analogous to what is observed for dissociative electron attachment to water, or by radiative emission. Although water clusters have positive electron affinities [70], the electron affinity of an isolated water molecule is either very small or zero [71]. Electron attachment to an isolated water molecule results in spontaneous dissociation to form predominantly H— with minor abundances of O— and OH— also observed [72]. With increasing incident electron energies, some internal vibration modes can be excited, but the majority of the dissociation energy is carried away by the fragments in the form of kinetic energy [73].
A caveat in this analysis is that the initial effective temperature of the small reduced clusters can be quite high. For , we estimate the effective temperature to be roughly 2900 K and 2000 K for n = 5 and 6, respectively, using calculated values for the electron recombination energy. To obtain a more accurate measure of internal energy deposition from these experimental data, temperature effects on both the bond dissociation energies and on the partitioning of internal energy into translational, vibrational and rotational modes of the products would need to be taken into account. The latter effects could be modeled using phase space theory [74].
The second piece of evidence in support of a nonergodic dissociation process for the smaller clusters is the different dissociation pathways of the precursor ions when thermally activated by BIRD [57] or by collisions with Xe [60] and when formed in an activated state by EC from the doubly charged precursor. As discussed previously, thermal activation of , n < 7 results in loss of water molecules (pathway I); loss of H is only observed for n between 7 and 21 (pathway II) [57]. In contrast, , n = 4 – 6, when formed by EC by the corresponding dissociates exclusively by pathway II. For n = 4, loss of H requires ~32 kcal/mol, whereas loss of a water molecule requires only 19 kcal/mol, and this difference in dissociation energies increases substantially for smaller clusters [50]. Although it is possible that the dissociation entropies are very different for these two processes, both processes are relatively “direct” and should occur through “loose” transition states.
A complicating factor is angular momentum effects that originate from the significantly different masses of H2O versus H that arise from dissociation via the two different pathways. Information about the energy dependence of the dissociation of small clusters has been reported by Armentrout and coworkers, who used guided ion beam mass spectrometry to measure the sequential binding energies of water to , M = Na, Mg, and Al, n = 1 – 4 [60]. For , loss of one or more water molecules was the only process observed with center of mass collision energies up to 1.5 eV. A second water molecule loss becomes apparent at about 1.2 eV [60]. The third and fourth sequential binding energies of water to Mg and Na are similar and only loss of water was reported for Mg under similar conditions [60]. These results indicate that , activated by collisions with center of mass collision energies up to 1.5 eV, results in only loss of water despite internal energies that are higher than the binding energy of H to these clusters. Although the maximum energy deposited in these guided ion beam experiments is less than that deposited by EC, it is surprising that this difference alone would result in exclusive dissociation by pathway I for the former and pathway II for the latter if both processes are statistical.
The dissociation of clusters using visible radiation has also been investigated [56,75,76]. For n = 4 and 5, both dissociation pathways were observed with a branching ratio for pathway II:I of ~4:1 over an energy range of 2.4 – 3.7 and 1.7 – 3.6 eV, respectively [75]. These results, in combination with the aforementioned data, suggest that the loss of H from these clusters occurs directly from electronic excited states formed either by absorption of visible photons by the monovalent cluster or by EC by the corresponding divalent cluster.
A confirmation of the nonergodicity of EC for these clusters would be to measure the collisionally activated dissociation products of the corresponding monovalent clusters at center of mass collision energies comparable to the maximum recombination energy into the divalent cluster upon EC. Different product ions formed from the same precursor ion upon activation to the same internal energy using two different activation methods provides compelling support for nonergodic dissociation.
A third piece of evidence for nonergodic dissociation, although very indirect, is the wider distribution of product ions formed as a result of pathway II versus I (see Figure 2c). The internal energy deposition by EC can be quite narrow for the larger cluster ions where often only a single product ion is observed indicating that the width of the energy distribution is less than 10 kcal/mol. This suggests that the kinetic energies of the water molecules that are lost from the cluster via pathway I are low. The broader distribution observed for dissociation via pathway II can be attributed to the H atom carrying away a variable amount of kinetic energy, or possibly a vibrationally excited water molecule accompanying the H atom loss, both of which are consistent with a nonstatistical process.
Double Resonance Experiments
To determine the order in which the H atom and water molecules are lost via pathway II, several double resonance experiments were performed. In a double resonance experiment [77, 78], a frequency corresponding to the cyclotron resonance frequency of an ion suspected to be an intermediate in a consecutive dissociation process is continuously irradiated over the course of a dissociation experiment. The disappearance of lower mass ions confirms that the irradiated ion is an intermediary in the formation of those ions. These experiments were done for EC of . Three separate experiments were done where CaOH+ with 1, 2 or 3 water molecules attached were continuously ejected with a single frequency waveform corresponding to the cyclotron frequency of these ions. This waveform had sufficient power to eject an ion from the cell within 100 μs. In each case, the final products were not perturbed by the single frequency waveform, except in the case of ejection of CaOH(H2O)+ where this is one of the final products. This suggests that either the ejection of the hydrogen atom occurs after loss of the water molecules, or more likely, that the loss of the hydrogen atom occurs on a timescale that is much shorter than 100 μs.
Conclusions
The results of the ECD experiments on hydrated divalent magnesium and calcium ions demonstrate that these ions can be used as nanocalorimeters over a wide range of cluster sizes. From the dissociation products, quantitative information about the average and maximum internal energy deposition resulting from EC is obtained. These results clearly show that the range of internal energies deposited is very narrow and that the vast majority of the recombination energy that is available from EC by the divalent precursor ions is converted into internal energy of the reduced precursor for the larger clusters. There is no significant difference in the internal energy deposition as a function of cluster size. The average internal energy deposited into , M = Mg and Ca, is approximately the same for n = 4 – 6 as it is for n = 32. In contrast, calculations of the ionization energy of [69] indicate that the recombination energy should increase rapidly for clusters below n = 10. These, and other results, suggest that not all the recombination energy that is available from EC is converted into internal modes of the ion and that the dissociation process for these smaller clusters is nonergodic.
The internal energy deposition values that we obtain from these experiments depend on the dissociation energies of the ligands lost. For the larger clusters, ~10 kcal/mol appears to be a good estimate for the dissociation energy corresponding to the loss of each water molecule from the reduced cluster, although we estimate the uncertainty in this value to be about ± 10%. For the smaller clusters that dissociate by both loss of a H atom and by loss of water molecules, we use calculated values for the dissociation energy because no experimental values are available. The internal energy deposition values that we obtain from these experiments can be revised if more accurate values for the dissociation energies are obtained either through experimental measurements or higher levels of theory. A more detailed investigation into the effects of high internal energy deposition on the translational, vibrational and rotational energies of the products would provide more accurate values for our estimates of the average internal energy deposition from these experimental data. Modeling of the dissociation process, including any partitioning into translational, vibrational and rotational degrees of freedom of the dissociation products with phase space theory, is currently ongoing.
It is interesting to note that the internal energy deposited into Mg and Ca clusters of a given size are essentially indistinguishable. When the electron recombines with the divalent cluster, it is likely that the resulting reduced cluster forms an ion pair consisting of a divalent metal cation with a solvated electron, at least for the larger cluster sizes. Such electrides, which are ionic salts with the electron as an anion [79, 80], have been investigated for many years and a single-crystal electride that is both thermally stable and unreactive has been recently reported [81]. A solvated electron Mg2+ pair has also been proposed for gas-phase for clusters with more than 17 water molecules to explain the change in dissociation reactivity that occurs for clusters of this size [57].
It is also interesting to postulate why dissociation of the small clusters is nonergodic whereas the dissociation of the larger clusters is statistical. Upon electron capture, the large clusters only lose water molecules whereas the smaller clusters lose a H atom and water molecules. The nonstatistical behavior may be due to the processes for loss of a H atom or it may depend on physical properties related to cluster size. Attachment of an electron to the cluster may result in spontaneous ejection of a “hot” H atom analogous to the dissociative electron attachment to an isolated water molecule. The efficiency with which the energy from EC is converted into vibrational modes may be attributable to other physical properties that change as a function of cluster size. Larger clusters have more vibrational modes which may make the transfer of the recombination energy into internal modes more efficient. The energy differences between electronic levels also depend on cluster size. For the octahedral form of , the HOMO-LUMO gap is 0.8 eV and there are 10 unoccupied molecular orbitals with energies that are within 2.5 eV of the HOMO. In contrast, the HOMO-LUMO gap is 2.9 eV for and there are only 7 unoccupied molecular orbitals that are within 5.0 eV of the HOMO. Thus, the energy differences between electronic excited states decreases with increasing cluster size and this may play a role in the efficiency of energy conversion between excited states and vibrational modes of the cluster.
Finally, it is important to note similarities and differences between these ECD experiments and those done with peptides and proteins. A key distinction between these experiments is that the dissociation processes for the hydrated divalent metal ions are clearly different from those of peptides and proteins. Loss of water molecules resulting from ECD of proteins has been observed [31], but this is a minor process. Product ions corresponding to the loss of a H atom can be the dominant process observed for ECID of diprotonated dipeptides [32], but loss of a H atom is less significant for larger peptides. In larger peptides and proteins, it has been postulated that a hot hydrogen atom may play a role in the formation of product ions [7]. The internal energy deposited into these cluster ions and peptides and protein ions from EC is similar and the process whereby this energy is converted into internal modes may be similar as well. Future experiments on EC of hydrated peptide and protein ions may provide important new information on how ECD occurs in these ions.
Supplementary Material
Acknowledgments
The authors thank Professors Peter B. Armentrout, Marcin Majda, William H. Miller, Daniel M. Neumark, Kenneth N. Raymond and Richard J. Saykally for helpful discussions and NSF (CHE-041593) and NIH (R01 GM064712-05) for generous financial support.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Sacksteder CA, Qian WJ, Knyushko TV, Wang HX, Chin MH, Lacan G, Melega WP, Camp DG, Smith RD, Smith DJ, Squier TC, Bigelow DJ. Endogenously nitrated proteins in mouse brain: Links to neurodegenerative disease. Biochemistry. 2006;45:8009–8022. doi: 10.1021/bi060474w. [DOI] [PubMed] [Google Scholar]
- 2.Valentine SJ, Kulchania M, Barnes CAS, Clemmer DE. Multidimensional separations of complex peptide mixtures: A combined high-performance liquid chromatography/ion mobility/time-of-flight mass spectrometry approach. Int J Mass Spectrom. 2001;212:97–109. [Google Scholar]
- 3.Valentine SJ, Liu XY, Plasencia MD, Hilderbrand AE, Kurulugama RT, Koeniger SL, Clemmer DE. Developing liquid chromatography ion mobility mass spectometry techniques. Expert Rev Proteomics. 2005;2:553–565. doi: 10.1586/14789450.2.4.553. [DOI] [PubMed] [Google Scholar]
- 4.Taraszka JA, Kurulugama R, Sowell RA, Valentine SJ, Koeniger SL, Arnold RJ, Miller DF, Kaufman TC, Clemmer DE. Mapping the proteome of drosophila melanogaster: Analysis of embryos and adult heads by LC-IMS-MS methods. J Proteome Res. 2005;4:1223–1237. doi: 10.1021/pr050038g. [DOI] [PubMed] [Google Scholar]
- 5.Han XM, Jin M, Breuker K, McLafferty FW. Extending top-down mass spectrometry to proteins with masses greater than 200 kiloDaltons. Science. 2006;314:109–112. doi: 10.1126/science.1128868. [DOI] [PubMed] [Google Scholar]
- 6.Ge Y, Lawhorn BG, ElNaggar M, Strauss E, Park JH, Begley TP, McLafferty FW. Top down characterization of larger proteins (45 kDa) by electron capture dissociation mass spectrometry. J Am Chem Soc. 2002;124:672–678. doi: 10.1021/ja011335z. [DOI] [PubMed] [Google Scholar]
- 7.Zubarev RA, Kelleher NL, McLafferty FW. Electron capture dissociation of multiply charged protein cations. A nonergodic process. J Am Chem Soc. 1998;120:3265–3266. [Google Scholar]
- 8.Zubarev RA, Horn DM, Fridriksson EK, Kelleher NL, Kruger NA, Lewis MA, Carpenter BK, McLafferty FW. Electron capture dissociation for structural characterization of multiply charged protein cations. Anal Chem. 2000;72:563–573. doi: 10.1021/ac990811p. [DOI] [PubMed] [Google Scholar]
- 9.Breuker K, Oh HB, Horn DM, Cerda BA, McLafferty FW. Detailed unfolding and folding of gaseous ubiquitin ions characterized by electron capture dissociation. J Am Chem Soc. 2002;124:6407–6420. doi: 10.1021/ja012267j. [DOI] [PubMed] [Google Scholar]
- 10.Coon JJ, Shabanowitz J, Hunt DF, Syka JEP. Electron transfer dissociation of peptide anions. J Am Soc Mass Spectrom. 2005;16:880–882. doi: 10.1016/j.jasms.2005.01.015. [DOI] [PubMed] [Google Scholar]
- 11.Syka JEP, Coon JJ, Schroeder MJ, Shabanowitz J, Hunt DF. Peptide and protein sequence analysis by electron transfer dissociation mass spectrometry. Proc Natl Acad Sci U S A. 2004;101:9528–9533. doi: 10.1073/pnas.0402700101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hvelplund P, Liu B, Nielsen SB, Tomita S. Electron capture induced dissociation of peptide dications. Int J Mass Spectrom. 2003;225:83–87. [Google Scholar]
- 13.Hvelplund P, Liu B, Nielsen SB, Tomita S, Cederquist H, Jensen J, Schmidt HT, Zettergren H. Electron capture and loss by protonated peptides and proteins in collisions with C-60 and Na. Eur Phys J D. 2003;22:75–79. [Google Scholar]
- 14.Zubarev RA. Reactions of polypeptide ions with electrons in the gas phase. Mass Spectrom Rev. 2003;22:57–77. doi: 10.1002/mas.10042. [DOI] [PubMed] [Google Scholar]
- 15.Zubarev RA, Haselmann KF, Budnik B, Kjeldsen F, Jensen F. Towards an understanding of the mechanism of electron-capture dissociation: A historical perspective and modern ideas. Eur J Mass Spectrom. 2002;8:337–349. [Google Scholar]
- 16.Zubarev RA. Electron-capture dissociation tandem mass spectrometry. Curr Opin Biotechnol. 2004;15:12–16. doi: 10.1016/j.copbio.2003.12.002. [DOI] [PubMed] [Google Scholar]
- 17.Cooper HJ, Hakansson K, Marshall AG. The role of electron capture dissociation in biomolecular analysis. Mass Spectrom Rev. 2005;24:201–222. doi: 10.1002/mas.20014. [DOI] [PubMed] [Google Scholar]
- 18.Breuker K, Oh HB, Lin C, Carpenter BK, McLafferty FW. Nonergodic and conformational control of the electron capture dissociation of protein cations. Proc Natl Acad Sci U S A. 2004;101:14011–14016. doi: 10.1073/pnas.0406095101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen XH, Turěek F. The arginine anomaly: Arginine radicals are poor hydrogen atom donors in electron transfer induced dissociations. J Am Chem Soc. 2006;128:12520–12530. doi: 10.1021/ja063676o. [DOI] [PubMed] [Google Scholar]
- 20.Syrstad EA, Turěek F. Hydrogen atom adducts to the amide bond. Generation and energetics of the amino(hydroxy)methyl radical in the gas phase. J Phys Chem A. 2001;105:11144–11155. [Google Scholar]
- 21.Syrstad EA, Stephens DD, Turěek F. Hydrogen atom adducts to the amide bond. Generation and energetics of amide radicals in the gas phase. J Phys Chem A. 2003;107:115–126. [Google Scholar]
- 22.Syrstad EA, Turěek F. Toward a general mechanism of electron capture dissociation. J Am Soc Mass Spectrom. 2005;16:208–224. doi: 10.1016/j.jasms.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 23.Turěek F, Syrstad EA, Seymour JL, Chen XH, Yao CX. Peptide cation-radicals. A computational study of the competition between peptide N-Cα, bond cleavage and loss of the side chain in the [GlyPhe-NH2+2H]+• cation-radical. J Mass Spectrom. 2003;38:1093–1104. doi: 10.1002/jms.527. [DOI] [PubMed] [Google Scholar]
- 24.Turěek F. N-Cα bond dissociation energies and kinetics in amide and peptide radicals. Is the dissociation a non-ergodic process? J Am Chem Soc. 2003;125:5954–5963. doi: 10.1021/ja021323t. [DOI] [PubMed] [Google Scholar]
- 25.Turěek F, Syrstad EA. Mechanism and energetics of intramolecular hydrogen transfer in amide and peptide radicals and cation-radicals. J Am Chem Soc. 2003;125:3353–3369. doi: 10.1021/ja021162t. [DOI] [PubMed] [Google Scholar]
- 26.Kruger NA, Zubarev RA, Carpenter BK, Kelleher NL, Horn DM, McLafferty FW. Electron capture versus energetic dissociation of protein ions. Int J Mass Spectrom. 1999;183:1–5. [Google Scholar]
- 27.Sobczyk M, Simons J. Distance dependence of through-bond electron transfer rates in electron-capture and electron-transfer dissociation. Int J Mass Spectrom. 2006;253:274–280. [Google Scholar]
- 28.Sobczyk M, Simons J. The role of excited Rydberg states in electron transfer dissociation. J Phys Chem B. 2006;110:7519–7527. doi: 10.1021/jp0604701. [DOI] [PubMed] [Google Scholar]
- 29.Anusiewicz I, Berdys-Kochanska J, Skurski P, Simons J. Simulating electron transfer attachment to a positively charged model peptide. J Phys Chem A. 2006;110:1261–1266. doi: 10.1021/jp052914j. [DOI] [PubMed] [Google Scholar]
- 30.Sawicka A, Skurski P, Hudgins RR, Simons J. Model calculations relevant to disulfide bond cleavage via electron capture influenced by positively charged groups. J Phys Chem B. 2003;107:13505–13511. [Google Scholar]
- 31.Robinson EW, Leib RD, Williams ER. The role of conformation on electron capture dissociation of ubiquitin. J Am Soc Mass Spectrom. 2006;17:1469–1479. doi: 10.1016/j.jasms.2006.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chakraborty T, Holm AIS, Hvelplund P, Nielsen SB, Poully J-C, Worm ES, Williams ER. On the survival of peptide cations after electron capture: Role of internal hydrogen bonding and microsolvation. J Am Soc Mass Spectrom. 2006;17:1675–1680. doi: 10.1016/j.jasms.2006.07.018. [DOI] [PubMed] [Google Scholar]
- 33.Liu H, Hakansson K. Electron capture dissociation of tyrosine O-sulfated peptides complexed with divalent metal cations. Anal Chem. 2006;78:7570–7576. doi: 10.1021/ac061352c. [DOI] [PubMed] [Google Scholar]
- 34.Liu H, Hakansson K. Divalent metal ion-peptide interactions probed by electron capture dissociation of trications. J Am Soc Mass Spectrom. 2006;17:1731–1741. doi: 10.1016/j.jasms.2006.07.027. [DOI] [PubMed] [Google Scholar]
- 35.Leymarie N, Costello CE, O’Connor PB. Electron capture dissociation initiates a free radical reaction cascade. J Am Chem Soc. 2003;125:8949–8958. doi: 10.1021/ja028831n. [DOI] [PubMed] [Google Scholar]
- 36.Lin C, O’Connor PB, Cournoyer JJ. Use of a double resonance electron capture dissociation experiment to probe fragment intermediate lifetimes. J Am Soc Mass Spectrom. 2006;17:1605–1615. doi: 10.1016/j.jasms.2006.07.007. [DOI] [PubMed] [Google Scholar]
- 37.O’Connor PB, Lin C, Cournoyer JJ, Pittman JL, Belyayev M, Budnik BA. Long-lived electron capture dissociation product ions experience radical migration via hydrogen abstraction. J Am Soc Mass Spectrom. 2006;17:576–585. doi: 10.1016/j.jasms.2005.12.015. [DOI] [PubMed] [Google Scholar]
- 38.Iavarone AT, Paech K, Williams ER. Effects of charge state and cationizing agent on the electron capture dissociation of a peptide. Anal Chem. 2004;76:2231–2238. doi: 10.1021/ac035431p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Griffiths IW, Mukhtar ES, March RE, Harris FM, Beynon JH. Comparison of photo-excitation of ions and collisional excitation using gases. Int J Mass Spectrom Ion Phys. 1981;39:125–132. [Google Scholar]
- 40.Baer T, Dutuit O, Mestdagh H, Rolando C. Dissociation dynamics of normal-butylbenzene ions - the competitive production of m/z 91-fragment and 92-fragment ions. J Phys Chem. 1988;92:5674–5679. [Google Scholar]
- 41.Chen JH, Hays JD, Dunbar RC. Competitive 2-channel photodissociation of normal-butylbenzene ions in the Fourier-transform ion-cyclotron resonance mass-spectrometer. J Phys Chem. 1984;88:4759–4764. [Google Scholar]
- 42.Kenttämaa HI, Cooks RG. Internal energy-distributions acquired through collisional activation at low and high-energies. Int J Mass Spectrom Ion Processes. 1985;64:79–83. [Google Scholar]
- 43.Dekrey MJ, Kenttämaa HI, Wysocki VH, Cooks RG. Energy deposition in Upon collision with a metal-surface. Org Mass Spectrom. 1986;21:193–195. [Google Scholar]
- 44.Beranova S, Wesdemiotis C. Internal energy-distributions of tungsten hexacarbonyl ions after neutralization-reionization. J Am Soc Mass Spectrom. 1994;5:1093–1101. doi: 10.1016/1044-0305(94)85070-4. [DOI] [PubMed] [Google Scholar]
- 45.Nguyen VQ, Turěek F. Protonation sites in gaseous pyrrole and imidazole: A neutralization-reionization and ab initio study. J Mass Spectrom. 1996;31:1173–1184. doi: 10.1002/(SICI)1096-9888(199610)31:10<1173::AID-JMS412>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- 46.Schnier PD, Jurchen JC, Williams ER. The effective temperature of peptide ions dissociated by sustained off-resonance irradiation collisional activation in fourier transform mass spectrometry. J Phys Chem B. 1999;103:737–745. doi: 10.1021/jp9833193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Price WD, Schnier PD, Jockusch RA, Strittmatter EF, Williams ER. Unimolecular reaction kinetics in the high-pressure limit without collisions. J Am Chem Soc. 1996;118:10640–10644. doi: 10.1021/ja961812r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wong RL, Paech K, Williams ER. Blackbody infrared radiative dissociation at low temperature: Hydration of X2+(H2O)n, for X = Mg, Ca. Int J Mass Spectrom. 2004;232:59–66. [Google Scholar]
- 49.Bush MF, Saykally RJ, Williams ER. Formation of hydrated triply charged metal ions from aqueous solutions using nanodrop mass spectrometry. Int J Mass Spectrom. 2006;253:256–262. doi: 10.1016/j.ijms.2006.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Siu CK, Liu ZF. Ab initio studies on the mechanism of the size-dependent hydrogen-loss reaction in Mg+(H2O)n. Chem Eur J. 2002;8:3177–3186. doi: 10.1002/1521-3765(20020715)8:14<3177::AID-CHEM3177>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 51.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JJA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03 Revision C. 02. Gaussian, Inc; 2004. [Google Scholar]
- 52.Cody RB, Freiser BS. Electron-impact excitation of ions from organics - alternative to collision-induced dissociation. Anal Chem. 1979;51:547–551. [Google Scholar]
- 53.Polfer NC, Haselmann KF, Zubarev RA, Langridge-Smith PRR. Electron capture dissociation of polypeptides using a 3 Tesla Fourier transform ion cyclotron resonance mass spectrometer. Rapid Commun Mass Spectrom. 2002;16:936–943. doi: 10.1002/rcm.664. [DOI] [PubMed] [Google Scholar]
- 54.Kjeldsen F, Haselmann KF, Budnik BA, Jensen F, Zubarev RA. Dissociative capture of hot (3-13 eV) electrons by polypeptide polycations: An efficient process accompanied by secondary fragmentation. Chem Phys Lett. 2002;356:201–206. [Google Scholar]
- 55.Harms AC, Khanna SN, Chen AB, Castleman AW. Dehydrogenation reactions in Mg+(H2O)n clusters. J Chem Phys. 1994;100:3540–3544. [Google Scholar]
- 56.Sanekata M, Misaizu F, Fuke K, Iwata S, Hashimoto K. Reactions of singly charged alkaline-earth metal-ions with water clusters - characteristic size distribution of product ions. J Am Chem Soc. 1995;117:747–754. [Google Scholar]
- 57.Berg C, Beyer M, Achatz U, Joos S, Niedner-Schatteburg G, Bondybey VE. Stability and reactivity of hydrated magnesium cations. Chem Phys. 1998;239:379–392. [Google Scholar]
- 58.Dzidic I, Kebarle P. Hydration of alkali ions in gas phase - enthalpies and entropies of reactions Mg+(H2O)n-1 + H2O = Mg+(H2O)n. J Phys Chem. 1970;74:1466–1474. [Google Scholar]
- 59.Shi Z, Ford JV, Wei S, Castleman AW. Water clusters - contributions of binding-energy and entropy to stability. J Chem Phys. 1993;99:8009–8015. [Google Scholar]
- 60.Dalleska NF, Tjelta BL, Armentrout PB. Sequential bond-energies of water to Na+ (3s(0)), Mg+ (3s(1)), and Al+ (3s(2)) J Phys Chem. 1994;98:4191–4195. [Google Scholar]
- 61.McLafferty FW, Wachs T, Lifshitz C, Innorta G, Irving P. Substituenteffects in unimolecular ion decompositions. 15. Mechanistic interpretations and quasi-equilibrium theory. J Am Chem Soc. 1970;92:6867–6880. [Google Scholar]
- 62.Leib RD, Donald WA, Bush MF, O’Brien JT, Williams ER. Internal energy deposition in electron capture dissociation measured using hydrated divalent metal ions as nanocalorimeters. J Am Chem Soc. 2007 doi: 10.1021/ja0666607. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kebarle P, Searles SK, Zolla A, Scarborough J, Arshadi M. The solvation of the hydrogen ion by water molecules in the gas phase. Heats and entropies of solvation of individual reactions: H+(H2O)n-1 + H2O -> H+(H2O)n. J Mass Spectrom. 1997;32:915–921. [Google Scholar]
- 64.Marsh KN. Recommended reference materials for the realization of physiochemical properties. Blackwell; Oxford: 1987. [Google Scholar]
- 65.Feistel R, Wagner W. A new equation of state for H2O ice Ih. J Phys Chem Ref Data. 2006;35:1021–1047. [Google Scholar]
- 66.Klots CE. Evaporative cooling. J Chem Phys. 1985;83:5854–5860. [Google Scholar]
- 67.Watanabe H, Iwata S, Hashimoto K, Misaizu F, Fuke K. Molecular-orbital studies of the structures and reactions of singly charged magnesium-ion with water clusters, Mg+(H2O)n. J Am Chem Soc. 1995;117:755–763. [Google Scholar]
- 68.Inokuchi Y, Ohshimo K, Misaizu F, Nishi N. Infrared photodissociation spectroscopy of [Mg • (H2O)1-4]+ and [Mg • (H2O)1-4 • Ar]+ J Phys Chem A. 2004;108:5034–5040. [Google Scholar]
- 69.Reinhard BM, Niedner-Schatteburg G. Ionization energies and spatial volumes of the singly occupied molecular orbital in hydrated magnesium clusters J Chem Phys. 2003;118:3571–3582. [Google Scholar]
- 70.Coe JV. Fundamental properties of bulk water from cluster ion data. Int Rev Phys Chem. 2001;20:33–58. [Google Scholar]
- 71.Märk TD. Free electron attachment to van der Waals clusters. Int J Mass Spectrom Ion Processes. 1991;107:143–163. [Google Scholar]
- 72.Fedor J, Cicman P, Coupier B, Feil S, Winkler M, Gluch K, Husarik J, Jaksch D, Farizon B, Mason NJ, Scheier P, Märk TD. Fragmentation of transient water anions following low-energy electron capture by H2O/D2O. J Phys B: At Mol Phys. 2006;39:3935–3944. [Google Scholar]
- 73.Belic DS, Landau M, Hall RI. Energy and angular-dependence of H-(D-) ions produced by dissociative electron-attachment to H2O (D2O) J Phys B: At Mol Phys. 1981;14:175–190. [Google Scholar]
- 74.Baer T, Hase WL. Unimolecular reaction dynamics: Theory and experiments. Oxford University Press; New York: 1996. [Google Scholar]
- 75.Misaizu F, Sanekata M, Fuke K, Iwata S. Photodissociation study on Mg+(H2O)n, n = 1-5: Electronic structure and photoinduced intracluster reaction. J Chem Phys. 1994;100:1161–1170. [Google Scholar]
- 76.Misaizu F, Sanekata M, Tsukamoto K, Fuke K, Iwata S. Photodissociation of size-selected Mg+(H2O)n ions for n = 1 and 2. J Phys Chem. 1992;96:8259–8264. [Google Scholar]
- 77.Anders LR, Beauchamp JL, Dunbar RC, Baldeschwieler JD. Ion-cyclotron double resonance. J Chem Phys. 1966;45:1062–1063. [Google Scholar]
- 78.Jurchen JC, Garcia DE, Williams ER. Gas-phase dissociation pathways of multiply charged peptide clusters. J Am Soc Mass Spectrom. 2003;14:1373–1386. doi: 10.1016/j.jasms.2003.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Dye JL. Electrons as anions. Science. 2003;301:607–608. doi: 10.1126/science.1088103. [DOI] [PubMed] [Google Scholar]
- 80.Dye JL. Electrides - ionic salts with electrons as the anions. Science. 1990;247:663–668. doi: 10.1126/science.247.4943.663. [DOI] [PubMed] [Google Scholar]
- 81.Matsuishi S, Toda Y, Miyakawa M, Hayashi K, Kamiya T, Hirano M, Tanaka I, Hosono H. High-density electron anions in a nanoporous single crystal[Ca24Al28O64]4+4e- Science. 2003;301:626–629. doi: 10.1126/science.1083842. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.