Hierarchies, multiple energy barriers, and robustness govern the fracture mechanics of α-helical and β-sheet protein domains

Abstract

The fundamental fracture mechanisms of biological protein materials remain largely unknown, in part, because of a lack of understanding of how individual protein building blocks respond to mechanical load. For instance, it remains controversial whether the free energy landscape of the unfolding behavior of proteins consists of multiple, discrete transition states or the location of the transition state changes continuously with the pulling velocity. This lack in understanding has thus far prevented us from developing predictive strength models of protein materials. Here, we report direct atomistic simulation that over four orders of magnitude in time scales of the unfolding behavior of α-helical (AH) and β-sheet (BS) domains, the key building blocks of hair, hoof, and wool as well as spider silk, amyloids, and titin. We find that two discrete transition states corresponding to two fracture mechanisms exist. Whereas the unfolding mechanism at fast pulling rates is sequential rupture of individual hydrogen bonds (HBs), unfolding at slow pulling rates proceeds by simultaneous rupture of several HBs. We derive the hierarchical Bell model, a theory that explicitly considers the hierarchical architecture of proteins, providing a rigorous structure–property relationship. We exemplify our model in a study of AHs, and show that 3–4 parallel HBs per turn are favorable in light of the protein's mechanical and thermodynamical stability, in agreement with experimental findings that AHs feature 3.6 HBs per turn. Our results provide evidence that the molecular structure of AHs maximizes its robustness at minimal use of building materials.

Proteins constitute critical building blocks of life, forming biological materials such as hair, bone, skin, spider silk, or cells (1), displaying highly specific hierarchical structures, from nano to macro. Some of these features are commonly found and highly conserved universal building blocks of protein materials. Examples include α-helices (AHs) (1, 2) and β-sheets (BSs) (1). Both the AH and BS domains are typically only one of the many domains within a larger protein structure.

The AH motif is commonly found in structural protein networks and plays an important role in biophysical processes that involve mechanical signals, including mechanosensation and mechanotransduction, and provide mechanical stability to cells (1–4). For instance, AH-rich intermediate filament networks forward signals from the cellular environment to the DNA (3, 4), aspects that are critical for cell mitosis or apoptosis. The BS motif is an integral component of spider silk, amyloids, and titin (1, 5). The mechanical properties of proteins and the link to associated atomistic-scale chemical reactions are not only of vital importance in biology but are also crucial for the de novo design and manufacturing of protein materials (6–8).

Mechanical loading of proteins can result in severe changes in the protein structure, inducing unfolding of the protein. Typically, a variety of unfolding processes exist for a given protein structure, each of which has a specific reaction pathway and an associated energy barrier (9). These unfolding modes can be understood as the interplay between processes with different activation barriers E_b operating at different activation distances x_b.

A variety of AH- and BS-based structures have been studied in experiment and molecular dynamics (MD) simulation (10–19). However, earlier MD simulations were carried out at rather large pulling rates, and therefore, no direct link between simulation and experiment has been reported. Transitions of unfolding mechanisms have been suggested (20, 21) but have thus far not been observed directly in either experiment or simulation. It remains controversial whether the free energy landscape of the unfolding behavior of proteins consists of multiple, discrete transition states or the transition states change continuously with a change in pulling velocity (20, 21).

Further, structure–property relationships for the force–extension behavior and associated strength models have not been reported. No links exist between the details of the molecular architecture, the resulting free energy landscape, and the mechanical properties. However, this understanding is crucial to developing strength models of protein materials.

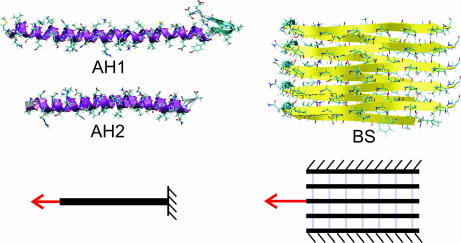
Here, we present studies of three model protein domains (for molecular geometries, see Fig. 1). We consider two AH models. AH1 is a domain from the 2B segment of the vimentin intermediate filament dimer (22–24), and AH2 is a domain from bacteriophage T4 fibritin (25). The BS model is a protein structure proposed for Alzheimer's amyloid β-fibril (5).

Fig. 1.

Atomistic geometries of the three protein domains studied here (AH1, AH2, and BS). Surrounding water molecules are not shown for reasons of clarity. The lower part of the plot indicates the boundary conditions (tensile loading for AH1 and AH2 and shear loading for BS). The BS structure consists of two stacks of β-sheets in the out-of-plane direction.

Results

Theoretical Model for Protein Unfolding Mechanics.

Several theories describe competing processes due to mechanically induced instabilities of protein structures. Most of these theories are derived from a phenomenological theory originally postulated by Bell (26), or Kramer's diffusion model (27). Here, we extend Bell's approach so that simulations at various pulling speeds can be used to gain information about the free energy landscape of a protein.

In Bell's theory, the off-rate χ is the product of a natural vibration frequency ω₀ ≈ 1 × 10¹³ s⁻¹ (26), and the quasi-equilibrium likelihood of reaching the transition state with an energy barrier E_b. The energy barrier is reduced by mechanical energy f·x_b·cos(θ) due to the externally applied force f, where x_b is the distance between the equilibrated state and the transition state, and θ is the angle between the direction of the reaction pathway of bond breaking (x direction) and the direction of applied load [f direction; see supporting information (SI) Fig. 6]. The angle can be determined by analyzing the protein geometry. The off-rate is given by

and describes how often a bond is broken per unit time (the reciprocal of the bond lifetime).

However, Eq. 1 does not describe the dependence of the pulling speed v (the controlled parameter in experiment and MD simulation) at which a bond breaks because of the pulling force f. We thus modify Eq. 1 based on the following idea. The speed v at which a bond is broken is equal to the distance that needs to be overcome to break the bond (x_b), divided by the time for the bond breaking. Consequently, v is the product of χ·x_b, thus v = χ·x_b = Δx/Δt. Macroscopically, the pulling speed is equal to the displacement Δx of the pulled atom divided by the pulling time Δt. This equation can be rewritten, leading to

with v₀ as the natural bond-breaking speed (speed of bond dissociation when no load is applied), defined as

This modified framework enables one to calculate the force at which a bond breaks, at a certain pulling rate:

where a₁ = k_B·T/(x_b·cos(θ)) and a₂ = −k_B·T/(x_b·cos(θ))·ln v₀. Eq. 4 predicts that the bond-breaking force depends logarithmically on the pulling speed in a nonequilibrated system. The parameters a₁ and a₂ can be calculated from the parameters x_b and E_b for a certain temperature and angle. Note that if the free energy landscape is dominated by several transition states, each of the states is characterized by a combination of E_b and x_b. This results in segments of multiple straight lines in the f–ln(v) plane. The model reduces to a phenomenological model when the cos(θ) term is removed; the phenomenological model contains only the energy barrier E_b and x_b and no structural information. Note that an expression similar to Eq. 4 was reported in ref. 28.

Results of MD Simulations.

We carry out a series of classical MD simulations (for details, see Materials and Methods). The goal is a systematic analysis of the unfolding behavior of the protein domains at varying pulling rates.

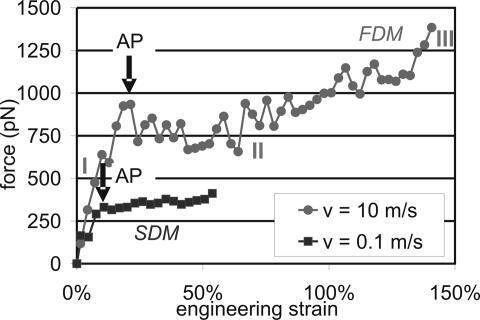
For the vimentin AH protein domain (AH1), two characteristic force–strain curves are shown in Fig. 2 for two pulling speeds. The simulations reveal existence of three distinct deformation regimes. The first regime shows a linear increase in strain until the angular point (AP) is reached. The second regime is a plateau of approximately constant force, during which unfolding of the entire protein occurs. The last regime displays a significant strain hardening due to pulling of the protein's backbone [only partly visible in the fast-deformation mode (FDM) plot]. A similar behavior is observed for the AH2 structure. The change from the first to the second regime is referred to as the AP, denoting the protein-unfolding force. Unfolding of the protein is characterized by rupture of hydrogen bonds (HBs) that destroys the protein structure as the displacement is increased. In the remainder of this article, we focus on the force at the AP as a function of the pulling speed.

Fig. 2.

Examples for force–extension curves of AH1. The fast deformation mode (FDM) is represented by a curve taken at a pulling speed of 10 m/s. The slow deformation mode (SDM) is represented by a pulling experiment at 0.1 m/s. The force–extension behavior consists of three regimes: (I) linear increase in strain until the AP is reached (indicated by arrows) when the first HBs rupture, leading to unfolding of one helical turn; (II) plateau of approximately constant force, during which unfolding of the entire protein occurs; and (III) strain hardening (only partly shown for the FDM).

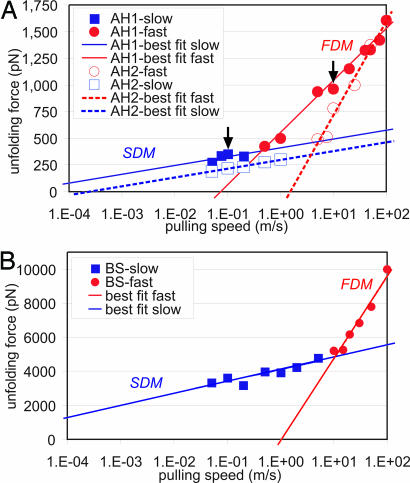
We carry out computational experiments by systematically varying the pulling velocity over four orders of magnitude, ranging from 0.05 to 100 m/s. The unfolding force is plotted as a function of the pulling speed in Fig. 3A for AH1 and AH2. Fig. 3B shows the unfolding force of the BS domain as a function of the pulling speed. We note that the force–extension curve of the BS structure does not show a large yield regime as in the AHs (regime II), but rather shows a maximum peak at which the structure fractures.

Fig. 3.

Unfolding force of single AHs from the vimentin coiled-coil dimers (A) and a BS amyloid domain (B), as a function of varying pulling speed over four orders of magnitude, ranging from 0.05 to 100 m/s. The results clearly reveal a change in protein-unfolding mechanism from the FDM to the SDM. The arrows in A indicate the representative pulling speeds used for the analysis reported in Figs. 2 and 4.

Notably, in all three cases we observe two distinct regimes, each of which follows a logarithmic dependence of the unfolding force with respect to the pulling rate. The existence of two discrete slopes indicates two different energy barriers and thus two different unfolding mechanisms over the simulated pulling velocity regime. The results clearly suggest a free energy landscape that consists of two transition states. In the following text we refer to these two regimes as the slow-deformation mode (SDM) and the FDM. The change in mechanism from the FDM to the SDM occurs at v = 0.4 m/s (AH1) and v = 4 m/s (AH2), and at a force of ≈350 pN (AH1) and ≈400 pN (AH2). For the BS structure, the transition occurs at v = 10 m/s at a force of ≈4,800 pN.

To the best of our knowledge, up to now, neither any unfolding behavior in the SDM nor the change from the FDM to the SDM has been observed in direct MD simulation or in experiment. We emphasize that the change in mechanism has thus far only been suggested or inferred (21, 29). For example, a comparison between MD simulation and experimental results revealed that force–pulling speed dependence must lie on two different curves in the f–ln(v) plane (21, 29), suggesting a change in unfolding mechanism.

By fitting the extended Bell theory to the MD results of the AH1 structure, we obtain for the FDM E_b = 4.7 kcal/mol and x_b = 0.20 Å. In the SDM (with θ ≈ 16°), E_b = 11.1 kcal/mol and x_b = 1.2 Å. Similar values are found for the AH2 structure, albeit the results for E_b are slightly lower (see Table 1). Considering that the bond-breaking energy E_b of a HB in water ranges typically from 3 to 6 kcal/mol (30), the results indicate that in the FDM, individual HBs rupture sequentially. In contrast, in the SDM approximately three HBs rupture at once. Studies of both AH structures clearly support this observation.

Table 1.

Summary of the differences between the SDM and FDM, for AH1, AH2, and BS

Parameter	AH1 (AH2) domain		BS domain
	SDM	FDM	SDM	FDM
Pulling speed, m/s	v < 0.4 (4)	v > 0.4 (4)	v < 10	v > 10
Unfolding force, pN	F < 350 (400)	F > 350 (400)	F < 4,800	F > 4,800
Eb, kcal/mol	11.1 (9.11)	4.87 (3.08)	11.08	1.82
xb, Å	1.2 (1.19)	0.2 (0.11)	0.138	0.019
HB-breaking mechanism	Simultaneous	Sequential	Simultaneous	Sequential

The values in parentheses in the AH columns represent the results for AH2.

For the BS structure, we obtain for the FDM E_b = 2.2 kcal/mol and x_b = 0.024 Å. In the SDM, E_b = 11.1 kcal/mol and x_b = 0.138 Å (the angular term is not considered here). Notably, the force levels in the BS domain are much higher than in the AH structure, indicating that this protein domain may be mechanically sturdy and approaches rupture forces of 1 nN at experimental and physiological pulling rates. These strength values agree quantitatively with recent experimental studies of amyloid structures, possibly explaining how the shear loading of arrays of HBs can lead to extremely strong resistance against rupture, reaching the strength of covalent bonds (31, 32).

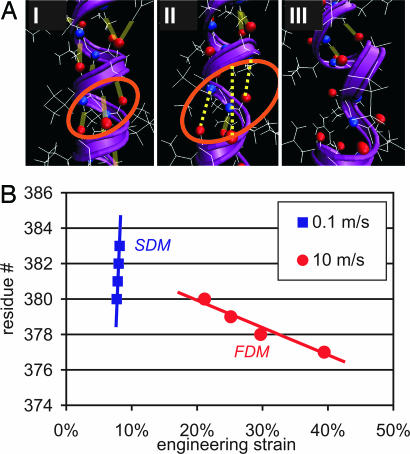
The details of the atomistic rupture mechanisms are summarized in Table 1. An analysis of the atomistic structure during the rupture event is shown in Fig. 4A for the SDM in the vimentin AH1 domain. In the SDM, three HBs rupture simultaneously, within <20-ps time scale. It was reported that the time for HB breaking is ≈20–40 ps (30), clearly supporting the notion that these HBs rupture at once.

Fig. 4.

Atomistic details of the unfolding mechanism of AH1 in the SDM (AP in Fig. 1 for v = 0.1 m/s). (A) Atomistic representation of the rupture dynamics. The time interval between these snapshots is 20 ps (between I and II) and 40 ps (between II and III). After 20 ps (I to II), all three HBs have ruptured simultaneously, leading to local unfolding of the protein in the next 40 ps (II to III). These snapshots strongly support the concept of cooperative bond rupture in the SDM. Surrounding water molecules are not shown for reasons of clarity. (B) Rupture sequence of the first four HBs as a function of the applied strain [residue number represents the amino acid of the O atom (H acceptor)]. In the FDM, HBs rupture one by one, whereas in the SDM, several HBs rupture almost simultaneously, within 20 ps. In the FDM, the unfolding wave runs from the pulled residue in the direction of the fixed residue, whereas in the SDM, the unfolding “wave” runs in the opposite direction, nucleating at a random residue within the protein sequence.

Further evidence for the change in mechanism is obtained by an analysis of the HB rupture dynamics. In Fig. 4B we plot the HB rupture as a function of the molecular strain for the vimentin AH1 domain. This provides a strategy to normalize the different time scales by the pulling velocity (here, 0.1 and 10 m/s). In agreement with the results shown in Fig. 2, the unfolding of the protein in the SDM starts at ≈10% strain, in contrast to 20% strain in the FDM regime. This difference is indicated in Fig. 4B by the rupture of the first HB. The data shown in Fig. 4 clearly show that, in the FDM, HBs rupture sequentially as the lateral load is increased from 20 to 40% tensile strain. In contrast, in the SDM, several HBs rupture almost simultaneously, within <20 ps, at a tensile strain of ≈10%. Even though the pulling speed is several orders of magnitude slower in the SDM, the HBs in the SDM rupture significantly faster. Similar observations are made in the BS structure. An analysis of the bond-breaking history reveals that sequential breaking of single HBs occurs in the FDM, and concurrent breaking of ≈6 HBs occurs in the SDM.

Notably, force spectroscopy results of individual AH or BS domains are rare, even though the first studies with atomic force microscopy were reported ≈10 years ago. This is partly due to experimental difficulties caused by the small size of the protein probes. For instance, it is difficult in an experiment to stretch individual proteins or protein domains rather than bundles (13, 33, 34). The unfolding forces measured in experiments are typically between 100 and 200 pN for pulling velocities in the SDM (13, 33, 34). This finding is close to the values obtained in our simulations, which predict forces below 350 pN in the SDM. Pulling experiments of coiled-coils, which consist of two AHs arranged in a helical geometry, can be carried out in a more controlled fashion. In these systems, the experimentally measured unfolding force ranges between 25 and 110 pN, also for deformation speeds in the SDM (10, 35). These force values are also in proximity to the unfolding forces predicted by our simulations and the theoretical model.

Hierarchical Strength Model for the AH Structure.

The remainder of this article is focused on the AH structure. Even though the phenomenological model (Eq. 1) explicitly considers chemical “bonds,” it does not distinguish between a single chemical bond and protein architectures that include several bonds. For instance, whether a single HB ruptures or several HBs rupture simultaneously is captured in an effective value of E_b; however, this change in mechanism is not explicitly noted in the theory.

To estimate the strength and the energy landscape of a protein without performing any simulations or experiments, we extend the theory to explicitly consider the structural hierarchies of the protein structure with the only input parameters being the energy of a HB and the rupture distance. The AH represents a hierarchical structure, reaching from individual HBs at the lowest, atomistic level to a collection of HBs at the next higher, molecular protein scale.

The lowest hierarchy is represented by individual HBs with an E_b⁰ and x_b, and the higher hierarchy consists of parallel HBs. Here we assume that b bonds in a structure are in parallel and d bonds out of these b bonds break simultaneously. Thus, _bC_d (the binomial coefficient is defined as _bC_d) possible combinations for this rupture mechanism exist. The probability that one of these combinations constitutes a particular rupture event is one divided by _bC_d. Also, if d bonds break simultaneously, the total energy barrier increases by a factor d, to d·E_b⁰. This leads to the following expression for the off-rate:

We rewrite Eq. 5 so that the binomial coefficient appears in the exponential, which enables us to compare Eq. 6 with Eq. 1,

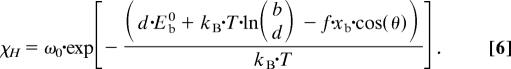The parameter E_b in Eq. 1 can thus be split up as

where E_b⁰ is the energy of a single bond and the term

is the contribution to the energy barrier due to the hierarchical structure. The unfolding force is

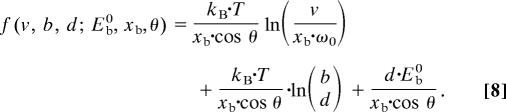Note that f = f_v + f_h1 + f_h0, where the f_v, f_h1, and f_h0 are the contributions to the force as a consequence of the pulling speed, the first hierarchy (number of parallel bonds, d), and the basic hierarchy (strength of bonds, E_b and x_b). This expression quantifies how the hierarchical design influences the rupture strength. In the following text we refer to this model as the hierarchical Bell model.

This approach can easily be extended to three hierarchies, which enables one to predict the rupture force of a tertiary structure consisting of 2, 3, …, n AHs, of which k unfold simultaneously (see SI Text, Extension of the Hierarchial Bell Model).

Because of the generic approach, the equations derived here are, in principle, valid for any protein structure that consists of several parallel bonds, for example, β-sheets or β-helices.

Here, we apply this theory to predict unfolding force of an AH domain. The AH is a two-hierarchy system, where the lowest hierarchical scale is represented by an individual HB. A collection of b bonds form the next higher hierarchical scale. Thus, Eq. 8 enables us to estimate the unfolding force at any pulling speed.

AHs Maximize the Robustness at Minimal Use of Building Resources.

Protein folding and thus the generation of hierarchical structures are essential for biological function. First, folding allows distant parts of the amino acid chain to come physically closer together, creating local sites with specific chemical properties that derive from the collection of particular residues. Second, folding permits collective, localized motion of different regions (36). The AH pattern is the most simple folding motif of a one-dimensional strand (2), forming a spring-like protein structure with high elasticity and large deformation capacity.

But why does an AH fold in such a way that 3.6 parallel HBs, instead of 2, 5, or 6, appear in parallel, per turn? Notably, all AHs universally show this particular molecular architecture. To the best of our knowledge, there has been no explanation for this particular molecular feature, despite the fact that the AH is such an abundant protein structure. Maybe the structural features can be explained by considering the robustness of the AH structure against mechanical and thermodynamical unfolding.

We calculate robustness based on the definition of robustness as parameter insensitivity, postulated by Kitano (37). This definition applied to the case of an AH structure corresponds to the sensitivity of the protein strength in regard to missing HBs. Starting with the hierarchical Bell model (Eq. 8), we calculate robustness as the ratio of strength of a failed system and an intact system. The intact system is defined as a system where all HBs contribute to strength, whereas in the failed system all except one HB contribute to the strength. Only the contributions due to the hierarchy in Eq. 8 are considered; the pulling speed part of this equation is not taken into account because we compare systems at identical pulling speeds. The robustness is defined as

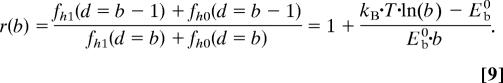The robustness converges toward fault tolerance when b → ∞.

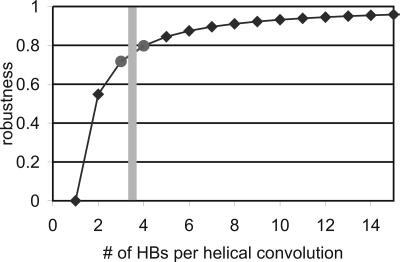
Fig. 5 depicts the robustness of an AH as a function of parallel HBs per turn. The analysis shows that for a AH structure with three to four HBs per turn, 80% robustness is achieved (0% robustness means that the system is highly fragile, and 100% represents complete fault tolerance). This level of robustness in a biological structure enables it to minimize waste of resources (that is, amino acids), weight, and volume, and thus makes the structure overall efficient and able to sustain extreme mechanical conditions (such as high loading rates and deformations).

Fig. 5.

Robustness of an AH as a function of parallel HBs per turn, b, predicted by the hierarchical Bell model. Robustness is defined as the ratio of strength of a failed system and an intact system. In the intact system, all HBs contribute to strength, whereas in the failed system, all except one HB contribute to the strength. The shaded bar indicates the number of parallel HBs per turn (3.6 HBs) as observed in nature. This particular molecular geometry corresponds to a robustness value of ≈80%, indicating that the AH is efficient in Pareto's sense (38, 39).

This finding is significant because the only input parameters in this model are the dissociation energy of an HB, E_b⁰, which is a fundamental, “first-principles” property of protein structures. This parameter can be determined reliably from either experiment or atomistic simulation (both approaches lead to similar values). The remainder of the parameters required to predict the robustness properties can be derived from the geometry of the protein structure.

Synthetic materials typically do not have such high levels of robustness. Lack of robustness makes it necessary to introduce safety factors that guarantee a structure's functionality even under extreme conditions. For instance, an engineering structure such as a tall building must be able to withstand loads that are 10 times higher than the usual load, even if this load will never appear globally. This safety factor is necessary because these structures are very fragile because of their extremely high sensitivity to material instabilities such as cracks, which might lead to such high local stresses. However, if a crack does not appear during operation, 90% of the material is wasted. This calculation shows the potential of engineering bio-inspired robust and efficient structures. The key may be to include multiple hierarchies and an optimal degree of redundancies, as illustrated here for the AH structure.

Forming three to four HBs in parallel instead of forming a single, much stronger bond is also energetically favorable, in particular, in light of the moderate assembly temperatures in vivo. However, this finding only makes sense if three HBs rupture simultaneously so that they can provide considerable mechanical and thermodynamical resistance, which has indeed been shown to be the case at physiological strain rates in Fig. 2 (33). The intimate connection of structural properties, assembly, and functional processes is an overarching trait of protein materials.

Discussion

Using an integrated approach of theory and simulation, we have systematically varied the pulling velocity and discovered a change in unfolding behavior during stretching of AH and BS protein domains. Our results prove that the unfolding mechanism at fast pulling rates is rupture of a single HB, whereas the unfolding mechanisms at slow pulling rates proceed by simultaneous rupture of several parallel HBs (Figs. 2–4 and Table 1). This phenomenon has been consistently observed for the three protein structures studied here, including AH and BS protein domains.

At present, MD simulations are the only means to directly observe these mechanisms, because experiments still lack appropriate spatial and temporal resolution. Advances in computing power have enabled us to carry out direct atomistic simulation of unfolding phenomena, including explicit solvent, at time scales approaching a significant fraction of a microsecond.

In previous atomistic simulations, unfolding forces were significantly larger than those measured in experiments, likely because they were carried out in the FDM so that forces increase to several nanonewtons for individual AHs. This finding is clearly an artifact of large pulling speeds (20, 21). Our analysis shows that, in addition to incorrect force estimates, the observed unfolding mechanism can also be significantly different if the pulling speed is too high. The estimate for v_σ provides a “maximum” pulling rate that could be used in MD studies to still allow a reasonable interpretation of MD results in light of biological relevance. The quantitative values derived here may provide guidance to set up other MD simulations. The SDM is most relevant for biological function, but the FDM could be important during tissue injuries that may be incurred under large deformation rates (e.g., shock impact, bullets, and fractures).

The fact that this behavior is observed for three protein structures under different loading conditions (tensile loading for the AH domains and shear loading for the larger BS domain) suggests that the discrete change in mechanism from single HB rupture to concurrent rupture of several HBs may be a universal phenomenon. In particular, the results obtained from the BS structure illustrate that this transition appears also at larger hierarchical levels. We thus believe that the results reported here are applicable to the mechanical behavior of many other protein domains and possibly larger protein structures.

Note that the interface of different proteins or even the supermolecular structure is significant and may be most relevant for many biological functions [for instance, the unfolding of globular domains in titin or unfolding of spectrin at the linker region between two AHs under strain (21)]. However, to predict the deformation mechanisms of more complex protein structures, studies like the one reported here are critical because they enable one to compare the strength of different competing deformation modes.

We have developed a hierarchical Bell theory that explicitly considers the hierarchical arrangement of HBs in the AH protein, providing the rigorous structure–property relationship for a protein structure, here exemplified for the vimentin AH motif. This theory features input parameters solely derived from the protein geometry and HB energy parameter E_b⁰ and x_b. Because the pulling speed is the characteristic parameter in capturing the time scale of protein-folding events, the theory enables one to link the geometry of the protein structure, distinct time scales, and consequently, experiment and simulation. This theory makes it possible to quantitatively extrapolate MD simulation results to experimental and in vivo deformation rates.

We have discovered that three to four parallel HBs are the most favorable bond arrangement in light of mechanical and thermodynamical stability, leading to a robustness of ≈80%. This result indicates that AHs are efficient according to Pareto's principle (38, 39), which is also known as the 80/20 rule. This rule is an empirical law that has found broad application in explaining social, economic, political, and natural phenomena. Our results indicate that this concept may also be applicable to explaining the nanoscopic architecture of the AH protein motif. In this study, we have found substantial evidence for the applicability of the Pareto principle to explain the molecular structure of proteins. In Pareto's sense, the more robust the structure becomes with each additional HB, the higher the barrier is to implementing an additional HB, because each HB introduces an additional “cost” due to increased material use, that is, the additional weight and volume. In light of these considerations, it is not surprising that a robustness value of 80% is found in AHs, which equals the optimal state due to these competing mechanisms. We note that other reasons, such as steric effects, may also be important in explaining the particular geometry of the AH protein motif.

The theoretical progress in understanding protein materials at the atomistic scale will enable us to understand, and eventually to exploit, the extended physical space that is realized by utilization of hierarchical features. These traits may be vital to enable biological systems to overcome intrinsic limitations due to particular building blocks: chemical bonds and chemical elements. By using a bottom-up structural design and synthesis approach, the hierarchical, extended design space could serve as a means to realize new physical realities that are not accessible at a single scale [e.g., material synthesis at moderate temperatures, fault-tolerant hierarchical assembly mechanisms, and robust and strong materials (40)].

A detailed analysis of hierarchical protein materials could further contribute to the understanding of which driving forces in nature are most important for the evolutionary development of biological materials, and what role the abundant nanoscopic features play in determining their properties at different scales.

Materials and Methods

Atomistic-Protein Structures.

The AH1 structure is taken from the 2B segment of the vimentin intermediate filament (IF) (22–24) coiled-coil dimer (length, 70 Å) [Protein Data Bank (PDB) ID code 1gk6). The AH2 structure is an AH domain from bacteriophage T4 (PDB ID code 1ox3) [length, 60 Å (25)]. The BS domain is taken from an Alzheimer's amyloid-β(1–42) fibril (5) (PDB ID code 2beg).

Atomistic-Simulation Methods.

We use a classical MD approach, implemented in NAMD (41) by using the CHARMM22 force field (42). All simulations were performed at a temperature of 300 K [NVT ensemble, Berendsen thermostat (43)], with a 1-fs time step. Careful energy minimization and finite temperature equilibration of all structures are simulated before the protein is loaded. The structure obtained from the Protein Data Bank is solved completely in a TIP3 water skin. In all cases, the entire protein is embedded in water, before and during deformation of the protein. The water is essential to capture the correct HB rupture dynamics.

Steered Molecular Dynamics (SMD) and Data Analysis.

To apply forces to the molecule to induce deformation, we use SMD (44), with the SMD spring constant k_SMD = 10 kcal·mol⁻¹·Å⁻². We obtain force-versus-displacement data by monitoring the time-averaged applied force (f) and the position of the atom that is pulled at (x) over the simulation time.

Force Application Boundary Conditions.

To apply load, C^α atoms at one end are fixed and the force is applied on the C^α atom at the other end in the AH structure, with a pulling speed v (Fig. 1 Bottom). The tensile boundary conditions chosen for the AH domain are closest to the physiological conditions. Several other boundary conditions have been used (changing fixed and pulled atoms, pulling at different turns). No changes in the AP forces have been observed, suggesting that the results reported here are robust with respect to changes in the boundary conditions. In the BS structure, we pull on the middle chain of the assembly (third chain from top or bottom) at the midpoint of the turn that connects the two β-strands. We fix all C^α atoms on the top and bottom chains during pulling (Fig. 1 Bottom). These boundary conditions are similar to those reported in recent atomic force microscopy experiments of a comparable amyloid structure (32).

Analysis of HB Rupture Dynamics.

We use Visual Molecular Dynamics (VMD) for visualization of protein structures (45), as well as for the analysis of the length of HBs. The rupture length of a HB is defined as 5 Å [the equilibrium length of HBs is ≈3 Å (46)]. The distance chosen from the equilibrium was higher than the transition state, as known from theory and experiment, in order not to capture the dynamics of bond breaking and rebinding caused by thermal fluctuations.

Abbreviations

AH

α-helical

AP

angular point

BS

β-sheet

HB

hydrogen bond

FDM

fast-deformation mode

MD

molecular dynamics

SDM

slow-deformation mode

SMD

steered molecular dynamics.