Patterns of Sequence Variability and Divergence at the diminutive Gene Region of Drosophila melanogaster: Complex Patterns Suggest an Ancestral Selective Sweep

Abstract

To identify putatively swept regions of the Drosophila melanogaster genome, we performed a microsatellite screen spanning a 260-kb region of the X chromosome in populations from Zimbabwe, Ecuador, the United States, and China. Among the regions identified by this screen as showing a complex pattern of reduced heterozygosity and a skewed frequency spectrum was the gene diminutive (dm). To investigate the microsatellite findings, nucleotide sequence polymorphism data were generated in populations from both China and Zimbabwe spanning a 25-kb region and encompassing dm. Analysis of the sequence data reveals strongly reduced nucleotide variation across the entire gene region in both the non-African and the African populations, an extended haplotype pattern, and structured linkage disequilibrium, as well as a rejection of neutrality in favor of selection using a composite likelihood-ratio test. Additionally, unusual patterns of synonymous site evolution were observed at the second exon of this locus. On the basis of simulation studies as well as recently proposed methods for distinguishing between selection and nonequilibrium demography, we find that this “footprint” is best explained by a selective sweep in the ancestral population, the signal of which has been somewhat blurred via founder effects in the non-African samples.

ONE of the central goals of population genetics is the identification of adaptively important regions of the genome in natural populations. Existing methods for detecting recent positive selection rely on the expectation that the substitution of a strongly selected advantageous mutation will change patterns of variation in linked neutral regions (Maynard-Smith and Haigh 1974; Kaplan et al. 1989; Stephan et al. 1992). A number of predicted effects of such a “selective sweep” on patterns of polymorphism have been proposed as tests for inferring the action of positive selection. These include a reduction in variation relative to divergence at the target of selection (Hudson et al. 1987), an excess of low-frequency variants localized around the target (Tajima 1989; Braverman et al. 1995; Fu 1997), and an excess of high-frequency derived alleles in regions flanking the target due to recombination (Fay and Wu 2000), as well as increased linkage disequilibrium (LD) in the flanking regions but reduced LD spanning the target (Przeworski 2002; Kim and Nielsen 2004; Stephan et al. 2006; Jensen et al. 2007), if gene conversion events are not considered. Given that these signatures are distinct relative to the location of the target of selection, a common approach has been to attempt to identify adaptively important loci by analyzing genomic patterns of polymorphism (e.g., Harr et al. 2002; Kim and Stephan 2002; Vigouroux et al. 2002).

Thus, a widely used method for detecting selection involves genomic scans, which take advantage of the signatures of selection on linked neutral variation. By identifying markers with skewed distributions or decreased variation, subsequent sequencing studies may be directed to determine if the observed patterns are consistent with a sweep hypothesis (e.g., Glinka et al. 2003; Bauer DuMont and Aquadro 2005; Haddrill et al. 2005; Pool et al. 2006; Thornton and Jensen 2007). Here we present an implementation of a subgenomic scan approach. Microsatellites were surveyed in population samples from Zimbabwe, China, the United States, and Ecuador in a 256-kb region of the X chromosome of Drosophila melanogaster, roughly corresponding to a microsatellite approximately every 10 kb throughout the region. The intent of this initial microsatellite screen was to identify loci that may have played a role in the process of adaptation. This region was chosen because it was both well annotated and highly recombining. By identifying microsatellites that were either reduced in variability or skewed toward rare alleles, the hope was to allow for well-directed sequencing efforts. Three regions were identified as potentially containing the targets of selective sweeps: the Notch region (Bauer DuMont et al. 2004), the dunce region, and diminutive (dm), the latter of which is analyzed here.

Around dm, several microsatellites showed reduced heterozygosity and/or skews in the frequency spectrum in all populations studied, although the observations are complex owing to heterogeneity in patterns between populations. To investigate whether the underlying gene genealogies show the signature of a selective sweep, 10 kb of sequence were generated in 10 segments across a 25-kb region centered around dm for population samples from both Zimbabwe and China (representing an African and a derived non-African population, respectively). Sequence was also generated for a number of additional species of varying divergence for the two coding exons of dm. While the patterns of both microsatellite and nucleotide polymorphism and divergence are somewhat complex, we conclude that major features are best explained by a selective sweep at or very near dm in the ancestral African range of the species (represented by Zimbabwe) and that the ancestral sweep patterns have been “blurred” in the non-African population via the widely accepted founder effect that accompanied the species' expansion out of Africa. Evidence of selection at this locus is intriguing given both the known role of diminutive as a positive regulator of body size (Craymer and Roy 1980), as well as the known clinal pattern of variation of this trait (Gockel et al. 2002; Calboli et al. 2003). Specifically, parallel body size clines have been shown to have a positive relationship with latitude across all major continents (Coyne and Beecham 1987; Imasheva et al. 1994; James et al. 1995; van't Land et al. 1999; Calboli et al. 2003). Whether variation at dm underlies these clines in body size will be the subject of future studies.

MATERIALS AND METHODS

Samples:

Four population samples of D. melanogaster were surveyed for microsatellite variability. These include Zimbabwe (Sengwa Wildlife Research Institute), the United States (Arvin and Soda Lake, California), Ecuador (Atacame), and China (Beijing). The sample sizes for the microsatellite study differed across the microsatellites in each population. For Zimbabwe 55–65 chromosomes were sampled, for the United States 34–35, for Ecuador 52–54, and for China 57–62. Two population samples of D. melanogaster were surveyed for nucleotide variability: Zimbabwe (Senegwa Wildlife Research Insitute) and China (Beijing). A single population of D. simulans (North Carolina) was also surveyed. The details of these collections have been described elsewhere (Begun and Aquadro 1991, 1994, 1995). For all D. melanogaster populations, extracted X chromosome lines were used (Begun and Aquadro 1994), while inbred lines were used for D. simulans. DNA sequences were determined in a sample of 24 lines of D. melanogaster (12 lines from Zimbabwe and 12 from China) as well as 12 lines of D. simulans (from North Carolina) across all loci to root branch-specific changes. At exon 2, the sample size collected for Zimbabwe was increased to a total of 28 to better quantify the site-frequency spectrum and address hypotheses concerning the selective neutrality of synonymous site evolution (see below). In addition, homologous sequence was generated for exon 2 in single lines of D. yakuba, D. teissieri, D. erecta, D. mauritiana, D. sechellia, and D. eugracilis. Sequences were deposited in GenBank under accession nos. EU167614–EU167733.

Analysis of microsatellite variability:

The microsatellite data presented here are a continuation of data presented for nine microsatellite loci centered on the Notch locus region of the X chromosome in D. melanogaster (Bauer DuMont and Aquadro 2005). Cosmid clones 163A10, 140G11, and BACN43K23 and the Celera 11/35 scaffold completely span between the Notch and dm gene regions of this chromosome. After omitting overlapping regions, these clones cover a total of 263,460 bp of which 10,092 bp extends upstream (and centromere distal) of Notch and 12,765 bp extends downstream (and centromere proximal) of dm. Using the “find” option of the DNASTAR program EditSeq, we searched this sequence for all dinucleotide motifs with lengths greater than five perfect repeats. A total of 26 microsatellites (including those presented in Bauer DuMont and Aquadro 2005) were chosen for further analysis on the basis of their length and location. The microsatellites were named on the basis of their location (in kilobases) within the combined sequence of these clones. The microsatellites surveyed for variability are denoted as follows: 7.9, 28.6, 33.3, 37.3, 45.7, 46.8, 50.7, 57.8, 67.8, 89.6, 99.3, 104.9, 113.4, 127.9, 135, 139.4, 165.4, 174.1, 183, 192.8, 201.5, 211.4, 223.4, 235.1, 244.2, and 255.6 (of which data from the first 9 were originally presented in Bauer DuMont and Aquadro 2005). Thus, our microsatellite survey spans 259.9 kb, which corresponds to bases 3024470–3284333 of the D. melanogaster genomic scaffold (Release 5.2). The primers used to amplify these microsatellites are given in supplemental Table 1 at http://www.genetics.org/supplemental/. Forward primers were labeled with the fluorescent dye FAM (Applied Biosystems, Foster City, CA). PCR product lengths were determined on an ABI 373XL automated sequencer using the ABI programs Genescan and Genotyper.

The Bottleneck program (Cornuet and Luikart 1996) was used to evaluate the relationship between the observed number of alleles and expected heterozygosity at each microsatellite. Negative deficiency of heterozygosity (DH)/SD values indicate an excess of rare alleles compared to neutral equilibrium expectations, while positive values indicate the opposite pattern. We report the two-phase model results, which were determined under the default settings of the program (variance = 30.0, probability = 70%). The LnRV and LnRH tests (Schlotterer 2002; Kauer et al. 2003) were also applied to the microsatellite data to test for population-specific reductions in variability. The tests were performed by comparing our 26 loci from the Notch to dm region to data from 118 other X-linked microsatellite loci reported by Kauer et al. (2003). For these tests, levels of variability at monomorphic loci were adjusted by replacing one allele with another that is one repeat unit different from the original allele length, following the suggestion of Schlotterer (2002) and Kauer et al. (2003).

PCR amplification and sequencing:

Ten regions spanning the dimunutive gene were sampled for nucleotide sequence variation in this study. Exons 1 (1 kb) and 2 (1 kb) of dm, the 5′-noncoding sequence (2 kb), intron (3 kb), 3′-noncoding sequence (1 kb), and the adjacent open reading frame (CG12535) were amplified using PCR. Primers (given in supplemental Table 1 at http://www.genetics.org/supplemental/) were used to generate sequence runs on an ABI3700 automated sequencer. For each of the regions sampled, a contiguous sequence was assembled for each individual and aligned using the computer program Sequencher (Gene Codes, Ann Arbor, MI). Details of region location and sequence length are given in the results section.

Data analysis:

Pairwise nucleotide diversity, θ_π (Nei and Li 1979), and θ_W, based on the number of segregating sites (Watterson 1975), were calculated using the program DnaSP 3.99 (Rozas and Rozas 1999) for each D. melanogaster sample. Insertion–deletion polymorphisms were excluded from the analysis of population diversity. Under neutral equilibrium conditions both summaries estimate the neutral parameter 3N_eμ for X-linked loci, where N_e is the effective population size and μ is the neutral mutation rate. Tajima's D (Tajima 1989), Fu and Li's D (Fu and Li 1993), and Fay and Wu's H (Fay and Wu 2000) were calculated to test for deviations from a neutral equilibrium frequency distribution at all loci. Ratios of polymorphism to divergence between nonsynonymous and synonymous sites were compared in coding regions using the McDonald–Kreitman (MK) test (McDonald and Kreitman 1991). Additionally, the HKA test (Hudson et al. 1987) was used to evaluate the fit of polymorphism and divergence data to neutral predictions. Tests were conducted via coalescent simulation using a program available from Jody Hey's website, designed to handle a large number of loci (http://lifesci.rutgers.edu/∼heylab/HeylabSoftware.htm#HKA).

One of the best known and most widely applied approaches for testing a selective sweep hypothesis is the Kim and Stephan (2002) composite-likelihood-ratio test (CLRT). The CLRT uses the spatial distribution of mutation frequencies and levels of variability among a population sample of DNA sequences to test for evidence of a selective sweep, with the composite likelihoods being calculated by applying the marginal likelihoods for each site along the length of the sequence. It is assumed that the beneficial mutation with selective advantage s arose on a single chromosome in a population of constant size, drifted to frequency ε, changed deterministically to frequency 1 − ε, and then drifted to fixation. In practice, this test is commonly applied to loci that are targeted for further resequencing from a genome-scan study. Maximum-likelihood estimates (MLEs) of the strength (α = 2N_es) and the location of the target (X) of selection are also obtained via maximization of their composite-likelihood function. To discriminate between hypotheses, the composite likelihood of the data under the model of a selective sweep, 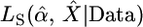, is compared to the likelihood of the data under the standard, neutral model, L_N(Data). The latter quantity depends only on the mutation rate, which is assumed known. The CLRT statistic employed is 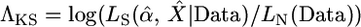. The null distribution of 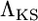is obtained by applying the CLRT to data sets obtained from simulation under the standard neutral model with fixed θ. The neutral model is rejected at level γ when the observed 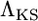is greater than the 100(1 − γ) percentile of the null distribution.

A problem with this test, however, is that it compares the standard, neutral model with a simplistic sweep model. As such, if the data look particularly nonneutral (as might be expected under a number of demographic scenarios), the null model might be rejected in favor of selection—even if the likelihood of the selection model is not particularly high. Jensen et al. (2005) demonstrated that this test is in fact sensitive to deviations from the assumptions of the standard neutral model, with both population substructure and bottlenecks leading to a high frequency of false-positive signals of selective sweeps. To address this problem, they proposed a composite-likelihood goodness-of-fit (GOF) test derived from the Kim and Stephan inference scheme. A GOF test is employed to determine if a random sample of data is drawn from a specific distribution of interest. In this case, the null hypothesis H₀ is that the data are drawn from the Kim and Stephan model, and the alternative hypothesis H_A is that the data are not drawn from a Kim and Stephan model. To decide between H₀ and H_A, they compare the ratio of the probability of the data given the null, P(Data | H₀), to the probability of the data given the alternative, P(Data | H_A). They employ a composite-likelihood scheme to approximate these probabilities on the basis of the site-frequency spectrum and then simulate under the null hypothesis to find the critical value of the composite-likelihood-ratio GOF statistic. Note that in this instance, the null model is the Kim and Stephan selective sweep rather than neutrality, as this test is used only if a data set has already rejected neutrality using the CLRT. Both the CLRT and the GOF software are available for download at http://bio4035747.dhcp.asu.edu/∼ykim55/YuseobPrograms.html.

In evaluating the performance of the CLRT in partially sequenced regions such as this, J. D. Jensen, K. R. Thornton and C. F. Aquadro (unpublished results) demonstrate that a parametric bootstrap of the estimated selection parameters, and thus confidence intervals of the predicted target location, can be obtained from the null distribution of the goodness-of-fit test proposed by Jensen et al. (2005). To extend their results to be applicable for our present study, we conducted a similar simulation study relaxing the usual assumption that the sweep just ended (τ = 0).

We additionally calculate the ω-statistic of Kim and Nielsen (2004), which quantifies a pattern of LD that has been argued to be unique to positive selection (Stephan et al. 2006). Specifically, this pattern includes strong LD flanking the target and reduced LD across the target. The statistic, defined as

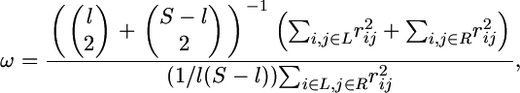divides the S polymorphic sites in the data set into two groups, one from the first to the lth polymorphic site from the left and the other from the (l + 1)th to the last site (l = 2, …, S − 2), where L and R represent the left and the right set of polymorphic sites, and 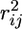is the squared correlation coefficient between the ith and jth sites. Thus, ω increases with increasing LD within each group and decreasing LD between groups (i.e., the larger the value of the statistic, the more “sweeplike” the underlying pattern). For a data set, the value of l that maximizes ω (ω_max) is found. Singletons were excluded prior to calculation.

Evaluating synonymous sites:

For D. melanogaster, D. simulans, and D. pseudoobscura, preferred codons had previously been determined by comparing codon usage between the 10% lowest- and the 10% highest-biased genes (Shields et al. 1988; Akashi 1994). Following Akashi (1995), an “unpreferred change” is a change within a synonymous family from a preferred to an unpreferred codon. Changes from an unpreferred to a preferred codon are called “preferred,” and those among unpreferred or preferred codons (a few synonymous families have two preferred codons) are called “equal.”

For exon 2 of dm the PAML program was used to provide a maximum-likelihood estimate of the ancestral state at each node of a multispecies tree (including only one sequence for D. melanogaster and D. simulans). These reconstructed sequences were then used to determine the derived nucleotide for each polymorphism observed within D. melanogaster. Performing analyses with the ancestral state assigned on the basis of parsimony leads to qualitatively similar results.

RESULTS

Microsatellite variability:

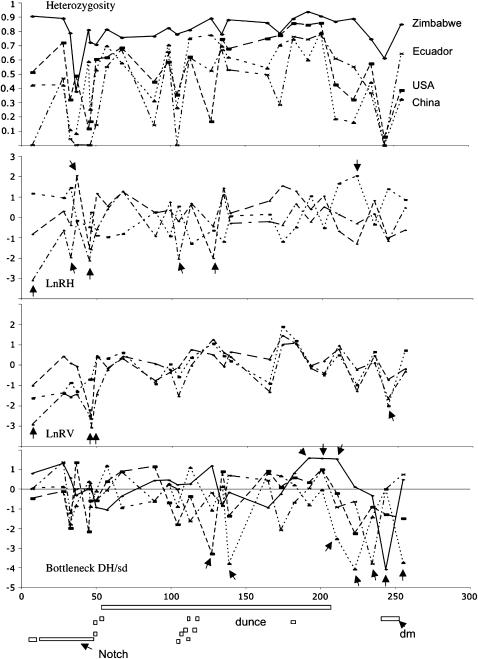
We present the results of a screen of variation across 26 microsatellites spanning 260 kb between the Notch and diminutive loci on the X chromosome of D. melanogaster for the following population samples: Zimbabwe, the United States, Ecuador, and China. Variability at the first 9 microsatellites within the Notch locus region of this chromosome has been previously reported in detail (Bauer DuMont and Aquadro 2005) and is included here as a frame of reference. Figure 1 and Table 1 present the locations of these 26 microsatellites together with measures of variability and test statistics for three methods used to detect deviations from the standard neutral model in each population. As has previously been noted (e.g., Pool et al. 2006), the non-African populations harbor on average fewer alleles and have lower heterozygosity than the Zimbabwe population. There is great heterogeneity across microsatellites in the levels of variability. Of particular note are the dips in heterozygosity and number of alleles around roughly positions 140 and 244 kb (in the dunce and dimunutive transcripts, respectively; Figure 1), in addition to the dips in these statistics previously reported at the Notch region (e.g., for positions 37–47 kb for Ecuador in Figure 1). However, microsatellites are notoriously heterogeneous in mutation rate among loci due particularly to different numbers of perfect repeats (e.g., Brinkmann et al. 1998; Schug et al. 1998a,b; Bachtrog et al. 2000; Ellegren 2000). In fact, many of the loci, which show lower levels of heterozygosity, also have shorter lengths, as deduced from the published D. melanogaster sequence. To circumvent this difficulty, we evaluated whether the neutral relationship between the number of alleles at a locus and the frequency distribution of those alleles (as measured by expected heterozygosity) were met at each microsatellite. We assess significance of a departure using the computer program Bottleneck (Cornuet and Luikart 1996). This program evaluates the probability of observing the expected heterozygosity at individual loci on the basis of allele frequencies given the observed number of alleles, assuming a two-phase mutation model (i.e., the majority of microsatellite mutations are stepwise but occasionally a larger jump in allele length occurs; results were similar when a stepwise-only model was assumed). A deficiency of heterozygosity (negative DH/SD value) indicates an excess of low-frequency alleles and would be consistent with linkage to a recent selective sweep. Positive DH/SD values suggest an excess of intermediate-frequency alleles.

Figure 1.—

Depiction of the levels of heterozygosity, LnRH, LnRV, and Bottleneck test statistics across the 26 Notch to dm microsatellites. Annotated open reading frames within the region are depicted by boxes along the bottom. Due to the scale of the figure we do not depict exon–intron boundaries. The open reading frames in order are kirre, Notch, CG18508, Fcp3C, CG3939, CG14265, ng2, ng3, ng1, dunce (represented as a box above other coding regions), ng4, pig1, sgs4, CG10793, and dm. For reference, the coordinates for open reading frames of Notch, dunce, and diminutive on the microsatellite sequence scale are 10093 to 45459, 110164 to 204572, and 240390 to 250695, respectively. Arrows indicate significant test results before Bonferroni correction.

TABLE 1.

Analysis of microsatellite variability within four populations of D. melanogaster

Zimbabwe
Microsatellite	7.9	28.6	33.3	37.3	45.7	46.8	50.7	57.8	67.8	89.6	99.3	104.9	113.4	127.9	135	139.4	165.4	174.1	183	192.8	201.5	211.4	223.4	235.1	244.2	255.6
Repeat no.	13	14	11	7	9	6	5\9	9\5	11	10	14	5	6\8	12	10	17	12	16	14	13	14	15	12	10	8	11
Sample size	49	49	49	49	49	49	61	49	49	63	64	65	62	62	62	61	60	58	59	57	55	61	61	61	60	53
No. alleles	13	10	7	3	9	6	8	11	8	7	9	8	9	11	10	14	14	9	12	15	11	8	14	8	10	10
Heterozygosity	0.905	0.889	0.787	0.376	0.809	0.721	0.706	0.812	0.755	0.765	0.822	0.778	0.808	0.889	0.779	0.879	0.859	0.785	0.887	0.936	0.906	0.867	0.887	0.745	0.61	0.848
Var. repeat no.	7.865	7.314	3.642	0.724	3.887	9.92	2.285	7.236	3.12	1.848	4.158	2.756	6.824	10.41	5.192	15.08	11.33	2.781	9.757	19.16	15.18	7.07	11.07	3.016	3.504	3.361
Bottleneck DH/SD	0.787	1.293	0.566	−0.33	−0.01	0.29	−0.95	−1.07	−0.37	0.432	0.448	0.216	0.246	1.178	−0.87	−0.17	−0.95	−0.26	0.797	1.572	1.553	1.525	0.11	−0.34	−4.09	0.475
P-value	0.233	0.033	0.343	0.341	0.419	0.469	0.153	0.12	0.283	0.407	0.39	0.507	0.499	0.054	0.146	0.363	0.142	0.306	0.2	0.004*	0.005*	0.002*	0.482	0.284	0.005*	0.369
California
Microsatellite	7.9	28.6	33.3	37.3	45.7	46.8	50.7	57.8	67.8	89.6	99.3	104.9	113.4	127.9	135	139.4	165.4	174.1	183	192.8	201.5	211.4	223.4	235.1	244.2	255.6
Repeat no.	13	14	11	7	9	6	5\9	9\5	11	10	14	5	6\8	12	10	17	12	16	14	13	14	15	12	10	8	11
Sample size	34	34	34	34	34	34	35	34	34	35	35	35	35	35	35	35	35	35	35	35	35	35	34	35	35	35
No. alleles	4	6	4	2	3	2	5	4	4	2	5	4	5	4	5	7	5	7	9	9	8	3	4	5	2	4
Heterozygosity	0.511	0.72	0.319	0.487	0.116	0.166	0.603	0.615	0.685	0.444	0.585	0.353	0.62	0.166	0.745	0.676	0.748	0.77	0.855	0.845	0.857	0.424	0.319	0.572	0.057	0.385
Var. repeat no.	0.682	4.988	1.527	0.243	0.061	0.083	1.608	2.142	1.801	0.222	0.904	0.84	7.4	7.77	1.726	13.89	6.129	8.153	15.88	6.558	7.387	7.946	0.652	2.134	0.457	0.941
Bottleneck DH/SD	−0.48	−0.11	−1.98	1.364	−2.16	−0.59	−0.58	0.387	0.895	1.15	−0.69	−1.79	−0.36	−3.29	0.897	−1.36	0.92	0.102	0.586	0.337	1	−0.21	−2.25	−0.91	−1.29	−1.5
P-value	0.262	0.363	0.065	0.171	0.032	0.417	0.229	0.437	0.172	0.215	0.189	0.075	0.275	0.008	0.172	0.095	0.156	0.46	0.319	0.444	0.105	0.352	0.045	0.157	0.194	0.104
LnRH	−0.86	0.282	−0.41	2.04	−1.57	−0.69	1.153	0.537	1.249	0.201	0.332	−0.22	0.589	−2.03	1.419	0.179	0.784	1.53	1.276	0.374	1.034	−0.7	−1.32	0.809	−1.04	−0.65
LnRV	−1.02	0.418	0.079	−0.08	−2.21	−2.65	0.44	−0.16	0.302	−0.79	−0.38	−0.14	0.742	0.481	−0.08	0.628	0.257	1.435	1.025	−0.06	0.183	0.767	−1.29	0.444	−0.74	−0.2
Ecuador
Microsatellite	7.9	28.6	33.3	37.3	45.7	46.8	50.7	57.8	67.8	89.6	99.3	104.9	113.4	127.9	135	139.4	165.4	174.1	183	192.8	201.5	211.4	223.4	235.1	244.2	255.6
Repeat no.	13	14	11	7	9	6	5\9	9\5	11	10	14	5	6\8	12	10	17	12	16	14	13	14	15	12	10	8	11
Sample size	45	45	45	45	45	45	53	45	45	54	53	54	54	54	54	53	53	45	53	53	53	53	53	52	53	53
No. alleles	1	2	2	1	1	1	2	4	4	2	5	1	7	4	7	3	3	4	9	7	6	6	5	6	1	4
Heterozygosity	0	0.469	0.044	0	0	0	0.142	0.549	0.67	0.14	0.655	0	0.615	0.521	0.669	0.528	0.493	0.283	0.761	0.742	0.777	0.607	0.551	0.366	0	0.642
Var. repeat no.	0	0.234	0.089	0	0	0	0.071	1.545	1.916	0.629	0.904	0	2.057	24.47	4.288	9.075	0.419	4.392	16.81	4.592	2.097	10.3	2.387	1.133	0	0.631
Bottleneck DH/SD	—	1.371	−1.23	—	—	—	−0.57	−0.08	0.871	−0.61	0.21	0	−1.64	−0.19	−0.85	0.69	0.436	−2.09	−0.7	0.032	0.963	−0.93	−0.64	−3.81	0	0.745
P-value	—	0.141	0.185	—	—	—	0.429	0.377	0.2	0.409	0.496		0.08	0.352	0.159	0.3	0.448	0.052	0.182	0.414	0.139	0.163	0.218	0.005*		0.254
LnRH	−3.12	−0.65	−1.99	−0.21	−2.14	−1.59	−0.6	0.383	1.266	−0.94	0.741	−2.05	0.675	−0.46	1.113	−0.31	−0.23	−0.4	0.655	−0.24	0.5	0.126	−0.32	0.159	−1.19	0.461
LnRV	−2.92	−1.42	−1.58	−1.44	−2.49	−3.07	−1.44	−0.24	0.412	0.047	−0.23	−1.53	−0.03	1.244	0.596	0.4	−1.33	0.998	1.052	−0.17	−0.51	0.948	−0.24	0.108	−1.66	−0.32
China
Microsatellite	7.9	28.6	33.3	37.3	45.7	46.8	50.7	57.8	67.8	89.6	99.3	104.9	113.4	127.9	135	139.4	165.4	174.1	183	192.8	201.5	211.4	223.4	235.1	244.2	255.6
Repeat no.	13	14	11	7	9	6	5\9	9\5	11	10	14	5	6\8	12	10	17	12	16	14	13	14	15	12	10	8	11
Sample size	72	72	72	72	72	72	60	72	72	62	62	61	62	62	62	62	60	51	60	60	61	61	60	61	57	61
No. alleles	3	3	3	2	4	3	4	4	6	3	6	3	5	10	6	10	3	5	7	6	9	4	5	5	1	6
Heterozygosity	0.421	0.421	0.108	0.081	0.587	0.252	0.527	0.697	0.578	0.311	0.704	0.263	0.749	0.773	0.695	0.617	0.541	0.703	0.745	0.599	0.791	0.185	0.16	0.441	0	0.323
Var. repeat no.	0.272	0.366	0.375	0.04	0.507	1.33	1.446	4.218	2.704	0.178	1.605	0.43	4.16	17.3	3.588	7.254	1.114	15.28	19.71	6.626	3.015	5.194	0.977	2.773	0	3.438
Bottleneck DH/SD	0.046	0.12	−1.78	−0.85	0.382	−0.89	−0.1	1.192	−0.94	−0.63	0.266	−0.88	1.103	−1.08	0.136	−3.78	0.799	0.666	0.212	−0.81	−0.04	−2.52	−4.07	−1.42	0	−3.73
P-value	0.45	0.467	0.075	0.35	0.425	0.239	0.365	0.064	0.155	0.287	0.492	0.228	0.081	0.143	0.477	0.007*	0.23	0.284	0.5	0.171	0.388	0.017*	0.001*	0.103		0.004*
LnRH	1.159	0.935	1.439	−0.18	−0.5	0.229	−0.91	−0.98	−0.84	0.248	−0.94	0.53	−1.31	−0.66	−1.21	0.041	0.133	−1.21	−0.51	1.036	−0.54	1.649	2.022	−0.37	1.381	0.847
LnRV	−1.63	−1.38	−0.88	−1.31	−0.72	−0.7	0.378	0.321	0.595	−0.93	0.035	−0.59	0.352	1.046	0.439	0.188	−0.91	1.874	1.181	−0.04	−0.42	0.481	−0.99	0.636	−2.01	0.71

Microsatellite names are based on their relative location within the genomic sequence used in this study. For each microsatellite, repeat number, sample size, number of alleles, heterozygosity, variance in repeat number, and the Bottleneck results with corresponding P-values are reported.. For the non-African populations, LnRH and LnRV values are given.

^*Values significant after Bonferonni correction.

The Bottleneck results for the 26 Notch to diminutive microsatellites are given in Table 1 and are visually depicted in Figure 1. It is noteworthy that while some values are positive, most are negative. The bottleneck test is one tailed and thus loci are significant when their P-values are <0.025. If a Bonferroni correction is applied to these data (a total of 64 tests were performed, 16 loci × 4 populations), the significant P-value is reduced to 0.0008. Under this criterion only microsatellite 223.4 is marginally significant (and negative) in the Chinese population (indicated by an asterisk in Table 1). However, given that this scan of variation was intended only as a course indication of regions potentially affected by positive selection, we consider any microsatellite with a P-value ≤0.025 as interesting. When considering only the 16 new microsatellites, there are two clusters of microsatellites for which we observe strongly negative DH/SD values and/or no variation. The first is located roughly at position 130 kb and is observed most strongly in the Chinese and United States populations. The other cluster is approximately between microsatellites 211.4 and 255.6. Particularly striking is the very strong (and significant) negative DH/SD value for Zimbabwe at microsatellite 244.2, and this is the region that we here focus on. Also within the Zimbabwe population we observe a cluster of strongly positive DH/SD values surrounding 200 kb. It is important to note that the DH test has a number of limitations, perhaps most significantly being that the performance appears to strongly depend on the underlying microsatellite mutation model.

We also applied the LnRV and LnRH multilocus tests (Schlotterer 2002; Kauer et al. 2003) to the microsatellite data. The goal of these tests is to detect loci that are outliers to the distribution of the ratio of observed microsatellite variation between two populations across loci (variation being measured either as variance in repeat number or expected heterozygosity per locus, respectively). Loci that are significant outliers show a population-specific excess or deficiency in variation, which is interpreted as the signature of population-specific balancing or directional selection, respectively, in that region of the genome. These statistics are used as an alternative to allele excess, and LnRV in particular has been argued to be particularly well suited for identifying regions affected by recent selection. This is owing to the fact that the statistic has an identical expectation for all loci that is independent of θ (Schlotterer et al. 2004).

We compared the microsatellites between Notch and diminutive to a set of 118 X-linked loci surveyed for variation in population samples from Zimbabwe and Europe (Kauer et al. 2003; data from supplemental material at http://www.genetics.org/cgi/content/full/165/3/1137/DC1). To perform the tests, our data from the United States, China, and Ecuador were individually combined with the European data of Kauer et al. (2003) and were compared to the combined Zimbabwe data set. Results of these tests are reported in Table 1 and visually depicted in Figure 1.

Within the United States population we detect a significant deficiency of heterozygosity as compared to Zimbabwe at microsatellite 127.9 (LnRH = −2.034). This is the same microsatellite where a significant excess of rare alleles is detected with the Bottleneck program. Within Ecuador, microsatellite 104.9 also appears to have a deficiency of heterozygosity compared to Zimbabwe. This is a monomorphic microsatellite in the Ecuador sample but has “normal” levels of variation in Zimbabwe. Within our Chinese population lower than expected variation is detected with the LnRV test at microsatellite 244.2. When considering LnRH, two microsatellites suggest a significant reduction in heterozygosity within the Zimbabwe sample (i.e., positive test statistics). One is within the Notch gene region (microsatellite 37.2 when compared to the United States) and one near the dips in the Bottleneck test statistic in the 211- to 255-kb region (microsatellite 223.4 when compared to China). These tests can be taken only as suggestive since, for our non-African populations, we are comparing Notch–dm region microsatellite variation within the United States, Ecuador, and China to variation observed at other X-linked microsatellites found in European samples. For instance, Asian populations have been shown to be particularly structured relative to other non-African populations (Schlotterer et al. 2005).

Nucleotide diversity:

Polymorphism data:

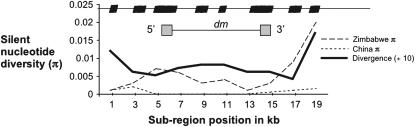
Although patterns of microsatellite variability appear generally neutral for many loci across the X chromosome in Zimbabwe, the microsatellite in the intron of dm (position 244.2) shows a strong skew toward rare alleles. In addition, several microsatellites within the dm region show reduced variation and a trend for variation to also be skewed toward rare alleles in different non-African populations. Subsequent sequence data were collected from the Zimbabwe and Chinese populations to further investigate this pattern (Figure 2). Levels of variability and neutral theory test statistics are given in Table 2 and visually depicted in Figure 3. The intron is less variable than would be anticipated by comparison with other genes similarly sampled in regions of high recombination in Zimbabwe (Begun and Aquadro 1994, 1995; Bauer DuMont and Aquadro 2005; Pool et al. 2006). In addition, the variable sites are segregating at very low frequencies. The intron also has reduced variation relative to the expectation inferred from levels of divergence (Figure 3). Thus, a low, localized mutation rate does not appear to account for the observed reduction.

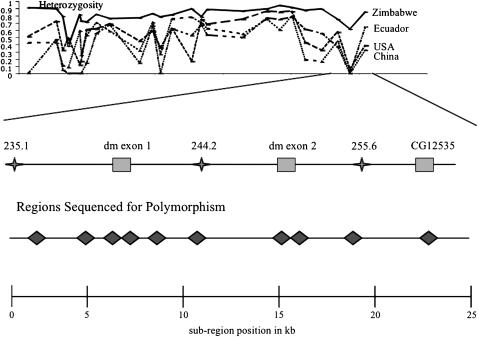
Figure 2.—

Schematic illustrating the position of the microsatellites (indicated as stars) specifically within the dm locus region relative to the two exons of dm as well as the coding region of a nearby annotated gene (CG12535). Below, the orientation of the sequenced regions relative to this schematic is shown, with each diamond representing ∼1 kb of sequencing. The total size of the region is 23 kb, with sequence position 0 corresponding to position 236788 in the microsatellite scan of Figure 1 (a portion of which is given at the top for the sake of orientation).

TABLE 2.

Nucleotide variation in two populations of D. melanogaster

			Zimbabwe					China
Region	Length	Description	n	Div	S	H	D	n	S	H	D
1302	987	5′ NCa	12	108	10	−0.89	+0.18	12	2	+1.20	−0.96
3303	1012	5′ NCa	12	79	18	+0.15	−0.91	12	4	−0.98	−1.33
5089	983	5′ NCa	12	61	8	+0.97	−1.12	12	0	NA	NA
6072	917	dm exon1	12	83	8	−0.37	−1.31	12	0	NA	NA
7324	988	Intron	12	101	7	+0.18	−0.97	12	0	NA	NA
9807	1003	Intron	12	78	10	+0.22	−0.66	12	0	NA	NA
15987	1016	Intron	12	95	27	−3.98*	−0.43	12	0	NA	NA
17003	1002	dm exon2	28	80	34	−12.32*	−0.22	12	4	+1.20	−0.22
19004	904	3′ NCa	12	48	23	−1.12	−0.87	12	4	−1.12	−0.32
21332	987	CG12535	12	163	29	−0.99	+1.1	12	3	−0.54	−1.98

The region's starting point, length of sequence, type of region (noncoding, exon, and intron), sample size (n), number of pairwise differences when comparing against D. simulans (Div), and number of segregating sites (S) for each population, as well as the relative values of Fay and Wu's H and Tajima's D, respectively, are shown. *Significance after Bonferonni correction.

^aNoncoding.

Figure 3.—

A plot of silent π for each of the sequenced populations, as well as pairwise divergence per nucleotide as estimated by comparison with D. simulans (divergence is divided by 10 for scaling purposes). On the x-axis is the location along the region under investigation, and overlaid is a schematic of the sequenced regions as well as the exon structure of diminutive.

Patterns of nucleotide polymorphism across the sampled regions in the Chinese population were largely consistent with the microsatellite 244.2 results in also being largely invariant. Although variability begins to recover moving away from dm in both the 5′ and 3′ directions, only 17 segregating sites were sampled in total from this population across the surveyed region, all in the flanking regions (Table 2).

While patterns of nucleotide variation at dm in both Zimbabwe and China are consistent with the effects of a selective sweep, another alternative hypothesis arises when considering that demographic processes are capable of producing very similar patterns in the frequency spectrum (e.g., Robertson 1975; Tajima 1989; Fu and Li 1993; Andolfatto and Przeworski 2000; Nielsen 2001; Przeworski 2002; Wall et al. 2002; Haddrill et al. 2005; Jensen et al. 2005; Thornton and Jensen 2007; and recently reviewed in Thornton et al. 2007). This result is of particular concern for D. melanogaster given that Thornton and Andolfatto (2006) have estimated that a severe bottleneck occurred during the migrations out of Africa ∼0.019 generations ago in units of 4N.

To further evaluate the hypothesis of a selective sweep at or near dm, the CLRT (Kim and Stephan 2002) and GOF test (Jensen et al. 2005) were applied to the diminutive polymorphism data from both Zimbabwe and China. These tests are appealing as they consider multiple features of the site-frequency spectrum and, in combination, have been shown to be robust to demography. A significant CLRT was observed for both populations, and the GOF P-values are found to be consistent with the selective sweep hypothesis (Table 3). Additionally, maximum-likelihood parameter estimates were obtained for both the strength (2N_es = 868 and 403 for China and Zimbabwe, respectively) and the target of selection (positions 13765 and 12132 for China and Zimbabwe, respectively, where position 1 corresponds to the first base pair of the first sequenced region).

TABLE 3.

The CLRT, Kim and Nielsen, and GOF P-values for each population, as well as the corresponding estimate of the selection coefficients

	CLRT P-value	Kim and Nielsen P-value	α	X	GOF P-value
Zimbabwe	0.039	0.022	403	12,132	0.9
China	0.043	0.057	868	13,765	0.561

While the CLRT is conservative when applied to partial sequence data (J. D. Jensen, K. R. Thornton and C. F. Aquadro, unpublished results), the resulting parameter estimates can be unreliable even when considering very recent selection (τ = 0). To examine the ancestral sweep predicted for dm, the assumptions regarding the age of the sweep were relaxed (the CLRT assumes that τ = 0). Data sets were simulated with selection using the diminutive parameters (θ, 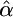, , 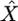n, R, as well as the precise configuration of sequenced regions) and used what has been suggested to be a minimum value of τ that would be necessary to accommodate a sweep prior to the splitting of the African from the non-African populations (τ = 0.019, Thornton and Andolfatto 2006). We find (Table 4) that while complete sequencing makes a large improvement in the precision of target site estimates when the sweep is very recent, it has a relatively minor impact when selection has occurred in the more distant past, owing to the loss of signal due to the subsequent impacts of drift, mutation, and recombination. For the estimate of the target of selection, for instance, the 95% confidence intervals with our current partial sequencing encompass ∼18 kb, while if the entire 22-kb region had been sequenced the confidence intervals would be reduced only to 14 kb (Table 4).

TABLE 4.

The 95% confidence intervals spanning the estimate of the target of selection (as ascertained from simulation) for partial and complete sequencing, as well as a common (n = 12) and large (n = 60) sample size, for τ = 0 and τ = 0.019

Sequencing	Sample size	95% C.I. (bp)
τ = 0
Partial	12	7,089–16,877
	60	8,132–16,111
Complete	12	11,137–13,672
	60	11,349–13,517
τ = 0.019
Partial	12	2,037–20,081
	60	2,654–19,234
Complete	12	3,876–18,453
	60	5,434–17,299

We also examined the impact of sample size on the MLE by evaluating the confidence intervals and relative mean square errors (RMSEs) under a number of different sample sizes. It is worth noting that while there is a marked improvement for larger sample sizes, the benefit appears to plateau around n = 60. Additionally, given the estimated strength and assumed age of the sweep in the dm region, even for a sample size of n = 110 and complete sequencing, the 95% confidence intervals would still encompass half (11 kb) of the 22-kb dm gene region under investigation here. Thus, while the CLRT has good power to detect sweeps of this age, the maximum-likelihood estimates are not very precise even with complete sequencing and extremely large sample sizes. Thus, these simulation results suggest that additional sequencing would not allow for a more precise localization of the target of selection. We note that even though the target of the dm sweep is inferred to be in the center of the intron, the confidence intervals span the entirety of the coding region.

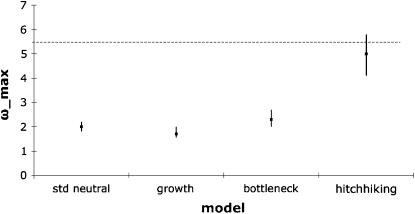
Additionally, LD patterns were examined for evidence of positive selection using the ω-statistic of Kim and Nielsen (2004). While we observe a large value that is consistent with a hitchhiking model according to the simulations of Jensen et al. (2007) (ω_max = 5.62), we have additionally examined the distribution of ω_max given our specific data structure and parameters, for the standard neutral model, the demographic model estimated for this population by Li and Stephan (2006), the demographic model estimated for this population by Haddrill et al. (2005), and a hitchhiking model in which selection parameters are taken from the MLEs obtained from the Kim and Stephan (2002) procedure. These simulations suggest the observed value to be uniquely consistent with the hitchhiking model (Figure 4).

Figure 4.—

The mean (square) and 95% confidence interval (line) of the LD test statistic, ω_max, under the four considered models: the standard neutral model, the growth model estimated for this population by Li and Stephan (2006), the bottleneck model estimated for this population by Haddrill et al. (2005), and a hitchhiking model using the MLEs of selection parameters estimated from our empirical data set (given in Table 3). One thousand replicates of each of the three neutral models were generated using ms (Hudson 2002), and 1000 replicates under the hitchhiking model were generated using ssw (Kim and Stephan 2002). The horizontal dashed line indicates the observed empirical value of ω_max. As shown, the observed value appears to be uniquely consistent with the hitchhiking model.

Divergence data:

The comparison of polymorphism to divergence can provide additional tests of an equilibrium neutral model. One such test is the HKA test (Hudson et al. 1987) that compares levels of polymorphism to divergence between regions. Comparing regions of dm to each other as well as to other genes on the X chromosome in regions of high recombination (Notch 5′, G6PD, and Vermillion) using a multilocus extension of the HKA test reveals a significant P-value (P = 0.0014) only for the China population sample. The data for these tests are presented in Table 2, where the lack of any segregating sites in the middle of the sequenced region, in contrast to normal divergence, appears to drive this rejection. While Zimbabwe does not reject, somewhat lower variation is apparent in this same region.

An additional polymorphism/divergence test of an equilibrium neutral model for protein-coding genes is the McDonald–Kreitman (MK) test (McDonald and Kreitman 1991). The null hypothesis of neutrality predicts that the ratios of polymorphism to divergence for synonymous and nonsynonymous sites are similar given that polymorphism is simply the transient phase of fixation. The polymorphism data considered are either from a combination of the two D. melanogaster populations or from a single population of D. simulans (Table 5). When considering total divergence between D. melanogaster and D. simulans, significant differences between ratios of synonymous and nonsynonymous polymorphism to divergence are observed in the former species for the entire dm coding region. With D. yakuba as an outgroup, and using parsimony to place fixations along the D. melanogaster or D. simulans lineages, the test was also performed using lineage-specific divergence. The results are marginally significant in both species for the entire dm coding region (the test is expected to lose power if lineage-specific divergence is relatively low). The MK test was also applied to the two exons of dm separately. The test remains marginally significant at exon 2 in D. melanogaster, suggesting that this region of dm has a tendency toward an excess of either nonsynonymous fixations or synonymous polymorphisms.

TABLE 5.

McDonald–Kreitman test results for the dm locus

	D. melanogaster		D. simulans
	Synonymous	Nonsynonymous	Synonymous	Nonsynonymous
Total locus
Total divergence
Polymorphism	21	2	15	11
Divergence	49	37	49	37
	P-value = 0.002		P-value = 0.948
Lineage-specific divergence
Polymorphism	21	2	15	11
Divergence	29a	12	10a	19
	P-value = 0.056		P-value = 0.084
Exon 1
Lineage-specific divergence
Polymorphism	7	2	4	7
Divergence	5	5	2	10
	P-value = 0.210		P-value = 0.283
Exon 2 (small sample, n = 12)
Lineage-specific divergence
Polymorphism	14	0	11	4
Divergence	24a	7	8a	9
	P-value = 0.053		P-value = 0.131
Exon 2 (large sample, n = 28)
Lineage-specific divergence
Polymorphism	47	19	11	4
Divergence	9a	4	2a	6
	P-value = 0.886		P-value = 0.026

^aComparisons for which there is a significant relative rates test (Tajima 1993) between the two species.

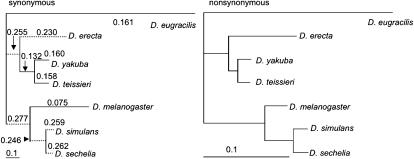
When the MK test suggests a deviation in the direction observed at exon 2 of dm, it is traditionally concluded to be due to positive selection on nonsynonymous mutations, although recent studies have illustrated the need to also consider selection acting on synonymous sites (e.g., Bauer DuMont et al. 2004; Comeron and Guthrie 2005). Interestingly, exon 2 also has an excess of synonymous fixations along the D. melanogaster lineage compared to the D. simulans lineage (Table 5), resulting in a significant relative rates test (Tajima 1993).Given the suggestive MK test result and significant relative rates test on synonymous fixations at exon 2 of dm, we sequenced this region in additional species and applied a genetic algorithm (GA) method to assess the relative rates across species in synonymous and nonsynonymous evolution (Kosakovsky Pond and Frost 2005). Models allowing up to six separate ω-ratios (d_N/d_S ratio) across the tree were explored. We observed no increase in likelihood beyond a three-ratio model. The three-ratio GA model reveals a significantly lower ω-ratio along the D. melanogaster branch relative to other branches of the tree (P-values ranging from 0.003 to 0.029). Figure 5 shows that this decreased ratio is as much due to an accelerated rate of synonymous fixations as it is to a decreased rate of nonsynonymous mutations in D. melanogaster, which corroborates the significant relative rates test for synonymous changes in this species represented in Table 5.

Figure 5.—

Synonymous and nonsynonymous trees at exon 2 of dm. Numbers in synonymous trees are d_N/d_S ratios for each branch. Dotted branches illustrate those with a significantly different d_N/d_S ratio from that of the D. melanogaster branch.

To further investigate the relative molecular evolution of synonymous and nonsynonymous mutations at exon 2 of dm, additional sequence was generated, increasing the sample size to n = 28 for this region in D. melanogaster. The addition of these sequences produced different MK test results because a large proportion of previously classified fixed differences between D. melanogaster and D. simulans are now found to be only near, but not at fixation (thus shifting to be counted as a higher frequency of polymorphisms). The MK test is no longer marginally significant for D. melanogaster, but becomes significant within D. simulans (Table 5). The effect of the larger sample size on reclassifying fixed differences was not consistent between synonymous and nonsynonymous mutations. Significantly, more new segregating sites are due to the conversion of fixed differences to polymorphisms for synonymous than for nonsynonymous changes (ratio of truly new polymorphism to those reclassified from “fixed” differences for synonymous and nonsynonymous changes, respectively: 7:40 and 12:8; Fisher's exact P-value <0.001).

The vast majority of the reclassified synonymous polymorphisms results in a high frequency of derived unpreferred mutations (changes from a preferred to an unpreferred synonymous codon). This pattern produces a significant difference in derived preferred (changes from an unpreferred to a preferred synonymous codon) and unpreferred frequencies within the Zimbabwe population (Wilcoxon test P-value = 0.014; 7.2 and 18.22 rank sum score mean for preferred and unpreferred, respectively). We note that the new, large sample-dependent polymorphisms are not associated randomly among the new alleles, but rather are mostly associated with two lines: Zimbabwe 21 and 25 (Table 6). In addition, the haplotype structure that these alleles introduce extends into the neighboring intron. This haplotype structure is consistent with the hypothesis that a selective sweep has occurred within this genomic region (Kim and Nielsen 2004). However, it is not expected that a sweep would change the relative frequencies of preferred and unpreferred mutations. These somewhat complex results do suggest that synonymous sites are not evolving in a strictly neutral fashion at exon 2 of dm.

TABLE 6.

Polymorphism table for the Zimbabwe population at exon 2 of diminutive nucleotide position

	Nucleotide position
Sequence	18	21	93	104	126	135	145	156	174	204	206	208	209	224	239	243	262	264	337	354	361	364	372	402
mel	G	G	C	G	G	C	C	G	G	G	G	G	C	C	C	C	C	G	C	A	A	C	C	C
46	T	A	T	T	.	T	.	A	A	.	.	A	.	.	.	A	.	A	G	.	.	.	T	.
47	T	A	T	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	T	T	T
48	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
20	T	A	.	T	.	T	T	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
21	.	A	.	.	.	T	.	.	.	A	A	.	G	T	A	.	.	A	G	.	.	.	T	.
23	T	A	.	T	.	T	T	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	.
25	.	.	.	.	A	.	.	.	.	A	A	A	G	T	.	.	A	.	.	G	T	.	.	.
26	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	T
27	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	T
28	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	.
29	T	A	T	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	.
30	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
31	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	T
33	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	T
34	T	A	T	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
43	T	A	T	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	.
45	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	T
10	T	A	T	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
13	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	.
15	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	.
16	T	A	T	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
18	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
22	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	T
36	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
39	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	A	.	A	G	.	.	.	T	.
41	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
42	T	A	.	T	.	T	.	A	A	A	A	A	G	T	.	.	.	A	G	.	.	.	T	.
sim	G	G	C	G	G	C	C	G	G	G	G	G	C	C	C	C	C	G	C	A	A	C	C	C
mel	C	G	G	G	G	C	A	G	T	C	G	C	C	C	T	C	A	C	T	A	C	C	T	T
46	T	.	.	A	.	T	.	A	G	T	A	.	T	.	.	G	G	.	.	C	T	.	G	.
47	.	A	.	A	.	.	.	A	G	.	A	G	T	.	.	G	G	A	C	C	T	.	.	.
48	T	.	.	A	.	.	.	A	.	T	A	G	T	.	G	G	G	A	C	C	T	.	.	.
20	T	.	.	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
21	.	.	.	A	.	T	.	.	.	T	.	.	.	T	.	.	.	.	.	C	.	.	.	.
23	T	.	.	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	.	.	.
25	.	.	.	A	.	.	.	A	.	T	A	G	T	.	.	G	G	.	.	.	.	.	.	.
26	.	.	A	.	.	.	.	A	.	T	A	.	T	.	.	G	G	A	C	C	T	T	.	.
27	.	.	A	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
28	T	.	A	.	.	.	.	A	.	T	A	.	T	.	.	G	G	A	C	C	T	T	.	.
29	T	.	.	A	.	T	T	A	.	T	A	.	T	.	.	G	G	A	C	C	T	.	.	.
30	T	.	.	A	A	.	T	A	.	T	A	.	T	.	.	T	G	A	C	C	T	T	.	.
31	.	.	A	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	.	.	.	.
33	.	.	A	A	.	T	T	A	G	T	A	G	T	.	G	G	G	.	.	C	T	T	.	.
34	T	.	A	.	.	.	.	A	.	T	A	.	T	.	.	G	G	A	C	C	T	.	.	.
43	T	.	.	A	.	.	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
45	.	.	A	A	.	T	.	A	.	T	A	G	T	.	.	G	G	A	C	C	T	T	.	A
10	T	.	.	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
13	T	.	A	A	.	T	.	A	G	T	A	.	T	.	.	G	G	A	C	C	T	.	.	.
15	T	.	.	.	.	.	.	A	.	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
16	T	.	.	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
18	T	.	.	A	.	.	.	A	.	T	A	.	T	.	.	G	G	A	C	C	T	T	.	.
22	.	.	A	.	.	.	.	A	.	T	A	.	T	.	.	G	G	A	C	C	T	T	.	.
36	T	.	.	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
39	T	.	A	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
41	T	.	A	A	.	T	.	A	G	T	A	.	T	.	.	G	G	A	C	C	T	T	.	.
42	T	.	.	A	.	T	.	A	G	T	A	G	T	.	.	G	G	A	C	C	T	T	.	.
sim	C	G	G	G	G	C	A	G	T	C	G	C	C	C	T	C	A	C	T	A	C	C	T	T

mel, melanogaster consensus sequence (and thus the inferred ancestral state); sim, simulans. Dots indicate that the site is the same as the melanogaster consensus sequence. Letters indicate that the site differs from the inferred ancestral state (and thus is inferred derived).

Regardless of the inherent evolutionary pressures acting on synonymous sites, the overall pattern of nucleotide sequence heterozygosity, the frequency spectrum, and the haplotype structure suggest that at least one (probably ancestral) selective sweep has occurred within the dm region of the X chromosome in D. melanogaster.

DISCUSSION

Detecting adaptive fixations via patterns of polymorphisms in demographically unstable populations that share a common history is a complex task. It is even more difficult when the sweep is ancestral, predating the bottleneck associated with the founding of the sampled derived populations. Nonetheless, this complex selective and demographic history appears to be the best explanation for the patterns observed at microsatellite and nucleotide sequence data spanning the diminutive gene region of an African and Chinese population of D. melanogaster. Microsatellite data from across the 260-kb region scanned here, together with an adjacent distal 330-kb region extending to the white gene screened by Pool et al. (2006), have led to the investigation of three subregions more thoroughly via complete sequencing. In these cases, the consensus of various analyses has supported the interpretation that selective sweeps have shaped patterns of variation. One footprint seems associated with an evolutionarily recent sweep most prominent in non-African samples (i.e., downstream of Notch; Bauer DuMont and Aquadro 2005). However, two other footprints (one upstream of roughest reported in Pool et al. 2005 and the other at diminutive from the present study) were first hinted at by microsatellite data from non-African samples, yet follow-up targeted sequencing revealed significant support for a more ancestral sweep evident in the African sample. The apparent inconsistency of results for some tests of neutrality that focus on individual components of the frequency spectrum or levels of variation (such as Tajima's D or the HKA test for sequence or DH/SD for microsatellites) may reflect both this older fixation within the representative African population (Zimbabwe) and the increased evolutionary variance imposed on aspects of variation in bottlenecked populations represented by China (for sequence and microsatellite data) and the United States and Ecuador (for microsatellite data only). Although sequence data have not been generated in the United States and Ecuador samples, their microsatellite data support the founder-effect-sweep-amplification hypothesis in showing a reduction in variability and a frequency spectrum skew toward rare alleles within the dm region.

The presence of an ancestral sweep, the signal of which is blurred in derived and bottlenecked populations, may also explain the lack of a clear statistical signal in the LnRV and LnRH test results for microsatellites, both of which focus on population-specific reductions in variation. Pool et al. (2006) have made a similar case for their results. Importantly, these tests are designed to detect deviations between populations relative to one another; thus, one would not necessarily expect to detect significant differences under a hypothesis in which all populations have been affected by the same selective sweep. This is largely consistent with our data, in which LnRH is not significant at dm, and LnRV is only marginally significant when comparing the Chinese and Zimbabwe samples. We suggest that the latter result is due to the fact that, while we propose the same selective event in the ancestral population common to both Zimbabwe and China, the Chinese population may have been additionally affected by a more recent population bottleneck, resulting in a greater loss of variation at linked neutral regions. For microsatellite 244.2, no variation is observed within the Chinese sample, which is not typical for this population (Bauer DuMont and Aquadro 2005; Pool et al. 2006).

The maximum-likelihood methods we have relied on heavily to analyze the nucleotide sequence data incorporate several aspects of variation and the frequency spectrum together and suggest that an ancestral sweep has occurred within the dm region of the X chromosome of D. melanogaster. This signal appears robust to the confounding effects of demography, and it is for this reason that we focus on these statistics. In addition, the observed haplotype structure and the pattern of LD in the Zimbabwe sample within the dm locus are also more consistent with selection than with nonequilibrium demography. There are at least three specific predictions for LD around the target of an adaptive fixation: (1) strong LD close, but not immediately adjacent, to the target of selection; (2) strong LD on both sides of, but not across, the target; and (3) a greater probability of observing high-frequency derived alleles where strong LD is observed (Kim and Nielsen 2004; Stephan et al. 2006; Jensen et al. 2007). This latter correlation between high-frequency derived alleles and strong LD is due to the common underlying genealogical structure that gives rise to both features. All three predictions are observed at dm, resulting in a large LD test statistic value, ω_max, which appears most consistent with a hitchhiking model. However, given the large confidence intervals on the target prediction, the selected site may be contained in either exon or in the intron of dm.

Interestingly, of the three regions for which selective sweeps have been inferred in this 256-kb region of the X chromosome, unusual patterns in synonymous site evolution have also been found at two of them (dm and Notch; e.g., Bauer DuMont et al. 2004; Bauer DuMont and Aquadro 2005). Could selection on synonymous sites at least partly explain the selective sweep signal at dm? The excess of high-frequency derived, unpreferred synonymous variants found at exon 2 with the large population sample is adjacent to the inferred target of selection. However, this pattern appears to be due to the presence of rare, ancestral haplotypes. This haplotype structure and associated linkage disequilibrium extend across exon 2 and into the neighboring intron. These patterns are expected with a selective sweep model, but not under a simple model of selection on synonymous sites in which selection coefficients on such mutations are predicted to be on the order of the reciprocal of the effective population size (e.g., Akashi and Schaeffer 1997; Comeron and Guthrie 2005; Nielsen et al. 2007). With our current data, we cannot exclude that a change in synonymous site selective pressure and/or a change in mutation bias along the D. melanogaster lineage (e.g., Nielsen et al. 2007), in association with a linked selective sweep, has led to our significant MK test results. Regardless, our results illustrate the potential importance of sample size in inference of fixed vs. polymorphic states and in assessing differences in frequency spectra between different types of mutations. To date, with typically used sample sizes (n = 10 or 12), the pattern at the second exon of dm of a significantly higher frequency of derived unpreferred mutations compared to preferred has not been previously observed in D. melanogaster (e.g., Akashi and Schaeffer 1997; V. Bauer DuMont and C. F. Aquadro, unpublished data). These results are worth additional investigation, but at present do not support the idea that pervasive selection at synonymous sites altered genealogies sufficiently to “look” like a single sweep footprint at dm.

In summary, we conclude that the most parsimonious explanation for both the observed microsatellite and sequence data in the diminutive region of the X chromosome is that an African sweep occurred prior to non-African founding events. While the composite-likelihood test we used appears to have good power to detect sweeps of this age, we have shown here that even for very large sample sizes the maximum-likelihood estimate of the target of selection still has a large confidence interval for ancestral sweeps. As such, there is disappointingly little power to localize the target within dm from polymorphism data alone. Our finding that selection has acted at this locus is, nonetheless, intriguing given the known role of diminutive as a positive regulator of body size (Craymer and Roy 1980), as well as the known clinal pattern of variation of this trait (Gockel et al. 2002; Calboli et al. 2003). Only a functional analysis of naturally occurring variation at dm, as well as more complete geographic sampling across these clines, will provide greater insight into the selective pressures producing the patterns of variability observed at this genomic region.