Abstract
Postural regulation is an important part of a variety of motor tasks, including quiet standing and locomotion. Muscle length feedback, both the autogenic length feedback arising from a muscle’s own spindles, and heterogenic length feedback, arising from its agonists and antagonists, is a strong modulator of muscle force and well suited to postural maintenance. The effects of this reflex feedback on 3-D force generation and limb mechanics are not known. In this paper, we present a mechanical model for relating 3-D changes in cat hindlimb posture to changes in muscle lengths. These changes in muscle length are used to estimate changes in both intrinsic muscle force generation and muscle activation by length feedback pathways. Few muscles are found to have directly agonist mechanical actions, and most differ by more than 20°. Endpoint force fields are largely uniform across the space investigated. Both autogenic and heterogenic feedback contribute to whole limb resistance to perturbation, autogenic pathways being most dramatic. Length feedback strongly reinforced a restoring force in response to endpoint displacement.
INTRODUCTION
The motor control system performs a wide variety of tasks. Its movements are supported by a network of reflex pathways. These pathways provide continuous feedback of limb position, muscle lengths, velocities, contact forces, muscle activations and allow the nervous system to correct for unexpected loads or displacements. However, this overwhelming connectivity makes it difficult to extract a meaningful analysis of the influence of any single pathway.
The autogenic stretch reflex (SR) was one of the first feedback pathways to be identified (Sherrington, 1907). It includes fast, monosynaptic input onto a motorneuron from 1a spindle afferents from the same (homonymous) muscle, and slower processes from other afferents and polysynaptic pathways (Houk & Rymer, 1981). Being a powerful, rapid modulator of muscle force, this pathway is an attractive mechanism for control tasks such as posture maintenance. The monosynaptic stretch reflex is central to the equilibrium point hypothesis (Feldman, 1966), and the foundation for the stiffness regulation hypothesis (Nichols & Houk, 1976).
In addition to excitation of the homonymous muscle, spindle 1a afferents make monosynaptic excitatory contacts with a range of other (heteronymous) muscles and presynaptically inhibit still other heteronymous motoneurons (Eccles and Lundberg, 1958). This network of heterogenic feedback consists primarily of mutual excitation between muscles with similar function and reciprocal inhibition of muscles with opposing action. For this reason, heterogenic length feedback from spindles has been described as coordinating individual muscles to generate a unified joint stiffness (Nichols et al., 1999).
The magnitude and distribution of the 1a pathway are fairly easily determined in reduced preparations (Eccles et al., 1957; Nichols, 1988). Eccles and coworkers (1957, 1958) have mapped the electrophysiological connections among motorneurons and spindles. Nichols (1989) and Bonasera and Nichols (1994, 1996) demonstrated similar connectivity using a mechanical approach. These experiments have shown that the concepts of the myotatic unit (Lloyd, 1946; Laporte & Lloyd, 1952) and stiffness regulation (Nichols & Houk, 1976) should be extended to describe the functions of a more complex network.
The mechanical behavior of a single muscle is frequently described in terms of its stiffness: the steady state increase in muscle force in response to an increase in muscle length (Feldman & Orlovsky 1972; Rack & Westbury, 1969). In the steady state, a muscle can be considered essentially a (nonlinear) spring, with its stiffness modulated by its intrinsic properties and reflex feedback. Similarly, the mechanical behavior of an intact limb may be described in terms of stiffness (Mussa-Ivaldi, et al., 1985; Hogan, 1985). Restoring forces in this multidimensional case are often represented as a vector field. The vector field presentation has also been used to describe the action of spinal motor primitives (Giszter et al., 1993; d’Avella & Bizzi, 1998).
These force fields have been used by several investigators attempting to extract the behavior and properties of the stretch reflex from intact preparations (Bennett, 1994; Fitzpatrick et al., 1992; Sinkjaer et al., 1988). Such attempts frequently depend on the use of perturbations imposed upon rapid voluntary movements (Bennett, 1994; Shadmehr et al., 1993), normal movement (Sinkjaer, 1997) or a static posture (Mussa-Ivaldi, et al., 1985). Any variation in EMG or force from unperturbed trials is attributed to the perturbation. However, an imposed perturbation necessarily impacts a wide range of sensory pathways, ranging from cutaneous afferents at the point of application (Vedel & Roll, 1982) to joint capsule afferents (Baxendale et al., 1988) to proprioceptors at distant segments. Further, analysis of whatever signals are recorded is complicated by the strong dynamic nonlinearities inherent in both the reflex control system and the muscular plant.
In spite of attempts to isolate reflex pathways in intact preparations, it remains difficult to relate the basic electrophysiology and mechanics from reduced preparations to the complex kinematics, forces, and EMG results of intact preparations. The ability to make such a relation would permit a more rigorous check on the assumptions made to analyze experiments on intact subjects and on the conditions under which reduced preparations are performed. The basic elements required relating the basic physiological experiments to planar performance have been available for some time (Loeb et al., 1989).
A step to understanding the mechanical role of the stretch reflexes is to use our knowledge of the group 1a feedback network, muscle architecture and limb anatomy to estimate the joint torques and endpoint forces. The purpose of this study was to develop a mathematical model of the cat hindlimb in order to evaluate the mechanical action of stretch evoked reflexes in resisting a mechanical perturbation. To this end, a three dimensional, anatomical model of the hindlimb was constructed. Individual muscle forces were predicted using separate Hill style models. Muscle activation patterns were determined by a control model mimicking autogenic and heterogenic length feedback arising from spindle primary afferents. Although the model included some dynamic aspects of muscle and reflex behavior, this report will focus on the steady-state results. Of particular interest are the mechanical actions of individual muscles, the influence of heterogenic length feedback on spring like behavior of the endpoint, and the shaping of the endpoint force field by reflex feedback.
Portions of this work have appeared in preliminary form (Burkholder & Nichols, 1998).
METHODS
Anatomical Model
The right hindlimb of a 3 kg female cat was harvested following euthanasia associated with another procedure. Although a single specimen was used in the preparation of these results, the structure of a second specimen is quite similar and produces similar results.
While the limb was still compliant, knee and ankle joint centers of rotation were estimated using a procedure similar to Hollister et al. (1992). A ball joint was fixed to the shank and a pin mounted in the joint. By rotating the ball joint, it was possible to alter the orientation of the pin with respect to the shank, and by adjusting the position of fixation of the ball joint, it was possible to alter the position of the pin relative to the shank. With the position and orientation of the pin held fixed relative to the shank, manipulation of the knee or ankle altered the position of the pin relative to the thigh or foot, respectively. When the motion of the pin with respect to the manipulated limb segment appeared to be at a minimum, indicating close alignment with the center of rotation, it was inserted into the limb. This procedure results in mechanical axes that are not parallel to the usual anatomic axes, nor perpendicular to each other. Based on manipulation of the limb, four mechanical axes were identified, roughly equating to knee extension, ankle extension, knee adduction, and ankle adduction.
Following identification of joint centers, pins were inserted into each limb segment. Using these pins, the limb was held in a stance-like position: knee at approximately 100 degrees of extension and ankle at approximately 110 degrees of extension. The limb was then fixed in 4% buffered formalin for five days before beginning anatomical measurements.
The limb and clamp assembly was mounted in the center of a 3-axis coordinate frame. The frame was constructed from stereotaxic frame parts, and allowed precise location of the end of a stylus. The stylus was used to record the position of muscle origins, insertions, and via points in a system similar to Delp et al. (1990). For broad origins and insertions, these points were approximated by the centroid of the muscle attachment area. The position of each muscle contact point was recorded on at least three separate trials, with the immobilized limb being removed from the frame between trials. Once the geometry of superficial muscles had been recorded, these muscles were removed to expose the deeper muscles below.
To facilitate combination of these repeated measurements, positions of the fixation pins were also recorded. Using these pins, it was possible to define a coordinate transformation that unified the description of each separate measurement trial into a single coordinate system. Once points were expressed in a common coordinate system, their locations could be averaged.
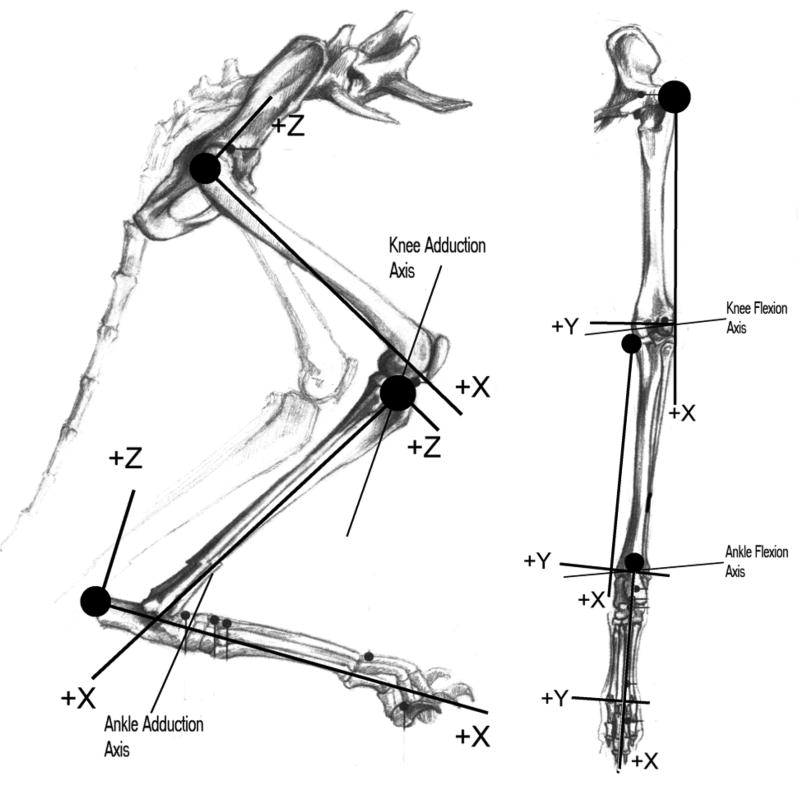
Coordinate systems were defined for each segment based on anatomical landmarks (figure 1). For the thigh, the X-axis was defined by the most proximal point on the greater trochanter and the lateral condyle. The Y-axis was defined by the X-axis and the medial condyle, and the Z-axis defined to be perpendicular to both. For the shank segment, the X-axis was defined by the medial epicondyle and the medial malleolus, with the Y-axis defined by the distal end of the fibula. For the foot, the X-axis was defined by the calcaneus and the midpoint between the 2nd and 5th metatarsal-phalangeal (MTP) joints. The Y-axis was defined by the X-axis and the 2nd MTP joint, and the Z-axis perpendicular to both.
Figure 1.
Sketch of the hindlimb showing reference frames for each segment and four defined axes of rotation.
To compare the anatomical model with previously reported data, muscle moment arms were calculated. Because joint axes did not correspond to anatomical axes moment arms could not be calculated directly, but had to be estimated using procedures similar to those used in physical measurement of moment arms (An et al., 1983). Both limb position and muscle origin to insertion distances were recorded as each of the four joint angles changed. This permitted calculation of apparent moment arms for motions in the common anatomical sagittal, transverse and coronal planes.
Muscle Model
Muscle forces were estimated using an architecture based Hill model similar to that described by Burkholder et al. (1994). Architecture reported in the literature (Sacks & Roy, 1982; Roy et al., 1997) or measured in our lab was used as a reference configuration. The model calculated sarcomere length from instantaneous muscle length using the formula:
| equation 1 |
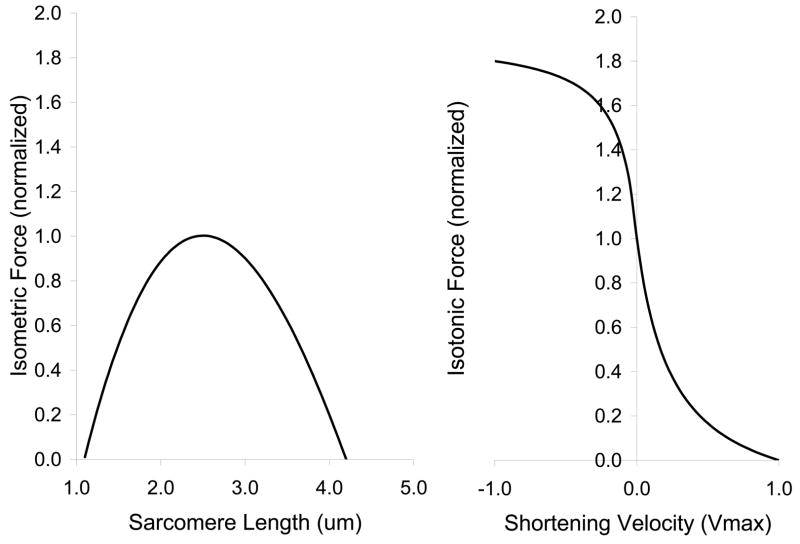
Where SL is sarcomere length; FL, fiber length; ML, muscle length; and the subscript 0 denotes the reference configuration. Muscle length was adjusted for tendon elasticity, assumed to be about 5% strain at maximum isometric force (P0). An activation dependent force-length relation was used, such that the sarcomere length of peak tension increased linearly by 0.5μm (20% of sarcomere L0) to 2.5μm as activation increased to maximum. Sarcomere length and velocity relations (figure 2) were scaled by muscle PCSA to yield whole muscle forces. The muscle model was implemented in MatLab 5.1 using Simulink 2.1 (MathWorks). A majority of the muscles crossing the knee and ankle were included (table 1).
Figure 2.
Sarcomere properties used in the muscle model.
Table 1.
Summary of muscles included in the model
| Muscle | Initial Activation (%Po) | Muscle | Initial Activation (%Po) |
|---|---|---|---|
| Biceps Femoris (BF) | 0.3 | Peroneus Tertius (PT) | 2.2 |
| Extensor Digitorum Longus (EDL) | 0 | Rectus Femoris (RF) | 0 |
| Flexor Digitorum Longus (FDL) | 2 | Semimembranosus (SM) | 1.4 |
| Flexor Halicus Longus (FHL) | 0 | Soleus (Sol) | 40 |
| Gracilis (Grac) | 4.7 | Semitendinosus (ST) | 4 |
| Lateral Gastrocnemius (LG) | 0 | Tibialis Anterior (TA) | 4.3 |
| Medial Gastrocnemius (MG) | 0 | Tibialis Posterior (TP) | 0 |
| Peroneus Brevis (PB) | 30 | Vastus Intermedius (VI) | 21.5 |
| Plantaris (Plan) | 0 | Vastus Lateralis (VL) | 0 |
| Peroneus Longus (PL) | 2.7 | Vastus Medialis (VM) | 12.1 |
Neural Model
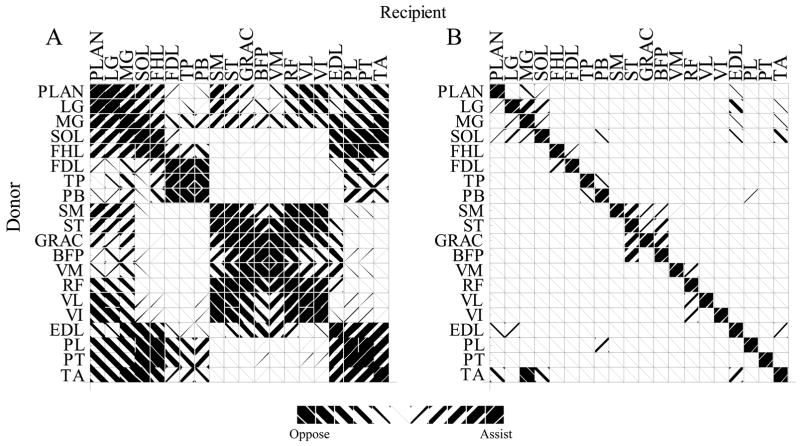
Each muscle was associated with an autogenic stretch reflex. Reflex activation varied smoothly as a function of , using the incomplete gamma function, Γ(1/8, x8). This activation was used both to scale force production and skew the length tension relation. Range was determined for each muscle from typical experimental ramp and hold stretches (Nichols. 1989; Bonasera & Nichols, 1994). Threshold was used as an input to adjust the initial activation of the muscle and to incorporate length feedback from other muscles. For example, heterogenic excitation of MG by LG was accomplished by reducing the MG threshold in proportion with changes in LG length. The pattern of heterogenic length feedback distribution (figure 4) was taken from the electrophysiological work of Eccles and coworkers (Eccles & Lundberg, 1958; Eccles et al., 1957) and mechanical stretches of Nichols and coworkers (Nichols, 1989; Bonasera & Nichols, 1994; 1996). Although muscles acting at the hip likely play an important role in the maintenance of posture, there is insufficient data describing their mutual interactions to reasonably include them in the present investigation.
Figure 4.
Angle between muscle moment arms (A) and strength of length feedback (B) between muscle pairs. Left hashing indicates similar muscle action and reflexive excitation. Right hashing indicates opposing mechanical actions and reflex inhibition. For example, to compare the MG and LG both flex the knee and extend and abduct the ankle, but they have opposing ab-adduction actions at the knee. The angle between these compound actions is 15°. Part B indicates that length feedback from LG onto MG is much stronger than length feedback from MG onto LG
Model Implementation
The anatomical data was used to generate a mechanical model using DADS 8.5 (CADSI, Coralville, IA). This model consisted of five segments: thigh, shank, foot, a thigh-shank linking body and a shank-foot linking body; four hinge/revolute joints: knee extension, knee adduction, ankle extension, and ankle adduction; and 32 muscle-tendon units (MTUs) in the form of DADS “PlantOut” and “PlantIn” element pairs. The muscle plant pairs were used to facilitate interchange of data between DADS and MatLab.
Each integration step began with DADS sending the current length of all 32 MTUs to Simulink. The Simulink neuromuscular model processed each MTU, using the secant method to iteratively determine tendon stretch, given muscle length, velocity and reflex activation. The resulting matrix of forces became the input to the DADS mechanical simulation, which determined a new configuration for the limb. The Simulink model was integrated by 4th order Runge Kutta method using a variable stepsize always smaller than 20 μs.
Reflex Evaluation
Simulations consisted of setting an initial pattern of muscle activation levels at the stance (initial) limb configuration, then moving the limb to a series of new endpoint positions. The initial activation pattern (table 1) was chosen to mimic the pattern of stance activation, i.e. predominantly the deep, “slow” anti-gravity muscles, (Roy et al., 1991; Abraham & Loeb, 1985) and to result in a stance-like force at the toe (Macpherson, 1994). The choice of initial activations is clearly critical to the results presented here, and little direct data are available. The pattern presented here represents a ‘best guess’: moderate changes to this pattern result in changes to the details of force generation, but the general trends remain the same. Altering the joint configuration produced changes in the lengths and moment arms of the model muscles. In response to the alteration of muscle lengths and moment arms, an altered pattern of force and torque production was developed at each position.
The role of reflex pathways was evaluated by successive simulations incorporating first: muscle intrinsic properties alone, second: muscle intrinsic properties with autogenic stretch reflex control, and finally: muscle intrinsic properties with autogenic stretch reflex control and heterogenic length feedback. The strength of autogenic feedback and distribution of heterogenic inputs were derived from electrophysiological experiments (Eccles et al., 1957; Eccles & Lundberg, 1958) and mechanographic measurements of reflex strength (Bonasera and Nichols, 1994;1996; Nichols, 1989). This stepwise approach allowed us to evaluate the role of each control level by examining alterations in the pattern of developed forces. For example, to determine the effect of autogenic length feedback, endpoint forces resulting from a ‘muscle only’ simulation would be subtracted from an ‘autogenic length feedback’ simulation. The change in force resulted from a combination of altered muscle activations and slightly altered limb configuration.
These fields of endpoint forces can be compared to the spring-like forces of Hogan (1985), and the displacement experiments of Macpherson (1988). Limb spring-like behavior can be evaluated by determining the curl, ∇ × F, of the force field. In these numerical simulations, Cartesian curl can be estimated by numerically differentiating the vector force field:
A spring like force field, which can be described as the gradient of a potential function, must have no curl in the coordinate system in which it is defined (Boas, 1983).
RESULTS
Anatomical Model
Two axes of rotation were identified at both the knee and ankle (figure 1). The knee flexion axis lay at an azimuth (angle in the X-Y plane from the X-axis of the thigh) of −96° and an inclination (elevation above the X-Y plane) of 1°, and passed through the medial femoral condyle. Thus, the “flexion” axis projected anteriorly, medially and distally. The second degree of freedom at the knee represented a combination of abduction and internal rotation. In the stance position, this axis lay at an azimuth of −73° and inclination of 137°, projecting posteriorly, medially, and anteriorly. The ankle flexion axis was at an azimuth of 82° in the shank X-Y plane and an inclination of 5°. The ankle abduction axis was found at azimuth 11°, inclination 22°: approximately parallel to the foot Z axis.
The primary concern in validating the anatomical model is that moment arms of the model muscles be similar in magnitude and direction as are those of previous reports. Moment arms for ankle crossing muscles can be seen in figure 3 to be similar to other reports (Young, et al., 1993; Lawrence, et al., 1993).
Figure 3.
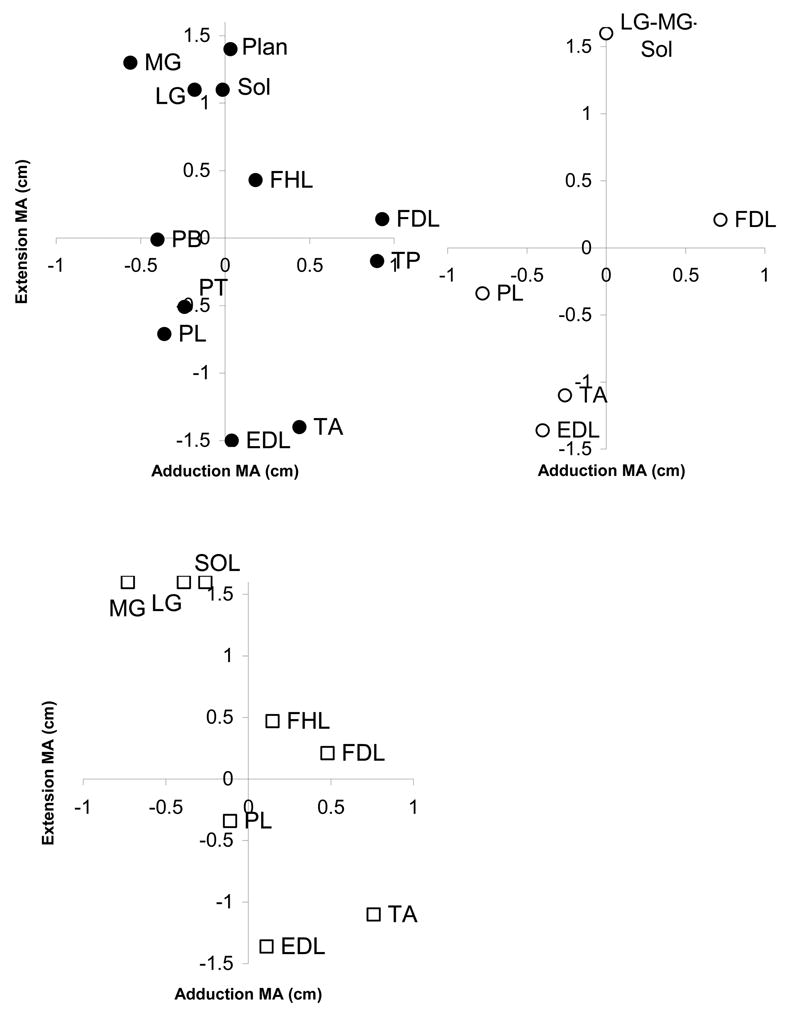
Moment arms of modeled ankle muscles (•), Young et al. (○) and Lawrence et al. (
 ). Abbreviations: EDL, extensor digitorum longus; FDL flexor digitorum longus; FHL, flexor halicus longus; LG, lateral gastrocnemius; MG, medial gastrocnemius; PB, peroneus brevis; PL, peroneus longus; PT, peroneus tertius; PLAN, plantaris; SOL, soleus.
). Abbreviations: EDL, extensor digitorum longus; FDL flexor digitorum longus; FHL, flexor halicus longus; LG, lateral gastrocnemius; MG, medial gastrocnemius; PB, peroneus brevis; PL, peroneus longus; PT, peroneus tertius; PLAN, plantaris; SOL, soleus.
One difficulty in comparing moment arms across multiple studies is the problem of coordinate systems. Defining a coordinate system that is reproducible across investigators and specimens is difficult, particularly in an intact specimen. One is frequently reduced to estimating the location and orientation of anatomic planes, introducing uncertainty about the direction of moment arms. The resulting rotation of axes may account for some of the discrepancies among the results of Young et al. (1993), Lawrence et al. (1993) and the present study. The similarities are of particular note, particularly the relative ordering of the MG-LG-Soleus muscles and TA-EDL muscles, which is uniform across studies.
Within the present study, surprisingly little mechanical redundancy was found. In this system, which contains four degrees of freedom, each muscle has a mechanical action or moment arm relative to up to four joints. For example, the medial gastrocnemius has actions of knee flexion, ankle extension, knee internal rotation and ankle abduction. These four axial moment arms can be considered the components of a four-dimensional moment arm, making it possible to define an angle between any pair of four dimensional vectors. This angle is a measure of the similarity of action of a pair of muscles (figure 4).
Muscle Model
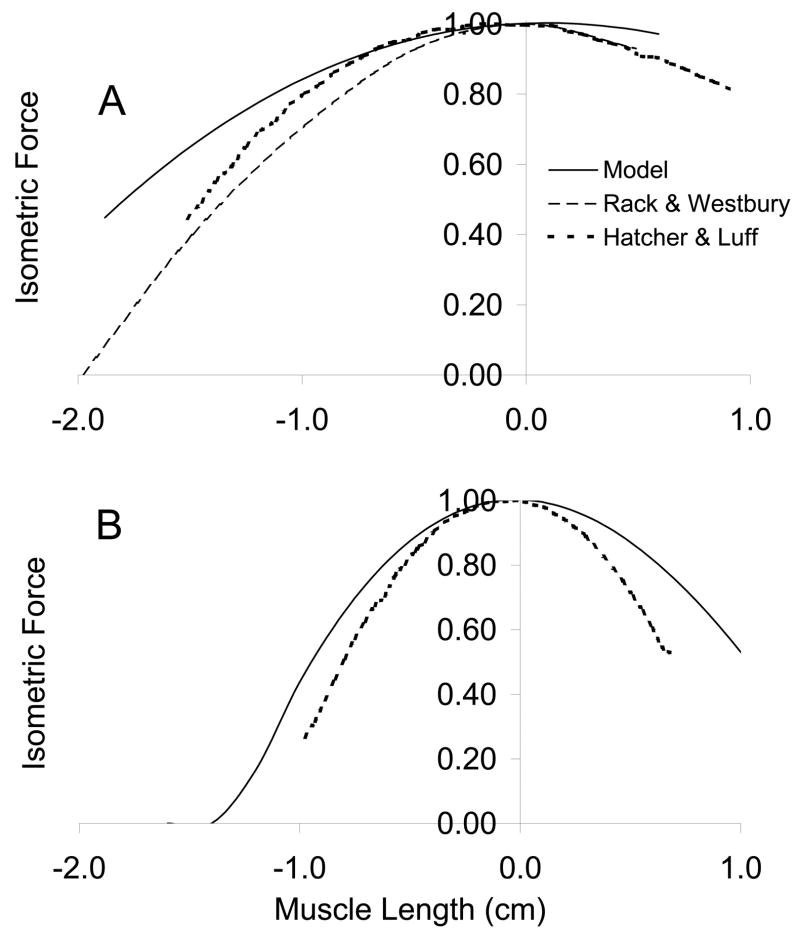
The muscle models predicted length-tension curves slightly broader than those experimentally described for several muscles (figure 5). The major goal of the muscle model is to account for gross muscle mechanics. Although the force length curves do not overlay the experimental data (Rack & Westbury, 1969; Hatcher & Luff, 1989), they do display an analogous variation with muscle fiber length. Some of the discrepancy lies in architectural differences between the muscles upon which the simulations are based (Sacks & Roy, 1982) and those of the experiments (Rack & Westbury, 1969; Hatcher & Luff, 1989). Rack and Westbury (1969) report soleus fiber lengths of approximately 2.5–3 cm, Hatcher and Luff report 3.1 cm, whereas Sacks and Roy report 4.2 cm.
Figure 5.
Model soleus (A) and FDL (B) length-tension relation compared to Rack and Westbury (1969) and Hatcher & Luff (1986).
Reflex Model
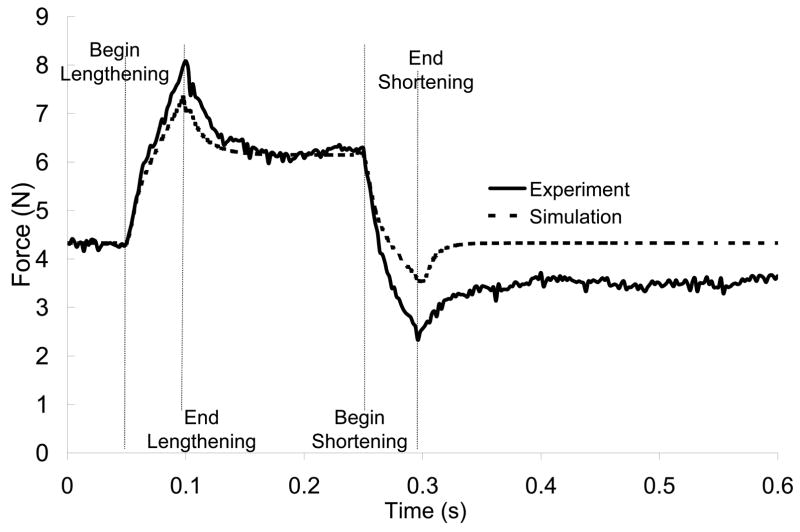
The critical aspect of the neuromuscular model is that it closely represents the response to stretch. As seen in figure 6, the combination of simple Hill muscle model and simple length feedback control give a close approximation of experimental results (Nichols & Koffler-Smulevitz, 1991). Although the length feedback model ignores such dynamic features as spindle stiction and dynamic sensitivity (Houk et al., 1981, Hasan, 1983), this simple feedback combined with nonlinear muscle behavior produces adequate stretch responses over a range of stretch velocities. As the present work focuses on steady state results, rather than forces and activations during the dynamic phase of a perturbation, these dynamic features are of minimal impact.
Figure 6.
Simulated EDL with autogenic stretch reflex model (--) closely mimics experimental data (—) (Nichols, 1989).
The addition of autogenic length feedback increased the stiffness of each simulated muscle (table 2). The reported stiffnesses depend on the initial activation levels chosen for each muscle (table 1). For example, the diminutive peroneus brevis (PB) displays greater stiffness than the massive medial gastrocnemius (MG) simply because the MG is minimally recruited. It is also for this reason that vastus lateralis (VL) has “0” stiffness: it is not recruited in these simulations, so has no change in force per change in length. Because all muscles operated on the ascending limb of their length tension relations (Sacks and Roy, 1982), each active muscle displays some stiffness related to its intrinsic mechanical function and baseline activation. This intrinsic stiffness depends on the architectural arrangement of the muscle: muscles with shorter fibers and larger PCSA will display higher intrinsic stiffness. Under the control of autogenic length feedback, that intrinsic stiffness is greatly magnified. The magnitude of this stiffness increase was different for each muscle, being largest for the strap-like hamstrings, smallest for the anti-gravity muscles and moderate for the ankle stabilizers. This increase in stiffness depended on the initial activation level and the stretch reflex gain chosen for each muscle.
Table 2.
Muscle active stiffness
| Muscle | Intrinsic Stiffness (N/cm) | Autogenic Stiffness (N/cm) | Ratio |
|---|---|---|---|
| FDL | 0.86 | 4.37 | 5.07 |
| FHL | 3.71 | 21.38 | 5.77 |
| Grac | 0.06 | 2.06 | 32.80 |
| LG | 7.63 | 17.47 | 2.29 |
| MG | 5.28 | 14.88 | 2.82 |
| PB | 22.73 | 40.43 | 1.78 |
| Plan | 0.84 | 3.59 | 4.29 |
| PL | 0.33 | 3.17 | 9.70 |
| PT | 0.55 | 1.62 | 2.94 |
| SM | 1.44 | 2.79 | 1.94 |
| Sol | 2.72 | 11.75 | 4.32 |
| ST | 0.57 | 5.99 | 10.51 |
| TA | 0.33 | 3.05 | 9.33 |
| TP | 3.65 | 12.11 | 3.31 |
| VI | 20.60 | 37.55 | 1.82 |
| VL | 0.00 | 0.00 | |
| VM | 29.02 | 40.64 | 1.40 |
Limb Control
When the endpoint of the two segment, four degree of freedom hindlimb model was displaced from its starting position, the orientation of each joint and length of each muscle changed. In response to these length changes, muscle force was altered, changing the resultant force at the endpoint. The kinematic response of the limb model to a given perturbation could be altered by the type of control model, because the anatomical model contained more degrees of freedom (4) than were specified during the perturbation (3).
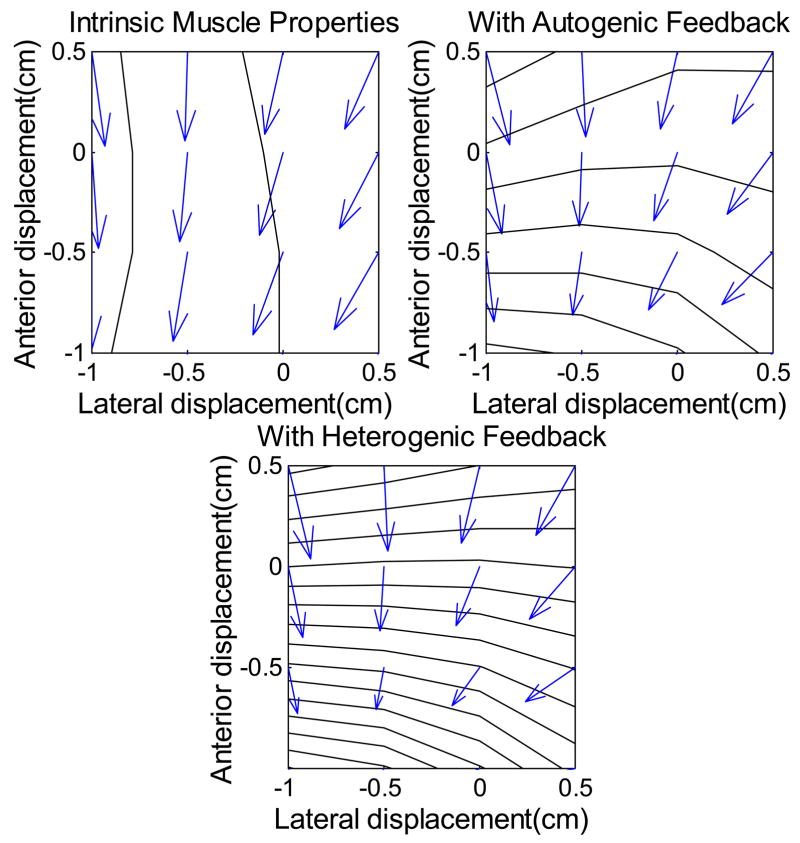
The field of steady state endpoint (toe) forces was dependent on both the choice of initial activation pattern and the type of control (figure 7, 8). Although the magnitude and direction of force responses could be altered by changing the initial activation pattern, the qualitative results are similar over a wide set of reasonable activation patterns. Figure 7 shows the horizontal components of toe forces for the initial activation pattern intended to mimic quiet stance. Throughout the region over which simulations were performed, endpoint force production is fairly uniform. Focusing on the change in endpoint force production following a displacement (figure 8), one sees that length feedback strongly enhances the postural stiffness of the lower limb.
Figure 7.
Total endpoint force under the influence of muscle intrinsic properites, muscle intrinsic properies and autogenic stretch reflex, and muscle intrinsic properties and heterogenic length feedback. Anterior-posterior displacements and forces are along the vertical axis, with abduction (+) and adduction (−) along the horizontal axis. Origin centered at the initial toe position.
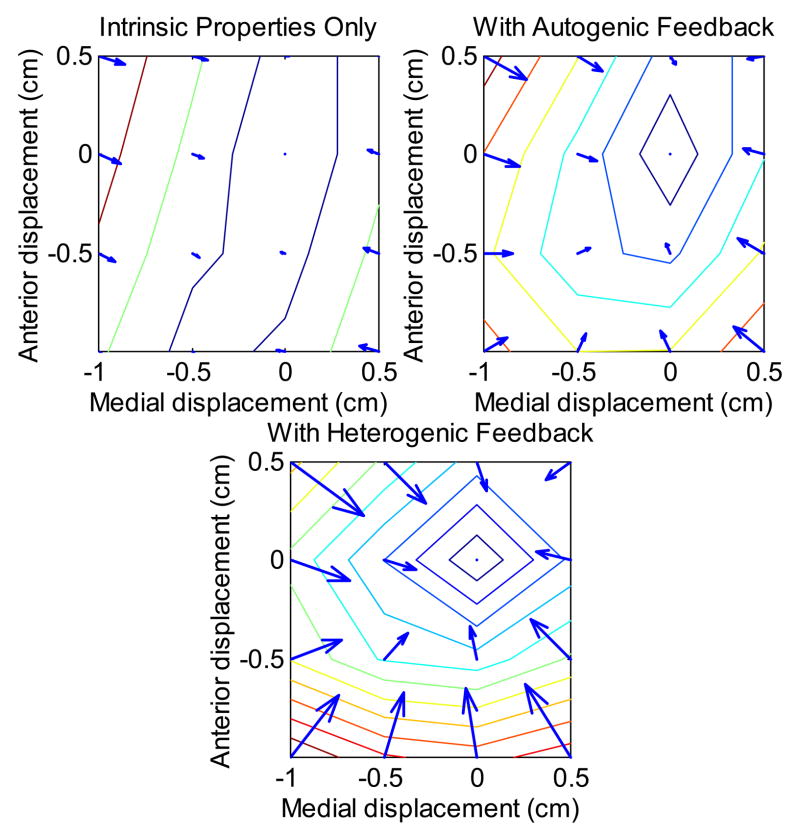
Figure 8.
Change in endpoint force in response to endpoint displacement with muscle forces determined by intrinsic muscle mechanics, muscle mechanics and autogenic length feedback, and muscle with autogenic and heterogenic length feedback. Contours represent 0.25 N increase in restoring force, and arrows show the A-P and M-L components. Reflex feedback strongly reinforces the restoring force field. Note that arrows are not generally perpendicular to contours, suggesting that restoring paths will not be straight.
The directional effect of reflex activation is most clearly seen in the lateral force components. The chosen pattern of starting activations includes little activity in stabilizing muscles such as TP and PB. As a result, these muscles contribute little to the pattern of forces in “muscle only” simulations (figure 7). The reflexive stiffness of these muscles is quite strong (Bonasera and Nichols, 1996), resulting in powerful lateral restoring forces when length feedback is included. The strong lateral stiffness contributed to the definition of a clear, preferred, nearly parasagittal path.
DISCUSSION
The intent of this work was to develop a model of the cat hindlimb for the purpose of investigating the interactions among the intrinsic mechanics of the musculo-skeletal system and neural length feedback control. The model components demonstrate reasonable agreement with experimental observations, while highlighting the limited mechanical redundancy of the neuromuscular system.
As in all mechanical models, the identification of axes of rotation is a significant issue. Knee and ankle motions were approximated using two hinge joints each, based on the motion of these joints during manipulation and by analogy to Hollister et al. (1992). The major flexion-extension motion of both intact joints is smooth and has a palpable preferred path. At the knee, this appears to be largely due to the actions of the medial and lateral collateral ligaments. At the knee in particular, there is strong coupling of abduction with internal rotation by the action of the cruciate ligaments. At least two methods have been described for identifying these axes in three dimensions. The screw displacement method (de Lange et al., 1990; Woltring et al., 1985) is an extension of the Rouleaux method (Rugg, et al., 1990) to three dimensions. To be reliable, it depends on a digitizing a fairly large number of points during displacement/rotation of the joint. It is mathematically justifiable but fraught with numerical uncertainties similar to its 2-D counterpart. The mechanical method used here, and described by Hollister et al. (1992, 1993), while not susceptible to numerical errors, does require significant operator skill to accurately locate the axes by feel and drill along the identified axis.
The definition of initial activation levels is another significant point of uncertainty. There are many activation patterns that would match the intended endpoint force pattern. Our choice of activations emphasized the deeper antigravity muscles – soleus and VI – while keeping the average activation level low (Sherrington, 1910; Abraham & Loeb, 1985; Roy et al., 1991). Changes in initial activation on the order of 10–15% had little effect on the qualitative results.
A major result from the anatomical model is the lack of redundancy in the musculoskeletal system. Fewer than 2% of the 180 moment arm pairs are within 20° of each other. Even muscles that share one common action, such as the triceps surae, differ in their complete function. The medial and lateral heads of the gastrocnemius, for example, differ in their non-sagittal action at both the knee and the ankle. The plantaris, which has an action very similar to lateral gastrocnemius at both the knee and ankle, has an additional action at the toes. The uniqueness of muscle actions is demonstrated in figure 4. Here, muscle pairs are coded by the angle between their four-component moment arms.
Functional agonist and antagonist groups are revealed by comparison of moment arms. Groups of red and blue muscles (figure 4) can be considered to be complementary pairs. In this way, it is possible to extract the classical agonist-antagonist groups, such as the similar group of PLAN, LG, MG, SOL, and FHL, opposed by EDL, PL, PT, and TA. Other mechanical pairings include quadriceps-hamstrings, quadriceps-triceps, and ankle ab-adductors. Some less considered synergies also appear, such as the similarity between TA and FDL, which both invert the foot.
Autogenic length feedback enhances the negative length feedback or stiffness, which a muscle on its ascending limb intrinsically displays. The simulations presented here demonstrate that length feedback has a strong effect of both the magnitude and direction of endpoint force responses. Both autogenic and heterogenic length feedback increase the restoring forces (figure 8), which would tend to stabilize the limb. The effect of reflex activation on the direction of force generation is somewhat more limited (figure 7). The principle reason for this is the intermuscular variation in the strength of length feedback. For example, the autogenic stretch reflex increases the stiffness of MG approximately 3-fold, but that of PL nearly 10-fold. In general, the “stabilizing” muscles – PL, PB, TP – were more excited by length feedback, so that under reflex control, these smaller muscles were better able to match the force changes of the larger plantarflexors.
Heterogenic length feedback tended to reinforce the action of the autogenic stretch reflex, generally increasing the lateral restoring force and slightly augmenting sagittal force production (figure 8). The actual impact of these modifications of endpoint force direction over the whole workspace, and particularly close to the preferred path, was comparatively minor, the mean direction change being generally less than 6°.
The present system appears to satisfy the requirements identified by Hogan (1985) for “springlike” behavior based on the properties of the muscles, even under autogenic length feedback control. Defining “spring-like” as possessing an integrable relation between force and displacement, Hogan (1985) argued that a system composed of spring-like muscles should possess spring-like behavior. Under the conditions imposed by the simulations presented here, the model muscles, in the absence of heterogenic feedback, are spring-like actuators. That is, they possess a one-to-one, monotonic, steady state relationship between length and force. There is also a unique relationship between limb configuration and each muscle length, and therefore a unique relation between limb configuration and each muscle force. The unique relation between limb configuration and muscle force imposes a unique relation between limb configuration and joint torques and, finally, endpoint forces. This system therefore appears to satisfy all the requirements for spring-like system behavior.
Simulations, however, result in force fields with non-zero curl indicating that this force field can not be completely described as the gradient of a Cartesian potential function. A non-zero curl implies, for example, that changes in lateral position alter sagittal force production by less than changes in sagittal position alter lateral force production. Displacement of the model toe within the plane of the ground results in changes in force production tending to restore the toe to its starting position (figure 8). These restoring forces have generally elliptical isotonic contours, similar to the restoring forces presented by Mussa-Ivaldi, et al., (1985) for the human forearm. The magnitude of curl in the present simulations is comparable to that measured by Mussa-Ivaldi and co-workers (1985), posing the possibility that the curl measured in those experiments is due not to reflex imbalances but to motion at joints presumed fixed. Averaged over the simulation plane, the magnitude of the curl vector increases from 3.5 N/m under the action of muscle intrinsic properties alone to 15 N/m with the addition of autogenic length feedback and 29 N/m with the further inclusion of heterogenic feedback. This is small, but not negligible, relative to a mean force of 2 N and mean divergence of −600 N/m.
The discrepancy between Hogan’s theoretical results and the present simulations lies in the transformation between joint coordinates and spatial coordinates. Hogan’s derivation depends on an invertable relation between joint coordinates and endpoint coordinates. In the present system, the four joint coordinates uniquely determine the three spatial coordinates of the toe, but that relation can not be inverted. The transformation from endpoint coordinates to joint coordinates is not unique. The configuration of the limb at the end of a perturbation depends on the path and dynamics of the perturbation. Since there are many possible configurations in joint-space represented by each endpoint position, the endpoint force can not be uniquely determined from endpoint position, and spring-like behavior in Cartesian space is not mathematically assured.
It should be noted that, while the behavior of the Cartesian endpoint of the system can not be completely described as the gradient of a 3-D potential function, it is stable and well behaved. The curl in this case indicates a tendency for the three dimensional projection of the four dimensional restoring paths to be curved relative to Cartesian space. As long as the divergence of the vector field is negative, the system will be stable, eventually returning to a resting position. This curvature of restoring force fields can be seen in physiological experiments (eg. fig 1 of Bizzi, et al., 1991; figs 4 & 9 of Shadmehr et al., 1993).
Macpherson (1988) found a strict limitation in the direction of limb force production. Following horizontal perturbations, regardless of the direction of the perturbation, each limb was found to generate a restoring force along a single axis. Although this result may be due to a propriospinal system linking the four intact limbs, it was of interest to determine whether each limb independently exhibits this anisotropic response. The present results demonstrate that the architecture of muscles crossing the knee and ankle, in conjunction with the anatomy of those joints strongly favors the generation of endpoint forces along a single axis. This is particularly clear in the trough-like shape of force magnitudes in figures 7a and 8a. In comparing our force fields with the results of Macpherson (1988), it became clear that the hip joint is extremely important to the specific direction of this preferred axis. Slight alterations in the attitude of the thigh can result in substantial differences in the direction of force generation at the toe due simply to the long distance from the hip to the endpoint. The importance of the more proximal segments is suggested by the relative constancy of knee and ankle angles relative to paw and pelvis angles as the cat is forced to adopt different postures (Fung and Macpherson, 1995). The distal segments included in the present simulations must be capable of transmitting and tuning the torques generated at the hip, requiring precise adjustment of both parasagittal and non-sagittal torques.
This paper has presented a three dimensional neuromechanical model of the cat hindlimb. The model was used to examine the mechanical influence of proprioceptive length feedback. It was found that length feedback enhances the stability of the distal hindlimb by hyperactivating the stabilizing muscles (PB, PL, PT, and TP). One possible role for length feedback is to reinforce or define the limb trajectory
Acknowledgments
This work was supported by NIH grants NS20855 and NS10520. The authors are grateful for insight and helpful discussion from David C. Lin and Thomas A. Abelew, and the anatomical expertise of Adnan Zulfiqar and Emily Schaeffer.
References
- Abraham LD, Loeb GE. The distal hindlimb musculature of the cat. Patterns of normal use. Exp Brain Res. 1985;58:583–93. [PubMed] [Google Scholar]
- An KN, Ueba Y, Chao EY, Cooney WP, Linscheid RL. Tendon excursion and moment arm of index finger muscles. J Biomech. 1983;16:419–425. doi: 10.1016/0021-9290(83)90074-x. [DOI] [PubMed] [Google Scholar]
- Baxendale RH, Ferrell WR, Wood L. Responses of quadriceps motor units to mechanical stimulation of knee joint receptors in the decerebrate cat. Brain Res. 1988;453:150–156. doi: 10.1016/0006-8993(88)90153-9. [DOI] [PubMed] [Google Scholar]
- Bennett DJ. Stretch reflex responses in the human elbow joint during a voluntary movement. J Physiol. 1994;474:339–351. doi: 10.1113/jphysiol.1994.sp020026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boas ML. Mathematical methods in the physical sciences. New York: John Wiley & Sons; 1983. [Google Scholar]
- Bonasera SJ, Nichols TR. Mechanical actions of heterogenic reflexes linking long toe flexors with ankle and knee extensors of the cat hindlimb. J Neurophysiol. 1994;71:1096–1110. doi: 10.1152/jn.1994.71.3.1096. [DOI] [PubMed] [Google Scholar]
- Bonasera SJ, Nichols TR. Mechanical actions of heterogenic reflexes among ankle stabilizers and their interactions with plantarflexors of the cat hindlimb. J Neurophysiol. 1996;75:2050–2070. doi: 10.1152/jn.1996.75.5.2050. [DOI] [PubMed] [Google Scholar]
- Burkholder TJ, Fingado B, Baron S, Lieber RL. Relationship between muscle fiber types and sizes and muscle architectural properties in the mouse hindlimb. J Morphol. 1994;221:177–190. doi: 10.1002/jmor.1052210207. [DOI] [PubMed] [Google Scholar]
- Burkholder TJ, Nichols TR. A three dimensional model of the cat hindlimb. Proceedings of NACOB’98.1998. [Google Scholar]
- d’Avella A, Bizzi E. Low dimensionality of supraspinally induced force fields. Proc Natl Acad Sci. 1998;23:7711–7714. doi: 10.1073/pnas.95.13.7711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Lange A, Huiskes R, Kauer JM. Effects of data smoothing on the reconstruction of helical axis parameters in human joint kinematics. J Biomech Eng. 1990;112:107–113. doi: 10.1115/1.2891160. [DOI] [PubMed] [Google Scholar]
- Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans Biomed Eng. 1990;37:757–767. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
- Eccles RM, Lundberg A. Integrative pattern of Ia synaptic actions on motoneurones of hip and knee muscles. J Physiol. 1958;144:271–298. doi: 10.1113/jphysiol.1958.sp006101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles JC, Eccles RM, Lundberg A. The convergence of monosynaptic excitatory afferents on to many different species of alpha motoneurones. J Physiol. 1957;137:22–50. doi: 10.1113/jphysiol.1957.sp005794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. III Mechanographic analysis of the execution by man of the simplest motor tasks. Biophysics. 1966;11:766–775. [Google Scholar]
- Feldman AG, Orlovsky GN. The influence of different descending systems on the tonic stretch reflex in the cat. Exp Neurol. 1972;37:481–494. doi: 10.1016/0014-4886(72)90091-x. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick RC, Taylor JL, McCloskey DI. Ankle stifness of standing humans in response to imperceptible perturbation: relfex and task-dependent components. J Physiol. 1992;454:533–547. doi: 10.1113/jphysiol.1992.sp019278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung J, Macpherson JM. Determinants of postural orientation in quadrupedal stance. J Neurosci. 1995;15:1121–1131. doi: 10.1523/JNEUROSCI.15-02-01121.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giszter SF, Mussa-Ivaldi FA, Bizzi E. Convergent force fields organized in the frog’s spinal cord. J Neurosci. 1993;13:467–491. doi: 10.1523/JNEUROSCI.13-02-00467.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasan Z. A model of spindle afferent response to muscle stretch. J Neurophysiol. 1983;49:989–1006. doi: 10.1152/jn.1983.49.4.989. [DOI] [PubMed] [Google Scholar]
- Hatcher DD, Luff AR. The effect of initial length on the shortening velocity of cat hindlimb muscles. Pflugers Arch. 1989;407:396–403. doi: 10.1007/BF00652624. [DOI] [PubMed] [Google Scholar]
- Hogan N. The mechanics of multi-joint posture and movement control. Biol Cybern. 1985;52:315–331. doi: 10.1007/BF00355754. [DOI] [PubMed] [Google Scholar]
- Hollister A, Buford WL, Myers LM, Guirinatano DJ, Novick A. The axes of rotation of the thumb carpometacarpal joint. J Orthop Res. 1992;10:454–460. doi: 10.1002/jor.1100100319. [DOI] [PubMed] [Google Scholar]
- Hollister AM, Jatana S, Singh AK, Sullivan WW, Lupichuk AG. The axes of rotation of the knee. Clin Orthop. 1993;290:259–268. [PubMed] [Google Scholar]
- Houk JC, Rymer WZ. Motor Control, part 1. II. Bethesda: American Physiological Society; 1981. Neural control of length and tension. Handbook of physiology, sec. I; pp. 509–596. [Google Scholar]
- Houk JC, Rymer WZ, Crago PE. Dependence of dynamic response of spindle receptros on muscle length and velocity. J Neurophysiol. 1981;46:143–166. doi: 10.1152/jn.1981.46.1.143. [DOI] [PubMed] [Google Scholar]
- Laporte Y, Lloyd DPC. Nature and significance of the reflex connections established by large afferent fibers of muscular origin. Am J Physiol. 1952;169:609–621. doi: 10.1152/ajplegacy.1952.169.3.609. [DOI] [PubMed] [Google Scholar]
- Lawrence JH, III, Nichols TR, English AW. Cat hindlimb muscles exert substantial torques outside the sagittal plane. J Neurophysiol. 1993;69:282–285. doi: 10.1152/jn.1993.69.1.282. [DOI] [PubMed] [Google Scholar]
- Loeb GE, He J, Levine WS. Spinal cord circuits: are they mirrors of musculoskeletal mechanics? J Mot Behav. 1989;21:473–491. doi: 10.1080/00222895.1989.10735495. [DOI] [PubMed] [Google Scholar]
- Lloyd DPC. Integrative pattern of excitation and inhibition in two-neuron reflex arcs. J Neurorphysiol. 1946;9:439–444. doi: 10.1152/jn.1946.9.6.439. [DOI] [PubMed] [Google Scholar]
- Macpherson JM. Strategies that simplify the control of quadrupedal stance. 1 Forces at the ground. J Neurophysiol. 1988;60:204–231. doi: 10.1152/jn.1988.60.1.204. [DOI] [PubMed] [Google Scholar]
- Macpherson JM. Changes in postural strategy with inter-paw distance. J Neurophysiol. 1994;71:931–940. doi: 10.1152/jn.1994.71.3.931. [DOI] [PubMed] [Google Scholar]
- Mussa-Ivaldi FA, Hogan N, Bizzi E. Neural, mechanical, and geometric factors subserving arm posture in humans. J Neurosci. 1984;5:2732–2743. doi: 10.1523/JNEUROSCI.05-10-02732.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols TR. The organization of heterogenic reflexes among muscles crossing the ankle joint in the decerebrate cat. J Physiol. 1989;410:463–477. doi: 10.1113/jphysiol.1989.sp017544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols TR, Houk JC. Improvement in linearity and regulation of stiffness that results from actions of stretch reflex. J Neurophysiol. 1976;39:925–935. doi: 10.1152/jn.1976.39.1.119. [DOI] [PubMed] [Google Scholar]
- Nichols TR, Lin DC, Huyghes-Despointes CMJI. The role of musculoskeletal mechanics in motor coordination. Prog Br Res. 1999 doi: 10.1016/s0079-6123(08)62871-x. in press. [DOI] [PubMed] [Google Scholar]
- Rack PMH, Westbury DR. The effects of length and stimulus rate on tension in the isometric cat soleus muscle. J Physiol. 1969;204:443–460. doi: 10.1113/jphysiol.1969.sp008923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy RR, Hutchison DL, Pierotti DJ, Hodgson JA, Edgerton VR. EMG patterns of rat ankle extensors and flexors during treadmill locomotion and swimming. J Appl Physiol. 1991;70:2522–2529. doi: 10.1152/jappl.1991.70.6.2522. [DOI] [PubMed] [Google Scholar]
- Roy RR, Kim JA, Monti RJ, Zhong H, Edgerton VR. Architectural properties of cat hip ‘cuff’ muscles. Acta Anat. 1997;159:136–146. doi: 10.1159/000147976. [DOI] [PubMed] [Google Scholar]
- Rugg SG, Gregor RJ, Mandelbaum BR, Chiu L. In vivo moment arm calculations at the ankle using magnetic resonance imaging (MRI) J Biomech. 1990;23:495–501. doi: 10.1016/0021-9290(90)90305-m. [DOI] [PubMed] [Google Scholar]
- Sacks RD, Roy RR. Architecture of the hind limb muscles of cats: Functional significance. J Morphol. 1982;173:185–195. doi: 10.1002/jmor.1051730206. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA, Bizzi E. Postural force fields of the human arm and their role in generating multijoint movements. J Neurosci. 1993;13:45–62. doi: 10.1523/JNEUROSCI.13-01-00045.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherrington CS. On reciprocal innervation of antagonistic muscles. Tenth note Proc Roy Soc B. 1907;79:337–349. [Google Scholar]
- Sherrington CS. Flexion reflex of the limb, crossed extension reflex and reflex stepping and standing. J Physiol. 1910;40:28–121. doi: 10.1113/jphysiol.1910.sp001362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinkjaer T. Muscle, reflex and central components in the control of the ankle joint in healthy and spastic man. Acta Neurol Scand Suppl. 1997;170:1–28. [PubMed] [Google Scholar]
- Sinkjaer T, Toft E, Andreassen S, Hornemann BC. Muscle stiffness in human ankle dorsiflexors: intrinsic and reflex components. J Neurophysiol. 1988;60:1110–1121. doi: 10.1152/jn.1988.60.3.1110. [DOI] [PubMed] [Google Scholar]
- Vedel JP, Roll JP. Response to pressure and vibration of slowly adapting cutaneous mechanoreceptors in the human foot. Neurosci Lett. 1982;34:289–294. doi: 10.1016/0304-3940(82)90190-2. [DOI] [PubMed] [Google Scholar]
- Woltring HJ, Huiskes R, de Lange A, Veldpaus FE. Finite centroid and helical axis estimation from noisy landmark measurements in the study of human joint kinematics. J Biomech. 1985;18:379–389. doi: 10.1016/0021-9290(85)90293-3. [DOI] [PubMed] [Google Scholar]
- Young RP, Scott SH, Loeb GE. The distal musculature of the cat: multiaxis moment arms at the ankle joint. Exp Brain Res. 1993;96:141–151. doi: 10.1007/BF00230447. [DOI] [PubMed] [Google Scholar]