Effect of protein dynamics on biological electron transfer

Abstract

Computer simulations of the effect of protein dynamics on the long distance tunneling mediated by the protein matrix have been carried out for a Ru-modified (His 126) azurin molecule. We find that the tunneling matrix element is a sensitive function of the atomic configuration of the part of the protein matrix in which tunneling currents (pathways) are localized. Molecular dynamics simulations show that fluctuations of the matrix element can occur on a time scale as short as 10 fs. These short time fluctuations are an indication of a strong dynamic coupling of a tunneling electron to vibrational motions of the protein nuclear coordinates. The latter results in a modification of the conventional Marcus picture of electron transfer in proteins. The new element in the modified theory is that the tunneling electron is capable of emitting or absorbing vibrational energy (phonons) from the medium. As a result, some biological reactions may occur in an activationless fashion. An analytical theoretical model is proposed to account for thermal fluctuations of the medium in long distance electron transfer reactions. The model shows that, at long distances, the phonon-modified inelastic tunneling always dominates over the conventional elastic tunneling.

Electron transfer is an integral part of many biological processes, such as photosynthesis and respiration. Much effort, therefore, has been directed toward understanding transport properties of various biological materials. In particular, recent experimental studies have provided information on the distance and structural dependence of electron transfer rates in various natural and modified proteins (1–4). In these systems, electron transfer typically occurs over distances of 10–30 Å and is due to tunneling mediated by the intervening medium between donor and acceptor.

It is commonly believed that fundamental principles of long distance electron transfer are essentially the same as those of any other electron transfer reaction (5). The only difference seems to be in the nature of electronic coupling; in short distance reactions, electronic orbitals of donor and acceptor directly overlap whereas in long distance reactions this coupling is indirect because of sequential overlaps of atomic orbitals of the donor, the intervening medium (bridge), and the orbitals of the acceptor. These sequential overlaps give rise to the concept of superexchange. It is assumed that all states in the bridging medium are virtual, i.e., there are no other resonant states in the system but those of donor and acceptor. The resonance between donor and acceptor occurs in the course of thermal fluctuations of the polar environment. The absence of real intermediate states and direct coupling physically means that electron transfer occurs via tunneling. In this picture, the overall rate of electron transfer is proportional to the frequency at which donor and acceptor states come to resonance and the probability to transfer an electron between donor and acceptor states at the transition state (i.e., donor–acceptor resonance) of the reaction. Such a direct application of classic Marcus theory has been very successful in characterizing major factors that control biological electron transfer (1–5).

The question, nevertheless, exists as to whether there is any conceptual difference at all between short and long range electron transfer reactions, in particular reactions in proteins. In this paper, we examine this question in computer simulations of electron tunneling in the Ru-modified azurin molecule, which recently has been synthesized and studied in Gray’s laboratory (3).

We are interested in the role of dynamics of the intervening medium through which an electron passes between donor and acceptor. One effect of the fluctuations in the medium is trivial; because of the flexibility of the bridge, every time donor and acceptor states meet in resonance, the configuration of the barrier separating donor and acceptor wells will be slightly different. The transfer matrix element (T_DA), therefore, will be also different for different configurations of the transition state, and an appropriate averaging of the square of T_DA has to be carried out in the rate expression to account for such inhomogeneity of the reaction.

This effect has been recognized early in the discussion of electron transfer in proteins (6, 7). The real challenge, however, always has been to evaluate how big the fluctuations of T_DA are in real systems and to understand whether or not the calculations of the electronic tunneling matrix element on a single configuration (x-ray data for a protein structure), which were the focus of many recent studies in this area, reliably represent actual electronic couplings in proteins. We examine this question in a molecular dynamics simulation by calculating the superexchange matrix element simultaneously with the dynamics trajectory of a protein in which electron transfer occurs. The magnitude of fluctuations of the matrix element observed in our calculations depends on the tunneling energy and on the part of the protein that is allowed to move. We find that, in general, the fluctuations of matrix element are so big that the averaging of the square of T_DA is unavoidable when a comparison with experimental data is made.

The second effect is more subtle. It has to do with the time scale of the fluctuations of the tunneling matrix element τ_b. The inverse of this time defines the typical energy quantum (ℏτ_b⁻¹) that the tunneling electron can exchange with vibrations of the medium in which the propagation of the tunneling electron is taking place. The effect of such an energy exchange is that the tunneling can occur not at the resonant position of donor and acceptor states but rather when the donor and acceptor states are mismatched by at least one quantum of the vibrational energy of the protein medium. Thus, tunneling becomes inelastic, in contrast to the usual elastic tunneling assumed in the conventional theory of electron transfer in proteins. We show here that the time scale of matrix element fluctuations, due to motion of the atoms of the protein matrix, can be as short as 10 fs, giving rise to a large energy quantum of the order of 1000 cm⁻¹. We find that these short time fluctuations are of the order of the matrix element itself, which indicates a strong coupling of the tunneling electron to the fast vibrational nuclear motions of the protein, such as CN, CC, CO, and CH stretch vibrations.

We also propose a simple analytical model, which is a natural modification of the Marcus model of electron transfer, that accounts for the effects found in our computer simulations. The study of this model shows that, when the distance between donor and acceptor increases, the contribution of inelastic tunneling always dominates over the usual elastic tunneling. One consequence of the inelastic tunneling is that the reaction becomes activationless in the conventional inverted region.

In the next section, results of computer simulations of the tunneling matrix element in Ru-modified azurin are presented. The following section is devoted to the discussion of the analytical model of electron transfer mediated by a fluctuating bridge.

2.0 Molecular Dynamics Simulations and Electron Tunneling in Ru-Modified Azurin

The main idea of the calculations was to simulate thermal fluctuations of the protein structure around equilibrium by running Nosè–Hoover dynamics on the protein matrix as well as to examine the tunneling matrix element for different configurations of the nuclear coordinates along the trajectory. At this stage of the work, the goal was to find how sensitive the tunneling amplitude would be to equilibrium fluctuations of the protein structure and to determine the relevant time scale of these fluctuations.

The calculations were performed on the His X–Ru-modified blue copper protein azurin molecules from recent experimental studies of Gray and coworkers (3). In these systems, electron tunneling occurs between the Cu⁺ and Ru³⁺ ions; Cu is a native metal center of the azurin molecule, and the Ru(bipy)₂im complex is attached to a His X residue at different positions on the surface of the molecule using site-directed mutagenesis. In particular, experimental studies have been carried out for three systems (His-122, His-124, and His-126) in which the Ru complex is attached along one of the eight anti-parallel β-strands of the azurin molecule, which has a distinctive β-barrel secondary structure. The metal-to-metal distance in these systems varies roughly between 15 and 26 Å for His-122 and His-126, respectively. These complexes have been used recently in our studies of protein pruning (8) and interatomic tunneling currents (9, 10) for a “frozen” crystal structure of the molecule. The results of dynamics simulation in His-126 molecule, with the longest distance between donor and acceptor, will be presented here.

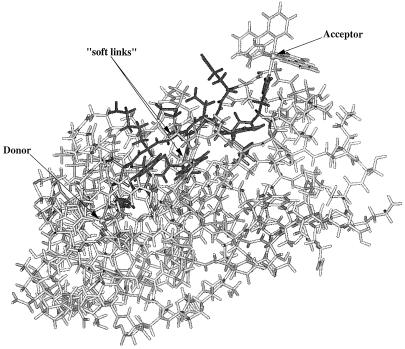
A computer model of the three-dimensional atomic structure of the system used in the calculations (Fig. 1) was based on the crystallographic data for azurin. Modifications of the original crystal structure of the azurin molecule by attaching the Ru complex were made using standard molecular simulation programs.§

Figure 1.

Ru(bipy)₂(Im)(His-126)–azurin system. Donor is a type II copper ion coordinated axially by a glycine oxygen and a methionine sulfur atom and in the equatorial positions by two histidine nitrogen atoms as well as a cysteine sulfur atom. Acceptor is in a virtually perfect octahedral crystal field coordinated by two bipyridines and two imidazole nitrogen atoms, one being the site-directed surface histidine. In dark, the 12-amino acid, pruned molecule is outlined. Donor and acceptor are separated by 26.7 Å. The arrows point to “soft links,” which are the Phe-110 (C_α–N) bond located on the Cys-112 strand and the Gly-123 (C_α–C) bond, which is part of the Met-121 strand. The pruned molecule and soft links were used in the dynamics simulations. The water molecules surrounding the protein are not shown.

We begin with a discussion of the method of tunneling matrix element calculation for a given configuration, i.e., for one snapshot of the protein structure along the trajectory. In fact, calculations of this type have been done and reported earlier (8–10). We therefore give here only a brief description of this part of the calculation.

2.1 Tunneling Matrix Element

Because of their size, direct ab initio studies of electronic coupling in realistic biological systems are not yet feasible although such studies have been carried out on small model systems (11–13). We will therefore use one of the semiempirical, one-electron methods developed for such calculations in our group (10).

In the matrix element calculations, the perturbation theory method (14–21) was used. This method avoids diagonalization of the protein Hamiltonian matrix and thereby allows for taking account of all atoms of the protein matrix in the calculation. The approach is based on the assumption of weak coupling between donor and acceptor orbitals and the orbitals of the intervening medium. We recently have tested the reliability of this method and found that it reproduces results of exact diagonalization for Ru-modified azurin within 30%, a reasonable accuracy for this type of calculation (10).

In this method, the tunneling matrix element is expressed in terms of the Hamiltonian matrix of the bridge H^B, its overlap matrix S^B, and the coupling coefficients of donor and acceptor orbitals to the bridge V,

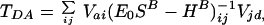2.1

where E₀ is the tunneling energy, and the couplings of donor and acceptor metal ion orbitals |d> and |a> to the bridge orbitals |i>, |j>, … are given by (17, 22)

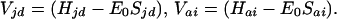2.2

The Hamiltonian matrix of the protein H_ij is set up using Slater-type atomic orbitals as in the extended Hückel method. The actual evaluation of Eq. 2.1 is carried out using the method of transition amplitudes (20, 21). This type of calculation for Ru-modified proteins and, in particular, for the His-126 derivative has been described in detail recently (10).

With the use of perturbation theory, it has been shown (8) that large portions of the protein are not participating in electron transfer and can therefore be excluded from the calculation of electronic coupling. The process of finding relevant amino acids on which the tunneling pathways are localized (“amino acid resolution” of tunneling pathways) is called “protein pruning” and has been described by Gehlen et al. (8). The pruned molecules consist only of important amino acids and are much smaller in size compared with the full protein. Further “atomic” details of the the tunneling pathways can be examined with the method of interatomic tunneling currents (9). Results of the pruning and examination of the tunneling currents in Ru–His-126–modified azurin have been reported (9).

From previous calculations by us and others, it has been shown that the major tunneling pathways in the His-126–azurin molecule are rather localized between two anti-parallel β-strands connecting donor and acceptor. One of the β-strands contains amino acids Met-121 and His-126, which are ligands to donor and acceptor ions, respectively. The other β-strand is ligated to the donor metal with Cys-112 and has a “through space” contact with the acceptor Ru complex (Fig. 1). We call these two strands Met-121 and Cys-112, respectively.

Pruning and tunneling currents allow one to identify important amino acids and to examine to what extent different atoms in these amino acids are involved in promoting the tunneling electron between donor and acceptor. Initially, such an analysis was performed on a crystal structure of a Ru–His- 126–azurin molecule. This information then was used in the dynamical studies as described below.

2.2 Protein Dynamics and Fluctuations of the Tunneling Barrier

We know that only a part of the protein is involved in tunneling, so the dynamics calculations were performed only on a particular group of atoms (determined by pruning and tunneling currents) that make up the tunneling bridge between donor and acceptor (Fig. 1). The tunneling matrix element was examined along the dynamic trajectory.

Standard canonical Nosè–Hoover dynamics (23) was performed with the cell–multipole method for nonbonding interactions. The protein dielectric constant ɛ was set to a value of 4.0. Several layers of movable water molecules were added to simulate the effect of the solvent. In addition, there was an outer water shell surrounding the simulation system. The coordinates of these water molecules were fixed to prevent long term escape of movable water from the simulation region.

All of the atoms in the molecule were frozen except those specified in Fig. 1, which were allowed to vibrate. The positions of the donor and acceptor metal ions and their nearest ligand atoms were also fixed, i.e., the total distance between donor and acceptor ions and the coupling coefficients to the nearest bridge atoms (Eq. 2.2) did not vary in the dynamics simulation.

It is clear that the frozen atoms in the molecule modify to some extent the low frequency vibrational patterns of the flexible bridge. The vibration of the whole molecule can only increase the amplitudes of low frequency fluctuations of the bridge (this increase indeed was observed in the calculation). To most clearly demonstrate the principal effect, and in particular the effect of high frequency modes of the bridge, we report here only results for the dynamics of the atoms that are directly involved in tunneling.

In the calculations, the ESFF force field (23) that allows inclusion of metal ions (Cu⁺ and Ru⁺³) in the calculations was used. The ESFF results were tested by comparing calculations using both CFF91 and ESFF on a protein model with metal ions removed. We have found that all qualitative results are the same for both force fields although details of the matrix element fluctuations are slightly different. There were no qualitative changes when ɛ varied in the range 1–4. The time step of the calculations was 0.25 fs. The system was equilibrated first, and then the dynamic trajectory was generated.

A remark is necessary on the applicability of the classical dynamics simulation of the fluctuations of high frequency modes, such as CC, CH, CN, and CO bonds, that clearly have a quantum character. As will be shown in the next section, to evaluate dynamic effects of fluctuations, one needs to calculate the correlation function of the tunneling matrix element. The Fourier harmonics of the correlation function, which are important for the dynamics of electron transfer, depend only on the frequencies of the vibrational modes. These frequencies are the same in both quantum and classical mechanics. Thus, the relevant time scale of fluctuations (the spectrum of fluctuations) of the tunneling matrix element can be obtained by classical simulation of the protein dynamics. Essentially the same idea was used in treating quantum mode contributions into the reorganization energy of electron transfer reactions in proteins (24, 25).

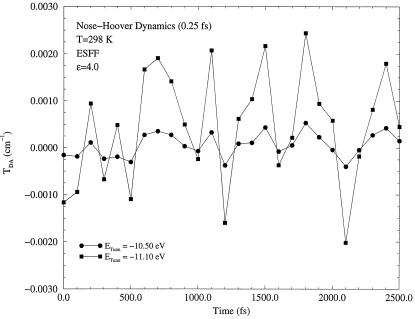
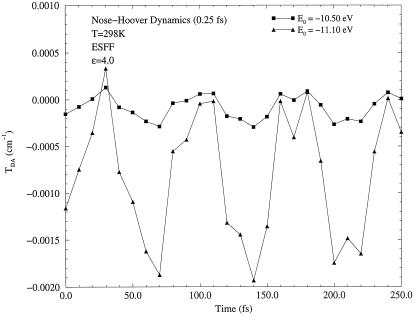
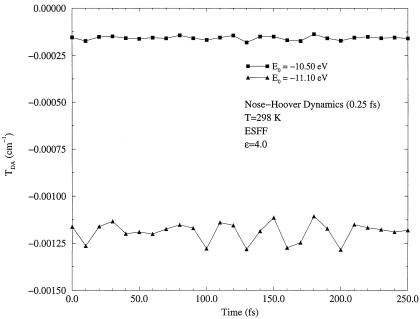
In Figs. 2, 3, 4, results of the dynamics calculations are shown. Fig. 2 presents a long term dynamics simulation, in which all amino acids of two β-strands relevant to electron transfer were allowed to move. To examine the shortest time scale of fluctuations, a short term dynamics was performed on the Gly-123 (C_α–C) bond on the Met-121 strand and on the Phe-110 (C_α–N) bond on the Cys-112 strand. These four atoms lie approximately the same distance from the donor (11.5–12.8 Å) and acceptor (13.0–14.5 Å) ions. Furthermore, these particular amino acids are well within hydrogen bonding distances (≃1.8 Å) to each other. These two strands were found previously to carry different amounts of tunneling current (9).

Figure 2.

Long term dynamics of matrix element fluctuations. The part of the molecule shown in dark in Fig. 1 was allowed to move together with surrounding water molecules (not shown in Fig. 1). The Cys-112 and Met-121 sulfur atoms, as well as the His-126 nitrogen atom, were held fixed in the dynamics simulation. Two different tunneling energies were used in the calculation. One (E₀ = −11.10 eV) is close to a gap edge, and the other (E₀ = −10.50 eV) is close to the middle of the gap. The gap in this model is located approximately between −11.7 and −9.6 eV.

Figure 3.

Matrix element fluctuations in short term dynamics of the Phe-110 (C_α–N) bond for two different tunneling energies, E₀ = −11.10 eV and E₀ = −10.50 eV.

Figure 4.

Matrix element fluctuations in short term dynamics of the Gly-123 (C_α–C) bond for two different tunneling energies, E₀ = −11.10 eV and E₀ = −10.50 eV.

As one can see from Figs. 2, 3, 4, the tunneling matrix element is a sensitive function of the configuration of the protein matrix. Fluctuations of the matrix element reflect variations of the barrier through which tunneling occurs at slightly different configurations of the protein. Typical thermal fluctuations of the protein structure are seen to be sufficient to cause significant fluctuations of the tunneling matrix element. The matrix element responds differently to motion of different parts of the protein, as shown in Figs. 3 and 4. This is related clearly to the probability that the tunneling electron will visit a given part of the protein as it makes a tunneling jump from donor to acceptor (9).

Two major conclusions can be drawn from the numerical results presented above. First, the fluctuations of the matrix element are sufficiently big, so when a comparison with experimental data is made, the averaging that reflects these fluctuations has to be included in the expression for the rate of electron transfer (5),

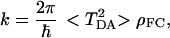2.3

where ρ_FC is the Franck–Condon density, and < T_DA² > is the averaged square of the transfer matrix element over all possible thermal fluctuations of the protein structure.

The second conclusion is that the fluctuations are in general sufficiently fast. The time scale τ_b on which variations of matrix element can be as large as 100% or even greater is ∼10 fs, as seen from Figs. 3 and 4. The corresponding energy quantum ℏ(τ_b)⁻¹ is ∼1000 cm⁻¹. As will be shown in the next section, such fast fluctuations result in energy exchange between a tunneling electron and vibrational modes of the medium in which tunneling occurs. The latter effect introduces a new important aspect into theory of long distance electron transfer reactions that results in a modification of the conventional expression (Eq. 2.3) for the rate.

3.0 Theoretical Model of Electron Tunneling in Fluctuating Medium

To account for thermal fluctuations of the bridge in long distance electron transfer reactions and for sensitivity of the tunneling matrix element to such fluctuations (i.e., the breakdown of the Condon approximation), a generalization of the Marcus model is required. Such a generalization is the subject of this section. In earlier literature, there were discussions of various aspects related to the breakdown of the Condon approximation and issues similar to those considered below, in particular in refs. 26–31.

3.1 Hamiltonian

The simplest treatment of electron transfer is obtained within a harmonic model of the medium. In this model, two states, donor and acceptor, are coupled to each other and to a harmonic bath that describes collective modes of polarization fluctuations of the medium surrounding the reaction complex. The Hamiltonian of this model (which sometimes is called the spin–boson Hamiltonian) is written in the form:

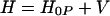3.1

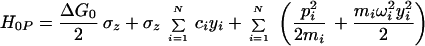3.2

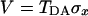3.3

where T_DA is the electronic matrix element coupling the reactant state |D〉 and the product state, |A〉, y_iand p_iare the coordinates and conjugated moment, respectively, referring to nuclear motions of the medium, and ΔG₀ is the driving force of the reaction. The symbols σ_z and σ_x are the Pauli operators (|A><A| − |D><D|) and (|D><A| + |A><D|), respectively, in a two-state (|D〉 and |A〉) representation.

Coordinates y_i describe “normal modes” of the solvent polarization and vibrations of the ligands of donor and acceptor ions. The connection of the model Hamiltonian to a real system is made by specifying the spectral density of the harmonic bath J(ω). The final result for the rate can always be expressed in terms of J(ω), which, in turn, can be expressed in terms of the longitudinal dielectric function of the solvent and parameters of the inner part of the reaction complex by well established formulas (32).

The nonadiabatic reaction corresponds to a weak electronic coupling T_DA in Eq. 3.3. In this case, the rate can be obtained using the Golden Rule or the equivalent expression in terms of the correlation function of electronic coupling V:

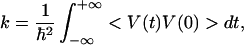3.4

where V(t) is the interaction representation of V and the averaging < … > is over a thermal distribution in the initial electronic state. A simple calculation (see, e.g., ref. 32) results in a well known quantum expression for the rate of nonadiabatic electron transfer reaction. Marcus theory is recovered as the classical limit of that expression.

In the above formulation of the conventional electron transfer model, two points are of particular importance for further discussion. First, in the above model, all vibrational modes y_i change their equilibrium positions as the electron jumps from donor to acceptor (otherwise a mode does not contribute to the reorganization energy and can be excluded from the model). The second point is that the electronic coupling T_DA is independent of the coordinates of the medium.

As calculations of the previous section show, the second assumption of the independence of electronic coupling of the system coordinates, namely the Condon approximation, is not necessarily valid for long distance electron transfer. Indeed, it is quite obvious that, in principle, thermal fluctuations of the bridge can result in fluctuations of the tunneling barrier and hence in variations of the electronic coupling. To account for this effect, the electronic coupling T_DA in the model should be made a function of coordinates of the bridge modes. The bridge modes, however, do not necessarily participate in polarization fluctuations or change their equilibrium positions upon electron transfer, in contrast to the modes in the standard model (Eqs. 3.1–3.3).

In long distance tunneling, electronic coupling is due to superexchange. The simplest expression of superexchange coupling is the McConnell product of the form (33, 34):

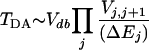3.5

where V_j,j+1 are the couplings between directly overlapping atomic orbitals of neighboring atoms along the tunneling path, and ΔE_j is the energy difference between the tunneling energy and the energy of orbital j promoting the long distance coupling. The coupling coefficients are exponential functions of the distance between atoms, so when the atoms make vibrational motions around equilibrium positions, the couplings V_j,j+1 change.

It is quite obvious then that a reasonable generalization of the above formulation, to account for fluctuations of the coupling coefficients V_j,j+1, is to write T_DA in the form:

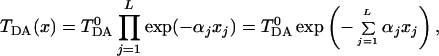3.6

where x_jare the deviations from equilibrium of the atomic coordinates of the bridge, α_j are some constants characterizing the strength of the coupling to a particular bridge mode j, and T_DA⁰ is the tunneling matrix element corresponding to the equilibrium configuration of the bridge. We assume that the electron makes a total of L virtual jumps between donor and acceptor. In general, L is proportional to the tunneling distance [or the length of a tunneling path (34)]. We further assume that coordinates x_i are harmonic oscillators [elsewhere (35) we show how to generalize the treatment to Morse oscillators]. Then, the new Hamiltonian of long distance electron transfer reactions takes the form:

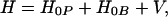3.7

where H_0P is the Hamiltonian of polarization modes and ligands that change equilibrium upon electron transfer; H_0B is the Hamiltonian of the bridge modes, which do not change their equilibrium position,

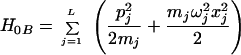3.8

and the coupling is

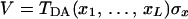3.9

with T_DA(x) given by Eq. 3.6.

3.2 Rate of Long Distance Inelastic Tunneling

To find the rate, one again can use the correlation function formalism (Eq. 3.4). We note that Eq. 3.5 does not involve any assumptions (such as the Condon approximation) in the functional form of the coupling V. Now V has an additional dependence on the bridge coordinates x_i. The group of bridge oscillators is assumed to be independent of other modes in the system, so the correlation function expression is factorized and can be written in the form:

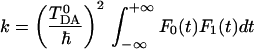3.10

where F₀(t) is the correlation function corresponding to the conventional electron transfer problem with constant coupling T_DA⁰, and F₁ is an additional correlation function of the bridge modes:

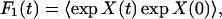3.11

where

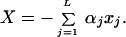3.12

Both F₀ and F₁ are easy to calculate using, e.g., the cumulant method (36). The full quantum expression for F₀ is well known (see, e.g., refs. 24, 25, 37). Its classical limit (ℏω_i/k_BT<<1 for all i in H_0P) has the form

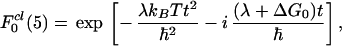3.13

where λ is the reorganization energy, and T is the temperature of the system. The rate constant corresponding to F₀^cl is given by the familiar expression (5)

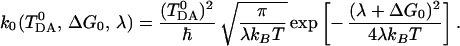3.14

For F₁(t), one obtains

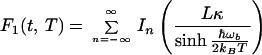3.15

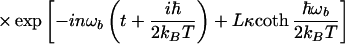where I_n(z) is the modified Bessel function, and all frequencies of the bridge were treated to be the same and equal to ω_b. A new constant κ was introduced, κ = ℏα²/2 mω_b. Using this correlation function and the expression for F₀^cl (Eq. 3.13 or a more general quantum expression), one obtains the following expression for the rate:

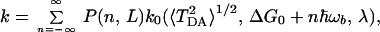3.16

where

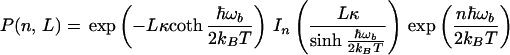3.17

and

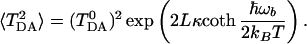3.18

The above formula has a clear physical meaning. The total rate is the sum of all multiphonon processes. The term with n = 0 corresponds to a usual electron transfer reaction, when no vibrational quanta are exchanged between the tunneling electron and the bridge. This is the usual elastic tunneling. The only consequence of fluctuations of the bridge here is that the effective tunneling matrix element is calculated for an “average” barrier, 〈T_DA²〉^1/2. This effect has been mentioned earlier (Eq. 2.3).

All other terms in the above formula describe inelastic processes, when one or more vibrational quanta are emitted or absorbed by the tunneling electron in the bridge. The factor P(n, L) is the probability to emit (positive n) or to absorb (negative n) |n| quanta of vibrational energy by the tunneling electron. For each of the multiquantum processes, the partial rate is given by the usual nonadiabatic formula (Eq. 3.14) with an averaged coupling constant and a shifted driving force. The reorganization energy remains the same.

The most significant change of the energetics of the reaction comes from the vibrational modes with high frequencies. For such modes, one can simplify the above expressions assuming ℏω_b/k_BT>>1. In this quantum limit, negative values of n can be neglected (there is no thermal excitation and, hence, no quanta to absorb), then for n ≥ 0, using the asymptotic expression of I_n(z) for small z, one obtains

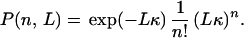3.19

The probability to emit n vibrational quanta in the bridge with L oscillators takes a Poisson form. In this limit, only terms with n ≥ 0 are present in Eq. 3.16.

Several important conclusions can be made from the above results. First, it is clear from the expressions for probabilities (Eqs. 3.17 and 3.19) that the probability of elastic tunneling quickly diminishes to 0 as the length of the tunneling path L increases. Thus, for long distance tunneling reactions, inelastic tunneling dominates over usual elastic tunneling when the distance between donor and acceptor becomes sufficiently large.

Second, because the activation energy for various inelastic reaction channels in Eq. 3.16 (with n quanta emitted) depends on n,

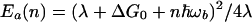3.20

for large and negative ΔG₀ (when the conventional reaction is in the inverted region) an inelastic reaction can be activationless because there will be always such an n^* (provided L is large) that, for n^*th channel, the activation energy will be close to 0. It is possible that such a phenomenon indeed occurs in proteins, such as Ru-modified azurin or cytochrome. According to recent data (38), the reaction rate in the Ru–Cyt system, for example, is surprisingly insensitive to variations of the driving force, which is consistent with the prediction of the present model.

The overall effect of multiphonon energy relaxation in the bridge (κL > 1) can be expressed in a simple formula that can be obtained by approximating P(n, L) (Eq. 3.19) by a continuous Gaussian function of n. Then, replacing the sum over n in Eq. 3.16 with an integral, one obtains:

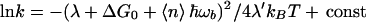3.21

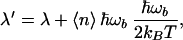3.22

where < n > = Lκ is the average number of quanta dissipated in the bridge. Thus, although the dependence of ln k on ΔG₀ is still quadratic in this approximation, as in the classic Marcus theory, the width of the parabola, λ′, can be significantly larger than that of the Marcus theory λ because one can have ℏω_b/k_BT>>1 for high frequencies in the bridge. Similar effects in principle exist for absorption channels (n < 0). However, for high frequency modes, the number of thermally excited vibrational quanta is too small to have practically significant effect.

We note that the inelastic bridge effects are qualitatively similar to quantum effects in the standard model of electron transfer discussed extensively in the literature in the past (e.g., ref. 37). Both quantum effects and inelastic effects can be incorporated within a single model (35).

The above formulas suggest that, when inelastic tunneling is contributing to the reaction, the dependence of the reaction rate on the driving force should be different for different distances of electron transfer. Also, the effective width, λ′, should be expected to be both temperature- and distance-dependent. These predictions provide an avenue for possible experimental verification of the discussed effects, for example, in a series of ΔG₀ measurements of the reaction rates in Ru-modified proteins with different distances between donor and acceptor.

There is no doubt that this effect should exist at large distances of electron tunneling. The main objective is to find a real example in which electron–bridge coupling κ is sufficiently strong. Present calculations, based on the extended Hückel model, indicate that it might be the case in Ru-modified proteins. More accurate calculations, however, would be desirable in the future to verify this conclusion.

We conclude that the dynamics of the medium in which long distance tunneling is taking place introduces a new perspective in our understanding of the mechanism of biological electron transfer worthy of further investigation.

ABBREVIATION

T_DA

transfer matrix element