Bayesian flux balance analysis applied to a skeletal muscle metabolic model

Abstract

In this article, the steady state condition for the multi-compartment models for cellular metabolism is considered. The problem is to estimate the reaction and transport fluxes, as well as the concentrations in venous blood when the stoichiometry and bound constraints for the fluxes and the concentrations are given. The problem has been addressed previously by a number of authors, and optimization based approaches as well as extreme pathway analysis have been proposed. These approaches are briefly discussed here. The main emphasis of this work is a Bayesian statistical approach to the flux balance analysis (FBA). We show how the bound constraints and optimality conditions such as maximizing the oxidative phosphorylation flux can be incorporated into the model in the Bayesian framework by proper construction of the prior densities. We propose an effective Markov Chain Monte Carlo (MCMC) scheme to explore the posterior densities, and compare the results with those obtained via the previously studied Linear Programming (LP) approach. The proposed methodology, which is applied here to a two-compartment model for skeletal muscle metabolism, can be extended to more complex models.

1 Introduction

Computational models for cellular metabolism play an important role in the quest for understanding the complex biochemical interactions between different organs, different cell types within an organ and the biochemistry within the cells. As our understanding of the functioning of the cells increase, the models become more complex and the number of parameters needed to identify them increase. The determination of a unique set of model parameters based on scarce and uncertain data is usually not possible, and the estimation of the parameters has to rely on additional information concerning the system. The model identification can thus be seen as a statistical inference problem and, in this context, a Bayesian statistical framework has turned out to be useful as it allows the incorporation of various levels of uncertain information into the model (Calvetti & Somersalo, 2006; Calvetti et al., 2006b).

In the study of the dynamic response of a metabolic system to varying conditions such as hypoxia or ischemia, it is common to assume that initially the system is at rest, corresponding to a biochemical steady state. The flux balance analysis (FBA) is used to determine the initial fluxes and consequently, a set of parameter values is often manually adjusted to satisfy the steady state. Due to the non-uniqueness of the parameter values identifying a steady state, the analysis of dynamic response based on the chosen values may depend strongly on how the values are chosen. Therefore, it is useful to understand to what extent the flux balance equations are able to identify the steady state and to what extent the steady state is stable with respect to perturbations in quantities which are assumed known. The present paper addresses this issues. The analysis is based on the Markov Chain Monte Carlo (MCMC) techniques, commonly used in statistical inference problems (Gilks et al., 1996; Kaipio & Somersalo, 2004; Liu, 2003).

In the literature it has been proposed to identify a feasible steady state by minimizing or maximizing a suitable objective function (Bonarius et al., 1997; Ramakrishna et al., 2001; Varma & Palsson, 1996; Ramakrishna et al., 2001). While such approach can usually single out a reasonable, feasible steady state, it is important to also investigate the stability of such solutions with respect to perturbations in the input parameters and to assess how representative statistically such solutions are.

The paper is organized as follows. In Section 2, we discuss the two-compartment metabolic model for skeletal muscle and the constraints that are appropriate for the fluxes. In Section 3, we review the steady state flux balance analysis from the classical optimization point of view. More specifically, we briefly describe the Linear Programming (LP) solution to FBA proposed in the literature, that will serve as a benchmark for the subsequent statistical analysis, and provides a feasible initial value for statistical simulations. In addition, we discuss the stability of the LP estimators estimators, i.e., the dependency of the result on the bound constraints and on uncertainties in the model input values. In Section 4, the statistical framework is presented, and the problem is recast in the form of Bayesian inference problem. Conclusions and comment on future work are found in Section 5. The details concerning the model are presented in Appendix A.

2 Multi-compartment models

The simplest example of the general multi-compartment models for cell metabolism is a two-compartment model consisting only of blood and lumped tissue compartments, see, e.g., Calvetti & Somersalo (2006); Calvetti et al. (2006b); Salem et al. (2004); Zhou et al. (2005). More complex models take into account the partitioning of the cells into cytosol and organelles such as mitochondria, and may differentiate between different cell types such as neurons and astrocytes in the brain metabolism models. Although in this paper we apply our Bayesian approach only to the case of a two-compartment model, the analysis can be extended to more complex models with the same structure.

2.1 Dynamic model and steady state

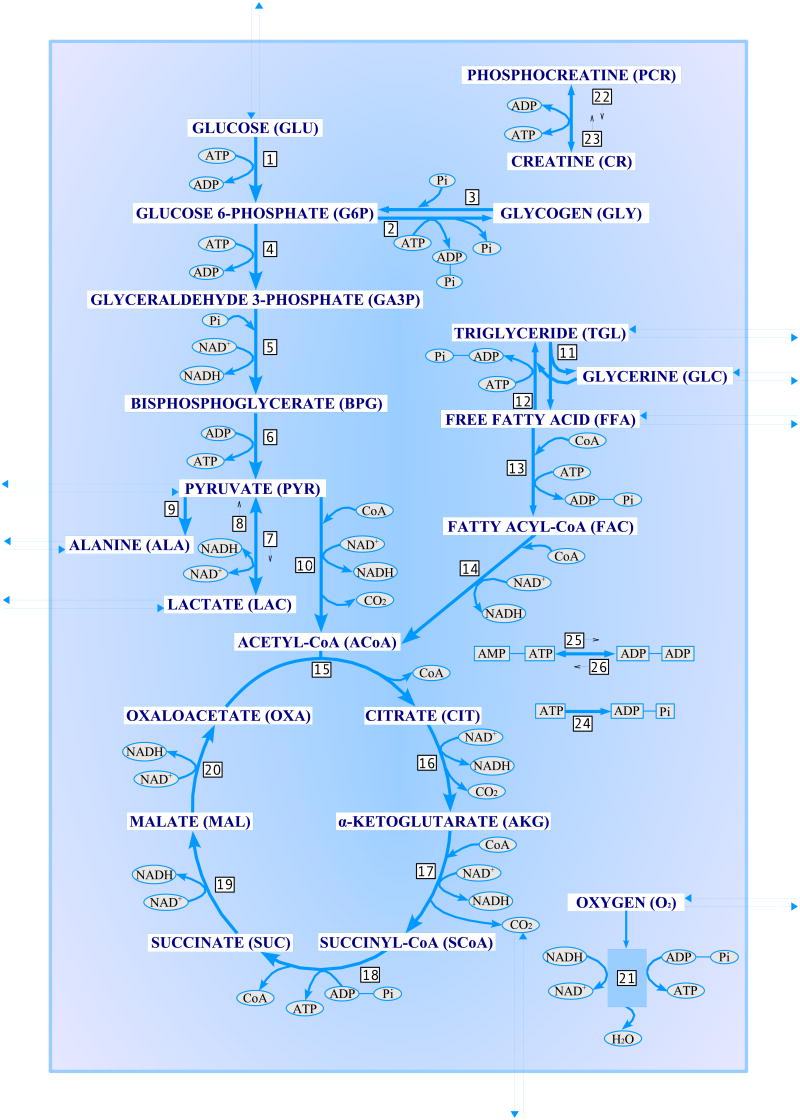
The model of metabolic system that we consider here consists of two domains, blood and a single cell type, where the cytosol and mitochondria are lumped together (see Appendix A, Figure 8). The state of the system at time t is described by vectors C_c(t) and C_b(t) that contain the concentrations of the biochemical species in the cell domain and the venous blood, respectively. As some of the species are interchanged between the compartments, their respective concentrations change. In the blood domain the concentrations change also due to convection, while in the cell domain, biochemical reactions consume or produce the metabolites and the intermediates. Thus, the dynamics of the concentrations are described by a system of differential equations of the form

Fig. 8.

A schematic diagram of the biochemical pathways in the two-compartment skeletal muscle model.

$$V_{\text{c}}\frac{{d\text{C}}_{\text{c}}}{dt}=\underset{\text{reaction}}{\underbrace{S\Phi (t)}}+\underset{\text{transport}}{\underbrace{M({\text{J}}_{\text{b}\to \text{c}}(t)-{\text{J}}_{\text{c}\to \text{b}}(t))}},$$ (1)

$$V_{\text{b}}\frac{d{\text{C}}_{\text{b}}}{dt}=\underset{\text{convection}}{\underbrace{\frac{Q(t)}{F}({\text{C}}_{\text{a},\text{tot}}(t)-{\text{C}}_{\text{b},\text{tot}}(t))}}+\underset{\text{transport}}{\underbrace{{\text{J}}_{\text{c}\to \text{b}}(t)-{\text{J}}_{\text{b}\to \text{c}}(t)}}.$$ (2)

The convection term depends on the difference of total arterial C_a,tot and venous C_b,tot concentrations of the species, where “total” means that in the oxygen and carbon dioxide concentrations, the oxy-hemoglobin, carbamino-hemoglobin and bicarbonate concentrations are taken into account in addition to the free dissolved concentrations (Dash & Bassingthwaighte, 2006; Lai et al., 2006). The factor Q(t) represents the blood flow, and F is the mixing ratio. The transport flux vectors J_c→b and J_b→c contain the non-negative transport fluxes of the species from cell to blood and blood to cell, respectively, and the matrix M describes which compounds participating in the metabolic processes in the cell domain are exchanged with the blood domain. Hence, if the jth compound in C_c is not transported to the blood domain, the corresponding row in the matrix M vanishes, otherwise the row contains a one in an appropriate place to pick the flux of the jth species. The reaction term consists of the product of a vector Φ of reaction fluxes, with each component accounting for one biochemical reaction, multiplied by the stoichiometric matrix S, whose nonzero components s_ij indicate how many units of compound i is created (s_ij > 0) or consumed (s_ij < 0) in reaction j. The coefficients V_c and V_b are the virtual volumes of the compartments, and since we represent them as diagonal matrices, we may assign different volumes to different species, e.g., to correct uneven distribution of the compounds or to take into account the hemoglobin/myoglobin concentrations.

In this study, we are interested in flux balance analysis at steady state condition, i.e., Q(t) = constant, C_a,tot = constant and dC_c/dt = 0, dC_b/dt = 0.

We write the steady state condition as the matrix equation

$$\underset{=\hspace{0.17em}A}{\underbrace{\left[\begin{array}{cccc}S& M& -M& 0\\ 0& I& -I& (Q/F)I\end{array}\right]}}\underset{=\hspace{0.17em}\text{u}}{\underbrace{\left[\begin{array}{c}\Phi \\ {\text{J}}_{\text{b}\to \text{c}}\\ {\text{J}}_{\text{c}\to \text{b}}\\ {\text{C}}_{\text{b}}\end{array}\right]}}=\underset{=\hspace{0.17em}\text{r}}{\underbrace{\left[\begin{array}{c}0\\ (Q/F){\text{C}}_{\text{a}}\end{array}\right]}},$$

or briefly,

$$A\text{u}=\text{r},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}A\in {ℝ}^{m\times n},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{u}\in {ℝ}^n,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{r}\in {ℝ}^m.$$ (3)

Note that we have dropped the subindex “total” to simplify the notation. For later reference, we partition the matrix A as

$$A=\left[\begin{array}{cccc}S& M& -M& 0\\ 0& I& -I& (Q/F)I\end{array}\right]=\left[\begin{array}{c}{A}_{\text{c}}\\ A_{\text{b}}\end{array}\right]\begin{array}{l}\in {ℝ}^{k\times n}\\ \in {ℝ}^{(m-k)\times n}\end{array}.$$ (4)

The steady state flux balance analysis is concerned with estimating the vector u when the vector r is known either exactly or approximately. Although the problem can be stated formally as a linear algebraic equation, the matrix does not have full rank and the entries of the solution need to obey a set of constraints which will be discussed later.

2.2 Parametric model: Michaelis–Menten formulas

The net transport fluxes between the blood and tissue domains are related to the substrate uptake that can be estimated from blood concentrations, for which some estimates have been presented in the literature, see, e.g., Calvetti et al. (2006a) and references therein. Reaction fluxes, on the other hand, are harder to estimate and information concerning them is often based on in silico experiments.

The reaction fluxes in our model are expressed in Michaelis–Menten form. If Φ represents the reaction flux of a single substrate facilitated reaction,

$$A+E\to B+\stackrel{\sim }{E},$$

where A, B are metabolites and E, $\stackrel{\sim }{E}$ are the facilitators and assuming that the reaction coefficients are unity for simplicity, we express the flux in the form

$$\Phi =V_{\text{max}}\frac{P}{\mu +P}\frac{C_A}{K+C_A},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}P=\frac{C_E}{C_{\stackrel{\sim }{E}}},$$ (5)

where V_max is the maximum reaction velocity, the C's are the corresponding concentrations and μ and K are reaction specific affinity coefficients. Similarly, for a facilitated bi-substrate reaction

$$A_1+A_2+E\to B_1+B_2+\stackrel{\sim }{E},$$

we use the modified Michaelis-Menten form

$$\Phi =\hspace{0.17em}{V}_{\text{max}}\frac{P}{\mu +P}\frac{C_{A_1}{C}_{A_2}}{K+C_{A_1}{C}_{A_2}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}P=\frac{C_E}{C_{\stackrel{\sim }{E}}}.$$

If the reaction is not facilitated, the factor P/(μ + P) is set to unity. The transport fluxes can be modeled similarly. The rate of a carrier facilitated transport of substrate A from compartment x to compartment y is expressed on the form

$$J_{A,x\to y}=T\frac{C_{A,x}}{M+C_{A,x}},$$ (6)

and for passive, diffusive transport, the rate is expressed as

$$J_{A,x\to y}=\gamma C_{A,x}.$$

These approximations were used earlier in the dynamic context, see Calvetti & Somersalo (2006); Calvetti et al. (2006b); Salem et al. (2004); Zhou et al. (2005). For a justification of such approximations, we refer to the textbooks Keener & Sneyd (1998); Marangoni (2003). If we stack all the model parameters V_max, K, μ, T, M and γ in a long vector that is denoted by θ, we can express the mapping F from these parameters to the flux vectors as

$$\text{u}=\text{F}\left(\theta ,\text{C}\right),$$ (7)

where C is a vector of the cell and blood concentrations of all the species.

2.3 Constraints

The components of the vector u need to satisfy a set of constraints. The most natural constraint coming from the assumptions in our model formulation, that the fluxes and concentrations are non-negative, u ≥ 0, already complicates the flux balance analysis, since it may exclude the pseudo-inverse solution of (3). Furthermore, since nonnegativity alone is not enough to specify a meaningful solution as it does not exclude the trivial solution where C_b = C_a and all fluxes vanish, we need to impose strictly positive lower bounds for some vital fluxes. Also, the reaction fluxes have natural upper bounds, which can be seen in the expressions of Michaelis–Menten forms: equations (5) and (6) imply that Φ ≤ V_max and J_A,x→y ≤ T, respectively. We can express the bound constraints in vectorial form as u_min ≤ u ≤ u_max. We remark that finding physiologically meaningful bounds is not a trivial issue, and that too strict and biasing bounds may result in misleading results.

In addition to the bound constraints described above, in general additional constraints on the fluxes arise from the requirement that the metabolic system respects the Second Law of Thermodynamics (Beard et al (2002); Nelson & Cox (2005); Siesjö (1978)). Checking the thermodynamic constraints requires that estimates of the concentrations of the substrates participating in reversible reactions are available. Since these concentrations are not estimated in the present work, we will not consider the thermodynamic constraints.

2.4 Optimality

The steady state condition (3) together with bound constraints is, in general, not enough to uniquely identify a steady state, and additional conditions are needed to single out the physiologically feasible steady state. In the literature, different criteria for optimality have been proposed to identify particular steady states (see, e.g., Bonarius et al. (1997); Ramakrishna et al. (2001); Varma & Palsson (1996)). In this article, following the optimality condition proposed by Ramakrishna et al. (2001), we assume that the metabolic chain is driven by the energetic efficiency principle: the system prefers a steady state where the mitochondriac ATP production via oxidative phosphorylation is at a maximum. Thus, we may pose the steady state problem as follows: find the solution u that satisfies the steady state condition (3), obeys a priori constraints and maximizes the reaction flux of the oxidative phosphorylation reaction.

3 Constrained Optimization Approach

In this section, we study the flux balance analysis from the classical optimization point of view, considering the optimality condition introduced in Section 2.4. If u_j is the reaction flux of oxidative phosphorylation Φ₂₁, (see Appendix A, Table 2), the objective function h to be maximized is

Table 2.

Biochemical reactions. The non-integer stoichiometry of oxidative phosphorylation corrects the effect of lumping together the concentrations in cytosol and mitochondria.

Reaction	Stoichiometry
1. Glucose Utilization	GLU+ATP → G6P+ADP
2. Glycogen synthesis	G6P+ATP → GLY + ADP + 2 Pi
3. Glycogen utilization	GLY + Pi → G6P
4. Glucose 6-phosphate breakdown	G6P+ATP→2 GA3P+ADP
5. Glyceraldehyde 3-phosphate breakdown	GA3P+Pi+NAD+ →BPG + NADH
6. Pyruvate production	BPG + 2 ADP → PYR + 2 ATP
7. Pyruvate reduction	PYR + NADH → LAC + NAD+
8. Lactate oxidation	LAC + NAD+ → PYR + NADH
9. Alanine production	PYR→ ALA
10. Pyruvate oxidation	PYR + CoA + NAD+ →ACoA + NADH +CO2
11. Lipolysis	TGL→GLC + 3 FFA
12. Triglyceride synthesis	GLC+3 FFA + 3 ATP→ TGL+3 ADP + 3 Pi
13. Free fatty acid utilization	FFA + CoA + 2 ATP→FAC +2 ADP+2 Pi
14. Fatty Acyl-CoA Oxidation	FAC + 7 CoA + (35/3) NAD+ → 8 ACoA + (35/3) NADH
15. Citrate production	ACoA + OXA → CIT + CoA
16. α-ketoglutarate production	CIT + NAD+ → AKG + NADH + CO2
17. Succinyl-CoA production	AKG + CoA + NAD+ → SCoA + NADH + CO2
18. Succinate production	SCoA + ADP + Pi → SUC + CoA + ATP
19. Malate production	SUC + (2/3) NAD+ →MAL + (2/3) NADH
20. Oxaloacetate production	MAL + NAD+ → OXA + NADH
21. Oxidative phosphorylation	O2 + 5.64 ADP + 5.64 Pi + 1.88 NADH → 2 H2O + 5.64 ATP + 1.88 NAD+
22. Phosphocreatine breakdown	PCR + ADP→CR+ATP
23. Phosphocreatine synthesis	CR + ATP→ PCR + ADP
24. ATP hydrolysis	ATP → ADP+Pi
25. AMP utilization	AMP+ATP→ADP+ADP
26. AMP production	ADP+ADP→ AMP+ATP

$$\begin{array}{ccc}h(\text{u})={\text{e}}_j^{\text{T}}\text{u},& {\text{e}}_j={[0\dots 0\underset{j}{\underbrace{1}}0\dots 0]}^{\text{T}},& j=21,\end{array}$$ (8)

and we seek to maximize the objective function h(u) among those vectors u satisfying

$$\begin{array}{cc}A\text{u}=\text{r},& {\text{u}}_{\text{min}}\le \text{u}\le {\text{u}}_{\text{max}}.\end{array}$$ (9)

The solution of this linear constrained optimization problem can be computed by Linear Programming (LP), a methodology that is briefly reviewed in the following section.

3.1 Linear Programming Solution

The Linear Programming problem can be formulated in its standard form as follows. Given $B\in {ℝ}^{m\times n}$, $\text{z}\in {ℝ}^m$, $\text{c}\in {ℝ}^n$, find the vector $\text{x}\in {ℝ}^n$, which maximizes c^Tx subject to constraints

$$B\text{x}\le \text{z},$$ (10)

$$\text{x}\ge 0,$$

see, e.g., Vanderbei (1996). The steady state flux estimation problem with the objective function (8) and the constraints (9) can be expressed as an LP problem of this form by using standard techniques. The details of the transformation to standard form can be found in the literature (see, e.g., Vanderbei (1996)) and therefore are omitted here. Numerous algorithms for the solution of the LP problems have been proposed in the literature, including interior point methods and the classical simplex algorithm. The flux balance problem has been solved by linear programming, see, e.g., Kauffman et al. (2003). In the present work, the LP solution will be used as a benchmark to which we compare to the results of the Bayesian FBA proposed in this article. In general, the data defining the bounds in LP problems are assumed to be exact. This is not necessarily the case in the FBA application that we consider here, in view of the natural fluctuations of the measurements over a population and the limitations of the collection and measurements procedure. Therefore, we will start with analyzing the stability of the LP solution with respect to uncertainties in the data, in our application consisting of the arterial concentration values. This sensitivity analysis will be a precursor to more extensive FBA that follows.

The sensitivity analysis of the LP solution contains two aspects: the sensitivity of the optimal solution to perturbations in the right-hand side of (10), and the possibility of having several optimal solutions without changing the value of the objective function. In this work, we are mostly interested in the former question.

Before computed examples, we conclude this section by mentioning that the LP approach is closely related to the extreme pathway analysis. In the past decade, a significant amount of research has been done to understand and describe a metabolic system using extreme pathway analysis, see Papin et al. (2002b, 2003, 2004); Schilling et al. (2000); Schilling & Palsson (1998). Similar to the flux balance analysis, the extreme pathways analysis imposes a steady state condition, but instead of a single optimal solution, it produces a set of feasible solutions in finite dimensional space. This is done by finding a system of basis pathways, called extreme pathways, that is unique for the metabolic network under consideration and which fully describes its properties. All possible steady-state flux solutions can then be represented as nonnegative linear combinations of these extreme pathways. Further analysis using a number of tools, such as SVD and α-spectrum analyses, is performed, see Price et al. (2003a); Wiback et al. (2003) for details.

A number of metabolic models, e.g., Haemophilus influenzae (Schilling & Palsson, 2000), the human red blood cell (Wiback & Palsson, 2002), Escherichia coli (Wiback et al., 2004), have been investigated with extreme pathway analysis. Since the number of extreme pathways can be very large for large-scale metabolic network systems (Papin et al., 2002a, 2003), a set of improved tools was developed to solve these problems (Barrett et al., 2006; Price et al., 2003b; Wiback et al., 2003).

3.2 Computed examples

In this section, we solve the steady state flux estimation problem for the skeletal muscle model (1)-(2) using the LP approach with the objective function (8) under the constraints (9). Note that, in general, several simultaneous objective functions can be considered, see, e.g., Vo et al. (2004).

To demonstrate the sensitivity of the LP solution to the upper and lower bounds, we calculate the solution with two different sets of lower bounds u_min and upper bounds u_max. The values of bound vectors are listed in Appendix B, Table 4. Figure 1 displays these two sets of bounds and the corresponding LP solutions. A more detailed discussion of the bounds, and in particular, their relation to bounds concerning the concentrations of the metabolites as well as model parameters will be discussed later in this work. At this stage, the bounds are applied without questioning how they were obtained. Figure 1 clearly shows that the LP solution depends on the boundary constraints. We remark that the two solutions obtained by using the two different sets of bounds yield different values for the objective function; more specifically, h(u) = 3.9377 for the wider bounds and h(u) = 1.2903 for the tighter bounds.

Table 4.

Bounds for the components u_j of the solution vector u.

	Tight bounds		Wide bounds			Tight bounds		Wide bounds
j	lower values	upper values	lower values	upper values	j	lower values	upper values	lower values	upper values
1	0.114	0.239	0.024	0.640	28	0.012	0.028	0.005	0.163
2	0.108	0.345	0.028	0.924	29	0.402	0.584	0.142	1.961
3	0.111	0.290	0.062	0.944	30	0.004	0.011	0.002	0.059
4	0.098	0.261	0.024	0.847	31	1.037	2.890	0.463	15.440
5	0.156	0.650	0.044	2.557	32	0.037	0.150	0.021	0.683
6	0.177	0.505	0.042	1.601	33	0.417	1.057	0.177	6.041
7	0.147	0.305	0.044	0.908	34	16.182	36.760	6.391	223.867
8	0.021	0.105	0.005	0.313	35	5.339	10.267	1.898	65.720
9	0.022	0.057	0.012	0.135	36	0.139	0.346	0.059	0.950
10	0.042	0.214	0.012	0.679	37	0.012	0.040	0.006	0.200
11	0.058	0.157	0.031	0.385	38	0.591	0.784	0.208	2.563
12	0.046	0.206	0.017	0.753	39	0.020	0.093	0.012	0.414
13	0.014	0.065	0.005	0.271	40	0.913	3.168	0.468	15.336
14	0.013	0.065	0.004	0.240	41	0.034	0.157	0.020	0.691
15	0.133	0.846	0.093	3.488	42	0.305	1.173	0.162	5.556
16	0.201	0.627	0.037	2.275	43	13.293	49.600	7.016	238.170
17	0.153	0.759	0.046	2.952	44	3.922	9.779	1.695	53.412
18	0.296	0.437	0.053	2.627	45	4.844	4.930	1.664	19.069
19	0.192	0.630	0.041	2.112	46	0.064	0.077	0.024	0.274
20	0.189	0.660	0.040	2.271	47	0.805	0.864	0.289	3.264
21	0.707	1.464	0.108	5.667	48	0.207	0.232	0.075	0.855
22	11.674	32.281	2.558	82.562	49	0.904	1.018	0.339	3.759
23	11.068	37.744	3.058	85.473	50	0.039	0.095	0.022	0.250
24	5.131	7.481	2.040	21.063	51	0.484	0.705	0.200	2.300
25	6.554	14.031	1.460	39.760	52	20.990	28.660	8.363	94.716
26	6.870	12.806	1.148	38.816	53	7.921	8.712	2.810	9.603
27	0.319	0.549	0.139	1.387

Fig. 1.

Two sets of the bounds and the corresponding solutions. The dotted curve is the LP solution for the wider bounds, the solid line is the LP solution for the tighter bounds. The plots are in logarithmic scale.

In addition to the bounds for the entries of the solution vector, the LP solution depends on the input values, i.e., on the concentrations of the biochemical compounds in arterial blood, whose values, in turn, may be contaminated by measurement noise and fluctuate over a population. We model this uncertainties in the input by replacing the equation (3) by r = Au + e, where $\text{e}\in {ℝ}^m$ is a noise vector. In order for (3) to hold in the mean value sense, we may assume that e is a zero mean random vector. In our numerical experiments, we shall assume that e is normally distributed with mutually independent components, e ∼ N(0, Γ), with covariance matrix $\Gamma =\text{diag}({\sigma }_1^2,{\sigma }_2^2,\mathrm{\dots },{\sigma }_m^2)$, where the diagonal element ${\sigma }_j^2$ is the variance of the jth component. Observe that the k first equations are related to the steady state condition in the cell domain. If we assume that the only uncertainties are in the input arterial concentrations, we must choose ${\sigma }_1^2=\mathrm{\dots }={\sigma }_k^2=0$, hence the steady state condition A_cu = 0 in the cell domain is strictly enforced.

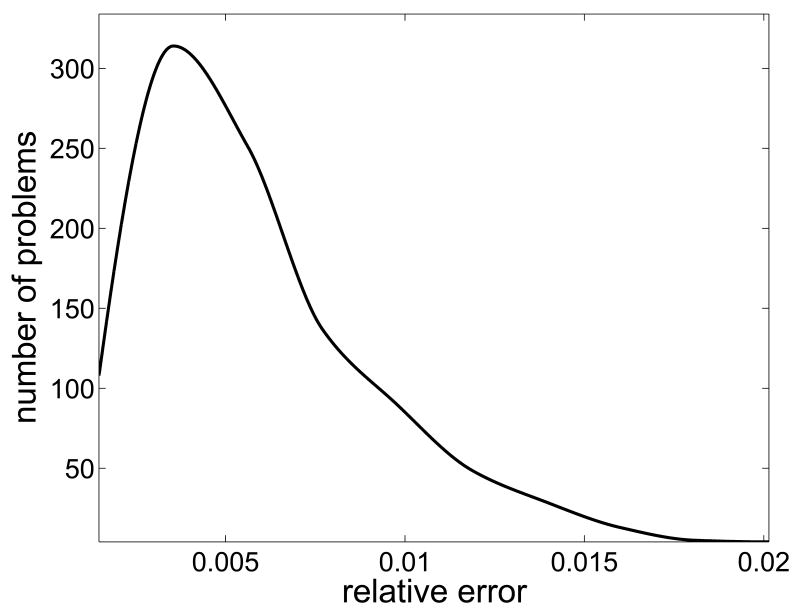
To numerically investigate the stability of the LP solution, we generated a sample of 1000 normally distributed random realizations of the arterial values around the known mean value r_b,mean = (Q/F)C_a with a given variance, and calculate the relative discrepancy of the corresponding LP solutions,

$$\begin{array}{cc}{d}_i=\frac{\Vert {\text{u}}_i-{\text{u}}_0\Vert }{\Vert {\text{u}}_0\Vert },& 1\le \text{i}\le 1000,\end{array}$$

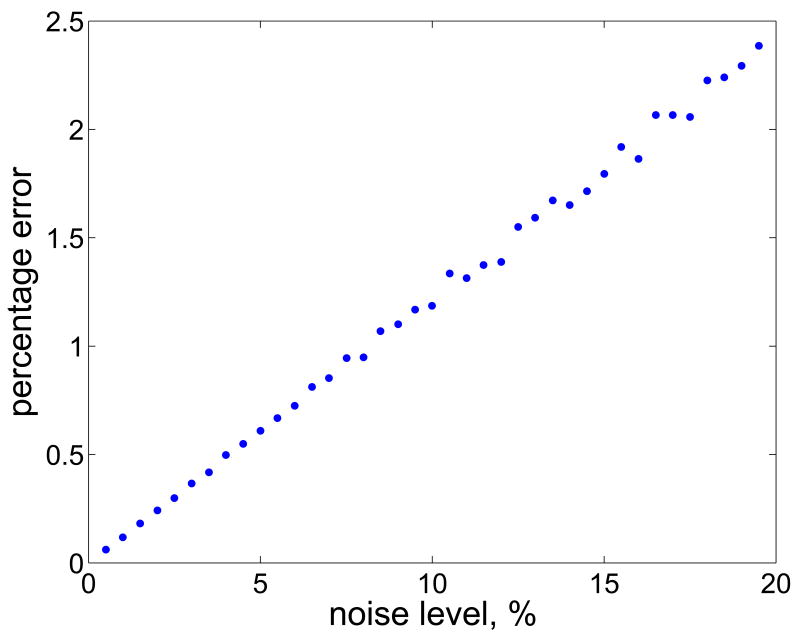
where u₀ is the LP solution corresponding to the mean value r_b,mean, and u_i is the LP solution corresponding to the ith realization of the noise vector. The left panel of Figure 2 shows the histogram of the relative discrepancies d_i when the standard deviation σ_j of the noise is 5% of the corresponding component of the noiseless vector r_b,mean. In the calculation of the LP solutions, which was done by using the built-in Matlab function linprog, we used the wider bound constraints. For each noise level ranging from 0.5% to 20% with the step 0.5%, we computed the mean of the discrepancies, as displayed in the right panel of Figure 2. Clearly the discrepancy of the LP solutions increases in a linearlike fashion as a function of the noise level.

Fig. 2.

Histogram of the discrepancies d_i with 5% noise level (left), and the dependency of the mean discrepancy on the noise level of the arterial concentration values (right).

In some cases it was not possible for the LP solver to find a feasible solution within the given bounds, and the frequency of non-feasible problems increased with the noise level. The tighter the bound constraints are, the more easily the problem fails to have a solution. For example, when using the tighter bounds of Table 4, with 5% noise level in the right-hand side the LP solver could not find a feasible solution in 83% of the cases.

4 Bayesian approach

In this section, we propose a Bayesian alternative for the constrained optimization based FBA. The advantage of a statistical framework is that it is naturally suited for modelling the uncertainties and variabilities inherent to a metabolic steady-state.

We begin by giving a brief overview of the basic principles of Bayesian parameter estimation.

4.1 General framework

In the Bayesian framework, we model uncertainties by random variables and encode the available information in terms of probability distributions. If $\text{x}\in {ℝ}^n$ and $\text{y}\in {ℝ}^m$ denote two multivariate random variables whose joint probability density is denoted by π(x, y), their marginal probability densities are related to the joint density by

$$\begin{array}{cc}\pi (\text{x})=\int \pi (\text{x},\text{y})d\text{y},& \pi (\text{y})=\int \pi (\text{x},\text{y})d\text{x}.\end{array}$$

The marginal densities express the probability distributions of the values of x and y, respectively, provided that no information about the other random variable is available. If y is a directly observable variable and x is the variable of primary interest, we call the marginal density of x the prior density and denote it by π(x) = π_prior(x). The prior density expresses the belief of the value of x prior to any observations of y.

The conditional probability densities π(x | y) and π(y | x) are defined via the formula

$$\pi \left(\text{x},\text{y}\right)=\pi \left(\text{y}|\text{x}\right)\pi \left(\text{x}\right)=\pi \left(\text{x}|\text{y}\right)\pi \left(\text{y}\right).$$

The conditional density expresses the distribution of one variable provided that the other takes on a given value. The above formula yields immediately the Bayes formula,

$$\pi (\text{x}|\text{y})=\frac{\pi (\text{x})\pi (\text{y}|\text{x})}{\pi (\text{y})}.$$ (11)

In statistical parameter estimation, this formula is fundamental, because it expresses the probability density of the variable x of primary interest given the observation of y and all possible prior information concerning x. The conditional density (11) is called the posterior density.

Since the posterior density is a probability density over a space whose dimension equals the number of components in the unknown x it cannot be immediately visualized. Instead, it is used for computing statistical estimates. One of the most commonly used estimates is the posterior mean,

$${\text{x}}_{\text{pm}}=\int \text{x}\pi (\text{x}|\text{y})d\text{x},$$

which is the expectation of x with respect to the posterior probability density. The posterior mean is optimal in the sense that it is the estimator with the minimum estimation error variance.

The computation of the posterior mean from the posterior density requires an integration which, in high dimensional space, cannot be done by numerical quadratures. The most popular method for computing this integral and more generally, to explore the posterior probability density, is to use Markov Chain Monte Carlo techniques. The basic idea is to generate a Markov chain whose realizations are asymptotically distributed according to the posterior probability density. This is achieved by defining a rule q of random draw: given the current point x_j, draw x_j+1 from the distribution $\text{t}\mapsto q(\text{t}|{\text{x}}_j)$. Repeating the random draw with some initial point x₀, one generates a large sample, S = {x₀, x₁, …, x_N}. If the drawing rule q is judiciously constructed, this ensemble is distributed asymptotically, as N → ∞, according to π(x | y). The most commonly used MCMC strategies are the variants of the Metropolis-Hastings scheme and Gibbs sampler. In this work we use the latter one. To describe the drawing strategy, we need only to specify the move x_j → x_j+1. Denoting the posterior density by π_post(x) = π(x | y), the Gibbs sampler is described as follows. Given x_j = (x_j,1, x_j,2, …, x_{j,n −1}, x_j,n),

$$\begin{array}{l}\text{draw}\hspace{0.17em}{x}_{j+1,1}\hspace{0.17em}\text{from}\hspace{0.17em}t\mapsto {\pi }_{\text{post}}\hspace{0.17em}(t,x_{j,2},\dots ,x_{j,n-1},x_{j,n}),\\ \text{draw}\hspace{0.17em}{x}_{j+1,2}\hspace{0.17em}\text{from}\hspace{0.17em}t\mapsto {\pi }_{\text{post}}\hspace{0.17em}(x_{j+1,1},t,\dots ,x_{j,n-1},x_{j,n}),\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}⋮\\ \text{draw}\hspace{0.17em}{x}_{j+1,n-1}\hspace{0.17em}\text{from}\hspace{0.17em}t\mapsto {\pi }_{\text{post}}\hspace{0.17em}(x_{j+1,1},x_{j+1,2},\dots ,t,x_{j,n}),\\ \text{draw}\hspace{0.17em}{x}_{j+1,n}\hspace{0.17em}\text{from}\hspace{0.17em}t\mapsto {\pi }_{\text{post}}\hspace{0.17em}(x_{j+1,1},x_{j+1,2},\dots ,x_{j+1,n-1},t).\end{array}$$

In other words, we update one component at a time, conditioning on the old, or the currently updated values of the remaining components. Details of the updating scheme are discussed later.

When basing estimates on an MCMC chain, it is important to assess whether the chain is long enough to guarantee convergence of computed estimates.

Sample based estimates of the type

$$\text{E}\left\{g(\text{x})\right\}=\int g(\text{x}){\pi }_{\text{post}}\hspace{0.17em}(\text{x})d\text{x}\approx \frac{1}{N}\sum _{j=1}^{N}g{(\text{x}}_j),$$

typically rely on convergence results derived from the Law of Large Numbers or from the Central Limit Theorem. The latter one asserts that if the samples x_j are independent and identically distributed, the convergence rate is $\sim 1/\sqrt{N}$. MCMC methods, however, do not necessarily yield independent realizations. Therefore, a complete analysis of the chain requires that we also estimate the correlation length. If the correlation length of the sampled values g(x_j) is k, every kth sample is approximately independent and we may assume that the rate of convergence is $\sim 1/\sqrt{N/k}$. For large k, the rate may be painfully slow; a slow convergence is seen also by looking at the sample history: rather than resembling a realization of white noise, the sample value keeps drifting.

To obtain an estimate for the correlation length, denote by g_c(x_j) the centered sample point,

$$g_{\text{c}}({\text{x}}_j)=g({\text{x}}_j)-\frac{1}{N}\sum _{i=1}^{N}g({\text{x}}_i),$$

and define the normalized autocovariance of the sample by the formula

$$\begin{array}{cc}{\gamma }_{\ell }^2=\frac{1}{\Vert g_{\text{c}}{\Vert }^2(N-\ell )}\sum _{j=1}^{N-\ell }{g}_{\text{c}}({\text{x}}_j)g_{\text{c}}({\text{x}}_{j+\ell }),& \ell \ge 0,\end{array}$$

where ${\Vert g_{\text{c}}\Vert }^2=\frac{1}{N}{\sum }_{j=1}^N{g}_{\text{c}}{({\text{x}}_j)}^2$.

The correlation length of the sample {g(x_j)} is then defined as the smallest integer for which ${\gamma }_{\ell }^2$ drops below a given threshold.

4.2 Setting up the statistical model

The Bayesian analysis consists of three key steps: (1) setting up the prior density that reflects our belief of the unknowns of primary interest, (2) definition of the likelihood function that links the unknown to any possible observed quantity, and, (3) exploration of the posterior density, including the computation of statistical estimates. In this section, we discuss the first two steps.

4.2.1 Likelihood

We start the discussion by defining the likelihood function. In the present context, the vector u represents the unknown of primary interest, and it is modeled as a random variable to reflect our lack of information of its value. The equation (3) is the starting point for observation equation, i.e., the vector r is interpreted as observation. When discussing the LP solutions, we already indicated that the vector r may be poorly known. We may not be sure about how strictly steady state condition holds, nor may we assume that the arterial concentration values are known exactly. In fact, it is quite reasonable to assume that concentrations of biochemical compounds fluctuate over a population.

Therefore, we write a stochastic extension of the equation (3), namely

$$\text{r}=A\text{u}+\text{e},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{e}\sim {\pi }_{\text{noise}}\left(\text{e}\right),$$ (12)

where the probability density π_noise reflects our degree of uncertainty about the data and strictness of steady state. Here, we model the uncertainty e as noise. From now on, we shall assume for simplicity that the vectors e and u are mutually independent, thus leading to a likelihood model

$$\pi \left(\text{r}|\text{u}\right)={\pi }_{\text{noise}}\left(\text{r}-\text{A}\text{u}\right).$$

To further simplify the discussion, we shall assume that e is zero mean Gaussian with covariance matrix Γ, yielding a likelihood function of the form

$$\pi (\text{r}|\text{u})\propto \text{exp}\hspace{0.17em}\left(-\frac{1}{2}{(\text{r}-A\text{u})}^{\text{T}}{\Gamma }^{-1}(\text{r}-A\text{u})\right).$$ (13)

Observe that here we are implicitly assuming that Γ is symmetric and positive definite. However, if we are confident that the steady state condition holds strictly and that the only uncertainty is in the arterial concentration values, the matrix Γ becomes singular. To cope with this situation, the model needs to be reduced so as to ensure that the steady state is strictly enforced. We shall discuss the details of such model reduction later in this section.

4.2.2 Prior

The prior probability density should contain all available information that we may have of the primary unknown before observations. In the application at hand, the prior contains our belief concerning the bounds and the belief that the cell metabolism is driven by the principle of maximizing ATP production.

The bound constraints u_min ≤ u ≤ u_max can be encoded into the prior by requiring that

$${\pi }_{\text{prior}}\propto \prod _{j=1}^n{\chi }_{[u_{\text{min},j},u_{\text{max},j}]}(u_j),$$ (14)

where χ_{[umin,j,umax,j]} denotes the characteristic function of the admissible interval [u_min,j, u_max,j] of the jth component. Observe that the form of the prior indicates that we are not expecting a priori any interdependence between the components of u.

Since in the Bayesian framework we are not interested in finding a single estimator, the principle of maximizing the ATP production cannot be enforced as an optimization objective. Rather, according to the general Bayesian philosophy, we take the energy principle as a prior belief and seek to construct a probability density that favors solutions with high oxidative phosphorylation flux, i.e., we let u ∼ π_phos(u), where the density π_phos is concentrated on energetically correct solutions. In particular, we choose the density to be

$${\pi }_{\text{phos}}(\text{u})\propto {\left(\frac{u_j-u_{\text{min},j}}{u_{\text{max},j}-u_{\text{min},j}}\right)}^2,$$ (15)

where u_j is the reaction flux corresponding to oxidative phosphorylation. This density attains its maximum at u_j = u_max,j and minimum at u_j = u_min,j, so it favors high ATP production.

4.3 Exploring the posterior

In this section, we explore the posterior distribution of the fluxes by generating representative samples via Gibbs samplers. Once the samples are available, we analyze the histograms, compute the posterior mean and compare it with the corresponding LP solution.

We first consider the case of a uniform prior (14), without including the part that favors high aerobic ATP production.

Traditionally, in FBA the steady state is strictly enforced, i.e., the concentrations of the biochemical species are assumed constant. This means that in the likelihood model above the matrix Γ is singular and therefore the model must be reduced. More precisely, consider the matrix A in the partitioned form (4). Strictly enforcing steady state implies, in particular, that

$$A_{\text{c}}\text{u}=0,$$ (16)

i.e., u must be in the null space of A_c.

To find a basis for the null space of A_c, we introduce its singular value decomposition $A_{\text{c}}=U_{\text{c}}{D}_{\text{c}}{V}_{\text{c}}^{\text{T}}\in {ℝ}^{k\times n}$, where $U_{\text{c}}\in {ℝ}^{k\times k}$ and $V_{\text{c}}\in {ℝ}^{n\times n}$ are orthonormal matrices and $D_{\text{c}}\in {ℝ}^{k\times n}$ is a diagonal matrix whose nonnegative diagonal entries, d_c,1 ≥ d_c,2 ≥ … ≥ d_c,k ≥ 0 are called singular values (Golub & Van Loan, 1989). Assume that d_c,r, r ≤ k is the last numerically nonzero singular value of A_c. Partitioning the matrix V_c accordingly,

$$V_{\text{c}}=\left[\begin{array}{ccccccc}{\text{v}}_{\text{c},1}& \dots & {\text{v}}_{\text{c},r}& ⋮& {\text{v}}_{\text{c},r+1}& \dots & {\text{v}}_{\text{c},n}\end{array}\right]=\left[\begin{array}{cc}{V}_{\text{c},1}& V_{\text{c},2}\end{array}\right]\hspace{0.17em},$$

and observing that the columns of $V_{\text{c},2}\in {ℝ}^{n\times \left(n-r\right)}$ form an orthonormal basis for the null space of A_c, in order for (16) to hold, u must be of the form

$${\text{u}=V}_{\text{c},2}\text{z},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{z}\in {ℝ}^{\ell },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\ell =n-r.$$

This representation reduces the dimension of the unknown vector, since we may now write the likelihood model for the ℓ-dimensional vector z.

Consider now the observation model where we assume that the arterial concentrations are corrupted by noise,

$${\text{r}}_{\text{b}}=A_{\text{b}}\text{u}+{\text{e}}_{\text{b}}=A_{\text{b}}{V}_{\text{c},2}\text{z}+{\text{e}}_{\text{b}}.$$

Here ${\text{r}}_{\text{b}}=\left(Q/F\right){\text{C}}_{\text{a}}\in {ℝ}^{m-k}$ is the observed vector, and ${\text{e}}_{\text{b}}\in {ℝ}^{m-k}$ is the noise vector which we assume normally distributed, with zero mean and covariance matrix ${\Gamma }_{\text{b}}\in {ℝ}^{\left(m-k\right)\times \left(m-k\right)}$. The reduced likelihood model for the new variable z is then

$${\pi (\text{r}}_{\text{b}}|\text{z})\propto \text{exp}\hspace{0.17em}\left(-\frac{1}{2}{(A_{\text{b}}{V}_{\text{c},2}\text{z}-{\text{r}}_{\text{b}})}^{\text{T}}{\Gamma }_{\text{b}}^{-1}(A_{\text{b}}{V}_{\text{c},2}\text{z}-{\text{r}}_{\text{b}})\right).$$

Since ${\Gamma }_{\text{b}}^{-1}$ admits a symmetric factorization of the form ${\Gamma }_{\text{b}}^{-1}=R_{\text{b}}^{\text{T}}{R}_{\text{b}}$, we can write the likelihood function as

$$\pi ({\text{r}}_{\text{b}}|\text{z})\propto \text{exp}\hspace{0.17em}\left(-\frac{1}{2}\Vert R_{\text{b}}{A}_{\text{b}}{V}_{\text{c},2}\text{z}-R_{\text{b}}{\text{r}}_{\text{b}}{\Vert }^2\right).$$

If m − k ≤ ℓ, as is the case in the application at hand, even after the reduction the problem remains underdetermined. Replacing $R_{\text{b}}{A}_{\text{b}}{V}_{\text{c},2}\in {ℝ}^{\left(m-k\right)\times \ell }$ by its singular value decomposition

$$R_{\text{b}}{A}_{\text{b}}{V}_{\text{c},2}=U_{\text{b}}{D}_{\text{b}}{V}_{\text{b}}^{\text{T}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{D}_{\text{b}}=\text{diag}(d_{\text{b},1},d_{\text{b},2}\dots ,d_{\text{b},m-k})\in {ℝ}^{\left(m-k\right)\times \ell },$$

and using the orthogonality of $U_{\text{b}}\in {ℝ}^{\left(m-k\right)\times \left(m-k\right)}$, it follows that

$$\begin{array}{ll}\pi ({\text{r}}_{\text{b}}|\text{z})& \propto \text{exp}\hspace{0.17em}\left(-\frac{1}{2}{\Vert \hspace{0.17em}{D}_{\text{b}}{V}_{\text{b}}^{\text{T}}\text{z}-U_{\text{b}}^{\text{T}}{R}_{\text{b}}{\text{r}}_{\text{b}}\Vert }^2\right)\\ & =\text{exp}\hspace{0.17em}\left(-\frac{1}{2}\sum _{j=1}^{m-k}{(d_{\text{b},j}{y}_j-b_j)}^2\right),\end{array}$$ (17)

where $\text{b}=U_{\text{b}}^{\text{T}}{R}_{\text{b}}{\text{r}}_{\text{b}}\in {ℝ}^{m-k}$ and $\text{y}=V_{\text{b}}^{\text{T}}\text{z}\in {ℝ}^{\ell }$. The original variable u can be expressed in terms of y as

$$\text{u}=\underset{=V\in {ℝ}^{n\times \ell }}{\underbrace{V_{\text{c},2}{V}_{\text{b}\hspace{0.17em}}}}\text{y}=V\text{y}.$$

In the remainder of this paper, we refer to this as the minimal likelihood model. Without any bound constraints on the components of u, the y_j are independent Gaussian random variables, and the components y_j, with j > m − k, have infinite variance since the likelihood (17) does not restrict them in any way. It is with the introduction of the prior that we restrict their variance.

We now outline a componentwise Gibbs sampling algorithm for this model. Starting from an initial vector y₀ that satisfies the componentwise bounds

$${\text{u}}_{\text{min}}\le V{\text{y}}_0\le {\text{u}}_{\text{max}}\hspace{0.17em},$$

we generate a sample S = {y₀, y₁, …, y_N} through the following componentwise updating scheme. The initial value y₀ can be found, e.g., by the LP solver, assuming that the system is consistent and a solution exists. Indeed, if u₀ is the LP solution, then A_cu₀ = 0 and we may set y₀ = V^Tu₀. Given the current vector y_k in the chain, generate y_k+1 componentwise by drawing y_k+1,j, for 1 ≤ j ≤ ℓ, from the distribution

$$t\mapsto {\pi }_{\text{post}}\hspace{0.17em}(y_{k+1,1},\dots ,y_{k+1,j-1},t,y_{k,j+1},\dots ,y_{k,\ell }).$$

Denote by $\text{y}\prime \in {ℝ}^{\ell -1}$ and $V\prime \in {ℝ}^{\ell \times \left(\ell -1\right)}$ the arrays

$$\text{y}\prime =\left[\begin{array}{c}{y}_{k+1,1}\\ ⋮\\ y_{k+1,j-1}\\ y_{k,j+1}\\ ⋮\\ y_{k,\ell }\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}V\prime =\left[\begin{array}{cccccc}{\text{v}}_1& \dots & {\text{v}}_{j-1}& {\text{v}}_{j+1}& \dots & {\text{v}}_{\ell }\end{array}\right].$$

and find the maximal interval [t_min, t_max] for which the system of inequalities

$${\text{u}}_{\text{min}}-V^{\prime }{\text{y}}_k^{\prime }\le t{\text{v}}_j\le {\text{u}}_{\text{max}}-V^{\prime }{\text{y}}_k^{\prime }$$

holds. For t ∈ [t_min, t_max], the vector v(t) = tv_j + V′y′ has positive prior probability. Then, if j ≤ m − k and d_b,j > 0, draw y_k+1,j from the truncated Gaussian distribution

$$t\mapsto {\chi }_{\left[t_{\text{min}},t_{\text{max}}\right]}\text{exp}\hspace{0.17em}\left(-\frac{1}{2}{(d_{\text{b},j}t-b_j)}^2\right)\hspace{0.17em},$$

while if d_b,j = 0 or j > m − k, draw it from the uniform distribution over the interval [t_min, t_max].

4.3.1 Relaxing the steady state condition

The strict enforcement of the steady state, although convenient from the computational complexity perspective, might not always be desirable or fully justified. In the present application, for example, it may not be known if the muscle is under constant energy demand during the experiment. Further, the initial value y₀ for the reduced model may not be available, as we do not know if the strict steady state is consistent with the imposed bound constraints.

By not requiring that the steady state condition holds strictly, we no longer restrict the vector u to the null space of A_c. As a result, in the additive noise model (12), the error covariance matrix Γ in the likelihood model is non-singular. Note that under these assumptions, in our application the components of the noise vector corresponding to the matrix A_b contain the uncertainty of the steady state plus possible measurement errors of the arterial concentrations. The Gibbs sampling can be applied to the whole model by relaxing the condition that the solution is in the null space of A_c. Introducing a symmetric decomposition for the inverse of the error covariance Γ⁻¹ = R^TR, we can express the likelihood function (13) in the form

$$\pi (\text{r}|\text{u})\propto \text{exp}\hspace{0.17em}\left(-\frac{1}{2}\Vert R\text{r}-RA\text{u}{\Vert }^2\right).$$

From the singular value decomposition RA = UDV^T, D = diag(d₁, d₂, …, dm), by using the orthogonality of U it follows that the likelihood function can be written in the form

$$\pi (\text{r}|\text{u})\propto \text{exp}\hspace{0.17em}\left(-\frac{1}{2}\sum _{j=1}^m{(b_j-d_j{y}_j)}^2\right)\hspace{0.17em},$$

where b = U^TRr and y = V^Tu. From here on, the componentwise Gibbs sampling with the bound constraints proceeds as before. In this case the dimensions of the problem are significantly larger than for the minimal model, thus requiring a greater computational load for the exploration of the posterior probability density via MCMC analysis.

Finally, we note that the Gibbs sampling of the full model can be done directly using the original coordinates u without passing to the new coordinates using the SVD.

4.3.2 Implementation of energy principle: rejection sampling

So far, our prior has only contained the upper and lower bound information on the unknowns, ignoring the portion that favors high oxidative phosphorylation flux values. The inclusion of (15) into the prior density is straightforward, but the Gibbs sampler algorithm requires modifications, in particular because the sampling is done in the y-space. One possibility is to implement the prior information sequentially: having computed the sample {u₁, …, u_N} using the bound constraint prior, we perform a resampling: for each vector u_j, we calculate the acceptance ratio, α = π_phos(u_j), 0 ≤ α ≤ 1, and accept u_j, with probability α, into the final sample. The resulting sample will be, in general, smaller and richer in vectors for which π_phos(u) is higher, i.e., that comply better with the energy principle. The above strategy is equivalent to what is known in the literature as rejection sampling, see, e.g., Liu (2003).

4.3.3 Parametric prior distributions

One of the motivations for adopting a Bayesian perspective for the flux estimation problem is that it allows the inclusion of a priori beliefs about the distribution of the vector u into the estimation. This prior belief may be based on preliminary studies, additional data sets or assumptions about the mathematical model.

For example, in Calvetti & Somersalo (2006) the probability density of the Michaelis-Menten parameters, collected in the model vector θ, was estimated by Bayesian sampling techniques using ischemic biopsy data from the literature (Katz (1988)). Since this information does not concern directly the fluxes at steady state, the question becomes then how to enter this available information about the Michaelis-Menten parameters in the form of a prior for the fluxes, which are the variables of primary interest in the present investigation. Observe that although in the cited article the steady state condition was included in the model before the onset of the ischemia, the flux balance was not enforced, and the steady state was assumed to be a resting steady state. Therefore, the FBA can provide complementary information of the system.

We propose the following straightforward procedure based on sampling. Consider the Michaelis-Menten model (7), and assume that we have a probability density $\stackrel{\sim }{\pi }(\theta ,\text{C})$ available for the model parameters and the steady state concentrations. We may draw a representative sample {(θ₁, C₁), …, (θ_M, C_M)} from this distribution, and then calculate the corresponding flux sample, {u₁, …, u_M}, where u_i = F(θ_i, C_i). The flux sample can then be used, e.g., to estimate upper and lower bounds for the fluxes or, more generally, to fit a given parametric model for the random variable u. Since in the Gibbs sampling methods presented above the sampling is done for the variable y, we can calculate the sample {y₁, …, y_M} using the formula y = V^Tu, and use it to fit a parametric model for the random variable y.

4.4 Results

This section presents the results of computed examples illustrating the Bayesian flux estimation method and compares them to the optimization based results discussed earlier. All computations were performed using Matlab.

4.4.1 Prior distributions and bounds

In order to set suitable bounds or parametric prior distributions for the components of the vector u, we proceed as described in Section 4.3.3. In the article Calvetti & Somersalo (2006), a Markov Chain Monte Carlo sample of the vector x = (C₀, θ) was calculated based on biopsy data of Katz (1988). Although we could use directly this sample to calculate a sample of vector u via the model (7), to avoid using a too committal prior, we follow a different approach. First, we assume that the components of the vector x are mutually independent. Then, using the sample generated in Calvetti & Somersalo (2006), we estimate a parametric distribution for each component separately, using a log-normal distribution for the Michaelis-Menten parameters, collected into the vector θ, and a uniform distribution for the initial concentrations over the interval $[(1/4){\overline{C}}_{0,j},4{\overline{C}}_{0,j}]$, where ${\overline{C}}_{0,j}$ is the componentwise mean. Similarly, for the log-normal distribution, we first compute the mean $\overline{{\theta }_j}$ and then select a lognormal density which preserves $\overline{{\theta }_j}$ and is such that 97.5% of the sample is below $4\hspace{0.17em}\overline{{\theta }_j}$. Having the parametric distributions for the components of x, we then generate a sample of 10 000 independently drawn vectors, calculate the corresponding flux vectors, and set the bounds for the fluxes so that 95% of the sample vectors are within the confidence interval.

We remark that fitting a log-normal prior to the sample in the maximum likelihood sense would lead to considerably tighter prior for the Michaelis-Menten parameters and for the flux vector u. The narrower bounds used in the LP computations are a result of the latter approach.

Before discussing the results of the MCMC sampling, a few comments concerning the priors for different parameters are in order. The first one concerns committal and non-committal priors. For simplicity, consider a Michaelis-Menten flux model without facilitators,

$$\Phi =V_{\text{max}}\frac{C}{K+C},$$

assuming that V_max and K are fixed, and denote Φ = Φ (C). In general, it is commonly believed that the wider the prior of the variable C is, the more uninformative and less committal it is. This is no longer obvious if the variable of primary interest is Φ instead of C. To understand why, denote by π_C(C) the probability density of C. After a change of variables, the probability density π_Φ of Φ is

$$\begin{array}{cc}{\pi }_{\Phi }(\Phi )=\frac{1}{\Phi \prime (C)}{\pi }_C(C),& C=C(\Phi )=K\frac{\Phi }{V_{\text{max}}-\Phi }.\end{array}$$

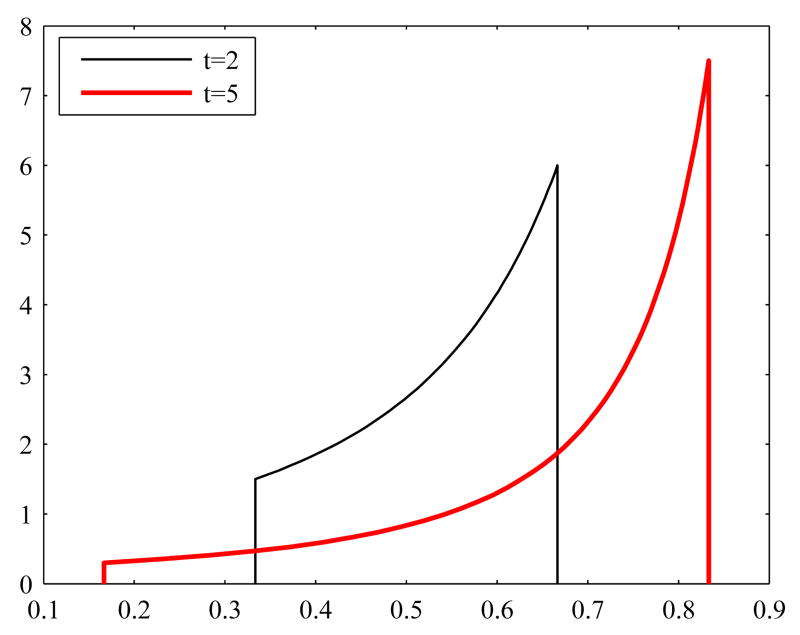
Since the mapping $C\mapsto \Phi (C)$ saturates for large values of C, the derivative tends to zero and hence, the probability density of Φ is large for large values of C. Therefore, the wider (noninformative) the probability density of C is, the more confident we are that Φ is close to its saturation value as C → ∞. This phenomenon is illustrated in Figure 3, where we have probability densities of Φ corresponding to uniform distributions of C over two different intervals.

Fig. 3.

Probability densities of Φ corresponding to uniform distributions of C over an interval [1/t, t], with two different values of t. Here, V_max = 1 and K = 1.

Our second point is that the uniform priors for the components of u could be replaced with other parametric priors. We found that, by using the Weibull distributions (see, e.g., Miller & Freund (1977)), we could get a relatively good fit to the histograms of the components of u, and further, for histograms of the minimal model vector y. However, since the use of different parametric priors had little effect on the final results, we will not discuss this issue any further.

4.4.2 Gibbs sampling computations

In our computed examples we applied Gibbs sampling MCMC for the analysis for the steady state to both the whole and the minimal model. For each model, we computed a sample of 200 000 elements.

The values for the arterial concentrations C_a were taken from Dash & Bassingthwaighte (2006) (see also Appendix A, Table 3). To set up the likelihood model, we assumed a standard deviation of 5% for the arterial concentration values. For the whole model, where we also needed to set uncertainties for the steady state condition, the standard deviation for the steady state conditions was chosen to be 1% of the value of the right-hand side of A_bu and A_cu, respectively, calculated at the mean of the prior density. The initial point for the sampling was calculated from the mean of the sample obtained in Calvetti & Somersalo (2006) (this sample was used also for the priors) using the Michaelis-Menten model (7).

Table 3.

Transport fluxes of species in the blood and arterial concentration values. For the transport fluxes, (f) refers to facilitated and (p) for passive transport.

Transport fluxes				Species in blood	Ca,tot value [mmol/1]
blood→cell		cell→blood
27. JGLU,b→ c	(f)	36. JGLU,c→b	(f)	45. GLU	5.000
28. JPYR,b→c	(p)	37. JPYR,c→b	(p)	46. PYR	0.0680
29. JLAC,b→c	(f)	38. JLAC,c→b	(f)	47. LAC	0.7200
30. JALA,b→c	(p)	39. JALA,c→b	(p)	48. ALA	0.1900
31. JTGL,b→c	(p)	40. JTGL,c→ b	(p)	49. TGL	0.9900
32. JGLC,b→c	(p)	41. JGLC,c→b	(p)	50. GLC	0.0600
33. JFFA,b→c	(p)	42. JFFA,c→b	(p)	51. FFA	0.6500
34. JCO2,b→c	(p)	43. JCO2,c→b	(p)	52. CO2	23.4066
35. JO2,b→c	(p)	44. JO2,c→b	(p)	53. O2	9.2000

We use the correlation length of the component sample as a measure of convergence. Thus, the correlation lengths are calculated using for g a function that picks a given component p from the vector x, i.e., g(x) = x_p (see Section 4.1). In our calculations, we define the correlation length using a threshold value of 0.25, i.e., γ_ℓ < 0.5. The calculation of the autocovariance is repeated up to the value ℓ=1000.

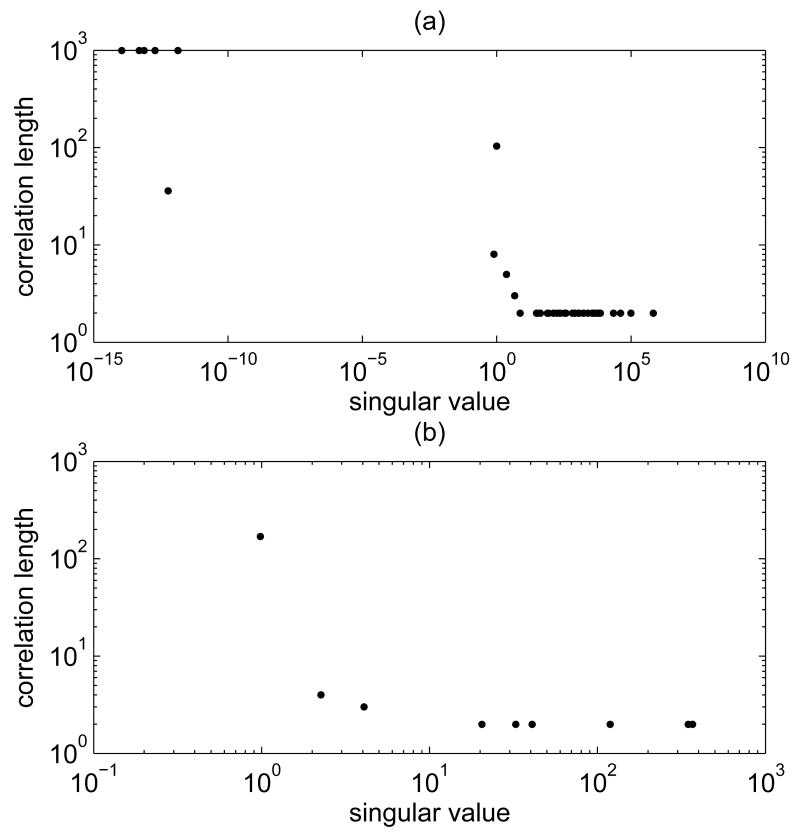
We recall that for both the minimal and the whole model, the sampling is done for y, while the variable of primary interest is u. From our numerical simulations, we saw that while some of the components of y converge fast, for others the convergence can be painfully slow. We also noticed that the correlation length of a y component clearly depends on the value of the corresponding singular value of the system matrix, with large singular values displaying low correlation length, thus good convergence rate, of the coefficient of the corresponding singular vector. This phenomenon, which we have observed for both the minimal and the whole model, is illustrated in Figure 4.

Fig. 4.

Singular values and correlation lengths for (a) the whole model and (b) the minimal model sampler. The values are based on samples with 200 000 elements. The correlation length was calculated as explained in Section 4.1, using a value ℓ = 1000 for the maximum value of the correlation length.

The singular values for the whole model that are clearly distinct from zero are very markedly separated from the near vanishing ones, and it is in correspondence of the gap that the correlation length increases dramatically. This phenomenon is independent of the Gibbs sampling strategy in the sense that it is present whether we perform the updating starting from the component corresponding to highest or lowest singular value.

In order to get a measure of the reliability of the estimates of u, we computed the correlation lengths for the components of u. Table 5 in Appendix B lists the correlation lengths of the components of the Gibbs samples for the whole and minimal model, respectively.

Table 5.

Correlation lengths of the components u_j of u from samples of 200000 elements calculated using the minimal model and the whole model with Gibbs sampling.

j	Minimal model	Whole model	j	Minimal model	Whole model
1	27	4	28	2	2
2	12	5	29	54	29
3	12	5	30	2	2
4	27	27	31	>1000	>1000
5	27	27	32	38	64
6	27	27	33	765	257
7	21	23	34	>1000	>1000
8	4	2	35	>1000	>1000
9	3	2	36	19	12
10	17	12	37	3	2
11	4	5	38	47	34
12	5	7	39	4	2
13	>1000	>1000	40	>1000	>1000
14	>1000	>1000	41	39	4
15	>1000	>1000	42	754	252
16	>1000	>1000	43	>1000	>1000
17	>1000	>1000	44	>1000	>1000
18	>1000	>1000	45	4	4
19	>1000	>1000	46	3	3
20	>1000	>1000	47	22	24
21	>1000	>1000	48	3	2
22	>1000	>1000	49	4	3
23	>1000	>1000	50	6	7
24	>1000	>1000	51	6	7
25	>1000	>1000	52	234	133
26	>1000	>1000	53	>1000	>1000
27	24	13

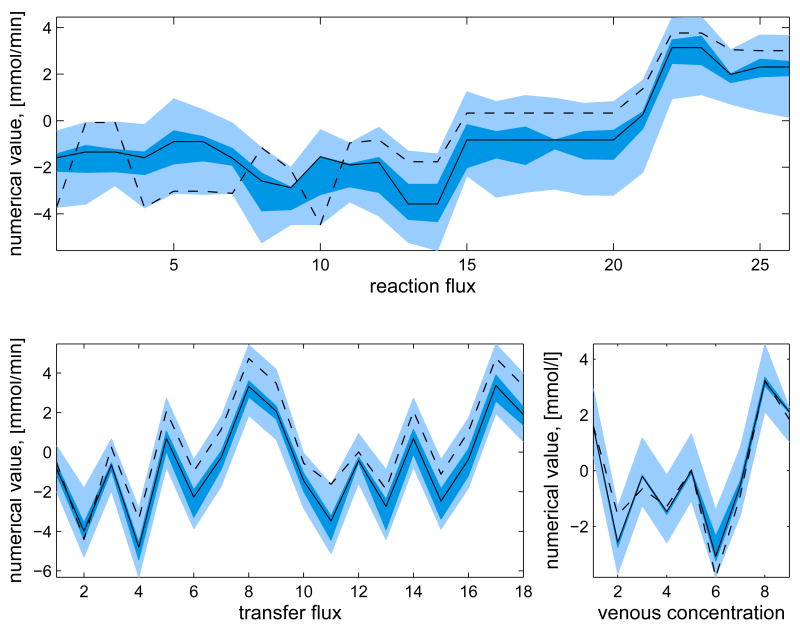
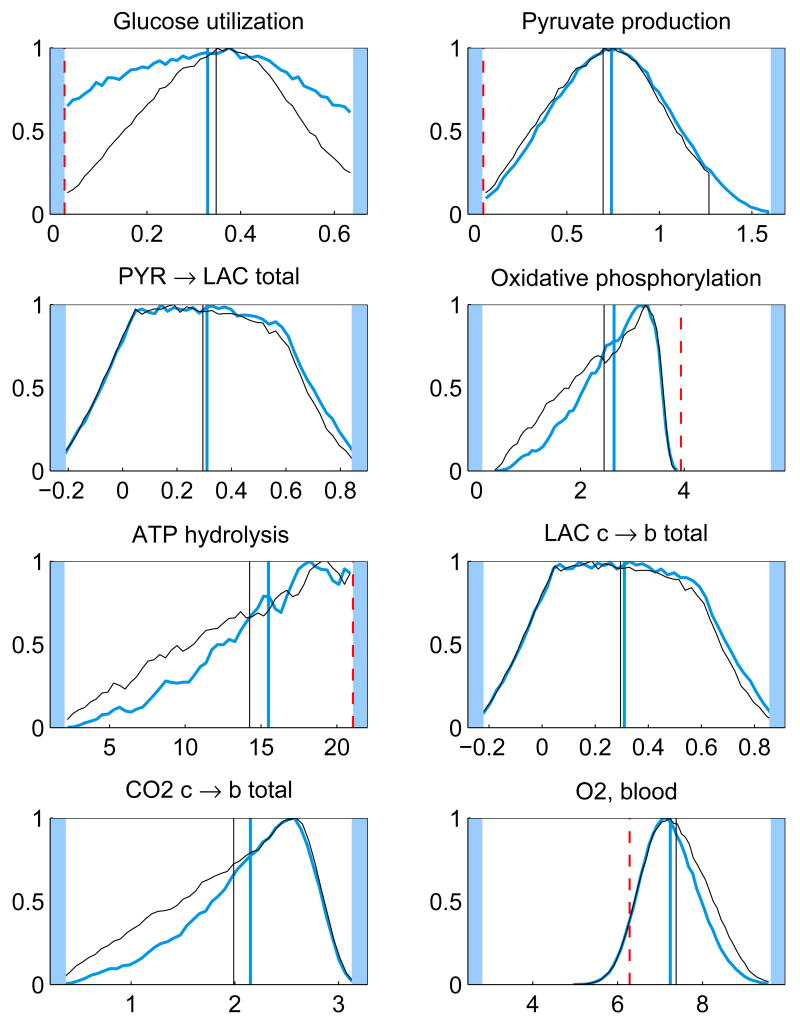
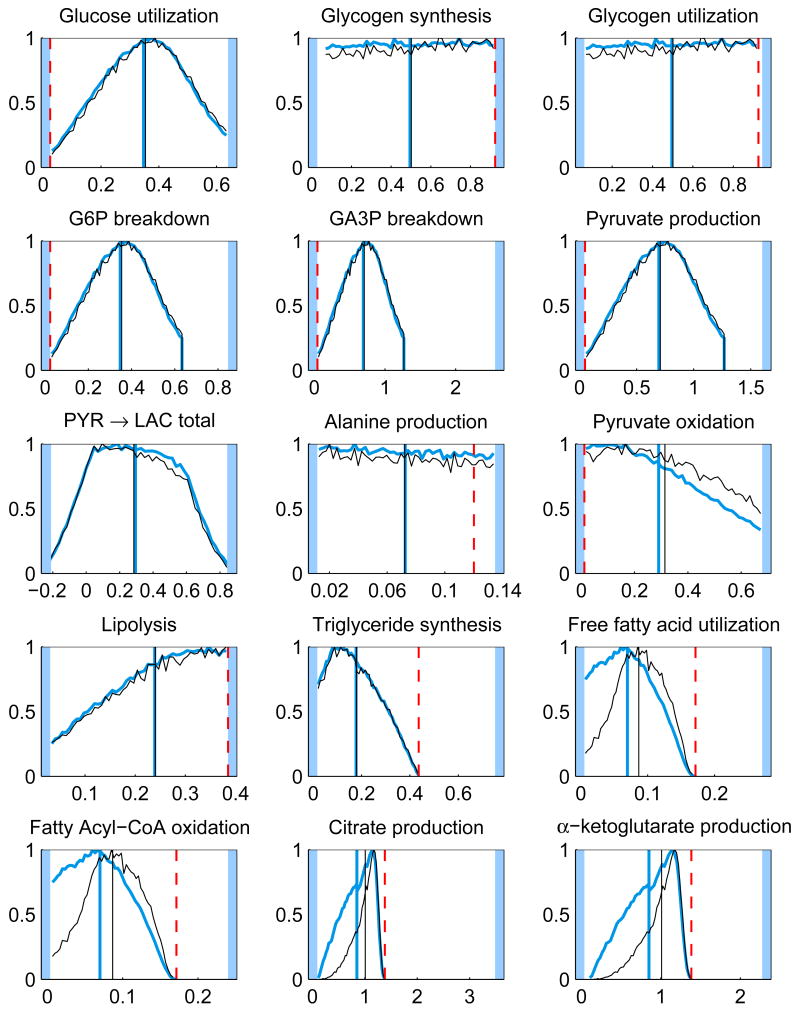
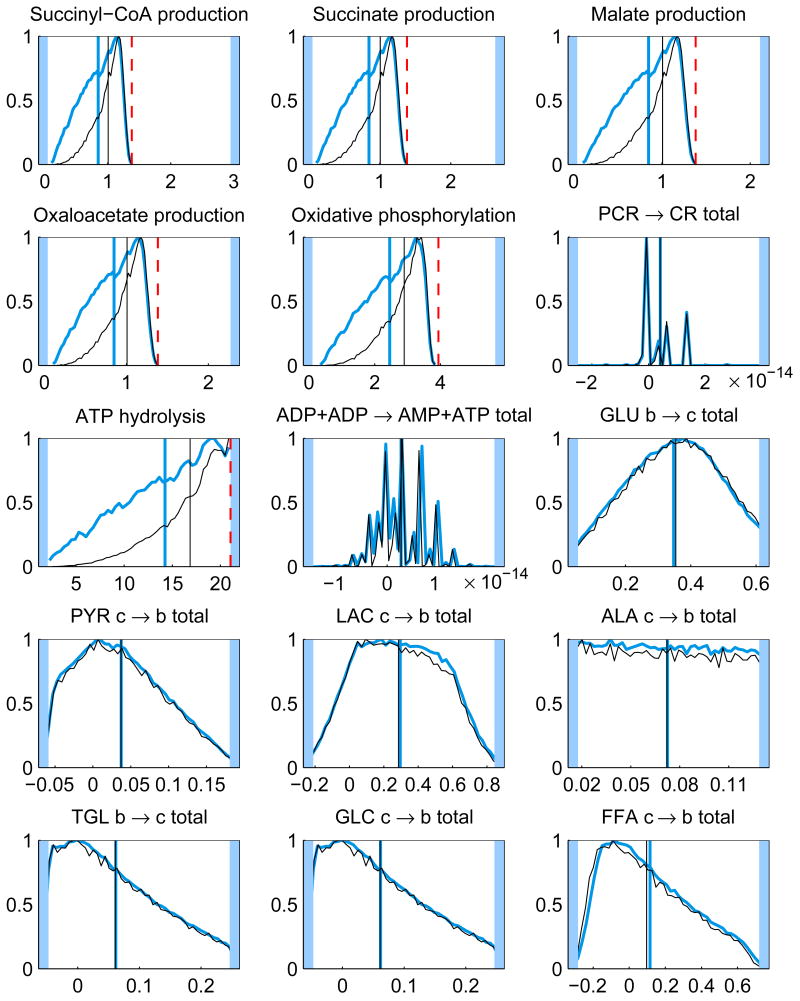
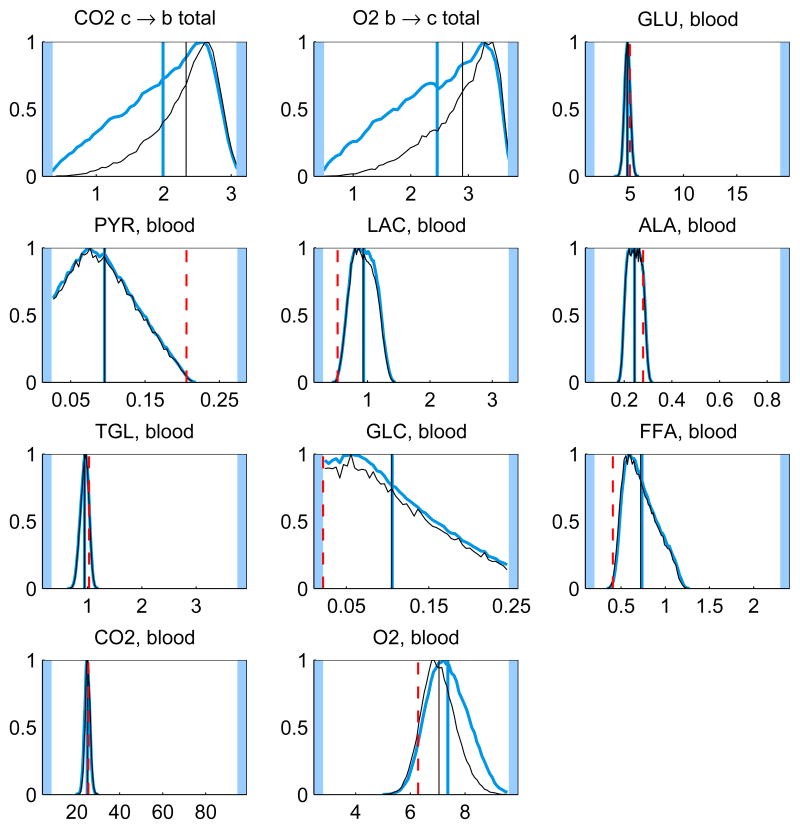
In addition to the posterior mean estimates, the histograms of the components of u from the samples {u_i}, i = 1, …, N, contain valuable information on how well the respective quantities are defined by the system. Figure 5 shows the histograms of some of the components of the solution u for the whole and minimal model. The posterior mean estimates and the corresponding LP solution are also shown. It should also be pointed out that different sampling strategies may lead into slightly different results.

Fig. 5.

The histograms and corresponding posterior mean estimates of some of the reaction and transport fluxes and the concentration of oxygen with Gibbs sampling using the whole model (thicker blue) and minimal model (thinner black). For reversible reactions and transport fluxes, the net flux is plotted. The maximum value of each histogram is normalized to unity. The units for the reaction and transport fluxes are mmol/min and for the concentrations mmol/l. The LP solution (dashed red) is also depicted (except for net fluxes). The highlighted area defines the bounds, or in case of net fluxes, the span of the histogram.

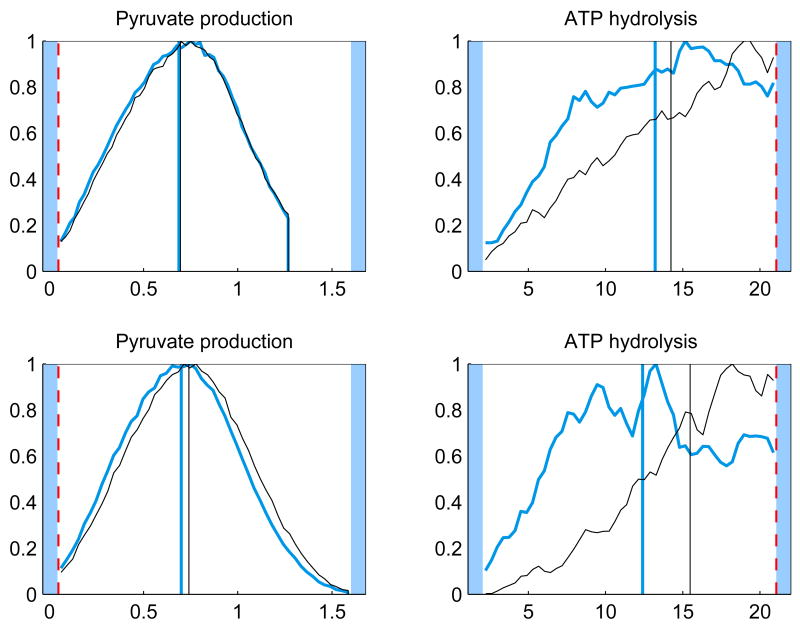
The initial point of the sampling may also affect the results in particular for the components that have not yet converged. To investigate the effect of the initial point, we calculated the Gibbs samples using two other initial points. For both the whole model and minimal model the LP solution was used. For the whole model, also the midpoint between the bounds was used, for the minimal model this natural choice for a starting point would not work as the initial point has to lie in the null space of A_c. The results show that for the components for which the correlation length is small, two different initial points produce in practice the same histograms, whereas for poorly converged components (high correlation length) the effect of the initial point is clearly visible. Figure 6 demonstrates the effect of the initial point.

Fig. 6.

The histograms of a well converged (left panels) and a poorly converged (right panels) component of u using the minimal model (top) and whole model (bottom) for different starting points of the sampling. For the minimal model the starting points were the LP solution (thicker blue) and the mean of the sample used for priors (thinner black). For the whole model the starting points were the midpoint between bounds (thicker blue) and the mean of the sample used for priors (thinner black). The LP solution (dashed red) is also shown. The units for the reaction fluxes are mmol/min and the maximum value of each histogram is normalized to unity.

In our computed simulations we implemented the prior belief that the system favors steady states with a high oxidative phosphorylation reaction flux by rejection sampling, i.e., we resampled the existing sample {u₁, …, u_N}, corresponding to the uniform prior, favoring those u for which π_prior(u) is large. Figure 7 shows the histograms from a Gibbs sample generated using the minimal model sampler before and after rejection sampling. We observe that the optimality criterion, as implemented here, has a visible but not dramatic effect on the posterior distribution, shifting the histograms slightly towards the energetically more efficient (higher aerobic ATP production) direction.

Fig. 7.

The histograms and the corresponding CM estimates of all the components of the solution u from Gibbs sampling using the minimal model before (thicker blue) and after (thinner black) applying rejection sampling. For reversible reactions and transport fluxes, the net flux is plotted. The maximum of each histogram is normalized to unity. The units for the reaction and transport fluxes are mmol/min and for the concentrations mmol/l. The LP solution (dashed red) is also depicted (except for net fluxes). The highlighted area in the plots defines the bounds, or in case of net fluxes, the span of the histogram.

5 Discussion and further studies

By looking at the histograms, it is clear that some of them have identical shapes. For instance, the histograms of the glycolytic reactions are all identical up to scaling, since at steady state the fluxes should indeed coincide. The same is true for the TCA cycle reaction fluxes. Mathematically, these fluxes depend linearly on the same underlying independent components, and it is possible to calculate correlation coefficients to find out the correlated fluxes. Note, that although the independent components are not necessarily equal to the singular vectors of the system matrix, since the coefficients of the singular vectors get correlated via the bound constraints in a non-trivial way, the singular vectors provide a good first approximation to the independent components.

The histograms of the reversible reactions, glycogen synthesis and utilization and phosphocreatine synthesis and breakdown, are identical and spread over the feasible region, indicating that the net flux vanishes while the one-way fluxes are not determined.

It is interesting to observe that the prior favoring high oxidative phosphorylation flux has a marginal effect on the means of the distributions. The LP solution, however, may differ dramatically from the mean, and it is often at a tail of the distributions. While it is not surprising that the optimization approach leads to a solution of high TCA fluxes, it is maybe less obvious that the glycolytic fluxes tend to the minimum in our computed example. This phenomenon may be due to the instability of the LP solution: from Figure 1, we observe that with the narrower bound constraints, the glycolytic fluxes (j = 1, 4, 5, 6) are closer to their maximum. This observation suggests that a distribution based estimation strategy, being less prone to instabilities, may be preferable to computing single estimates. Notice also that the LP solution requires that the steady state condition and the bound constraints are consistent, which may not be easy to check, in particular when bound constraints from different sources are used. The Bayesian approach is more flexible in the sense that since the steady state is not enforced strictly, inconsistency with the prior bounds leads only to low likelihoods.

The trade-off in using sampling methods is that sampling strategies are generally slower than methods that produce single point estimates such as LP solution. However, the obtained solution is also much more informative; the estimate of the probability density of the solution, rather than a single point estimate that may be rather unstable. To give more practical feeling on computational effort, the computing time of a sample of 200 000 elements was approximately 160 minutes for the whole model, which amounts to roughly 0.05 seconds per sample point, and 72 minutes for the minimal model, which amounts to roughly 0.02 seconds per sample point, on a PC with 2 GHz processor and 2 Gb of RAM. The computing time of a single LP solution at the same setup was of the order of a fraction of a second.

There are several directions where this analysis can be extended. The most straightforward one is the study of more complex models, including sub-compartments of different cell types and sub-domains within them. Another natural extension is the analysis of independent components, since they define subsystems in the metabolic networks that can be estimated separately. The study of conditional distributions is also of interest if we have partial information about the system available. Furthermore, a Bayesian FBA which take into account concentration data (Katz, 1988; Korth et al., 2000) as well as thermodynamic constraints, will be the topic of future work.

Appendix A. Skeletal muscle model

This appendix gives the details of the two-compartment skeletal muscle model considered in this article. Table 1 lists the biochemical species included in the model with their abbreviations. All 30 species are present in the tissue domain, and the first 9 also in the blood domain. The 26 biochemical reactions implemented in the model are listed in Table 2. Table 3 specifies the type of transport flux (facilitated or passive) between blood and tissue for each species in the blood domain, and gives the numerical values (from Dash & Bassingthwaighte (2006)) for the arterial blood concentrations. In our calculations, the units for the concentrations are mmol/l, for the reaction and transport fluxes mmol/min and for the blood flow l/min. The numerical values used for the blood flow Q(t) and the mixing ratio F are 0.9 l/min and 2/3, respectively. Finally, Figure 8 presents a schematic diagram of the two-compartment skeletal muscle model.

Table 1.

Biochemical compounds.

1. GLU (glucose)	16. CIT (citrate)
2. PYR (pyruvate)	17. AKG α-ketoglutarate
3. LAC (lactate)	18. SCoA (succinyl-CoA)
4. ALA (alanine)	19. SUC (succinate)
5. TGL (triglyceride)	20. MAL (malate)
6. GLC (glycerine)	21. OXA (oxaloacetate)
7. FFA (free fatty acid)	22. PCR (phosphocreatine)
8. CO2 (carbon dioxide)	23. CR (creatine)
9. O2 (oxygen)	24. Pi (inorganic phosphate)
10. G6P (glucose 6-phosphate)	25. CoA (coenzyme A)
11. GLY (glycogen)	26. NADH
12. GA3P (glyceraldehyde 3-phosphate)	27. NAD+
13. BPG (bisphosphoglycerate)	28. ATP
14. FAC (fatty acyl-CoA)	29. ADP
15. ACoA (acetyl-CoA)	30. AMP

Appendix B. Bounds and correlation lengths

Table 4 presents the numerical values for the bounds for the solution vector u. The LP solution was calculated with both the set of tight bounds and the set of wide bounds. In the Bayesian statistical computations, the set of wide bounds was used. Table 5 presents the numerical values of the correlation lengths for the components of u from the Gibbs sampling.