Activity-dependent changes in temporal components of neurotransmission at the juvenile mouse calyx of Held synapse

Abstract

The temporal fidelity of synaptic transmission is constrained by the reproducibility of time delays such as axonal conduction delay and synaptic delay, but very little is known about the modulation of these distinct components. In particular, synaptic delay is not generally considered to be modifiable under physiological conditions. Using simultaneous paired patch-clamp recordings from pre- and postsynaptic elements of the calyx of Held synapse, in juvenile mouse auditory brainstem slices, we show here that synaptic activity (20–200 Hz) leads to activity-dependent increases in synaptic delay and its variance as well as desynchronization of evoked responses. Such changes were most robust at 200 Hz in 2 mm extracellular Ca²⁺ ([Ca²⁺]_o), and could be attenuated by lowering [Ca²⁺]_o to 1 mm, increasing temperature to 35°C, or application of the GABA_BR agonist baclofen, which inhibits presynaptic Ca²⁺ currents (I_Ca). Conduction delay also exhibited slight activity-dependent prolongation, but this prolongation was only sensitive to temperature, and not to [Ca²⁺]_o or baclofen. Direct voltage-clamp recordings of I_Ca evoked by repeated action potential train template (200 Hz) revealed little jitter in the timing and kinetics of I_Ca under various conditions, suggesting that increases in synaptic delay and its variance occur downstream of Ca²⁺ entry. Loading the Ca²⁺ chelator EGTA-AM into terminals reduced the progression rate, the extent of activity-dependent increases in various delay components, and their variance, implying that residual Ca²⁺ accumulation in the presynaptic nerve terminal induces these changes. Finally, by applying a test pulse at different intervals following a 200 Hz train (150 ms), we demonstrated that prolongation in the various delay components reverses in parallel with recovery in synaptic strength. These observations suggest that a depletion of the readily releasable pool of SVs during high-frequency activity may downregulate not only synaptic strength but also decrease the temporal fidelity of neurotransmission at this and other central synapses.

Since the early studies of Bernard Katz et al. in the 1960s (Katz, 1969), a large body of work has established that the process of fast neurotransmission, across a variety of chemical synapses, is highly conserved. Action potentials (APs) in the presynaptic cell are usually initiated from the axon hillock and propagate along the axon. Upon arrival of an AP at the nerve terminal, voltage-gated Ca²⁺ channels (VGCCs) open and flux Ca²⁺ ions, raising intracellular Ca²⁺ concentration ([Ca²⁺]_i) and triggering engagement of release machinery (i.e. SNAREs) on synaptic vesicles (SVs) and within active zones (AZs). This process leads to membrane fusion and ultimately unloading of neurotransmitter from SVs. When transmitters diffuse across the synaptic cleft, they bind to, and activate, ligand-gated ion channels in the postsynaptic density, generating responses in the target neuron. Over the past several decades, tremendous insight has been gained into the mechanisms underlying the regulation of synaptic strength and plasticity by Ca²⁺ influx (Augustine et al. 1987; Zucker, 1996; Meinrenken et al. 2003; Schneggenburger & Neher, 2005). Despite these advances, little is known about how, or even whether, the temporal delays associated with the various steps in neurotransmission exhibit plasticity (Lin & Faber, 2002). Lack of understanding in this regard is particularly evident for mammalian central synapses which are small in size, difficult to access with electrodes, and have thus largely precluded quantitative delineation of the various temporal components of neurotransmission. Given that the fidelity of neurotransmission at any synapse depends both on the magnitude and timing of synaptic inputs, understanding the temporal building blocks for signal propagation and transduction is therefore of central importance in understanding the physiology of synapses.

Classical studies at the frog neuromuscular junction (NMJ) have indicated that the latency distribution histogram of synaptic delay, which refers to the time interval between the arrival of an AP at the nerve terminal and the onset of a postsynaptic response, is stable under a variety of conditions (Katz & Miledi, 1965; Barret & Stevens, 1972; Datyner & Gage, 1980; Parnas et al. 1989). However, recent evidence from other synapses, including the goldfish Mauthner cell synapse and crayfish NMJ, suggests that synaptic delay is modifiable. Paired-pulse depression in the Mauthner cell synapse is associated with a prolongation in synaptic delay (Waldeck et al. 2000), while facilitation at the crayfish NMJ leads to an activity-dependent shortening in synaptic delay (Vyshedskiy et al. 2000). These studies raise the possibility that the temporal components of neurotransmitter release, including synaptic delay, may undergo changes, either in parallel with or independently of, changes in synaptic strength.

The calyx of Held synapse is an axosomatic synapse located in the medial nucleus of the trapezoid body (MNTB) and specialized for preserving timing information along sound localization pathways in the auditory brainstem (Trussell, 1999; von Gersdorff & Borst, 2002). This synapse is known to be capable of high-fidelity transmission at extraordinarily high rates (up to several hundred hertz). The giant size of this synapse permits direct simultaneous recordings of both pre- and postsynaptic responses, presenting an excellent model to clearly dissect various temporal delays in the context of its physiological functionality (Forsythe, 1994; Borst et al. 1995). Using paired recordings from the mouse calyx of Held-MNTB synapse in acute brainstem slices, we show here that stimulation of the presynaptic axon, at a broad spectrum of frequencies, leads to activity-dependent prolongation in certain temporal components of neurotransmission. Build-up of intraterminal Ca²⁺, and depletion of SVs in the readily releasable pool during repetitive stimulation, are likely to underlie this activity-dependent short-term temporal plasticity.

METHODS

Slice preparation

Mice were housed in a facility certified by the Canadian Council of Animal Care and used for this study according to a protocol approved by the Hospital for Sick Children Animal Care Committee. Brainstem slices were prepared from postnatal day 14 to day 17 (P14–17) mice (CD1/C57 black hybrid) as previously described for rats (Forsythe, 1994). Following decapitation with a small guillotine, brains were immediately immersed into semifrozen artificial cerebral spinal fluid (ACSF) containing (mm): NaCl (125), KCl (2.5), glucose (10), NaH₂PO₄ (1.25), sodium pyruvate (2), myo-inositol (2), ascorbic acid (0.5), NaHCO₃ (26), MgCl₂ (1), and CaCl₂ (2), at a pH of 7.3 when oxygenated (95% O₂ and 5% CO₂), followed by rapid dissection. Transverse slices of the auditory brainstem containing the MNTB were cut at a thickness of 200–250 μm using a microtome (Leica VT1000S), followed by incubation at 37°C for 1 h prior to experimentation. For EGTA-AM experiments, slices were subsequently immersed in a solution (as above) containing 50 μm EGTA-AM for 30 min at room temperature just before experiments. Most experiments were performed at room temperature (20–22°C), except for those denoted in Fig. 5, in which recording solutions were heated to 35°C using an inline heater with a feedback thermistor (Warner TC-324B).

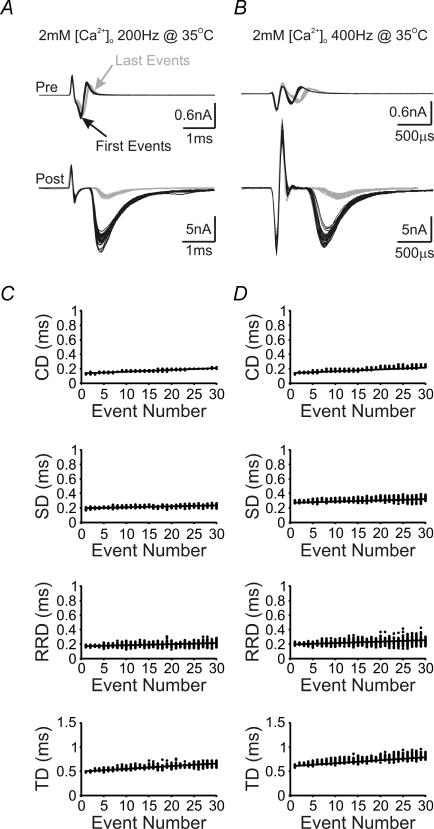
Figure 5. Temperature dependence of neurotransmission delay components.

A and B, first (black lines) and last (grey lines) pairs of presynaptic current deflections and postsynaptic EPSCs from 30 repeated stimulation trains at 200 (A) and 400 Hz (B) are aligned and superimposed to illustrate the frequency dependence of changes in presynaptic and postsynaptic responses at 35°C. Note that time scales are different in A and B. C and D, plots for each measurable delay component against the number of stimuli in a train under the two experimental conditions described in A and B. Lines in these plots represent linear regression to scattered data points of 30 sweeps.

Electrophysiology

Presynaptic APs and EPSCs were generated through stimulation of afferent axons using a Master 8 stimulator (AP Instruments) coupled to a bipolar platinum electrode. All recordings were made with a dual-channel amplifier (MultiClamp 700A; Axon Instruments). Presynaptic cell-attached recordings (voltage-clamp mode) were performed to facilitate long-lasting, high accuracy recordings of presynaptic APs and to leave the presynaptic terminal undisturbed. ACSF was supplemented with bicuculline (10 μm) and strychnine (1 μm) to block inhibitory inputs during recording with [Ca²⁺]_o adjusted as noted. For recording of presynaptic Ca²⁺ currents, tetrodotoxin (TTX, 0.5 μm), tetraethylammonium (TEA, 10 mm) and 4-aminopyridine (4-AP, 0.3 mm) were added to block Na⁺ and K⁺ channels, respectively, while [Ca²⁺]_o was adjusted to 1, 2 or 2 mm with 50 μm baclofen. Patch electrodes typically had resistances of 4–6 and 2.5–3 MΩ for presynaptic and postsynaptic recordings, respectively. For whole-cell voltage-clamp recordings, presynaptic and postsynaptic series resistances were 6–12 MΩ (<10 MΩ in the majority of recordings) and 4–8 MΩ, respectively, compensated to 90%, with cells showing higher resistances being omitted from analysis. Intracellular recording solution used for cell-attached voltage-clamp and whole-cell current-clamp recordings contained (mm) potassium gluconate (97.5), KCl (32.5), EGTA (0.5), Hepes (10), and MgCl₂ (1), at a pH of 7.2 (adjusted with KOH). Intracellular recording solution for presynaptic Ca²⁺ currents contained (mm) CsCl₂ (110), Hepes (40), EGTA (0.5/10), MgCl₂ (1), ATP (2), GTP (0.5), phosphocreatine (12), TEA (30), potassium glutamate (3), at a pH of 7.3 (adjusted with CsOH). Intracellular solution for postsynaptic recordings contained (mm) potassium gluconate (97.5), CsCl (32.5), EGTA (5), Hepes (10), MgCl₂ (1), TEA (30) and lidocaine N-ethyl bromide (QX314; 3) (pH 7.2). Holding potentials were −70 and −60 mV for presynaptic terminals and postsynaptic neurons, respectively. Presynaptic Ca²⁺ currents (I_Ca) were evoked using a train of real APs as a voltage-command protocol (200 Hz, 150 ms) with leak subtraction performed with a P/4 protocol. AP trains were recorded from a current-clamped calyx (P15) in response to afferent stimulation (200 Hz, 200 ms), sampled at 50 kHz and filtered at 4 kHz. After manually removing stimulation artefacts preceding the APs, the digitized voltage values were fed back into the amplifier as a stimulation file (.atf, Axon Text File, pCLAMP 8.2) at the same frequency as their acquisition (50 kHz), evoking I_Ca from voltage-clamped terminals. All reagents were purchased Sigma, Tocris and Alomone Laboratories.

Data analysis

Data were acquired on-line, digitized at 50 kHz, filtered at 4 kHz, and analysed off-line using the pCLAMP 8.2 software package (Axon Instruments), Maple 7.2 (Waterloo Maple), and Excel 2000 (Microsoft). Conduction delay (Fig. 1A, segment 1) was defined as the delay between the peak of the stimulation artefact and the negative deflection of the presynaptic volley, which represents the maximum rate of depolarization of the presynaptic AP (Sabatini & Regehr, 1997; Yang & Wang, 2006). Synaptic delay (Fig. 1A, segment 2) was defined as the delay between the downward deflection of the presynaptic volley and the onset of the EPSC (see Appendix). Response rise delay (Fig. 1A, segment 3) was defined as the delay between the onset of EPSC and its peak. Finally, transmission delay (Fig. 1A, segment 4) was defined as the sum of the delays above. Fitting for the determination of the EPSC onset was performed in Clampfit 8.2 using a Levenberg–Marquardt search algorithm minimizing the sum of squared errors for the chosen function (Fig. 1C; also see eqn (13) in Appendix). Linear fitting, for error analysis and delay/variance progression, was also performed using a least-squares minimization. Baseline averages were sampled from a 10 ms portion of the recording preceding stimulation. Envelope plots (Figs 4, 5 and 7, and Supplemental Fig. 1) show individual delay values, as a function of event number, for 30 repeated trains at specified frequencies. Progression of delay was calculated as the slope of the least-squares linear fit through the 900 points displayed on each envelope plot and results are reported in microseconds per event. Variance of the reported delays was calculated for each event and plotted against event number (data not shown), a linear least-squares fit was then used to determine the progression of the variance, reported as the slope in microseconds squared per event. The recovery time constants for both EPSC area and the delay components (Fig. 9) were fitted with one- or two-term standard exponential equations, with their asymptote fixed at 100%, and using a Levenberg–Marquardt search algorithm minimizing the sum of squared errors. Statistical tests of significance were two-tailed unpaired Student's t tests assuming unequal variances with a P value cut-off of <0.05. Data are expressed as the mean ± standard error of the mean (s.e.m.) from a population of synapses (n). A summary of significance tests between all tested stimulation frequencies and experimental groups is provided in Supplemental Table 1. Significance is assessed for delay (blue) and variance (green), within the same comparison matrix, for each delay component.

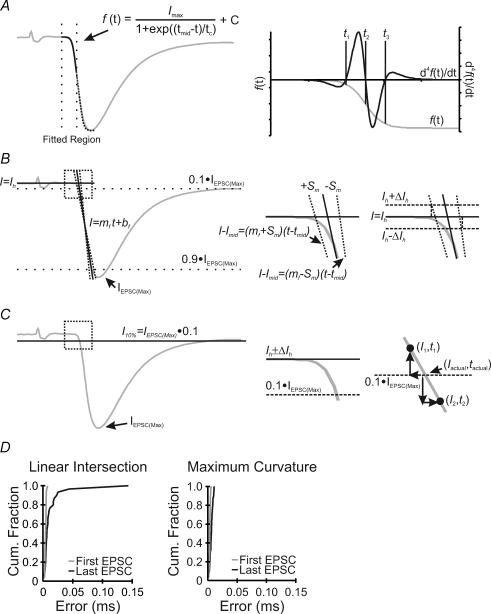
Figure 1. Experimental arrangement and analytical approaches for quantifying temporal delays of synaptic transmission.

A, simultaneous recording from a presynaptic calyx, in cell-attached configuration, and a postsynaptic neuron in whole-cell configuration (top). Example current traces (middle) are also shown, in which the deflections are marked with dotted lines to define conduction delay (1, CD), synaptic delay (2, SD), response rise delay (3, RRD), and transmission delay (4, TD). B, the first (black line) and last (grey line) EPSCs recorded during a stimulation train (200 Hz, 150 ms) are superimposed to show activity-dependent changes in size, kinetics and timing of synaptic responses. Two analytical approaches, namely the ‘threshold method’ (top) and ‘intersection method’ (bottom), are depicted for determination of EPSC onset (arrows). Dotted lines showing the 10% of maximum line are used to determine the onset of EPSCs in the former, whereas dotted lines, fit to the baseline and the 10–90% rise portion of the EPSC, define the intersection point as the onset of EPSCs in the latter. C, graphic presentation of the ‘maximal curvature method’ for determination of synaptic delay. The rise phase of an EPSC (dotted line) is first fit with an equation of the form of the Boltzmann charge–voltage equation, and the fitted curve is shown (black line). The 4th derivative of the fitted curve is then set equal to zero and solved for its three solutions (right), of which t₁ or t₃ define the maximal curvature point as the onset of an EPSC.

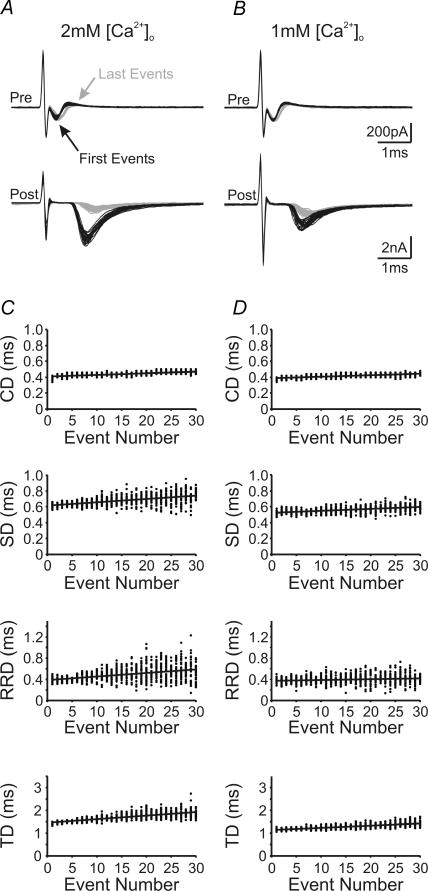
Figure 4. Activity and Ca²⁺ dependence of neurotransmission delay components.

A and B, first (black lines) and last (grey lines) pairs of presynaptic current deflections and postsynaptic EPSCs from 30 repeated stimulation trains (200 Hz, 150 ms) are aligned and superimposed to illustrate activity-dependent changes in presynaptic and postsynaptic responses in 2 mm[Ca²⁺]_o (A) and 1 mm[Ca²⁺]_o (B). C and D, plots for each measurable delay component against the number of stimuli in a train under the two experimental conditions described in A and B. Lines in these plots represent linear regression to scattered data points of 30 sweeps.

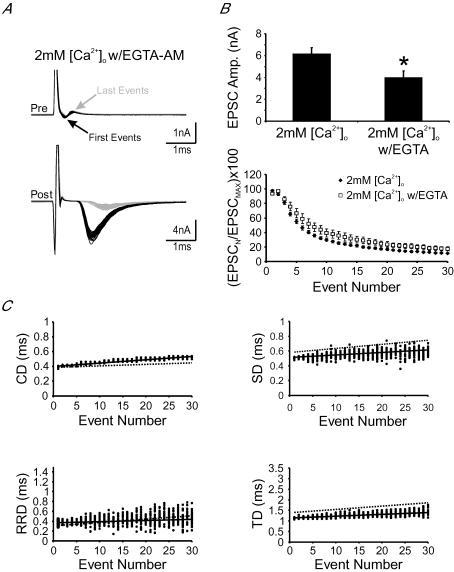
Figure 7. Intraterminal accumulation of residual Ca²⁺ underlies activity-dependent prolongation in neurotransmission delay components.

A, examples of first (black lines) and last (grey lines) pairs of presynaptic current deflections and postsynaptic EPSCs from 30 repeated stimulation trains (200 Hz, 150 ms) in 2 mm[Ca²⁺]_o w/EGTA-AM pretreatment. B, pooled data showing the amplitude of the first EPSCs (top) and a plot of normalized EPSC amplitude against event number in 2 mm[Ca²⁺]_o with and without EGTA-AM pretreatment (bottom). C, plots for delay components against the number of stimuli in a train under the experimental conditions described in A. Continuous black lines represent linear regression to scattered data points shown. Dashed lines represent linear regression to scattered data shown in Fig. 4C.

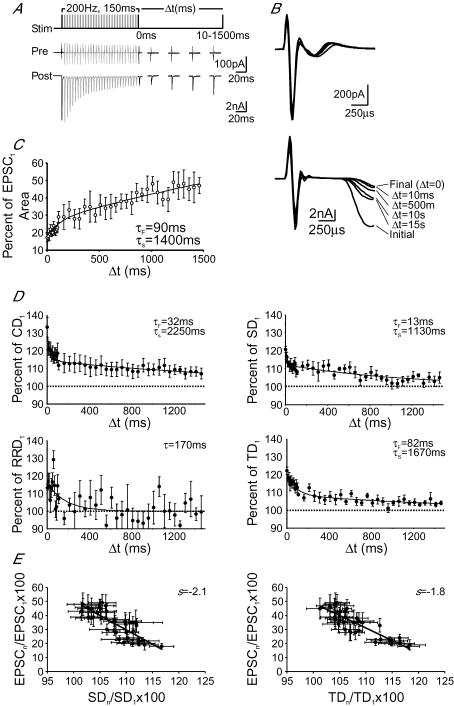
Figure 9. Recovery of delay components from activity-dependent prolongation.

A, stimulation protocol (top) for determining the recovery kinetics of delay components; 200 Hz, 150 ms trains were followed by a single test pulse at varying Δt from 10 to 1500 ms. Example traces showing averaged presynaptic current deflections (middle) and postsynaptic EPSCs (bottom), in response to the stimulation protocol in A, for Δt = 10, 500, 1000 and 1500 ms. B, magnification of the events shown in A are aligned by presynaptic stimulation artefact for the Δt in A (as marked). C, pooled data plotting EPSC area, as a percentage of the initial EPSC area, against Δt. Points were fitted with a biphasic exponential (continuous line). D, pooled data plotting delays, as a percentage of the initial delay, against Δt. Points were fitted with a biphasic exponential (solid lines) in all cases except for response delay, which was fitted with a single exponential. E, correlation plots of EPSC recovery versus recovery of synaptic delay (left) and transmission delay (right) as a percentage of the initial events. Continuous black lines represent linear regression to scattered data points shown.

Results

Definition of the temporal components of synaptic transmission

To experimentally separate the timing landmarks of signal propagation at the calyx of Held-MNTB synapse, we made dual-electrode recordings in which one electrode was sealed onto the presynaptic membrane, in the cell-attached voltage-clamp configuration, while the other electrode was used to establish a whole-cell voltage-clamp configuration in the postsynaptic neuron. We chose to use the cell-attached configuration, rather than whole cell current-clamp recordings of presynaptic APs, to minimize disruption of intraterminal homeostasis while maintaining long-lasting recordings. Presynaptic axons were stimulated with a platinum bipolar electrode placed less than 200 μm away from the recorded cells. Figure 1A shows an example of simultaneous pre- and postsynaptic recordings in response to a single stimulus. Following the stimulation artifact, the presynaptic pipette registered an AP invasion in the form of a compound current with inward and outward deflections, reflecting the depolarization and repolarization phases of the AP. The peaks of these currents, corresponding to the time point at which the maximal rate of AP depolarization/repolarization occurs, approximate the AP half-width (Sabatini & Regehr, 1997; Yang & Wang, 2006). Shortly afterwards, an excitatory postsynaptic current (EPSC) was recorded from the postsynaptic neuron. From such an experimental arrangement, we separated three temporal components of transmission delay (TD), as illustrated in Fig. 1A: (1) conduction delay (CD), the time interval between the peak of the stimulation artifact and that of the presynaptic inward current deflection, reflecting the time required for AP propagation; (2) synaptic delay (SD), the time interval between the peak of the presynaptic inward current deflection and the onset of an EPSC in the postsynaptic cell, representing the time required for Ca²⁺-dependent vesicular release of transmitter and the diffusion of that transmitter to postsynaptic receptors; and (3) response rise delay (RRD), the time interval between the onset of EPSC and its peak, providing a measure of the synchronicity of release events.

Amongst the three delay components, accurate determination of SD is the most difficult to achieve. The onset of EPSCs, unlike other measurement points with defined peaks, has no clear inflection as a reference. Two previous methods have been used to determine the onset of single EPSCs (Fig. 1B). The first method is based on setting an arbitrary proportion of the EPSC peak (e.g. 5 or 10%), at which the time point for the EPSC onset is taken (Taschenberger & von Gersdorff, 2000) (Fig. 1B, top trace) (named herein as the threshold method). The second takes the intersection point of two linear regression lines, one fit to the baseline and the other fit to the rise phase of the EPSC (10–90%), as the onset of EPSCs (Wu & Borst, 1999) (Fig. 1B, bottom trace, named herein as the intersection method). However, both methods tend to carry significant errors and methodological bias, especially when the EPSC rising phase is shallow, which makes their accuracy questionable under certain circumstances (see Fig. 10 for details). Here, we developed a novel method for determining the onset of EPSCs that improves the degree of detection accuracy and eliminates rise-phase-dependent bias. In this method, we define the onset of an EPSC as the point of maximal curvature along the EPSC rise phase. To mathematically resolve the maximal curvature point, we first fit the rise phase of the EPSC with an equation of the form of the Boltzmann charge–voltage function (Fig. 1C, left) and then solve this equation for its 4th derivative (Fig. 1C, right). Three solutions are generated as shown in Fig. 1C (and also in Fig. 10A, right), representing the two points of maximum curvature for the symmetric function (i.e. t₁ and t₃), and the other being the inflection point (half-maximal time, t₂). Choosing the solution that occurs earliest in time gives a highly accurate measure of the EPSC onset independent of the slope of the EPSC rise phase (see Appendix). Such an approach, which we have termed the maximal curvature method, reduces intrinsic errors and eliminates potential time biases associated with the other two methods (see Fig 2C and D; also Fig. 10D), as is confirmed in the following analyses of representative experiments in which both the amplitude and time course of recorded EPSCs exhibit profound changes during repetitive activity.

Figure 10. Quantitative assessment of three analytical methods for determination of the onset of EPSCs.

A, example EPSC (grey line, left trace), with fitted the Boltzmann equation (black line), and dotted lines highlighting the region used for the curve fitting process. The fitted function (grey line) and the 4th derivative (black line), aligned in time, are shown (right trace) with solutions to the 4th derivative given as vertical dotted lines (t₁, t₂ and t₃). B, same trace as in A analysed with the linear intersection method. The EPSC onset is determined by the intersection point of the two black lines, with the upper and lower error limits shown by dotted lines (left trace). The boxed region is magnified (right traces) to show the shift in the calculated EPSC onset time, with and without the inclusion of error in the horizontal baseline. The nomenclature refers to the appendix. C, same trace as in A analysed with the threshold method. The black line in the left trace indicates 10% of the EPSC peak. Magnification of the boxed region is shown (right traces) to illustrate the error inherent due to digitization. D, cumulative histograms of the error distributions in the determination of the EPSC onset from the first (grey line) and last (black line) EPSCs in response to train stimuli (200 Hz, 150 ms) using the linear intersection (left) and maximal curvature methods (right).

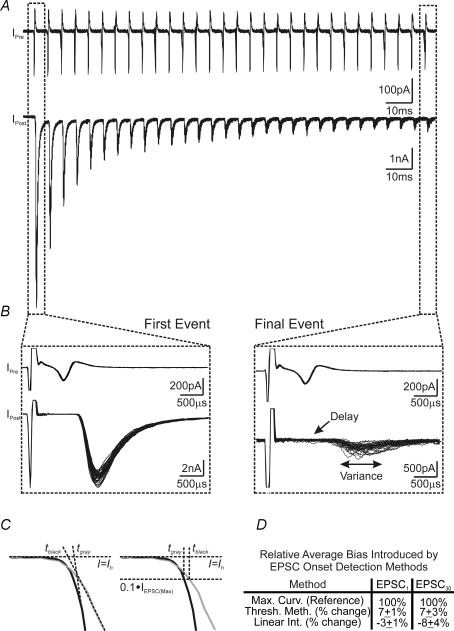
Figure 2. Quantitative comparison of different analytical methods for determining dynamic changes in the onset of EPSCs evoked by high-frequency stimuli.

A, example of paired presynaptic cell-attached (top) and postsynaptic whole-cell voltage-clamp recordings (bottom). Thirty current traces, in response to high-frequency afferent stimulation trains (200 Hz, 150 ms), are superimposed to illustrate activity-dependent changes in synaptic responses. Stimulation artefacts preceding presynaptic and postsynaptic currents have been removed for clarity. B, magnified view of first (left) and final (right) stimuli from the traces shown in A. Note the increase in both synaptic delay and variance in events towards the end of trains. C, an example contrasting two EPSCs with fast (black line) and slow rise phases (grey line), for which the linear intersection method (left) and threshold method (right) both bias the temporal onset of EPSCs. D, summary data showing the bias inherent in each of the methods shown in C as compared with the maximal curvature method for the determination of the EPSC onset.

Validity of the maximal curvature method for analysis of dynamic changes in SD during high-frequency neurotransmission

When afferent axons of the calyx of Held synapse were stimulated with high-frequency trains (200 Hz, 150 ms), we observed a robust synaptic depression with EPSC amplitudes declining to about 10% of the initial amplitude near the end of the train, in line with previous reports using similar stimulation protocols (Borst et al. 1995; Wang & Kaczmarek, 1998; Taschenberger & von Gersdorff, 2000). However, when the first and last events of paired pre- and postsynaptic recordings (30 sweeps superimposed) were contrasted, we noted that the last EPSCs appeared to have a delayed onset and increased variance in its timing (Fig. 2A and B). The small amplitude and highly variable rise phase of the last EPSCs in the train made it difficult to accurately quantify SD with the threshold method or the intersection method. As illustrated in Fig. 2C and D, when the EPSC rising phase slows, determination of the EPSC onset biases forward in time with the threshold method, and backward in time with the intersection method. To evaluate the accuracy of the maximal curvature method for determination of the EPSC onset, using the experiment exemplified in Fig. 2A, we estimated and compared the expected error in the EPSC onset using each of the detection methods (see Fig. 10D). Briefly, the linear intersection and maximum curvature methods have similar errors for the first event in the train (accuracy of several microseconds), with the error inherent in the threshold method being one order of magnitude larger. For the final event in the train, the linear intersection method showed a fourfold increase in error (tens of microseconds accuracy), while the maximum curvature method showed only a modest (∼1.5-fold) increase in error (still microseconds accuracy). The accuracy of the threshold method was unchanged during the train as it is independent of the shape of the EPSC and dependent only on the sampling rate of the digitizer. Both the threshold and linear intersection methods had errors one order of magnitude higher than those of the maximum curvature method for late events. With the EPSC onset depending on the slope of the EPSC rising phase, for both the linear intersection and threshold methods, we questioned whether either of these methods would bias their determination when the rising phase of the EPSC slows during repetitive stimulation. Analysis was performed to determine the EPSC onset and associated bias of the first and final events, shown in Fig. 2A and B, using each of the detection methods. As illustrated in Fig. 2C (left), when the slope of the EPSC rising phase decreases, the linear intersection method identifies the point of intersection as occurring earlier in time, although the actual onset may be identical. In contrast, the threshold method biases the EPSC onset forward in time, relative to EPSCs with steep rising phases. Using each of the methods to calculate the position of the EPSC onset from the traces shown in Fig. 2A, we found that the threshold method biased and average of 7 ± 1% forward in time for first and 7 ± 3% for final EPSCs, while the linear intersection method biased backwards in time an average of 3 ± 1 and 8 ± 4% for first and final EPSCs, respectively, as compared with the maximum curvature method (Fig. 2D). While the bias averages to small discrepancies in the EPSC onset, these discrepancies vary from 2 to 20% and −24 to 44% for the threshold method (first and last events, respectively) for some traces. The linear intersection method showed a range of discrepancies of −9 to 11% and −61 to 31%, for first and last events, respectively, over the 30 sweeps analysed. When both the error and methodological bias were considered, in the context of delay changes of generally less than 500 μs during high-frequency transmission, it was evident that these methods were insufficient to resolve small changes in delay from event to event. Furthermore, bias, depending on the detection method chosen, may mask or enhance small changes in delay, producing misleading results. Given the results of such comparative analyses, we suggest that the maximal curvature method provides a significant advantage over previous methods and can measure small changes in the various temporal components of synaptic transmission with accuracy in the order of microseconds throughout stimulus trains.

Frequency-dependent prolongation in transmission delays and variance

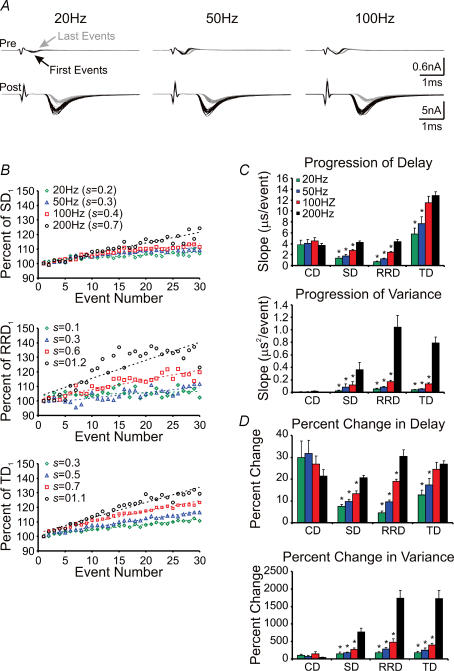
Inspection of pre- and postsynaptic recordings revealed that, in contrast to the profound jitter of the last EPSCs, current traces reflecting presynaptic APs showed little variation in shape and size between sweeps (Fig. 2B, right), suggesting that activity-dependent changes in SD and variance occur downstream of AP arrival at the calyx terminal. Armed with our novel analytical approach, we next quantified three temporal components, namely CD, SD and RRD, of synaptic transmission. Thirty sweeps of pre- and postsynaptic events, in response to stimulus trains at 20, 50, 100 and 200 Hz (30 stimuli per train), were recorded and analysed for each experimental condition designed to explore the potential mechanisms underlying these short-term temporal changes in delay components.

Figure 3A illustrates an example of paired pre- and postsynaptic recordings in response to 30 sweeps of train stimuli at various frequencies in 2 mm extracellular Ca²⁺ ([Ca²⁺]_o). Sweeps from the 1st (black) and 30th (grey) events are superimposed. Initial events from this recording were found to have basal TD (the sum of the three component delays) of approximately 1.34 ms, with CD, SD and RRD comprising about 0.44, 0.51 and 0.39 ms, respectively (Fig. 3A and D). When these temporal components were quantified from each pair of events, and plotted against the stimulus number, we found that all three delays were prolonged by about 5–30% in a frequency-dependent manner, being most robust at 200 Hz (Fig. 3B). These changes were well described by a linear function with a slope or rate of delay progression (s, microseconds per event), being 3.6, 1.0, 0.5 and 5.0 μs event⁻¹ at 20 Hz, and 4.0, 4.2, 7.0 and 15.0 μs event⁻¹ at 200 Hz for CD, SD, RRD and TD, respectively. When pooled, across all frequencies tested, the progression of delay was 3.8 ± 0.8, 1.4 ± 0.2, 0.6 ± 0.1 and 6.0 ± 1.0 μs event⁻¹ (n = 7) at 20 Hz, 4.1 ± 0.7, 1.8 ± 0.2, 1.3 ± 0.1 and 7.0 ± 1.0 μs event⁻¹ (n = 7) at 50 Hz, 4.0 ± 0.5, 2.7 ± 0.2, 2.4 ± 0.1 and 12.0 ± 1.0 μs event⁻¹ (n = 7) at 100 Hz, and 3.6 ± 0.3, 4.2 ± 0.2, 4.3 ± 0.4 and 13.4 ± 0.2 μs event⁻¹ (n = 11) at 200 Hz for CD, SD, RRD and TD, respectively (Fig. 3C, top). In parallel, these delays also showed frequency-dependent increases in their variance (in microseconds squared per event), which also followed a linear functions with slopes of 0.006 ± 0.001, 0.02 ± 0.01, 0.05 ± 0.01 and 0.04 ± 0.007 μs² event⁻¹ (n = 7) at 20 Hz, 0.008 ± 0.002, 0.08 ± 0.04, 0.084 ± 0.008 and 0.053 ± 0.007 μs² event⁻¹ (n = 7) at 50 Hz, 0.010 ± 0.006, 0.12 ± 0.05, 0.17 ± 0.03 and 0.14 ± 0.02 μs² event⁻¹ (n = 7) at 100 Hz, and 0.007 ± 0.001, 0.3 ± 0.1, 1.0 ± 0.2 and 0.79 ± 0.09 μs² event⁻¹ (n = 11) at 200 Hz for CD, SD, RRD and TD, respectively (Fig. 3C, bottom). Furthermore, we calculated the percentage change in both delay and variance for each of the stimulation frequencies tested. Delay increased by 30.0 ± 8.0, 7.5 ± 0.9, 4.6 ± 0.9 and 13.0 ± 2.0% at 20 Hz, 32.0 ± 6.0, 10.0 ± 1.0, 9.6 ± 0.9 and 17.0 ± 3.0% at 50 Hz, 27.0 ± 4.0, 13.0 ± 1.0, 19.0 ± 0.9 and 25.0 ± 3.0% at 100 Hz, and 21.0 ± 3.0, 21.0 ± 1.0, 30.0 ± 3.0 and 27.0 ± 2.0% at 200 Hz for CD, SD, RRD and TD, respectively (Fig. 3D, top). Variance increased by 100 ± 39, 150 ± 51, 170 ± 41 and 160 ± 48% at 20 Hz, 80 ± 29, 180 ± 22, 290 ± 35 and 250 ± 66% at 50 Hz, 150 ± 64, 270 ± 44, 480 ± 98 and 400 ± 49% at 100 Hz, and 45 ± 7, 700 ± 100, 1700 ± 215 and 1700 ± 228% at 200 Hz for CD, SD, RRD and TD, respectively (Fig. 3D, bottom). As a result of prolongations in individual delay components and their variance, TD and its variance displayed significant increases, as illustrated in Fig. 3C and D. The magnitude of activity-dependent prolongation in SD, RD, and therefore TD, depend strongly on the frequency of the activity with stronger activity evoking more prolongations in delays and increases in variance. Our observations at the calyx of Held synapse demonstrate that the temporal components of synaptic transmission, including SD, are highly sensitive to activity and can undergo short-term plastic changes in central synapses.

Figure 3. Frequency-dependence of increases in neurotransmission delay and variance during repetitive stimulation.

A, first (black lines) and 30th (grey lines) pairs of presynaptic current deflections and postsynaptic EPSCs, from 30 repeated stimulation trains at 20 (left), 50 (middle) and 100 Hz (right), are aligned and superimposed to illustrate the frequency dependence of delay in pre- and postsynaptic responses (P15, 2 mm[Ca²⁺]_o). B, average change in synaptic (top), response rise (middle) and transmission (bottom) delays, as a function of stimulus number, for 20 (green diamonds), 50 (blue triangles), 100 (red squares) and 200 Hz (black circles) stimulation frequencies shown in A. Data shown for 200 Hz are taken from the example shown in Fig. 2A. Dashed lines are least-squares regressions through data shown. C, summary data showing the progression of delay (μs event⁻¹, top) or variance (μs² event⁻¹, bottom) for each delay component at each frequency shown in B. D, summary data showing the percentage change in delay and variance, compared between the first and final three events in a train, for each delay component at each frequency shown in B. *P < 0.05 (Students t test) vs 200 Hz group (black bars).

Lowering Ca²⁺ influx into the nerve terminal reduces activity-dependent increases in transmission delays and variance

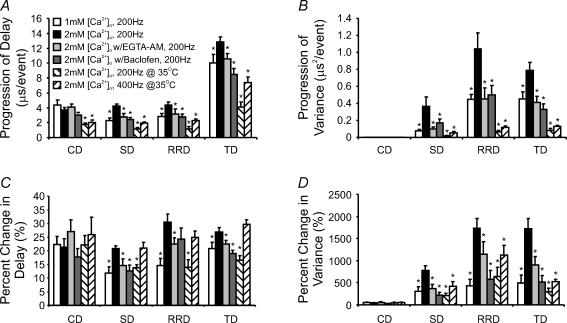
Given that the calyx of Held synapse exhibits the most profound changes in temporal delay components at 200 Hz, where synaptic depression is also strongest over the tested frequency spectrum, we asked whether reducing the extent of synaptic depression can attenuate temporal changes in delays and their variances. To this end, we reduced [Ca²⁺]_o from 2 to 1 mm, thereby reducing the driving force for Ca²⁺ entering the nerve terminal and attenuating synaptic depression during high-frequency stimulation. Overlaying the 1st and 30th pairs of events, as in Fig. 4A and B, showed that neither the size nor the shape of presynaptic APs was significantly affected by lowering [Ca²⁺]_o, but initial synaptic strength and synaptic depression were reduced as expected. Analyses of the various temporal delays revealed that the activity-dependent increase in CD was not affected by lowering [Ca²⁺]_o, while both the progression of SD and RRD, as well as their variances, decreased significantly (s and variance in 2 mmversus 1 mm[Ca²⁺]_o: sd: 4.2 ± 0.2 versus 2.3 ± 0.3 μs event⁻¹, variance: 0.4 ± 0.1 versus 0.08 ± 0.01 μs² event⁻¹; RRD: 4.4 ± 0.4 versus 2.8 ± 0.4 μs event⁻¹, variance: 1.0 ± 0.2 versus 0.50 ± 0.06 μs² event⁻¹; P < 0.05 in all cases, n = 11 versus 6) (Fig. 4C and D, also see Fig. 8). Slowed activity-dependent prolongation in SD and RRD also caused a resultant decrease in the progression of the sum TD and its variance (TD: 13.0 ± 0.7 versus 10 ± 1.0 μs event⁻¹, variance: 0.80 ± 0.09 versus 0.40 ± 0.08 μs² event⁻¹, for 2 mmversus 1 mm[Ca²⁺]_o, respectively, P < 0.05, n = 11 versus 6). If we compare the percentage increase, in either delay or variance, between the 1st and 30th events, lowering [Ca²⁺]_o from 2 to 1 mm reduced the increase in SD from 21 ± 1 to 12 ± 2%, and its variance from 800 ± 100 to 300 ± 100%, the increase in RRD from 30 ± 3 to 15 ± 3% and its variance from 1700 ± 200 to 400 ± 150%, and the increase in TD from 27 ± 2 to 21 ± 2% and its variance from 1700 ± 200 to 500 ± 200% (P < 0.05 in all cases) (also see Fig. 8). Neither the delay nor the variance of the conduction component was affected by altering [Ca²⁺]_o (Fig. 4C and D, top; Fig. 8). In line with these results, we found that the progression rate of delays, and the increase in their variances, were reduced in 2 mm[Ca²⁺]_o with the addition of 50 μm of the GABA_BR agonist baclofen (See Fig. 8 and Supplemental Fig. 1), which acts through a G-protein-mediated signalling cascade (G_βγ) to inhibit P/Q-type Ca²⁺ channels (Isaacson, 1998; Takahashi et al. 1998; Kajikawa et al. 2001), the type predominantly mediating release of neurotransmitter in the calyx of Held at this developmental stage (Forsythe et al. 1998; Iwasaki et al. 2000). These data collectively suggest that a reduction in the influx of Ca²⁺ into the nerve terminal attenuates the rate and degree to which delay and variance increase during high-frequency synaptic activity.

Figure 8. Comparison of activity-dependent changes in temporal delays and their variance.

A and B, pooled data showing the progression rate of delay (A) for all temporal components, and their variance (B) for various experimental conditions. C and D, pooled data showing the relative extent of the prolongation in various delay components (C) and their variance (D), as in A and B. *P < 0.05 (Student's t test) against the 2 mm[Ca²⁺]_o data set. Comparisons between other data sets are shown in Supplemental Table 1.

Increasing temperature reduces activity-dependent increases in transmission delays and variance

Because elevating temperature shortens presynaptic AP width, reduces Ca²⁺ influx and short-term depression during train stimuli (Taschenberger & von Gersdorff, 2000; Kushmerick et al. 2006; Yang & Wang, 2006), we next examined activity-dependent changes in delay for the three temporal components, and their variances, at the near physiological temperature of 35°C in 2 mm[Ca²⁺]_o. At 200 Hz, we found that synaptic transmission was accelerated with all temporal delay components shortened at the onset of the stimulus train (i.e. 1st events). Activity-dependent increases in delays, and their variances, remained, though to a lesser extent than that at room temperature (Fig. 5A and CversusFig. 4A and C, and Fig. 8). SD, RRD and TD progressed during the train at a rate of 1.1 ± 0.2, 1.2 ± 0.3 and 4.1 ± 0.6 μs event⁻¹ (n = 6), while variance of these components also increased at a rate of 0.018 ± 0.006, 0.07 ± 0.02 and 0.08 ± 0.02 μs² event⁻¹, respectively. The extent to which the delay and variance increased in 2 mm[Ca²⁺]_o at 35°C was similar to that recorded at room temperature in 1 mm[Ca²⁺]_o, with SD and RRD being 14 ± 1 and 14 ± 3%, and their variance being 200 ± 50 and 600 ± 200%, respectively (n = 6). However, when we increased the stimulation frequency to 400 Hz at 35°C, prolongation in delay components and their variance again increased markedly, with progression rates being 2.0 ± 0.1, 2.2 ± 0.2 and 7.3 ± 0.7 μs event⁻¹ (n = 8), and their variance being 0.05 ± 0.01, 0.12 ± 0.01 and 0.13 ± 0.01 μs² event⁻¹ (n = 8) for SD, RRD and TD, respectively (Fig. 5B and D). On average, delays increased by 21 ± 2, 25 ± 2 and 30 ± 2% (n = 8), while variance increased 400 ± 100, 1100 ± 200 and 500 ± 50% (n = 8) for SD, RRD and TD, respectively. In contrast, CD and its variance were unaltered by such a manipulation (see Fig. 8). These data suggest that activity-dependent increases in temporal delays and the propensity for temporal jitter, during high-frequency stimulation, are intrinsic physiological properties of this synapse and can occur at near physiological temperatures.

Prolongation in delay and increase in variance occurs downstream of Ca²⁺ influx

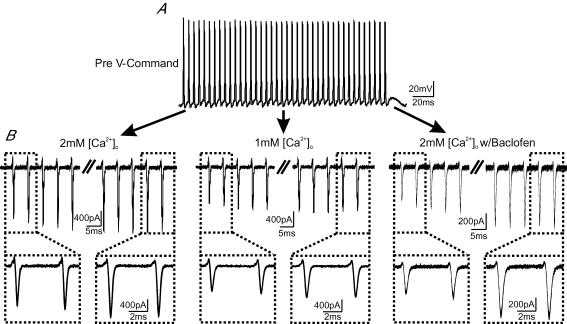
Although high-frequency train stimulation led to an increase in CD, presynaptic recordings showed that the 30th APs displayed little variation in their waveform or temporal jitter (e.g. Fig. 2B), implying that the prolongation in SD and RRD, and progressive increases in their variance, must originate downstream of APs themselves. One source of such changes may be that the size and timing of Ca²⁺ currents evoked by AP trains fluctuates between sweeps, introducing variations in quantal output and temporal asynchrony of fusion events. To test this, we performed whole-cell voltage-clamp recordings of Ca²⁺ currents from the calyx terminal, for which we have previously demonstrated that good space-clamp can be achieved (Yang & Wang, 2006). Ca²⁺ currents were evoked in response to a train of real APs used as a voltage-clamp command waveform. These APs were previously recorded from a current-clamped calyx (P15) in response to axonal stimulation at 200 Hz for 200 ms (Fig. 6A). Ca²⁺ currents were then examined for fidelity in amplitude and timing. Figure 6B shows recordings of 10 superimposed traces of Ca²⁺ currents evoked, as above, in 2 mm[Ca²⁺]_o (left), 1 mm[Ca²⁺]_o (middle) and 2 mm[Ca²⁺]_o with 50 μm baclofen (right). Although the amplitude and facilitation of Ca²⁺ currents differed in the three conditions, their shape and size exhibit extremely high fidelity during repeated sweeps, with no observable jitter in the timing at any stage during the high-frequency AP trains (Fig. 6B, insets). These observations were highly reproducible among different calyces (n = 5–10 for each condition). The fact that AP-evoked Ca²⁺ currents display such high fidelity suggests that the source of the observed activity-dependent increases in delay and variance occurs downstream of Ca²⁺ channel gating.

Figure 6. Temporal plasticity of synaptic transmission is mediated by mechanisms downstream of AP-evoked Ca²⁺ influx.

A, voltage-clamp template of an AP train (200 Hz, 200 ms) used for evoking Ca²⁺ currents from calyces. Note that these real APs were previously recorded in whole-cell current-clamp configuration from a nerve terminal (P15), in response to afferent stimulation, and digitally converted into a voltage-clamp command file (see Methods). B, Ca²⁺ currents evoked by the AP train template in 2 mm[Ca²⁺]_o (left), 1 mm[Ca²⁺]_o (middle) and 2 mm[Ca²⁺]_o w/50 μm baclofen (right) solutions are shown. In each case, 10 repeated sweeps of Ca²⁺ currents are overlaid to demonstrate their temporal fidelity. Insets (B, bottom) contrast the first and last two Ca²⁺ currents magnified from those shown in the top traces.

Reducing intra-terminal Ca²⁺ accumulation attenuates activity-dependent increases in delay and variance

Knowing that Ca²⁺ currents preserve fidelity in their timing during high-frequency synaptic transmission, we next asked whether accumulation of residual Ca²⁺, during repetitive activity, underlies the observed activity-dependent temporal plasticity. To investigate this possibility, we made use of EGTA-AM, a membrane-permeable Ca²⁺ buffer, which accumulates intracellularly following cleavage of its AM-ester group by endogenous esterases. Because EGTA has a slow forward rate constant for the binding of Ca²⁺ ions, it is assumed that it may effectively buffer accumulation of residual Ca²⁺ in the terminal (Adler et al. 1991; Kamiya & Zucker, 1994; Regehr et al. 1994; Naraghi & Neher, 1997; Fedchyshyn & Wang, 2005). Although it is difficult to know the exact amount of buffer that has accumulated in the presynaptic terminal, following pretreatment of slices with EGTA-AM (50 μm) for 30 min, we noted that the amplitude of EPSCs were noticeably attenuated from 6.1 ± 0.6 to 4.0 ± 0.6 nA (Fig. 7A and B, top), consistent with previous observation that EGTA can block a fraction of transmitter release either with direct loading into the terminal through patch pipette or incubation of AM-ester form for synapses at the developmental stage used for this study (Fedchyshyn & Wang, 2005; Korogod et al. 2005). Furthermore, EGTA-AM pretreatment also led to a slight facilitation in EPSCs while the extent of synaptic depression was reduced and its kinetics slowed, in line with the effects of this buffer at the nerve terminal (Fig. 7B, bottom). In pretreated synapses, high-frequency stimulation of afferent axons resulted in attenuated progression rates for SD, RRD and TD (Fig. 7C) (s in 2 mm[Ca²⁺]_oversus 2 mm[Ca²⁺]_o w/EGTA-AM: 4.2 ± 0.2 versus 2.8 ± 0.4 μs event⁻¹ for SD; 4.4 ± 0.4 versus 3.2 ± 0.6 μs event⁻¹ for RRD; 13.0 ± 0.7 versus 10.5 ± 0.7 μs event⁻¹ for TD; P < 0.05, n = 11 versus 6). The extent to which delay increased was also reduced for all delays (s in 2 mm[Ca²⁺]_oversus 2 mm[Ca²⁺]_o w/EGTA-AM: 21 ± 1 versus 15 ± 2% for SD; 30 ± 3 versus 22 ± 2% for RRD; TD: 27 ± 2 versus 22 ± 1%; P < 0.05). In parallel, the progression rate of variance for each delay component was also attenuated by pretreatment with EGTA-AM (SD variance: 0.4 ± 0.1 versus 0.10 ± 0.02 μs² event⁻¹; RRD variance: 1.0 ± 0.2 versus 0.4 ± 0.1 μs² event⁻¹; TD variance: 0.79 ± 0.09 versus 0.41 ± 0.07 μs² event⁻¹ for 2 mm[Ca²⁺]_o and 2 mm[Ca²⁺]_o w/EGTA-AM, respectively, P < 0.05). Similarly, the extent of increase in the variance declined (SD variance: 700 ± 100 versus 370 ± 90%; RRD variance: 1700 ± 200 versus 1100 ± 200%; TD variance: 1700 ± 200 versus 900 ± 200%; for 2 mm[Ca²⁺]_o and 2 mm[Ca²⁺]_o w/EGTA-AM, respectively, P < 0.05) (see Fig. 8). These observations demonstrate that activity-dependent changes in delays, and their variances, strongly depend on the build-up of residual Ca²⁺ in the calyx terminal. Since APs and Ca²⁺ currents precisely preserve timing during repetitive activity, we suggest that this build-up underlies the breakdown of synchrony and reproducibility of fusion events.

Mechanisms underlying activity-dependent prolongation in temporal delays

Reducing Ca²⁺ influx into the calyx or buffering intraterminal accumulation of Ca²⁺ in the aforementioned experiments all led to decreases in activity-dependent prolongation of temporal delays of transmission and their variances, as well as the extent of short-term synaptic depression in synaptic strength. Given these observations, we hypothesized that changes in synaptic strength and temporal delays during high-frequency activity may be related. To test this, we measured the recovery time course of synaptic strength and delay components by delivering single test pulses at different time intervals (Δt) after repeated high-frequency trains (Fig. 9A and B). Figure 9A shows a typical experiment in which the amplitude of EPSCs declined in response to the test train (200 Hz, 150 ms), but gradually recovered in as Δt increased. When pre- and postsynaptic responses, evoked by single test pulses at different intervals, were superimposed and aligned by stimulus artefact (Fig. 9B), we noted that the temporal delays recovered in parallel with the recovery of synaptic strength (Fig. 9C and D). Recovery of the delay components showed that CD, SD and TD followed a biphasic exponential time course with fast and slow time constants ranging from 13 to 82 ms and 1100 to 2300 ms, respectively. Recovery of RRD was fit with single exponential function (τ= 170 ms) since RRD data appeared to be scattered, probably due to significant asynchrony of quantal release and small amplitude of EPSCs (Fig. 9D). These values are similar to those for the recovery time course of synaptic strength (Fig. 9C). Plotting the recovery of SD (Fig. 9E, left) and TD (Fig. 9D, right) against the recovery of EPSCs yielded linear correlations significantly past 95% confidence (R = 0.82 and 0.87 for SD and RD, respectively), and suggest that the recovery of both delay and EPSCs may share an underlying mechanism. Upon closer inspection of our data on changes in SD, RD and TD, we noted that prolongations in these parameters and their variance became most apparent when the amplitude of EPSCs during high-frequency train was depressed to about 30% of the initial quantal output (e.g. Figure 4C). Furthermore, when the amplitude of the EPSC evoked by the test pulse returned to about 30% of the first EPSC, the fast component of recovery for prolongations in SD, RD and TD was also complete. We interpreted these lines of evidence to suggest that high-frequency activity leads to a depletion of the readily releasable pool of SVs, and/or a reduction of release probability. Depletion transforms transmitter release from fast synchronous events, near the beginning of the train, to slower asynchronous stochastic events towards the end. Following the cessation of a train, replenishment of depleted release sites with SVs from the peripheral reserve pool at least partially restored synaptic strength and temporal fidelity of fusion events.

Discussion

With a novel and unbiased analytic approach, termed the ‘maximal curvature method’, to precisely dissect out different delay components of synaptic transmission (Figs 1 and 10), we have revealed a new form of activity-dependent, short-term plasticity at the calyx of Held synapse. We found that high-frequency axonal stimulation prolongs the various temporal components underlying SV release and increases their variance in a frequency-dependent manner (Fig. 3). We have further demonstrated that such changes at 200 Hz can be attenuated by reducing the amount of Ca²⁺ influx via lowering [Ca²⁺]_o, raising experimental temperature, or inhibiting VGCCs with GABA_BR agonist baclofen (Figs 4 and 5, and Supplemental Fig. 1). Changes in delays and their variance are independent of presynaptic I_Ca (Fig. 6), but facilitation of I_Ca during a train of APs may contribute to intraterminal accumulation of residual Ca²⁺. As calyceal preloading of the slow Ca²⁺ buffer EGTA-AM effectively reduces the progression rate of activity-dependent increases in various delay components and their variances, we suggest that the build-up of residual Ca²⁺ downstream of Ca²⁺ entry during APs is likely to be the key mediator of such changes (Fig. 7). A quantitative description of the various temporal delays and their variances under different experimental conditions are presented in Fig. 8. Both the slope, representing the progression rate in each component delay and its variance (Fig. 8A and B), and the relative increase in each delay and variance component, from the beginning to the end of test train (i.e. 1st versus 30th event) (Fig. 8C and D), are compared. These results present compelling evidence that central synapses can exhibit temporal changes in the form of activity- and Ca²⁺-dependent increases in delay and variance, along with changes in synaptic strength.

Among the three delay components that we have separated, with paired recordings from pre- and postsynaptic elements of the same synapses, CD shows similar prolongation to the other delay components but little change in its delay or variance under most experimental conditions (Fig. 8). This is evident from the observation that the presynaptic AP waveform remains highly superimposed, between sweeps and throughout the trains (e.g. Fig. 2B), despite slight AP broadening during each stimulation train (i.e. increased peak-to-peak time interval between inward and outward current deflections in presynaptic cell-attached recordings). Large axons leading to the calyceal terminals presumably play an important role in maintaining temporal fidelity in CD. Nevertheless, absolute time for CD can be significantly shortened by increasing temperature, but activity-dependent prolongation in CD remains and is resistant to experimental manipulations. It is possible that axons still experience fatigue due to the build-up of K⁺ and/or undergo Na⁺ channel inactivation during repetitive high-frequency activity or a process sensitive to temperature but not Ca²⁺, as suggested by our observations under different conditions in this study.

In contrast to CD, SD and RRD are highly sensitive to manipulations that affect intraterminal Ca²⁺ levels. By lowering [Ca²⁺]_o, or attenuating Ca²⁺ currents with baclofen, activity-dependent prolongation in these two delays and their variances decreased significantly, suggesting that temporal changes in these parameters are Ca²⁺ dependent. Direct voltage-clamp recordings of Ca²⁺ currents, in response to repeated trains of high-frequency APs, revealed that these currents are highly faithful in timing and waveform, indicating that the progressive increase and fluctuations in the latency of EPSCs originates downstream of Ca²⁺ entry. Indeed, our observation that EGTA-AM pretreatment attenuates activity-dependent increases in SD and RRD, and their variances, suggests that residual accumulation of intraterminal Ca²⁺ is a critical factor underlying such temporal plasticity. Because conditions that influence the rate and extent to which synaptic depression occurs also appear to influence the rate of progression of delay and variance (e.g. [Ca²⁺]_o), we suggest that both these forms of short-term plasticity may share common underlying mechanisms. Indeed, recovery kinetics in synaptic strength, following synaptic depression by high-frequency trains, appears to correlate with those of SD and TD (Fig. 9). We interpret these observations such that high-frequency activity sequentially depletes the readily releasable pool (RRP) of SVs, which are coupled most tightly to release sites and are released with the shortest latencies. Release of SVs, recruited from the periphery of the RRP, follows this rapid release (Wang & Kaczmarek, 1998; Sakaba & Neher, 2001; Schneggenburger et al. 2002; Otsu et al. 2004; Sakaba, 2006). Because of the heterogeneous distance of peripheral SVs to the release sites, the increased time required for the recruitment and release of these SVs may therefore introduce not only prolongations in sd, but also variability or asynchrony in the timing of release events. Increased jitter in SD towards the later part of trains may simply mirror the inherent stochastic nature of vesicular release when tightly docked vesicles are depleted and/or release probability is substantially reduced, as has been demonstrated at the end bulb of Held synapse with Ca²⁺ channel blocker cadmium (Isaacson & Walmsley, 1995). However, we cannot exclude the possibility that temporal changes in SD and RRD could result from an activity-dependent refractory period of release sites (Stevens & Wang, 1995) or exhaustion of the release machinery (e.g. Ca²⁺ sensor) (Hsu et al. 1996), leading to short-term transient prolongations in temporal delays.

Previous work has shown that first latency distribution histograms of release events at the NMJ display remarkable stability under different experimental conditions, implying that the minimal SD is rather static and therefore the timing of exocytosis following AP invasion is not plastic (Katz & Miledi, 1965; Barret & Stevens, 1972; Datyner & Gage, 1980; Parnas, 1989). However, those studies were done primarily with single or pairs of stimuli. Little is known regarding whether the various temporal components of neurotransmission show activity-dependent plasticity when synapses are presented with more physiological stimuli such as high frequency trains. Indeed, when this issue was investigated in non-mammalian synapses using other protocols such as paired-pulse stimuli or trains, it was demonstrated that SD could be modified under appropriate conditions (Vyshedskiy et al. 2000; Waldeck et al. 2000). At the calyx of Held-MNTB synapse, increases in both AP latency and EPSC onset have also been observed following prolonged tetanic stimulation (Habets & Borst, 2005; Kim et al. 2007). However, it is not know whether such changes are due to changes in the timing and magnitude of Ca²⁺ currents or depend on factors residing downstream of Ca²⁺ entry. Our study has clearly demonstrated that increases in SD and its variance are both a result of residual Ca²⁺ accumulation downstream of AP-evoked Ca²⁺ influx during repetitive activity. Interestingly, Wu & Borst (1999) showed in the immature calyx-of-Held synapses (P8–10) that SD, in response to a pair of brief APs (half-width, 0.5 ms; amplitude, −80 to +30 mV), was not altered during synaptic depression. However, SD was prolonged when assayed with a prolonged pair of voltage steps with longer duration (10 ms), and of smaller amplitude (−80 to 0 mV), than real APs. This observation lends support to our interpretation that activity-dependent increases in SD and its variance reflect sequential depletion and recruitment of SVs during train stimuli. High-frequency activity mimics the effects of prolonged steps, where the first step largely depletes the SVs in the RRP, and the second step recruits latent peripheral SVs to the depleted release sites increasing the SD.

Physiological relevance

By paired recordings directly from the nerve terminal and its postsynaptic target neuron, we have provided insights into understanding the constraints of temporal fidelity of neurotransmission. We have also provided the proof-in-principle that activity-dependent changes in the temporal delay components of synaptic transmission can occur in mammalian central synapses. One can envision that such temporal changes may be common and more profound for typical en passant synapses with thin axons and tiny boutons containing limited number of SVs. AP propagation along thin axons may experience significant increase in CD during repetitive activity, while small size of readily releasable pool of SVs may be depleted quickly to cause prolongations in SD and RD. Furthermore, presynaptic boutons are spatially innervating different parts of dendrite branches of the same target neuron, potentially expanding the window for temporal summation of inputs. Temporal delays in such circumstances may in fact be of physiological significance for neural computation (Lu & Trussell, 2000; Markram et al. 1998). Being a critical relay station specialized in preserving timing information for sound localization, the calyx of Held-MNTB synapse must be superior to other synapses in preserving the temporal fidelity of synaptic input. Our experiments at near physiological temperature of 35°C demonstrate that temporal changes in three delay components is indeed limited at 200 Hz, but exacerbated with an increase in stimulation frequency (e.g. 400 Hz), indicating that such changes are inherent properties of synapses. Nevertheless, knowing that this synapse can operate at much higher frequencies (>600 Hz), our observations lead us to suggest that there are several important strategic adaptations, which the calyx of Held synapse may develop for best preserving timing information. First, we have demonstrated in this study that synaptic depression and prolongations in temporal delays are two well-correlated processes (Fig. 9). Developmental narrowing APs at the calyx would make Ca²⁺ transients very brief and reduce the extent of short-term depression in synaptic strength during high-frequency transmission, thereby minimizing delays and maximizing their reproducibility. Such effects are reminiscent of those by shortening the half-width of APs at higher temperature (Fedchyshyn & Wang, 2005; Kushmerick et al. 2006; Yang & Wang, 2006). Second, efficient clearance of Ca²⁺ by buffering and extrusion may help reduce the effects of residual Ca²⁺ build-up on prolongations in delays, as implicated by our EGTA-AM experiments (Fig. 7). In fact, developmental upregulation of endogenous calyceal Ca²⁺ buffering proteins, such calretinin and parvalbumin, beyond the postnatal stage used in this study (i.e. P14–16), has been demonstrated (Felmy & Schneggenburger, 2004). Ca²⁺ pumps/exchangers may also operate more efficiently at physiological temperature to accelerate removal of residual Ca²⁺ (Helmchen et al. 1997). Finally, it should also be noted that although 2 mm[Ca²⁺]_o is generally used in a majority of studies performed in brain slices, physiological [Ca²⁺]_o is likely to be closer to 1 mm (Jones & Keep, 1988). Lower [Ca²⁺]_o can reduce the drive force for Ca²⁺ influx during each spike, and further minimize the temporal changes of neurotransmission as observed in this study (Fig. 4). Taken together, these factors may be potentially crucial for curtailing accumulation of intraterminal [Ca²⁺]_i, and preserving temporal fidelity of synaptic transmission at the calyx of Held synapse.

Appendix: sources of error in determining the EPSC onset

Intersection method

The intersection method defines the EPSC onset as the intersection point of two lines fit to the experimental data. The first is a horizontal line fit to the baseline region preceding the onset of the EPSC, the choice of what constitutes the baseline being arbitrary. The second is fit to the rising phase of the EPSC, and this is defined as an arbitrary range, usually either 10–90 or 20–80% of the EPSC peak (Fig. 10B). The equations of the lines are given as:

(1)

(2)

where I_h is the baseline current, m_f is the slope of the line fitted to the EPSC rising-phase, and b_f is the I intercept of the line fitted to the EPSC rising phase. Setting eqns (1) and (2) equal allows for the determination of t at the intersection point which is the defined EPSC onset using this method.

Sources of error

While this method is algebraically simple, it has sources of error in both eqns (1) and (2) that affect its overall accuracy. Eqn (2) is subject to error in both of its parameters, m_f and b_f, which depend on deviations of the source data (EPSC rising phase) from linearity. The sum of squared errors is minimized when the parameters are given by:

(3)

(4)

With standard deviations given by:

(5)

(6)

Where s_I is the residual standard deviation. Then, the standard error in each parameter can be calculated depending on the confidence interval chosen (95% for all analyses). The error in the EPSC onset is then the range between t intercepts calculated using the upper and lower error limits of the fitted slope (Fig. 10B, left).

(7)

(8)

Where (I_mid, t_mid) is the midpoint of the fitted line and are common with both boundary lines above (eqns (2), (7) and (8)). Setting I =I_h, and subtracting eqns (7) and (8) yields the standard error in the estimation of the EPSC onset. It can also be shown that, by setting t = 0 in eqns (2), and (7) or (8), the difference in the I intercept is equal to eqn (6).

When we consider that eqn (1) also carries error from the averaging of I_h, the error in the EPSC onset is increased further. Determination of the error in I_h (ΔI_h) involves averaging over a region in which I fluctuates normally (noise) around I_h. Thus the error in I_h is the standard error of the mean, where σ is the standard deviation.

(9)

Although this error only occurs in the I dimension, it affects the accuracy of the EPSC onset through its effect on the intersection of eqn (1) with eqn (2). The magnitude of this error is dependent on the level of ‘noise’ contained within the chosen baseline region and the degree to which it is stationary. Setting I =I_h−ΔI_h in eqn (8), or I =I_h+ΔI_h in eqn (9) increases both the upper and lower limit of t beyond S_m (Fig. 10B, rightmost panel). Thus eqns (7) and (8) become:

(10)

(11)

which, when solved for t, represent the upper and lower errors for the EPSC onset with error in eqns (1) and (2) considered.

The threshold method

The threshold method defines the EPSC onset as the time point at which the EPSC is an arbitrary percentage of its maximum, usually 10% (Fig. 10C).

Sources of error

The accuracy of the method is determined by the rate at which the analog current signal is digitized. The temporal spacing between samples [i.e. (I₁,t₁) and (I₂,t₂), Fig. 10C rightmost panel) creates an interpolated region in which the 10% point will almost always fall. The 10% point must then be taken as the known digitized point (I₁ or I₂) closest to the calculated value (I_actual). Choosing either of these points also means choosing the corresponding time point (t₁ or t₂) as the EPSC onset. Since the probability of I_actual occurring at any point between t₁ and t₂ is uniform, the error in the EPSC onset is:

(12)

Where S_dig is the intersample interval of the digitizer. Thus, the error in the determination of the EPSC onset is uniform using this method.

The maximum curvature method

The maximum curvature method defines the EPSC onset as the point of maximum curvature occurring during the rising phase of the EPSC. To determine this point, an equation in the form of the Boltzmann function is used (Fig. 10A).

(13)

Since we are concerned only with the initial portion of the EPSC, the fitted region can be chosen such that it maximizes the fit quality in this region (continuous line in Fig. 10A, left panel, within fitted region indicated by dashed lines). This sacrifices accuracy in other regions of the fitted curve (red dotted line) that are inconsequential to the determination of the EPSC onset. With the parameters determined, we determine the point of maximum curvature by solving the 4th derivative of eqn (13) and set it equal to 0. Evaluation of the 4th derivative gives three solutions (Figure 10B, bottom panel):

(14)

(15)

(16)

where the solution that occurs earliest in time is defined as the EPSC onset.

Sources of error

The accuracy of the maximum curvature method is determined by the accuracy in the determination of t_mid and t_c through the fitting process (Levenberg–Marquardt with least-squares minimization). Here, the error is determined from the evaluation of a covariance matrix of the general form:

(17)

Where μ is the mean, and E is the matrix of expected values for X. In the condition where i = j, eqn (17) reduces to:

(18)

which is the variance of the parameter matrix X_i. Following standard error propagation rules, we can evaluate t₁ or t₃, whichever occurs earlier in time, and summate the standard error returned from eqn (18) to determine the overall error in the EPSC onset.

Example error determination

Choosing the 30 example traces shown in Fig. 2A, we determined the accuracy of each EPSC onset detection method for the first and final event in the train (200 Hz, 150 ms).

Intersection method

The maximal EPSC amplitude was determined for each event from which the 10 and 90% points were also determined. The digitized point nearest the 10/90 values was then chosen as the upper and lower range, respectively, for the linear least-squares fit to the rising phase. A 300 μs region preceding the EPSC and following the stimulation artefact was chosen as the baseline and used to determine I_h. Regression analysis was performed (as above) for data points within the 10 and 90% range, from which the equation of the fitted line and the error in its parameters were returned. The range of t intercepts was then calculated with and without error in I_h for each of the traces. The analysis was then repeated for the final (30th) event in each sweep.

In the absence of error in I_h, the error in the determination of the EPSC onset was 0.0044 ± 0.0002 ms for the first event and 0.014 ± 0.005 ms for the final event. The increase in error of the final event can be attributed directly to the increased noise inherent in the rising phase of small depressed EPSCs which occur late in trains where release synchronization has broken down. Under these conditions, the error in the slope of the rising phase increases (S_m), increasing the error in the t intercept.

When the error in I_h was calculated it had average values of 1.58 ± 0.07 and 2.0 ± 0.1 pA for first and last events, respectively. Adding this to the previous error, we observe a small increase in average error to 0.0046 ± 0.0005 ms for the first events and a more significant increase in the error of the final events to 0.016 ± 0.005 ms. That is, as the slope of the line fitted to the rising-phase decreases, the length of time travelled between I_h and ΔI_h increases, resulting in the increased error. The distribution of the errors in both the first and final event are compared as a cumulative histogram in Fig. 10D (left panel).

Threshold method

Error determination for the threshold method is directly related to digitizing speed. For the experiment in question, and those throughout, the sampling rate was 50 kHz producing a time gap between acquired points of 0.02 ms. Using eqn (12), a consistent error of 0.01 ms is inherent in the time point reported near 10% of EPSC_max.

Maximum curvature method

The error in the determination of the EPSC onset, using the maximum curvature method, results from the propagation of error contained the t_mid and t_c parameters. For the first events the average error was 0.0035 ± 0.0002 ms with only a modest increase for the final events, being 0.0051 ± 0.0005 ms on average. The distribution of the errors in both the first and final events are compared as a cumulative histogram in Fig. 10D (right panel). In summary, the maximum curvature method can detect the EPSC onset with accuracy as much as two orders of magnitude better than either of the other methods.

Special cases and methodological bias

For large, fast EPSCs, both the intersection method and the maximum curvature method allow for determination of time points with microsecond accuracy. The threshold method is approximately one order of magnitude less accurate for the first event but is of similar accuracy late in trains, when the accuracy of the linear intersection method degrades significantly. However, the maximum curvature method maintains microsecond accuracy independent of the stimulus number within the train.

Independent of their accuracies, both the intersection method and the threshold method depend on parameters that can bias their determination of the EPSC onset. In particular, they depend on the slope of the EPSC rising phase. A slowing in the kinetics of the EPSC rise often results during high frequency stimulation due to desynchronization of release events or receptor desensitization towards the end of stimulation trains. To illustrate this bias, we chose two EPSCs of equal amplitude but differing rising-phase slope and compared the analytic solutions obtained with three methods (Fig. 2C).

For the intersection method, as the slope of the EPSC rise phase decreases, the intersection point is pushed back in time (t_blackversus t_gray, Fig. 2C, left panel) despite near identical EPSC onsets. Thus, this method cannot be used to compare EPSC onset when m_f changes, as it would mask potential increases in SD in traces with mild rising-phase slopes.

In contrast, the threshold method biases forward in time as the rising-phase slope decreases (t_blackversus t_gray, Fig. 2C, right panel). This is due to the fact that it takes more time to reach 10% of EPSC_max when the rising-phase slope is lower, exacerbating SD in traces with mild m_f. Use of this method, to evaluate the EPSC onset, should then also be restricted to conditions in which the EPSC rise-phase slope does not change.

The maximum curvature method depends only on the shape of the EPSC, in the region of its onset, to establish the parameters that will be used to evaluate the 4th derivative. Taking the 4th derivative of eqn (13) we get:

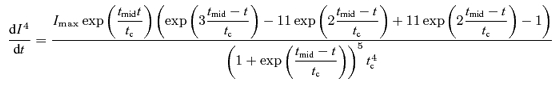(19)

and the 1st derivative, representative of the slope of I(t);

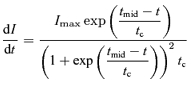(20)

which can be separated from eqn (19). Setting eqn (20)=β we have:

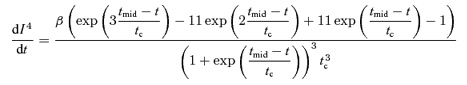(21)

Setting eqn (21)= 0 and solving for t we get solutions (eqns (14)–(16)) which are independent of β and thus the slope of the EPSC.

This analysis suggests that the maximum curvature method can be used to evaluate the EPSC onset under conditions where the rising phase of the EPSC changes. Furthermore, determination of the EPSC onset can be made with higher accuracy than by either of the other determination methods.

Supplemental material

Online supplemental material for this paper can be accessed at:http://jp.physoc.org/cgi/content/full/jphysiol.2007.129833/DC1 and http://www.blackwell-synergy.com/doi/suppl/10.1113/jphysiol.2007.129833

tjp0581-0581-fs1.pdf ^{(1.7MB, pdf)}

tjp0581-0581-ts1.pdf ^{(23.9KB, pdf)}