Structural motifs of biomolecules

Abstract

Biomolecular structures are assemblies of emergent anisotropic building modules such as uniaxial helices or biaxial strands. We provide an approach to understanding a marginally compact phase of matter that is occupied by proteins and DNA. This phase, which is in some respects analogous to the liquid crystal phase for chain molecules, stabilizes a range of shapes that can be obtained by sequence-independent interactions occurring intra- and intermolecularly between polymeric molecules. We present a singularity-free self-interaction for a tube in the continuum limit and show that this results in the tube being positioned in the marginally compact phase. Our work provides a unified framework for understanding the building blocks of biomolecules.

The structures and phases adopted by inanimate matter have traditionally been understood and predicted by simple paradigms; e.g., seemingly disparate phenomena such as phases of matter, magnetism, critical phenomena, and neural networks (1) have been successfully studied within the unified framework of an Ising model (2). Liquid crystals (3), whose molecules are not spherical, form several distinct stable, yet sensitive, structures. They possess translational order in fewer than three dimensions and/or orientational order and exist in a phase between a liquid with no translational order and a crystal with translational order in all three directions. The liquid crystal phase is poised in the vicinity of the transition to the liquid phase and accounts for its exquisite sensitivity. Any material that resides in a particular phase of matter exhibits the general properties characteristic of that specific phase, and there are just a few essential ingredients—such as the symmetry of the atoms or molecules comprising the material and certain macroscopic parameters, such as the pressure and temperature—that determine the relevant phase.

Biomolecules, such as DNA and proteins, form the basis of life and exhibit simple forms such as a single, double, or a triple helix and almost planar sheets assembled from zigzag strands (4). The latter are also implicated in amyloid structures that play a role in diseases such as Alzheimer's and type II diabetes (5). The origin of these structures is now well understood based on details of the constituent atoms and the quantum chemistry that governs their assembly (6–8). The common use of these modular structures by nature begs for a simple unified explanation for their ubiquity. Here we show that not only single, double, and triple helices but also planar sheets made up of biaxial strands are natural forms in a marginally compact phase of matter of a flexible tube, the simplest description of a chain molecule that incorporates the correct symmetry. Remarkably, this phase of matter is analogous to a liquid crystalline phase but for chain molecules and is assembled from emergent anisotropic building blocks. Our work provides a unified description, which transcends chemical details, of the structural motifs of biomolecules. We elucidate the role played by discreteness in promoting the creation of biaxial strands through spontaneous symmetry breaking. An important consequence of our work is that it suggests that physical scientists and engineers who wish to build nifty machines akin to proteins would do well to design their devices so that they are poised in this phase of matter with all of its advantages.

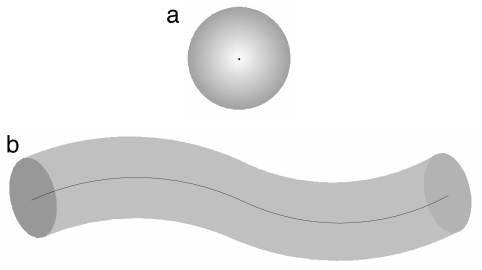
The fluid and crystalline phases of ordinary matter are well described by a simple model of a collection of beads or hard spheres (2). A hard sphere can be thought of as a point, a zero-dimensional object, in space with an excluded volume region obtained by symmetrically inflating it to a size equal to its radius. The packing of spheres is a classic optimization problem (9) with a long and venerable history and many important applications. There are a large number of important synthetic materials, such as plastic, rubber, gels, and textile fibers, comprised of polymer molecules (10). Life is also based on chain molecules such as DNA and proteins. The generalization of the hard sphere to a one-dimensional manifold consists of taking a curve and symmetrically inflating it to form a flexible tube of thickness Δ characterized by uniaxial symmetry (Fig. 1). We will show that the tube paradigm provides a unified and natural explanation for helical forms and sheets in biomolecules.

Fig. 1.

Sketch of a hard sphere (a) and a tube (b). The self-avoidance of an ensemble of hard spheres, each of radius Δ, can be ensured by considering all pairs of spheres and requiring that none of the distances between the sphere centers is <2Δ. The self-avoidance of a tube of thickness Δ can be enforced through a suitable three-body potential (11, 12). We denote the tube axis by a smooth curve, r(s), where the arc-length s satisfies 0 ≤ s ≤ L, and L is the total length of the tube. For a tube, one considers all triplets of points r_i = r(s_i), i = 1, 2, 3 on the tube axis and draws circles through them and requires that none of the radii r(r₁, r₂, r₃) of these circles is less than the tube radius Δ.

Results and Discussion

Buried Area of Tubes.

We begin by describing the discrete version of a tube of thickness Δ represented by a chain of coins, whose planes coincide with equally spaced circular cross-sections of the tube. The self-avoidance of the tube is implemented by the three-body prescription (11, 12) described in the legend of Fig. 1. A classic way to take into account the solvophobic effect is to introduce an attractive pairwise interaction between the coin centers with an interaction range R₁. In refs. 13 and 14, it was shown that, when Δ ∼ R₁, a short tube had relatively few low-energy conformations compared with the generic compact phase (Δ ≪ R₁) and the swollen phase (Δ ≫ R₁). Structures in this novel marginally compact phase were found to be constructed from two building blocks, helices and zigzag strands, and able to possess liquid crystal-like sensitivity because of being poised in the vicinity of a transition to the swollen phase.

In the continuum limit, two-body interactions are necessarily singular because there is a continuum of pairs, close by along the chain, that are within the interaction range (12). A singularity-free formulation of the attractive interaction follows from the following physical situation. Let us suppose that the tube is immersed in a poor solvent whose molecules are approximated by spherical balls of radius R. For any given tube configuration, there are regions of the tube surface that the solvent molecules can come in contact with and other regions that are inaccessible. The latter constitutes the buried surface of the tube configuration. The bigger the radius of the solvent molecule, the larger the buried surface. We will show that an interaction based on the buried area is sufficient to lead to ground state tube conformations in the marginally compact phase with a variety of secondary motifs.

The simplest potential for the solvophobic interaction is given by

where r(s) defines the smooth curve corresponding to the tube axis, s is the arc-length, Σ_B(R) is the buried area in presence of solvent molecules of radius R, and κ_sol is an effective interaction strength that we set equal to 1 without loss of generality. An analytical derivation is given in Methods.

The interaction as given by Eq. 1 describes a tube with a uniform solvophobicity. As discussed below, for proteins it is more appropriate to introduce a mixed solvophobicity tube. In its simplest version, this tube has two types of surface regions, each characterized by a different degree of solvophobicity, as described by Eq. 9 in Methods.

Uniform Solvophobic Tubes.

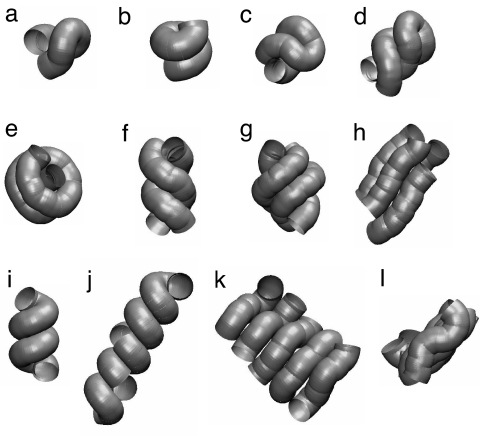
Fig. 2 a–h depicts the conformations adopted by short tubes subject to compaction. Our results are obtained by maximizing the buried surface area (15–17) of the tube (see Eqs. 1 and 8). Such an optimization requirement is generically encountered when a tube shows a higher affinity to itself than to a solvent; e.g., in poor solvent conditions (10). Strikingly, the conformations of choice are single, double, and triple helices, all characterized by chirality and adopted by nature in the context of biomolecules such as proteins and DNA. It is remarkable that the shapes of closely packed single and double helices adopted by flexible tubes match those of α-helices (18, 19) and the DNA double helix (20), respectively. At somewhat higher temperatures, one obtains the conformation in Fig. 2h, as a result of the interplay between the simultaneous maximization of both the buried area and the entropy, comprising almost parallel elongated tube segments. Fig. 3 shows an optimal arrangement of several segments of continuous tubes arranged in a hexagonal array. [Such an arrangement is called an Abrikosov flux lattice in the field of superconductivity (21).] One would expect that the helical state of a few tubes would be supplanted by such an ordering when many tubes are packed together.

Fig. 2.

Optimal conformations of tubes subject to compaction. In our simulations, we considered a discretized representation with N segments separated by a distance b = Δ/2, where Δ is the tube radius. The continuum limit is obtained when b ≪ Δ—we have verified that our results are substantially the same on reducing the value of b down to Δ/3. The conformations are obtained by using metropolis Monte Carlo simulations by annealing or by long simulations at constant temperature. The simulations are performed with standard pivot and crank-shaft move sets (25). For systems of multiple chains, the tubes are placed inside a hard-wall cubic box of side of 40Δ—we verified that the walls of the box did not influence the conformations shown. (a–e) Conformations of single solvophobic tubes (c = 0) of various lengths and for different solvent molecule radius R that maximize the buried area (Eq. 8). (a) N = 20 and R = 0.1Δ. (b) N = 20 and R = 0.2Δ. (c) N = 30 and R = 0.1Δ. (d) N = 40 and R = 0.1Δ. (e) N = 50 and R = 0.2Δ. (f–h) Optimal conformations of multiple solvophobic tubes (c = 0) of length N = 20 and for R = 0.1Δ obtained in long simulations at constant temperatures. (f) Two tubes at a low temperature. (g) Three tubes at a low temperature. (h) Four tubes at an intermediate temperature. (i–l) Conformations of mixed solvophobicity tubes (c = 5) that minimize the energy (Eq. 9). R = Δ/2 for all cases. (i) A single helix of length N = 30 and θ₁ = 15° obtained by slow annealing (one obtains the same conformation for θ₁ = 30° or 45°). (j) A stack of four helices of length N = 15 and θ₁ = 45° obtained by slow annealing. (k and l) Two views of a planar sheet arrangement of five chains of length N = 15 and θ₁ = 30° obtained in a constant temperature simulation run at T = 0.4.

Fig. 3.

Optimal arrangement of several segments of continuous tubes arranged in an Abrikosov flux lattice-like state (21) with straight tube segments parallel to each other. In the plane orthogonal to the tube axes, the tube cross sections are arranged in a hexagonal array.

Mixed Solvophobic Tubes.

We turn now to a consideration of two distinct mechanisms that promote sheet formation within the context of the tube picture. The first mechanism is directly inspired from the observation that the side chains of amino acids stick out in a direction approximately opposite of the bending direction of the protein backbone (22), yielding an effectively mixed solvophobic tube. In other words, certain parts of the solvophobic tube, determined by the instantaneous tube conformation, are already protected from the solvent by the side chains, whereas the rest of the tube needs to shield itself from the solvent by means of the compaction process. The structures in Fig. 2 i–l, obtained by minimizing the energy given by Eq. 9, are optimal conformations for a single tube (i) and for multiple tubes at low temperature (j) and at a higher temperature (k and l). Our studies have been carried out at c = 5, which corresponds to the region P being solvophilic and the region H being solvophobic. The resulting sheet structure is characterized by planarity as well as strands that zigzag normal to the plane of the sheet, as observed in real protein structures.

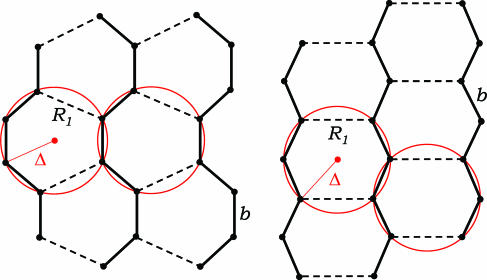
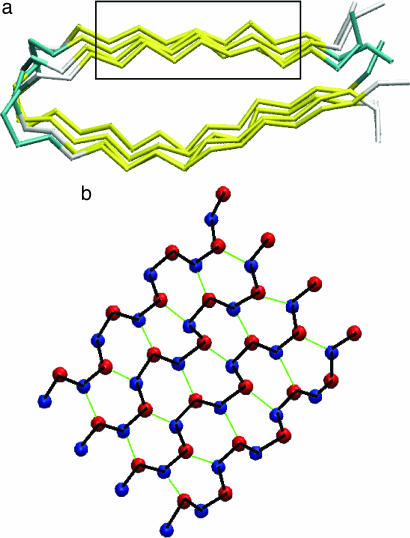
The second mechanism is more subtle and does not invoke mixed solvophobicity but instead arises from the consideration of a discrete version of the tube as described above. Instead of maximizing the buried surface area of the continuous tube, we now seek to maximize the number of pairwise contacts between nonconsecutive coin centers within a prescribed mutual distance of the order of the tube thickness to be within the marginally compact phase (13, 14). The optimal packing for the discrete case at its edge of compaction is shown in Fig. 4—one obtains a planar arrangement of chains that zigzag within the plane. In the continuum, one retains the uniaxial anisotropy characteristic of a tube, whereas in the discrete case, the symmetry between the two directions perpendicular to the principal strand direction is spontaneously broken (in the mixed solvophobic tube, this symmetry is broken overtly). Strikingly, the out-of-plane zigzag pattern shown in Fig. 2 for continuous tubes is realized in protein β-sheets when viewed in the C^α representation (see Fig. 5a), whereas the in-plane zigzag pattern of the discrete case shown in Fig. 4 is obtained in a different representation with interaction centers on both the N−H and C−O bonds (see Fig. 5b).

Fig. 4.

Sketch of optimally packed short segments of three tubes (solid lines) obtained from metropolis Monte Carlo annealing simulations at the edge of compaction. The self-avoidance of a discrete tube [defined through a set of N points along the discretized tube axis {r₁, r₂, …, r_N} with unit spacing (b = 1) between consecutive points] is enforced through the three-body potential defined in the legend of Fig. 1. The number of pairwise contacts between nonconsecutive beads is maximized. Any two such beads are forbidden to come closer than 1.1 units and are defined to form a contact when they come closer than 1.6 units (R₁ = 1.6) (these numbers have been selected to conform to the known length scales associated with real proteins). For convenience, the three tube segments are placed inside a hard-wall spherical box of radius 9 units—the conformations shown are not affected by the presence of the walls. Our simulations were performed with standard pivot, crank-shaft, and tail slithering move sets. Random translations of one of the chains were also attempted. All tubes have a radius Δ = 1.1. To minimize edge effects, the tubes were of different lengths, and the first and last points, which are not shown in the figure, were not allowed to form any contact. One obtains eight pairwise contacts for both of the ground state arrangements shown in the figure as dashed lines. Also drawn, in red, are some of the circles of radius Δ going through several local and nonlocal triplets.

Fig. 5.

Parallel β-sheets from a structural model of CA150.WW2 protofilaments forming amyloid fibrils [Protein Data Bank (26) entry 2NNT]. The model is based on distance constraints obtained by means of magic angle spinning (MAS) NMR spectroscopy (27). (a) Side view of the two β-sheets (in yellow) forming the hairpin structure of the whole protofilament. C^α backbone representation is used (28). (b) Top view of the β-sheet included in the rectangular box in a. The representation used in b employs virtual interaction centers based on main backbone atom positions. Blue (red) spheres are placed in the middle of the N–H (C–O) bonds and lie approximately in the same plane. Thick black lines are drawn to connect interaction centers along the same β-strand. Thin green lines are drawn to represent interactions (i.e., virtual hydrogen bonds) between neighboring strands.

Conclusions

Our work suggests that protein native state structures occupy a novel phase of matter corresponding to that of compact conformations of a flexible tube. This marginally compact phase is analogous in several respects to the liquid crystal phase but this time for chain molecules. The liquid crystal phase is exquisitely sensitive to perturbations because it is poised close to the transition to the liquid phase. Likewise, protein structures are able to facilitate the range of functions that proteins perform in the living cell because a tube at the edge of compaction is in the vicinity of a swollen phase in which the attractive potential is no longer operational. In addition, just as liquid crystals are made up of anisotropic molecules, protein native state structures are made up of emergent anisotropic building blocks—uniaxial helices and almost planar sheets comprised of biaxial strands. It is tempting to speculate that nature, through evolution and natural selection, has been able to exploit the marginally compact phase of flexible tubes under the constraints of quantum chemistry governing covalent and hydrogen bonds.

Methods

We derive an analytical expression for the buried area of a tube of length L (0 ≤ s ≤ L) and radius Δ. A generic point on the tube surface is given by

where n̂(s) and b̂(s) are the normal and binormal vectors, respectively, at position s, and θ is an azimuthal angle running from 0 to 2π (23). The surface element is given by $\sqrt{g\left(s,\theta \right)dsd\theta }$, where

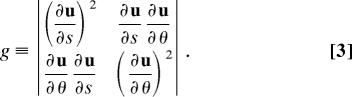Note that ∂²r/∂s² = κn̂(s), R_c(s) ≡ 1/κ(s) is the local radius of curvature, and ∂b̂/∂s = −τn̂(s), where τ is the torsion (24). One obtains

For the tube R_c(s) = 1/κ(s) ≥ Δ, ∀s, thus 1 − Δκ cos θ ≥ 0, and

The total area of the tube is

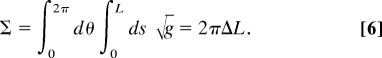The buried surface is determined by the inequality

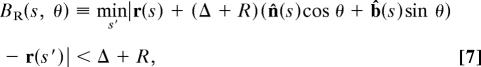yielding an expression for the buried area:

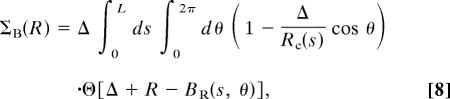where ϴ(x) is equal to 1 if x > 0, and 0 otherwise.

The simplest version of a mixed solvophobicity tube has two types of surface regions, each characterized by a different degree of solvophobicity. We denote these regions as P (for solvophilic) and H (for solvophobic), respectively. We consider the generalized Hamiltonian

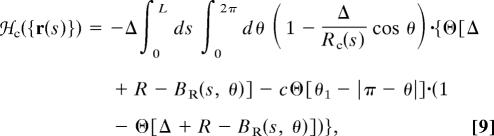where θ₁ defines half the angular width of region P centered around θ = π and c is a measure of the coupling between this region and the solvent. The case c = 0 corresponds to the uniform tube described previously.

Note Added in Proof.

Hansen-Goos et al. (29) have studied the solvation free energy of proteins in the tube model and have identified the parameter regions in which one obtains the optimal helix and β-sheets.