Abstract
Among the multiple steps constituting the kinesin mechanochemical cycle, one of the most interesting events is observed when kinesins move an 8-nm step from one microtubule (MT)-binding site to another. The stepping motion that occurs within a relatively short time scale (≈100 μs) is, however, beyond the resolution of current experiments. Therefore, a basic understanding to the real-time dynamics within the 8-nm step is still lacking. For instance, the rate of power stroke (or conformational change) that leads to the undocked-to-docked transition of neck-linker is not known, and the existence of a substep during the 8-nm step still remains a controversial issue in the kinesin community. By using explicit structures of the kinesin dimer and the MT consisting of 13 protofilaments, we study the stepping dynamics with varying rates of power stroke (kp). We estimate that kp−1 ≲ 20 μs to avoid a substep in an averaged time trace. For a slow power stroke with kp−1 > 20 μs, the averaged time trace shows a substep that implies the existence of a transient intermediate, which is reminiscent of a recent single-molecule experiment at high resolution. We identify the intermediate as a conformation in which the tethered head is trapped in the sideway binding site of the neighboring protofilament. We also find a partial unfolding (cracking) of the binding motifs occurring at the transition state ensemble along the pathways before binding between the kinesin and MT.
Keywords: cracking, neck-linker zippering, power stroke, rectified diffusion
First recognized by means of their close relationship between ATPase activity and organelle transport along microtubules (MTs) (1, 2), kinesins have received broad attention as a prototype of molecular motors for the past two decades. Recent single-molecule (SM) experiments have shown that, with each stepping motion being strongly coupled to the ATP, the kinesin moves toward the (+) ends of MTs by taking discrete 8-nm steps (3–7) in a hand-over-hand fashion (4, 7, 8). Although the ultimate understanding of kinesin's motility is still far from completion, the SM experiments (3–9), together with the series of kinetic ensemble measurements (10–13) and theoretical studies (14–19), begin providing glimpses to the physical principle of how kinesin walks.
Along the kinesin mechanochemical cycle (supporting information (SI) Fig. 7), one of the main observations of the SM experiments is the stepping dynamics that enables the kinesin to move forward. The actual time spent for the stepping motion itself (≲100 μs), compared with the ATP binding and hydrolysis (≳10 ms), is too short, however, to detect the details of the dynamics with the spatial and temporal resolution of current instruments. Thus, it is still difficult to answer many basic questions (20) related to the stepping dynamics. Some of those questions are: (i) During the 8-nm step, how does the swiveling motion of the tethered head occur? Does any detectable substep exist that reflects a transient intermediate (5, 21, 22)? (ii) What fraction of the time and length scales is contributed from the power stroke and the diffusional search? (iii) Does the kinesin walk parallel to the single protofilament (PF) or walk astride by using two parallel PFs (23, 24)? To shed light on these questions, we propose to take advantage of the native topology of kinesins and MTs. For instance, our earlier study clarified the regulation mechanism between the two heads (6, 25) by using the native topology-based, two-head bound model of kinesin on the MT (19). Following the same line of thought, we show that even the dynamical pathways of kinesins reflect “the topological constraints emanating from the molecular architecture.” In the present work, we have adapted our previous two-head bound model (19) to study the stepping dynamics of kinesins on the 13-PF MT.
According to the “neck-linker docking model” (26–28), the stepping motion of kinesin is initiated by the undocked-to-docked transition of the neck-linker at the MT-bound head (power stroke), and the rest of the binding process of the tethered head to the next MT-binding site is accomplished by a diffusional search. The whole stepping dynamics is typically interpreted as a combination between the directional motion of power stroke and the nondirectional diffusional search. At the molecular level, the length of the neck-linker shrinks gradually, with the progress of the power stroke, making a transition from a disordered to an ordered state; the resulting configurations bias the diffusional motion of the tethered head in one direction. Thus, we can rather interpret the power stroke as a time-dependent boundary condition that biases the diffusional motion, considering that the tethered head diffuses on the time-dependent energy landscape to search for the next MT-binding site.
To study the dynamics, through simulations, we first obtain potentials of mean force (PMFs) felt by kinesin's tethered head on the MT at two extreme cases: one is the PMF with fully disordered neck-linker [Fλ=0(x, y, z)] and the other is the PMF with ordered neck-linker [Fλ=1(x, y, z)], where λ is a parameter that specifies the degree of the neck-linker being zippered. The kinesin structures with a disordered (λ = 0) and an ordered neck-linker (λ = 1) at the MT-bound head are generated by switching on and off the native contacts inside the green circles in Fig. 1B (see Results and Methods for more details). We subsequently perform Brownian dynamics simulations of a quasi-particle representing the tethered head on a PMF that is mixed between the two extreme cases. The disordered-to-ordered transitions are mimicked by mixing the two PMFs, Fλ=0(x, y, z) and Fλ=1(x, y, z), in a time-dependent manner. We show that, because of the multiple binding sites on the MT surface, the tethered head has a chance of misbinding to other MT-binding sites. To avoid such an intermediate, we argue that the rate of power stroke (kp) should be faster than the sampling rate on the MT surface (kE). Throughout the article, we designate the rate of power stroke and the rate of space exploration by diffusion as kp and kE, respectively.
Fig. 1.
Topology of MT, kinesin, and their interface. (A) Geometry of MT surface showing the distances between the neighboring binding sites. | | = |
| = | | = 8.0 nm, |
| = 8.0 nm, | | = |
| = | | = 10.9 nm, |
| = 10.9 nm, | | = |
| = | | = 6.3 nm, |
| = 6.3 nm, | | = |
| = | | = 9.4 nm. The distances are measured by using the position of the residue 400 at each α-tubulin subunit. (B) The native contact map of kinesin model. The native bias between the neck-linker and its neck-linker binding site (neck-linker zipper contacts inside the green circles) is retained for the MT-bound head to have the neck-linker ordered (λ = 1), whereas it is removed for the tethered head to make the neck-linker of the tethered head disordered. For structures with a disordered neck-linker in the MT-bound head (λ = 0), the neck-linker zipper contacts are made repulsive. The contacts for the coiled-coil are purple. (C) Native contacts between the residues of kinesin (yellow) and MT-binding sites (magenta).
| = 9.4 nm. The distances are measured by using the position of the residue 400 at each α-tubulin subunit. (B) The native contact map of kinesin model. The native bias between the neck-linker and its neck-linker binding site (neck-linker zipper contacts inside the green circles) is retained for the MT-bound head to have the neck-linker ordered (λ = 1), whereas it is removed for the tethered head to make the neck-linker of the tethered head disordered. For structures with a disordered neck-linker in the MT-bound head (λ = 0), the neck-linker zipper contacts are made repulsive. The contacts for the coiled-coil are purple. (C) Native contacts between the residues of kinesin (yellow) and MT-binding sites (magenta).
The present work provides scenarios on how the dynamic pathways of the tethered head depend on the rate of the power stroke, based on the landscape of stepping and the molecular details that the current experiment cannot easily access. Importantly, the present work will give further insights to resolve the recent experimental debate (5, 20–22) on the existence of a substep within kinesin's 8-nm step.
Results
Topological Constraints in Stepping Dynamics.
On ATP binding to the empty MT-bound head (positioned at the binding site o in Fig. 1A), the allosteric communication between the strained nucleotide-binding pocket and the disordered neck-linker leads to the docking of the neck-linker to the β7 and L10 neck-linker binding motifs. As a result, the tethered head swings forward from one MT-binding site (a in Fig. 1A) to the other (e in Fig. 1A), whereas the MT-bound head remains at the same position (see SI Fig. 8 for the snapshots of a kinesin during the stepping). For the tethered head to bind to the MT-binding site, the ruggedly shaped kinesin head having specific MT-binding motifs should explore the MT surface and fit into the MT-binding site in a right orientation under topological constraints. The two neck-linkers (one from the MT-bound head and the other from the tethered head) and the steric hindrance between the two heads restrain the search space available for the tethered head. The topology of MT also makes unique the association process between the tethered head and the MT-binding site. In the MT made of 13 PFs (29) the lateral binding interfaces between the adjacent PFs are shifted by ≈0.95 nm, which makes the MT helical (Fig. 1A). The distances between the diagonally located tubulins become asymmetric (| |(= 9.4 nm) < |
|(= 9.4 nm) < | |(= 10.9 nm). The distance between the interfaced tubulins at the side (|
|(= 10.9 nm). The distance between the interfaced tubulins at the side (| | = |
| = | | = 6.3 nm) is shorter than the distance between the tubulins along the same PF (|
| = 6.3 nm) is shorter than the distance between the tubulins along the same PF (| | = 8.0 nm). In light of the contour length of a neck-linker (15 aa × 0.38 nm/aa ≈5.5 nm), two fully extended neck-linkers (≈11 nm) allow the tethered head to cover a wide range of the MT surface.
| = 8.0 nm). In light of the contour length of a neck-linker (15 aa × 0.38 nm/aa ≈5.5 nm), two fully extended neck-linkers (≈11 nm) allow the tethered head to cover a wide range of the MT surface.
Because every MT-binding site on the MT interacts equally with the tethered head, one cannot totally rule out the possibility of binding to the neighboring PFs, but the experiments suggest that the kinesin moves straight along the MT (23, 24).
PMF Between Kinesin Tethered Head and MT.
During the disordered-to-ordered transition, the length of disordered neck-linker decreases gradually. Depending on the length of the disordered neck-linker, there are substantial variations in the search space available for the tethered head (Fig. 2A and Fig. 3 A). We sample the conformational space by using the centroid of tethered head from the multiple trajectories with varying temperatures (see Methods for the energy function) and calculate the two-dimensional (2D) PMF between the tethered head and the MT, projected on the xy, xz, and yz planes, at two extreme cases (see SI Text for the computational details of PMF construction). One 2D PMF results from search processes under which the neck-linker of the MT-bound head is practically in the zippered state (λ = 1). We expect that this process is realized when the neck-linker zippering rate is faster than the rate of space exploration (kp ≫ kE). Whereas, the other 2D PMF results when the neck-linker is in a disordered state throughout the search process (kp ≪ kE, λ = 0). Although the exact values of kp and kE are not known, we presume that the stepping dynamics should occur on a PMF linking between these two regimes.
Fig. 2.
PMF between the tethered head of kinesin and the MT surface for λ = 1. (A) A structure of kinesin when λ = 1, with a yellow arrow depicting the accessible search space. (B) 1D PMFs in x, y, and z projections are shown at various temperatures. (C) 2D PMFs in xz, yz, and xy projections at T = 295 K. Binding sites e and d and entropic basin S are marked with circles and arrows. (D) 2D PMFs at T = 355 K. The energy scale is color-coded in the kBT unit from dark brown to white in C and D.
Fig. 3.
PMF between the tethered head of kinesin and the MT surface for λ = 0. (A) A structure of kinesin when λ = 0, with a yellow arrow depicting the accessible growth space. (B) 2D PMFs in xz, yz, and xy projections at T = 295 K. Binding site c, which results in an intermediate state, is marked with circles. (C) 1D free-energy profile F0(x) is fitted by a harmonic potential 1/2 kx2 where k ≈ 0.02 kBT/nm2 (dashed line).
From the structures with λ = 1, we find two major basins of attraction in the 3D space (Fig. 2). One is the MT-binding site e and the other is a broad basin (S) formed at the forward-right corner relative to the MT-bound head [Fig. 2C, F1(x, z)]. Between the two basins exists the free-energy barrier of ≈1–2 kBT in F1(x, z) or F1(x, y), and ≈4–5 kBT in F1(y, z), depending on the projection. The basin S stems from the large conformational degrees of freedom that the tethered head should explore before reaching the binding site e (Fig. 2C, blue circles). The energetic bias to binding site d (Fig. 2C, magenta arrows) is also present but negligible (<1 kBT). With an increasing temperature the stability of basin S relative to binding site e increases, which indicates that the nature of the broad basin is entropic (Fig. 2D). Note that the one-dimensional (1D) free-energy profiles (Fig. 2B) projected from higher dimensional representation of free-energy surface underestimates the barrier height by merging the various possible dynamic pathways.
From the structures with λ = 0, which is obtained by making repulsive the attractive neck-linker zipper contacts (the native contacts inside the green circles of Fig. 1B; see also Methods), we find that the most frequently visited binding site is the site c that belongs to the adjacent PF (Fig. 3). Explicit analysis on the bound complex shows that the binding of the tethered head to site c is not as complete as the one binding to site e. Interestingly, the structure at c has only about one-third of the interfacial native contacts (see Fig. 4). We find that a strained neck-linker induces a significant distortion in the α6-helix, preventing a full binding.
Fig. 4.
The conformation of kinesin dimer [view from the back (A), top (B), and front (C)] when the tethered head is trapped at binding site c. The tethered head are partially bound to site c, using only one-third of the native contacts.
Modeling the Stepping Dynamics.
The most straightforward strategy to monitor the real-time stepping dynamics of our model is to integrate the equation of motion for each coarse-grained unit of kinesin molecule in an overdamped environment. The inclusion of hydrodynamics in the simulations, which is essential to naturally retrieving a correct behavior of the translational diffusion for the tethered head (see SI Text with SI Fig. 9), is however computationally too expensive for a model with >700 coarse-grained units. Thus, we take an alternative method to study the real-time dynamics by using the two PMFs obtained above.
Conceptually, the stepping dynamics coupled to the power stroke is considered as a diffusional process with a moving reflecting boundary condition that restrains the search space, which is illustrated in Fig. 5A. The blue shade and the red dots depict the energetic cost for extending the neck-linker and the multiple MT-binding sites, respectively. The progress of the neck-linker zippering is depicted by dotted lines with parameter λ. The reflecting boundary moves from λ = 0 to λ = 1 in a finite rate. Depending on the rate of the variation from λ = 0 to λ = 1, as well as the motility of the kinesin head, the dynamic pathway of the binding process changes because of the influence of the sideway binding site c. The rate of variation from λ = 0 to λ = 1 is defined as kp = τp−1 = dλ/dt, that is, λ = kpt with 0 ≤ t ≤ τp.
Fig. 5.
Results of the Brownian dynamics simulations of the quasi-particle representing the tethered head on the PMF defined in Eq. 1. (A) Conceptual representation of kinesin's stepping dynamics (see text). (B) The fraction of trajectories (fdirect) directly reaching the target binding site e as a function of τp. (C Left) The ensemble average of 100 trajectories generated for varying τp. Substeps are manifested for 〈x〉(t) values with τp > 20 μs. (Inset) The substep in the 〈x〉(t) values for τp = 100 μs. (C Right) An actual time trace xi(t) is plotted in black with the time interval of 0.1 μs from which the ensemble average is obtained as 〈x〉(t) = 1/100 Σi100 = 1xi(t). The ensemble average of trajectories for τp = 20.0 μs is fitted to 〈x〉(t) = 14.7 nm × [1 − 0.74e−t/15.3 μs − 0.26 e−t/149 μs] − 6.0 nm.
We propose that the PMF time-dependently linking between the two extreme cases be modeled by using the following ansatz adapting the dual-Go potential (30, 31),
 |
where the switching rate between F0(x, y, z) and F1(x, y, z) is controlled by τp(= kp−1). We perform Brownian dynamics simulations of a quasi-particle, representing the centroid of tethered head, on the “time-dependent” PMF, F(x, y, z, t), from the initial position of the head at (xi, yi, zi) = (−6.0, 4.0, −2.0) nm. We update the position at time t by using
where R⃗(t) is a vector of Gaussian random number satisfying 〈R⃗〉 = 0 and 〈R⃗·R⃗〉 = 6DKeff Δt. We choose DKeff = 2 μm2/s for the effective diffusion coefficient of the tethered head to reproduce a time scale similar to the one in the recent SM experiment by Yanagida and coworkers (21), where they monitored the stepping dynamics of kinesin in the time resolution of ≈20 μs and suggested that the kinesin take substeps at the displacement of Δx ≈ 4 nm.
Simulating the dynamic trajectories by varying the τp, we count the number of trajectories trapped in binding site c (Fig. 5B). The fraction of trajectories directly reaching site e decreases almost exponentially as τp increases. We find that when τp ≲ 20 μs, 90% of the stepping dynamics occurs without being trapped to the intermediate. The signature of such an intermediate, manifested as a “substep” in the averaged trace, is captured only when τp > 20 μs (Fig. 5C). Note the similarity between the patterns of averaged time traces by Yanagida and coworkers (see figure 4a in ref. 21) and the present results plotted in Fig. 5C. Interestingly, the averaged trace for τp = 20 μs fits to the double-exponential function (Fig. 5C) where the time scale of the fast phase corresponds to that of the power stroke, and the slow phase represents the rate process to overcome the barrier from broad basin to the target basin shown in F1(x, y, z).
Partial Unfolding (Cracking) of Structure Facilitates the Binding Process.
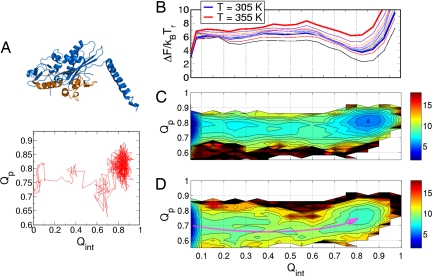
In the sections above, we studied the association between the tethered kinesin head and the MT-binding site by using the centroid of the tethered head. When we probe the kinesin conformation and the binding interface by using native contacts, we observe partial unfolding (32) of the MT-binding motifs in the kinesin head at the transition state ensemble before the complete binding. The flexibility of the structure eases the binding process by reducing the entropic barrier to overcome, which is a well known phenomenon in protein–protein or protein–DNA association process (33–35). To quantify the degree of cracking in the kinesin structure during binding, we use the fraction of native contacts for the MT-binding motifs of kinesin (Qp) and the fraction of interfacial native contacts between the kinesin and the MT (Qint) (Fig. 6). In an exemplary trajectory (Fig. 6A), starting from Qp ≈ 0.75, the MT-binding motifs are disrupted to Qp ≈ 0.65. When the kinesin is completely bound to the MT, Qp ≈ 0.82(± 0.08). By collecting the configurations and applying the histogram-reweighting technique (see SI Text), we obtain the 2D free-energy surface F(Qp, Qint). Fig. 6 C and D shows that the Qp value of the kinesin–MT complex is greater than the value of the transition state ensemble. At higher temperatures, the trend of cracking before the binding is more pronounced, showing a downward curvature in the pathways connecting the separated molecules and the complex. Interestingly, the 1D free-energy profile F(Qint) (Fig. 6B) shows that the free-energy barrier for the binding is ≈6 kBT, which is higher than the barriers measured as a function of spatial reaction coordinates in Fig. 2.
Fig. 6.
PMF between the tethered head and the MT-binding site e as a function of two order parameters, Qp and Qint. (A Top) The MT-binding motifs of the kinesin are orange. (A Bottom) An exemplary binding trajectory as functions of Qp and Qint. (B) ΔF(Qint), 1D free-energy profile as a function of Qint at varying temperatures. (C) ΔF(Qint,Qp) at T = 305 K (= Tr). As the binding progresses, minor structural disruption is observed. The free-energy difference is color-coded from blue to red in kBTr units. (D) ΔF(Qint,Qp) at T = 355 K. The partial unfolding along the binding process is more pronounced than at a lower temperature. The overall binding pathway is drawn with a curved arrow.
Discussion
To study the dynamics of kinesin's stepping motion, first, we made full use of the topological information available from the structures of kinesin and MT to build the PMF, and second, we considered the whole stepping dynamics as a “rectified diffusional motion” (36, 37) by envisioning the power stroke as a moving reflecting boundary condition for the diffusional motion of the tethered head. Although the level of our description is hinged solely on the native topology, lacking in the chemical details, several key issues on the stepping dynamics can be discussed in a semiquantitative fashion.
(i) The PMF between the tethered head and the MT showed that the leftward diagonal stepping ( ) is forbidden because of structural constraints (see Figs. 2 and 3). Also, the alternation between the sideway stepping (
) is forbidden because of structural constraints (see Figs. 2 and 3). Also, the alternation between the sideway stepping ( stepping) and the parallel stepping would generate a helical path in the long run, which contradicts the previous experimental findings (24). Thus, the likelihood for using two parallel PFs is ruled out. An interesting finding in this study is that the intermediate structure trapped in the sideway binding site c has only ≈30% stability compared with the correctly bound complex at e. We expect that under the action of the power stroke, the intermediate state found for kp ≪ kE becomes further destabilized and readily loses its binding with site c. A direct comparison between F0(x, y, z) and F1(x, y, z) at (x, y, z) ≈ (0, 4, 5) nm indicates that binding site c is destabilized by ≳5 kBT on λ = 0 → λ = 1.
stepping) and the parallel stepping would generate a helical path in the long run, which contradicts the previous experimental findings (24). Thus, the likelihood for using two parallel PFs is ruled out. An interesting finding in this study is that the intermediate structure trapped in the sideway binding site c has only ≈30% stability compared with the correctly bound complex at e. We expect that under the action of the power stroke, the intermediate state found for kp ≪ kE becomes further destabilized and readily loses its binding with site c. A direct comparison between F0(x, y, z) and F1(x, y, z) at (x, y, z) ≈ (0, 4, 5) nm indicates that binding site c is destabilized by ≳5 kBT on λ = 0 → λ = 1.
(ii) With the speed limit of protein folding rate ≈O(1) (μs)−1 (38–40) and the number of amino acids consisting of neck-linker N ≈ (12 − 15), one can roughly estimate the rate of power stroke by using the scaling relation for the folding rate of proteins with N (kF ≈ kF0 exp(−1.1N1/2) with (kF0)−1 ≈ 0.4 μs (38, 41), or kF ≈ kF0 exp(−0.36N2/3) with [(kF0)−1 ≈ 8 μs (42)]. The agreement of kF−1 (≈20–70 μs) with kp−1 (≈20 μs) shows that the power stroke is closely connected with the conformational change of neck-linker whose activation barrier is estimated as ΔG‡/kBT(≈1.1N1/2 or 0.36N2/3) ≈ 2 − 4.
(iii) Given the diffusion constant (DKeff) and the approximate shape of PMF, one can estimate kE, the exploration rate over the PMF, by approximating kinesin's motion as a Brownian motion in a harmonic potential (F(x) ≈ 1/2 × kx2, i.e., Ornstein–Uhlenbeck process), whose conditional probability is solved as follows (43).
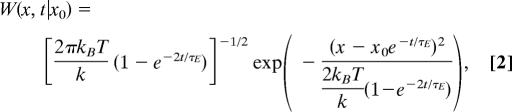 |
where τE = kBT/DKeffk. When t ≫ τE, W(x, t | x0) → Peq(x), 〈x〉eq → 0, and 〈(δx)2〉eq → kBT/k. Because k ≈ 0.02 kBT/nm2 from the fit of 1D F0(x) to a quadratic potential (Fig. 3C), and DKeff = 2 μm2/s, one gets τE = 25 μs. The lower bound for the rate of power stroke (kp) is similar to the upper bound for the exploration rate of harmonic potential (kE = τE−1). If the PMF switching is too fast, the molecules sample only the subregion of the landscape, reflecting the signature of the far-from-equilibrium dynamics.
(iv) The experimentally measured time traces for the rising phase, averaged over the different stepping time scales, by Yanagida and coworkers (21) showed the signatures of intermediates. The comparison between the data of Yanagida and coworkers and our time traces generated over varying kp values suggests that the kp values distribute broadly, given by a distribution of rate constant g(kp). Because of the molecular origin of the power stroke, associated with a complex energy landscape representing the molecular architecture, it is natural to speculate that the stepping dynamics occurs via the kinetic partitioning mechanism (44). The multiple basins (binding sites c and d and entropic basin S) in the PMF suggests that kinesins reach the target binding site e along multiple parallel pathways. By not dividing the time traces into the different classes in the way that Yanagida and coworkers adopted (21), one should be able to fit the full ensemble average of the time traces to the finite number of multiexponential function as 〈x〉 (t) = ∫0∞ dkpg(kp)e−kpt (45). Although a visual signature of intermediate (a substep in the averaged time trace) is masked if the contribution from the fast kinetics (τp <20 μs) is dominant, a careful statistical analysis of 〈x〉(t) averaged over the entire time traces would give a glimpse to the g(kp) that encodes the underlying energy landscape associated with the stepping dynamics.
Methods
To generate the configurations of kinesin on the MT, we performed hybrid Monte Carlo–molecular dynamics simulations by adapting an ADP-complexed crystal structure of rat kinesin dimer (PDB ID code 3kin) on the 13-PF MT structure (see SI Text for further details). The 13-PF structure is built with multiple tubulin dimers fitted to the 8-Å resolution electron density map of Downing and coworkers (29).
Energy Function.
The energy function for the kinesin/MT system is modeled as Vtot = VK + VK·MT where VK(= VKB + V KT + VKBT) is the energy function for the kinesin dimer and VK·MT is the interaction between the kinesin and the MT. B and T denote the MT-bound head and the tethered head, respectively. VKBT describes the interaction between the B and T head. To design each kinesin monomer we use the self-organized polymer model (31, 46),
 |
where ξ = B or T. The first term models the chain connectivity with k = 100 kcal/(mol·Å2), Ro = 2 Å. The second term describes the attraction between the native contact pairs i and j. The native pairs are defined by using Δij = 1 for the residue pairs within Rc = 8 Å at the native structure, and rijo is the corresponding distance. εh(i, j) controls the strengths of native pairs. We choose εh(i, j) = 1.8 kcal/mol for the residues i and j(= i + 3) within an α-helix, and εh(i, j) = 1.2 kcal/mol for all other cases, for example, β-sheets, loops, and residue pairs between the secondary structural elements. The third term prevents the volume overlap between the residues i and i + 2. The last term is for the repulsive potential between the nonnative pairs, modeled by using εl = 1 kcal/mol and σ = 3.8 Å. We design the L12 loop, disordered in the crystal structure, as a self-avoiding chain, employing the same Hamiltonian as Eq. 3 with Δij = 0 for i = 240 − 255 and all other j, or vice versa, which makes the L12 loop neutral to other parts of kinesin monomer (see also the SI Text). The coiled-coil interaction responsible for dimerization between two neck-helices (residues 341–370) is modeled by using
 |
with εhαα = 1.2 kcal/mol. We defined Δijαα = 1 only for “i,j ≥ 341” with rijo < Rc, otherwise Δijαα = 0, so that the two motor domains other than neck–helix repel each other. Because the two monomers are identical as a fold, we should impose the “same” topological bias to the both heads, which is achieved by setting Δij(T) = Δij(B) and rijo(T) = rijo(B) for all i and j. This condition was used when we studied the role of internal strain on the regulation mechanism of kinesin dimer (19). To study the stepping dynamics, in particular, however, we want the neck-linker of the tethered head in a disordered state, so that the tethered head can search and reach the next MT-binding site. This is realized by making the neck-linker (residues 327–338) of the tethered head always repulsive to the residues constituting the neck-linker binding site (see Fig. 1B). To generate the kinesin configurations with λ = 1 and λ = 0, we retain (λ = 1) or discard (λ = 0) the neck-linker zipper contacts (contacts inside green circles in Fig. 1B) of the MT-bound head. The interaction between the kinesin and the MT is designed by using
 |
NMT is the number of all of the residues, belonging to the tubulin heterodimers, that are within the interaction range from kinesin when the MT-bound head is poised at the central tubulin (o) (see Fig. 1A). The topological information of the binding interface between the MT-bound head and the central tubulin (o) is replicated in other surrounding tubulins (a–h) by using Δik*, so that the tethered head feels the identical potential on every MT-binding site. The native contacts between the kinesin and MT are defined between the i, k pairs within RcK·MT = 9 Å. Δik* = 1 for the native pairs, and Δik* = 0 otherwise. In addition to the nonbonded interaction (εhK·MT = εlK·MT = 1 kcal/mol), the electrostatic interaction between the kinesin and the MT is considered because of the large amount of net negative charge (−35 e) in each tubulin unit. To preserve the native contact distance as the one in the crystal structure even with electrostatic potentials, we adjust the parameter χik in Eq. 5 by choosing χik = 2 + (lBkBT/6εhK·MT)[1/riko + 1/lD]e−riko/lD. At r = riko, the energy for the native pair with the opposite charges is given as V(riko) = −εhK·MT − lBkBT (7/6riko + 1/lD)e−riko/lD. The strength of electrostatics is controlled by the salt concentration c, that determines the Debye screening length lD = (8πlBc)−1/2 ≈ (3/) Å where lB = 7 Å and c is in the unit of M (mol/liter). For a pair formed at riko ≈ 8 Å, the energy stabilization due to the electrostatics is lBkBT(7/6riko + 1/lD)e−riko/lD ≈ 0.14 kcal/mol at c ≈ 1 M, but the same value becomes ≈1.4 kcal/mol at c ≈ 0.1 M, which is comparable to εh = 1.0 kcal/mol. At physiological condition, c ≈ (0.1 − 0.2) M for monovalent salt. Careful consideration is required, however, in choosing the c near the MT surface because of the counterion condensation (47). Near the highly charged rod, the counterion concentration can be much higher than that of bulk. Therefore, we choose c = 1 M, which makes the electrostatics negligible throughout all of the simulations (see SI Text with SI Fig. 10 for the details). Eq. 5 accomodates nonspecific interactions due to electrostatics even for the nonnative contacts.
Sampling the Free-Energy Surface.
We combine Monte Carlo and molecular dynamics simulations to efficiently sample the kinesin configurations on the MT. We first generate an ensemble of initial configurations by both pivoting (48) a random position of neck-linkers (residues 327–339 for the MT-bound head, residues 328–337 for the tethered head) and translating the center of position of the tethered head. The acceptance of following a trial move is decided by standard Metropolis criteria with the potentials defined in Eqs. 3, 4, and 5. The subsequent hybrid Monte Carlo–molecular dynamics simulations are performed from a host of initial kinesin configurations. During the 1,000 simulation steps, we perform the Monte Carlo simulations for the first 50 steps, and integrate the subsequent 950 steps by using a velocity-Verlet algorithm. The kinesin configuration is collected every 1,000 steps.
Supplementary Material
Acknowledgments
We thank Dr. Stefan Klumpp for insightful conversation and Dr. Ken Downing for kindly providing the coordinate of 13-PF MT. This work was funded by National Science Foundation Grant MCB-054396 and by the National Science Foundation-sponsored Center for Theoretical Biological Physics (Grants PHY-02165706 and PHY-02255630).
Abbreviations
- MT
microtubule
- PF
protofilament
- PMF
potential of mean force
- SM
single molecule.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0708828104/DC1.
References
- 1.Brady ST. Nature. 1985;317:73–75. doi: 10.1038/317073a0. [DOI] [PubMed] [Google Scholar]
- 2.Vale RD, Reese TS, Sheetz MP. Cell. 1985;42:39–50. doi: 10.1016/s0092-8674(85)80099-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Visscher K, Schnitzer MJ, Block SM. Nature. 1999;400:184–187. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 4.Asbury CL, Fehr AN, Block SM. Science. 2003;302:2130–2134. doi: 10.1126/science.1092985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Carter NJ, Cross RA. Nature. 2005;435:308–312. doi: 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- 6.Guydosh NR, Block SM. Proc Natl Acad Sci USA. 2006;103:8054–8059. doi: 10.1073/pnas.0600931103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kaseda K, Higuchi H, Hirose K. Nat Cell Biol. 2003;5:1079–1082. doi: 10.1038/ncb1067. [DOI] [PubMed] [Google Scholar]
- 8.Yildiz A, Tomishige M, Vale RD, Selvin PR. Science. 2004;303:676–678. doi: 10.1126/science.1093753. [DOI] [PubMed] [Google Scholar]
- 9.Block SM, Asbury CL, Shaevitz JW, Lang MJ. Proc Natl Acad Sci USA. 2003;100:2351–2356. doi: 10.1073/pnas.0436709100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gilbert SP, Johnson KA. Biochemistry. 1994;33:1951–1960. doi: 10.1021/bi00173a044. [DOI] [PubMed] [Google Scholar]
- 11.Ma YZ, Taylor EW. Biochemistry. 1995;34:13242–13251. doi: 10.1021/bi00040a040. [DOI] [PubMed] [Google Scholar]
- 12.Moyer ML, Gilbert SP, Johnson KA. Biochemistry. 1998;37:800–813. doi: 10.1021/bi9711184. [DOI] [PubMed] [Google Scholar]
- 13.Cross RA. Trends Biochem Sci. 2004;29:301–309. doi: 10.1016/j.tibs.2004.04.010. [DOI] [PubMed] [Google Scholar]
- 14.Jülicher F, Ajdari A, Prost J. Rev Mod Phys. 1997;69:1269–1281. [Google Scholar]
- 15.Fisher ME, Kolomeisky AB. Proc Natl Acad Sci USA. 2001;98:7748–7753. doi: 10.1073/pnas.141080498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fisher ME, Kim YC. Proc Natl Acad Sci USA. 2005;102:16209–16214. doi: 10.1073/pnas.0507802102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shao Q, Gao YQ. Proc Natl Acad Sci USA. 2006;103:8072–8077. doi: 10.1073/pnas.0602828103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kolomeisky AB, Fisher ME. Annu Rev Phys Chem. 2007;58:675–695. doi: 10.1146/annurev.physchem.58.032806.104532. [DOI] [PubMed] [Google Scholar]
- 19.Hyeon C, Onuchic JN. Proc Natl Acad Sci USA. 2007;104:2175–2180. doi: 10.1073/pnas.0610939104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Block SM. Biophys J. 2007;92:2986–2995. doi: 10.1529/biophysj.106.100677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nishiyama M, Muto E, Inoue Y, Yanagida T, Higuchi H. Nat Cell Biol. 2001;3:425–428. doi: 10.1038/35070116. [DOI] [PubMed] [Google Scholar]
- 22.Coppin CM, Finer JT, Spudich JA, Vale RD. Proc Natl Acad Sci USA. 1996;93:1913–1917. doi: 10.1073/pnas.93.5.1913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ray S, Meyhofer E, Milligan RA, Howard J. J Cell Biol. 1993;121:1083–1093. doi: 10.1083/jcb.121.5.1083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang Z, Khan S, Sheetz MP. Biophys J. 1995;69:2011–2023. doi: 10.1016/S0006-3495(95)80071-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hancock WD, Howard J. Proc Natl Acad Sci USA. 1999;96:13147–13152. doi: 10.1073/pnas.96.23.13147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rice S, Lin AW, Safer D, Hart CL, Naber N, Carragher BO, Cain SM, Pechatnikova E, Wilson-Kubalek EM, Whittaker M, et al. Nature. 1999;402:778–784. doi: 10.1038/45483. [DOI] [PubMed] [Google Scholar]
- 27.Asenjo AB, Weinberg Y, Sosa H. Nat Struct Mol Biol. 2006;13:648–654. doi: 10.1038/nsmb1109. [DOI] [PubMed] [Google Scholar]
- 28.Tomishige M, Stuurman N, Vale RD. Nat Struct Mol Biol. 2006;13:887–893. doi: 10.1038/nsmb1151. [DOI] [PubMed] [Google Scholar]
- 29.Le H, deRosier D, Nicholson W, Nogales E, Downing K. Structure (London) 2002;10:1317–1328. doi: 10.1016/s0969-2126(02)00827-4. [DOI] [PubMed] [Google Scholar]
- 30.Best RB, Chen YG, Hummer G. Structure (London) 2005;13:1755–1763. doi: 10.1016/j.str.2005.08.009. [DOI] [PubMed] [Google Scholar]
- 31.Hyeon C, Lorimer GH, Thirumalai D. Proc Natl Acad Sci USA. 2006;103:18939–18944. doi: 10.1073/pnas.0608759103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Miyashita O, Onuchic JN, Wolynes PG. Proc Natl Acad Sci USA. 2003;100:12570–12575. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shoemaker BA, Portman JJ, Wolynes PG. Proc Natl Acad Sci USA. 2000;97:8868–8873. doi: 10.1073/pnas.160259697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dyson HJ, Wright PE. Nat Rev Mol Cell Biol. 2005;6:197–208. doi: 10.1038/nrm1589. [DOI] [PubMed] [Google Scholar]
- 35.Levy Y, Onuchic JN, Wolynes PG. J Am Chem Soc. 2007;129:738–739. doi: 10.1021/ja065531n. [DOI] [PubMed] [Google Scholar]
- 36.Peskin CS, Odell GM, Oster GF. Biophys J. 1993;65:316–324. doi: 10.1016/S0006-3495(93)81035-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Taniguchi Y, Nishiyama M, Yoshiharu I, Yanagida T. Nat Chem Biol. 2005;1:342–347. doi: 10.1038/nchembio741. [DOI] [PubMed] [Google Scholar]
- 38.Thirumalai D. J Phys I (French) 1995;5:1457–1467. [Google Scholar]
- 39.Onuchic JN, Wolynes PG. Curr Opin Struct Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 40.Kubelka J, Hofrichter J, Eaton WA. Curr Opin Struct Biol. 2004;14:76–88. doi: 10.1016/j.sbi.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 41.Li MS, Klimov DK, Thirumalai D. Polymer. 2004;45:573–579. [Google Scholar]
- 42.Bryngelson JD, Wolynes PG. Biopolymers. 1990;30:177–188. [Google Scholar]
- 43.Uhlenbeck GE, Ornstein LS. Phys Rev. 1930;36:823–841. [Google Scholar]
- 44.Thirumalai D, Hyeon C. Biochemistry. 2005;44(13):4957–4970. doi: 10.1021/bi047314+. [DOI] [PubMed] [Google Scholar]
- 45.Zwanzig R. Acc Chem Res. 1990;23:148–152. [Google Scholar]
- 46.Hyeon C, Dima RI, Thirumalai D. Structure (London) 2006;14:1633–1645. doi: 10.1016/j.str.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 47.Manning GS. J Chem Phys. 1969;51(3):924–933. [Google Scholar]
- 48.Bishop M, Clarke JHR, Rey A, Freire JJ. J Chem Phys. 1991;95:4589–4592. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.