Drought mediates the importance of stochastic community assembly

Abstract

Historically, the biodiversity and composition of species in a locality was thought to be influenced primarily by deterministic factors. In such cases, species' niches create differential responses to environmental conditions and interspecific interactions, which combine to determine that locality's biodiversity and species composition. More recently, proponents of the neutral theory have placed a premium on how stochastic factors, such as birth, death, colonization, and extinction (termed “ecological drift”) influence diversity and species composition in a locality independent of their niches. Here, I develop the hypothesis that the relative importance of stochastic ecological drift and/or priority effects depend on the harshness of the ecological filter in those habitats. I established long-term experimental ponds to explore the relative importance of community assembly history and drought on patterns of community compositional similarity among ponds that were otherwise similar in their environmental conditions. I show considerable site-to-site variation in pond community composition in the absence of drought that likely resulted from a combination of stochastic ecological drift and priority effects. However, in ponds that experienced drought, I found much higher similarity among communities that likely resulted from niche-selection filtering out species from the regional pool that could not tolerate such environmental harshness. These results implicate the critical role for understanding the processes of community assembly when examining patterns of biodiversity at different spatial scales.

As the human footprint continues to grow, understanding the factors that influence patterns of biodiversity across the earth is essential to understand and remedy these effects (1). However, many of the critical factors that create variation in species diversity and composition among localities remain unresolved (2). Historically, community ecologists focused on deterministic factors, including how species' niches interact with environmental conditions and interspecific interactions (e.g., competition, predation) to determine how species diversity and composition vary along environmental and/or spatiotemporal gradients (3). More recently, Hubbell's (4) “neutral” theory has challenged this view by suggesting that many natural patterns can be recreated only by considering stochastic processes of birth, death, colonization, and extinction (and speciation) (see also refs. 5 and 6). Although the biodiversity and composition of an ecological community is most likely governed by a balance between stochastic (including neutral) and deterministic (niche-related) processes (7, 8), progress will require an expanded framework that explicitly includes both processes and explores the factors that will influence the relative importance of each.

At the core of the neutral theory is the concept of “ecological drift” (analogous to genetic drift) leading to dispersal-assembled communities (4–6). The structure of such communities results from stochastic colonization and extinction processes and is not influenced by species traits. Dispersal-assembled communities are expected to have considerable site-to-site variation (unpredictability) in their community composition among otherwise similar environments (9, 10). This unpredictability can be intensified if early colonizing species are able to disproportionately stave off invasion by subsequent colonizing species through priority effects leading to multiple stable states (11). In contrast, “niche-selection” (3) predominates if species' abilities to establish in a locality are more strongly determined by their traits, regardless of stochastic colonization and extinction dynamics. Such niche-assembled communities are expected to have more predictable community composition among sites that are similar in environmental conditions (12, 13).

Ecologists have treated niche versus dispersal assembly as a dichotomous debate (e.g., refs. 5, 6, 9, and 12–21). Here, I propose reconciliation to this debate by identifying critical features of habitats that create conditions that favor or disfavor the relative importance of these processes. In population genetics, the relative importance of genetic drift in shaping patterns of gene frequencies is determined by the balance between the strength of regional processes (dispersal), by population size, and by the strength and nature of local natural selection (22). By analogy, the relative importance of ecological drift, leading to dispersal-assembled communities, should be greater when dispersal is low, when niche-selection is weak, and/or when priority effects are strong.

One simple way to predict the relative importance of ecological drift is based on the effect of the environmental filter on the number of species that can potentially exist in a given locality combined with stochastic colonization and extinction processes. For example, in relatively benign environments, a majority of the species in the regional species pool can tolerate the physical conditions of the environment. So long as local richness is considerably less than the size of the regional pool and ecological drift is important, then the null expectation is that community composition will be quite different among localities and that communities will be highly dispersal-assembled. Alternatively, in communities with harsher environmental conditions, a large proportion of the regional species pool can be eliminated (filtered) from the “realized” pool of species. In this case, even if the process of assembly from the realized pool of species is completely random, the smaller available pool of species that can persist in the harsher conditions (due to niche-selection) leads to higher site-to-site similarity among communities, making their structure more niche-assembled.

Stochasticity in community assembly can also give rise to multiple stable states (11). Multiple stables states are not mutually exclusive from the concept of ecological drift, because variation in colonization processes leads to priority effects that are a primary mechanism creating variation in community structure. However, the multiple stable-states paradigm does not consider variation in communities through time, whereas the ecological-drift paradigm allows for extinction to create temporal changes in local community structure. In this case, communities that experience harsher environmental conditions, and a smaller realized pool of species as a result, are hypothesized to exhibit fewer potential multiple stable states than more benign communities with larger regional species pools (11, 23).

Small freshwater pond communities represent an ideal venue to explore the effects of environmental harshness on patterns of community assembly, because they harbor high levels of biodiversity and important ecosystem functions (24); their community compositions are sometimes highly variable, suggesting a possible role for stochastic community assembly (11, 25); and drought can greatly alter community structure by acting as an environmentally harsh filter (26, 27). In a long-term experiment in artificial ponds, I allowed communities to assemble over a 2-year period (see Methods). After all species had multiple opportunities to colonize each pond, albeit in different timings to enhance the potential for priority effects to manifest, I experimentally imposed drought on 10 (one half) of these ponds by slowly allowing the water to drain completely in late summer and refill over the winter/spring to simulate the effects of infrequent drought on pond communities (27) [supporting information (SI) Fig. 3]. This experiment allowed me to test whether drought, by imposing a strong environmental filter and potentially eliminating species from the species pool, reduces the relative importance of ecological drift and/or priority effects and therefore reduces the among-site variability in community composition relative to ponds that do not experience drought.

Results and Discussion

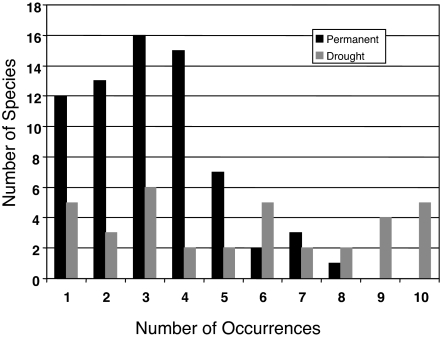
I compared community composition among each of the ponds after the experiment had run for 4 years (2 years following the drought treatment). Drought had a moderately negative influence on the average local (within-pond) species richness. Permanent ponds had on average 22.9 [±3.21 (SD)] species, whereas ponds that experienced drought in the second year of the experiment had on average 20.5 [±2.87 (SD)] species (ANOVA: F_1,18 = 8.82, P = 0.09), an ≈10% reduction. However, at the regional level, 71 species were observed in at least one of the permanent ponds, whereas only 39 species were observed in at least one of the ponds that experienced drought, an ≈45% reduction. Importantly, the difference in the effect size of drought on species richness at local (α-diversity) and regional (γ-diversity) spatial scales implies that drought also reduced among-site compositional differences of the ponds (β-diversity) (11). In addition, the frequency of occurrence of species among the replicate ponds differed between the treatments; species occurrences in permanent ponds were considerably more sporadic than those in drought ponds (Fig. 1).

Fig. 1.

The number of species that occurred in each pond (of 10 possible) for the permanent (black) and drought (gray) ponds. In permanent ponds, the majority of species occurred in <1/2 of the ponds, and no single species occurred in every pond. Of the species observed in at least one of the permanent ponds, each was observed in 3.21 [±1.65 (SD)] of the 10 permanent ponds, whereas of the species observed in at least one of the disturbed ponds, each was observed in 5.26 [±3.1 (SD)] of the 10 drought ponds (ANOVA: F_1,108 = 20.78, P = 0.001).

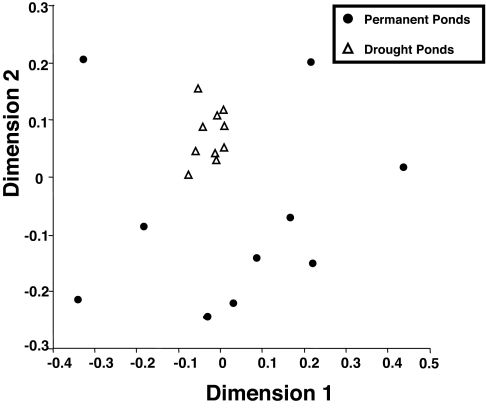
I tested whether communities that experienced a harsh environmental filter through drought would be more similar to each other than communities not exposed to drought by using Jaccard's index of community similarity, J. J ranges from 0 (when no species are shared between any two communities) to 1 (when all species are shared) and serves as a metric of β-diversity. Low similarity among communities that are otherwise identical in environmental conditions would imply a large role for dispersal assembly, whereas high similarity would imply a large role for niche assembly. Nonmetric multidimensional scaling (NMDS) portrays the relationship among each of the pond communities simultaneously based on the matrix of their community similarities, J. The pond communities exposed to drought cluster tightly in the NMDS ordination space, indicating similarity of species composition, whereas pond communities lacking drought are much more dispersed in the NMDS space, indicating large variability in species composition despite identical environmental conditions (Fig. 2).

Fig. 2.

Nonmetric multidimensional scaling (NMDS) allows the visualization of the multidimensional composition of communities in two-dimensional space. The Euclidean distance between any two points represents the difference in Jaccard's similarity between those two communities. Drought ponds are indicated by open triangles, and permanent ponds are indicated by filled circles.

Differences in similarity, J, values among and between treatments were tested using randomization tests (see Methods), which demonstrated that the species composition of ponds in each treatment (disturbed or drought) more closely resembled ponds in the same treatment than ponds in the other treatment (permutation ANOVA: F ratio = 2.13, P < 0.001). This result confirms that the drought treatment had a large effect on the assortment of species that could persist in those habitats (27). More importantly, permanent ponds were considerably more variable in their species composition than were ponds that experienced drought (permutation dispersion: F ratio = 34.07, P < 0.001). These results were consistent among similarity metrics and different groupings of species (SI Table 1).

Because community similarity estimated from species' incidence (e.g., J) is biased by the number of species in the different communities (28), and because local species richness differed between the ponds that experienced drought and those that were permanent, I developed an additional null-model approach (see Methods). This approach allowed me to test the hypothesis of whether within-treatment similarity differed from that expected from a purely random model of dispersal assembly alone (9). Thus, I was able to quantify the relative influence of niche assembly as the deviation of the actual similarity among communities relative to the similarity expected by random chance due to dispersal assembly alone. In permanent ponds, the observed similarity among all communities averaged 0.21, whereas the null expectation was 0.19 [0.18–0.21, 95% confidence interval (CI)]. In drought ponds, the observed similarity averaged 0.50, whereas the null expectation was 0.17 (0.15–0.19, 95% CI). By comparing the effect size of the difference between the observed similarity and the null expectation [ln(observed J) − ln(null expected J)] in a randomization test, I found that the effect size of the deviation from the null expectation was considerably higher for the drought ponds (1.08; 0.97–1.17, 95% CI) than for the permanent ponds (0.07; −0.02 to 0.15, 95% CI) (randomization test: P < 0.001).

There are several possible interpretations of these results. First, it is possible that ecological drift (defined here to include demographic stochasticity and other intrinsic stochastic effects, such as migration; ref. 4) played a prominent role in the assembly of the permanent ponds, because the actual community similarities (J) were statistically indistinguishable from the null expectation on the basis of dispersal assembly alone. Second, priority effects leading to multiple stable states could explain this result. Among the drought ponds, compositional similarity, J, was much higher than expected for dispersal assembly alone, possibly indicating a more prominent role for niche selection in the assembly of these communities and/or a reduction in the importance of priority effects and multiple stable states. Because community structure did not vary significantly in each pond during the final 2 years of the study (SI Text), this finding suggests a possible role for priority effects and multiple stable states in these communities. Importantly, these two interpretations are not mutually exclusive; priority effects that lead to multiple stable states are based on the same stochastic processes that create ecological drift.

It is also important to note that variation in ecological drift and/or multiple stable states are not the only two explanations for the observed results. For example, it is possible that in the absence of drought, heterogeneities in one or more environmental factors (light levels, allochthonous inputs) could have lead to more divergent community compositions. Alternatively, in the presence of drought, even the same magnitude of heterogeneity may be less important in determining the composition of the community. In addition, the magnitude of the heterogeneities themselves could have been altered by the drought. Although this experiment was established to minimize the majority of such heterogeneities and although none of the variables measured showed strong variation in the environmental conditions among the experimental ponds, I cannot rule out this alternative.

One final alternative explanation that could confound the interpretation of the results is that, after the drought, I allowed only natural resistance and/or resilience to the drought to influence community assembly, whereas during the initiation of the assembly process, I introduced species in a stochastic way. Thus, it is possible that communities in permanent ponds were less similar because of experimentally imposed initial differences, whereas ponds that received drought were only subject to species that were resistant to the drought and remained in the ponds (as diapausing life stages) or were resilient to the drought and recolonized the ponds. My intention with this design was to maximize the potential for ecological drift and priority effects to exert a legacy in community structure if it existed. However, after the drought, I did not manipulate community recolonization to simulate the effects of such harsh conditions on already assembled communities. Thus, even though the experimentally imposed assembly process was different before and after the drought, this manipulation is relevant to understanding the effects of a harsh environmental filter on the structure and similarity among communities. In addition, natural observations of permanent pond communities (11, 25), as well as a series of simultaneously running experimental ponds that received only natural (stochastic) colonizations (J.M.C., unpublished data), showed that permanent ponds maintained a much higher degree of compositional variation than did those exposed to drought. This indicates that the results of this study are likely to be due to drought effects filtering the species pool, making communities more niche-assembled, and not due to experimental artifacts.

Drought represents an important environmental filter for species in natural ponds and wetlands (26). Species that can persist after drought do so by either resisting it through life stages that can withstand drought (e.g., diapausing eggs) and/or by being resilient to drought by being capable of rapid recolonization (26). For example, in my experiment, the producers that dominated permanent ponds included a diverse array of submerged vascular plants (e.g., Elodea canadensis, Ceratophyllum demersum, Najas flexilis, Myriophyllum sibiricum, and several Potamogeton species). These species have no obvious mechanisms to resist drought, and are also very poor dispersers unable to disperse readily among ponds. Alternatively, following drought, the dominant producers were much less diverse and included filamentous (e.g., Oedogonium, Cladophora, Spirogyra) and macrophyte-like (Chara vulgaris) green algae, and a single macrophyte species (Zannichellia palustris). All of these species can tolerate drought as cells (in the case of algae) or diapausing seeds (in the case of Z. palustris) and can readily disperse from nearby habitats. Similar diversity and compositional shifts were repeated across functional and taxonomic groupings. Because drought created such a harsh filter, reducing the pool of species able to persist in those habitats, deterministic niche-selective forces were more prominent in drought ponds than in permanent ponds. In permanent ponds with less of an environmental filter, niche selection was weaker, and ecological drift and priority effects left a more prominent signature on community composition.

Understanding the relative roles of dispersal versus niche assembly in the development of community structure should provide important practical information for biodiversity restoration, which heretofore has had mixed results (29). If ecological drift leading to dispersal assembly is important, as I show in permanent ponds, restoration projects aimed at particular ecological communities will need to carefully consider stochastic processes and may require intervention (e.g., seed additions, removals) to achieve a desired state. Alternatively, when dispersal assembly is less important, as I show in communities that experienced drought, restoration projects may not need to consider the vagaries of community assembly, but focus more on the restoration of desired habitat properties.

In conclusion, I have shown that the environmental harshness imposed by drought on pond communities increases the similarity, reducing β-diversity. As such, even if local species diversity is able to recover following drought, regional diversity may be compromised. As human activities alter natural disturbance rates both locally (e.g., land development, forest harvesting) and globally (altering the intensity of El Niño events; ref. 30), it is imperative that ecologists recognize the varied influences of ecological forces, such as disturbance, on patterns of biodiversity at different spatial scales.

Materials and Methods

Experimental Setup.

I established a 4-year experiment manipulating community assembly and drought in artificial ponds. In the spring of 1999, I established 20- to 1,140-liter mesocosms (cattle tanks; Rubbermaid, Wooster, OH) (amidst a larger array of other mesocosms) in a large old-field near the University of Pittsburgh's Pymatuning Laboratory of Ecology (Crawford County, PN) (SI Fig. 3A). Each mesocosm was initiated with ≈5 cm of topsoil and nutrient-poor well water. Nutrient levels after the water and soil had settled were intermediate relative to surrounding pond habitats (25 ± 4 μg/liter P; 625 ± 43 μg/liter N). Each spring, I added 1/10 the amount of nutrients (nitrogen in the form of NaNO₃ and phosphorus in the form of NaH₂PO4) to each mesocosm to simulate spring runoff and to replace nutrients lost to the atmosphere, bound in the sediments, and lost to species that metamorphosed and left the experimental arena.

Manipulating Community Assembly and Drought.

To maximize the potential for stochastic ecological drift and priority effects to leave a signature on the resulting structure of the community, over a 2-year period, I randomly introduced a large number of species of producers and invertebrates into each experimental pond. Specifically, 25% of species from this total pool of species were randomly selected to be introduced in May of 1999, 25% in August of 1999, 25% in May of 2000, and 25% in August of 2000. After their introductions into some of the ponds, many of these species were observed to readily disperse among ponds. Furthermore, a wide variety of taxa (e.g., winged insects and amphibians with complex life-cycles) that were not experimentally manipulated colonized the mesocosms on their own, and these species were monitored alongside those that were introduced. Following the first introduction of all species, I introduced each species to each mesocosm a second time in May of 2001. All species were introduced at low numbers (3–20 individuals, depending on size and mating system) to simulate colonization. In all, my intention was to allow communities to assemble such that all species had access to every experimental pond but that colonization history was stochastic, so that any priority effects, if they existed, could manifest themselves.

After allowing these communities to assemble for 2 years, I imposed a drought (27) at the end of the growing season (August–September) in 2001 to one-half of the experimental ponds. To impose drought, I connected an L-shaped (5-cm diameter, 1-m tall) PVC pipe to the bottom drain of each mesocosm so that I could drain them over the course of the summer (by angling the PVC pipe) to simulate the natural phenology of a pond drying during a drought (see SI Fig. 3). Drying was initiated in early August and completed by early to mid-September. A 0.5-mm mesh screen was placed over the drain to minimize loss of individuals. After 1 month of being completely dry, the PVC pipe was repositioned, so that fall and winter precipitation could refill the mesocosms.

Censusing Pond Communities.

After 4 years (2 years following the experimentally imposed drought), ponds were censused to determine whether there were any legacies of stochastic assembly history (ecological drift and/or priority effects) and whether drought influenced the strength of those legacies.

Macroinvertebrates and amphibians were censused by pulling a 10 cm × 10 cm sweep net (0.33-mm mesh) perpendicularly through the center of the mesocosm. Sweeps were repeated two times perpendicularly at the bottom, middle, and surface of the water to ensure equal sampling of taxa with different microhabitat preferences. In all, this sampled ≈15% of the volume of the water. In addition, 10 more sweeps were made haphazardly throughout the volume of the pond to ensure that rare and or otherwise elusive organisms were captured. All collected macroscopic organisms (other than zooplankton) were preserved in 70% EtOH for enumeration and identification (31). Numbers/sizes of individuals of each taxon were extrapolated to the volume of the entire tank and compared with size- and species-specific dry-weight conversions (J. M.C, unpublished data) to calculate biomass of each species for abundance-based similarity analyses (see below).

Zooplankton were censused using a 5-cm diameter × 1-m tall integrated tube sampler (32). Five samples were taken from the edges and center of the ponds for a total of ≈15 l of sampled water, which was then filtered through an 80-μm mesh zooplankton net. Samples were preserved in acid Lugol's solution and identified and enumerated under a dissecting microscope (32–34).

Producers (macrophytes and filamentous green algae) were censused using five 0.1-m² quadrats (≈15% of the area). Vascular macrophytes and plant-like macroalgae (e.g., C. vulgaris) were removed from quadrats, sorted to species in the laboratory (35), dried at 60°C, and weighed. Filamentous green algae were removed from their entanglements, sorted to species (often with the aid of a dissecting microscope) (36), dried, and weighed as above. To include rare species that were not collected in the above sampling, I visually scanned ponds for ≈5 min.

Similarity Metrics.

Although all of the data presented in the main text discuss Jaccard's index of similarity, which is an incidence-based metric, I also computed several other metrics of similarity that can be calculated using the EstimateS software package (37). These included Sorenson's incidence metric, as well as Chao's abundance-based indices, and the Bray–Curtis abundance-based metric. Numbers of individuals of each species were extrapolated to the entire mesocosm and compared with species-specific biomass conversions (J.M.C., unpublished data) to calculate biomass for the abundance-based similarity metrics. I also calculated similarity matrices separately among each of the functional groups of the species, including producers, zooplankton, benthic herbivores, and predators. Although all of these similarity metrics possess different statistical properties, all of them showed similar results (see SI Table 1), justifying my focus on one metric in the text.

Comparing Compositional Similarity Between Disturbed and Permanent Ponds.

If drought affects species composition, then communities in the disturbed treatment should be more compositionally similar to communities in the same treatment than to the other treatment. To test this, I used a nonparametric, multivariate test, permutation ANOVA [available as a Fotran program (38, 39)]. The test statistic is a multivariate analog to Fisher's F ratio. To do this, I created similarity matrices for all experimental communities. Next, I calculated an F ratio that compares the variability in species similarity among communities within a treatment versus the variability in species similarity among communities across treatments. The larger the value of F, the more likely it is that the null hypothesis is false. The F ratio is not distributed like Fisher's F ratio because (i) individual species are not normally distributed (e.g., rare species contribute many zeros to the dataset) and (ii) similarity is not calculated from a single experimental unit. Thus, traditional P values cannot be used. Instead, a randomly generated F value (called F^π) is calculated by randomly shuffling the similarity matrix without regard to treatment 999 times. The P value is calculated by comparing the value of F obtained with the actual labeling of experimental treatments to the distribution created by permuting the labels.

Comparing Similarity Within Treatments.

A significant P value in the above permutation ANOVA analysis could arise because treatments differ in their across treatment similarity, in their within-treatment similarity, or both (39, 40). To examine the relative influence of dispersal assembly, I was primarily interested in exploring within-treatment similarity, and as such, the next statistical test is designed to disentangle these.

To test whether treatments differ in their within-treatment similarity, I used a second nonparametric permutation analysis, permutation dispersion, available as a FORTRAN program (41). This analysis uses the similarity matrix for all experimental communities (as above) and calculates the spatial median value of community composition (centroid) and the distance of each experimental community to that centroid. Calculating distance-to-centroid (dispersion) values for each treatment gives the F ratio. A P value is then obtained by comparing the actual F ratio to 999 randomly generated (treatment randomly assigned to each community in the similarity matrix) F ratios.

Comparing Within-Treatment Similarity to the Null Expectation.

Significantly different within-treatment similarity values among treatments could be generated, in part, due to differences in the species richness of those treatments. Because there was a trend for higher local species richness in permanent ponds, I developed a null model that explicitly incorporates differences in species richness among treatments.

If ecological drift and priority effects leading to dispersal-assembled communities alone determine species composition, then the similarity observed across these communities will not be statistically distinguishable from the random expectation. Alternatively, if community assembly is more influenced by deterministic niche selection, actual similarity values should be greater than the null expectation. I quantified the average observed within-treatment similarity by using Jaccard's similarity index for both disturbed and permanent ponds. I quantified the within-treatment similarity expected via a random assembly model by doing the following: (i) quantifying the total species richness present in the final year of study (2003) for each experimental pond, (ii) randomly assigning species to each experimental pond until the richness of the randomly assembled pond equaled the richness observed in that pond, and (iii) calculating the average within-treatment similarity for these randomly assembled communities. I repeated this randomization process to achieve 1,000 randomly generated within-treatment similarity values for each treatment. Significant deviation in within-treatment similarity from that expected in a neutral assembly scenario is indicated if the actual value for within-treatment similarity lies outside the 95% confidence intervals of the randomly generated values.

I predicted that ecological drift and priority effects will play a larger role in determining the composition of permanent ponds than drought ponds, and thus, that the actual value of average within-treatment similarity will differ more from the randomly generated value for the communities in the drought treatment. To test this, I randomly assembled communities and generated average within-treatment similarity values for each treatment (as above). For each run of this randomization process and for each treatment, I calculated the difference (effect size) between the actual and the randomly generated average within-treatment similarity: Effect size = ln(actual similarity) − ln(randomly generated similarity). I repeated this process for 1,000 runs to obtain a P value from the proportion of the runs in which the effect size of permanent ponds was greater than the effect size of drought ponds.

Separate statistical analyses were conducted for the entire community and for subsets of the community (i.e., plants, herbivores, predators, etc.) as above, but this analysis was only performed on the incidence-based similarity metrics, because abundance-based similarity metrics are not as influenced by changes in species richness. Statistical analyses were conducted using a program written in MATLAB.