THREE-DIMENSIONAL CHEMOARCHITECTURE OF THE BASAL FOREBRAIN: SPATIALLY SPECIFIC ASSOCIATION OF CHOLINERGIC AND CALCIUM BINDING PROTEIN-CONTAINING NEURONS

Abstract

The basal forebrain refers to heterogeneous structures located close to the medial and ventral surfaces of the cerebral hemispheres. It contains diverse populations of neurons, including the cholinergic cortically projecting cells that show severe loss in Alzheimer’s and related neurodegenerative diseases. The basal forebrain does not display any cytoarchitectural or other structural features that make it easy to demarcate functional boundaries, a problem that allowed different investigators to propose different organizational schemes. The present paper uses novel three-dimensional reconstructions and numerical analyses for studying the spatial organization of four major basal forebrain cell populations, the cholinergic, parvalbumin, calbindin and calretinin containing neurons in the rat. Our analyses suggest that the distribution of these four cell populations is not random but displays a general pattern of association. Within the cholinergic space (i.e. the volume occupied by the cortically projecting cholinergic cell bodies) the three other cell types form twisted bands along the longitudinal axis of a central dense core of cholinergic cells traversing the traditionally defined basal forebrain regions, (i.e. the medial septum, diagonal bands, the substantia innominata, pallidal regions and the bed nucleus of the stria terminalis). At a smaller scale, the different cell types within the cholinergic space occupy overlapping high-density cell clusters that are either chemically uniform or mixed. However, the cell composition of these high-density clusters is regionally specific.

The proposed scheme of basal forebrain organization, using cell density or density relations as criteria, offers a new perspective on structure–function relationship, unconstrained by traditional region boundaries.

Using various tracer and histochemical techniques, Heimer and his colleagues (Heimer and Wilson, 1975; Heimer et al., 1985, 1991; Zaborszky et al., 1985; Heimer, 2000) were among the first to realize that the main part of the forebrain that was previously referred as the substantia innominata belongs to nearby and better defined anatomical systems. These include the ventral aspects of the basal ganglia, i.e. the ventral striatopallidal system (consisting of the ventral pallidum and the core/shell subdivisions of the nucleus accumbens) and the so-called ‘extended amygdala’ which refers to the subpallidal cell bridges extending from the centromedial amygdala to the bed nucleus of the stria terminalis. Using sophisticated combinations of a dozen or more chemical markers, a refined parcellation of the various forebrain areas is possible (Riedel et al., 2002). However, many of these regions are traversed by the continuous collection of aggregated and non-aggregated cholinergic projection neurons referred as the basal nucleus of Meynert in humans. We will refer to the volume occupied by the cholinergic cell bodies in rats as cholinergic space. The cholinergic space is shared by several other chemically defined cell populations, including neurons containing various calcium-binding proteins, e.g. calbindin (CB), calretinin (CR) and parvalbumin (PV). PV-positive neurons represent a significant population of basalo-cortical projection neurons and most PV cells are GABAergic (Gritti et al., 2003). Another substantial proportion of corticopetal and septohippocampal neurons contains CB, but only a small proportion of CR cells projects to the cortex. In contrast to PV cells, only a small proportion of CB and CR cells contains GABA in the basal forebrain (Gritti et al., 2003). These four cell markers label non-overlapping cell populations in the basal forebrain (Kiss et al., 1997).

Whether or not a systematic spatial relationship exists among the different cell populations along the entire extent of the cholinergic space has not been addressed in previous studies. In this study, we used computational neuroanatomical tools for studying the spatial arrangement and numerical relations of the four major neurochemically distinct cell populations of the basal forebrain. Our analyses suggest that the distribution of the four cell populations is not random but displays a general pattern of association.

EXPERIMENTAL PROCEDURES

Animals and tissue preparation

The reconstructions and statistical analysis presented in this paper were prepared from three male Sprague-Dawley rats (375–466 g; Zivic Miller Laboratories, Portersville, PA, USA). All animal procedures were in compliance with PHS policy on Humane Care and Use of Laboratory Animals and the NIH Guide for the Care and Use of Laboratory Animals and approved by the Rutgers University Institutional Review Board. Special care was taken to minimize the number of animals used and their suffering. In deep anesthesia (sodium pentobarbital, 50 mg/kg i.p.), rats were perfused transcardially with 50 ml of saline, followed by 250 ml of an ice-cold solution containing 4% paraformaldehyde, 15% picric acid and 0.05% glutaraldehyde in 0.1 M phosphate buffer (pH 7.4). Brains were removed immediately after perfusion and post-fixed in a similar fixative without glutaraldehyde for 4–12 h. Two brains (cases #96001 and #96002) were cut into 50 μm coronal sections on an Oxford Vibratome® and collected into six vials. Alternate sections were stained with antibodies against choline acetyltransferase (CH: 1:100, courtesy of Dr. F. Eckenstein, University of Washington), PV (1:1000, courtesy of Dr. K. G. Baimbridge, University of British Columbia), CR (1:4000, courtesy of Dr. J. H. Rogers, University of Cambridge, UK) and CB (1:750, courtesy of Dr. K. G. Baimridge) according to the ABC technique of Hsu and Soban (1982), followed by nickel intensified diaminobenzidine reaction as described earlier (Cullinan and Zaborszky, 1991). Altogether, we obtained 44 (#96002) and 48 (#96001) sections, consisting of 11 and 12 series of four sections, stained for each marker. An additional set of sections was stained for Cresyl Violet to consult for cytoarchitectonic landmarks and the last series of sections were used for immunocytochemical controls. The distance between two consecutive sections stained with identical markers was 250 μm. The third brain (#97048) was cut into three series of 50 μm coronal sections on a freezing sliding microtome. From this brain we recovered 21 series, each consisting of two sections stained for CH and CR, thus the distance between two consecutive sections stained for identical markers was 100 μm.

Data acquisition

For data acquisition an image combining computerized microscope system and the Neurolucida® software package (Micro-BrightField, Williston, VT, USA) was used. Contours of the sections and fiducial markers were drawn under a 5× Plan-NEOFLUAR lens. In brains #96001 and #96002 cholinergic cell bodies were plotted with a 20× Plan-NEOFLUR lens. After plotting all cholinergic cell bodies in both hemispheres, basal forebrain areas containing cholinergic cells were delineated using relatively simple cytoarchitectonic criteria (Paxinos and Watson, 1986). Such borders were then superimposed on adjacent sections stained for the other three markers. Labeled cells within such defined areas were also exhaustively plotted. In brain #97048 the two cell types were traced by using ‘unbiased sampling’ and optical fractionators principles (West et al., 1991) with the Stereo Investigator® software (MicroBrightField). Briefly, CH and CR neurons were scanned under a 100× objective lens (Zeiss Plan-NEOFLUAR) using the following stereological parameters: sampling grid area: 2250 μm², counting frame: 75× 75 μm, section thickness: 20–21 μm, counting box height: 16 μm. The original Neurolucida® data files (database) contain 30,359 plotted cells in #96001; 30,926 neurons in #96002 and 4516 perikarya in #97048.

Statistical analysis of multivariate spatial interactions

To establish the overall tendency for random or non-random spatial interactions among the investigated cell populations, we used the analysis described by Bjaalie et al. (1991). By comparing two cumulative distribution functions of distances between cells (defined by their x, y, z point coordinates), this method distinguishes neutrality (random distribution) from non-random distribution between two cell populations. One function, H₁₂(t), is the cumulative distribution function of the distance t between a pair of randomly selected cells of type 1 and 2. The other, H₀₀(t), is the corresponding function for a pair of cells randomly selected among the two neuronal populations, without reference to type. A statistical test based on simulations of 100 random distributions was used to see whether deviations from neutrality were significant (for further details, cf. Bjaalie et al., 1991).

Construction of volumetric data of neuronal densities

For the data analysis described below, we extracted the x, y, and z coordinates of the cell bodies from the Neurolucida® database and saved them in ASCII format, each cell type in different data files. Structure outlines were stored separately. The medial, lateral, dorsal, and ventral extremes of the cholinergic cell distribution were taken as a three-dimensional (3D) framework to incorporate the entire dataset. Cells of different types mapped from four (#96001 and #96002) or two (#97048) adjacent sections were collapsed into a two dimensional plane (‘layer’) by removing the within-section depth coordinates but preserving the x and y coordinates for the individual perikarya. The distance from bregma of each of these composed layers was calculated using the average of the original four (#96001, 96002) sections. This way we created a set of 11–12 layers, each containing four different cell populations with their original x, y coordinates with a discontinuity of 250 μm between the layers. For expressing regional density changes the 3D framework was subdivided into virtual blocks of identical size denoted as ‘voxels’ of 250 × 250 × 50 μm for cases 96001, 96002. Section thickness served as unit size for the z dimension. In brain #97048 we constructed 21 layers, each containing two different markers with a discontinuity of 100 μm between the layers. The voxel size in this brain was 400 × 400 × 50 μm. The cells were counted in each of these lattices for each of the cell types. A mathematical description of the volumetric data construction is given in a recent publication (Nadasdy and Zaborszky, 2001) and in the Appendix.

Iso-density surface rendering

Cells counts of identical cell types were entered to a 3D matrix according to the i, j, and k indices of the voxels where i and j are the voxel’s position within the layer and k is the position of the layer within the series of layers. Since cell density is defined by cell counts within unit spaces, this 3D matrix represents a volumetric data of cell densities for a given cell type. Note that the discontinuity and gaps between sections are eliminated in the volumetric data. The local density differences in the volumetric data were visualized by defining a density threshold. Voxels with density larger or equal to the threshold were selected. Next, a surface was rendered around the selected voxels by interpolation between the i, j, k coordinates of voxels. For surface rendering we used functions written in C++ and the 3D-visualization toolbox of MATLAB R11® (MathWorks, Inc., Natick, MA, USA). To gain insight of the gradient of density changes in the 3D data we constructed a set of iso-density surface models where the density threshold was varied systematically (Nadasdy and Zaborszky, 2001; Zaborszky et al., 2002).

Iso-relational surface rendering

The construction of volumetric data of cell densities for each individual cell type is identical to the iso-density surface rendering. However, instead of calculating the cell densities of individual cell types here we consider the relative cell density of two different cell types. Voxels were selected if two conditions were met: (1) cell density must be larger than or equal to a threshold value for both cell types and (2) the ratio of the two cell counts must be larger than or equal to a predefined value. Using the double-constraint we localized voxels where the relative density of the two cell markers was specific; the implication of association of two cell types. The algorithm of surface rendering used here is similar to the iso-density surface rendering except that a surface is rendered around voxels only where the double-constraint was met.

Rendering a surface around heterogeneous density structures always involves the chance of capturing hollow spaces. However, layer-by-layer splicing of the volumetric data indicated no hollow spaces. Whenever iso-surfaces of the different cell types were combined, the larger surface area may have included iso-surfaces of the other cell type. Therefore, separate renderings of the individual cell populations were consulted and the threshold for cell count ratios was varied systematically. The overlapping areas were quantified using the overlap analysis method. A more detailed discussion of these methods can be found in two recent publications (Nadasdy and Zaborszky, 2001; Zaborszky et al., 2002).

Overlap analysis

We used an algorithm designed for quantitative analysis of the distribution of two populations of coordinate pairs from serial sections in brains #96001 and #96002. Similar approaches have been used by Alloway et al. (1999) and Leergard et al. (2000). In essence, the density and overlap between two cell populations (‘population 1’ and ‘population 2’) digitized from serial sections were compared. Each digitized section was subdivided into an array of voxels of a given size, and the numbers of coordinate pairs of each category were counted per voxel. Voxels containing a defined number of ‘population 1’ or ‘population 2’ points as well as voxels containing a similarly defined number of cells of both categories were classified. The numbers of voxels for each category were counted for each section and also summed across sections. The number of cells per voxel is influenced by the size of the voxel and cell count threshold criteria. Using small voxels and high threshold resulted in selecting a smaller number of high density clusters that do not reflect the organization of the whole data. Likewise, using large voxels and low threshold will generate a few large clusters that do not discriminate between spaces of different cell density. Our choice of voxel size (250 × 250 × 50 μm) was the smallest unit volume within which local density differences could be revealed while preserving major structural features. In our visualizations, we chose threshold levels of 5, 10 or 15 cells per voxel; higher threshold values would have obscured the general pattern of organization. One-way ANOVA and Tukey’s post hoc tests were used to compare the percentage of pair-wise overlap between different structures. The post hoc tests used a conservative test to take into account error due to multiple comparisons. Our custom made program for overlap analysis was developed in JAVA, with cross platform support (Windows, Mac, Unix) can be download from website: www.ratbrain.org. There are several outputs of the program including visualization of bin distributions and summarized cell and bin numbers in Excel format.

Cross-animal validity

The brain-to-brain co-registration of high density clusters of the individual and joint-marker distributions was tested by calculating the global voxel-to-voxel correlation coefficient of the cell density (absolute and relative) between brains #96001 and #96002. Individual and joint marker (CH-CB; CH-CR and CH-PV) density was quantified with the same voxel frame for the two brains. The density correlation between corresponding voxel positions was computed on two types of database. One contained the whole basal forebrain and the other type consisted of three databases containing individual structures (horizontal limb of the diagonal band, medial septum/vertical diagonal band and ventral pallidum). Both types of database were a full 3D definition of the basal forebrain consisting of six to 11 layers. The 250 × 250 μm voxel grid was aligned to the coronal midline for each coronal section individually in both brains. An affine transformation was applied between the two brains. Cells were counted within the 3D voxels for each marker separately. Then iso-relational threshold was applied and voxels with n ≥ 5 cells of both types were selected. Within each selected voxel the exact ratios of two specific markers of all combinations were determined and assigned to the voxel. A Gaussian blur of 750 μm (3 × 3 voxels) was applied to attenuate binning artifacts. Pearson’s correlation coefficient of the blurred density was calculated between corresponding voxels of the two brains. Only voxels with cell density or joint density distribution above threshold were included in the correlation analysis.

RESULTS

We have taken five different approaches to reveal principles of spatial organization among the four basal forebrain cell populations studied. First, we present a series of coronal sections through the basal forebrain, showing the distribution of the individual labeled neurons. Second, we have searched for statistical evidence for non-random distributions of the cell populations, pair-wise compared. Third, using cell density measure, we have explored the 3D structure of each of the four cell populations; we then examined the spatial association between the individual cell populations. Finally, a numerical analysis of the overlaps of different cell populations was applied.

Section-by-section, rostrocaudal, distribution of CH, CR, CB, and PV cells

The four cell types investigated show a heterogeneous distribution across rostro-caudal levels and across different subregions of the basal forebrain. For example, in the substantia innominata-bed nucleus of the stria terminalis continuum (so-called ‘extended amygdala’) the dominant cell population is the CB, while the globus pallidus is mostly populated by PV cells. All four chemically-identified cell populations show characteristic distribution patterns, and their relative distribution will be described briefly. The distribution pattern of the different cell populations was similar in all brains analyzed.

Medial septum/vertical limb of the diagonal band (MS/VDB)

A regular arrangement of the different cell types is especially apparent in panel B, Fig. 1, where most of the PV cells are located medially, and the majority of CB neurons are placed laterally. CR and CH neurons are in a partially overlapping position in between the bulk of PV and CB cells.

Fig. 1.

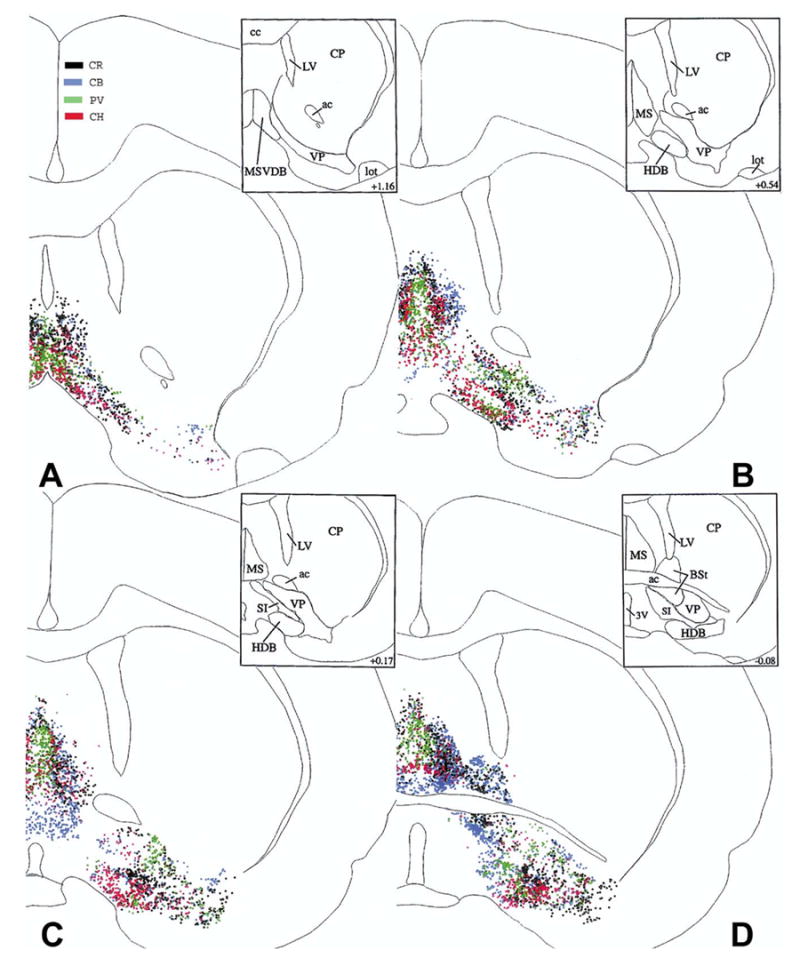
The distribution of cholinergic (CH, red), PV (green), CR (black) and CB (blue) cells at four caudal levels from the right side of brain #96001. These maps were generated by superimposing the original Neurolucida® maps plotted from sets of four sections alternately stained for CH, PV, CR, and CB, using landmarks and alignment techniques. Upper right insets show the outlines of individual basal forebrain areas applied in this study. Numbers in the insets represent distances in mm from the bregma, based upon the atlas of Paxinos and Watson (1986, 2005).

Horizontal limb of the diagonal band (HDB)

As described earlier (Zaborszky et al., 1986; Schwaber et al., 1987; Kiss et al., 1997) cholinergic cells show a doughnut shape arrangement in this region (Fig. 1B). Rostrally, CR cells are located mainly at the medial and ventral border of the HDB (Fig. 1A and B). More caudally, the border area between the HDB and the ventral pallidum is especially rich in CR cells (Fig. 1C). Further caudally, CR cells tend to be located primarily in the ventral part of this structure (Fig. 2A–C). CB cells are located at mid-rostral level (Fig. 1D) primarily at the medial border of this structure, while these cells tend to be diffusely distributed more caudally (Fig. 2A–D).

Fig. 2.

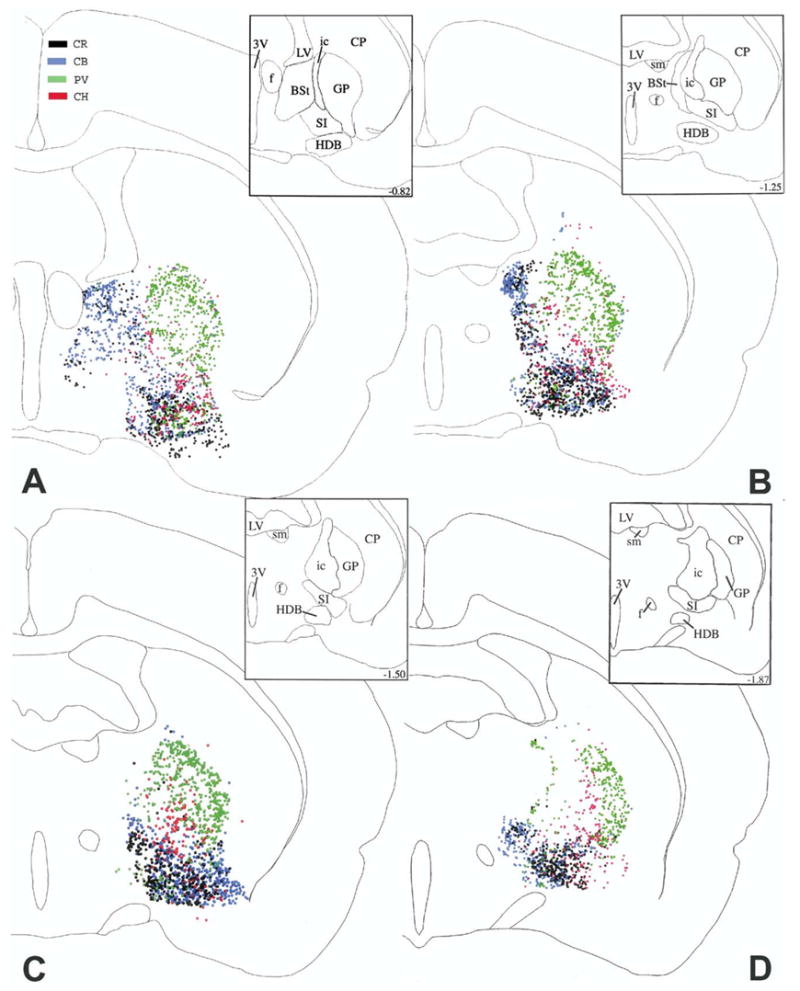
The distribution of cholinergic (CH, red), PV (green), CR (black) and CB (blue) cells at four caudal levels from the right side of brain #96001. These maps were generated by superimposing the original Neurolucida® maps plotted from sets of four sections alternately stained for CH, PV, CR, and CB, using landmarks and alignment techniques. Upper right insets show the outlines of individual basal forebrain areas applied in this study. Numbers in the insets represent distances in mm from the bregma, based upon the atlas of Paxinos and Watson (1986, 2005).

Ventral pallidum

PV cells are often concentrated in clusters in the medial (Fig. 1B) or lateral part of the ventral pallidum (Fig. 1C), while CB and CH cells are more diffusely distributed in this structure, with some local inhomogeneities and empty territories. CR cells are located in conspicuous clusters just ventrolateral to the anterior commissure (Fig. 1C).

Substantia innominata

This structure is especially rich in CB and CR cells and is characterized by relatively few cholinergic and PV cells (Fig. 2A–D). From these maps, a clear preferential localization of the different cell populations is not apparent.

Bed nucleus of the stria terminalis (BSt)

This nucleus contains relatively few cholinergic and PV cells, but it is mostly populated by CR and CB cells. These latter two cell types show an overlapping distribution, although CR cells tend to be shifted from a central position rostrally (Fig. 1D) to a more lateral position caudally (Fig. 2B).

Globus pallidus

The most prevalent population in this area is represented by PV neurons. The other three cell populations make up only a minority of its cells (Fig. 2A–D). Cholinergic cells are characteristically positioned medially in relation to the bulk of PV cells.

Internal capsule

The internal capsule contains relatively few cells, the majority of which are cholinergic and PV cells (Fig. 2A–D). PV cells tend be localized more medially in a thin layer, adjacent to the thalamic reticular nucleus.

Random or non-random distributions of cell populations?

Studies using mapping as well as stereological methods suggest an inhomogeneous distribution of the four cell populations across different basal forebrain structures. However, these techniques are, unable to detect basic rules of spatial associations among the four cell populations. To elucidate the tendency for random or non-random spatial interactions, we applied a pair-wise comparison of two cumulative distribution functions of distances between coordinate points, using the database from which Figs. 1–2 were prepared (see Experimental Procedures). This analysis included the six possible pair-wise combinations of cell types (CR/CB; CH/CR; CH/CB; CH/PV; PV/CB and PV/CR) in seven brain regions, including the MS/VDB, HDB, substantia innominata, globus pallidus, ventral pallidum, internal capsule and BSt. If the average distance of identified pairs does not differ from that of unidentified pairs the association is considered to be neutral. In contrast, if the distances of identified pairs are smaller than that of the unidentified pairs then a positive association is assumed, while distances between identified pairs larger than the unidentified pairs indicate a negative association. The null hypothesis was that the association between a given cell type pair is neutral. Altogether, 42 hypothesis tests were conducted. Deviations from neutrality were statistically significant (P < 0.01) in 38 of 42 cases. We could not reject neutrality of distribution in three pairs (CR/CB, CH/CR and PV/CR) in the internal capsule and in CH/CB in the BSt. Overall, this analysis demonstrated a significant spatial interactions between the cell populations.

Spatially specific density distribution within the various cell populations

Iso-density surface rendering was used to identify locations with similar density levels for each of the cell populations. The first row of Fig. 3 shows the spatial distribution of three cell populations, including CH, PV and CB-containing neurons, in animal #96001 (approximately 15,000 cells, right hemisphere). The lower three rows display separate surface renderings at different density thresholds (d ≥ 5, 10, 15) with the same voxel size (250 × 250 × 50 μm). Each cell population shows an overall continuous distribution consisting of characteristic U- or W-shape amalgamation with variations in the location that breaks down to smaller clusters when higher density thresholds (d ≥ 15) were imposed on the surface rendering. The large-scale structure of the cholinergic cells (‘red column’) consists of a high-density core (Fig. 3D) that can be considered as the major axis of the basal forebrain, from rostromedial to caudolateral. PV cells (‘green column’) are concentrated in several high-density clusters (Fig. 3H), bridging the two major assemblies of cells in the rostral and caudal part of the basal forebrain, e.g. in the septum and globus pallidus, respectively. CB neurons (‘blue columns’) display a ‘W’-shape distribution, with major amalgamations in the septum, in the BSt, and in the substantia innominata. As Fig. 3L suggests, the large CB amalgamation in the substantia innominata of Fig. 3K, consist of parallel bands of higher density clusters (labeled by arrows). Similarly, CR cells show several major amalgamations and smaller clusters (not shown).

Fig. 3.

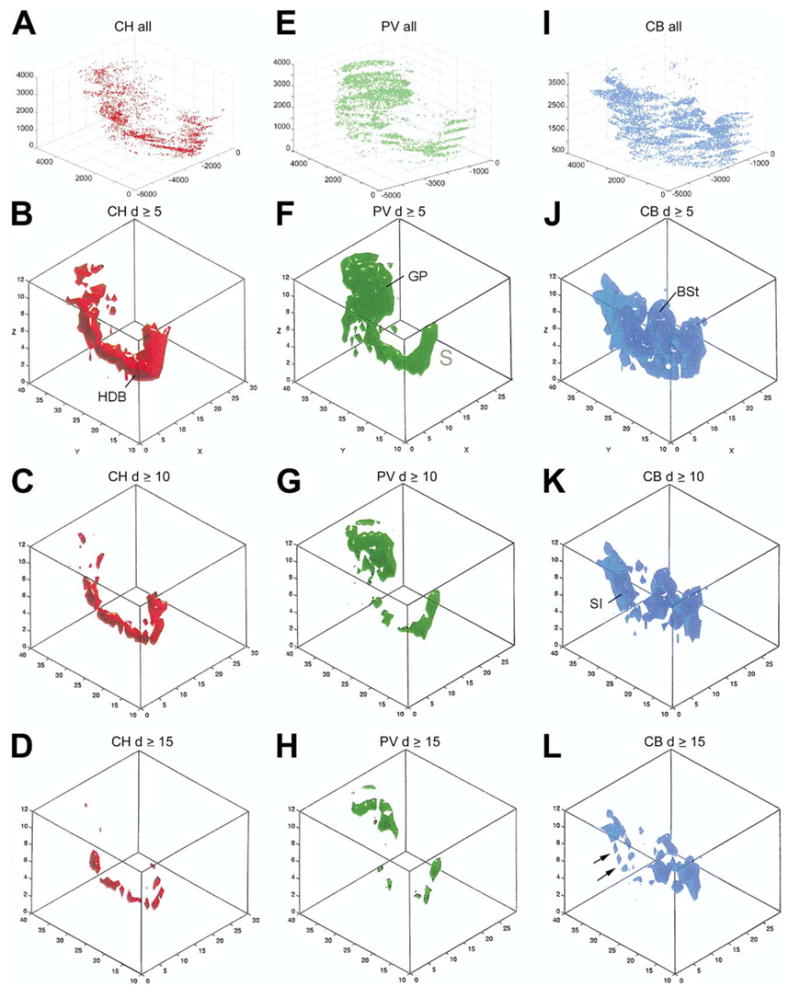
(A, E, I) Spatial distribution of all cholinergic (CH, red), PV (green) and CB (blue) cells from the right side of case #96001 as shown in separate coordinate systems. The numbers along the axes represent distances in micron of a given point from the reference point as traced in the Neurolucida® system. Flakes are due to the section steps along the z axis. B, C, D cholinergic; F, G, H PV and J, K, L CB iso-density surfaces. Threshold density: 5 ≥ (B, F, J), 10 ≥ (C,G, K) 15 ≥ (D, H, L) cells per unit space (250 × 250 × 50 μm). The numbers in the box plots represent voxel indices along the x and y axis. Numbers along the z axis are the layers. x-Axis: medio-lateral, y-axis: antero-posterior, z-axis: rostro-caudal.

Large scale spatial arrangement and association of the four cell populations

Figure 4 displays the iso-density surface renderings of three cell populations relative to the cholinergic neurons in various combinations. The first row shows models from brain #96001, the second row from brain #96002. Panel H was constructed from brain #97048. Panels G and I are compositions of all the four cell population from brains #96001 and #96002, respectively. From a 3D perspective, these four cell types seem to occupy longitudinal, obliquely (lateromedially) oriented U- or W-shaped band-like subspaces. The different cell bands seem to be twisted and attached to each other in a complicated fashion; however, a closer observation suggests that the four cell groups display a pattern of association in the entire basal forebrain. The twisted pattern of CB, CR, and PV bands is apparent relative to the axis of CH distribution (red). Regarding the caudal two thirds of the basal forebrain (e.g. globus pallidus), the lateromedial order of cell groups is PV-CH-CR-CB, while in the septum this pattern is clearly reversed. This is in accord with the observation by Kiss et al. (1997, Fig. 4D) in the septum where PV cells were reported to be located most medially and CB neurons most laterally. Cholinergic and CR cells are deposited in between with CR medial relative to CH.

Fig. 4.

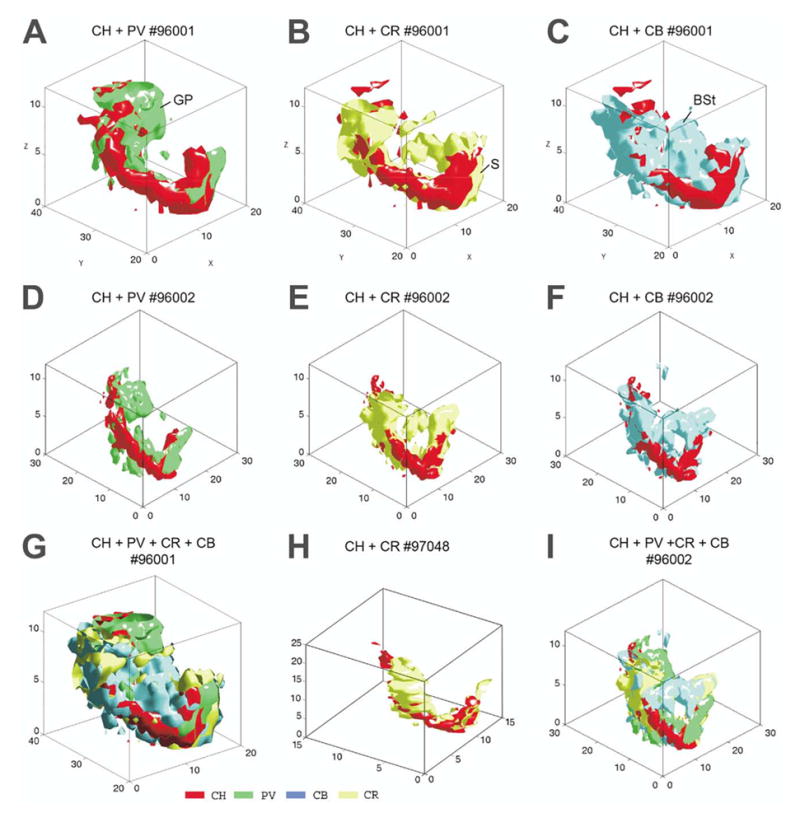
Merging of iso-density surfaces of different cell types. (A–C) Case #96001; D–F: case 96002. (G) All four cell types merged, case #96001. (H) CR and cholinergic markers, case 97048. (I) Case 96002. The iso-density surfaces render volumes of cell density ≥ 5 in the unit space (250 × 250 × 50 μm) in all models, except in H where the unit space is 400 × 400 × 50 μm and d ≥ 3.

Comparison of the combinational plot of iso-density surfaces between animals indicates that the global arrangement of the different cell groups is essentially similar (Fig. 4G–I). However, there are local differences due to technical factors detailed in the Discussion.

Spatial overlap between pairs of cell populations

In order to reveal the volume where the above-described cell groups overlap we used iso-relational surface rendering. This method imposes a combination of criteria that renders a surface around volumes where two cell types occur with a specified overall density and density ratio. The pairs compared were CH/PV, CH/CR, and CH/CB. In the analysis shown in Fig. 5, only voxels containing five or more cells from both cell populations in the pairs are shown. The upper row shows all voxels containing five or more cells from both populations. The ratio of CH/PV cells varied from 0.29:1–3.6:1 in the individual voxels. Similar ratios were found for the other combinations investigated. Thresholds for density ratios between the two extremes were arbitrarily introduced (middle and lower rows). In the second row, we arbitrarily introduced a threshold of 0.5:1 (cholinergic:other). Thus, voxels with ratios lower than 0.5:1 are not shown in this rendering. In the third row, the threshold was set to 1:1. Choosing a ratio of 2:1 (not shown), the renderings would contain only those few voxels where the number of cholinergic cells were at least twice as high as that of the other cell type. By increasing threshold we highlight subspaces where high-density groups of cholinergic neurons co-distribute with one of the other categories of high density non-cholinergic neurons, below referred to as mixed clusters.

Fig. 5.

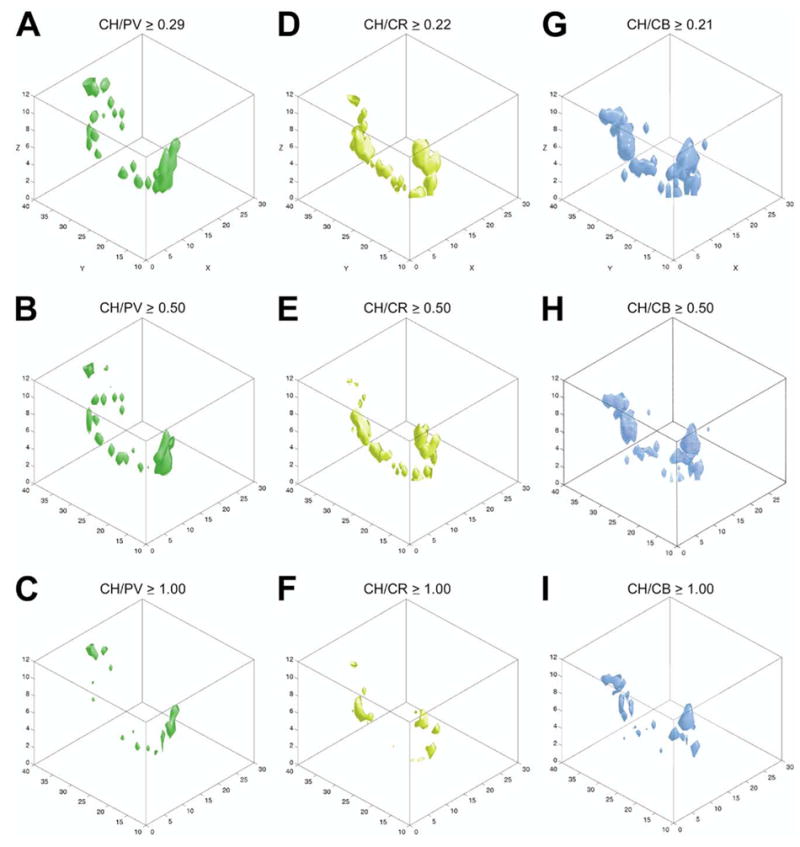
Iso-relational maps. The spatial relationship of cholinergic neurons to the other three cell types was determined by mapping the change in their density ratios. The ratios between the cholinergic and other markers were calculated considering only those unit spaces where both cell types have a density ≥ 5 cells. Iso-relational surfaces of CH/PV (green), CH/CB (yellow) and CH/CB (blue) are shown from the lowest local ratio in the upper row (0.29:1 for CH/PV, 0.22:1 for CH/CR and 0.21:1 for CH/CB), through intermediate ratios in the middle row (B: CH/PV, E: CH/CR, H: CH/PV: 0.5:1 or higher). (C, F, I) For all cell types cell ratio: 1:1 or higher.

Using this iso-relational surface rendering technique, regions with high density of PV, CR or CB cell populations that contain only few cholinergic cells were eliminated from the rendering. Comparing, for example, the ‘green’ columns in Fig. 3 (PV only) and Fig. 5 (cholinergic and PV cells) or the appropriate ‘blue’ columns in these figures, one can realize that the large blue amalgamations (CB) in the BSt or the green cell aggregate (PV) in the globus pallidus disappeared; thus the spatial and numerical relationships between the cholinergic neurons and the other three cell populations are easier to appreciate.

Combining the volume defined by the iso-relational surface rendering (Fig. 5) with the total distribution of the corresponding two cell populations clearly shows that these surfaces construct a central core surrounded by regions containing gradually decreasing cell densities. This is exemplified with the CH/CB cell populations shown in Fig. 6.

Fig. 6.

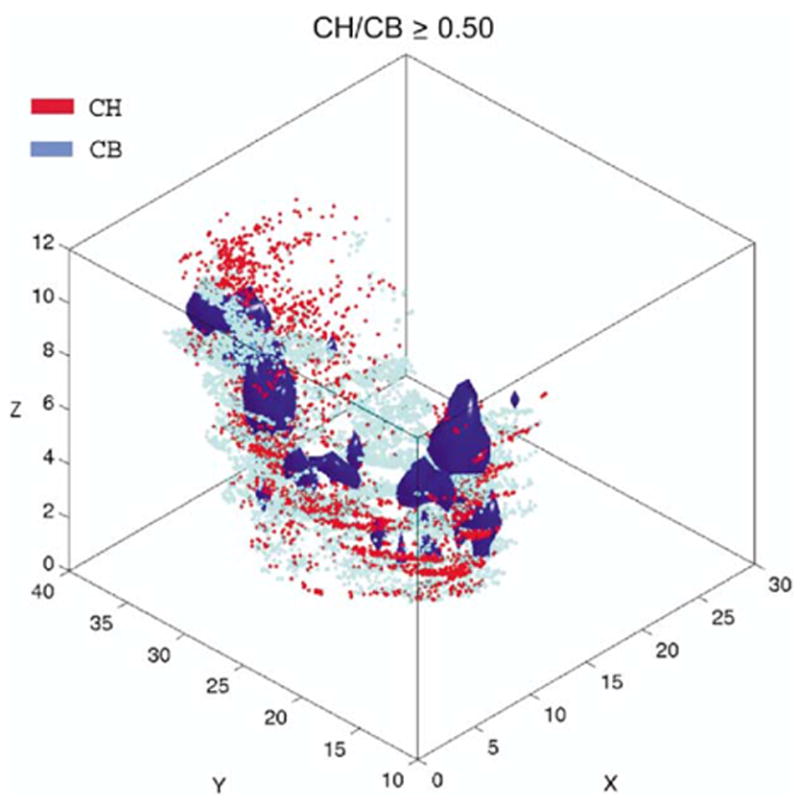
The iso-relational volumes of CH/CB rendered with violet surfaces (d ≥ 5 cells/250 × 250 × 50 μm unit spaces) were superimposed with scatter plot maps of all cells from the two neuronal populations.

By combining the volumes where pairs of the four cell types occur with a certain density from Fig. 5B-E-H we obtained a mosaic of high density voxels, as shown in Fig. 7A. This mosaic represents the overlapping core of the four cell population in Fig. 4. For better orientation, in Fig. 7B the combined rendering of panel 7A is placed into the wire frame of the section outlines. Comparing similar type of renderings between two brains, a similar global pattern was observed, however, there are local differences (compare Fig. 7A and C).

Fig. 7.

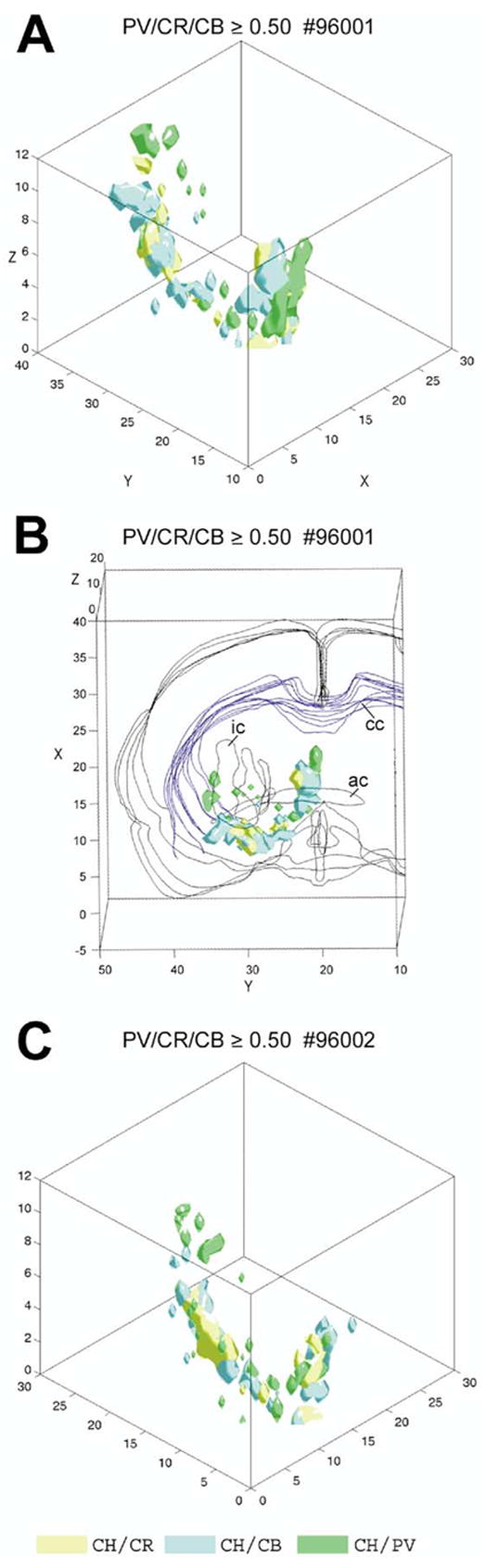
(A) Merging the three iso-relational surfaces of case #96001 from Fig. 5B, E, H into one scheme reveals that the cholinergic ‘column’ can be parcellated into clusters of different sizes and compositions. These surfaces cover the space where the relationship of cholinergic cells to PV (green), CR (yellow) and CB (blue) neurons is identical. The sequence of clusters corresponds to the sites where the three cell populations are attached to the cholinergic column (see Fig. 4A–C). (B) The iso-relational rendering of panel A is placed into the wire frame of the section outlines including other fiducial markers to show their real position in the original brain. (C) Similar composite rendering as in A from case #96002.

Numerical estimate of spatial overlap between different cell populations

To extract the systematic numerical relationships among the four cell populations at the different basal forebrain regions, we applied a method that has been used successfully to quantify overlapping cell populations. Using the same voxel size as in the density analysis (250 × 250 × 50 μm) and thresholding (unit spaces that contain ≥ 5 cells), we have mapped the number and fraction of voxels that contain high densities of the different cell groups. These data reveal that, as a total in brain #96001, about 50% of the high-density cholinergic voxels are shared with high-density CB voxels and 26% of the high density PV voxels occupy the same space as CB voxels (Table 1). However, the structure-by-structure analysis revealed that the number and location of the high-density voxels are uneven across structures. For example, in the medial septum, 48% of high-density cholinergic voxels share space with CB voxels, but this ratio is only 11% in the ventral pallidum. On the other hand, 57% of the high-density PV voxels in the HDB are shared with CB voxels; this ratio is in the ventral pallidum only 15% and these differences are significant (P < 0.05, Table 1). Despite the high percentage of mixed high-density voxels, a substantial proportion (23–45%, depending on the cell marker) of the high-density voxels for each cell types remains ‘lonely’; i.e. contain only one marker above the set threshold level density. The consequence of this arrangement is that each cell type and structure possesses a characteristic ‘signature’ combination of overlapping and lonely voxels. Fig. 8 shows the distribution of high-density segregated and overlapping voxels at three different levels from the CH/CB analysis. As it can be seen, the medial septum (Fig. 8A–D) and HDB (Fig. 8E–H) are rich in overlapping voxels as compared with that of the ventral pallidum (Fig. 8J–L) where these two cell markers occur mostly in separate voxels.

Table 1.

Comparison of pair-wise percentage overlap in the basal forebrain in case 96001^*

	Total	MS/VDB	HDB	VP
CH/CB	50.13 ± 22.3a	48.30 ± 32.0b	27.95 ± 21.4	11.1 ± 17.1a,b
CH/CR	46.17 ± 20.7	62.05 ± 20.4	36.91 ± 33.2	26.38 ± 24.9
PV/CB	26.36 ± 22.5	28.98 ± 22.25	57.13 ± 35.7c	15.96 ± 18.6c
PV/CR	15.54 ± 13.0d	32.90 ± 25.8	51.78 ± 32.7d	28.78 ± 34.2

^*Values are expressed as mean and standard deviation. Same superscript letters denote significant differences between corresponding structures.

^a,bOne-way ANOVA revealed that CH/CB overlap percentage from MS/VDB and VP differed significantly (F(3,27) = 1.38, P < 0.05). Tukey’s post hoc revealed that the MS/VDB had significantly more CH/CB overlap than the VP.

^cThe PV/CB overlap percentage between HDB and VP differed significantly (F(3, 28) = 2.25, P < 0.05). Tukey’s post hoc revealed that the HDB had significantly more PV/CB overlap than the VP.

^dThe PV/CR overlap percentage between the total and HDB differed significantly (F(3,28) = 3.54, P < 0.05). Tukey’s post hoc test revealed that the HDB had significantly more PV/CR overlap than using the total database.

Fig. 8.

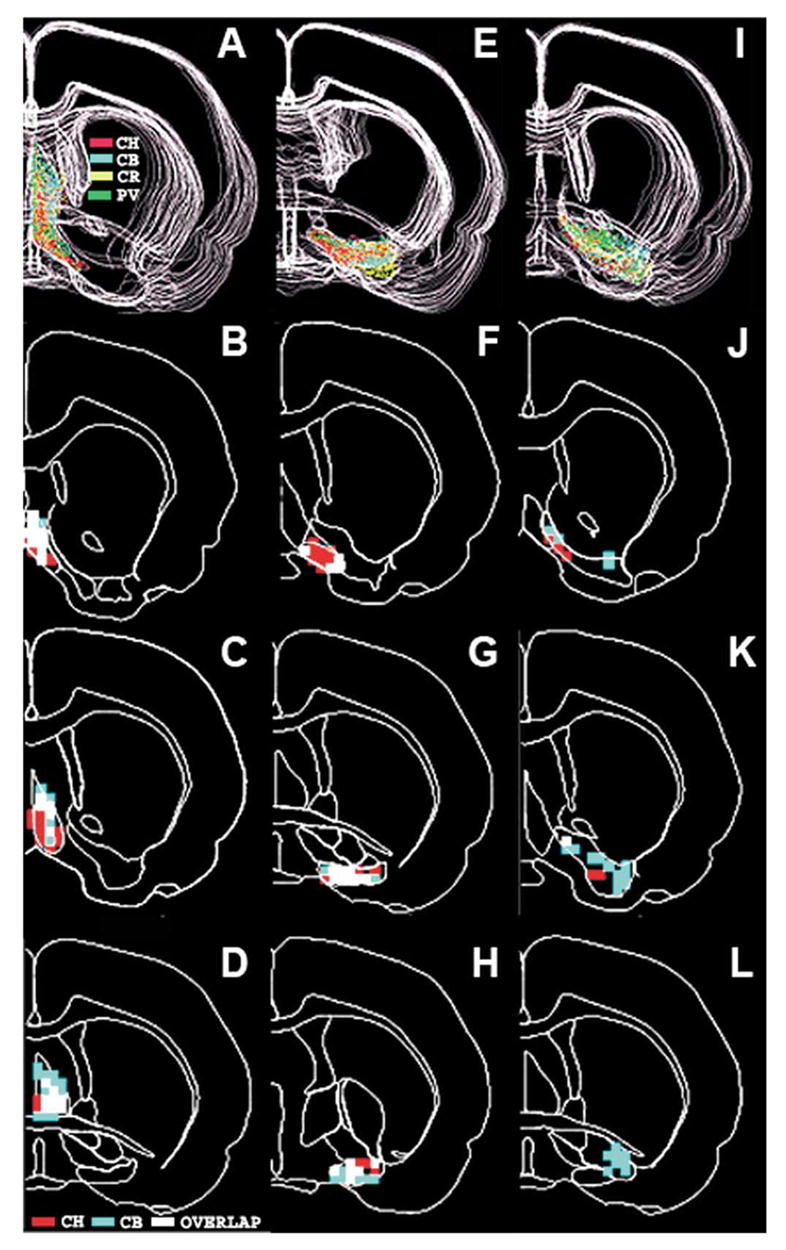
Distribution of the high density and overlapping voxels between cholinergic and CB neurons in the medial septum (B–D), the HDB (F–H) and in the ventral pallidum (J–L) from case 96001. Density threshold is five cells and voxel size of 250 × 250 × 50 μm. Red voxels: high density cholinergic, blue: high density CB and white voxels: high-density overlapping voxels. The panels in (A, E, I) in the upper row show all four cell markers in the septum (A), in the HDB (E) and in the ventral pallidum (I). In these panels cholinergic cells are red, CB neurons blue, CR cells yellow and PV cells green.

Cross-animal validity

The per voxel cell density correlation between the two brains was significant for each marker (r_PV = 0.79 P_PV= 0.01, r_CR = 0.64 P_CR = 0.01, r_CB = 0.87 P_CB = 0.01, r_CH = 0.92 P_CH = 0.01). The joint distribution of each marker with CH (CH-CB, CH-CR and CH-PV) was also significant at P < 0.01 (r = 0.73, 0.48, 0.51, respectively). The joint marker density correlation was significant for each marker pair regardless of the two database type, e.g. containing all layers and structures or structure by structure databases. However, large difference in correlation coefficient was observed between different structures and within structures ranging from r_CH-PV= 0.36 between the two MS/VDBs to r_CH-CB = 0.81 between the two HDBs. The correlation was the highest within HDB (r_CH-CB = 0.81 r_CH-CR = 0.75 r_CH-PV = 0.78) and the lowest within MS/VDB (r_CH-CB = 0.52 r_CH-CR = 0.67 r_CH-PV = 0.36). The co-registration of different marker pairs also varied within the same structure (see MS/VDB above), and different marker pairs have different registration correlation regarding the whole brain (Fig. 9).

Fig. 9.

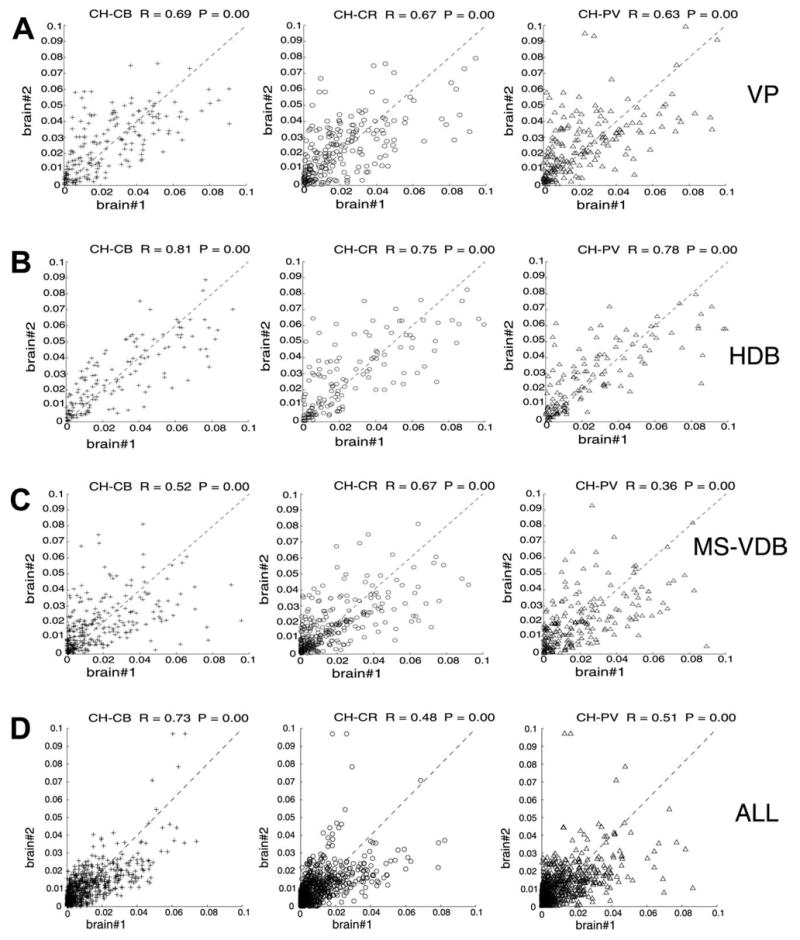
Voxel-by-voxel cell density correlation between cases 96001 and 96002. Abscissa: per voxel cell density for brain #96001; ordinate: per voxel cell density for brain #96002. The joint marker density correlation was significant for each marker pairs regardless of the database type: the entire basal forebrain volume (ALL) or only a particular structure volume (VP, HDB, MS-VDB). However, large difference in correlation coefficient was observed between different structures and within structures. The co-registration of different marker pairs also varied within the same structure. See text for further description of this analysis.

DISCUSSION

The present paper uses novel 3D reconstructions and numerical analyses for studying the spatial relationship of four major cell populations of the basal forebrain. The main results are as follows: 1) each cell system displays a characteristic non-homogeneous distribution that was consistent across animals (Fig. 3); 2) the large-scale organization of the populations of different cell types displays twisted bands around the cholinergic column (Fig. 4); 3) within the cholinergic space the different cell types occupy both chemically specific uniform and mixed overlapping regions along the axis of the cholinergic ‘column’ (Fig. 7). The overlapping regions are composed of various cell types of all combinations but the cell type composition is regionally specific (Table 1).

What made these observations possible was to apply novel statistical methods (iso-density surface rendering and iso-relational surface rendering) for analyzing the 3D distribution of different cell markers. This group of methods relies on the 3D reconstruction of cell bodies and the goal is to extract the hidden architecture of cell populations that may not be evident from simple visual observation. The key principle was to convert the Cartesian cell coordinates to a volumetric database which allowed us to perform various statistics on the cell density domain, including selective visualization of high density cell populations and localize regions where a specific combination of cell-markers was predominant. These high-density regions and specific combination of cell types suggest putative functional architecture of the neurons that was not evident from the single section reconstructions. A more detailed description of these methods is included in the Appendix.

Technical considerations

Cluster artifacts resulting from layer distances

Since the layers were derived from discontinuous tracing with 250 μm gaps of untraced tissue our sampling was not gapless in the z-dimension. This factor may cause two types of errors. One is segregation of a continuous cell population into two clusters. The other is to miss cell population borders that were located between adjacent sections. In order to generate a gapless database we collapsed each cell’s original z-coordinate to a layer identification number, thus eliminating within layer z-coordinates. This method may also generate artifacts such as failing to identify within-layer structural details in the z-dimension. However, this does not affect the spatial resolution in the x and y coordinates because the choice of voxel size in those dimensions was free. In principle, since the voxel size was set to 250 μm, equal to the gap, this reduction of resolution led to an equal bias in all x, y, z coordinates. To control for the effect of this type of error we compared the iso-density distribution of brain #97048 which had 100 μm gaps with brains #96001 and #96002 that have 250 μm gaps between sections containing the same two markers. Based on this analysis we were able to rule out that the global configuration is affected by the gap frequency.

Data acquisition using mapping or unbiased sampling

The purpose of unbiased sampling is to eliminate sampling errors derived from the ‘lost cap,’ over-projection effects, and from the differential probability of sampling neurons with different sizes (West, 1999). This method was designed to improve the efficacy of cell counting procedure on a smaller sample size. Despite of the substantial reduction of the sample size in brain #97048, a similar spatial configuration of the two cell types was obtained (compare Fig. 4B, 4E and 4H).

Across animal validity

Despite the inevitable minute differences in the immunocytochemical protocol if brains are separately processed and the difficulty in manual alignment of sections, there is a remarkable inter-individual similarity in the global organization of the four cell types investigated. For example, when the four iso-density renderings were combined into one scheme (Fig. 4G and 4I), misalignments would particularly alter the configuration of specific attachments in different animals. Local differences between cases #96001 and #96002, especially the difference of the middle CB amalgamation (Fig. 4C and Fig. 4F) in the rendering was due to a partial plotting of CB cells in the BSt in case #96002. The lack of the middle aggregate in the CR population in case #97048 is caused by the complete omission of the BSt in tracing. The similarity of the overall percentage distributions of the joint-markers and the significant per voxel density correlation between the two brains support the notion that the novel computational analyses reveal specific associations among the investigated cell types across basal forebrain regions.

A hypothetical 3D model of basal forebrain organization

It was evident from the comparison of iso-density distribution of individual and combined cell populations across different animals that the major pattern of cholinergic column surrounded by a twisted bundle of the other three cell types is preserved across different animals (Fig. 4). Consistent with the twisted bundle arrangement of cells, our earlier cholinergic reconstruction from gapless series of sections suggested that the cholinergic column itself is composed of several longitudinally oriented twisted bands (see Fig. 2E in Nadasdy and Zaborszky, 2001). Likewise, multiple retrograde tracer labeling of cortical areas suggests that neurons projecting to medio-laterally located stripes of the neocortex in rodents are organized into oblique, longitudinal twisted bands in the basal forebrain (Zaborszky, 2002). We suggest that the mixed composition of the four cell types inside the cholinergic space derives from the intersection of twisted multiple bands composed of single cell types. The inverse topographical relationship along the ascending hypothalamoseptal fibers (see p. 656 in Cullinan and Zaborszky, 1991) suggest that a twisted connectional pattern could be a general building principle in the forebrain. At present, it is unknown how signaling factors along the longitudinal and transverse domains of the forebrain regulate gene expression and migration of clonally related cells (Rubinstein et al., 1998) to establish the observed sequence of cellular pattern. However, our studies are compatible with the notion that the global and local configuration of basal forebrain clusters and amalgamations are developmentally determined.

Concluding remarks

The basal forebrain does not display any cytoarchitectural or other structural features that make it easy to demarcate functional boundaries, a problem that led to several proposed organizational schemes (e.g. compare the different delineation schemes of the basal forebrain in the two most popular anatomical atlases of the rat: Swanson, 1992; Paxinos and Watson, 2005). Neuronal density is an important dimension of the functional architecture of brain since neurons in close proximity of one another are sharing input and output thus supporting related functions. We offer a cellular-based parcellation scheme using cell density or density relations as criteria. This will afford a new perspective on structure-function relationships in the basal forebrain, unconstrained by traditional region boundaries.

The high density clusters, or amalgamations, showing regionally specific distributions in the basal forebrain, bear some resemblance to ‘interface islands’ found in other areas of the CNS, such as the striosoma-matrix compartments of the striatum (Gerfen, 1985; Graybiel and Penney, 1999), the interdigitating, frequency-specific cell clusters in the auditory brainstem nuclei (Malmierca et al., 1998), or the AChE patches in the superior colliculus (Chevalier and Mana, 2000) that have been suggested to represent processing channels. It is interesting to note that stimulations in spatially different locations in the basal forebrain have been shown to result in different modulation of ongoing cortical activity (Jimenez-Capdeville et al., 1997). Future electrophysiological studies must take into consideration that stimulations with vertically penetrating electrodes in the basal forebrain may affect heterogeneous neuronal aggregates with different targets and chemical compositions. Consequently, stimulation could modulate spatially and functionally disparate cortical areas.

Abbreviations

BSt

bed nucleus of the stria terminalis

CB

calbindin

CH

choline acetyltransferase

CR

calretinin

HDB

nucleus of the horizontal limb of the diagonal band

MS/VDB

medial septum/nucleus of the vertical limb of the diagonal band

PV

parvalbumin

3D

three-dimensional

Abbreviations used in the figures

ac

anterior commissure

BSt

bed nucleus of the striá terminalis

CB

calbindin

cc

corpus callosum

CH

choline acetyltransferase

CP

caudate putamen

CR

calretinin

f

fornix

GP

globus pallidus

HDB

horizontal limb of the horizontal band

ic

internal capsule

lot

lateral olfactory tract

LV

lateral ventricle

MS

medial septum/vertical nucleus of the diagonal band

PV

parval bumin

S

septum

SI

substantia innominata

sm

stria medullaris

VP

ventral pallidum

3V

third ventricle

APPENDIX

Construction of volumetric data of neuronal densities

For the data analysis, all Neurolucida® databases were exported as ASCII files and these files were parsed for cell body and structure outline coordinates where cell bodies {b_t} of a given cell type t were represented by single points individually by their Cartesian point coordinates {p_xyz} and section identifier s. If z-coordinates were not available or different cell types belonging to the same layer were mapped from adjacent sections, the section identifier was taken as z-coordinate. So each cell was represented as a point

$$b_t=p_{xyz}$$ (1)

Conversely, since a given position could be occupied only by one cell body, the Cartesian coordinates with the cell type together completely determined a given cell b_t as x_b, y_b, z_b, t. Structure outlines were compiled to separate files. For discretization of the space occupied by cholinergic cells, the medial, lateral, dorsal and ventral extremes of the entire cholinergic cell population were taken as the edges of a 3D framework. The total volume V occupied by neurons (neuronal space) is expressed as a vector r⃗ with a minimal p_r⃗ density function.

$$V=\{\overrightarrow{r}:p_{\overrightarrow{r}}\ne 0\}.$$ (2)

For quantization of regional density differences, V was subdivided into identical size virtual blocks denoted as ‘voxels’ and defined as follows.

$$v=d_x,d_y,d_z$$ (3)

where d is the edge of the voxel. The thickness of the original sections served as d_z. If different cell types were mapped from different but adjacent sections, then their z_b coordinates were collapsed into a common two-dimensional plane (master plane) by removing the within-section depth coordinates, however, preserving the x and y coordinates and redefining z-coordinates as section identifier s of cells. Thus, voxel and cell definitions have been simplified as v_s = d_x, d_y and b₁ = p_xys, respectively.

The i, j, k indices of a voxel containing a b_i = p_xys cell body is calculated as

$$i=d_x(x_p/V_{\mathit{length}}),j=d_y(y_p/V_{\mathit{width}})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}k=s$$ (4)

Cells were then counted in each voxel for each cell type separately providing a local density function ρ.

$${\rho }_{(v_{\mathit{ijk}})}={\mathit{count}}_{(v_{\mathit{ijk}})}=n{b}_i$$ (5)

For visualization, we defined a volume Ω based on a function of minimum density σ.

$$\mathrm{\Omega }=\{v_{\mathit{ijk}}:{\rho }_{(v_{\mathit{ijk}})}\ge \sigma \}$$ (6)

Note that the critical step was the conversion of the 3D point-coordinate database, where the entries were the cells, to a density data (Equation 4) which became a volumetric database. In contrast to the original parametric database where cell bodies are represented by their x, y, z-coordinates, the entries of the volumetric database are cell-counts. More precisely, the volumetric database is described by an at least four dimensional vector where the first three coordinates are the voxel coordinates and the forth is a variable, here cell density. One advantage of the volumetric database that it can be sliced in any angle and visualized from any point of view. The cell density distribution was visualized by defining a density threshold and voxels larger than threshold were identified (Eq. 6). For surface rendering we used custom written C++ programs and the 3D-visualization toolbox of Matlab R11® (MathWorks, Inc.).

Iso-density surface rendering

The spatial distribution of different cell types may be very complicated as neuronal populations interdigitate, intersect or overlap with one another. Instead of using scatter plots, the spatial organization of density differences is better visualized by rendering a surface around high-density cell groups, especially when multiple cell types are concerned. We developed an algorithm that renders a surface around voxels of larger than certain cellular density. The procedure of subdividing the 3D database onto voxels (unit spaces) and calculating the voxel cell densities is described under ‘Construction of volumetric data of neuronal densities.’ In the visualization of iso-density surfaces the numbers along the large box, which represents the total volume occupied by the neurons, are voxel coordinates. Figure^* 3B, uses individual rendering of the cholinergic cell population at a given density threshold (d ≥ 5) and voxel size (250 × 250 × 50 μm). The rendering in Fig. 4G was constructed by merging the individual iso-relational surfaces of the cholinergic, PV, CR and CB cell populations from Fig. 3.

Iso-relational surface rendering

In order to reduce complexity and extract the associative relationship of different cell types, we calculated the density ratio of the two cell types in each voxel. Highlighting the locations at which the density ratio exceeds a certain level reveals the spatial configuration of cell-to-cell associations between different cell types. First, we constructed volumetric databases of density for each cell type and discretized the space with dividing it to voxels. For this, the different cell types must be carefully mapped in a common 3D coordinate system. If the different cell types were traced from different sections, it must be considered that inference of the joint density from separated sections may be affected by section distortion. If density changes between adjacent sections are negligible, the within-section z-coordinates of different cell types can be collapsed into the same section s to obtain an estimate for the real joint-density. The next step was to calculate local density ratios between the cell types for each voxel. When density ratios had been assigned to each voxel of the volumetric database, we imposed a predefined density ratio criterion and selected voxels which met this criterion for visualization. The volume of these voxels represented a specific numerical association between cell types. Voxels, where the predefined density ratio of cell types had been established, were surface rendered. Thus, cell bodies with density ratios larger than a specific value were covered by the surface. Conversely, voxels with density ratios smaller than the critical one were located outside of the surface. The unique feature of the ‘iso-relational surface rendering’ method is the visual representation of an abstract relationship that may be more important for understanding the functional architecture of neurons than the exact locations of cell bodies. For visualization purposes, a range of critical density values must be applied for testing the integrity of clouds and to make sure that there are no hollow spaces covered. Density relations of multiple cell types can be decomposed into pair-wise relations, such as the plots^* in Fig. 5B, displaying iso-density surfaces around CH-PV, cells. To appreciate more complex spatial relationships, the separate iso-relational surfaces (CH-PV; CH-CR and CH-CB) can be merged into one model such as the plots in Fig. 7A.