Evolution of the primate lineage leading to modern humans: Phylogenetic and demographic inferences from DNA sequences

Abstract

To date major divergences that occurred in the primate lineage leading to modern humans and to infer a demographic parameter (effective population size) of the ancestral lineage that existed at each divergence, a maximum likelihood method was applied to autosomal DNA sequence data currently available for pairs of orthologous genes between the human and each of the chimpanzee, gorilla, Old World monkey (OWM), and New World monkey (NWM). A statistical test is carried out to support the assumption that silent substitutions have accumulated in a clock-like fashion over loci between primate taxa or even among sites within a locus. It is shown that the human ancestral lineage became distinct from the NWM 57.5 million years (Myr) ago, the OWM 31 Myr ago, the gorilla 8.0 Myr ago, and the chimpanzee 4.5 Myr ago, and that the effective population size at these divergences was generally much greater than that of modern humans. It is argued that the human ancestral lineage branched off from the NWM and OWM earlier than once thought and that significant demographic changes might have occurred at different evolutionary stages, particularly at the hominid stage.

The dating of the emergence of primate species has been a subject of controversy (1). A previous estimate of the divergence time of hominoids from the Old World monkey (OWM) is 25 millions years (Myr) ago and that of Catarrhini (hominoids and OWM) from Platyrrhini (New World monkey; NWM) is 35 Myr ago (2). However, recent discoveries of early fossil primates and theoretical considerations of the effects of gaps in the fossil record have challenged such relatively recent divergences of OWM and NWM and have pushed these divergences back by at least 10 Myr (1).

In addition, since a pioneering work on “Blood Immunity and Blood Relationships (Cambridge)” by G. H. F. Nuttal in 1904, molecular approaches to primate evolution often have led to discordant conclusions with the then-authoritative view based on fossil records and have fueled the controversy (3). Particularly controversial have been the phylogenetic relationships among hominoids (4–9). Not all molecular data yielded the same conclusion and Rogers (10) summarized phylogenetic studies of seven autosomal DNA sequences from humans, chimpanzees, and gorillas: four support the human and chimpanzee clade, two support the chimpanzee and gorilla clade, and one is ambiguous. There are several causes for this discrepancy (11). Besides the causes that may stem from inaccuracy of inferred molecular phylogenetic trees, one is particularly relevant to our case: molecular phylogenetic trees can intrinsically differ from locus to locus as well as from the species tree (10–13). This is because orthologous genes sampled from different species must have diverged before the species divergence and the persistence time of the gene lineages in a common ancestral species might have differed greatly from locus to locus. Conversely, the divergence time estimated from nucleotide substitutions between orthologous genes can provide an upper limit for the species divergence time (12), but there is no way to set a lower limit.

To infer the species divergence time accurately, it is necessary to separate nucleotide substitutions between orthologous genes into two categories: substitutions that have accumulated before the species divergence (ancestral polymorphism) and those after it. For many independent pairs of orthologous genes in a given species pair, such separation becomes feasible, at least in principle, because the process of accumulating nucleotide substitutions is different between the two categories. In particular, the former type of nucleotide substitutions is expected to have a larger variance than the latter. N. T. (14) developed a moment method, and N. T., Y. S., and J. Klein (13) developed a maximum likelihood (ML) method. However, both loci and species used in these studies were limited. In addition, possible heterogeneity in the nucleotide substitution rate over sites or across loci was not considered. In this paper, we apply the ML method to 23, 14, 46, and 8 pairs of DNA sequences (EMBL-GenBank database Rel. 44) in comparisons of the human with the chimpanzee, gorilla, OWM, and NWM, respectively, after examining the rate heterogeneity and the statistical power of the ML method by computer simulation.

METHODS

Test of Rate Heterogeneity over Loci.

The process of nucleotide substitutions is usually modeled by a Markov chain (e.g., ref. 15). Most models assume that individual nucleotide sites at a locus evolve independently from each other and that the waiting time for successive nucleotide substitutions at a site is exponentially distributed or the number of nucleotide substitutions per unit time is Poisson distributed. From the site-independence assumption, a Markov chain can be established by specifying 4 × 4 transition matrix among four different nucleotides. Jukes and Cantor (16) proposed a simple model that assumes that a nucleotide at a site is substituted with equal probability by one of the remaining three or that the diagonal and off-diagonal elements of the transition matrix, in the following specification, take the value of 0 and 1/3, respectively. A number of extensions since have been made: first to incorporate unequal substitution patterns among the four nucleotides (15), which is particularly conspicuous in mitochondrial (mt) DNA (e.g., ref. 17). The second extension has focused on constraints of secondary structure in rRNA and tRNA genes (18) or of codon frames on synonymous and replacement substitutions (19, 20) in each of which 16 × 16 or 61 × 61 (excluding stop codons) transition matrix is manipulated. The third extension has been concerned with the waiting time distribution of nucleotide substitutions. For instance, because the nucleotide substitution rate in the D-loop region of mtDNA varies substantially from site to site (21), it was assumed that the rate parameter in Poisson models is not constant among sites, but it varies according to a certain probability distribution (e.g., the gamma distribution in ref. 22). The mathematical procedure involved the derivation of Poisson-based formulas and then taking their averages (randomization) with respect to the rate parameter (see p. 53 in ref. 23).

Here we retain the site-independence assumption and thus model the pattern of nucleotide substitutions by 4 × 4 transition matrix M. We then express transition matrix M^k for k nucleotide substitutions per site per unit time as

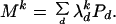1

In the above, λ_d and P_d are eigen values and matrices of M, respectively, and k is a random variable. If k follows the Poisson distribution, the probability of having k substitutions during 2s generations is given by

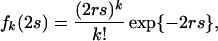2

where for convenience r is defined as the nucleotide substitution rate per site per generation. Averaging M^k in Eq. 1 with respect to f_k(2s) in Eq. 2, we have

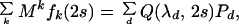3

where Q(z, 2s) = Σ_k[2rsz^k/k!]exp(−2rs) = exp[−2rs(1 − z)] is the probability generating function of f_k(2s). Eqs. 1-3 allow us to handle M and k separately, and can be extended easily to the case where k is not Poisson distributed.

We would rather consider the total number (K) of nucleotide substitutions per locus defined by K = k₁ + k₂ + … + k_n where k_i (i = 1, 2, … , n) is the number of nucleotide substitutions at the ith site at a locus and n is the total number of sites compared. To derive the probability generating function of K, we must specify the linkage relationships and rate heterogeneity of nucleotide substitutions among the sites. There are two extreme situations under which r may vary: (a) from locus to locus and (b) from site to site. There are also two extreme situations about linkage among sites within a locus: (a) complete linkage and (b) free recombination. Of these four combinations, we focus for the moment on the situation in which all n sites are completely linked and r varies from locus to locus, but a constant rate is taken for the sites at a locus. Under this situation, we can express the probability generating function of K as Q_P(z, 2s) = Q(z, 2s)ⁿ = exp[−2nrs(1 − z)] and take the average of Q_P(z, 2s) with respect to r. If r in Q_P(z, 2s) follows the gamma distribution with mean a/b and variance a/b², we use Q_G(z, 2s) = [1 + 2ns(1 − z)/b]^−a instead of Q_P(z, 2s) (22, 24).

For a pair of orthologous genes sampled from different species that diverged t generations ago, gene divergence time s necessarily exceeds t and is given by t + τ where τ is the persistence time (in units of generations) of the two gene lineages in the ancestral species. Because τ is an exponentially distributed random variable with mean 2N when the effective population size of the ancestral species is N (25), we take the average of either Q_P(z, 2s) or Q_G(z, 2s) with respect to τ, because all n-linked sites have experienced the identical genealogical history. In the former case, we have

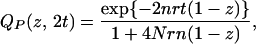4

and the coefficient of z^K in Eq. 4 is the probability of taking a particular value of K, which is given by

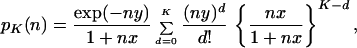5

where x = 4Nr and y = 2rt (13). On the other hand, the same procedure taking the average of Q_G(z, 2s) over τ does not lead to a concise formula, but it is easy to derive formulas for moments of K (14). Let E{Z} stand for taking the average of random variable Z with respect to its given probability distribution. If r is gamma distributed, E{r} = a/b, we redefine x = 4NE{r} and y = 2E{r}t and obtain the averages of K and K(K − 1) as

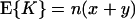6

and

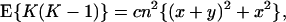7a

or the variance of K as

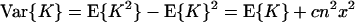7b

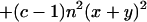where c = 1 + 1/a, independent of scaling parameter b. To estimate x and y from the observed mean and variance of K, Takahata (14) used Eqs. 6 and 7b with c = 1.

We examined whether or not c is close to 1 (or a ≫ 1) in actual DNA sequence data, i.e., whether or not we need to take account of rate heterogeneity across loci. Let m be the number of loci examined and K_j be the number of nucleotide substitutions at the jth locus consisting of n_j sites (j = 1, 2, … , m). We replace Eqs. 6 and 7a by

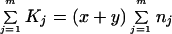8

and

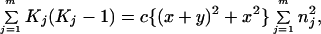9

respectively. If we define S = c[1 + {x/(x +y)}²], which ranges from c (y = ∞) to 2c (y = 0), we may estimate S from Eqs. 8 and 9 as

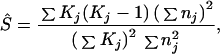10

in which a hat on the left-hand side stands for an estimate. This estimation of S is an approximation, and the reliability was examined by computer simulation (see next section). In the actual DNA sequence analysis, we used silent sites only, and to estimate K from the nucleotide differences, we corrected multiple-hit substitutions per site and summed them up over the sites. Because of relatively small extents of nucleotide differences per site even in the comparison of the human with the OWM and NWM as well as of small biases in base compositions, most correction methods made essentially the same estimate of K. We then computed Ŝ in Eq. 10 for 48 pairs of DNA sequences within humans (y = 0) as well as for 23, 14, 46, and 8 pairs of orthologous DNA sequences (y > 0) between the human and four nonhuman primates (chimpanzee, gorilla, OWM, and NWM). Table 1 shows that the value is about 2 (y = 0) in the within-human comparison while it is about 1 (y ≫ x) in the human vs. nonhuman comparisons. This indicates that c is close to 1 and the rate heterogeneity across loci is insignificant. We therefore concluded that the process of silent nucleotide substitutions is well approximated by Poisson and hence Eq. 5 is applicable. For a set of observed values [K_j, n_j; j = 1, 2, … , m], we determined x and y so as to maximize the log likelihood function

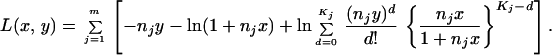11

Table 1.

The value of Ŝ estimated from Eq. 10 and the DNA sequence data described in Table 3

Human vs.	No. of loci (m)	Ŝ
Human (y = 0)	48	2.151
Chimpanzee	23	0.960
Gorilla	14	0.792
OWM	46	1.011
NWM	8	1.124

If the substitution process is Poisson (c = 1), the value of Ŝ should range from 1 to 2 depending on the relative values of x and y. 

Simulation Study.

We examined the power of our ML method by computer simulation. In each replication for a given set of parameters, N, t, n, and m, we generated a random variable τ after the exponential distribution with mean 2N. For given τ and constant r, the expected number of nucleotide substitutions for a pair of sequences with n silent sites is 2(t + τ)nr. A Poisson random number with mean 2(t + τ)nr was generated and stored as a realized value of K. We repeated this process m times, keeping n constant. At the end, the above procedure generated a simulation data set of [K_j, n; j = 1,2, … , m] for m loci each with n silent sites. We then applied Eq. 11 to [K_j, n; j = 1,2, … , m] and searched the ML estimates of x and y, x̂ and ŷ. Because we used the total number of nucleotide substitutions per locus, the important parameters in our simulation were nx = 4nNr and ny = 2nrt rather than three individual values of x, y, and n. For constant n, x̂ + ŷ = Σ_j=1^m K_j/(nm) must be satisfied and could be used to search x̂ and ŷ.

Owing to finite values of n and m, the ML estimates naturally differed from the assumed true values of x and y. We counted the number of cases in which x̂ lies between 0.1x to 10x and at the same time ŷ lies between 0.8y and 1.2y, assuming y = 1% and x = 0.06% or 0.6% (Table 2). As expected, the larger the n and m values, the more accurate estimates we can make. It is necessary that the expected value of both nx and ny is not smaller than 1. For instance, when n = 1,000, x = 0.06% and y = 1%, ny = 10 and nx = 0.6. In this case, more than 20 loci are sufficient for an accurate estimate of y, but not for x. As x increases up to 0.6%, 1,000 sites are sufficient for an accurate estimate of x (nx = 6) with m ≥ 20. However, it was observed that the reliability of ŷ is somewhat lowered. It appears that the accuracy of ŷ depends on not only ny but also nx and m; the larger nx, the less accurate ŷ for small m. Thus, even when nx > 1 and ny > 1 are satisfied, use of many loci is required.

Table 2.

Simulation results of the ML estimates of x = 4Nr and y = 2rt based on Eq. 11

n	m = 10				m = 20				m = 50
x = 0.06% and y = 1%
	0.136	0.008	0.002		0.131	0.003	0.000		0.070	0.000	0.000
100	0.093	0.025	0.011		0.169	0.049	0.011		0.238	0.119	0.002
	0.135	0.332	0.258		0.071	0.384	0.182		0.021	0.446	0.104
	0.001	0.000	0.000		0.000	0.000	0.000		0.000	0.000	0.000
1,000	0.095	0.263	0.005		0.071	0.356	0.002		0.017	0.489	0.000
	0.005	0.561	0.070		0.000	0.560	0.011		0.000	0.493	0.001
	0.000	0.000	0.000		0.000	0.000	0.000		0.000	0.000	0.000
2,000	0.071	0.356	0.002		0.031	0.467	0.000		0.003	0.601	0.000
	0.000	0.560	0.011		0.000	0.501	0.001		0.000	0.396	0.000
x = 0.6% and y = 1%
	0.000	0.000	0.000		0.000	0.000	0.000		0.000	0.000	0.000
100	0.250	0.099	0.111		0.261	0.186	0.119		0.239	0.339	0.173
	0.017	0.101	0.422		0.001	0.049	0.384		0.000	0.007	0.242
	0.000	0.000	0.000		0.000	0.000	0.000		0.000	0.000	0.000
1,000	0.112	0.532	0.230		0.050	0.720	0.210		0.020	0.930	0.050
	0.000	0.010	0.116		0.000	0.005	0.015		0.000	0.000	0.000
	0.000	0.000	0.000		0.000	0.000	0.000		0.000	0.000	0.000
2,000	0.115	0.665	0.170		0.080	0.800	0.110		0.010	0.980	0.010
	0.000	0.015	0.035		0.000	0.000	0.010		0.000	0.000	0.000

The 3 × 3 matrix for specified n and m represents the proportion of ML estimates that lie in (x̂ ≥ 10x, 10x > x̂ > 0.1x, x̂ ≤ 0.1x in rows) × (ŷ ≤ 0.8y, 0.8y < ŷ < 1.2y, ŷ ≥ 1.2y in columns). The central element in each matrix is an indicator for reliable estimates. The number of replications is 1,000. 

The above simulation study is based on the assumption of constant r. As an example, we examined the case in which r follows the exponential distribution with mean 1/b or the gamma distribution with mean 1/b and variance 1/b² (a = 1). The simulation result shows that x tends to be overestimated even when y is accurately estimated (data not shown). This reflects the fact that Eq. 11 attributes the deviation in the number of nucleotide substitutions from the Poisson expectation to the ancestral polymorphism. We therefore examined sensitivity of Ŝ in the above non-Poisson model and found that the value becomes significantly greater than 1 (the mean is about 2, as expected if c = 1 + 1/a = 2, and the coefficient of variation is less than 0.3 for n ≥ 500 and m ≥ 20). This result is in direct opposition to the observation in Table 1, supporting the previous conclusion that silent substitutions in the present data set are compatible with those under the Poisson model.

In the above treatment, the order of taking the product of Q(z, 2s) over n sites at a locus and of averaging the product over r and τ depends on the assumptions about the linkage relationships and rate heterogeneity among the sites. When r varies over n linked sites, we must take the average of Q(z, 2s) with respect to r before computing Q(z, 2s)ⁿ. This procedure results in Eq. 7 with c = 1 + 1/(an) instead of c = 1 + 1/a. Because an is much greater than 1 in actual data (generally n > 100 and a ≈ 0.1 in ref. 22), rate heterogeneity among linked sites, if present, should have minor effects on the ML estimates. In this respect, Eq. 10 gives a conservative way of evaluating effects of rate heterogeneity. On the other hand, when n sites are freely recombined and r varies either from site to site or from locus to locus (cf. ref. 26), E{K(K − 1)} becomes even smaller than (n² + n/a)[(x + y)² + x²] by n(n − 1)x². In all these situations, the mean value of K is the same as in Eq. 6, but the variance becomes smaller than that given in Eq. 7 and the estimate of x becomes correspondingly larger [e.g., when c = 1, Var{K} = E{K} + n²x² for tight linkage and Var{K} = E{K} + nx² for no linkage]. Thus, the present moment and ML methods tend to underestimate x (ancestral polymorphism) and overestimate y (species divergence time). However, the extent of these biases is expected to be small for realistic values of 4Nr, because the probability generating function of K for n unlinked sites is given by exp[−2nrt(1 −z)]/[1 + 4Nr(1 − z)]ⁿ and the difference between this formula and Eq. 4 is small for 4Nr ≪ 1.

RESULTS AND DISCUSSION

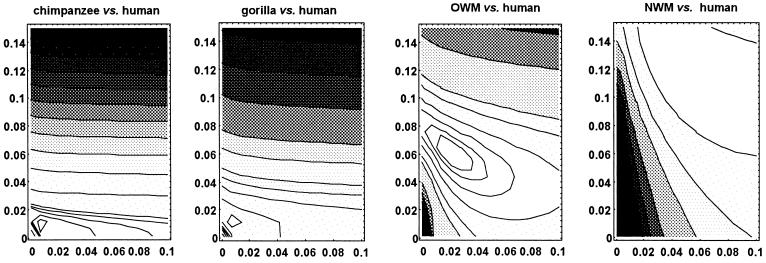
Based on the ML method in the preceding section, we estimated x and y in the four comparisons of the human with the nonhuman primates. The result is given in Table 3, which also includes the ML estimate of x based on Eq. 11 with y = 0 and 48 pairs of DNA sequences sampled from the extant human population. We recall x = 4Nr and y = 2rt so that for given r, N and t can be estimated as x̂/(4r) and ŷ/(2r), respectively, in units of generation time g. The value of N thus estimated is the effective population size of the ancestral species, which likely reflects the demographic history between t̂ and t̂ + 2N generations ago (25). In what follows, we use the per-generation rate of silent substitutions r defined by the per-year rate 10⁻⁹ multiplied by g (28, 29). The estimated divergence time between Catarrhini and Platyrrhini then becomes 57.5 Myr ago (for ŷ = 11.4%, irrespective of the value of g), although because of the small number of loci compared, the 90% confidence limit of ŷ is broad (Fig. 1). Such an early divergence of Platyrrhini is in good agreement with the revised version of more than 55 Myr ago (1) and much older than the previous estimate of 35 Myr ago (2). However, the emergence of Platyrrhini in South America remains puzzling because the continent began to drift away from Africa more than 100 Myr ago (30, 31). The estimated divergence time between hominoids and OWM (ŷ = 6.2% or 31 Myr) is also older than the previous estimate of 25 Myr ago (2), although the value of y = 5% corresponding to 25 Myr is again on the margin of the 90% confidence limit (Fig. 1). It is therefore suggested that although Africa might have been close to Eurasia 31 Myr ago, the divergence between these superfamilies occurred in Africa before its rejoining Eurasia since the continents had been separated during the period from 100 Myr ago to 30 Myr ago (30). In either event, the molecular data are more consistent with the earlier divergences of NWM and OWM than previously thought; unless otherwise, the ancestral population size is required to be as large as 10⁶-10⁷, or the rate of silent substitutions is required to be faster in NWM and OWM than in hominoids (see below).

Table 3.

The estimated y = 2rt and x = 4Nr represent parameters t and N scaled by silent substitution rate r per site per generation

Human vs.	Moment method, %	ML, %
Human (y = 0.000)	x̂ = 0.08	x̂ = 0.08
Chimpanzee	x̂ + ŷ = 1.57	x̂ = 0.76 ŷ = 0.9
Gorilla	x̂ + ŷ = 1.79	x̂ = 0.22 ŷ = 1.6
OWM	x̂ + ŷ = 8.17	x̂ = 2.0  ŷ = 6.2
NWM	x̂ = 4.4 ŷ = 12.7	x̂ = 6.1  ŷ = 11.4

The moment method could not estimate x and y separately in comparison of the middle three. The generation time g of ancestral primates is uncertain, but presently it is 7-14 years in the chimpanzees and gorilla, and 3.5-4 years in the OWM (27). These generation times were used in text to estimate N from x̂. The data sources are described in ref. 13 in addition to the following genes retrieved from the GenBank and EMBL database: chimpanzee, carbonic anhydrase I (CAI), triose phosphate isomerase (TPI), β₂-microglobulin (β₂m), intercellular adhesion molecule 1 (ICAM1), interleukin 3 (IL3), urate oxidase (UO), protamine 1 (P1), protamine 2 (P2), ζ-globin, epididymal secretory protein precursor (EPI1), eosinophyil cationic protein (ECP), and neurotoxin; gorilla, CAI, β2m, UO, P1, P2, and α-fetoprotein (AFP), ECP, neurotoxin, and ɛ-globin; OWM, ɛ-globin, apolipoprotein CII (ApoCII), cholesteryl ester transfer protein (CETP), p53, chorionic gonadtropin (CG) subunit, urokinase plasminogen (UKP), c-mos, TGF, TPI, UO, P2, IL3, FIX, CAI, ADH, TFα, ATI, amyloidβ, ApoA1, ApoA2, ApoA4, ApoBLDL, CD4, Prosep, ApoC3, EP, FSHR, HSDI, IL11, KAL, PBP, SOM, SPC, PRL, Amylin, GH, Histon1 (H1t), INFG, IL10, IL4, IL6, Lysozyme, PLSM, PROS, ALB, TRD, and PON; NWM, δ-globin, cystic fibrosis transmembrane conductance regulator protein (CFTR), corticosteroid-binding globulin (CSBG), CD59, alanine:glyoxylate aminotransferase (AGAT), α-1-3-galactosyltransferase (α-1-3-GT), insulin, and β-hydroxysteroid dehydrogenase (β-HD). The number (n) of synonymous sites is generally more than 200 for most sequence pairs. A table for the estimated number of silent substitutions and the number of nucleotide sites at individual loci is available upon request. 

Figure 1.

Contour maps of the log likelihood function of x = 4Nr (abscissa) and y = 2rt (ordinate) in Eq. 11 where N is the effective population size before species divergence time t and r is the rate of silent substitutions, both measured in units of generations. The 90% confidence limit is depicted by the innermost contour line. Log likelihood values of all other contour lines are rather arbitrary. The data used in the comparisons between human and four nonhuman primates are given in Table 3.

Regarding the timing of the origin of hominid lineages, our estimates support that the human is more closely related to the chimpanzee than to the gorilla. The gorilla and chimpanzee lineages appear to have become distinct from the human 8.0 Myr ago (ŷ = 1.6%) and 4.5 Myr ago (ŷ = 0.9%), respectively. The possibility that the human and chimpanzee pair diverged from each other as early as 8.0 Myr ago is rejected for any value of x (p < 0.05). Likewise, the possibility that the human and gorilla pair or the chimpanzee and gorilla pair diverged as recently as 4.5 Myr ago is rejected with p < 0.01 or p < 0.1, respectively (see also Fig. 1). There are 12 loci available for the comparison between chimpanzees and gorillas. The ML method yielded ŷ = 1.4%, or 7.0 Myr, which is insignificantly different from the estimated divergence time between humans and gorillas (13). Also, all these results are consistent with those that were inferred from the whole mtDNA sequences of hominoids (9). The divergence time between humans and chimpanzees has been of particular interest for dating the most recent common ancestor of human mtDNAs and thereby examining competing hypotheses on the origin of modern humans (32). For example, the most recent common ancestor of human mtDNAs is only as old as 143,000 ± 18,000 years, thus supporting the single origin hypothesis of modern humans (9).

The estimated value of N in the lineage leading to modern humans is of the order of 10⁵ through the Pliocene to the late Miocene (for x̂ = 0.22–0.76%, ŷ = 0.9–1.6%, and g = 7–14 years in ref. 27) and of 10⁶ through the Oligocene to the Palaeocene (for x̂ = 2–6.1%, ŷ = 6.2–11.4%, and g = 3.5–4 years in ref. 27). Although the 90% confidence limit of these x̂ or N̂ is fairly large (Fig. 1), the log likelihood value at n = 10⁴ is significantly smaller than that at n = 10⁵ or 10⁶. Because n = 10⁴ is the ML estimate from the data for the extant human population (x̂ = 0.08% and g = 15–20 years) and the 90% confidence limit ranges from 5,700 to 17,000 (33, 34), the rather small value of N reflects the demographic history of past 20,000 generations or 300,000–400,000 years during which Homo erectus dispersed over Eurasia. Thus, there might have been a reduction in N after H. erectus first migrated out of Africa, although the reduction might not be severe as suggested by the long persistence of polymorphism at major histocompatibility complex loci (35). Our estimates indicate roughly a 10-fold reduction in N, providing corroborative evidence for the absence of drastic bottleneck effects in primate evolution. More importantly, our estimates can specify at which stages of primate evolution polymorphism was abundant or equivalently demographic parameter N was large. Such specification allows us to link primate evolution to geological events and/or global environmental changes.

If our ML values of x in the ancestral species are substantially overestimated for some reasons, the true values of y would be larger than the present estimates. Were x as small as 0.08% throughout primate evolution, y for NWM would be 18% or 90 Myr. No fossil records suggest such an early divergence of NWM. However, Li and his colleagues (36) reported a higher substitution rate in the NWM and OWM than in the human lineage. We note that this high rate comes from their assumption that the NWM and OWM became distinct 35 and 25 Myr ago, respectively. If the NWM and OWM diverged as early as we presented here, their estimate of substitution rate per site per year should be about 10⁻⁹, and there seems to be no evidence against the rate constancy among primate lineages. We could not perform the relative rate test (12) because of the lack of appropriate outgroup DNA sequences. The relative rate test is free from the assumption of species divergence times, but the test may be sensitive to many factors such as sampling errors, outgroup DNA sequences, and genomic regions used. In fact, even for nearly the same data set after excluding unusual ψη-globin genes, Herbert and Easteal (37) and Li et al. (38) have reached the opposite conclusions about the rate constancy between primate taxa.

The effective population size (N) is roughly equal to the actual number of breeding individuals in a population, but only under the assumption of random mating (39). Such an ideal situation may not obtain in any real species and N depends on various demographic factors, including sex ratio, mating systems, geographic separation of subpopulations, and extinction-recolonization of subpopulations (39, 40). For instance, subdivided structure may hinder individuals between subpopulations from random mating, so that genes sampled from different subpopulations might be derived from the most recent common ancestor much earlier than expected under the condition that all individuals in the whole population are assumed to mate at random. Conversely, the value of N in subdivided populations can be much larger than the total number of breeding individuals (11). By contrast, frequent extinction-recolonization of subpopulations is an effective process that increases the chance that genes sampled from different subpopulations might recently come from a common subpopulation. In an extreme case, N decreases to the number of breeding individuals within a single subpopulation (11). We could not identify which factors have been most responsible for causing fluctuations in N over evolutionary time. Nonetheless, it seems certain that the primate lineage leading to modern humans has not been demographically stable throughout.

DNA is a molecular archive of the organism history. Together with the sequence differences in orthologous genes, methods like these presented here and their refinements (41) could lead soon to a new understanding of ancient population dynamics and ancient ecosystems.

ABBREVIATIONS

NWM

New World monkey

OWM

Old World monkey

ML

maximum likelihood

Myr

million years