Diffusion control in an elementary protein folding reaction

Abstract

The cold-shock protein CspB (from Bacillus subtilis), a very small protein of 67 residues, folds extremely fast in a reversible N ⇋ U two-state reaction. Both unfolding and refolding are strongly decelerated when the viscosity of the solvent is increased by adding ethylene glycol or sucrose. The folding of CspB thus seems to follow Kramers’ model for reactions in which the reactants must diffuse together. It indicates that the compaction of the protein chain occurs in the rate-limiting step of folding. Chain diffusion to a productively collapsed form and the crossing of a high energy barrier are thus tightly coupled in this folding reaction, and the measured reaction rate depends on both the diffusion of the protein chain in the solvent and the magnitude of the activation energy. We suggest that in protein folding an energetic barrier is essential to separate the native from the unfolded conformations of a protein. This barrier protects the ordered structure of a native protein against continuous unfolding by diffusive chain motions and leads to apparent two-state behavior.

Most protein chains reach their native conformations during folding rapidly and with high precision, even though the native state is only marginally stable and even though an unfolded protein can adopt very many conformations. Often it is assumed that the folding process is so efficient, because it occurs in two distinct stages (1–4). In the first stage the extended protein chain collapses rapidly into a compact form (often called a molten globule), which is already native-like, but still loosely packed (4, 5). In the second, slow stage the protein chain rearranges to the native state, possibly by a restricted search through the compact conformations. This stage shows a high energy barrier and determines the overall rate of folding. Until recently it was assumed that the rapid formation of compact intermediates is a prerequisite for fast and efficient folding (2, 4–8).

Several small proteins fold extremely fast within a millisecond or even less, but no partially structured intermediates could be detected in these folding reactions (9–17). This seems puzzling. Either these proteins do not follow the two-stage model in their folding, or the initial collapse is so specific that the second stage becomes extremely fast. Thus, the compact intermediate would not accumulate, and the diffusive collapse would become rate-limiting for the entire folding reaction. In this case folding should not follow a monoexponential time course. As a third possibility, chain compaction and crossing of the energy barrier could be tightly coupled in folding. Kramers (18) developed a kinetic model for reactions in which the reactants diffuse together in the rate-limiting step, and he found that the time constants of such processes should depend linearly on the viscosity of the medium. Kramers’ theory was used by Karplus and Weaver (19, 20) when they formulated the diffusion–collision model for protein folding. Folding reactions that are limited in rate by rearrangements in an already compacted molecule should be independent of solvent viscosity.

To find out whether the extremely rapid folding of a small protein could indeed be limited in rate by chain diffusion through the solvent, we measured the dependence on solvent viscosity of the folding kinetics of the cold shock protein CspB (21, 22). This small protein from Bacillus subtilis contains 67 amino acid residues and in its native state consists of a five-stranded β-barrel structure (23, 24). At 25°C CspB reaches the native state with a time constant of about 1 ms, and even in the middle of the unfolding transition the native and the unfolded molecules equilibrate with a time constant of 30 ms (13). The folding of CspB follows a monoexponential time course. It is well described by a N ⇋ U two-state mechanism, and the activated state of folding is unusually native-like in its interactions with the solvent (25).

We varied the viscosity of the solvent by adding ethylene glycol or sucrose. These viscosogenic molecules are well miscible with water and lead to a high viscosity at both the macroscopic and the microscopic level. We studied also the influence of ethylene glycol on the folding reaction of apo-α-lactalbumin, which folds via a stable compact molten globule intermediate (4, 26, 27).

Unfolding and refolding of CspB are indeed strongly decelerated when the viscosity of the solvent is increased, which suggests that the collapse of the polypeptide chain occurs in the rate-limiting event of its folding.

MATERIALS AND METHODS

Materials.

Guanidinium chloride (GdmCl) was from ICN, and holo-α-lactalbumin, type III, was purchased from Sigma. Ethylene glycol and sucrose (both of analytical grade) as well as all other chemicals were from Merck. Concentrations of ethlyene glycol and sucrose are given as percent (wt/vol). The concentration of GdmCl was determined by measuring the refraction of the solution and using the equation of Pace (28). This equation was extended experimentally to solutions containing different amounts of ethylene glycol. The solvent viscosities were measured by using an oscillating capillary rheometer (OCR-D from Chempro, Hanau, Germany). Values for the viscosity of sucrose solutions were taken from reference 29. CspB from Bacillus subtilis was overexpressed in Escherichia coli and purified as described (13, 24).

Spectroscopic Measurements.

CD spectra were recorded with a Jasco (Tokyo) model J600A spectropolarimeter in 0.01-cm cells at a CspB concentration of 180 μM (in the absence) and 312 μM (in the presence of 70% ethylene glycol) as described (13). The one-dimensional NMR spectra were measured with a Bruker (Karlsruhe, Germany) AMX-600 spectrometer. For the experiments 0.7 mM solutions of CspB were prepared in either 70 g ethylene glycol per 100 ml of a 50 mM phosphate buffer (pH 7.0) in D₂O or in a 9:1 mixture of H₂O and D₂O (containing 50 mM phosphate buffer, pH 7.0). The pH values were determined with a glass electrode without correction for D₂O or ethylene glycol. Water suppression was achieved with weak presaturation or with the pulse sequence WATERGATE (30). The ethylene glycol resonance at 3.58 ppm was suppressed by weak off-resonant presaturation. Five hundred scans per free induction decay (FID) were acquired with a sweep width of 7812.5 Hz. Prior to Fourier transformation a 90° shifted squared sinebell window function was applied.

GdmCl Induced Unfolding Transitions.

Samples of CspB were incubated at 25°C in solutions of 0.1 M Na cacodylate-HCl (pH 7.0) and varying concentrations of GdmCl. The fluorescence of the samples was then measured at 343 nm (5 nm band width) after excitation at 278 nm (3-nm band width). The unfolding transitions were analyzed assuming a two-state transition between the folded (N) and the unfolded (U) conformation by using the procedure of Santoro and Bolen (31).

Stopped-Flow Kinetic Experiments.

A DX.17MV sequential mixing stopped-flow spectrometer from Applied Photophysics (Leatherhead, U.K.) was used for all kinetic measurements. Conditions and procedures were as described (25). All measurements were performed in solutions containing 0.1 M Na cacodylate-HCl (pH 7.0) at 25°C. Unfolding of native protein (in buffer only) or refolding of unfolded protein (in 6.0 M GdmCl) were initiated by 6- or 11-fold dilutions with solutions containing varying concentrations of GdmCl to give the appropriate folding conditions and a final protein concentration of 1 μM. The concentrations of ethylene glycol or sucrose were the same before and after mixing. Individual kinetics were measured about 10 times, averaged and analyzed as monoexponential functions by using the software provided by Applied Photophysics. The dependences on GdmCl concentration of the measured rate constants λ were analyzed as described (13) by assuming that the folding of CspB follows a two-state mechanism and that the logarithms of the microscopic rate constants of unfolding k_NU and of refolding k_UN depend linearly on denaturant concentration. The fitted curves resulting from this analysis are shown in the figures.

RESULTS

An Increase in Ethylene Glycol Concentration Decelerates Both Unfolding and Refolding of CspB.

Instead of urea as in our previous work (13, 25) we used GdmCl because it is a much stronger denaturant for CspB, and because it remains well soluble when ethylene glycol is added. Thus the unfolding and refolding kinetics could be studied in a much wider range of solvent viscosity than would have been possible with urea.

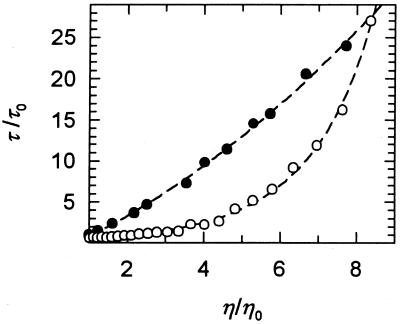
In a first test for viscosity-dependent folding the rates of unfolding and refolding were measured at 0.5 M GdmCl and at 5.0 M GdmCl, respectively, by the change in protein fluorescence in the presence of ethylene glycol at increasing concentration (Fig. 1). The equilibrium unfolding transition of CspB at 25°C shows a midpoint at 1.43 M GdmCl. The time constant τ (τ = λ⁻¹) of refolding (Fig. 1) remained almost constant between 0 and 30% ethylene glycol, but when the ethylene glycol concentration was further increased the refolding of CspB became progressively decelerated. In the presence of 73% ethylene glycol, which is equivalent to a relative viscosity η_rel of 5, folding was 5-fold decelerated. The time constant of unfolding increased strongly in a nonlinear fashion with the viscosity of the solvent (Fig. 1), and unfolding was 20-fold slower when the relative viscosity was increased from 1 to 7.

Figure 1.

Dependence on solvent viscosity of the folding kinetics of CspB. The relative time constants τ/τ₀ (τ = λ⁻¹) of refolding at 0.5 M GdmCl (○) and of unfolding at 5.0 M GdmCl (•) are shown as a function of the relative viscosity of the solvent (η_rel = η/η₀). The viscosity of the solvent was adjusted by the addition of ethylene glycol. η₀ refers to the viscosity of the solvent in the absence of ethylene glycol, but in the presence of 0.5 M GdmCl in refolding and 5.0 M GdmCl in unfolding. Folding was measured by fluorescence in 0.1 M Na cacodylate-HCl (pH 7.0) at 25°C at 1 μM CspB.

Ethylene Glycol Stabilizes CspB.

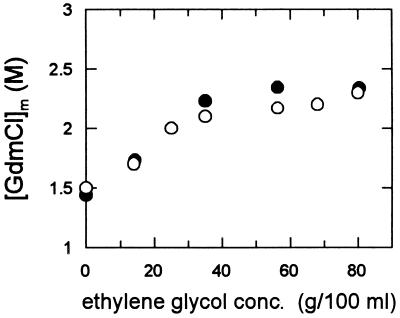
Ethylene glycol does not only increase the viscosity of the solvent, but it can also affect the conformational stability of a protein (32). Indeed, the midpoint of the unfolding transition of CspB increased from 1.43 M GdmCl at 0% to a constant value of about 2.35 M which is reached above 30% ethylene glycol (Fig. 2). The structure of the folded protein is not affected by ethylene glycol. The addition of 70% ethylene glycol did not change the dispersion of the ¹H resonances in the NMR spectrum or the CD spectrum in the amide region (data not shown).

Figure 2.

Influence of ethylene glycol on the stability of CspB. The midpoints of the GdmCl-induced equilibrium unfolding transitions [GdmCl]_m (•) and the kinetic transition midpoints (○) are shown as a function of the concentration of ethylene glycol. The kinetic transition midpoints are derived from the data in Fig. 4. They are defined as the GdmCl concentration at which the microscopic rate constants of unfolding and refolding are equal. All measurements were carried out in 0.1 M Na cacodylate-HCl (pH 7.0) at 25°C at 1 μM CspB. The folding equilibria were measured by fluorescence at 343 nm after excitation at 278 nm.

Stabilizing and Viscosogenic Effects of Solvent Additives.

The increases in both solvent viscosity and protein stability (as in Fig. 2) have to be considered when the retardation by ethylene glycol of unfolding and refolding (as shown in Fig. 1) is analyzed. According to Kramers’ theory (18), the time constant τ of a chemical reaction, which involves linear diffusion, is directly proportional to the viscosity η (Eq. 1).

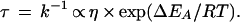1

The viscosogenic effect of a solvent additive should thus lead to a linear increase in τ because η contributes to the preexponential factor in the rate equation (Eq. 1). This is distinct from the stabilizing effect of a solvent additive. This effect changes the unfolding and refolding kinetics, because it affects the energies of the folded, the activated, and the unfolded state, and thus the activation energies of unfolding and refolding (E_A in Eq. 1).

For a N ⇋ U folding reaction the logarithm of the microscopic rate constant of unfolding logk_NU increases and that of refolding logk_UN decreases linearly with the denaturant concentration, and thus the measured folding rate logλ (λ = k_NU + k_UN) follows a chevron-like profile with a minimum near the midpoint of the folding transition (33, 34). In an ideal case (when the position of the activated state along the reaction coordinate is not changed), a stabilizing additive should accelerate refolding and decelerate unfolding, and thus shift the chevron observed for λ horizontally to higher denaturant concentrations, without changing the minimal folding rate near the midpoint of the transition. This has been outlined previously (33–36), and Hurle et al. (37) provided a mathematical formulation for this “horizontal shift” of the chevron profiles by a stabilizing agent.

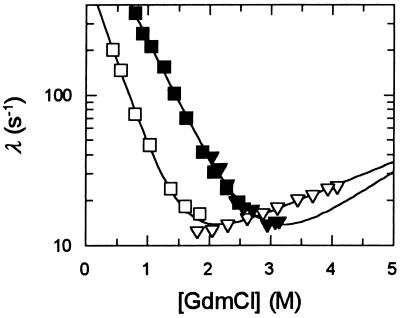
Phosphate stabilizes CspB, but hardly affects the solvent viscosity. In the presence of 0.4 M potassium phosphate the midpoint of the unfolding transition increases from 1.4 M to 2.4 M GdmCl, and the chevron profile for the folding kinetics is indeed shifted horizontally (Fig. 3)

Figure 3.

Folding kinetics of CspB in the absence (open symbols) and in the presence (filled symbols) of 0.4 M potassium phosphate. The measured rate constants of refolding (□, ▪) and of unfolding (▿, ▾) are shown as a function of the GdmCl concentration. Folding was measured in 0.1 M Na cacodylate-HCl (pH 7.0) at 25°C at a final protein concentration of 1.0 μM. The lines represent fits based on the two-state mechanism as described in Materials and Methods.

GdmCl-Dependent Folding Kinetics at Different Solvent Viscosities.

Based on the above considerations it should be possible to dissect the stabilizing and the viscosogenic effects of a solvent additive on a simple two-state folding reaction (37). The stabilization should displace the kinetic chevron profile horizontally to higher GdmCl concentrations (as in Fig. 3), and the increase in viscosity should displace it vertically to lower rates.

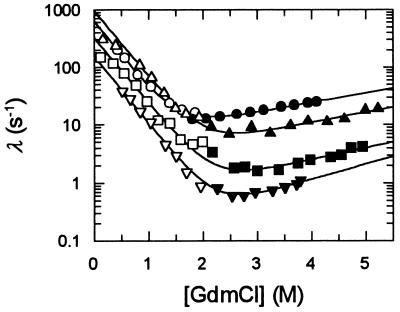
Chevron plots measured for CspB at several concentrations of ethylene glycol are shown in Fig. 4. The variation of these chevrons with the ethylene glycol concentration reveals both the stabilizing and the viscosogenic effect of this additive. Between 0 and 30% ethylene glycol the stabilizing effect dominates (see Fig. 2), and the minima of the chevrons are shifted to higher GdmCl concentrations. This horizontal shift is combined with a strong vertical displacement to smaller rates. This is clearly seen above 30% ethylene glycol, where the stability remains almost constant. The minimal value for λ decreases 30-fold from about 20 s⁻¹ in the absence of ethylene glycol to about 0.6 s⁻¹ in the presence of 68% ethylene glycol.

Figure 4.

Effect of viscosity on the folding kinetics of CspB. The measured rate constants of refolding (open symbols) and of unfolding (filled symbols) in the presence of 0 g/100 ml (○, •, relative viscosity η_rel = 1), 25 g/100 ml (▵, ▴, η_rel = 1.9), 56.3 g/100 ml (□, ▪, η_rel = 4.5), and 68 g/100 ml (▿, ▾, η_rel = 5.5) of ethylene glycol are shown as a function of the GdmCl concentration. Folding was measured in 0.1 M Na cacodylate-HCl (pH 7.0) at 25°C at a final protein concentration of 1.0 μM. The lines represent fits to the data based on the two-state mechanism (as described in Materials and Methods). η_rel refers to the viscosity measured at 0 M GdmCl.

The kinetic and the equilibrium data were mutually consistent under all conditions, and the kinetic transition midpoints (where the rate constants of unfolding and refolding k_NU and k_UN are equal) follow the same profile as the midpoints of the equilibrium transitions (see Fig. 2). The limiting slopes of the kinetic profiles in Fig. 4 (which approximate the kinetic m values for unfolding and refolding) did not change when the concentration of ethylene glycol was increased. Together this suggests that the folding of CspB follows a simple two-state mechanism, and that the thermodynamic properties of the activated state do not change significantly, when the ethylene glycol concentration is increased. Thus the strong retardation of both unfolding and refolding in Fig. 4 (above 30% ethylene glycol) clearly reflects the viscosogenic effect of ethylene glycol.

Analysis of the Folding Kinetics of CspB at Constant Stability.

Because the two-state folding mechanism of CspB seems not to be changed by ethylene glycol, we accounted for its stabilizing effect by analyzing the viscosity dependence of the folding kinetics at identical stability of the folded protein. We chose three different conditions for this comparison: (i) the midpoints of the respective unfolding transitions, where the stability constant K_N = [N]/[U] = 1 and where the rate constants of unfolding k_NU and of refolding k_UN contribute equally to the measured kinetics; (ii) mildly destabilizing conditions (K_N = 0.1), where the kinetics are largely determined by the rate constant of unfolding k_NU; and (iii) mildly stabilizing conditions (K_N = 10), where the measured kinetics are dominated by the rate constant of refolding k_UN. In addition the folding kinetics were also investigated in the presence of sucrose as a viscosogenic agent. The results of this analysis show that at low solvent viscosity the time constants of unfolding and refolding are almost linearly related with viscosity (Fig. 5A), as expected from Kramers’ model. The retardation became progressively stronger when the viscosity was further increased, and at a relative viscosity of 6 folding of CspB was already 25-fold decelerated. Virtually identical results were obtained when the viscosity was increased by adding either ethylene glycol or sucrose, and, as expected for a reversible two-state reaction, the deceleration was almost equally strong in unfolding and refolding.

Figure 5.

Dependence on solvent viscosity of the unfolding and refolding of CspB at constant protein stability. The relative retardation of folding (τ/τ₀) is shown as a function of the relative viscosity η_rel = η/η₀ at an equilibrium constant K (K = [N]/[U]) of 0.1 (□), 1 (•), and 10 (○). The viscosity was adjusted by adding ethylene glycol in various concentrations. ▪, Experiments in the presence of sucrose as the viscosogenic agent at K = 1. The folding was measured in 0.1 M Na cacodylate-HCl (pH 7.0) at 25°C at a final protein concentration of 1.0 μM. (A) An expanded view of the data at low values of η_rel. (B) The entire data set. The broken line represents a linear relationship between τ/τ₀ and η/η₀ with a slope of 1.13.

The polarity of the solvent decreases when ethylene glycol is added, and, in principle, this could also be the source for the observed deceleration of folding. In control experiments we therefore measured the folding kinetics of CspB in the presence of 30% methanol, which, similar to 60% ethylene glycol, reduces the dielectric constant to 60. Methanol shifts the minimum of the chevron profile to a lower GdmCl concentration, and at its minimum folding was slightly accelerated and not decelerated. Changes in the surface tension as a possible source for the observed retardation can be ruled out as well, because the surface tension is reduced in the presence of ethylene glycol but increased in the presence of sucrose. These results, together with the experiments in the presence of phosphate, confirm that the folding of CspB is retarded by ethylene glycol and by sucrose primarily because these additives increase the viscosity of the solvent.

Folding Kinetics of Apo-α-Lactalbumin in the Presence of Ethylene Glycol.

A folding reaction should be independent of viscosity when the collapse and the rate limiting step of folding are separated in time. We tested this prediction by using α-lactalbumin as a model protein. Below 1 M GdmCl apo-α-lactalbumin attains a compact molten globule conformation very rapidly in its folding (4, 5, 26, 27), and, indeed, the refolding kinetics of this protein (at 1 M GdmCl) remained unchanged when 46% ethylene glycol were added (Fig. 6). Above 1 M GdmCl unfolding and refolding are progressively decelerated by ethylene glycol, probably because the compact intermediate becomes destabilized and folding turns into a two-state process. It should be noted that the stability of apo-α-lactalbumin was also not affected by 46% ethylene glycol.

Figure 6.

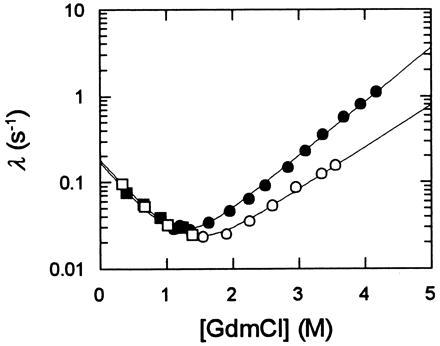
Folding kinetics of apo-α-lactalbumin in the absence (filled symbols) and in the presence (open symbols) of 46 g/100 ml ethylene glycol (η_rel = 4). The measured rate constants of refolding (□, ▪) and of unfolding (○, •) are shown as a function of the GdmCl concentration. Folding was measured by fluorescence in 0.1 M Na cacodylate-HCl (pH 7.0) at 25°C at a protein concentration of 1.0 μM. The lines represent fits to a two-state mechanism as described in Materials and Methods.

DISCUSSION

Folding of CspB Depends Strongly on Solvent Viscosity.

The rapid folding reaction of CspB is strongly decelerated when the viscosity of the solvent is increased. As expected for a simple and reversible N ⇋ U two-state reaction without intermediates, the retardation is observed in unfolding and in refolding and does not depend on the nature of the viscosogenic agent (ethylene glycol or sucrose). At low solvent viscosities the time constant of folding increases linearly with viscosity as expected from Kramers’ theory (18) for diffusion-limited processes. At high solvent viscosity folding is progressively retarded, and at η_rel = 6 folding is already 25-fold decelerated.

This deviation from linearity cannot be explained readily. In Kramers’ theory (18) and in the diffusion–collision model (19, 20) linear diffusion of two reactants or of two folding domains is considered. Domain–domain interactions and the association of subunits during folding are such linear diffusion processes, and indeed their time constants depend linearly on solvent viscosity (37–42). The collapse of the extended polypeptide chain in the folding of a small protein (such as CspB) is probably a process of higher dimensionality than considered in Kramers’ model (18, 43), and this might lead to a nonlinear relationship between reaction time and solvent viscosity.

Other sources for the strong decrease in folding rates at high solvent viscosity can, however, not be ruled out. The viscosogenic cosolvents are present in these experiments at very high concentrations (68% ethylene glycol are required to reach η_rel = 5.5) and thus additional factors may contribute to the observed retardation of folding. It should be noted that under these conditions refolding seems to be more strongly retarded than unfolding (see Fig. 5).

Consequences of Viscosity-Dependent Folding.

The maximal rate of folding should be reached when the diffusion-controlled coalescence of the extended protein chain is rate-limiting. This is not the case for CspB. Its diffusion-controlled folding transition is coupled with the simultaneous crossing of a high energy barrier. Our previous work has already shown that there is indeed a barrier between the native and the unfolded forms of CspB (25). It is responsible for the exponential time course of this folding reaction. In this work we have demonstrated that chain diffusion in the activated state also contributes to the measured folding kinetics. Kramers’ model (18) describes these two aspects of folding well: the measured reaction rate depends on both the diffusion in the solvent, as expressed by η in the pre-exponential factor of Eq. 1 and on the height of the activation energy barrier, as expressed in the exp(E_A/RT) term.

It may seem puzzling that the rate of unfolding of CspB is viscosity-dependent, although the activated state of folding appears to be fairly native-like, as indicated by the kinetic ΔC_p^≠ and m^≠ values (13, 25). However, in a two-state process the forward and reverse reactions are equally viscosity-dependent as a consequence of the principle of microscopic reversibility. The ΔC_p^≠ and m^≠ values of a folding reaction reflect other properties than the dependence on solvent viscosity of the folding rates. ΔC_p^≠ and m^≠ are pseudothermodynamic parameters that report on the averaged (“static”) properties of the entire ensemble of activated states. The viscosity-dependence, however, reports on the importance of the dynamics of the protein chain when it passes through the activated states of folding. It is conceivable that at high viscosity a protein chain can explore only a very small fraction of the conformational space which in principle would be available for the activated molecules.

Both the friction with the solvent (as shown here for CspB), or the internal friction of the folding chain itself (as assumed for apo-α-lactalbumin) could be limiting for the chain dynamics in the activated state. Only in the first case is folding retarded by an increase in solvent viscosity.

Various estimates have been given recently for the time which is required for a protein chain to collapse in the absence of an energy barrier (44). Helices can form in 10–100 nanoseconds (45, 46)—i.e., the linear collapse of a polypeptide chain can be 10⁵-fold faster than the folding of CspB. Thirumalai and Woodson (47) proposed that a protein chain of the size of CspB could collapse in 100 μs, which would be only 10-fold faster than the rate-limiting event in its folding. Pascher et al. (48) suggested that a 40-μs phase in the folding of cytochrome c could represent the collapse, but this was disputed recently (49). Hagen et al. (50) estimated that it takes 30–40 μs to form a diffusion-limited contact between two residues that are separated by 50 residues in sequence. Together, this suggests that collapse should occur in the range of microseconds.

The Role of Collapse for Protein Folding.

Physiological solvents, which favor the compact native form of a protein, are poor solvents for unfolded and extended forms and thus force the protein chains to collapse (51). This force is probably strong for long chains with high hydrophobicity and low polarity, but weak for small hydrophilic proteins. Accordingly, compacted forms, such as molten globules are found for large proteins, but usually not for small ones.

Intuitively we would expect that for a protein with perfectly optimized folding kinetics every chain collapse should be productive and lead immediately to the native state. Such a purely diffusion-limited folding without an energy barrier was certainly not a goal in protein evolution. A high barrier of activation energy between the native and the unfolded state is certainly required for the functioning of a protein. In the absence of such a barrier the native conformation would not be protected against continuous unfolding by diffusive motions of the protein chains. It seems that the question about the maximal rate of folding (44, 52) cannot be answered by investigating natural proteins, because they evolved to fold at the optimal, not the maximal rate. Folding at the maximal rate in the absence of an energy barrier would lead to a “molten globule” conformation.

For real proteins folding is most efficient when non-native, unproductive globules are highly unstable and when they “re-equilibrate” rapidly with the pool of extended conformations—i.e., when the energy landscape of the non-native forms is fairly smooth—as seems to be the case for CspB. This allows a rapid transient screening of many collapsed states. Only those with native-like, stabilizing interactions revert so slowly to the unfolded state that further folding to the native state can occur. The native-like activated state in the folding of CspB (25) is probably a consequence of this folding mechanism: only when most of the native-like contacts have already formed is re-unfolding slow and further progression to the native state can effectively compete.

This scenario for protein folding is not new. In Go’s theoretical model (53) the rapid sampling of many partially folded conformations and the instability of “intermediates” with incorrect interactions were salient features of an ideally folding protein. Our kinetic data support his model.

It is an advantage for the small proteins not to collapse readily under native conditions, because transiently formed globules with nonproductive contacts will rapidly disintegrate. The search for the folding-competent conformations can therefore take place while the protein chains are extended and not in a molten globule intermediate. This makes folding very efficient. The potential of stable local structure as a guide for further folding is not exploited in this mechanism, but kinetic traps are avoided. It is possible that such a mechanism is most closely approached by small β-sheet proteins, such as CspB.

Larger proteins with a high hydrophobicity cannot escape from a rapid and possibly nonproductive collapse (54, 55). These proteins fold more slowly. They probably acquired strategies to use local sequence information to favor productive collapse and to search efficiently through the compact conformations to find the native state. In the cell they also accept help from chaperone systems, such as GroE, to melt out incorrectly collapsed structure (56–59).

ABBREVIATIONS

CspB

cold-shock protein from Bacillus subtilis

GdmCl

guanidinium chloride

λ

measured rate of a reaction

τ

time constant of a reaction (τ = λ⁻¹)

k_ij

microscopic rate constant

η

solvent viscosity

η_rel

relative viscosity (η_rel = η/η₀)