A Kinetic Analysis of DNA Ejection from Tailed Phages Revealing the Prerequisite Activation Energy

Abstract

All tailed bacteriophages follow the same general scheme of infection: they bind to their specific host receptor and then transfer their genome into the bacterium. DNA translocation is thought to be initiated by the strong pressure due to DNA packing inside the capsid. However, the exact mechanism by which each phage controls its DNA ejection remains unknown. Using light scattering, we analyzed the kinetics of in vitro DNA release from phages SPP1 and λ (Siphoviridae family) and found a simple exponential decay. The ejection characteristic time was studied as a function of the temperature and found to follow an Arrhenius law, allowing us to determine the activation energy that governs DNA ejection. A value of 25–30 kcal/mol is obtained for SPP1 and λ, comparable to the one measured in vitro for T5 (Siphoviridae) and in vivo for T7 (Podoviridae). This suggests similar mechanisms of DNA ejection control. In all tailed phages, the opening of the connector-tail channel is needed for DNA release and could constitute the limiting step. The common value of the activation energy likely reflects the existence for all phages of an optimum value, ensuring a compromise between efficient DNA delivery and high stability of the virus.

INTRODUCTION

Bacterial viruses (phages or bacteriophages) are complex macromolecular assemblies. Successful infectivity of the phage particle relies on the high resistance of its proteinaceous structure, which protects the viral genome from environmental aggression, and on its ability to infect a specific host. These particles are built to be highly stable but also as sophisticated devices that use a precisely regulated mechanism to efficiently deliver their genome into the host cytoplasm. The large majority of phages presently identified (1) consists of a tail attached to a head containing a genome composed of a double-stranded DNA (dsDNA). For these phages (Caudovirales), heads are icosahedral capsids with isometric or elongated forms and have no envelope. Their predominance in the bacterial world indicates that this structure has been retained during evolution as a highly effective device for infection of bacteria. Tailed phages are divided into three families according to their tail morphology. Siphoviridae (61% of tailed phages) are characterized by a flexible noncontractile tail of several hundred nanometers, Myoviridae (25%) by a contractile tail composed of a sheath surrounding a central tube, and Podoviridae by a short tail (1).

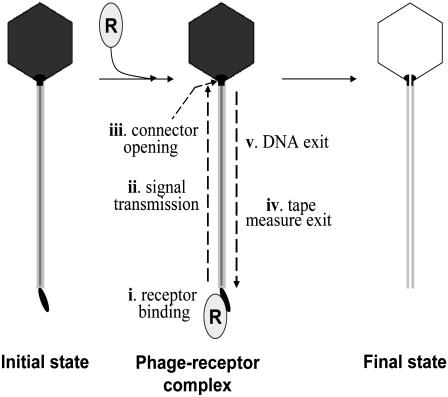
Tailed phages' infection of bacteria follows a common general strategy. The process is initiated by the interaction of a protein of the phage tail with a surface component of the bacterium, the specific host receptor. Once bound to its host, a signal is transduced from the tail region in contact with the receptor to the head-to-tail connector (Fig. 1). Opening this structure allows DNA to exit from the phage head through the tail structure into the bacterial cytoplasm. A strict coordination between both processes is necessary for delivery of the viral genome to the host cell. Control of DNA ejection by the phage structure is thus an essential requirement for efficient infection.

FIGURE 1.

DNA ejection in phages with a long tail. Mixing bacteriophages with their receptor(s) leads to strong binding of the receptor to the tail extremity distal from the phage head (step i), generating a sequence of molecular events that culminate in DNA release: (ii) a signal is transmitted along the helical tail structure to the head-to-tail connector; (iii) the connector opens; (iv) the tape measure protein that occupies the tail interior is released from the tail structure; and (v) the DNA moves down the connector and tail central channel to exit the phage particle. Theoretically any of these individual steps can control DNA ejection.

Several hypotheses have been proposed to explain DNA transport. Recent experiments and theories (2,3) support the idea that DNA is propelled outside the phage by the high pressurization resulting from the strong compression imposed by the capsid onto the genome (4). Even if this mechanism plays a documented role in genome delivery into the bacteria, the important differences observed from phage to phage during infection of bacteria call for comparative studies to identify the common principles that control DNA release from phage particles and the specificities of individual systems (5). In this article, we focus on Siphoviridae because they constitute the most common morphology among tailed phages and are prevalent over a wide variety of hosts (6). We use two bacteriophages, λ and SPP1, belonging to this family but which infect a Gram-negative and a Gram-positive bacterium, Escherichia coli and Bacillus subtilis, respectively. For these phages, the DNA release in the surrounding solution can be simply triggered in vitro by interaction of the virus with its purified receptor protein (7,8). An initial study on bacteriophage T5, another Siphoviridae, showed that it was possible to measure the kinetics of the in vitro DNA ejection using light scattering (9). The activation barrier that limits the DNA release was obtained by studying the dependence of the ejection rate as a function of the temperature. Temperature effect was also recently observed on phages λ (10).

This study aims to understand which mechanisms limit the exit of DNA from the phage capsid through the tail and to find out a general rule for Siphoviridae that could apply to all tailed phages. Despite recent advances, this mechanism essential for phage infection is still poorly understood. Without contribution of the host cell and no external energy supply, the in vitro DNA release in the surrounding solution by interaction with the protein receptor is a passive process driven only by the pressure inside the capsid. Its study allows a detailed characterization of the molecular mechanisms employed by the phage particle to control DNA ejection. Such mechanisms are very likely operative in the more complex process of the phage infection of bacteria.

MATERIAL AND METHODS

Preparation of bacteriophages and receptor proteins

Phage stocks were prepared as described previously in (3) and (11). Bacteriophage λ cI857 wild-type (DNA length 48.5 kbp) was multiplied in E. coli strains AE1 and bacteriophage SPP1 wild-type (DNA length 44.9 kbp; R. Lurz, Max-Planck Institut für Molekulare Genetik, Berlin, Germany, personal communication) in B. subtilis YB886. Both phages were purified using caesium chloride gradients. The final titer determined by plaque assay was 6.6 × 10¹² pfu/ml for λ and to 1.8 × 10¹³ pfu/ml for SPP1.

The λ-receptor LamB was purified from pop 154, a strain of E. coli K12 in which the lamB gene was transduced from Shigella sonnei 3070 (8,12). For ejection measurements, phage λ and LamB were diluted in TM buffer (10 mM MgSO₄, 50 mM Tris-HCl, pH 7.4) supplemented with 1% oPOE (octyl polyoxyethylene) to solubilize the receptor proteins. TM buffer containing oPOE was centrifuged at 11,000 × g 10 min before the addition of phages and receptors.

The purified protein YueB780 was used to release DNA from phage SPP1 (6). YueB780 is a truncated form of the membrane protein YueB that only contains the ectodomain extending outside the membrane of the bacteria. For ejection measurements, phage SPP1 and YueB780 were diluted in a buffer containing 300 mM NaCl, 50 mM Tris-HCl, pH 7.5, 10 mM MgCl₂. Divalent cations ensure SPP1 stability, and the high salt concentration guarantees YueB 780 solubility (7).

Light scattering

The kinetics of DNA ejection from phages was measured on a homemade light-scattering device using a He-Ne laser (632.8 nm) (9). The samples were placed in a thermostated cell located at the center of a goniometer. The scattering intensity was recorded with a photodetector at an angle equal to 90° from the incident laser beam. For light-scattering experiments, samples containing a few 10¹⁰ phage particles were prepared by diluting aliquots of λ and SPP1 stocks in 0.3 ml of their respective ejection buffers. The receptor proteins were added to create a final concentration equal to 10 μg/ml for YueB and from 5 to 10 μg/ml for LamB. These concentrations correspond to a nominal receptor/phage ratio equal to 4000 for SPP1 and between 50 and 200 for λ. The addition of the receptors defines the start time of the kinetics recording. For the λ-samples, we observed at long times, when all DNA was already ejected, a decrease of the signal that could come from sedimenting phages attached to their receptors surrounded by the surfactant oPOE.

Data were analyzed as described (9) with the exception that our expressions of the scattered intensity take into account the fact that the number of phages is constant during the ejection process. This is contrary to our first approach (9) where only the phage concentration (expressed in g/l) was wrongly supposed to be constant.

RESULTS AND DISCUSSION

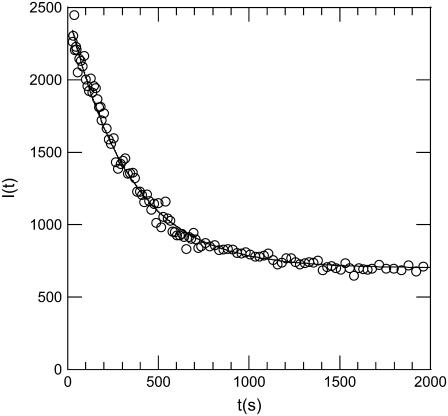
Fig. 2 shows a typical kinetics recorded with our light-scattering setup when a large amount of receptors is mixed with a phage solution. The curve was obtained at 37°C for phage SPP1 in the presence of its receptor protein YueB780. Similar curves were obtained for phage λ and its receptor LamB. When adding the receptor protein at time t = 0, the detected intensity drops progressively to a low level, indicating that phages are losing their genome. Interestingly a simple exponential decay 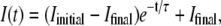where 1/τ denotes the decay rate constant, fits very well with the experimental curve (τ = 270 s in Fig. 2). The initial intensity I_initial stands for the intensity scattered by phages when they are filled with DNA, and I_final represents scattering by empty phages and by the small fraction of residual phages unable to eject their genome.

FIGURE 2.

Kinetics of SPP1 DNA ejection followed by light scattering. YueB780 was added at time t = 0 to a dilute solution of bacteriophage SPP1. The scattering intensity reduced as a function of time. The signal recorded here at 37°C reflects the kinetics of DNA ejection from phages. A simple exponential decay with a characteristic time τ = 270 s fits very well with the data.

At this phage concentration, ejected DNA does not contribute to the final signal, as can be verified by adding DNase (not shown). The reason for this comes from the change in DNA size during the ejection process: nonejected DNA is strongly confined in the capsid (with a diameter of <100 nm) and ejected DNA swells in the surrounding medium (typically to ∼1 μm). As our light wavelength is 633 nm, interferences between the light scattered by the different portions of a DNA chain are different when DNA is or is not confined. When confined, the total DNA mass contributes to the high level signal whereas destructive interferences greatly reduce the signal level when DNA is ejected. Therefore, phages in dilute solution scatter light with an intensity that mostly depends on their DNA content. If we omit all the optical factors, the variation I(t) − I(0) of the scattered intensity after a time t may be written as a function of the number and mass of phages

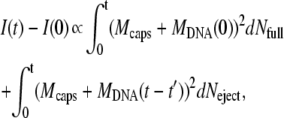(1)

where the initial intensity reads I_initial = I(0) ∝ N₀ (M_caps + M_DNA(0))², with N₀ the total number of phages, M_caps the capsid mass, and M_DNA(0) the DNA mass encapsidated at time t = 0, i.e., the mass of the entire genome. The first term in Eq. 1 describes the intensity change due to the decreasing number 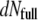of fully filled phages of mass M_caps + M_DNA(0) during the interval dt′. The second term corresponds to the contribution to the signal of the other phages, which started to eject their DNA at the different earlier times t′(t′ ≤ t). The symbol 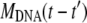represents their DNA mass still encapsidated (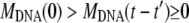). Their number increases with time as 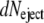= − 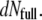In the Appendix, we formulate a detailed analysis of Eq. 1 based on the different assumptions concerning the steps that could occur.

As detailed in Fig. 1, a succession of steps follows the addition of receptors to the phage solution. In our experimental conditions, we eliminate the receptor binding step (step i in Fig. 1) by adding YueB780 or LamB at such a high final concentration that the kinetics does not depend on their concentration. In such a large excess of receptors, binding can be neglected compared to the other steps. Concerning the DNA exit (step v), the in vitro DNA ejection rate (13) has recently been measured by fluorescence microscopy for phage T5. This technique allows a direct visualization of DNA release from single phages. The movement through the tail of approximately half the genome's length was found to take place in a time period shorter than 750 ms, and the corresponding translocation rate was estimated to be at least equal to 75,000 bp/s at 23°C. Estimations based on in vivo measurements found in the literature for different phages (5,14) are more than one order of magnitude lower than the rate measured for T5. The reason for this apparent divergence is that the in vivo data include all the steps required for the whole DNA internalization and not only the step of DNA movement. The DNA ejection rate measured on T5 should give a reasonable estimation for other phages like SPP1 and λ with equivalent morphology and maximum capsid pressurization.

A simple exponential decay is observed for a multistep process when a first order reaction constitutes the rate-limiting step. If DNA movement and the sequence of events leading to the opening of the connector-tail channel (i–iv in Fig. 1) occur in comparable time ranges, one should consider the convolution of the channel opening with the DNA release. In this case, the kinetics would deviate from a simple exponential curve, being a function of the characteristic times τ_o and τ_ej for aperture and DNA ejection, respectively (see case iii of the Appendix). The general expression results in a simple exponential behavior only if the DNA ejection rate is at least 10 times higher than the channel opening rate. In our experiments, the kinetics corresponds to a perfect exponential decay with a characteristic time of 270 s at 37°C. This observation leads to a minimum value for the DNA exit rate of 16,000 bp/s (see Appendix). This is compatible with the high value measured for T5 and much higher than the values estimated from in vivo measurements. As a consequence, it is a reasonable approximation to neglect the time taken by the DNA movement in the overall process of ejection. The limiting step of the process can therefore be attributed to changes in protein conformation necessary to open the connector-tail channel (ii–iv in Fig. 1).

The simple feature observed for in vitro DNA ejection of phages SPP1 and λ in this study strongly differs from our previous study on phage T5 for which a complex shape was observed (9). It was shown that the kinetics of T5 is far from being a simple exponential decay. This was not due to a reduced speed of DNA movement exiting the phage (9). We hypothesized that the kinetics reflected a succession of rapid DNA release steps separated by pauses at some defined lengths. A model describing each step by a first order reaction was in good agreement with the experimental results (9). Such pauses were directly visualized by fluorescence microscopy (13). In vivo, T5 is known to present the unique characteristic of transferring its DNA to the host cell in two steps (15). Even if a clear relation is not yet established, it is tempting to link the in vitro pauses of DNA ejection to the in vivo two-step transfer.

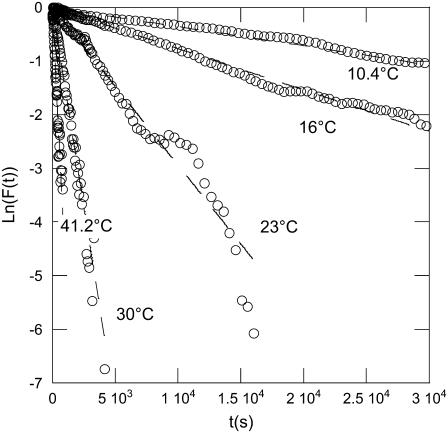
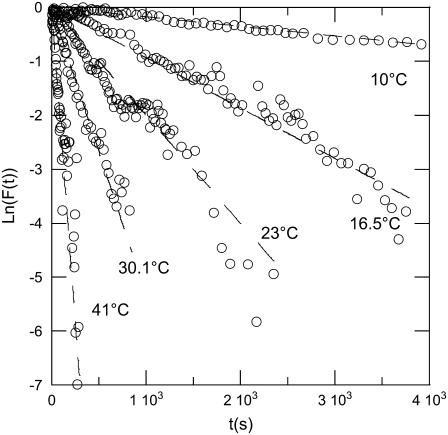
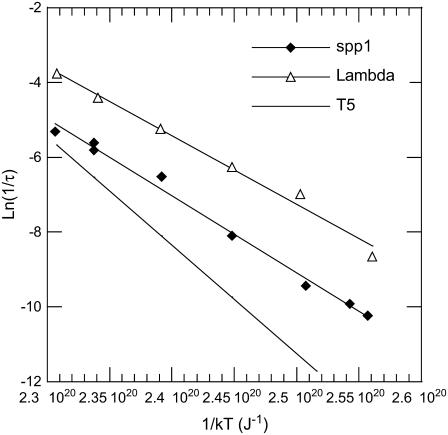
The DNA release from phages SPP1 and λ was recorded at different temperatures varying between 10°C and 41°C. The unejected DNA fraction F(t) is calculated as the ratio 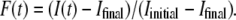The natural logarithm of F(t) is reported for both phages in Figs. 3 and 4. In this representation, an exponential decay corresponds to a straight line of slope equal to 1/τ. For both phages and at any temperature, we observed a straight line from which the characteristic time τ was extracted with an accuracy of ∼10%. Fig. 5 shows a linear variation for ln(1/τ) versus 1/T for both phages. The temperature dependence of the rate constant 1/τ is consistent with an Arrhenius law 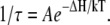The activation energy ΔH is found to be equal to 2.06 × 10⁻¹⁹ J (29.5 kcal/mol) for SPP1 and to 1.84 × 10⁻¹⁹ J (26.4 kcal/mol) for λ. These two values are of the same order of magnitude as the value 2.9 × 10⁻¹⁹ J (41.6 kcal/mol) previously measured for phage T5 (13). For T5, the DNA is released with several pauses at some defined lengths, and the same energetic barrier has to be overcome after each step. We conclude that in all Siphoviridae phages DNA ejection requires a similar energetic barrier to be overcome.

FIGURE 3.

Kinetics on phage SPP1 DNA ejection measured at different temperatures (from 10°C to 41°C). The data follow an exponential decay for each temperature. To accurately determine the different characteristic times, the natural logarithm of the normalized intensity F(t) is plotted versus time.

FIGURE 4.

Kinetics on phage λ DNA ejection. The experimental setup and data analysis are as in Fig. 3.

FIGURE 5.

Plot of the natural log of 1/τ against the inverse of the temperature. The observed linear relation for the two phages λ (▵) and SPP1 (♦) indicates that the decay rate constants 1/τ follow an Arrhenius law. From the slope, we extract the activation energy for each phage. By comparison, we also indicate by a solid line the activation energy previously determined in de Frutos et al. (9) for phage T5.

During packaging of DNA in phages the end of the genome remains attached to the head-to-tail connector structure (Fig. 1; (11) and references therein). Opening the connector provides a continuous conduit for DNA passage defined by the connector and tail central channel. This channel has a diameter of ∼3–4 nm in different phages (16–19), but some regions have diameters as narrow as 1.8 nm (20). These dimensions are close to or smaller than, respectively, the diameter of the dsDNA helix (2.3 nm), implying likely contacts between exiting DNA and the channel walls. It is thus tempting to associate the temperature dependence with frictional forces on DNA during its motion through this narrow channel. Nevertheless as demonstrated in Gabashvili and Grosberg (21), the different sources of friction can only give dependence proportional to 1/T, and an exponential dependence cannot be associated with such mechanisms. The Arrhenius law observed for 1/τ as a function of the temperature strengthens further the idea that the ejection is limited by protein conformational changes required to promote ejection and not by the DNA movement in itself.

In phages with a long tail the receptor binding site is separated from the head-to-tail connector by the helical tail tube that has a length typically longer than 90 nm (92 nm for T4, a Myoviridae, and 135, 160, and 175 nm for the Siphoviridae λ, SPP1, and T5, respectively (19,22)). The tube of Siphoviridae is composed of >100 subunits forming the tubular helical lattice organized around the internal tape measure protein that is present in <10 copies. After receptor binding, this structure undergoes structural rearrangements necessary for signal transduction across its full length. The signal triggers the opening of the head-to-tail connector for genome ejection and exit of the internal tape measure, a necessary prelude for DNA traffic through the tube (Fig. 1).

These structural events can potentially provide the energy barrier found in this study. However, the energies of activation estimated here for DNA ejection from Siphoviridae are of the same order of magnitude as the one found for a mutant of phage T7 able to passively deliver its entire genome into the E. coli cytoplasm (28.3 kcal/mol) (23). This barrier was attributed by the authors to a “reaction-determining step in T7 genome entry that establishes the means for DNA transport, rather than the process of genome internalization itself”. Since T7 has a short tail (Podoviridae) without a tube structure, the rate-limiting step for DNA ejection cannot result from signaling events across the helical tail (steps ii and iv in Fig. 1). The results for phage T5 draw the same conclusion: steps ii and iv occur only once during the ejection process, but the same energy barrier is measured for each ejection pause. Even though DNA traffic in vivo requires additional steps necessary for passage of the cellular envelope when compared to genome ejection in vitro (6,23), the similarity between the activation energies suggests that the process is controlled by the same mechanism in both experimental conditions.

A common requirement for DNA ejection in tailed phage systems with different morphologies is opening the head-to-tail connector. In all tailed phage families the portal of the head is physically closed by proteins that form this structure. This stopper is composed of 6 or 12 subunits organized as a radial disk in the connector structure (17,18,24). Its opening allows propulsion of DNA to the phage head exterior driven by the high internal pressure built by DNA phosphate backbone repulsions and strong DNA bending imposed by the genome confinement inside the head. Tight control of this step is of major importance for the phage. The channel aperture must imply mechanisms that require an energy low enough to be thermally activated. As seen for the tail contraction of the phage T4 (22), bacteriophages can undergo large conformational modifications without energy supply.

The question is then to determine where the energy is stored for these huge structural changes. The proteins responsible for the connector channel aperture are most likely folded in a metastable form when the channel is closed, separated by an energetic barrier from the lowest energy state corresponding to an open channel. The interaction with the receptor would lower the energetic barrier to one that can be simply overcome by thermal activation. This feature is essential to guarantee the survival of bacteriophages whose structure is a compromise between a highly robust assembly to protect the integrity of their genome and a functional machine for its efficient delivery into their host. For instance, the energy barrier can be important for the survival of phages at low temperatures where the host does not support phage growth; under these conditions, phages can adsorb to host cells without ejecting their genome. In addition, it would be highly instructive to compare activation energies for phages with very different morphologies or those infecting bacteria living at extreme temperatures.

The requirement of an energy barrier as found here for phage genome ejection is a common feature in many systems for which a time-stable and controllable state is required. In biology, a typical example concerns enzymes that are able to promote a reaction by lowering the activation energy separating substrates from products. Enzymes can be viewed as cellular tools to control and regulate the concentrations of certain molecules. The enthalpic barrier generally reported in the literature varies from 15 to 40 kcal/mol for different proteins (25). In solid state physics, the magnetization of 50–100 nm sized grains may be reversed by overcoming an energy barrier (26,27). Because the barrier height can be controlled simply by adjusting the applied magnetic field, these materials are of great interest in magnetic recording devices. Therefore the barrier height must be high enough to ensure the magnetization stability and avoid the spontaneous reversal by thermal fluctuations and consequently the uncontrollable data loss. Interestingly the minimal energy barrier of 1.5–3 × 10⁻¹⁹ J (20–40 kcal/mol), which is commonly reported in the literature, is identical to the value determined here for viruses. This leads to the intriguing possibility that systems requiring a controllable transition of state converge to a common energy of activation.

APPENDIX

In this appendix, we examine in detail three different cases concerning the phage population ejection and leading to different variations of the measured scattered intensity. In Eq. 1, the intensity splits into two parts because at each moment t, the signal integrates the light scattered by all phages, fully or partially filled. During the ejection process, their total number N₀ is constant and reads N₀ = N_full(t) + N_eject(t); only the respective proportion of the two populations changes as dN_eject = − dN_full. Here it is convenient to introduce n(t′)dt′ = dN_eject(t′), the number of phages starting to eject their DNA between t′ and t′ + dt′ . The DNA mass variation of one phage may be written as M_DNA(t − t′) = M_DNA(0) f(t − t′). The function f(t − t′) describes the dynamics of the DNA translocation between the beginning of the ejection at t′ and the detection time t. When phages are still full of DNA for t′ ≥ t, f(t − t′) = 1, and when DNA is completely ejected at t′ ≪ t, f(t − t′) = 0. Introduction of n(t′) and f(t − t′) in Eq. 1 gives the relation

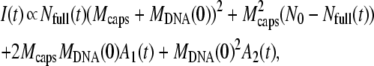(2)

where the two integrals A₁(t) and A₂(t) are given by A₁(t) = 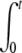f(t − t′) n(t′)dt′ and A₂(t) = 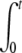f(t − t′)² n(t′)dt′.

Now the general Eq. 2 may be used to calculate the intensity variation expected in three specific cases:

i. DNA ejection from all phages is synchronized. Therefore ejection starts after adding the receptors at time t′ = 0, and the number of phages starting to eject N_eject(t′) may be expressed as a Heaviside step function θ(t′): N_eject(t′) = N₀ θ(t′). The derivative of N_eject(t′) reduces to a simple Dirac function, and by inserting the expression for n(t′) into the two integrals, we get A₁(t) = N₀ 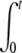f(t − t′) δ(t′)dt′ = N₀ f(t) and A₂(t) = N₀ 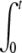f(t − t′)² δ (t′)dt′ = N₀ f(t)². And finally, since N_full(t ≥ 0) = 0, the intensity in Eq. 2 becomes equal to

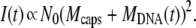(3)

Since all phages are synchronized, at each time t, they have the same mass M_caps + M_DNA(t) and, as a result, the detected intensity should correspond to a simple scattering by N₀ monodisperse particles as expressed by Eq. 3. Note that getting a simple exponential decay for the measured kinetics imposes a dependence on the ratio M_DNA(0)/M_caps on the function f(t). This dependence is very unlikely. Hence, because of the square dependence of the mass, the detected exponential decay cannot be assigned to the case where all phages are synchronized.

ii. Phages are desynchronized and the DNA ejection is instantaneous. Instantaneous ejection for one phage at a time t′ implies that its mass equals M_DNA(0) when t < t′ and 0 when t ≥ t′. The function f(t − t′) satisfies the step function f(t − t′)= 1 − θ(t − t′). It follows that f(t − t′) is always equal to zero when t ≥ t′, which in turn cancels the two integrals A₁(t) and A₂(t) in Eq. 2

(4)

Introducing the initial and final intensities expressions, I_initial ∝ N₀ (M_caps + M_DNA(0))² and 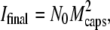Eq. 4 may be transformed into the relation F(t) = (I(t) − I_final)/(I_initial − I_final) = N_full(t)/N₀. Therefore, if the number of fully filled phages decreases exponentially with time as expected for a first order reaction, the normalized function F(t) should be a simple exponential decay described by the characteristic time τ₀.

iii. Phages are desynchronized and DNA ejection is not instantaneous. Unlike the previous case, the two integrals A₁(t) and A₂(t) cannot cancel here, and therefore the kinetics given by Eq. 2 depends also on the DNA release itself, that is, on the variation of f(t − t′). The exact variation of f(t − t′) is unknown, but as might be expected from the DNA pressurization state, DNA translocation should be faster at the beginning than at the end of the process. Although arbitrary, we can assume, for simplicity, an exponential decay for f(t − t′) once the phage starts to eject its DNA at t = t′. As a consequence, the function may be written as f(t − t′) = 1− θ(t − t′) + θ(t − t′)exp(−(t − t′)/τ_ej) with τ_ej the characteristic time of ejection, which allows us to easily calculate the two integrals A₁(t) and A₂(t). That gives a contribution of the form

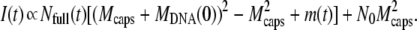(5)

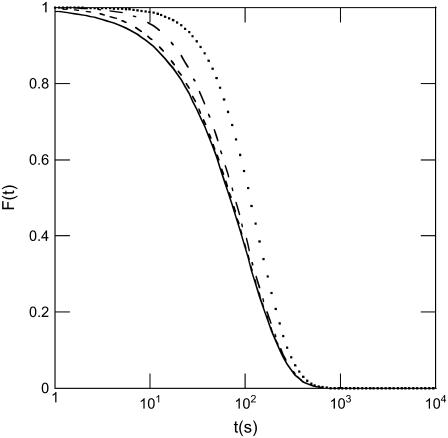
For clarity, we do not express here the explicit form of the contribution m(t) which, as can be seen in Eq. 5, induces a deviation from the previous result in Eq. 4. As seen in Fig. 6, m(t) contributes mainly to the intensity in the short-time range and the magnitude of the deviation from the exponential behavior depends on the ratio τ₀/τ_ej. Experimentally, the difference can only be perceived if τ_ej exceeds τ₀/10.

FIGURE 6.

Effect of desynchronization and of the duration of DNA movement on the expected signal for a population of phages ejecting their DNA. Modeling shows that when DNA ejection from one phage is not instantaneous and when phages are also desynchronized due to the energy barrier described in the article, the detected kinetics deviates from a simple exponential (solid line). If τ_ej and τ₀ denote the two respective characteristic times, curves expected for different ratios τ_ej/τ₀ (with τ₀ = 100 s) are illustrated: τ_ej/τ₀ = 1/2 (dotted line), 1/10 (dashed-dotted line), and 1/50 (dashed line).