The Effect of Charge-Charge Interactions on the Kinetics of α-Helix Formation

Abstract

The formation of the monomeric α-helix represents one of the simplest scenarios in protein folding; however, our current understanding of the folding dynamics of the α-helix motif is mainly based on studies of alanine-rich model peptides. To examine the effect of peptide sequence on the folding kinetics of α-helices, we studied the relaxation kinetics of a 21-residue helical peptide, Conantokin-T (Con-T), using time-resolved infrared spectroscopy in conjunction with a laser-induced temperature jump technique. Con-T is a neuroactive peptide containing a large number of charged residues that is found in the venom of the piscivorous cone snail Conus tulipa . The temperature-jump relaxation kinetics of Con-T is distinctly slower than that of previously studied alanine-based peptides, suggesting that the folding time of α-helices is sequence-dependent. Furthermore, it appears that the slower folding of Con-T can be attributed to the fact that its helical conformation is stabilized by charge-charge interactions or salt bridges. Although this finding contradicts an earlier molecular dynamics simulation, it also has implications for existing models of protein folding.

INTRODUCTION

Recent years have seen an increased interest in the study of the folding kinetics of α-helices (1–29), β-hairpins (30–33), and other small folding motifs (34–42). Not only do such studies provide insight into the folding mechanism of protein secondary/supersecondary structural elements, but they also yield invaluable information that could help decipher, in a bottom-up manner, the underlying principles that govern protein folding. Additionally, results obtained from such studies often serve as benchmarks for computer simulations.

Among the studied protein structures, the α-helix motif has received considerable attention because its folding is simplified, to an extent, by involving mainly local interactions (43). For example, a variety of spectroscopic methods have been employed to examine the nanosecond folding dynamics of monomeric α-helices in response to a conformational trigger, such as a temperature jump (T-jump) (2–10,14,16,23), a pH jump (22), or a photo-triggering event (17). In addition, numerous theoretical studies and computer simulations have also been carried out, with the aim of understanding the underlying energy landscape and mechanism governing α-helix folding (1,11–13,15,18–21,24–28). However, our current understanding of the folding dynamics of monomeric α-helices in solution is mostly founded upon studies of alanine-based peptides. This is because alanine has the highest helix-forming propensity and is therefore frequently used in synthetic α-helical peptides (44). As shown in Table 1, most of the peptides used in early kinetic studies had rather similar sequences, in that alanine was the dominant residue. However, in naturally occurring helical peptides and proteins, alanine is not the most abundant residue (45), and many interactions work together to stabilize individual helical structures (46–48). Although studying alanine-rich peptides has provided invaluable information on the kinetics and mechanism of α-helix formation, a comprehensive understanding of how monomeric α-helices fold requires the study of helical peptides with drastically different sequences. More important, in the context of existing protein-folding models (49), a survey of how helix folding time varies with peptide content will help distinguish the role of secondary-structure formation. With these goals in mind, we have studied the T-jump-induced relaxation kinetics of a 21-residue α-helical peptide, Conantokin-T (Con-T), which is rich in charged amino acids.

TABLE 1.

Sequences and relaxation times of several α-helices reported previously

Peptide	Sequence	Relaxation time (ns) (Tf, (°C))*	Reference
AR peptide	(AARAA)4GY	184 (28)	2
AK peptide	(AAKAA)4GY	194 (28)	2
AE peptide	(AAEAA)4GY	147 (28)	2
AQ peptide	(AAQAA)4GY	117 (28)	2
Suc-FS peptide	Suc-A5(A3RA)3A	160 (27)	3
YGG-3Ai	YGGK(A4K)3	130 (30)	6
W1H5-21	WA3H(A3RA)3A	240 (27)	4
D-Arg peptide	YGG(KA4)3-CO-D-Arg	140 (27)	14
FS peptide	A5(A3RA)3A	240 (37)	7
AKA2	YGAKA4(KA4)2G	80 (28)	5
SPE2	YGSPEA3(KA4)2-D-Arg	80 (28)	5
AKA3	YGAKA4(KA4)3G	125 (28)	5
SPE3	YGSPEA3(KA4)3-D-Arg	100 (28)	5
AR4	A5(A3RA)4A	164 (24)	23

^*T_f corresponds to the final temperature.

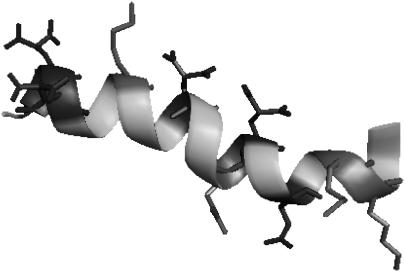
Con-T is a neuroactive peptide found in the venom of the piscivorous cone snail Conus tulipa (50), developed for rapid immobilization of fast-moving prey (51). Although most Conus venom peptides contain disulfide bonds, Con-T is structurally unusual, as it lacks the disulfide motifs and instead contains four base-stable but acid-labile γ-carboxyglutamic acids (Gla) in its sequence (GEγγYQKMLγNLRγAEVKKNA, where γ denotes Gla, a residue originally identified in blood-clotting factors such as prothrombin (51)). The NMR structure of Con-T (Fig. 1) indicates that it folds into a twisted α-helical structure in aqueous solution (52). Consistent with previous studies (52,53), our circular dicroism (CD) and infrared (IR) results also show that at neutral pH Con-T adopts a helical conformation; however, our IR T-jump study indicates that the relaxation rate of Con-T is significantly slower than that of alanine-based peptides of similar length, suggesting that formation of salt bridges slows down the folding of α-helices.

FIGURE 1.

NMR structure of Con-T (PDB code 1ONT). The charged residues are shown. The figure was generated using the program PyMol (http://pymol.sourceforge.net/).

EXPERIMENTAL SECTION

Materials and sample preparation

Conantokin-T was synthesized based on standard Fmoc (9-fluorenylmethyloxycarbonyl) protocols on a PS3 automated peptide synthesizer (Protein Technologies, Woburn, MA) and purified to homogeneity by reverse-phase chromatography. The identity of the peptide sample was further verified by matrix-assisted laser desorption ionization mass spectroscopy. The exchangeable hydrogens and residual trifluoroacetic acid from peptide synthesis, which absorbs around 1678 cm⁻¹, were removed by multiple rounds of lyophilization against a 0.1 M DCl/D₂O solution. Peptide solutions used in both CD and IR measurements were prepared by directly dissolving the lyophilized peptide samples in either 20 mM phosphate buffer (pH 7) or 20 mM phosphate buffer (pH 7) containing 2.0 M NaCl. The final peptide concentrations, determined optically by tyrosine absorbance at 276 nm, using ɛ₂₇₆ = 1450 cm⁻¹ M⁻¹, were ∼50 μM and 2 mM for CD and IR, respectively.

CD measurements

The CD data were collected on an Aviv 62A DS circular dichroism spectrometer (Aviv Instruments, Piscataway, NJ) using a 1-mm sample cuvette. Mean residue ellipticity was calculated using the equation [θ] = (θ_obs/10lc)/N, where θ_obs is the ellipticity in millidegrees, l is the optical path length (cm), c is the concentration of the peptide (M), and N is the number of residues.

Absorption measurements

All ultraviolet (UV)-visible spectra were measured on a Lambda 25 UV-Vis spectrometer (Perkin Elmer, Wellesley, MA).

FTIR measurements

Static Fourier transform IR (FTIR) spectra were collected on a Magna-IR 860 spectrometer (Nicolet, Madison, WI) equipped with a HgCdTe detector using 2 cm⁻¹ resolution. A homemade CaF₂ sample cell that was divided with a 52-μm Teflon spacer into two compartments and mounted on a programmable translation stage was used to allow separate measurement of the sample and the reference under identical conditions. Temperature control with ±0.2°C precision was obtained by a thermostated copper block. Typically, 256 scans were averaged to generate one spectrum.

Infrared T-jump apparatus

The T-jump technique uses a burst of IR photons to heat up a sample solution within a very short period of time, e.g., a few nanoseconds. As a result, the sudden increase in temperature induces a population redistribution among conformational ensembles that are initially at equilibrium. Hence, the time course in which the nonequilibrium state evolves toward a new equilibrium position contains information regarding the kinetics of folding and unfolding. The time-resolved T-jump IR apparatus used in this study has been described in detail elsewhere (8). Briefly, a 1.9-μm laser pulse, generated via Raman shifting of the fundamental output of a Q-Switched Nd:YAG laser in H₂, was used to generate a T-jump of 8–10°C, and the T-jump-induced transient absorbance changes were measured by a continuous-wave IR diode laser in conjunction with a 50-MHz HgCdTe detector and a digital oscilloscope. A thermostated, two-compartment sample cell with 52-μm path length was used to allow separate measurement of the sample and buffer under identical conditions. The buffer measurements provide information for both background subtraction and T-jump amplitude determination. The latter was achieved by using the T-jump-induced absorbance change of the D₂O buffer solution at the probing frequency ν, ΔA(ΔT, ν), and the following equation: ΔA(ΔT, ν) = a(ν) × ΔT + b(ν) × ΔT², where ΔT corresponds to the difference between the final (T_f) and initial (T_i) temperatures, and a(ν) and b(ν) are constants determined by analyzing the temperature dependence of the FTIR spectra of the buffer.

RESULTS

Static CD studies

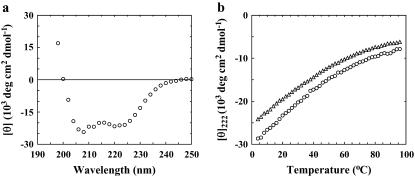
As shown (Fig. 2 a), the far-UV CD spectrum of Con-T at 25°C and pH 7 exhibits the characteristic double minima of α-helices at 222 and 208 nm, respectively, indicating that the helical conformation is significantly populated under this condition. Similar to those observed for other monomeric α-helical peptides, the CD thermal unfolding transition of Con-T measured at 222 nm is quite broad (Fig. 2 b). The fractional helicity (f_H) of Con-T was further estimated using the relationship

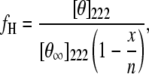(1)

where [θ]₂₂₂ is the measured mean residue ellipticity at 222 nm, [θ_∞]₂₂₂ is the mean residue ellipticity at 222 nm of an ideal peptide with 100% helicity, n is the length of the potential helical region, and x is an empirical correction for end effects. Using the x and [θ_∞]₂₂₂ values given by Luo and Baldwin (54) (i.e., x = 2.5 and [θ_∞]₂₂₂ = −44000 deg cm² dmol⁻¹), the fractional helicity of Con-T at 4°C was estimated to be ∼74%, 21% lower than that reported by Lin et al. (53) for pH 5. The temperature at which the average helicity reaches 50% is ∼33°C. As expected, the helicity of Con-T decreases with increasing ionic strength (Fig. 2 b). For example, addition of 2.0 M NaCl to the peptide solution lowers the fractional helicity to 62% at 4°C.

FIGURE 2.

(a) Far-UV CD spectrum of Con-T at 25°C. (b) Mean residue ellipticity of Con-T at 222 nm as a function of temperature. Open circles correspond to peptide samples of low ionic strength (i.e., in 20 mM phosphate buffer, pH 7), whereas open triangles represent a peptide sample of high ionic strength (i.e., in 20 mM phosphate buffer, pH 7, and 2.0 M NaCl).

Static FTIR studies

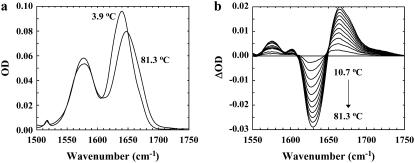
Similar to those obtained with alanine-based α-helical peptides, the amide I′ band of Con-T, which mainly arises from the backbone C=O stretching vibrations, is centered at ∼1632 cm⁻¹ at 3.9°C (Fig. 3 a), whereas increasing temperature shifts the peak position toward a higher wavenumber. Consequently, the FTIR difference spectra of Con-T (Fig. 3 b), calculated by subtracting the 3.9°C spectrum from those obtained at higher temperatures, exhibit a negative feature centered around 1632 cm⁻¹ and a positive feature centered at ∼1665 cm⁻¹, respectively. The former results primarily from loss of α-helical conformations with increasing temperature, whereas the latter is due to the concurrent formation of the nonhelical conformational ensemble (55,56). Since temperature-induced variations in backbone solvation also shift the amide I′ band toward higher frequency and thus contribute to the aforementioned spectral changes, we did not attempt to determine the thermal denaturation of Con-T using its amide I′ band. However, these spectral features shown in Fig. 3 b can serve as IR markers of the underlying conformational changes and have been used in the subsequent kinetic studies to monitor the conformational relaxation kinetics of Con-T in response to a T-jump.

FIGURE 3.

FTIR spectra of Con-T were collected in the temperature range 3.9–81.3°C at approximately every 7°C. (a) Two representative spectra (in the amide I′ region), collected at 3.9 and 81.3°C, respectively. (b) The difference FTIR spectra generated by subtracting the spectrum collected at 3.9°C from those collected at higher temperatures.

T-jump-induced relaxation kinetics

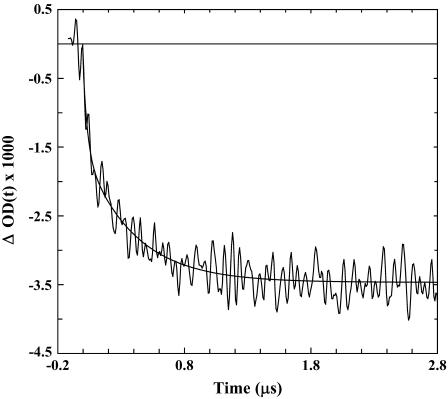
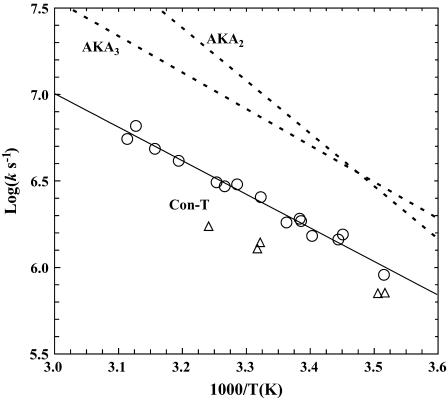
The T-jump-induced relaxation kinetics of Con-T were probed at 1632 cm⁻¹ using an infrared transient absorption apparatus, which has been described in detail elsewhere (8). Similar to those observed for alanine-based α-helical peptides (14), the IR relaxation kinetics of Con-T in response to a T-jump exhibit two distinct phases (Fig. 4). The fast phase rises concomitantly with the response of the infrared detector of the IR T-jump apparatus and, therefore, was not resolved in time. In accord with our previous interpretation (5,8,32) and also the work of Hamm and co-workers (17), we attributed this phase to an IR signal arising from a T-jump-induced spectral shift (57). The slow phase was well resolved in the temperature range of the experiment and was attributed to a conformational redistribution process in response to the T-jump. In addition, the slow phase was well fit by a single-exponential function (Fig. 4), and the resultant rate constant exhibits Arrhenius temperature dependence with an apparent activation energy of ∼8.9 kcal/mol (Fig. 5). Interestingly, however, the T-jump-induced relaxation rate of Con-T is distinctly slower than that of alanine-based α-helical peptides measured under similar conditions. For example, at 27.8°C, the relaxation time constant of Con-T is 390 ns (Fig. 4), whereas an alanine-based α-helical peptide of the same length relaxes in 160 ns in response to a T-jump from 10 to 28°C (3). Therefore, these results suggest that the charge-charge interactions or salt bridges in Con-T greatly affect the folding/unfolding kinetics of its α-helical conformation.

FIGURE 4.

A representative T-jump relaxation trace of Con-T measured with a probing frequency of 1630 cm⁻¹. The corresponding T-jump is 7.4°C, from 20.4 to 27.8°C. The smooth line is a convolution of the instrument response function with ΔOD(t) = A × [1 − B × exp(−t/τ)], with A = −0.0035, B = 0.56, and τ = 0.39 μs.

FIGURE 5.

Arrhenius plot of the T-jump-induced conformational relaxation rates of Con-T under different conditions: (open circles) 20 mM phosphate buffer (pH 7); (open triangles) 20 mM phosphate buffer (pH 7) and 2.0 M NaCl. A linear regression (solid line) to the data obtained for the low-ionic-strength solution yields an apparent activation energy of 8.9 ± 0.3 kcal/mol. Also shown for comparison are the relaxation rates of two alanine-based α-helical peptides, AKA₂ and AKA₃ (5).

DISCUSSION

The folding kinetics of α-helices has been a subject of great interest in recent years (1–29). The goal has been not only to measure the folding timescale for isolated α-helical structures but also to identify the key determinants of their folding kinetics and mechanism. For example, Volk and co-workers (2) have shown that even a single mutation in an alanine-based peptide affects its folding kinetics; and Wang et al. (5) have further shown that the folding times of a series of monomeric α-helices depend on the peptide chain length as well as end-capping motifs. Because most α-helices found in proteins often adopt nonhelical conformations in isolation as a result of the loss of stabilizing tertiary interactions, previous kinetics studies have focused mainly on model peptides consisting mostly of alanines, because of their high helicity around room temperature (Table 1). Therefore, our current understanding of the folding dynamics of the α-helix motif is mainly based on studies of model peptides with very limited sequence variation (2,5). To determine whether the peptide sequence strongly affects the folding kinetics of α-helices, especially the effect of charge-charge interactions, we studied the T-jump-induced relaxation kinetics of Con-T, a naturally occurring α-helical peptide isolated from the venom of C. tulipa (50).

Compared to the widely studied alanine-based α-helical peptides, a distinct feature of Con-T is that it contains a large number of charged residues, i.e., Glu, Gla, Lys, and Arg, which all take their respective charges at neutral pH. Gla is a modified glutamic acid, and its primary function has been suggested to be calcium binding (53,58). Although charged and/or polar residues (e.g., Lys and Arg) have also been used in alanine-based peptides, they are often introduced to increase peptide solubility (44). As shown (Fig. 1), Con-T contains 10 charged residues and adopts a nonlinear α-helical structure wherein the hydrophilic residues reside on the exterior surface, resulting in alternating regions of positive and negative charges (52). As indicated (Fig. 6), these charged residues can potentially form two i, i + 4 and five i, i + 3 salt bridges (53). Indeed, a mutational study has shown that replacing all Gla residues with Glu significantly diminishes the peptide helicity, indicating the stabilizing role of these salt bridges in the helical conformation (53). Consistent with these studies, our static CD and IR results also show that Con-T adopts an α-helical conformation at neutral pH and relatively low temperatures.

FIGURE 6.

Schematic illustration of charge-charge interactions in Con-T. (Solid line) i, i + 4 salt bridges; (dotted line) i, i + 3 salt bridges; (bold) acidic residues; (italic) basic residues.

The folding-unfolding kinetics of Con-T were studied by a T-jump IR technique (14). Because the helicity of Con-T depends on temperature (Fig. 2), a rapid increase in temperature thus allows, via an appropriate spectroscopic probe, the measurement of the time course of its conformational relaxation, which contains information regarding its folding and unfolding kinetics (59). Specifically, the T-jump-induced relaxation kinetics of Con-T were probed by monitoring the optical density change at 1632 cm⁻¹, where solvated α-helices absorb. As shown (Fig. 4), within experimental uncertainties, the T-jump-induced conformational relaxation of Con-T follows a single-exponential time course (see below). In addition, the T-jump-induced relaxation rate of Con-T exhibits Arrhenius temperature dependence with an apparent activation energy of 8.9 kcal/mol, similar to that observed for alanine-based peptides (5,14). Although several factors have been suggested to contribute to such energetic barriers in α-helix formation (5,18), the nature of the enthalpic cost encountered in α-helix folding is still not entirely clear.

Although an isolated α-helix is one of the simplest structural motifs in proteins, its folding dynamics are nevertheless complex. Both computational and experimental studies have suggested that the folding-unfolding process of monomeric helices may proceed in a non-two-state manner (8,17,21,26). For example, several studies have shown that the T-jump-induced relaxation kinetics of alanine-based α-helical peptides deviate from simple exponential kinetics (5,8,10,17), and the termini exhibit a faster relaxation rate than the middle of the peptide (6,8). Although it is not entirely clear at the molecular level what causes this deviation from single-exponential relaxation kinetics, several factors, such as conformational distribution, folding intermediates, or multiple folding/unfolding pathways, may contribute to this complexity. Interestingly, Wang et al. (5) have shown that the T-jump-induced relaxation of short helical peptides, the helical conformation of which is only marginally stable, is significantly nonexponential, whereas longer helical peptides tend to exhibit relaxation kinetics that are closer to single-exponential. These studies therefore suggest that although the single-exponential relaxation kinetics of Con-T are consistent with a two-state folding mechanism, this interpretation may not be rigorously true. However, if we were to assume that the folding of Con-T follows a two-state process, its relaxation rate constant (k_R) could be further separated into the corresponding folding (k_f) and unfolding (k_u) rate constants using the helicity (i.e., equilibrium constant K_eq) estimated from the CD measurements and the relationships: k_R = k_f + k_u and K_eq = k_f/k_u. For example, at 28°C the relative helical population of Con-T was estimated to be ∼54% and the relaxation time constant was measured to be 390 ± 40 ns; thus the corresponding folding and unfolding time constants are 722 and 848 ns, respectively. These results are particularly interesting, considering the fact that several small helical proteins have been shown to fold in ∼1 μs (37,60).

If the folding of Con-T follows a more complicated mechanism, the above analysis becomes invalid or less rigorous. However, it is apparent that the T-jump-induced relaxation of Con-T is distinctly slower than that of alanine-based peptides under the same conditions (see Table 1). For example, the single-exponential relaxation time of the Fs peptide at 28°C is 160 ns (3), less than one half that of Con-T. Furthermore, the 19-residue helical peptide AKA₂ relaxes in ∼80 ns at 27°C (5), which is roughly five times faster than the relaxation time of Con-T. Moreover, Volk et al. have shown that a series of 22-residue alanine-based α-helices exhibits T-jump-induced relaxation times in the range of 117–194 ns (2), which is also much shorter than that of the Con-T peptide. Taken together, these results thus suggest that Con-T does fold on a timescale that is slower than that of alanine-based peptides and the requirement for formation of salt bridges in the rate-limiting step retards the rate of helix formation. Interestingly, this picture is contrary to the conclusion of Wei et al. (27), who performed molecular dynamics simulations of Con-T folding. When compared to results of folding simulations of alanine-based peptides of the same length (36), their results suggest that Con-T folds at a faster rate as a result of the salt bridges.

Although it is clear that native salt bridges are often beneficial to the stability of the folded state (61), the underlying effects of individual charge-charge interactions on the folding kinetics of a protein could be very different. For example, Matthews and co-workers (62) have shown that although the salt bridge formed between E22 and R25 in the homodimeric coiled-coil peptide GCN4-p1 might play a critical role in stabilizing the C-terminal nascent helices that drive the association reaction, the remaining salt bridges stabilize the coiled-coil architecture only after the rate-limiting step. The study of Daggett and co-workers (63) has also indicated the important role of salt bridges in forming long-range tertiary contacts that assist helix formation in the engrailed homeodomain. On the other hand, several studies have indicated that burying polar side chains and salt bridges in a relatively hydrophobic environment is generally an unfavorable process and, therefore, could slow down folding (37,41,64), even though the desolvation penalty of burying the charged residues may be compensated to some degree by their interaction energy (65). Apparently, breaking up nonnative salt bridges, either present in the denatured conformational ensemble (66) or formed during the folding process, would also retard the rate of folding. Considering the fact that Con-T does not possess a hydrophobic core, its slower folding rate, when compared with that of alanine-based peptides, could arise from two possible scenarios: 1), the formation of salt bridges is an intrinsically slower process; or 2), folding requires breaking up nonnative charge-charge interactions. Since the T-jump-induced relaxation process of Con-T encounters an activation energy (∼9 kcal/mol) that is comparable to that observed for alanine-base peptides (5), it is therefore unlikely that we can attribute its slower folding rate to the formation of nonnative salt bridges. This conclusion is further supported by the fact that increasing the ionic strength of the peptide solution (i.e., by addition of 2.0 M NaCl) leads to a decrease in the relaxation rate of Con-T (Fig. 5), an indication that the free energy barrier for both folding and unfolding is increased. In other words, increasing ionic strength has a larger effect on the transition state than on the unfolded state in the case presented here. Interestingly, it has been shown that for alanine-based peptides the addition of salt increases the relaxation rate after a T-jump (23).

Our results seem to suggest that the overall folding rates of monomeric helices correlate with their intrinsic helical propensities, with faster folding corresponding to a higher propensity. Although this correlation requires further verification in future studies, the idea that the rate of helix formation is sequence-dependent is not new and may carry important implications for protein folding mechanisms and models. For example, a recent simulation study by Daggett and co-workers (67) has shown that individual helical segments in barnase and protein A exhibit very different folding times, and the folding of those segments having low intrinsic helical propensities is initiated by side-chain interactions through the formation of salt bridges or hydrophobic contacts. Akin to the role of the folding nucleus in the nucleation-condensation model of protein folding (49), such side-chain contacts, either native or nonnative, could provide a scaffold for further growth of the native structure. On the other hand, those segments with higher helical propensity may fold independently, thereby providing a framework for constructing the tertiary structure.

CONCLUSION

In summary, using CD and FTIR spectroscopies and a laser-induced T-jump IR technique, we have studied the thermal unfolding transition and folding kinetics of Con-T, a 21-residue, naturally occurring helical peptide whose native conformation is largely stabilized by charge-charge interactions or salt bridges. Compared to that of alanine-based model helical peptides, the folding rate of Con-T is distinctly slower. Therefore, this result suggests that the folding time of monomeric helices is sequence-dependent and that the formation of one or multiple salt bridges in the rate-limiting step retards the rate of helix formation.