Distributivity and Processivity in Multisite Phosphorylation Can Be Distinguished through Steady-State Invariants

Abstract

Multisite protein phosphorylation and dephosphorylation are key cellular regulatory mechanisms but their system properties have been difficult to study in vivo and in vitro. Here we show by mathematical analysis that steady-state invariants enable the mechanism of the kinase or the phosphatase to be determined from steady-state measurements. Invariants exist when both enzymes act distributively (i.e., nonprocessively), making at most one modification in each molecular encounter. For instance, in the sequential case, in any experiment involving the same ingredients, the quantity [S_i−1][S_i+1]/[S_i]² always has the same value, where [S_i] denotes the steady-state concentration of the i-th phospho-form. For a two-site substrate, if either enzyme exhibits processivity, so that more than one modification can be made in each molecular encounter, the degree of processivity can be estimated from changes in this invariant. We discuss the experimental and theoretical challenges in extending these results.

INTRODUCTION

Ever since the discovery of reversible protein phosphorylation (1), its importance as a key cellular regulatory mechanism has been increasingly appreciated (2). Disregulation of phosphorylation is implicated in several human diseases and both kinase and phosphatase inhibitors are important in the clinic (3,4). Prokaryotes predominantly use two-component histidine, aspartate phospho-transfer, whereas eukaryotes predominantly rely on serine, threonine, and tyrosine phosphorylation (5–7). Significantly, eukaryotes exhibit a striking difference in multisite modification (8,9). Bacterial and archaeal proteins are phosphorylated on at most a few sites under normal conditions (10,11), whereas eukaryotic proteins can be heavily phosphorylated (7): p53, which integrates the cell's DNA damage response, has 16 phosphorylation sites, targeted by several kinases and phosphatases (9).

A substrate molecule with n phosphorylation sites may be in one of 2ⁿ states and a population of molecules may contain a mixture of these different phospho-forms. Furthermore, the system of kinases, phosphatases, and substrate is maintained far from equilibrium in vivo by a steady supply of ATP. This is a recipe for complex emergent behavior but this has rarely been seen either in vivo or in vitro. In vivo studies are hampered by the need for single-cell resolution and the absence of real-time sensors for phosphorylation state. In vitro studies are normally done with either kinase or phosphatase. Recent exceptions to this have been the development of extract systems for phosphorylation studies (12) and the remarkable in vitro recapitulation of the cyanobacterial circadian oscillator (13), which manifests itself as an oscillation in multisite phosphorylation. These experimental studies hint at the complexity that is to be found with just three components: kinase, phosphatase, and substrate.

Despite their dynamical complexity, such systems can satisfy algebraic invariants at steady state. Invariants are algebraic expressions, which only involve measurable state variables, whose values are independent of the conditions under which the system is initiated, such as the total amounts of enzymes or substrate (Eq. 5). We show here that these invariants provide a method for determining the mechanism of action of both kinases and phosphatases. This method has many advantages over current techniques, as summarized in the Discussion.

We consider a kinase E and phosphatase F acting on a substrate S with n phosphorylation sites. The enzymes are initially assumed to act distributively on S and to maintain a sequential order of phosphorylation. Distributivity means that at most one modification (addition or removal of phosphate) takes place in each encounter between substrate molecule and enzyme molecule (14). Accordingly, each phospho-form competes for both enzymes. Sequentiality means that sites are phosphorylated in a specific order and dephosphorylated in the reverse order, so that there are only n + 1 phospho-forms, S₀, ⋯, S_n. Here, S_i denotes the phospho-form with i sites phosphorylated in order. These assumptions give rise to a chain of reactions

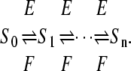(1)

The enzymes are assumed to operate through a standard biochemical reaction scheme with reversible formation of an enzyme-substrate complex and irreversible formation of product:

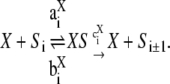(2)

Here, X = E, 0 ≤ i < n and the product is S_i+1, or, X = F, 0 < i ≤ n and the product is S_i−1. Assuming mass-action kinetics, the reactions are labeled with their corresponding rate constants (“a” for association, “b” for breakup, and “c” for catalysis), with the subscript corresponding to the substrate of the reaction.

These assumptions are frequently used for multisite phosphorylation (14,15) although Eq. 2 is sometimes approximated by a Michaelis-Menten rate function (16–18). We make no approximations here. The relevance of our assumptions to current experimental understanding is reviewed in the Discussion.

Equations 1 and 2 give rise to a (3n + 3)-dimensional dynamical system in which the state variables are the concentrations of the n + 1 phospho-forms, S₀, ⋯ S_n; the 2n enzyme-substrate complexes, ES_i for 0 ≤ i < n and FS_j for 0 < j ≤ n; and the two free enzymes, E and F. As modeled, the system is closed; ATP is assumed to be held constant, through a mechanism that is not explicitly modeled, and its effects absorbed into the rate constants. It follows, assuming a fixed reaction volume, that the total concentrations of substrate, [S_tot], and enzymes, [E_tot] and [F_tot], remain constant during any time evolution of the system. When started from some initial condition, the system would be expected to relax onto a stable steady state, in which the actions of the kinase and the phosphatase are in balance. Although it contains no explicit feedback, the system can exhibit multistability: there may be more than one steady state having the same total amounts of substrate and enzymes (17). Indeed, the maximal number of steady states increases with n (M. Thomson and J. Gunawardena, unpublished data).

Although this dynamical system is nonlinear, there is an analytic solution for it at steady state. We review this below but its main consequence is that, if [−] denotes concentration in any steady state,

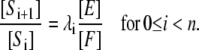(3)

Here, using the notation introduced in Eq. 2, λ_i is the site-specific relative catalytic efficiency,

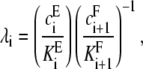(4)

and 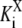is the site-specific Michaelis-Menten constant for X = E or X = F,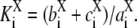

Equation 3 has the following remarkable consequence. Dividing the formulas for i + 1 by that for i, we see that

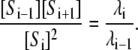(5)

The left-hand side of Eq. 5 depends only on the measurable state variables, S₀, ⋯, S_n, whereas the right-hand side depends only on the rate constants. Hence, in any experiment involving the same ingredients, no matter what amounts are used, no matter how the system is started and no matter what steady state is reached, the left-hand side must always have the same value. We refer to such quantities as invariants of the system. (There are further invariants of the form [S_i+1][S_j]/([S_i][S_j+1]) but these can be written in terms of those in Eq. 5.)

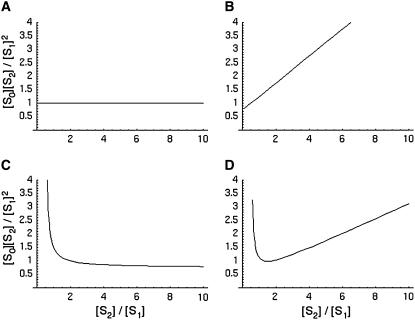
The main focus of this article is to ask what happens when Eq. 5 is not satisfied. One of the key assumptions made above is that both enzymes act distributively. An alternative hypothesis is that one or the other of the enzymes acts processively, allowing more than one modification to be made in each molecular encounter. Suppose given a kinase, phosphatase, substrate system with two phosphorylation sites, for which a variety of steady states are constructed having different total amounts of substrate and enzymes and different initial conditions and that, for each steady state, [S₀][S₂]/[S₁]² is plotted against [S₂]/[S₁]. We show below (see Fig. 1) that if both enzymes are distributive, the resulting graph is flat; if the kinase is distributive and the phosphatase is processive, the graph increases linearly; if the kinase is processive and the phosphatase distributive, the graph decreases hyperbolically; and if both enzymes are processive, the graph has a minimum, so that it first decreases and then increases. It follows that the mechanism of action of the enzymes can be determined by measurements carried out at steady state.

FIGURE 1.

Distinguishing distributive from processive. Plots of [S₀][S₂]/[S₁]² against [S₂]/[S₁] for systems with catalytic constants and Michaelis-Menten constants all 1, as described in the text. (A) Kinase distributive, phosphatase distributive. The constant value is the ratio of the relative catalytic efficiencies at the two sites, λ₁/λ₀. (B) Kinase distributive, phosphatase processive. The slope increases with the degree of processivity of the phosphatase. (C) Kinase processive, phosphatase distributive. The position of the singularity moves to the right as the degree of processivity of the kinase increases. (D) Kinase processive, phosphatase processive. The position of the singularity and of the minimum, along with the value of the minimum, determine the parameters in Eq. 15.

Extending this result to n > 2, or to systems that are not sequential, is surprisingly difficult and requires different mathematical techniques. For instance, for a nonsequential system with two sites, which corresponds to the case of several interesting biological examples, the invariant is considerably more complicated than Eq. 5 (see Eq. 16). We review these issues in the Discussion along with the challenges of experimentally verifying these predictions.

METHODS

The results were obtained by algebraic calculation. Fig. 1 was generated in Mathematica (Wolfram Research, Champaign, IL).

THEORY

Proof of Eq. 3

Consider the enzymatic chain in Eq. 1 at steady state. Let e_i be the net flux of substrate from S_i to S_i+1 due to enzyme E and let f_i be the net flux of substrate in the same direction due to enzyme F. Since the system is at steady state, the net flux into S_i+1 from the left, given by e_i − f_i, must equal the net flux out of S_i+1 to the right, given by e_i+1 − f_i+1. Hence e_i − f_i = e_i+1 − f_i+1 for 0 ≤ i < n. However, there is no net flux into S₀ from the left, nor net flux out of S_n to the right. (Sequentiality is essential here.) It follows that e_i = f_i for 0 ≤ i < n. In other words, at steady state, each individual loop in the chain is at steady state. This observation, which has been repeatedly made in different mathematical contexts, is well known to experts in biochemical kinetics (20).

The net fluxes are given by 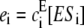and 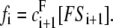It follows from Eq. 2 that at steady state, 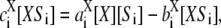so that

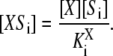(6)

Since e_i = f_i,

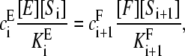from which Eq. 3 follows.

Model of processive phosphorylation and dephosphorylation

Consider the case n = 2. We explain the difficulties with the general case in the Discussion. If E acts processively, then it only makes a difference to its phosphorylation of S₀. We assume the following reaction scheme,

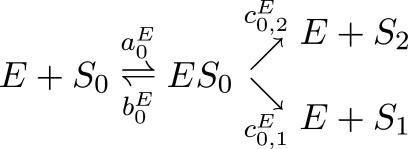, (7)

in which the decision as to how many phosphorylations to undertake is determined after binding of substrate molecule and kinase molecule. This is consistent with the experimental intuition emerging from studies of processive phosphorylation (21). It is conceivable that the decision could be made earlier, during the binding event, which would lead to a different reaction scheme, but it makes no difference to our results (not shown).

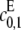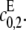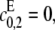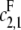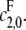The different possibilities for product formation in Eq. 7 each have their own mass-action rate constants, and If then the scheme reverts to that in Eq. 2 for a distributive kinase. We assume a symmetrical scheme to Eq. 7 for the processive dephosphorylation of S₂, with catalytic rate constants and If 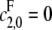then the phosphatase reverts to being distributive.

We further assume that eithe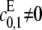r or 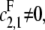for if both are zero then there is no way to produce S₁. The case of full processivity for both enzymes (that is, when exactly two modifications are done in each molecular encounter, so that 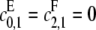) can be easily handled, since it is equivalent to having only a single site. We will ignore this possibility here. It is in any case more reasonable to assume that full processivity means that the single modification rate is very small compared to the double modification rate, so that 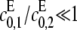for the kinase and 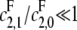for the phosphatase and these conditions can be handled by the results below.

Steady-state analysis

We will calculate [S₀][S₂]/[S₁]², assuming both kinase and phosphatase are processive, as described in Eq. 7. Because of the flux from S₀ to S₂ implied by this, the simple argument for the distributive case can no longer be used. However, balancing the net fluxes at S₀ at steady state in a similar way, we see that

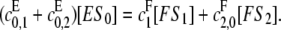(8)

If the definitions of the Michaelis-Menten constants 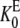and 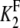are slightly modified so that

then it can be checked that Eq. 6 continues to hold for X = E, 0 ≤ i < 2 or X = F, 0 < i ≤ 2. Hence, Eq. 8 gives

which may be rearranged to give

(9)

A similar balancing of steady-state fluxes at S₂ gives a formula symmetric to Eq. 9 with subscript 0 interchanged with 2 and E interchanged with F:

(10)

Equations 9 and 10 are a pair of simultaneous linear equations for [S₂]/[S₁] and [S₀][S₁] in terms of the rate constants and [E]/[F]. To solve them, it is convenient to introduce relative catalytic efficiencies similar to λ_i in Eq. 4,

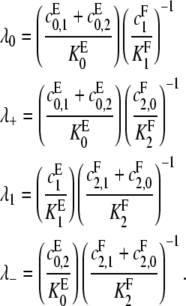(11)

When the kinase is distributive, so that 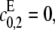λ₀ as defined in Eq. 11 reduces to λ₀ as defined in Eq. 4 for the distributive case and similarly for λ₁ when the phosphatase is distributive. The parameters λ₊ and λ₋ are specific to the processive case. Since we have assumed that eithe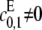r or 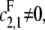it follows that λ₊ > λ₋.

Solving for [S₂]/[S₁] and [S₀][S₁] in Eqs. 9 and 10, we find that

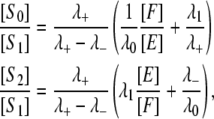(12)

from which it follows that

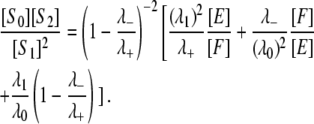(13)

Distinguishing distributive from processive

Equation 13 provides a way to distinguish between the four possibilities for the mechanism of action of E and F. However, although the experimentalist can control [E_tot], [F_tot], and [S_tot] and measure [S₀], [S₁], and [S₂], the quantities [E] and [F] are determined by the dynamics of the system and cannot readily be measured or controlled. The second formula in Eq. 12 shows that [E]/[F] is a linear function of [S₂]/[S₁] and the latter can be measured. To exploit this, it is helpful to further simplify the algebra. Let

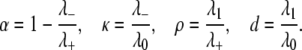(14)

Note that 1 − α = κρ/d. If the kinase is distributive then 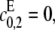λ₋ = 0, and κ = 0; if the phosphatase is distributive then 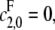λ₊ = ∞, and ρ = 0; since λ₊ > λ₋, 0 < α ≤ 1 and if either kinase or phosphatase is distributive then α = 1; d reverts to the value that [S₀][S₂]/[S₁]² has when both enzymes are distributive. Let x = [S₂]/[S₁]. Substituting for [E]/[F] in terms of x in Eq. 13, we find that

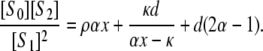(15)

Note from the second equation in Eq. 12 that αx − κ > 0. There are four cases to consider.

E distributive, F distributive

In this case κ = ρ = 0 and α = 1. Hence, [S₀][S₂]/[S₁]² = d, in accordance with Eq. 5. It does not change with x.

E distributive, F processive

In this case κ = 0 and α = 1. Hence, [S₀][S₂]/[S₁]² = ρx + d, which increases linearly with x. When graphed, this gives a straight line whose intercept on the vertical axis is d, the value that [S₀][S₂]/[S₁]² would have if F were distributive with a catalytic rate of 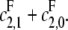The slope of the graph is

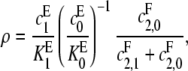which increases hyperbolically with increasing 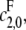the catalytic rate for producing S₀ from S₂. In particular, no matter how processive F is (that is, no matter how small 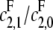is), the slope of the graph cannot exceed the ratio of the catalytic efficiencies of E at sites 1 and 0. If this latter number can be estimated, then measurement of the slope gives an estimate of the degree of processivity of F, 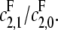In particular, full processivity of the phosphatase, where 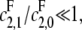can be detected.

E processive, F distributive

In this case, ρ = 0 and α = 1. Hence, [S₀][S₂]/[S₁]² = κd/(x − κ) + d. When graphed, this gives a hyperbola, whose singularity occurs at

This point increases hyperbolically with increasing 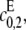the catalytic rate for producing S₂ for S₀. In particular, it can never exceed the ratio of the catalytic efficiencies of F at sites 1 and 2. If this number can be estimated, then measurement of the position of the singularity gives an estimate of the degree of processivity of the kinase, 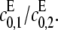In particular, full processivity, where 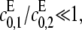can be detected. The asymptote as 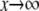is d, the value that [S₀][S₂]/[S₁]² would have if E were distributive with a catalytic rate of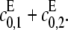

E processive, F processive

In this case, the right-hand side of Eq. 15 defines a function whose graph first decreases as x increases away from x = κ/α but then increases as 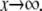It has a singularity at x = κ/α and a minimum at

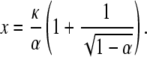The ratio of the position of the minimum to the position of the singularity gives an estimate of α, which then allows κ to be recovered. The minimum value is 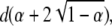which allows d to also be estimated.

Provided a sufficiently broad range of [S₂]/[S₁] values can be obtained by varying the total concentrations and initial conditions then not only can the mechanisms of action of E and F be deduced but values of the relevant compound parameters in Eq. 14 can also be estimated, without the need for any fitting.

Fig. 1 shows the graphs of [S₀][S₂]/[S₁]² against [S₂]/[S₁] for four systems in which all nonzero catalytic constants are 1 and all Michaelis-Menten constants are 1 (units may be chosen arbitrarily provided they are consistent between the two sets of constants). When both enzymes are processive the parameter values in Eq. 15 are

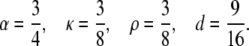Fig. 1 shows how easily the different cases can be distinguished by qualitative comparison and how the parameters can be quickly estimated, as described above.

DISCUSSION

Experimental determination of distributivity or processivity has been based on time course experiments. If the rate of production of highly phosphorylated phospho-forms is unchanged as the concentration of unphosphorylated substrate is increased or if production of highly phosphorylated phospho-forms cannot be interrupted by a competitor, that provides evidence for a highly processive mechanism (21–25). Although these methods can detect processivity, additional experiments are usually required at either end of the processivity scale, when the system is distributive or fully processive (22).

The method introduced in this article has several advantages. 1), Only a single set of steady-state measurements is required, using both kinase and phosphatase. If only one of the enzymes is of interest, the other can be chosen arbitrarily. 2), It gives the mechanism of both kinase and phosphatase simultaneously. 3), Classification of the mechanisms is by qualitative distinctions in the shapes of graphs, as in Fig. 1. 4), It does not require careful control of initial conditions or concentrations, which may be chosen in any convenient way to generate a broad range of [S₂]/[S₁] values. 5), It does not require additional experiments at the distributive end of the processivity scale, irrespective of the mechanism of the other enzyme. 6), The degree of processivity of one of the enzymes can be quantitatively determined without the need for any fitting, provided that site-specific catalytic efficiencies of the other enzyme can be estimated. In this case, full processivity of the first enzyme can also be determined. 7), Once the site-specific catalytic efficiencies have been estimated for one standard kinase or phosphatase, they can be used in conjunction with any cognate phosphatase or kinase, respectively. 8), In all cases, the relevant compound parameters in Eq. 15 can be estimated without the need for any fitting.

The results of this article focus attention on two principles: first, the importance of studying multisite phosphorylation as a system, with both kinase and phosphatase present. Although this is always the case in vivo, in vitro studies, with the notable exception of recent work in extracts (12), have customarily focused on each enzyme individually. Second, there are polynomial invariants at steady state, which encode useful information about enzyme mechanisms. Further development of these ideas must confront both experimental and theoretical challenges.

The experimenter must deal with two issues. First, as mentioned, steady states need to be generated. Bringing kinase and phosphatase together creates a futile cycle, which churns ATP. The resulting buildup of ADP and inorganic phosphate can poison the reactions, effectively compromising the biochemical scheme in Eq. 2. A similar problem is experienced in high-throughput in vitro translation systems for which a remedy was found by using reaction chambers separated from a larger buffer volume by a dialysis membrane, thereby allowing dilution of reaction products (26). In our laboratory, we are adapting a commercial in vitro translation system for multisite phosphorylation studies, which we expect to give improved reproducibility of steady states.

Second, given a substrate with n sites, it is necessary to distinguish and quantify all 2ⁿ potential phospho-forms. Although antibodies are frequently used to detect phosphorylation, they can be ill-suited to distinguishing phosphorylation patterns. For instance, Erk2 (the p42 MAP kinase) is one of the most frequently studied phospho-proteins. It is doubly phosphorylated on threonine (T) and tyrosine (Y) in a three residue T-Y motif in its activation loop. Although commercial antibodies exist to the intermediate phospho-forms, (pT)-Y and T-(pY), we have found that they show unacceptable cross-reactivity on quantitative Western blots. (In contrast, antibodies against the maximally phosphorylated phospho-form, (pT)-(pY), and the unphosphorylated substrate, T-Y, are much more specific.) Mass spectrometry (MS) holds much promise for phospho-protein analysis (7,10,27). One problem with MS, as with other forms of protein separation such as isoelectric focusing, is that different phospho-forms may have the same mass/charge ratios. Moreover, since proteins must first be digested into peptides, even if the phospho-peptides can be distinguished, the phospho-proteins still have to be deconvoluted from the phospho-peptides. We believe that a combination of isoelectric focusing, followed by high-performance liquid chromatography and tandem MS, will be able to distinguish and quantify all 2ⁿ phospho-forms on a substrate with n sites, for low values of n. We are developing such a protocol in collaboration with Hanno Steen.

On the theoretical side, it turns out to be surprisingly awkward to extend the results of this article to n > 2 or to nonsequential systems. The latter would be most useful initially, because, even for n = 2, it brings important biological examples within the scope of our methods.

Of the two assumptions made in our analysis, degrees of processivity in posttranslational modification are well attested in the literature. Both distributive and processive enzymes are known and these properties can significantly impact cellular regulation (14,28,29). Phosphorylation of Erk2 by the MAP kinase kinase Mek is distributive (22,23), as is dephosphorylation of Erk2 by the phosphatase MKP3 (30). The p38 MAP kinase also doubly phosphorylates the transcription factor ATF2 through a distributive mechanism (31). Phosphorylation of p130Cas on 15 sites by Src appears highly processive (24), as does phosphorylation of the alternative splicing factor ASF/SF2 on nine sites by serine-arginine protein-specific kinase SRPK1 (25). Phosphorylation of the phosphate regulator Pho4 on five sites by the Cyclin-CDK complex Pho80-Pho85 is partially processive, with an average of 2.1 phosphorylations per molecular encounter (21).

The other assumption, of sequentiality, has been less well documented. This assumption is commonly made in theoretical studies of multisite phosphorylation (14–18,32) (a recent exception being Salazar and Höfer (33)). Sequential kinases are certainly known. For instance, GSK3, in its mode of primed phosphorylation, phosphorylates SXXXS repeat motifs on several substrates in a strict C to N order (34). The receptor tyrosine kinase FGFR1 also auto-phosphorylates in a strict order (35). These examples suggest that cognate phosphatases may cooperate to maintain a sequential system of kinase, phosphatase, and substrate. However, no such phosphatase is currently known.

Nonsequential systems are more difficult to analyze because the calculations required are nonlinear. In broad terms, methods of algebraic geometry, rather than linear algebra, are needed. In joint work with Arjun Manrai, we have been able to show that a two-site system in which both kinase and phosphatase are distributive has the following invariant:

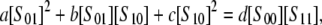(16)

where the subscript on S indicates which sites are phosphorylated and a, b, c, and d depend only on the rate constants. However, it remains unclear how this changes when one or both of the enzymes is processive and whether that change can be used to determine the degree of processivity. Erk2 is phosphorylated on its two activating sites by Mek and dephosphorylated by MKP3, both of which are known to be distributive, as mentioned above. The Mek, MKP3, Erk2 system would therefore provide a test of Eq. 16, provided the experimental issues discussed above can be resolved.

The case n > 2 presents similar difficulties. The steady-state equations corresponding to Eqs. 9 and 10 are no longer linear in the [S_i+1]/[S_i] and their reciprocals. Furthermore, with increasing numbers of sites, the nature of the processivity becomes more complicated. Is there a processivity bound, so that no more than k modifications are made in any encounter? If the system is nonsequential, can any pattern of modifications be made or does this depend on the pattern of modifications already made? Such questions can only be answered by detailed experiments on specific kinase, phosphatase, substrate systems. This is work in progress in our laboratory.

Multisite protein phosphorylation and dephosphorylation are key cellular regulatory mechanisms. We hope that the results of this article will encourage both theoreticians and experimentalists to further unravel their emergent complexity.