Transport direction determines the kinetics of substrate transport by the glutamate transporter EAAC1

Abstract

Glutamate transport by the excitatory amino acid carrier EAAC1 is known to be reversible. Thus, glutamate can either be taken up into cells, or it can be released from cells through reverse transport, depending on the electrochemical gradient of the co- and countertransported ions. However, it is unknown how fast and by which reverse transport mechanism glutamate can be released from cells. Here, we determined the steady- and pre-steady-state kinetics of reverse glutamate transport with submillisecond time resolution. First, our results suggest that glutamate and Na⁺ dissociate from their cytoplasmic binding sites sequentially, with glutamate dissociating first, followed by the three cotransported Na⁺ ions. Second, the kinetics of glutamate transport depend strongly on transport direction, with reverse transport being faster but less voltage-dependent than forward transport. Third, electrogenicity is distributed over several reverse transport steps, including intracellular Na⁺ binding, reverse translocation, and reverse relocation of the K⁺-bound EAAC1. We propose a kinetic model, which is based on a “first-in-first-out” mechanism, suggesting that glutamate association, with its extracellular binding site as well as dissociation from its intracellular binding site, precedes association and dissociation of at least one Na⁺ ion. Our model can be used to predict rates of glutamate release from neurons under physiological and pathophysiological conditions.

Glutamate transporters belong to the class of Na⁺-driven secondary-active transporters. They couple the uphill uptake of glutamate into cells to the movement of three Na⁺ ions down their ion concentration gradient (1). Neurons, like many other cells, express glutamate transporters, allowing them to keep a 10⁶-fold glutamate concentration gradient across their cell membranes (2). This steep concentration gradient is essential for neuronal signaling, because it ensures submicromolar resting concentrations of extracellular glutamate.

Glutamate transporters are not strictly unidirectional and are able to change the direction of glutamate transport (3). Under physiological conditions, forward transport from the extracellular side to the cytosol is favored. However, if the driving force for glutamate uptake decreases, glutamate can be released from cells through reverse glutamate transport (3, 4). This situation may arise in oxygen-deprived cells when the Na⁺ concentration gradient across the membrane runs down, and/or when cells depolarize. In ischemic neurons, the majority of glutamate release upon oxygen/glucose deprivation was shown to be caused by reverse glutamate transport and not by vesicular release (5, 6). Considering the severe neurotoxic effects of elevated extracellular glutamate concentrations, it is of major importance to understand the mechanism of how glutamate is released through reverse transport.

Here, we investigated with high time resolution the steady- and pre-steady-state kinetics of reverse glutamate transport by the neuronal glutamate transporter excitatory amino acid carrier 1 (EAAC1). We found that transport kinetics depend strongly on transport direction. At steady state, reverse glutamate transport is faster than forward transport but less voltage-dependent. Reverse transport also differed from forward transport in its Na⁺ dependence, suggesting a “first-in-first-out” mechanism for at least one of the cotransported Na⁺ ions. The pre-steady-state kinetics revealed four reverse-transport processes occurring on time scales ranging from 300 μs to ≈4 ms. Three of these processes were associated with the reverse-translocation process, indicating that glutamate can be released from cells rapidly, within milliseconds. We propose a kinetic model that can explain the experimental data.

Results

The Steady-State Kinetic Properties of EAAC1 Depend Strongly on Transport Direction.

We studied reverse glutamate transport by measuring transporter-associated currents in response to glutamate application to the cytosolic face of EAAC1-containing membranes. Inside-out patches from EAAC1-transfected cells responded to 5 mM glutamate with outward transport currents (not shown). The majority of patches (>80%) displayed currents with <10 pA (at 0 mV) and therefore were not practicable to measure. Because glutamate in addition activates an at least 2-fold larger anion current carried by SCN⁻ (thiocyanate) in inside-out patches (7), we used this anion current as a measure for the kinetic properties of EAAC1 reverse transport [Fig. 1; see discussion in supporting information (SI) Text on why the anion conductance can be used to assay transport activity]. In the presence of 140 mM extracellular SCN⁻, 5 mM glutamate induced an outward patch current of 29 ± 15 pA (Fig. 1A, n = 20, V = 0 mV), which is a sum of transport and anion current components. These currents are not seen in nontransfected cells (Fig. 1 A and B).

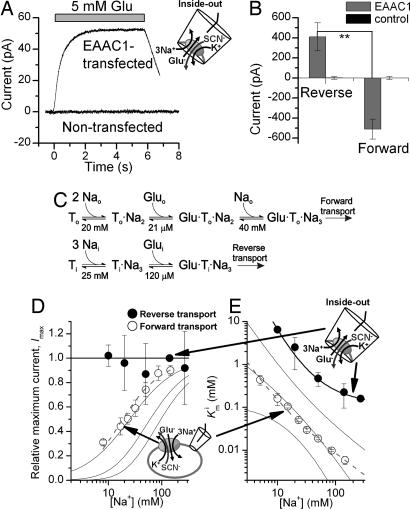
Fig. 1.

The steady-state kinetic properties of the EAAC1 anion current depend on the direction of glutamate transport. (A) Typical traces of anion currents evoked by the application of 5 mM glutamate (indicated by the bar) to inside-out patches from an EAAC1-transfected cell and a nontransfected cell. (B) Average whole-cell anion currents at saturating [glutamate] in EAAC1-expressing cells and nontransfected cells. In the reverse transport mode, glutamate was applied by intracellular photolysis, as detailed in Fig. 5A. (C) Proposed Na⁺-glutamate binding sequences in the forward and reverse transport modes. (D and E) The maximum anion current at saturating glutamate concentrations and the apparent K_m for glutamate are plotted as a function of [Na_i⁺] (reverse mode, closed circles) and [Na₀⁺] (forward mode, open circles). The solid lines represent calculations according to the possible Na⁺-Glu-binding sequences as described in SI Text. The thick solid and dashed lines represent the best approximations of the experimental data according to the Na⁺-Glu-binding sequences and parameters (K_m values) shown in C for reverse and forward transport, respectively. The solutions contained 140 mM NaMes on the cis-side and 140 mM KSCN on the trans-side of the membrane, respectively (all at V = 0 mV).

In the forward transport mode, both the apparent dissociation constant (K_m^o) of EAAC1 for glutamate and the maximum glutamate-induced anion current depend strongly on the extracellular [Na⁺] ([Na_o⁺]) [SI Fig. 7 (8)]. Consistent with this, the dose–response curve of glutamate activation of the anion current in the reverse transport mode was shifted to the right at 20 mM [Na_i⁺], as compared with the control conditions of 140 mM Na_i⁺ (SI Fig. 7), indicating that the apparent dissociation constant of glutamate from its intracellular binding site, K_mⁱ, also depends on [Na_i⁺]. As expected, K_mⁱ values are 20- to 40-fold larger for reverse transport than the K_m^o for forward transport (7). In contrast to the K_m values, the maximum glutamate-induced anion current, I_max, determined at saturating [glutamate_i] was independent of [Na_i⁺] (SI Fig. 8). This result indicates a strong asymmetry of the Na⁺ activation kinetics of the anion current, depending on to which side of the membrane Na⁺ is applied.

Therefore, we determined K_mⁱ and the I_max values over a range of [Na⁺] (Fig. 1 D and E). I_max was independent of [Na_i⁺] down to a concentration of 10 mM (we were unable to reach I_max at [Na_i⁺] lower than 10 mM because of the high K_mⁱ at such low concentrations). In contrast, K_mⁱ strongly depended on [Na_i⁺] in the same concentration range, increasing 41-fold from 270 to 10 mM Na_i⁺. Whereas log(K_m^o) showed an almost linear relationship with log[Na_o⁺] (slope = −1.3 ± 0.04), this relationship was curved for the log(K_mⁱ) vs. log[Na_i⁺] plot (Fig. 1E). The [Na_i⁺] independence of I_max may indicate that Na_i⁺ activates the anion current with a very high apparent affinity (<2 mM) as proposed in ref. 3. However, this explanation is unlikely because of the strong [Na_i⁺] dependence of K_mⁱ. Alternatively, I_max may be independent of [Na_i⁺], because saturating concentrations of glutamate lock all of the cotransported Na⁺ ions into their cytoplasmic binding site. This would be consistent with a model in which glutamate can bind to its cytoplasmic binding site only once all cotransported Na⁺ ions are bound to EAAC1, as illustrated in Fig. 1C. Calculations according to this second possibility and alternative models are shown as solid lines in Fig. 1 D and E and are detailed in SI Text.

Cytosolic Na⁺ Binding to the Empty Transporter Is Electrogenic.

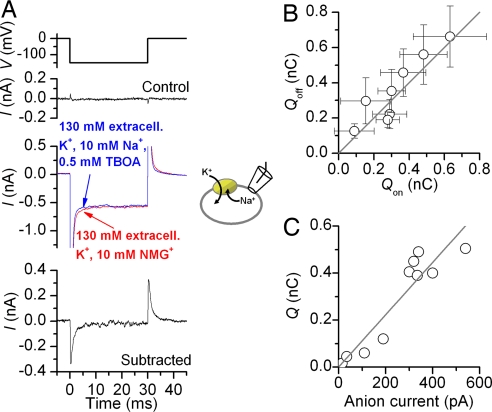
When Na⁺ binds extracellularly, it moves through part of the membrane electric field (8–11). Because at least two Na⁺-binding sites of the glutamate transporter are assumed to be buried in the membrane (12, 13), cytoplasmic Na⁺ may also move through parts of the transmembrane electric field. To test this hypothesis, we performed voltage-jump experiments to rapidly change the electrical driving force for cytoplasmic Na⁺ association with EAAC1, while forcing the Na⁺-binding site(s) to face the cytoplasmic side (using 130 mM extracellular K⁺). Stepping the voltage from 0 to −150 mV resulted in EAAC1-specific inwardly directed transient currents (Fig. 2A, red trace), in addition to a large background of unspecific current. The magnitude of the unspecific currents depends on the seal quality and the existence of non-EAAC1 conductances also present in nontransfected cells. A small but significant part of this transient current was inhibited in the presence of the nontransportable blocker, DL-threo-β-benzyloxyaspartate (TBOA) (14) (Fig. 2A, blue trace), locking the transporter in the TBOA-bound state (see SI Fig. 7). Subtraction of the current in the presence of TBOA from that in its absence yielded the EAAC1-specific current component (Fig. 2A Bottom), eliminating effects of the nonspecific background current. Although block of EAAT2 currents by kainate is voltage-independent (11), a possible small-voltage dependence of TBOA block of EAAC1 should not affect interpretation of the data, because the [TBOA] was supersaturating at 0.5 mM (1,000-fold K_i). Thus, the TBOA block should be 100% within the voltage range studied. When the membrane potential was returned to 0 mV, the cell responded with a transient outward current, which carried the same charge, Q, as the initial inward current (Fig. 2B), indicating that the charge movement is of capacitive nature. Q correlates well with the glutamate-induced anion current recorded from the same cells (Fig. 2C), indicating that the transient current is specifically carried by EAAC1.

Fig. 2.

Voltage jumps to EAAC1 produce transient currents when the Na⁺-binding site is exposed to the cytosplasm. (A) Extracellular TBOA (0.5 mM) inhibits transient charge movement in response to a voltage jump (compare red and blue traces). The voltage-jump protocol is shown (Top). Subtraction of the blue trace from the red trace yields the EAAC1-specific charge movement (Bottom). (B) The total charge, Q, moved in the off response equals that in the on response. (C) Q of individual cells scales with the magnitude of the exchange anion current. The exchange anion current was measured in the presence of 140 mM NaSCN and 0.2 mM glutamate (extracellular). Charging times for the membrane were 150 μs.

The transient current measured in response to voltage jumps may be caused by the association of intracellular Na⁺ with EAAC1. To test this, we measured the [Na_i⁺] dependence of Q (SI Fig. 9). The midpoint potential of this charge movement changed with [Na_i⁺], as expected for a Na_i⁺-dependent binding process with an apparent valence of z_Q = 0.29 (detailed in SI Text).

Reverse Steady-State Transport by EAAC1 Is Faster Than Forward Transport, but Less Voltage-Dependent.

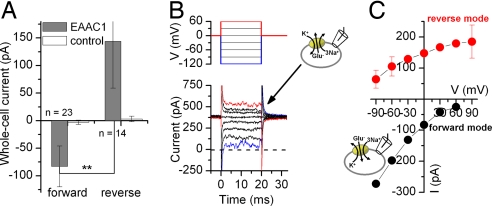
To measure reverse transport current, which should be proportional to the reverse-transport rate, we trans-inhibited reverse transport by applying TBOA to the extracellular (trans) side of the membrane (10 mM [glutamate_i]). Currents measured in the absence of TBOA were then corrected by subtraction with unspecific currents in the presence of TBOA to obtain the EAAC1-specific reverse transport current (Fig. 3 A and B). When the average reverse transport currents were compared with forward transport currents, the reverse transport currents were significantly larger (at V = 0 mV, Fig. 3 A and C; Student's t test P value = 0.005). These data indicate that the same driving force applied in opposite directions across the membrane results in reverse glutamate transport being faster than forward glutamate transport.

Fig. 3.

Reverse glutamate transport is faster than forward glutamate transport and is less voltage-dependent. (A) Average transport currents in the forward and reverse transport modes in EAAC1-transfected and nontransfected control cells (V = 0 mV). Intracellular glutamate was applied by photolysis from caged glutamate, as detailed in Fig. 5A. (B and C) Voltage dependence of steady-state transport currents in the reverse (red circles) and forward modes (black circles). Transport currents were induced by voltage jumps (B Upper) for voltage protocol. B Lower shows typical original data in the reverse mode obtained by subtraction of currents in the presence of 130 mM K⁺, 10 mM Na⁺, and 0.5 mM TBOA in the external solution from those in the presence of 130 mM K⁺ only. The counterion was Mes⁻.

Na⁺-driven transporters can show dramatically different voltage dependencies of substrate forward and reverse transport (15). Therefore, we determined the voltage dependence of the EAAC1 reverse transport current (Fig. 3C). Reverse glutamate transport was significantly less voltage-dependent (varying 3-fold from +60 to −90 mV) than forward transport (31-fold variation). Furthermore, the reverse transport current leveled off at increasingly positive potentials (V > 0 mV), indicating that transport becomes rate-limited by a weakly electrogenic process. In contrast, the forward transport current does not show any tendency to level off with increasing electrical driving force (apparent valence = 0.74; Fig. 3C, black circles). Rate limitation of reverse transport by an electroneutral step was also seen at 50 mM intracellular Na⁺ (SI Fig. 10), whereas at 20 mM [Na⁺]_i, the current voltage relationship was linear. These reverse transport data (Fig. 3C, four times slower than forward transport at −90 mV) agree well with a previous report on glutamate exchange by EAAT2, which is ≈2 times slower for reverse than for forward exchange at −88 mV (16).

Pre-Steady-State Kinetics in the Reverse Transport Mode.

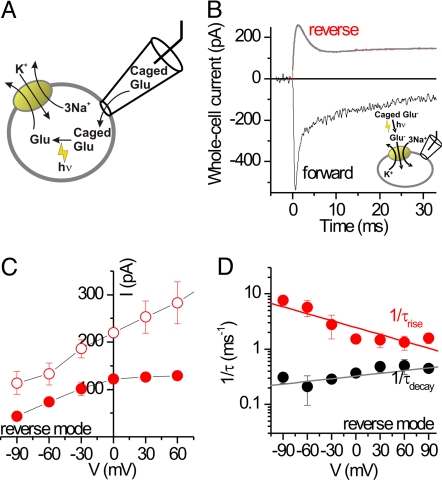
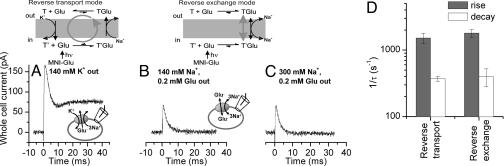
In the forward transport mode, determination of EAAC1 pre-steady-state kinetics revealed a wealth of information on the glutamate transport mechanism (8, 17–20). Here, we used the same laser photolysis approach as applied previously (8, 18), however in the reverse transport mode (Fig. 4A). Inactive caged glutamate [4-methoxy-7-nitroindolinyl (MNI)-glutamate (21)] entered the cell by diffusion from the recording pipette (Fig. 4A; SI Fig. 11), and free glutamate was released on the intracellular side by photolysis, rapidly activating reverse transport current (Fig. 4B). Control experiments revealed no effects on EAAC1 either of MNI-glutamate (SI Fig. 7) or of the laser pulse alone. The reverse transport current showed a significant pre-steady-state overshoot component (Fig. 4B, red trace). In contrast to the inward pre-steady-state current in the forward transport mode (Fig. 4B, black trace), which decayed with biphasic kinetics, the outward pre-steady-state current decayed with only one phase but relaxed to the steady state with a time dependence resembling a damped oscillation. The current could be fit with a sum of three exponentials with time constants of 0.6 ± 0.1 ms for the rising phase, 2.7 ± 0.1 ms for the decaying phase, and 6.3 ± 0.5 ms for the return of the damped oscillation to the steady state (all n = 10). This demonstrates that at least three fast reverse transport processes precede steady-state outward transport of glutamate.

Fig. 4.

The pre-steady-state kinetics of reverse glutamate transport differ from those in the forward transport mode. (A) Illustration of the rapid delivery of glutamate to the cytosolic face of the membrane by laser photolysis of intracellular caged glutamate. (B) Typical currents in response to photolysis of caged glutamate applied to the intracellular (reverse transport, 6 mM MNI-Glu) and extracellular sides (forward transport, 1 mM MNI-Glu) at t = 0 ms (V = omV). The smooth line represents a fit to a sum of three exponentials plus a current offset, as explained in the text. (C) Voltage dependence of the photolysis-induced reverse transport current at the peak of the response (open circles) and at steady state (closed circles). (D) Voltage dependence of the relaxation rate constants for the transport current rise and decay in the reverse transport mode. All experiments were performed in the whole-cell configuration with 140 mM Na⁺ on the cis-side and 140 mM K⁺ on the trans-side of the membrane, respectively.

In line with data from voltage jumps, the steady-state outward current started leveling off at membrane potentials >0 mV (Fig. 4C, closed circles; original data in SI Fig. 13), indicating rate limitation by an electroneutral or only weakly voltage-dependent process. In contrast, the peak outward current increased monotonically with increasing electrical driving force (Fig. 4C, open circles). The voltage dependencies of the relaxation rate constants for the three phases of the reverse transport current are shown in Fig. 4D. Whereas the rate associated with the rising phase decreased with increasing membrane potential (equivalent to an apparent valence of the underlying reaction, z_Q, of −0.45 ± 0.09), the rate associated with the decaying phase had an opposite and weaker voltage dependence (z_Q, = 0.20 ± 0.02). The relaxation rate associated with the return of the damped oscillation to the baseline was basically independent of the voltage (not shown), indicating that the underlying transporter process is electroneutral.

Pre-Steady-State Currents in the Reverse Transport Mode Are Associated with the Glutamate-Dependent Half-Cycle.

Kinetically, the overall transport cycle can be separated into two independent branches, the glutamate/Na⁺ translocation branch and the K⁺ relocation branch. In the forward transport mode, glutamate translocation was proposed to be associated with inward charge movement (8, 16). To isolate the glutamate/Na⁺-dependent branch of the transport cycle, we performed glutamate concentration jump experiments in the reverse exchange mode (see Fig. 5 A–C, at the top). To establish this mode, high concentrations of Na⁺ and glutamate were used on the extracellular side in the absence of extracellular K⁺ to ensure that the majority of transporter-binding sites were initially exposed to the cytoplasm (8). Subsequent rapid application of mM [glutamate_i] led to a redistribution of states in the glutamate/Na⁺ translocation branch, which was associated with transmembrane charge movement (Fig. 5B). When compared with the transient component of the reverse transport current in the presence of extracellular K⁺, which carried a charge of 500 fC (in the specific cell of Fig. 5), the exchange current was smaller with a total charge movement of 240 fC. Generally, the charge associated with the transient current was 1.65 ± 0.4 larger in the reverse transport mode than in the exchange mode (n = 3). This suggests that some of the rapid charge movement in the reverse transport mode is caused by extracellular dissociation of Na⁺ and/or substrate, which should be inhibited in the exchange mode. To make sure that extracellular Na⁺ and/or substrate inhibition is, in fact, inhibited in these experiments, we raised the extracellular [Na⁺] to 300 mM (Fig. 5C), which should fully saturate the extracellular Na⁺-binding site of the glutamate-bound transporter [K_m = 22 mM (8, 13)]. The total glutamate-induced charge movement was 230 fC (for the cell shown in Fig. 5), showing that the increased extracellular [Na⁺] did not further inhibit the charge movement. Together, these results demonstrate that charge movement is associated with intracellular Na⁺ association and/or reverse glutamate translocation.

Fig. 5.

Outward charge movement is associated with the glutamate-dependent half-cycle and is not caused by extracellular Na⁺/substrate dissociation. (A) Reverse transport current induced by photolysis of 6 mM MNI-Glu at t = 0 ms (140 mM KMes external). (B and C) Transport currents recorded from the same cell as in A in the reverse exchange mode in the presence of 0.2 mM glutamate and 140 mM (B) and 300 mM Na⁺ (C) external. (D) Relaxation rate constants associated with the rise and decay of the current in the reverse transport and reverse exchange modes. All experiments were done at V = 0 mV. At the top is an illustration of the transport and exchange mode used in these experiments.

The above results suggest that the rapid glutamate-induced charge movements in the reverse transport and exchange modes reflect similar state transitions in the EAAC1 transport cycle. Thus, we determined the relaxation time constants associated with the exchange current. The time constant for the rising phase was 0.6 ± 0.1 ms (n = 6), and that for the decaying phase was 2.7 ± 0.8 ms (n = 6). These time constants are similar to those observed in the reverse transport mode (Fig. 5D), indicating similarity of the underlying transport reactions. Interestingly, the third phase observed in the reverse transport mode (return of the damped oscillation to the steady state) was not present in the exchange current, suggesting that it is associated with extracellular Na⁺/substrate dissociation and/or K⁺-induced completion of the transport cycle.

A Simplified First-In-First-Out Model Can Explain the Experimental Data.

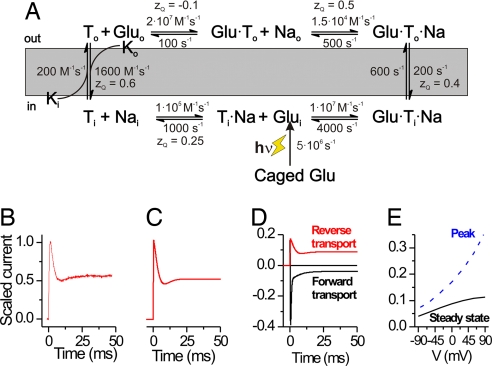
In our simplified kinetic scheme based on a first-in-first-out mechanism (Fig. 6A), one of the three cotransported Na⁺ associates first with EAAC1 on the cytoplasmic side (before glutamate_i binding) and dissociates first from its extracellular binding site (before glutamate_o dissociation). For simplicity, the additional two cotransported Na⁺ ions and the cotransported proton were not included into the scheme, and the K⁺-induced relocation reaction was lumped into one bimolecular step. To account for the weak voltage dependence of the reverse transport kinetics, we distributed electrogenicity over a number of weakly voltage-dependent reaction steps, including intracellular Na⁺ binding, reverse glutamate translocation, extracellular Na⁺ dissociation, and relocation of the empty transporter. We cannot rule out that other partial reactions not included in the scheme are also voltage-dependent, because the total charge transported per cycle is +2, whereas the total charge from the scheme in Fig. 6 is +1.65. However, these additional electrogenic reactions are probably fast and do not contribute to the overall voltage dependence of the pre-steady-state kinetics. In the forward transport mode, the K⁺-induced relocation reaction is predicted to be the single rate-limiting step for overall transport (16–18). In contrast, our model predicts that at 0 mV, three steps contribute to the rate limitation in the reverse transport mode, including reverse relocation, reverse translocation, and possibly extracellular glutamate dissociation. Because of this difference in the rate limitation, the turnover rate at 0 mV is predicted to be larger in the reverse transport mode (55 s⁻¹) than in the forward transport mode (24 s⁻¹), given identical but opposite glutamate, Na⁺, and K⁺ concentration gradients. The model predicts the experimentally observed behavior at pre-steady state and steady state, including the oscillatory time response of the transport current (Fig. 6 B and C), the time dependence of the transport current in the forward transport mode (Fig. 6D), and the leveling off at positive potentials of the current–voltage relationship of the steady state but not the peak current (Fig. 6E). The model also predicts the exchange mode behavior.

Fig. 6.

Kinetic scheme and numeric simulations of glutamate reverse and forward transport. A simple kinetic model based on a “first-in-first-out” mechanism can explain the experimental data (A). (B and C) Experimental reverse transport current (left trace, B), scaled to a peak amplitude of 1 is compared with results from numeric simulations (right trace, C) according to the scheme shown in A. (D) Simulation of reverse and forward transport current under conditions that match the experiments in Fig. 5B. (E) Simulated voltage dependence of the reverse transport current at the peak of the response and at steady state (data are shown in Fig. 4C).

Discussion

Glutamate release from cells through the reversal of plasma-membrane glutamate transporters is an important process that is thought to account for the majority of glutamate release in the brain after oxygen-glucose deprivation (5, 6). Nevertheless, our knowledge of the kinetics and the mechanism of reverse transport of glutamate is limited because of the difficulty of applying glutamate to the intracellular side of the membrane. Here, we have used current recordings from inside-out patches together with rapid solution exchange (time resolution, 100–200 ms) and from whole cells after ultrafast application of glutamate by photolysis from intracellular caged glutamate (time resolution, ≈20 μs), to determine the kinetics and the mechanism of reverse glutamate transport.

The major findings of this study can be summarized as follows: (i) Glutamate association with its intracellular binding site requires that the binding sites for all three cotransported Na⁺ ions be occupied. This is in contrast to the binding sequence from the extracellular side, in which one or two occupied Na⁺-binding site(s) are required for glutamate binding, whereas the remaining cotransported Na⁺ ion(s) associate then with the glutamate-bound transporter (8, 22). Together, these results indicate that glutamate and at least one of the cotransported Na⁺ are moved across the membrane in a “first-in-first-out” mechanism, i.e., glutamate binds first extracellularly, followed by binding of the Na⁺ ion and translocation, followed by initial dissociation of glutamate and the subsequent dissociation of Na⁺ to the cytosol (Fig. 6A). Because [glutamate_i] in neurons can reach millimolar levels, it appears counterintuitive that glutamate dissociates first into the cytosol, locking EAAC1 in a glutamate exchange mode. However, our data predict that glutamate_i binds to EAAC1 weakly in the presence of physiological cytosolic [Na⁺] (K_mⁱ > 100 mM), indicating that glutamate dissociation to the cytosol is irreversible and forward transport will still take place. Because of this high K_mⁱ for glutamate in the absence of Na_i⁺, our model is also consistent with previously published data showing an effect of intracellular glutamate on anion current kinetics in the presence of intracellular Na⁺, but not K⁺ (18). Based on these data, Otis and Jahr (19) proposed that at least one Na⁺ must unbind before glutamate dissociates into the cytoplasm. (ii) Glutamate transport at steady state is faster in the reverse than in the forward transport mode. This difference in the rates in the two transport directions is caused by a difference in rate limitation. Whereas forward transport is strongly rate limited by one single reaction step, the K⁺-induced relocation (17, 18), the reverse transport rate is limited by a number of reactions, including the K⁺-induced relocation, glutamate reverse translocation, and possibly glutamate dissociation to the extracellular solution. Our model (Fig. 6A) reproduces these differential turnover rates in the forward and reverse modes without violating the thermodynamic principles of detailed balancing. (iii) The kinetic properties and voltage dependence of glutamate transport strongly depend on the transport direction. (iv) As found for the forward transport mode (7), electrogenicity of reverse glutamate transport is spread over several individual reaction steps in the transport cycle, all of which are relatively weakly voltage-dependent (Fig. 6A). Our results suggest that intracellular Na⁺ binding, reverse glutamate translocation, extracellular Na⁺ dissociation, and K⁺-induced reverse relocation are electrogenic in the reverse direction. We placed only weak voltage dependence on extracellular glutamate dissociation (z_Q = −0.1).

Our results suggest that reactions associated with the glutamate translocation reaction and most likely the translocation reaction itself are electrogenic. This interpretation is consistent with results of previous work on the glutamate translocation step in the forward mode, which was found to be voltage-dependent (8, 16, 18). Furthermore, the deactivation of the anion current in response to extracellular glutamate removal in the exchange mode of EAAT2 is voltage-dependent (16). This deactivation most likely represents reequilibration of the glutamate translocation equilibrium, resulting in the majority of the binding sites facing the extracellular side. Our data agree well with these EAAT2 results.

The kinetic model (Fig. 6A), although very simplified, reproduces the majority of the experimental results obtained in the reverse transport direction. It also reproduces some of the key data in the forward transport mode, such as the time and voltage dependencies of transport and anion currents. The kinetic model can be used to predict the behavior of EAAC1 to be tested in future experiments, as detailed for the following two examples: (i) The model predicts that when saturating concentrations of glutamate and Na⁺ are present on both sides of the membrane, as is typically the case in crystallographic experiments where ion and potential gradients across the membrane cannot be established, 75% of the transporters will be in the outward-facing configuration, whereas 25% will have inward-facing Na⁺ and glutamate-binding sites (at 0 mV). Therefore, it will be challenging to isolate EAAC1 in one specific conformational state in the absence of a transmembrane ion concentration gradient. Thus, to isolate specific conformational states, mutant transporters may have to be used that stabilize either the outward- or the inward-facing configuration. The bacterial glutamate transporter homologue GltPh was crystallized in what appeared to be an outward-facing or occluded conformation (12, 23). In contrast to EAAC1, GltPh therefore seems to prefer one conformational state over the other, suggesting a strongly asymmetric translocation equilibrium. Interestingly, our kinetic model predicts a reversal of the conformational preference in the presence of symmetrical and saturating concentrations of K⁺. Under these conditions the inward-facing configuration is predicted to be strongly favored by a factor of 8:1. (ii) The model can be used to predict the kinetics of glutamate release from EAAC1-expressing cells upon depolarization. Assuming a sudden arbitrary depolarization from −80 to −40 mV ([Na⁺]_i = 5 mM, [Na⁺]_o = 140 mM, [K⁺]_i = 140 mM, [K⁺]_o = 5 mM, [Glu⁻]_i = 5 mM, and [Glu⁻]_o = 1 nM), the steady-state release rate of glutamate (1.2 molecules per EAAC1 per second) is predicted to increase 20-fold at short times after the depolarization (SI Fig. 14) and also increases significantly as intracellular [Na⁺] and extracellular [K⁺] increase. Glutamate transporters are expressed at densities of 15,000–20,000/μm² in HEK293 cells (18), as well as in the vicinity of glutamatergic synapses (24). Thus, the large number of transporters present at the synapse may significantly and rapidly release hundreds of molecules of glutamate per millisecond and per micrometer² upon depolarization.

Conclusions

Our results present a kinetic framework for understanding the mechanism of glutamate release from cells through reverse transport by the neuronal glutamate transporter EAAC1. The results suggest that glutamate and at least one of the three cotransported Na⁺ ions associate and dissociate from EAAC1 in a first-in-first-out fashion. We also show that reverse glutamate transport at steady state is faster than forward transport, and that it is less voltage-dependent. The kinetic model presented not only explains the data here but also may be used for prospective experiments in view of structure predictions or the physiological role of reverse transport processes in the brain.

Methods

Molecular biology, transient expression of EAAC1 in HEK293 cells, and electrophysiological recordings of EAAC1 currents were performed as described in detail (13). In the forward transport mode experiments, the extracellular solution contained: 140 mM NaMes, 2 mM CaCl₂, 2 mM MgCl₂, and 30 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (Hepes), pH 7.3. In the reverse transport mode, NaMes was replaced by KMes. In the exchange mode, 0.2 mM glutamate was added to the Na⁺-containing extracellular solution. To measure anion currents, Mes⁻ was substituted by SCN⁻. The pipette solution contained 140 mM NaMes, 2 mM MgCl₂, 10 mM EGTA, and 10 mM Hepes, pH 7.4.

Rapid Solution Exchange and Laser-Pulse Photolysis.

Rapid solution exchange was performed as described (18). Rise times were 20–50 ms (10–90%) for whole-cell currents and 200–500 ms for inside-out patches, most likely because of the invagination of the patch resulting in delayed diffusion of compounds to the membrane. Laser-pulse photolysis experiments are detailed in SI Text.

Data analysis was performed as described in detail (8, 18). Simulations were performed by using Berkeley Madonna software by numerically integrating the differential equations pertaining to the reaction scheme shown in Fig. 6A, as described (8, 18).