Efficient and verified simulation of a path ensemble for conformational change in a united-residue model of calmodulin

Abstract

The computational sampling of rare, large-scale, conformational transitions in proteins is a well appreciated challenge—for which a number of potentially efficient path-sampling methodologies have been proposed. Here, we study a large-scale transition in a united-residue model of calmodulin using the “weighted ensemble” (WE) approach of Huber and Kim. Because of the model's relative simplicity, we are able to compare our results with brute-force simulations. The comparison indicates that the WE approach quantitatively reproduces the brute-force results, as assessed by considering (i) the reaction rate, (ii) the distribution of event durations, and (iii) structural distributions describing the heterogeneity of the paths. Importantly, the WE method is readily applied to more chemically accurate models, and by studying a series of lower temperatures, our results suggest that the WE method can increase efficiency by orders of magnitude in more challenging systems.

It has long been appreciated that conformational changes in proteins are critical to biological function. Examples including allosteric proteins like hemoglobin, enzymes like adenylate kinase, signaling proteins like calmodulin, and motor proteins like myosin are only the most famous textbook cases (1). The dynamic nature of biological processes observed from the organ level to the intracellular level is equally evident at the molecular level.

Traditional molecular simulations are limited to <100 ns (2), making them inadequate to the task of studying large conformational transitions in macromolecules, which may occur on microsecond to millisecond time scales or beyond (3). Yet, the situation is actually worse than it first appears: even if such long simulations could be achieved, the observation of a single transition event would hardly be a full scientific description of the process. Because structural transitions are driven in part by thermal fluctuations, some degree of variability among events must be expected, in turn requiring the observation of many events to draw statistically satisfactory conclusions. Indeed, a key unanswered question is, What degree of variation exists in biological transition dynamics? Experiments are only beginning to probe the details of transition variability (4). Therefore, the present work maintains a statistical viewpoint (5–8) as we explore pathways and variability in long-time protein dynamics. Such a statistical outlook has most famously been exploited in studies of protein folding paths (e.g., refs. 9–12).

Three basic approaches to the problem of long-time macromolecular dynamics have been explored by a number of investigators. Coarse-graining is probably the oldest strategy, dating from the very earliest molecular simulations (13, 14). By reducing the number of degrees of freedom, coarse-grained models of proteins can drastically reduce the intrinsic cost of simulating a time step, as well as increasing the duration of each step. The strategy has been pursued for many different problems over the years from protein folding to aggregation to conformational change (8, 15–27). Although coarse-grained models fail to capture atomistic detail and may have limited biochemical accuracy, recent work may permit the use of simplified ensembles in accelerating atomistic sampling (28, 29).

A second approach pursues a severe discretization of conformation-state space that enables the use of master-equation stochastic kinetics (30–32). Although an exact kinetic description can be obtained, a comprehensive and accurate discretization of configuration space is required. In other words, all states must be known with equilibrium probabilities and transition rates. Thus, at present, such a description is limited to cases where rather complete sampling can be obtained by some other means.

The third strategy, path sampling, is of greatest relevance to the present work. Path sampling approaches (5–7, 33–42) can, in principle, employ models of any level of detail, without approximation to the correct statistical mechanics. The potential for efficiency in these approaches stems from an extreme separation of time scales: rare events are rare because they are infrequent, not because the events are slow. As shown in Fig. 1, the duration of an event itself (denoted here as t_b) typically is orders of magnitude less than the associated waiting time between events (i.e., the first passage time or inverse rate k⁻¹), so that t_b ≪ k⁻¹ (5, 43). Path-sampling approaches make practical use of this separation by focusing computer resources exclusively on rare transition events, as opposed to random equilibrium motions that prove unproductive of transitions. We note that a number of ad hoc path-generating approaches have been developed for biological systems (38, 44–51), but these do not lead to properly distributed path ensembles or time scales. Many earlier efforts have also been directed to determining single, optimal paths (50, 52–58). Path-sampling approaches, it should be noted, have recently been applied to atomistic models of proteins and nucleic acids (38, 41, 42).

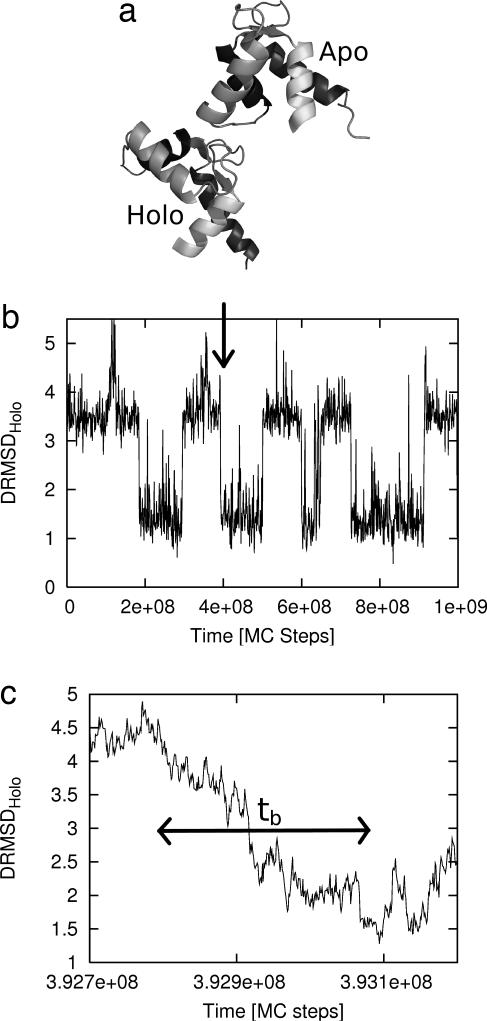
Fig. 1.

The N-terminal domain of calmodulin undergoes a large-scale structural change when it binds calcium. (a) The calcium-free Apo structure (1CFD) and the calcium-bound Holo structure (1CLL) are shown. (b) A sample trajectory from the simulation of the “double-native” Gō model of calmodulin exhibits several transition events, one of which is detailed in c. The approximate duration of the event t_b is indicated by the arrow.

Despite these important studies, a critical question remains: Do the path sampling methods work? That is, do they yield unbiased results that would be obtained with sufficient resources by means of brute-force simulation? Although the question has been answered in the affirmative for some toy models (36, 43, 59, 60), molecular systems include major difficulties not present in simpler cases. The present study appears to be unique among path-sampling investigations of proteins because we verify the results by comparison with brute-force simulations.

We study conformational transitions in a “double-native” Gō model introduced in ref. 8 and since adapted to other contexts (61–63). It is a united-residue model of calmodulin's N-terminal domain constructed to be stable in two highly distinct experimentally determined conformations (8), one corresponding to the calcium-bound state (Holo) and the other being calcium-free (Apo). These structures are depicted in Fig. 1. Despite its simplicity, the 72-residue model possesses 72 × 3 − 6 = 210 degrees of freedom and incorporates the basic conformational complexity of a protein. Calmodulin itself is an ideal system for our study: It is a key signaling protein involved in many cellular processes (e.g., ref. 64), it is small, and it exhibits a particularly large structural rearrangement.

We employ the “weighted ensemble” (WE) approach (36) to generate an unbiased ensemble of paths for the calmodulin transition and, simultaneously, the reaction rate. Previously, WE sampling has been applied to study diffusion effects in binding (36, 65) and the folding of a simple protein model (66). The WE method was chosen to investigate conformational transitions for three reasons. First, among path sampling algorithms, it is particularly elegant and straightforward to implement. Second, the WE method appears to be particularly well suited for sampling multiple, structurally distinct pathways in a statistically correct way. Third, it yields both a path ensemble and the reaction rate from a single simulation. The WE method embodies a strategy of replicating success (“enrichment”), which had earlier been introduced in the construction of polymer configurations (ref. 67; also see ref. 68). As illustrated in Fig. 2, the strategy has three essential steps and maintains a rigorous statistical weighting throughout: (i) initiation of multiple trajectories; (ii) replication of trajectories that advance along a progress coordinate; and (iii) occasional pruning of low-weight trajectories. The pruning ensures manageable computational cost. Issues surrounding the selection of a progress coordinate, which need not be a reaction coordinate in the traditional sense, are discussed in detail below.

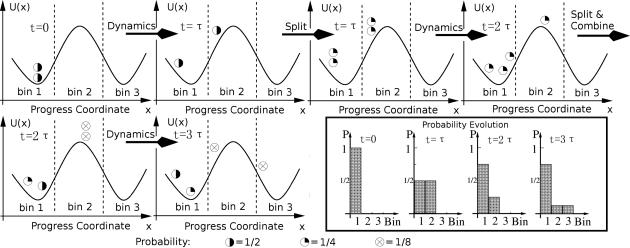
Fig. 2.

Schematic illustration of the WE method, using n = 3 bins and M = 2 simulations per bin following ref. 65. After initiating M trajectories, unbiased dynamics are simulated for a time τ, after which the locations (bins) are checked. Trajectories are split or combined to maintain M trajectories per bin, while preserving the correct probabilities in each bin. Dynamics are again initiated, and the process is repeated. The box at the lower right shows the corresponding evolution of the probability histogram.

Our data show that WE path-sampling of calmodulin transitions provides excellent quantitative agreement with brute-force results, which include substantial pathway heterogeneity. Because the WE simulations consume a fraction of the brute-force simulation time, they appear to be a promising choice for the study of more realistic protein models.

Results

To validate the WE method, we first considered the temperature k_BT/ε = 0.5 as in the previous study (8). As a reference for comparison, brute-force simulations were run on several CPUs, yielding 373 independent transition events from the Apo to Holo structure of our model of calmodulin. The total cost of these simulations is equivalent to ≈18 months of single-processor CPU time (Xeon, 3.2 GHz).

WE simulation, by contrast, required considerably less computer time, although identical code was used for running the embedded dynamical Monte Carlo (MC). The WE simulation was run on a single CPU (Xeon, 3.2 GHz) for 4 weeks, yielding 33,576 correlated transitions. We made the simple choice of using the distance RMSD (DRMSD) [see supporting information (SI) Text] (69) to the Holo state (DRMSD_Holo) as the progress coordinate and cut this one-dimensional space into 40 bins, with M = 40 simulations allowed in each bin. After every τ = 72,000 MC steps, the embedded brute-force simulations are paused, then combined and split without introducing bias, as described in Materials and Methods (also see Fig. 2).

Distribution of Event Durations.

We first studied the distribution of transition event durations ρ_b(t) (43, 70). The duration of a transition event is a short time scale characteristic of the reaction pathway itself (by contrast to the more common first-passage time). It is defined as the time elapsed from the last exit from the initial/reactant state until the first entry to final/product state (see Fig. 1). The distribution of these durations is the simplest quantitative measure of the heterogeneity expected in the ensemble of transition events. For conformational change in calmodulin, transition event durations were calculated based on a reactant state defined such that DRMSD_Apo < 1.5 Å and the product state by DRMSD_Holo < 1.5 Å.

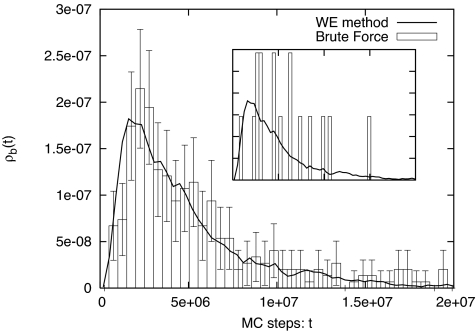
In Fig. 3, we show the WE simulation result for ρ_b(t) compared with that from brute-force simulation. They match well. Fig. 3 Inset shows results from the two methods using equal quantities of CPU time. It is clear that the WE method is more efficient than the brute-force simulation even at the relatively high temperature k_BT/ε = 0.5.

Fig. 3.

Distribution of transition event durations ρ_b(t) from WE and brute-force simulations. The event duration is the time interval between the last time a trajectory leaves the reactant state (DRMSD_Apo < 1.5 Å) and the first time it reaches the product state (DRMSD_Holo < 1.5 Å) (see Fig. 1). (Inset) Results from the two methods using equal amounts of CPU time, ≈4 weeks, which is not sufficient for brute-force simulation to obtain a good statistical distribution.

The Transition Rate.

For chemical and biological reactions and transitions, the reaction rate k is one of the most important quantities and is impossible to obtain by brute-force simulation if the first-passage time is long (71). Distinguished from other path-sampling methods, WE simulation yields not only the path ensemble but also the reaction rate simultaneously. In WE simulation, after a transient period reflecting the finite event durations, the average current arriving to the product state (Holo) gives the transition rate. For k_BT/ε = 0.5, we obtained k_WE = (1.9 ± 0.4) × 10⁻¹⁰ per MC step, which is in excellent agreement with the brute-force result, k_BF = (2.1 ± 0.2) × 10⁻¹⁰ per MC step.

Structural Cross-Sections of the Path Ensemble.

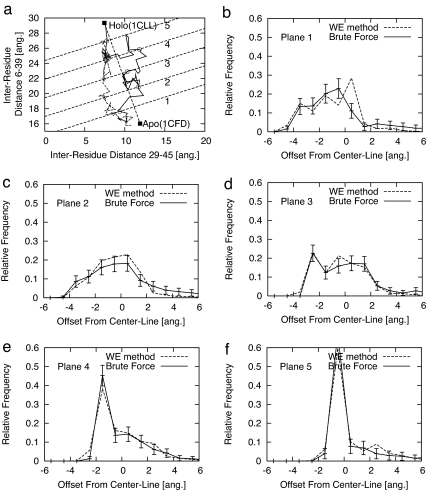
We also compared structural properties of the path ensembles generated by the two methods, following the approach taken in our previous work (8). Specifically, we examined the distributions of intermediate structures isolated along several “cross-sections” of a two-dimensional reaction surface. The two coordinates of this surface—each a distance between residues located at the ends of helices—were chosen to assay heterogeneity in the path ensemble (8). As shown in Fig. 4a, five cross-sectional “planes” were placed orthogonally to a straight line drawn between the two states. Histograms were made of the position, relative to the center line, at which each trajectory first crossed a given plane.

Fig. 4.

Structural distributions describing the heterogeneity of the path ensemble connecting the Apo and Holo states of calmodulin, based on both WE and brute-force simulations. a shows two sample Apo → Holo transitions, with open symbols indicating points at which the five parallel (dashed) “planes” are first crossed. Plots b–e show the ensemble-based distributions of the first crossing points of the paths on each of the five planes from a.

These cross-sectional histograms were produced by both simulation methods and again compare favorably. They also demonstrate the structural heterogeneity in the path ensemble of this simple model system. Fig. 4 b–e shows the distributions, with the error bars representing an ≈90% confidence interval. This sensitive structural analysis further underscores the accuracy of the WE method.

Efficiency.

The previous results indicate the accuracy of the WE approach—i.e., that it properly corrects for bias as claimed. Nevertheless, the “bottom line” measure of a path-sampling approach is its efficiency, and especially its potential for efficiency in more chemically realistic and larger systems. We measured efficiency by calculating the ratio of single-processor CPU times required by WE and brute-force simulations to estimate the reaction rate with a given statistical precision. Similar results are found if the average event duration is used.

By studying a range of lower temperatures to assay the promise of WE simulation in more challenging systems, we found very encouraging results. First, for the temperature studied above (k_BT/ε = 0.5), we found a modest efficiency gain of somewhat more than a factor of five; that is, WE simulation requires less than one-fifth of the CPU expenditure for a given level of statistical precision. However, as the system becomes more difficult to simulate by brute-force simulation at lower values of k_BT/ε, the WE approach becomes relatively more efficient. Equally importantly, the WE simulations require essentially the same overall amount of CPU time regardless of the temperature. For k_BT/ε = 0.45, we found an efficiency gain of a factor of ≈15, and for k_BT/ε = 0.4, it increased to ≈100.

In greater detail, for k_BT/ε = 0.45, 3 weeks of WE simulation yielded 32,464 correlated transition trajectories, along with the estimate k_WE = (6.4 ± 1.3) × 10⁻¹¹ per MC step. By contrast 30 months of brute-force simulation generated 172 trajectories and k_BF = (7.4 ± 1.2) × 10⁻¹¹ per MC step. The distributions of event durations also agree very well. For k_BT/ε = 0.4, the WE method gives the reaction rate k_WE = (8.4 ± 1.8) × 10⁻¹² per MC step from 3 weeks of simulation, whereas brute-force simulation was too slow to yield even a single transition event in the time we allotted to it. However, based on the reaction rate from WE simulation and the simple statistics of Poisson processes expected for brute-force simulation, the efficiency gain can be estimated as ≈100. (We also confirmed that such estimation based on Poisson statistics reproduced the efficiency estimates of the higher temperatures.)

Use of a Two-Dimensional Progress Coordinate.

To investigate whether the WE simulations for calmodulin were sensitive to the choice of progress coordinate—and also to explore potentially useful strategies for more complex systems—we investigated a two-dimensional progress coordinate. Specifically, we used two-dimensional bins where the first coordinate was the DRMSD_Holo distance as described in Materials and Methods, and the second coordinate was DRMSD_Apo. Our results were essentially indistinguishable from those based on a one-dimensional coordinate for the k_BT/ε = 0.5 condition we investigated.

Although using DRMSD_product as a single coordinate might be expected to be a fairly robust choice for many systems, generally one cannot expect a single dimension to be sufficient because there could be barriers transverse to the chosen coordinate (59) (i.e., free energy saddle points within a single bin). We further probes this issue in the next section.

Discussion: Applying WE to More Complex Systems

Whereas WE simulation has proven highly successful in the present application of a simplified protein model, strategies for applying the approach robustly in more complex systems are important to consider. However, before describing such strategies, it should be recognized that the WE algorithm is statistically correct for sufficiently long simulations regardless of the choice of progress coordinate. This can be seen heuristically by noting that, because the WE approach records statistical weights and does not use a biasing force or potential, unnatural transitions will only occur rarely and with very low weight. Each full transition trajectory is simply a concatenation of unbiased segments with proper statistical weights. Eventually, the important transition trajectories will occur, and their weights will (correctly) dominate the results. In other words, the choice of coordinate(s) and binning should affect the efficiency of the WE approach but not its asymptotic correctness.

There are many possible strategies for using for using higher-dimensional binning while maintaining the overall number of bins at a practicable level. To be concrete, assume that an initial one-dimensional progress coordinate, such as DRMSD_product, has already been divided into bins. Additional “sub-bins” can be added that will encourage transitions across possible saddles in the free energy landscape that may be orthogonal to the initial coordinate. For instance, the first bin (only) can be divided into sub-bins based on DRMSD₁, the distance from the starting structure in the first bin. Once a trajectory arrives in the second bin, a set of sub-bins there can be defined based on DRMSD₂, the distance from the first configuration recorded in bin 2. By repeating this process, “transverse” sub-bins are always defined locally to maximize the chances for transverse motion with each bin.

Other strategies may also be useful. For instance, one could use just a single (“reactant”) structure and the corresponding DRMSD_reactant as an initial coordinate, along with orthogonal sub-bins defined on-the-fly, as above. In other words, one can let the simulation find the product state(s). Furthermore, one can use bins of nonuniform sizes, possibly adjusted on-the-fly, or populate bins with different numbers of particles—and still maintain conformity with the statistical assumptions of the WE method.

The main point is that there is enormous flexibility to construct structurally suitable bins. We believe that this flexibility will ultimately lead to robust strategies suitable for a wide range of biomolecular systems.

Conclusions

We have applied the WE approach of Huber and Kim (36) to the study of a protein conformational transition and shown that it is a remarkably straightforward and successful approach. Because we used a tractable united-residue model for a 72-residue domain of calmodulin (8), we verified the quantitative correctness of the results, by comparison to brute-force simulations. The WE results were also obtained in a fraction of the brute-force simulation time. To our knowledge, no previous path-sampling study of a nontrivial protein model performed such comparisons. Furthermore, efficiency relative to brute-force simulation was found to increase dramatically as the system was made “difficult” by lowering the temperature, with minimal increase in absolute cost.

Although our model exhibits substantial heterogeneity in its transition-path ensemble, it remains an open and fundamental biochemical question as to whether real proteins are more precisely tuned. Although proteins need to be robust (insensitive to many mutations), they are also precisely calibrated to their specific function. How is the balance achieved?

It is certainly premature to choose a single method as best for path sampling in biomolecular systems, but the WE approach appears to be quite promising: (i) it estimates the reaction rate simultaneously with generating the transition path ensemble; (ii) it has the ability to sample heterogeneous pathways independently, avoiding trapping; and (iii) it is extremely easy to implement. Additionally, we have described a method that overcomes a potential weakness of the approach: effective, low-dimensional progress coordinates can be defined for any system in a simple, automated way that does not require any previous knowledge of the system beyond two structures of interest (or even just one). Of course, the ultimate proof will be in the future application to more difficult problems, but these initial, verified results in a nontrivial model mark the passing of a critical test. We also note that structurally diverse pathways determined via WE, possibly in simplified models, can be refined using transition path sampling (59).

Materials and Methods

Path Sampling Using the WE Approach.

Full theoretical details of the WE method are given in the original paper by Huber and Kim (36), but we briefly summarize the approach. Fig. 2 illustrates the basic idea—to propagate trajectories along a “progress coordinate” divided into bins by replicating (splitting) those trajectories that move to empty bins. The progress coordinate is so named because it need not correspond to a reaction coordinate, which is a strength of the WE method and elaborated on in Discussion.

The following steps are used in the WE method.

1. Divide an arbitrarily chosen progress coordinate into N bins or regions. Each bin will contain no more than M simulations.

2. Initially, M independent trajectories are started from the same configuration. Each carries a weight 1/M.

3. Run all of the simulations for a fixed time τ.

4. Check each bin to see whether it has become populated. If there are fewer than M trajectories, split the trajectory (or trajectories) in the bin so that there are M total. The weights must also be split accordingly. If a bin contains more than M trajectories, combine the lowest-weight simulations. These steps are performed without introducing statistical bias (see ref. 36 for details).

5. Go back to step 3.

In Fig. 2, we show a schematic example of the WE method for a double-well potential in one dimension. The progress coordinate is divided into n = 3 bins, and each bin will allow M = 2 simulations. After 3τ, one trajectory carrying probability P = 1/8 has arrived to the third bin.

For our calmodulin simulations, the progress coordinate was chosen to be the negative of the DRMSD (see SI Text) (69) to the Holo state. The simulation starts from the Apo state and progresses toward Holo. SI Fig. 5 shows the evolution of the probability in one WE simulation of calmodulin.

Bistable Gō Model of United-Residue Calmodulin (N-Terminal Domain).

One of the authors previously designed a united-residue potential and associated software to enable brute-force generation of an ensemble of unbiased large-scale conformational transitions (full details are given in ref. 8). As in the previous study, only the N-terminal domain (residues 4–75) of calmodulin was studied (72). Although a Gō model will not capture realistic biochemistry or detailed kinetics, it serves as an ideal system for testing algorithms. Furthermore, the degree of activation can be tuned by lowering the temperature as we have done.

In brief, our united-residue “double-Gō” model (see SI Text and SI Figs. 6 and 7) (8) consists of α-carbon interaction centers with pairwise contact interactions. Infinite wells ensure chain connectivity, and, for nonbonded pairs, standard square-well (contact) interactions occur below an 8.0-Å cutoff, along with hard-core repulsions. When two residues are in contact, the interactions are attractive if the pair is also in contact in either of the reference structures (Apo and Holo, here) but repulsive for nonnative contacts. This potential guarantees that the two native structures (1CFD and 1CLL) have low total energies and that the transition between the two is possible. The temperature is given in units of k_BT/ε, where ε describes the well depths. To make the brute-force simulations run as quickly as possible, the model was implemented on a fine grid—importantly, with grid spacing much smaller than any other length scale (8).

We used “dynamical MC” for the calmodulin model; i.e., Metropolis MC employing only small, physically reasonable trial moves. This is a natural choice for any square-well potential; but furthermore, when small trial steps are used, one can expect dynamical MC to provide dynamics similar to overdamped Langevin dynamics (73, 74). The reason is that, considering an energy landscape consisting of many barrier-separated basins, small-step dynamical MC should cross barriers according to the standard Arrhenius factor without any unphysical, large jumps. In our simulations, the only trial move attempted was a single-particle translation of one grid-spacing (0.13 Å) to a randomly chosen grid point among the 26 closest in the surrounding 3 × 3 × 3 cube.

Although neither the model nor the dynamics is fully accurate, the key point is that both our WE and brute-force simulations were performed with the identical computer code, ensuring a fair comparison in a tractable system.

Error Analysis by Block Averaging.

The transition paths generated by the WE method are correlated, ruling out the use of simple statistical analyses. We therefore used a standard statistical block-averaging approach based on that of ref. 75, which is a reliable algorithm for calculating the statistical errors embodied in time-correlated data. In brief, one divides the sequence of data into n blocks and calculates the standard deviation among the block averages, σ_n, for the quantity of interest. The length of blocks is continually increased until the quantity $\text{SE}={\sigma }_n/\sqrt{n}$ reaches a plateau, which indicates that the blocks have become significantly longer than any correlation times and yields the effective standard error (i.e., scale of statistical uncertainty) of the estimate. All statistical uncertainties and error bars in the figures are given as ±2 SE.

Abbreviations

WE

weighted ensemble

DRMSD

distance RMSD

MC

Monte Carlo.