Direct observation of the reversible unwinding of a single DNA molecule caused by the intercalation of ethidium bromide

Masahito Hayashi; Yoshie Harada

doi:10.1093/nar/gkm529

. 2007 Sep 28;35(19):e125. doi: 10.1093/nar/gkm529

Direct observation of the reversible unwinding of a single DNA molecule caused by the intercalation of ethidium bromide

Masahito Hayashi ^1,^*, Yoshie Harada ^1,2

PMCID: PMC2095801 PMID: 17905818

Abstract

Ethidium bromide (EtBr) is the conventional intercalator for visualizing DNA. Previous studies suggested that EtBr lengthens and unwinds double-stranded DNA (dsDNA). However, no one has observed the unwinding of a single dsDNA molecule during intercalation. We developed a simple method to observe the twisting motions of a single dsDNA molecule under an optical microscope. A short dsDNA was attached to a glass surface of a flow chamber at one end and to a doublet bead as a rotation marker at the other end. After the addition and removal of EtBr, the bead revolved in opposite directions that corresponded to the unwinding and rewinding of a dsDNA, respectively. The amount of intercalating EtBr was estimated from the revolutions of the bead. EtBr occupied 57% of base pairs on a single dsDNA at 1 mM of EtBr, indicating that EtBr molecules could bind at contiguous sites to each other. The isotherm of intercalation showed that negative cooperativity existed between adjoining EtBr molecules. The association constant of EtBr and dsDNA (1.9 (±0.1) × 10⁵ M⁻¹) was consistent with that of previous results. Our system is useful to investigate the twisting of a single dsDNA interacting with various chemicals and biomolecules.

INTRODUCTION

Nucleic acid intercalators, such as ethidium bromide (EtBr), bind specifically to double-stranded DNA (dsDNA). Intercalators have been used as anticancer drugs since they inhibit transcription and replication of the DNA to which they bind (1). They have also been used as DNA staining dyes because they fluoresce upon binding to DNA (2). Sequence-specific intercalators have been developed for the detection of a specific sequence or the site-specific inhibition of transcription or replication (3).

EtBr binds between adjacent base pairs of dsDNA; the binding mode is termed intercalation. The distance between base pairs flanking an EtBr molecule increases 0.34 nm, and the angle between them decreases 26°. Then EtBr intercalation elongates and unwinds dsDNA. This structural information was derived from the mobility in solution (4) or the crystal structure (5) of the EtBr/dsDNA complex. Coury et al. measured the contour length change of a single dsDNA during EtBr intercalation (6). The isotherm of intercalation was obtained using the absorbance, fluorescence or buoyant densities of the EtBr/dsDNA complex in bulk (4,7). Previous studies on EtBr intercalation explained its isotherm by the nearest neighbor exclusion model assuming that EtBr molecules cannot bind to next binding sites and that no cooperativity exists between EtBr molecules on the same DNA molecule (8).

The effects of external forces on EtBr intercalation were investigated using several methods. In order to reveal the torque effect, the conformations of closed circular DNA before and after EtBr intercalation were observed using electrophoresis (9) or an electron microscope (10). Recently, optical and magnetic tweezers were used for single DNA manipulation and measurement (11–18). Vladescu et al. investigated the amount of intercalating EtBr from the changes in length of a stretched DNA molecule using optical tweezers. They demonstrated that under high tension (>10 pN) EtBr can bind to dsDNA more than expected value (50%) from the nearest neighbor exclusion model (14). Strick et al. used magnetic tweezers to measure the twist change of a single dsDNA molecule (15,16). A single dsDNA was attached to a glass surface of a flow chamber at one end and to a magnetic bead at the other end. The DNA could be stretched and twisted using magnetic tweezers. Rotations of the bead resulted in the coiling of DNA upon itself. The length of the DNA shortened as it coiled. The relative twist of the DNA was estimated from the height change of the bead. The tension and torque of the DNA had to be kept during measurement. We also used magnetic tweezers to observe the revolutions of a single DNA molecule during transcription (17) and recombination (18). However, in order to reveal the tension and torque effects on EtBr intercalation, we need to measure the amount of intercalating EtBr under various tensions and torques, including a no-tension and a no-torque condition.

In this report, we developed a simple method to measure the number of twists in a single DNA molecule under no external force. We estimated the amount of intercalating EtBr on the DNA from its twists. Then the isotherm of intercalation was obtained at a single DNA level. We discussed whether the nearest neighbor exclusion model holds true for a single DNA as well as for bulk DNA.

MATERIALS AND METHODS

Materials

Streptavidin-coated beads (500 nm in diameter) were constructed as described before (17). The streptavidin-coated beads randomly formed doublets and larger aggregates. About 10% of aggregates were doublet beads. Coverslips (24 × 24 mm, 18 × 18 mm, Matsunami, Japan) were dipped into 0.5% (w/v) collodion (Nacalai Tesque, Japan) in isoamyl acetate and dried in air. N,N-dimethylcasein (Sigma, USA) diluted in Milli-Q water (10 mg/ml) was autoclaved at 121°C for 20 min and centrifuged at 15 000 × g for 10 min at 4°C. The supernatant was filtered through a 0.2 μm pore size polyvinylidene difluoride (PVDF) filter (Whatman, USA), stored at −20°C, and used within 6 months. The concentration of EtBr (E-8751, Sigma, USA) stock solution was determined by the absorbance at 480 nm, using an absorbance coefficient ε = 5800 M⁻¹cm⁻¹.

DNA preparation

DNA was amplified by PCR using a pair of primers, a digoxigenin-labeled primer and a biotin-labeled primer. The three digoxigenin and three biotin labels on the amplified DNA were used for connecting the DNA to a glass surface and a doublet bead, respectively. These multiple labels at both ends prevented the DNA from rotating freely. The PCR template was constructed by inserting the following sequence, which had eight repeats of 50 bp sequence each, between KpnI and SacI sites of pBluescriptIISK(-);

CCTAAAGTATCCTCCTAAAG Inline graphic CACCTCCTAACGTCCATCCGGATCCC(TCGAGTAATACGACTCACTATAGGGAGACCACAACGGTTTAAATCTAGCG)₈TCGACGAATTCTAACCGAACTAAATCAGGCCTTGAGCATCAAGATTGGTGG.

The 5′ underlined region was the sequence of the digoxigenin-labeled primer; three digoxigenins were conjugated to two nucleotides (in bold) and the 5′ end of the primer. The 3′ underlined part was the complementary sequence of the biotin-labeled primer; three biotins were conjugated to two nucleotides (in bold) and the 5′ end of the primer. The total length of the sequence was 499 bp. The length between the digoxigenin- and biotin-labeled nucleotide in boxes was 458 bp. The template was amplified by ExTaq PCR system (Takara, Japan). The PCR product was purified using 8% polyacrylamide gel electrophoresis.

Construction of DNA-tethered beads

The DNA was attached to a glass surface of a flow chamber and a doublet bead as follows: a flow chamber was made of two collodion-coated coverslips separated by 50 μm thick spacers. The volume of the chamber was ∼5 μl. At first, anti-digoxigenin antibody (20 μg/ml) in H buffer (10 mM HEPES·KOH, pH 7.8/100 mM KCl/1 mM EDTA) was infused into the chamber and incubated for 5 min. Unbound antibodies were washed out with blocking buffer (0.1 mg/ml N,N-dimethylcasein in H buffer). After 5 min incubation, 10 pM of the DNA in blocking buffer was infused into the chamber. The DNA molecules attached to the antibodies on the glass surface at their digoxigenin-labeled ends during 5 min incubation. The chamber was flushed with blocking buffer. Here, 0.1% (w/v) of streptavidin-coated beads were infused into the chamber. Beads attached to the biotin-labeled ends of the DNA molecules on the glass surface during 5 min incubation. Unbound beads were washed out with blocking buffer. In order to simplify the calculation of the surface density of DNA molecules, the top and bottom coverslip were coated using the same procedure. Because the observation chamber was deeper than the objective focus, the beads that tethered to the top coverslip were invisible during the observation of the beads attached at to the bottom coverslip. The surface density of DNA was ∼0.15 molecules/μm² when all the DNA molecules attached randomly to the glass surface. Almost all (>97%) tethered-doublet beads were connected with a single DNA following a Poisson distribution. The DNA-tethered beads rotated randomly. About 80% of the tethered beads rotated within two turns while the other tethered beads rotated without any restriction. The rest of the beads were assumed to be tethered with a nicked DNA. Therefore, we observed the tethered-doublet beads that displayed rotational fluctuations within two turns on a focal plane.

Measurement of the rotating angle of a tethered bead

A DNA-tethered doublet bead was observed on an inverted microscope (IX70, Olympus, Tokyo, Japan) with a 60x oil immersion objective. The bright field image of the bead was projected on a CCD camera (XC-ST50, Sony, Tokyo, Japan) and recorded on videotape. The shutter speed of the camera was 1/250 s. Buffers in the chamber were changed with 10 μl of EtBr in blocking buffer within 10 s. The chamber was flushed out with 20 μl of blocking buffer within 20 s. DNA-tethered beads were observed in the flow chamber at 26 ± 2°C.

We analyzed each field of the video images and got rotating angles of the beads every 1/60 s. An image-processing program ImageJ (http://rsb.info.nih.gov/ij/) was used for the following analysis. The rotating angle of the bead was determined by its major axis. The bright field image of the bead was transformed to a binary image, which was fitted to an ellipsoid. We regarded the major axis of the ellipsoid as being that of the bead. This measurement algorithm was very robust against the translational-Brownian motions of the beads and drifts and vibrations of the sample stage.

Spectral analysis of thermal fluctuations

A power density spectrum (PDS) of the rotational fluctuations of a tethered-doublet bead is expressed as a Lorentzian curve, Φ(f) = 4ξk_BT/k²/[1 + (f/f_c)²], f_c = k/2πξ, where f is the frequency; ξ is the friction coefficient of a DNA-tethered doublet bead against solution; k_BT is the thermal energy; k is the torsional spring constant of the DNA; f_c is the corner frequency of the curve (19). ξ is given by (7/2)πβηD³, where β = 1.82 is the factor of a surface effect (20) on the doublet bead whose center is at a distance of (D/2) + L = 405 nm from the chamber surface; L = 155 nm (= 0.34 nm × 458 bp), the length of DNA between the digoxigenin tags and the biotin tags; η = 8.8 × 10⁻⁴ Pa·s is the bulk viscosity of water at 26°C; D = 500 nm is the diameter of the bead. Therefore, ξ = 2.2 pN·nm·s. k = 1.4 pN·nm is given by κ/L, where κ = 220 pN·nm² is the torsional rigidity of the DNA (21); k_BT = 4.1 pN·nm is the thermal energy at 26°C. Thus f_c = 0.1 Hz, and the relaxation time of the fluctuations τ = 1/2πf_c = 1.8 s. The SD of the rotational fluctuations is obtained by 〈θ²〉^1/2 = (k_BT/k)^1/2 = 1.71 radian = 97°. The experimental value of 〈θ²〉^1/2 was calculated from the time course of the rotational fluctuations. We obtained a PDS of the rotational fluctuations using a fast Fourier transform (FFT) algorithm on a numerical-calculation software package, Octave (http://www.gnu.org/software/octave/). We fitted the PDS to a Lorentzian curve and obtained the experimental value of f_c.

Analysis of the isotherm of EtBr intercalation

To analyze the EtBr-DNA binding isotherm, we used the neighbor exclusion model of McGhee and von Hippel incorporating the cooperative binding of DNA intercalators (8). The equations in the model can be rearranged as follows:

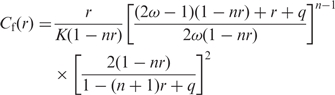(1)

(2)

where C_f is the free EtBr concentration; r is the ratio of bound EtBr to total concentration of DNA in base pairs; K is the association constant for the intercalation of an EtBr molecule with an isolated site; n is the number of base pairs occupied by a bound EtBr molecule; ω is the cooperativity parameter, which may be greater than 1 (positive cooperativity), equal to 1 (non-cooperativity) or less than 1 (negative cooperativity).

Under our experimental conditions, C_f was approximated with the total concentration of EtBr in the chamber since the concentration of DNA, ∼5 nM in base pair, was much smaller than C_f, from 1 to 1000 μM. The ratio r was expressed as r = N_b/N, where N_b was the number of intercalating EtBr molecules on a DNA molecule; N was the length of the DNA, 458 bp. N_b was expressed as N_b = R/φ, where R was the number of revolutions of a tethered bead and φ was a unit angle of unwinding per EtBr molecule, 26° (4,5). This was because N_b was in proportion to the twists of the DNA, which equaled R.

To fit the theoretical model to the experimental data, we used an inverse function method. In previous studies about intercalators, the isotherm was fitted to the model on a Scatchard plot. However, complicated algorithms had to be applied to estimate experimental errors (23). A simple method was used for estimating the measurement errors of r. Equations (1) and (2) give us C_f as an explicit function of r. We calculated the inverse function r(C_f) by a numerical solution using the golden section search algorithm (24) for minimization of (C_f(r) − C_f)². r(C_f) was fitted to a set of data using the non-linear least squares method (24). The weight given to each data point was the standard deviation of r. We analyzed data by using numerical computing software, Octave.

RESULTS

Random twisting of a single DNA molecule

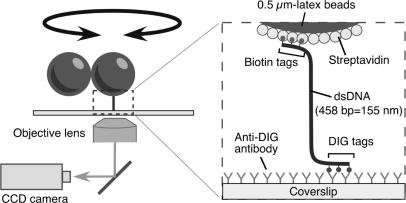
In order to observe twisting motions of a single DNA molecule, we constructed a simple experimental setup as shown in Figure 1. A dsDNA was attached to a glass surface of a flow chamber at one end and to a doublet bead at the other end. The rotation of the bead reflected the twisting motions of the DNA. Each end of the DNA had three tags of biotin or digoxigenin, preventing the bead from free rotations. We did not use optical or magnetic tweezers to pull up the bead or to stretch the DNA.

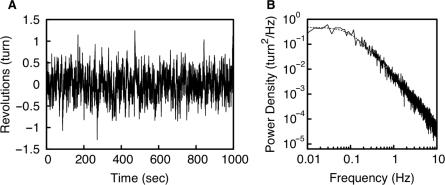
The rotations of a DNA-tethered bead reflected accurately the twists of the DNA. Since the DNA was shorter than the diameter of the bead, the bead moved randomly on a focal plane. Translational fluctuations on the focal plane were smaller than the radius of the bead. The translational fluctuations had a small effect on the measurement of the rotational angle since we measured directly the axis of the doublet bead. About 80% of tethered beads rotated randomly within about two turns (Figure 2A) while the other tethered beads rotated without any restriction. The amplitude of the fluctuations of the former beads had a constant variance at all times during observation. The SD of the fluctuations 〈θ²〉^1/2 was 104°, which was as much as its expected value, 97°.

A PDS of the rotational fluctuations is shown in Figure 2B. It followed a Lorentzian curve, which is a characteristic of restricted Brownian motion. Its corner frequency f_c was 0.1 Hz. The relaxation time of the fluctuations τ (=1/2πf_c) was 1.6 sec, which was as much as its expected value, 1.8 s.

Reversible revolutions of a DNA-tethered bead caused by the addition and removal of EtBr

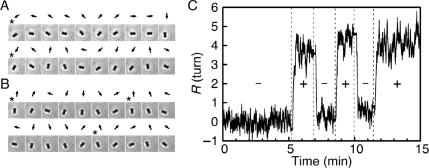
We tried to determine whether dsDNA twisted clockwise or counterclockwise during intercalation. DNA-tethered beads were observed from the top as described in Figure 1. We exchanged the solution in a flow chamber for one containing EtBr. During the exchange of solutions, tethered beads pointed downstream since they were pushed aside by the streaming of the solution. Immediately after the streaming stopped, the bead started to revolve clockwise (Figure 3A, Movie S3 in Supplementary Data). The revolving bead slowed down and fluctuated around a certain orientation within about two turns. On the other hand, after the removal of EtBr, the bead revolved counterclockwise and fluctuated around the original orientation (Figure 3B, Movie S3 in Supplementary Data). The changes in the direction of the bead's revolution were reversible and could be repeated more than three times (Figure 3C). The clockwise and counterclockwise revolutions of the bead corresponded to the unwinding and rewinding, respectively, of right-handed helices.

Figure 3. — Reversible revolutions of a DNA-tethered bead caused by EtBr. (A and B) Snapshots of rotating beads for 2 s at 200 ms intervals after the addition (A; from 8′56′′ in C) or the removal (B; from 10′10″ in C) of 1 μM EtBr. Arrows indicate the directions of the bead. Asterisks indicate completion of a turn. (C) Time course of bead rotation during the repeated change of EtBr concentration, 0 (−) and 1 μM (+). See also Movie S3 in Supplementary Data.

Number of twists of a dsDNA molecule at various EtBr concentrations

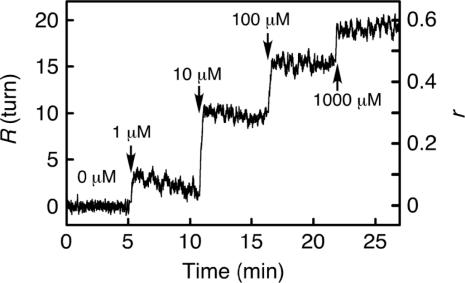
DNA-tethered beads revolved a certain number of turns at various concentrations of EtBr. Figure 4 shows the time course of the revolutions, R, in a stepwise increase of EtBr concentration. Immediately after the increase of EtBr concentration, R increased and reached a certain value within several seconds. At concentrations of EtBr lower than 10 μM, R reached a maximal value within several seconds and then decreased slowly. The glass surface of the flow chamber became weakly fluorescent as caused by EtBr after washing it out. The fluorescence intensity became saturated with concentrations of EtBr higher than 10 μM (data not shown) at which point the decrease was probably a result of the adsorption of EtBr to the glass surface. The half-life of the decrease was ∼300 s and was much slower than that of the initial increase, which was ∼3 s. Then, to minimize the adsorption effect, we used R in 15 s after the solution exchange. R was reproducible with SDs as large as the rotational fluctuations of the DNA-tethered beads, about two turns. When using longer DNA, tethered beads revolved more (Figure S1 in Supplementary Data). The bead revolutions R and the length of dsDNA L were directly proportional.

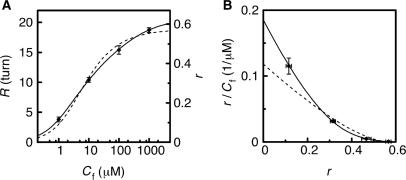
Isotherm of EtBr intercalation at a single DNA level

Next, we evaluated the kinetic parameters of EtBr intercalation at a single DNA level. We calculated the number of intercalating EtBr molecules to dsDNA assuming that the tethered bead rotated clockwise φ = 26° when one molecule of EtBr intercalated (4,5). Then r, the ratio of the intercalating EtBr to base pairs, was calculated as r = 360R/φ/N, where N was the length of the DNA. The dependence of r on EtBr concentration C_f is shown in Figure 5A and B. The Scatchard plot of the isotherm (Figure 5B) was a downward concave, which was the characteristic shape of the isotherm of intercalation in bulk experiments (4,8,22). EtBr bound to DNA at the ratio r of more than 0.5 when added at a high concentration; r = 0.57 at 1 mM EtBr. The isotherm was fitted to the neighbor exclusion model of McGhee and von Hippel incorporating the cooperative binding of DNA intercalators, as described in the Materials and Methods section (22). Assuming no-cooperativity (ω = 1), the model did not fit the data (Figure 5, broken lines). When using a cooperative model (ω ≠ 1), however, the data agreed with the model (Figure 5, solid lines). The fitting parameters of the cooperative model were n = 1.60 ± 0.03, K = 1.9 (±0.1) × 10⁵ M⁻¹, ω = 0.38 ± 0.07. The parameter n indicated that EtBr could bind to up to 67% (=1/n) of base pairs. The association constant agreed with that in the bulk measurement at 100 mM KCl (25). r increased as the concentration of KCl decreased at a fixed concentration of EtBr (Figure S2 in Supplementary Data). Negative cooperativity (ω < 1) existed between bound EtBr molecules on the same DNA.

Figure 5. — Direct plot (A) and Scatchard plot (B) of the data derived from the time course of bead revolutions such as that shown in Figure 4. Each data point is the average of four data with SDs. Theoretical curves were the best fits to the data. The fitting parameters were n = 1.60 ± 0.03, K = 1.9 (±0.1) × 10⁵ (M⁻¹), ω = 0.38 ± 0.07 (with cooperativity; the solid lines); n = 1.8 ± 0.1, K = 1.2 (±0.4) × 10⁵ (M⁻¹), ω = 1 (without cooperativity; the broken lines).

DISCUSSION

We developed a simple method to measure the twists of a single DNA molecule using an optical microscope (Figures 1 and 2). This system enabled us to observe that EtBr unwinds the double helical structure of dsDNA at a single molecule level (Figure 3). The amount of intercalating EtBr into each DNA molecule was calculated from the twists of the DNA. The isotherm of intercalation was obtained from a single DNA molecule (Figures 4 and 5).

A DNA-tethered bead reflected accurately the twisting motions of the DNA molecule. The dsDNA was attached to a glass surface of a flow chamber at one end with three digoxigenin tags and to a doublet bead at the other end with three biotin tags. The multiple tags prevented the DNA from rotating freely. About 80% of tethered beads rotated randomly within about two turns. The amplitude of the rotational fluctuations of the beads coincided with the expected amplitude of the DNA's twisting motions that was caused by the thermal energy. This coincidence indicated that the twists of the DNA molecule were transmitted accurately to the motions of the bead. The twists of the DNA molecule can be measured by the revolutions of the tethered bead without stretching or coiling it. This was made possible by the short DNA (155 nm) and the large doublet bead (500 nm in diameter). Since the DNA was three times as long as its bending-persistence length, 50 nm (21), the DNA transmitted its twists to the bead like a universal joint. The large doublet bead, whose diameter was larger than the length of the DNA, kept the DNA on a vertical axis. The twisting angle of the DNA molecule during EtBr intercalation had an error as large as the rotational fluctuations of the bead. The error was small enough to evaluate the isotherm of EtBr intercalation as described later. The response time of the bead to the twist of the DNA was as much as the relaxation time of the bead's rotation, τ = 1.6 s. Although this was much slower than the dissociation of EtBr from dsDNA, which was ∼30 ms (26), it was sufficient for the investigation about the equilibrium state of EtBr intercalation.

Using the tethered bead method, we succeeded in observing the unwinding of each DNA molecule caused by EtBr intercalation. Previous studies using electrophoresis (9) and electron microscopy (10) showed that the compactness of closed circular dsDNA changes with the concentration of EtBr. The change in compactness can be explained by the unwinding of the DNA. The crystal structure of the EtBr/dsDNA complex indicated the direction and dimension of the unwinding (5). In this article, we observed the unwinding and rewinding during EtBr intercalation. When EtBr molecules bound to a dsDNA molecule, it twisted in a counterclockwise direction, which coincided with the unwinding of the right-handed DNA helix. On the other hand, the dissociation of EtBr from dsDNA resulted in clockwise twists of the DNA. Our observations were consistent with the model of intercalation that was derived from previous studies using bulk DNA (4,5).

The tethered-bead method enabled us to estimate the amount of intercalating EtBr molecules at a single DNA level. Previous studies measured indirectly the amount of EtBr bound to bulk DNA using fluorescence or buoyant densities of the EtBr/dsDNA complex. Since our method measured the structural change of a single DNA molecule, we could only count intercalating EtBr molecules. The linear relationship between the bead revolutions R and the length of dsDNA L indicated that R reflected the number of intercalating EtBr molecules.

We calculated n, K and ω from the titration data of EtBr intercalation using the McGhee and von Hippel model (22). We obtained the association constant K = 1.9 (±0.1) × 10⁵ M⁻¹ which had a coefficient of variation (CV) of 5%. In a previous report using the absorbance titration of bulk EtBr/dsDNA (27), K = 6.52 (±0.63) × 10⁴ M⁻¹ (including 10% CV); in a report measuring the contour length change of a single dsDNA during EtBr intercalation (6), K = 3.6 (±0.5) × 10⁴ M⁻¹ (including 14% CV). Hence, the K obtained in our method was as accurate as that of previous methods. The variation of K among these reports might be due to the composition of solutions. For example, the amount of intercalating EtBr was sensitive to the salt concentration (Figure S2 in Supplementary Data).

In the nearest neighbor exclusion model (8), EtBr can bind to every other base pair (n = 2), and there is no cooperativity between EtBr molecules on the same dsDNA (ω = 1). We showed that EtBr molecules could bind to neighboring sites (n < 2) with negative cooperativity (ω < 1), in violation of the previous model. The negative cooperativity indicated the instability of neighboring EtBr molecules on dsDNA. The instability is explained by the fine conformational imbalance of two DNA backbones (8). Vladescu et al. (14) showed that EtBr could bind to every base pair (n = 1) under high tension (>10 pN) with a large association constant (K = 10⁷ M⁻¹). They explained that the strong tension, which imposed the backbone conformation of dsDNA, released the requirement for site exclusion and promoted further EtBr intercalation. The determination of n, K and ω in a wide range of dsDNA tension and EtBr concentration will reveal much about the site exclusion mechanism of EtBr intercalation.

In this report, we determined the kinetic parameters of EtBr intercalation under no external force. In order to reveal the torque and tension effects on EtBr intercalation, we have to evaluate the parameters about stretched or twisted dsDNA molecules using optical or magnetic tweezers. Our system can be applied to other chemicals and biomolecules which have DNA-twisting activity.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

ACKNOWLEDGEMENTS

We thank Drs K. Kinosita Jr, T. Tani, H. Yokota and Y. Sasuga for helpful discussion. We appreciate the assistance of Ms K. Terada and Mr T. Kobayashi for correcting the English. This work was supported in part by a research grant from Core Research for Evolutional Science and Technology (CREST) of the Japan Science and Technology Agency (JST), and by Grand-in-Aid for Scientific Research by the Ministry of Education Culture, Sports, Science and Technology of Japan (to M.H. and Y.H.). Funding to pay this Open Access publication charges for this article was provided by Grand-in-Aid for Scientific Research by the Ministry of Education Culture, Sports, Science and Technology of Japan.

Conflict of interest statement. None declared.

REFERENCES

1.Hurley LH. DNA and its associated processes as targets for cancer therapy. Nat. Rev. Cancer. 2002;2:188–200. doi: 10.1038/nrc749. [DOI] [PubMed] [Google Scholar]
2.Stuart KR, Cole ES. Nuclear and cytoskeletal fluorescence microscopy techniques. Methods Cell Biol. 2000;62:291–311. doi: 10.1016/s0091-679x(08)61538-1. [DOI] [PubMed] [Google Scholar]
3.Choudhury JR, Bierbach U. Characterization of the bisintercalative DNA binding mode of a bifunctional platinum-acridine agent. Nucleic Acids Res. 2005;33:5622–5632. doi: 10.1093/nar/gki869. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Wang JC. The degree of unwinding of the DNA helix by ethidium. I. Titration of twisted PM2 DNA molecules in alkaline cesium chloride density gradients. J. Mol. Biol. 1974;89:783–801. doi: 10.1016/0022-2836(74)90053-9. [DOI] [PubMed] [Google Scholar]
5.Tsai CC, Jain SC, Sobell HM. X-ray crystallographic visualization of drug-nucleic acid intercalative binding: structure of an ethidium-dinucleoside monophosphate crystalline complex, ethidium: 5-iodouridylyl(3′-5′)adenosine. Proc. Natl Acad. Sci. USA. 1975;72:628–632. doi: 10.1073/pnas.72.2.628. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Coury JE, McFail-Isom L, Williams LD, Bottomley LA. A novel assay for drug-DNA binding mode, affinity, and exclusion number: scanning force microscopy. Proc. Natl Acad. Sci. USA. 1996;93:12283–12286. doi: 10.1073/pnas.93.22.12283. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Waring MJ. Complex formation between ethidium bromide and nucleic acids. J. Mol. Biol. 1965;13:269–282. doi: 10.1016/s0022-2836(65)80096-1. [DOI] [PubMed] [Google Scholar]
8.Cantor CR, Schimmel PR. Biophysical Chemistry, Part III: The Behavior of Biological Macromolecules. New York, USA: W.H.Freeman and Company; 1980. pp. 1239–1261. [Google Scholar]
9.Shure M, Pulleyblank DE, Vinograd J. The problems of eukaryotic and prokaryotic DNA packaging and in vivo conformation posed by superhelix density heterogeneity. Nucleic Acids Res. 1977;4:1183–1205. doi: 10.1093/nar/4.5.1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Liu LF, Wang JC. On the degree of unwinding of the DNA helix by ethidium. II. Studies by electron microscopy. Biochim. Biophys. Acta. 1975;395:401–412. [PubMed] [Google Scholar]
11.Bustamante C, Bryant Z, Smith SB. Ten years of tension: single-molecule DNA mechanics. Nature. 2003;421:423–427. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]
12.Gore J, Bryant Z, Stone MD, Nöllmann M, Cozzarelli NR, Bustamante C. Mechanochemical analysis of DNA gyrase using rotor bead tracking. Nature. 2006;439:100–104. doi: 10.1038/nature04319. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Sischka A, Toensing K, Eckel R, Wilking SD, Sewald N, Ros R, Anselmetti D. Molecular mechanisms and kinetics between DNA and DNA binding ligands. Biophys. J. 2005;88:404–411. doi: 10.1529/biophysj.103.036293. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Vladescu ID, McCauley MJ, Rousina I, Williams MC. Mapping the phase diagram of single DNA molecule forse–induced melting in the presence of ethidium. Phys. Rev. Lett. 2005;95:158102. doi: 10.1103/PhysRevLett.95.158102. [DOI] [PubMed] [Google Scholar]
15.Strick TR, Croquette V, Bensimon D. Single-molecule analysis of DNA uncoiling by a type II topoisomerase. Nature. 2000;404:901–904. doi: 10.1038/35009144. [DOI] [PubMed] [Google Scholar]
16.Revyakin A, Ebright RH, Strick TR. Single-molecule DNA nanomanipulation: improved resolution through use of shorter DNA fragments. Nat. Methods. 2005;2:127–138. doi: 10.1038/nmeth0205-127. [DOI] [PubMed] [Google Scholar]
17.Harada Y, Ohara O, Takatsuki A, Itoh H, Shimamoto N, Kinosita K., Jr Direct observation of DNA rotation during transcription by Esherichia coli RNA polymerase. Nature. 2001;409:113–115. doi: 10.1038/35051126. [DOI] [PubMed] [Google Scholar]
18.Han YW, Tani T, Hayashi M, Hishida T, Iwasaki H, Shinagawa H, Harada Y. Direct observation of DNA rotation during branch migration of Holliday junction DNA by Escherichia coli RuvA-RuvB protein complex. Proc. Natl Acad. Sci. USA. 2006;103:11544–11548. doi: 10.1073/pnas.0600753103. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Kittel C. Elementary Statistical Physics. New York: J. Wiley and Sons; 1958. [Google Scholar]
20.Happel J, Brenner H. Low Reynolds Number Hydrodynamics. 2nd. Dordecht, the Netherlands, p. 553: Kluwer Academic; 1991. [Google Scholar]
21.Heath PJ, Clendenning JB, Fujimoto BS, Schurr JM. Effect of bending strain on the torsion elastic constant of DNA. J. Mol. Biol. 1996;260:718–730. doi: 10.1006/jmbi.1996.0432. [DOI] [PubMed] [Google Scholar]
22.McGhee JD, von Hippel PH. Theoretical aspects of DNA-protein interactions: co-operative and non-co-operative binding of large ligands to a one-dimensional homogenous lattice. J. Mol. Biol. 1974;86:469–489. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]
23.Correia JJ, Chaires JB. Analysis of drug-DNA binding isotherms: a Monte Carlo approach. Meth. Enzymol. 1994;240:593–614. doi: 10.1016/s0076-6879(94)40065-2. [DOI] [PubMed] [Google Scholar]
24.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes in C. Cambridge: Cambridge University Press; 1988. [Google Scholar]
25.Wilson WD, Krishnamoorthy CR, Wang YH, Smith JC. Mechanism of intercalation: ion effects on the equilibrium and kinetic constants for the interaction of propidium and ethidium with DNA. Biopolymers. 1985;24:1941–1961. doi: 10.1002/bip.360241008. [DOI] [PubMed] [Google Scholar]
26.Macgregor RB, Jr, Clegg RM, Jovin TM. Pressure-jump study of the kinetics of ethidium bromide binding to DNA. Biochemistry. 1985;24:5503–5510. doi: 10.1021/bi00341a034. [DOI] [PubMed] [Google Scholar]
27.Qu X, Chaires JB. Analysis of drug-DNA binding data. Meth. Enzymol. 2000;321:353–369. doi: 10.1016/s0076-6879(00)21202-0. [DOI] [PubMed] [Google Scholar]

[B1] 1.Hurley LH. DNA and its associated processes as targets for cancer therapy. Nat. Rev. Cancer. 2002;2:188–200. doi: 10.1038/nrc749. [DOI] [PubMed] [Google Scholar]

[B2] 2.Stuart KR, Cole ES. Nuclear and cytoskeletal fluorescence microscopy techniques. Methods Cell Biol. 2000;62:291–311. doi: 10.1016/s0091-679x(08)61538-1. [DOI] [PubMed] [Google Scholar]

[B3] 3.Choudhury JR, Bierbach U. Characterization of the bisintercalative DNA binding mode of a bifunctional platinum-acridine agent. Nucleic Acids Res. 2005;33:5622–5632. doi: 10.1093/nar/gki869. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B4] 4.Wang JC. The degree of unwinding of the DNA helix by ethidium. I. Titration of twisted PM2 DNA molecules in alkaline cesium chloride density gradients. J. Mol. Biol. 1974;89:783–801. doi: 10.1016/0022-2836(74)90053-9. [DOI] [PubMed] [Google Scholar]

[B5] 5.Tsai CC, Jain SC, Sobell HM. X-ray crystallographic visualization of drug-nucleic acid intercalative binding: structure of an ethidium-dinucleoside monophosphate crystalline complex, ethidium: 5-iodouridylyl(3′-5′)adenosine. Proc. Natl Acad. Sci. USA. 1975;72:628–632. doi: 10.1073/pnas.72.2.628. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] 6.Coury JE, McFail-Isom L, Williams LD, Bottomley LA. A novel assay for drug-DNA binding mode, affinity, and exclusion number: scanning force microscopy. Proc. Natl Acad. Sci. USA. 1996;93:12283–12286. doi: 10.1073/pnas.93.22.12283. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B7] 7.Waring MJ. Complex formation between ethidium bromide and nucleic acids. J. Mol. Biol. 1965;13:269–282. doi: 10.1016/s0022-2836(65)80096-1. [DOI] [PubMed] [Google Scholar]

[B8] 8.Cantor CR, Schimmel PR. Biophysical Chemistry, Part III: The Behavior of Biological Macromolecules. New York, USA: W.H.Freeman and Company; 1980. pp. 1239–1261. [Google Scholar]

[B9] 9.Shure M, Pulleyblank DE, Vinograd J. The problems of eukaryotic and prokaryotic DNA packaging and in vivo conformation posed by superhelix density heterogeneity. Nucleic Acids Res. 1977;4:1183–1205. doi: 10.1093/nar/4.5.1183. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B10] 10.Liu LF, Wang JC. On the degree of unwinding of the DNA helix by ethidium. II. Studies by electron microscopy. Biochim. Biophys. Acta. 1975;395:401–412. [PubMed] [Google Scholar]

[B11] 11.Bustamante C, Bryant Z, Smith SB. Ten years of tension: single-molecule DNA mechanics. Nature. 2003;421:423–427. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]

[B12] 12.Gore J, Bryant Z, Stone MD, Nöllmann M, Cozzarelli NR, Bustamante C. Mechanochemical analysis of DNA gyrase using rotor bead tracking. Nature. 2006;439:100–104. doi: 10.1038/nature04319. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] 13.Sischka A, Toensing K, Eckel R, Wilking SD, Sewald N, Ros R, Anselmetti D. Molecular mechanisms and kinetics between DNA and DNA binding ligands. Biophys. J. 2005;88:404–411. doi: 10.1529/biophysj.103.036293. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B14] 14.Vladescu ID, McCauley MJ, Rousina I, Williams MC. Mapping the phase diagram of single DNA molecule forse–induced melting in the presence of ethidium. Phys. Rev. Lett. 2005;95:158102. doi: 10.1103/PhysRevLett.95.158102. [DOI] [PubMed] [Google Scholar]

[B15] 15.Strick TR, Croquette V, Bensimon D. Single-molecule analysis of DNA uncoiling by a type II topoisomerase. Nature. 2000;404:901–904. doi: 10.1038/35009144. [DOI] [PubMed] [Google Scholar]

[B16] 16.Revyakin A, Ebright RH, Strick TR. Single-molecule DNA nanomanipulation: improved resolution through use of shorter DNA fragments. Nat. Methods. 2005;2:127–138. doi: 10.1038/nmeth0205-127. [DOI] [PubMed] [Google Scholar]

[B17] 17.Harada Y, Ohara O, Takatsuki A, Itoh H, Shimamoto N, Kinosita K., Jr Direct observation of DNA rotation during transcription by Esherichia coli RNA polymerase. Nature. 2001;409:113–115. doi: 10.1038/35051126. [DOI] [PubMed] [Google Scholar]

[B18] 18.Han YW, Tani T, Hayashi M, Hishida T, Iwasaki H, Shinagawa H, Harada Y. Direct observation of DNA rotation during branch migration of Holliday junction DNA by Escherichia coli RuvA-RuvB protein complex. Proc. Natl Acad. Sci. USA. 2006;103:11544–11548. doi: 10.1073/pnas.0600753103. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B19] 19.Kittel C. Elementary Statistical Physics. New York: J. Wiley and Sons; 1958. [Google Scholar]

[B20] 20.Happel J, Brenner H. Low Reynolds Number Hydrodynamics. 2nd. Dordecht, the Netherlands, p. 553: Kluwer Academic; 1991. [Google Scholar]

[B21] 21.Heath PJ, Clendenning JB, Fujimoto BS, Schurr JM. Effect of bending strain on the torsion elastic constant of DNA. J. Mol. Biol. 1996;260:718–730. doi: 10.1006/jmbi.1996.0432. [DOI] [PubMed] [Google Scholar]

[B22] 22.McGhee JD, von Hippel PH. Theoretical aspects of DNA-protein interactions: co-operative and non-co-operative binding of large ligands to a one-dimensional homogenous lattice. J. Mol. Biol. 1974;86:469–489. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]

[B23] 23.Correia JJ, Chaires JB. Analysis of drug-DNA binding isotherms: a Monte Carlo approach. Meth. Enzymol. 1994;240:593–614. doi: 10.1016/s0076-6879(94)40065-2. [DOI] [PubMed] [Google Scholar]

[B24] 24.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes in C. Cambridge: Cambridge University Press; 1988. [Google Scholar]

[B25] 25.Wilson WD, Krishnamoorthy CR, Wang YH, Smith JC. Mechanism of intercalation: ion effects on the equilibrium and kinetic constants for the interaction of propidium and ethidium with DNA. Biopolymers. 1985;24:1941–1961. doi: 10.1002/bip.360241008. [DOI] [PubMed] [Google Scholar]

[B26] 26.Macgregor RB, Jr, Clegg RM, Jovin TM. Pressure-jump study of the kinetics of ethidium bromide binding to DNA. Biochemistry. 1985;24:5503–5510. doi: 10.1021/bi00341a034. [DOI] [PubMed] [Google Scholar]

[B27] 27.Qu X, Chaires JB. Analysis of drug-DNA binding data. Meth. Enzymol. 2000;321:353–369. doi: 10.1016/s0076-6879(00)21202-0. [DOI] [PubMed] [Google Scholar]

PERMALINK

Direct observation of the reversible unwinding of a single DNA molecule caused by the intercalation of ethidium bromide

Masahito Hayashi

Yoshie Harada

Abstract

INTRODUCTION