Low Frequency Spectral Density of Ferrous Heme: Perturbations Induced by Axial Ligation and Protein Insertion

Abstract

Femtosecond coherence spectroscopy is used to probe low frequency (20–400 cm⁻¹) modes of the ferrous heme group in solution, with and without 2-methyl imidazole (2MeIm) as an axial ligand. The results are compared to heme proteins (CPO, P450_cam, HRP, Mb) where insertion of the heme into the protein results in redistribution of the low frequency spectral density and in (∼60%) longer damping times for the coherent signals. The major effect of imidazole ligation to the ferrous heme is the “softening” of the low frequency force constants by a factor of ∼0.6 ± 0.1. The functional consequences of imidazole ligation are assessed and it is found that the enthalpic CO rebinding barrier is increased significantly when imidazole is bound. The force constant softening analysis, combined with the kinetics results, indicates that the iron is displaced by only ∼0.2 Å from the heme plane in the absence of the imidazole ligand, whereas it is displaced by ∼0.4 Å when imidazole (histidine) is present. This suggests that binding of imidazole (histidine) as an axial ligand, and the concomitant softening of the force constants, leads to an anharmonic distortion of the heme group that has significant functional consequences.

INTRODUCTION

Heme proteins are involved in a wide variety of physiological processes in living systems. The active site of this class of proteins consists of a heme cofactor (Fe-protoporphyrin IX (FePPIX)), with the iron atom covalently linked to the protein through an “axial” amino acid ligand (typically histidine (1,2) or cysteine (3,4) fulfill this role, although other axial ligands like proline (5,6) or methionine (7,8) are also found). Over the years, there has been a continuous effort to study the structure, function, and dynamics of heme containing systems using a wide variety of techniques (9–24). Important progress in understanding the functionality of heme proteins has been achieved by studying heme model compounds (25–33), where the effect of the surrounding protein is eliminated. Here we report studies that focus on the low frequency (<300 cm⁻¹), thermally accessible, vibrational modes of several heme systems. The low frequency density of states (LFDOS) is probed using an ultrashort laser pump-probe impulsive stimulated Raman scattering technique referred to as femtosecond coherence spectroscopy (FCS).

FCS utilizes the broad bandwidth of a femtosecond pump pulse to create coherences between the vibrational eigenstates of the heme system under investigation (34–46). The delayed probe pulse creates a third order electronic polarization modulated by the vibrational coherence, which gives rise to a self-heterodyned coherent signal along the probe beam direction. When electronic resonance is involved (e.g., excitation in the Soret band), the coherences that are coupled to the electronic excitation are strongly enhanced, in analogy to resonance Raman spectroscopy. The observed signal depends upon the timing between pump and probe pulses and can be thought of as a monitor of the pump-induced transient absorption as the delay is changed. The bandwidth of the typical laser pulses used in the current experiments is 200–300 cm⁻¹. This bandwidth optimizes the excitation and detection of low frequency modes in the region between 20 and 300 cm⁻¹, which are not accessible using traditional Raman techniques.

FCS experiments on heme systems have demonstrated the presence of rich information content in the low frequency region, along with the somewhat surprising observation that heme modes below 100 cm⁻¹ are not overdamped and diffusive. Since heme modes in this region of the spectrum are significantly excited at ambient temperature, and FCS measurements have demonstrated that they do not rapidly dissipate their vibrational energy to the environment, they are likely candidates for reaction coordinates associated with the broad class of biochemical reactions mediated by heme proteins. It has also been suggested that directed energy transfer to distant protein sites can be mediated by such modes (23). Further studies of low frequency modes in heme model systems are presented here to achieve a better understanding of functionally important motions in heme protein systems. We report on a series of experiments involving Fe²⁺PPIX, complexed with either 2-methyl imidazole (2MeIm) or water, with the objective of classifying the low frequency heme spectrum and its dependence on the strength of the axial ligand.

One of the motivations for this study was the observation that the low frequency spectrum of heme proteins is systematically affected by the specific heme axial ligand. We present below the low frequency vibrational spectra of myoglobin (Mb) and horseradish peroxidase isoenzyme C (HRPC), which have histidine as the axial iron ligand, along with cytochrome P450 and chloroperoxidase (CPO), which have cysteine as the axial ligand. Such experiments have led us to hypothesize that distortions of the heme geometry, possibly induced by the strength of the axial ligand, play a significant role in determining the low frequency mode structure of the heme group.

Because the LFDOS can be affected by the interaction of the chromophore with the surrounding protein environment, it is necessary to separate the contributions of axial ligation from those of the protein surroundings. As a result, we investigate heme model compounds, where protein interactions are absent. The results suggest that the addition of a strong axial ligand “softens” the low frequency modes and at the same time increases the barrier for the binding of CO, presumably because of increased heme distortion that moves the iron further out of the heme plane (33). Comparisons of femtosecond coherence spectra of the isolated heme (complexed with strong and weak axial ligands) allow us to estimate the changes in force constants associated with the low frequency heme distortions. The softening of the low frequency force constants evidently makes the heme more flexible and allows for a larger iron out-of-plane (doming) displacement. The magnitude of the equilibrium heme doming displacement between the CO-bound and unbound states (i.e., the linear coupling reorganization energy) remains the dominant factor in determining the enthalpic barrier (47–49).

MATERIALS AND METHODS

Sample preparation

Horse heart myoglobin and HRPC were purchased from Sigma Chemical (St. Louis, MO) as lyophilized salt-free powder and used directly without further purification. To prepare the reduced species the proteins are first dissolved in potassium phosphate buffer (pH 7.5, 0.1 M) and degassed for 20 min under argon atmosphere. The concentration of protein is adjusted so that the final absorbance of the reduced species is ∼1 OD/mm of pathlength, at the pump wavelength. Subsequently, the samples are transferred into a glove box and 3 μl of 1 M sodium dithionate (Na₂O₄S₂) is added to 250 μl of buffered sample to obtain the deoxy species. The reduced samples are then transferred into the sample cell and insulated against oxygen contamination. The ferric cytochrome P450_CAM sample was provided by Professor T. L. Poulos and the reduced species were prepared following the same procedure as described above. The ferric chloroperoxidase (CPO) sample was provided by Professor J. H. Dawson. The sample was dissolved in 50% glycerol (v/v) potassium phosphate buffer (pH 5, 0.1M), degassed, and transferred into the glove box. The reduced species was obtained by adding 7 μl of 1 M sodium dithionate to 250 μl of buffered sample. For all samples, the absorption spectra were recorded (Hitachi U-3410) after the preparation procedure to confirm that heme iron reduction was achieved and that it was complete.

Ferric protoporphyrin IX chloride (hemin) was purchased from Porphyrin Products (Logan, UT) and dissolved in 1 M NaOH. Small aliquots of this highly concentrated solution were then added to an 80% (v/v) glycerol solution with final concentration of hemin between 50 and 100 μM, depending on the laser excitation wavelength. Samples were degassed for 30–35 min under argon atmosphere to remove the dissolved oxygen and then transferred into the glove box and reduced by addition of a small amount of degassed sodium dithionite. When preparing the 2MeIm-(Fe²⁺)PPIX sample, 50 μl of saturated 2MeIm solution was added to the sample before degassing, so that the imidazole concentration in the final sample is ∼0.1 M. The final samples were transferred into an airtight spinning cell and the absorption spectra were recorded before and after the FCS experiments.

Laser system

The laser system used for FCS measurements consists of a tunable (750–960 nm) Ti-Sapphire oscillator (MIRA 900, Coherent (Santa Clara, CA)) pumped by a diode laser (Verdi 10, Coherent (Santa Clara, CA)). The oscillator is able to generate 50–100 fs pulses at a repetition rate of 76 MHz with energy of ∼10 nJ/pulse. To resonantly excite the samples in the Soret band, the infrared output of the laser is frequency doubled in a 250-μm BBO crystal and then chirp compensated by a pair of SF10 prisms to within 10% of the transform time-bandwidth limit. Subsequently, the laser light is split into a pump arm and a probe arm, with a power ratio of 2:1 between the two. The pump beam is modulated using an acousto-optic modulator (AOM) (Neos Technologies, Melbourne, FL) at 1.5 MHz. Before reaching the sample, the pump and probe beam polarizations are adjusted to be perpendicular. The time delay between the pump and probe pulses is controlled by a Newport Klinger (Irvine, CA) translation stage in steps of 1 μm (6.66-fs steps in the time domain). Both beams are focused into the spinning sample cell using a three-inch achromatic lens in a near parallel geometry. After the sample, the beams are recollimated and the pump light is spatially blocked (using a pinhole) and extinguished by a polarization analyzer that only allows the probe light to pass.

The detection step of the experimental procedure allows us to focus on different frequency ranges of the coherent signal. In an “open band” detection scheme we employ a photodiode to measure the entire spectral bandwidth of the pulse probe. This kind of measurement results in better fidelity for the detection of low frequency modes. The “detuned” or “dispersed” detection scheme, on the other hand, allows us to selectively enhance higher frequency regions of the coherent signal (8,36,45,50). In this case, a photomultiplier tube (PMT) coupled to a monochromator is employed for detection, resulting in increased amplitude and superior detection of the higher frequency components in the coherent signal. The detuned detection scheme lets us compare the FCS results against frequency domain techniques like resonance Raman spectroscopy, which can be helpful in the data analysis process.

Data analysis

The experimental FCS data have two components that result from different sources, population transfer and vibrational coherence. The dominant population transfer components are represented by exponential decays. Although these components carry important information regarding various dynamic processes (e.g., ligand rebinding dynamics and/or cooling and spectral diffusion of the lineshape) they must be removed to reveal the residual coherence signal. Due to the large amplitude of the electronic population signals (generally about two orders of magnitude larger than the coherence signal) special precautions have to be taken for the fitting procedure. The data analysis follows a sequential approach. We first employ a maximum entropy method (MEM) algorithm to fit and subtract the monotonic decay, to retrieve the oscillatory signal. The MEM approach removes assumptions regarding the number of exponential decay processes that might be present.

The oscillatory coherence signal comes from the superposition of vibrational states coupled to the resonant electronic transition. This coherent superposition is lost a few picoseconds after the excitation due to homogeneous and inhomogeneous decoherence processes that cause the oscillatory signal to damp as a function of time. To quantify the coherent signals, the residual left after the removal of exponential decay is fit to a sum of damped cosine functions using a linear predictive single value decomposition (LPSVD) algorithm. There are a few parameters that can be controlled during the fitting procedure, such as the number of oscillations or the time domain of the data. Given the fact that a small amount of noise is always present in the experimental data, we use the low frequencies observed in the Raman spectrum to help avoid over- or underfitting of the data.

We first analyze the detuned data (which optimizes the detection of the higher frequencies within the pulse bandwidth) to make sure that the global fitting parameters (such as the number of oscillators, noise level, and time domain of the data) optimize the correlation with the frequencies determined independently from the Raman spectrum. The power spectra obtained from the detuned measurements generally extend below 200 cm⁻¹, which represents the lower limit cutoff for Raman measurements. After analysis of the detuned data, we consider the open band experiment and compare the frequencies in the overlapping regions. Examination of the data from numerous independent samples has generally produced strong correlations between the frequencies extracted using the three experimental conditions (Raman, detuned FCS, and open band FCS). However, data from protein samples have better signal/noise than the heme model compounds because the damping timescale of the coherence signal is found to be longer in the protein environment. As a result, the correlations of the femtosecond coherence and Raman spectra are generally better in proteins than for heme model compounds.

EXPERIMENTAL RESULTS

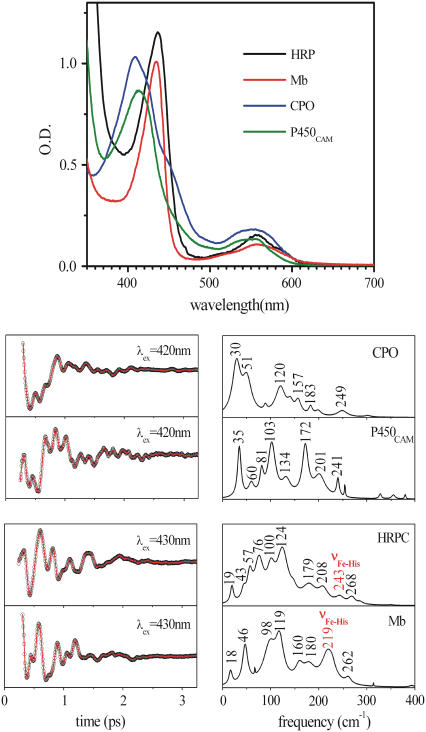
Fig. 1 shows the absorption spectra and the low frequency femtosecond coherence spectra, obtained using Soret band excitation, of four ferrous heme protein samples (five-coordinate, high-spin) having either histidine (HRP, Mb) or cysteine (CPO, P450_cam) as axial ligands. Most of the modes in the low frequency region have not been formally assigned, although density-functional theory calculations of model compounds suggest that the modes below ∼150 cm⁻¹ are associated with out-of-plane motions of the heme, such as doming, ruffling, saddling, and waving (M. Kubo, unpublished data). The iron-histidine (Fe-His) stretching modes of the histidine ligated samples are labeled as such in the figure. It is noteworthy that, for the cysteine bound species, the lowest frequency mode appears between 30 and 35 cm⁻¹, whereas in the histidine bound samples modes appear near 40–45cm⁻¹. Such differences at low frequency are significant because the percentage change in the mode frequencies is on the order of 25–50%.

FIGURE 1.

Top panel shows the absorption spectra of the reduced species of HRP, Mb, CPO, and P450_cam. The lower left panels display the FCS data (circles) and fits (solid line). The lower right panels show the corresponding LPSVD power spectra.

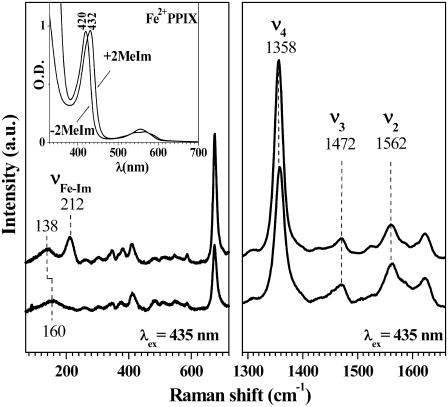
To single out the effect of axial ligation on the low frequency modes of isolated heme systems, FCS measurements on Fe²⁺PPIX in the presence (2MeIm-Fe²⁺PPIX) or absence (H₂O-Fe²⁺PPIX) of 2MeIm were performed. When 2MeIm is bound to FePPIX, this model system closely mimics the active site of myoglobin and preserves many important physical characteristics found in the native protein molecule. We use optical absorption and resonance Raman spectroscopy to probe the heme models as can be seen in Fig. 2. The 2MeIm bound sample has a Soret peak at 432 nm and its absorption spectrum closely resembles that of deoxy-myoglobin (Soret peak at 435 nm). The sample without 2MeIm has a Soret peak that is shifted to the blue, with a maximum near 420 nm. Both optical absorption spectra exhibit features (e.g., asymmetric lineshape) characteristic of a ferrous five-coordinated heme (51). This assignment is confirmed by the position of Raman marker bands (52) presented in Fig. 2. Both samples are in a ferrous five-coordinate, high spin state (S = 2) configuration. In addition, the Raman spectrum of the 2MeIm-Fe²⁺PPIX sample has a strong peak at 212 cm⁻¹, which has been previously assigned as the Fe-2MeIm stretching band (2,53,54). This mode does not appear in the Raman spectrum of the Fe²⁺PPIX sample without added 2MeIm, which is consistent with this assignment. From the above measurements we conclude that a water molecule is bound to the ferrous heme iron atom as the fifth axial ligand. (In the absence of 2Melm, the hydroxide anion is another possible heme ligand. However, it is more likely to bind to the positively charged ferric heme than to the charge neutral ferrous heme. We refer to “water” ligation throughout the text, with the understanding that hydroxyl ligation is also a possibility.) Although there are distinct changes in the heme electronic structure in the absence of the 2MeIm ligand (as reflected by changes in the Soret peak position), the Raman data show the central metal ion preserves its five-coordinate high-spin structure.

FIGURE 2.

Raman spectra of the +2MeIm (upper) and the −2MeIm (lower) Fe²⁺PPIX samples with laser excitation at 413.1 nm. The inset shows the corresponding absorption spectra of the two species.

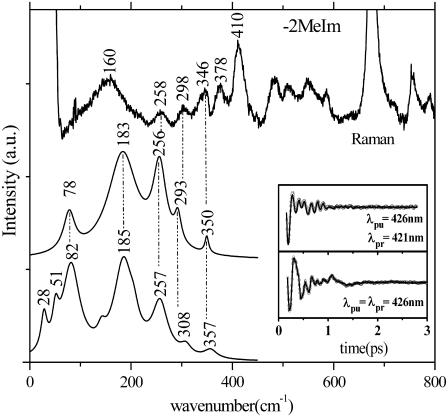
We performed a series of FCS experiments on Fe²⁺PPIX with and without 2MeIm (referred to as +2MeIm and −2MeIm, respectively) using both the open band and detuned experimental configurations. To optimize the comparison of oscillatory signals, we excite and probe the ±2MeIm samples with 60-fs laser pulses at 426 nm, in resonance with the Soret band. Both samples show excellent stability in time, with no changes recorded during the experimental FCS measurements. Fig. 3 shows a set of experiments in the absence of 2MeIm that utilize Raman, detuned, and open band FCS. The Raman experiments are unable to probe effectively below 150 cm⁻¹ due to limitations brought on by Rayleigh and quasielastic light scattering and the uncertainties associated with the low frequency cutoff filters used to limit the large light flux in the region of laser excitation. As can be seen from the FCS data in the figure, there is significant vibrational activity between 20 and 300 cm⁻¹. In the region above 200 cm⁻¹ the Raman spectrum agrees reasonably well (to within few cm⁻¹) with the detuned FCS experiment (upper curves). Recall that the detuned experimental configuration selects for the higher frequency vibrational components contained in the third order polarization signal (36). The open band experiment (lower curves) reveals the lowest frequency components (<200 cm⁻¹) of the spectrum with greatest fidelity, so the higher frequency components are somewhat less reliable under these conditions. Below 200 cm⁻¹, it can be seen that modes at ∼80 cm⁻¹ and ∼180 cm⁻¹ dominate the spectrum. The broad Raman mode in the 150–180 cm⁻¹ region is found at a somewhat lower frequency than the 180 cm⁻¹ mode observed using FCS. This behavior is not understood, but it could potentially arise from artifacts induced by the laser cutoff filter used in the Raman experiment.

FIGURE 3.

Correlations between Raman and FCS for the −2MeIm sample. The inset shows the FCS data and the LPSVD fits corresponding to an open band detection (lower) and to a dispersed detection scheme (upper). The Raman data were measured with a 413.1-nm excitation wavelength whereas the FCS data were measured using a 426-nm excitation. The dispersed data were measured with a 0.5-nm spectral window, detuned 5 nm to the blue of the carrier frequency maximum (λ_pr = 421 nm).

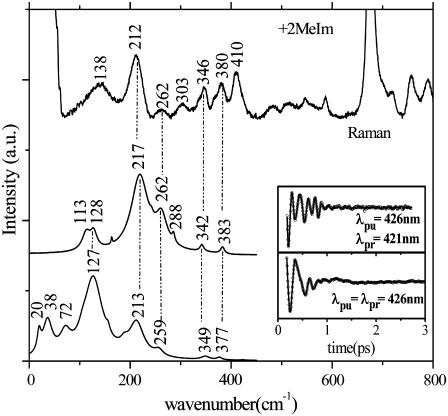
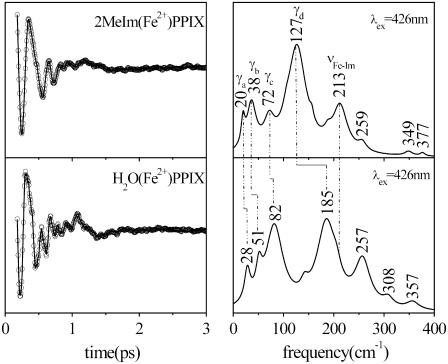
Fig. 4 displays the results for experiments with 2MeIm as the heme axial ligand and again explores correlations between Raman and FCS spectra. Here we see the appearance of the 2MeIm-Fe stretching frequency near 213 cm⁻¹ in both the detuned and open band experiment, as well as in the Raman spectrum. At lower frequencies the spectrum is dominated by peaks near ∼40 cm⁻¹ and ∼130 cm⁻¹ demonstrating how the low frequency heme modes “soften” when a strong ligand such as imidazole (or histidine) binds to the heme iron. This is shown more clearly in Fig. 5, where the two samples are directly compared and the general upshift in low frequency modes of H₂O(Fe²⁺)PPIX relative to 2MeIm(Fe²⁺)PPIX can be more easily discerned.

FIGURE 4.

Correlations between Raman and FCS for the +2MeIm sample. The inset shows the FCS data and the LPSVD fits corresponding to an open band detection (lower) and to a dispersed detection scheme (upper). The Raman data were measured with a 413.1-nm excitation wavelength whereas the FCS data were measured using a 426-nm excitation wavelength. The dispersed data were measured with a 0.5-nm spectral window, detuned 5 nm to the blue of the carrier frequency maximum. (λ_pr = 421 nm).

FIGURE 5.

FCS data, fits (left panel), and LPSVD power spectra (right panel) of the ±2MeIm samples. The experiments were run in an open band detection scheme, with a 426-nm excitation wavelength. The shifts between the main frequencies of the two samples are displayed. The Fe-Im stretching frequency near 213 cm⁻¹ is absent in the −2MeIm sample.

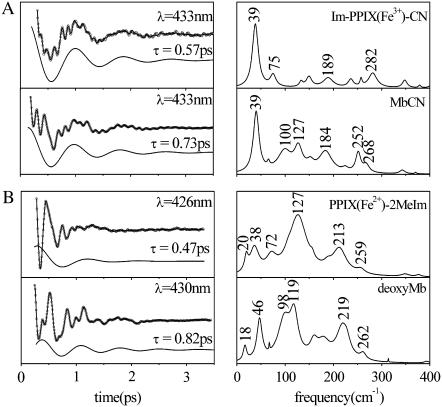
When the heme chromophore is placed into a protein matrix, it can result in geometric distortions that lead to interesting redistributions of the frequencies and amplitudes in the coherence spectra. The observed redistributions will be discussed in more detail elsewhere, in the context of theoretical calculations that are based upon normal mode decomposition of the heme distortions. Another interesting observation is that the time needed to damp the coherent signals is significantly lengthened when the heme is inserted into the protein, as can be seen in Fig. 6. We have observed this phenomenon in many samples and Fig. 6 compares some typical data for ferric and ferrous hemes. The LPSVD fits of the mode near 40 cm⁻¹ indicate that the average damping time is ∼0.5 ps for the “bare” heme compounds and ∼0.8 ps for the protein bound systems (a ∼60% increase in the damping time constant). The more rapid decay of the coherent signal in the “bare” heme model compounds is a major reason that the signal/noise achieved with these samples is somewhat less than that observed in analogous protein samples. The reduced signal/noise in the model compounds also manifests itself by a poorer correlation between the Raman and FCS data (e.g., Figs. 3 and 4) than is achieved when spectra of proteins are considered (F. Gruia, unpublished data).

FIGURE 6.

(A) FCS data, fits, and LPSVD power spectra of MbCN and its corresponding model compound. The 39 cm⁻¹ spectral component and its damping time are shown displaced from the data. (B) FCS data, fits, and LPSVD power spectra of deoxyMb and its corresponding model compound. The ∼40 cm⁻¹ spectral component and its damping time are shown displaced from the data.

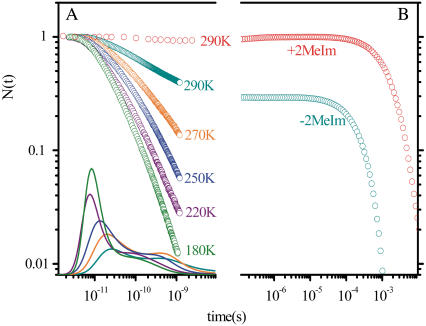
To test the functional significance of axial ligation on the heme model compound dynamics, we have also investigated (33) the rebinding kinetics of carbon monoxide (CO) to the two heme systems under investigation here (i.e., Fe²⁺PPIX ±2MeIm). Diatomic ligand rebinding studies have been used extensively as tools for understanding various aspects of heme dynamics and CO has been an especially useful ligand because its rebinding spans many orders of magnitude in time. Fig. 7 displays the CO rebinding to the Fe²⁺PPIX ±2MeIm samples. It is clear that the addition of 2MeIm as a proximal ligand drastically affects the timescales of the CO binding as can be seen from the dramatically reduced geminate amplitude and rate at 290 K (33). Thus, we conclude that there is a significant increase in the free energy barrier for CO rebinding when 2MeIm is the axial ligand.

FIGURE 7.

(A) The CO rebinding kinetics for the −2MeIm sample measured above the glass transition temperature and the resulting rebinding time constant distribution rates, obtained from the MEM fits to the experimental kinetics data. (B) The CO rebinding kinetics for the ±2MeIm samples measured at room temperature.

The enthalpic and entropic barriers can be determined by measuring temperature-dependent CO rebinding kinetics. A set of temperature-dependent data is shown in Fig. 7 for the H₂O-Fe²⁺PPIX-CO sample along with the results of a maximum entropy method (MEM) analysis. The CO rebinding kinetics were recorded at temperatures above the solvent glass transition near 180 K and show a strong temperature dependent rate reduction as the temperature is increased. The data are normalized and the MEM time constant distributions are shown on a semilog scale at the bottom of Fig. 7. Analysis of the nonexponential temperature dependence, using either the MEM distributions or a more quantitative heme model potential (55), indicates that heme structural relaxation is taking place in this temperature region. Heme structural relaxation is also supported by observed changes in the Band III region of the optical spectrum (55). The quantitative analysis of this relaxation (55) indicates that the enthalpic rebinding barrier for H₂O-Fe²⁺PPIX-CO increases from ∼1 kJ/mol to ∼6 KJ/mol between 180 and 290 K.

DISCUSSION

The FCS measurements of the low frequency spectrum in Fe²⁺PPIX model compounds, with and without 2MeIm, show a general “softening” of the low frequency heme modes when the imidazole is bound as an axial ligand to the heme iron. These findings are supported by the Raman data shown in Fig. 2, where there is a noticeable shift from ∼160 cm⁻¹ to 138 cm⁻¹ after the addition of the 2MeIm axial ligand. With the exception of this shift, and the appearance of the 2MeIm-Fe mode at 212 cm⁻¹, the Raman spectra of the Fe²⁺PPIX(±2MeIm) samples are very similar. Although the broad low frequency Raman features could potentially be affected by the strong quasielastic light scattering and the details of the cutoff filters used in the Raman experiments, they do exhibit the same trend as seen in FCS data (i.e., a general shift to lower frequency when the 2MeIm is added).

The kinetic studies of CO rebinding to Fe²⁺PPIX(±2MeIm) also show a strong effect of the axial ligand, especially on the geminate rate and amplitude, which can be understood as an increase in the recombination barrier when 2MeIm is present (33). This difference demonstrates the importance of the so-called “proximal contribution” to the ligand rebinding barrier (33,55).

However, the softening of the heme force constants, along with an increase in the CO rebinding barrier, when 2MeIm is added, appear to be mutually opposed observations. The Raman spin and coordination marker bands strongly support the idea that the two samples (±2MeIm) have very similar geometries. Both samples appear to have the central iron atom in a five-coordinate high-spin configuration (S = 2). The band frequencies of propionate (380 cm⁻¹) and vinyl (410 cm⁻¹) bending modes are also virtually the same between the two samples, suggesting very similar substituent geometry. Thus, the kinetic changes must be correlated with fairly subtle changes in the geometry of the heme plane due to axial ligand strength and steric interactions. The high-spin state of heme iron is generally associated with an out-of-plane displacement from the porphyrin macrocycle. We believe that this displacement can be different when ligands with different strength and structure bind in the axial position (e.g., 2MeIm and H₂O).

For example, the steric influence of the 2-methyl group is known to disrupt heme planarity so that the bis-2MeIm complex is not formed. Moreover, the 2MeIm is a strong ligand and it should lead to more disruption of the planar porphyrin structure and pull the iron further out-of-plane compared to a smaller and weaker ligand such as water. A larger out-of-plane iron displacement would likely affect the chemical bond strength and the geometry of the entire heme structure. In the case of 2MeIm (bulky and with strong chemical affinity toward ferrous ion) we expect the iron to be moved as much as 0.4 Å out of plane, in the direction of the ligand (56). This will weaken the four Fe-N_por bonds and possibly other chemical bonds of the heme as well. As can be seen from Fig. 5, the shifts in the FCS spectra after replacement of the H₂O axial ligand by 2MeIm suggest a general weakening of the bonds responsible for the observed (out-of-plane) low frequency heme modes.

A simple harmonic approximation can be used to estimate the decrease in the value of the heme distortion force constants, k, when 2MeIm replaces H₂O. As k is reduced, the frequency decreases according to Eq. 1 (where the reduced mass of the normal mode oscillator is denoted as μ).

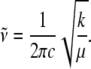(1)

Because most of the very low frequency modes remain unassigned, it is difficult to estimate the absolute force constants because it is unclear which nuclear motions within the porphyrin molecule are associated with the observed mode frequencies. Moreover, it is difficult to calculate the reduced mass μ in Eq. 1. On the other hand, we can estimate the relative effect on the force constants when H₂O is replaced with 2MeIm. After making a one-to-one correspondence between the frequencies observed in the power spectra of the two samples (cf. Fig. 5), and neglecting changes in the reduced mass we can write:

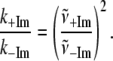(2)

Table 1 presents the numerical values for the strongest modes (γ_a, γ_b, γ_c, γ_d) identified in the FCS power spectra along with the relative change in the force constants for each mode. Note that the assigned correspondence between 127 cm⁻¹ (+2MeIm) and 185 cm⁻¹ (−2MeIm) is also based on the Raman spectra. We can calculate the average ratio of these force constants to find:

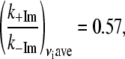so that, on average, the 2MeIm axial ligand appears to soften the low frequency force constants by nearly a factor of 2.

TABLE 1.

Low frequency modes of Fe²⁺PPIX(±2MeIm)

γi	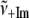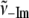(cm−1)	(cm−1)		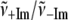k+Im/k−Im
γa	20	28	0.71	0.50
γb	38	51	0.75	0.56
γc	72	82	0.87	0.77
γd	127	185	0.68	0.46

Alternatively, we can find an “average frequency” for the ±2MeIm samples by taking the first moment of the power spectra (i.e., treating the low frequency domain as an Einstein oscillator). This treatment allows us to average over all low frequency modes without having to worry about the specific details of the one-to-one correspondence between spectra employed in the previous calculation. We find the average frequency by using:

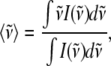(3)

and integrating the data shown in Fig. 4 over the spectral range 0–400 cm⁻¹. The result for the sample without 2MeIm is 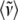_−Im = 160 cm⁻¹ and for the sample with 2MeIm 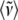_+Im = 132 cm⁻¹ (which, coincidentally, is very similar to the Raman shifts observed independently in Fig. 2). The square of the ratio of Einstein oscillator frequencies again leads to a ratio for the low frequency force constants:

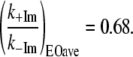This suggests a somewhat smaller change in the low frequency heme force constants than the previous calculation. This is probably because we integrated out to 400 cm⁻¹ and the frequency shifts occur mainly in the region below 200 cm⁻¹, where out-of-plane motions occur. Taken together, the two calculations imply that the ratio for force constant “softening” upon 2MeIm ligation to the heme is:

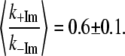(4)

Evidently the effect of the 2MeIm ligation to heme is twofold. On one hand, the axial ligation of the imidazole appears to make the heme potential “softer” and probably more anharmonic. On the other hand, this softening makes the heme more susceptible to deformation at higher temperatures and this deformation leads to a larger iron out-of-plane displacement. A quantitative analysis of the temperature-dependent kinetics of CO binding to heme model systems in the presence and absence of 2MeIm demonstrates (55) that increased iron out-of-plane displacement (linear coupling) plays the dominant role in determining the enthalpic rebinding barrier. This indicates that the softening of the heme force constants (quadratic coupling) is primarily an enabling effect, which helps to facilitate the iron displacement, although the curvature of the potential surface obviously contributes to the transition state energies as well.

For example, the room temperature kinetics (33) demonstrate that the addition of the 2MeIm results in an increase of the free energy barrier for CO binding by ∼10kJ/mol (ΔG = G_+Im − G_−Im ∼10 kJ/mol). In addition, the temperature dependence of CO rebinding to H₂O-Fe²⁺PPIX, as shown in Fig. 7, allows the estimation of the average enthalpic barrier, 〈H_−Im〉 ∼ 6 kJ/mol, at room temperature (55). If we assume that the Arrhenius prefactor, and the associated entropic barrier, are independent of the 2MeIm binding, ΔG ∼ ΔH ∼10 kJ/mol (33) so we can estimate the room temperature enthalpic barrier for the +2MeIm sample as H_+Im ∼ 16 kJ/mol.

However, it is quite possible that, due to the ultrafast nonequilibrium conditions present in these experiments, the entropic and the enthalpic barriers are not independent. The slower CO rebinding to the 2MeIm bound sample allows more time for the photolyzed CO and the heme to sample the full range of system states, leading to the possibility that the entropic rebinding barrier is larger for 2MeIm-FePPIX than for the more rapidly binding sample without 2MeIm. As a result, the estimate of H_+Im ∼ 16 kJ/mol probably represents an upper limit because some of the free energy barrier difference at room temperature (ΔG = G_+Im − G_−Im ∼ 10 kJ/mol) may be associated with a relative increase in the entropic barrier of the +2MeIm system.

It is possible to obtain a lower limit for the enthalpic barrier for CO binding to 2MeIm-Fe²⁺PPIX by using a more quantitative analysis (55), which indicates that the “distal” component to the enthalpic barrier for CO binding in the heme model systems is absent. A simple comparison to the results for MbCO, which has a total enthalpic barrier of ∼18 kJ/mol (57,58)) with 7 kJ/mol attributed to “distal” effects (55), suggests that roughly ∼11 kJ/mol might be expected for the proximal barrier of an isolated imidazole-ligated heme. Thus, we suggest that a reasonable estimate for the enthalpic barrier for CO binding to 2MeIm-Fe²⁺PPIX can be given as: H_+Im ∼ 13.5 ± 2.5 kJ/mol.

The source of the enthalpic barrier in the heme model samples has been shown (55) to be dominated by the heme iron out-of-plane displacement deformation, a₀, so we neglect the “distal” enthalpic term (H₀) and approximate the average barrier:

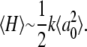(5)

By assuming that, when the 2MeIm is present, the Fe is displaced from the heme plane by ∼0.4 Å (56,59) we can estimate the out-of-plane displacement for the heme iron in the absence of the 2MeIm ligand by using:

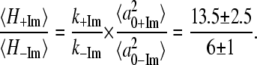(6)

From Eq. 4, a simple calculation leads to the value of 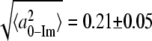Å for the bare heme without a bound imidazole ligand. Thus, the kinetics and FCS data are consistent with a model where 2MeIm binding to the heme both increases the iron out-of-plane displacement and softens the force constants. The results of this very simple analysis predict that the iron out-of-plane distortion of the “bare” heme is ∼0.2 Å (when the analogous distortion for the 2MeIm bound sample is ∼0.4 Å) and that the force constants of the 2MeIm bound heme soften to ∼60% of their value without imidazole. These results seem quite reasonable and it would be of interest to independently determine the bare heme structural parameters using other techniques, if possible.

Beyond histidine ligation and the subsequent heme distortion, the insertion of the heme into the protein leads to two other clear effects. As can be seen from Fig. 6, there is a redistribution of mode frequencies and intensities, which is presumably a direct consequence of the interaction between the heme group and the surrounding protein material. In addition, the longer dephasing times that are systematically observed for heme within the protein environment can be attributed to either decreased structural inhomogeneity or to decreased coupling to the phonon spectrum of the surroundings (pure dephasing). Measurements of the damping times as a function of temperature (F. Gruia, unpublished data) suggest that pure dephasing is an important source of damping of the low frequency modes in the protein environment. However, if there is an “induced fit” of the heme when it binds to the protein, a more homogeneous environment than found for free heme in solution is also a possibility. Additional temperature dependent studies of heme model compounds would be helpful in assessing the role of structural inhomogeneity in the damping of low frequency heme modes in solution. If inhomogeneity is the dominating source of decoherence in these systems, then the damping will be “frozen in” and independent of temperature below the glass transition. However, if solvent dephasing processes are involved, the damping times should lengthen at lower temperatures.

In summary, we have demonstrated that the low frequency spectra of the heme group are quite strongly affected when an imidazole is ligated to the iron atom. Insertion of the heme into the protein environment leads to additional perturbations, such as significantly increased dephasing times and further redistribution of the LFDOS due to heme geometric distortions induced by the protein environment and the possibility of mixing with protein modes. The results indicate that the heme bonding force constants generally soften upon imidazole or histidine binding, allowing for an easier geometric distortion of the prosthetic group. One example of the potential functional significance of these distortions involves the larger iron out-of-plane displacements that occur when 2MeIm replaces water as the axial heme ligand, resulting in a significant increase of the CO rebinding barrier. For hemoglobin, such doming displacements function as the trigger of T-R allosteric transition and cooperative ligand binding (60). Additional functional consequences can arise from other environmentally induced heme distortions. For example, heme ruffling has been proposed (61) as a stabilizing distortion for the ferric heme, and this could have significance for the understanding of NO and electron transport processes (e.g., in nitrophorin and cytochrome c). We are currently exploring the relation between various types of heme distortion and the redistribution of the LFDOS as probed by femotsecond coherence spectroscopy.