Abstract
The experiments presented in this study address the problem of how the cytoplasmic surface (proton-input side) of cytochrome c oxidase interacts with protons in the bulk. For this purpose, the cytoplasmic surface of the enzyme was labeled with a fluorescein (Flu) molecule covalently bound to Cys223 of subunit III. Using the Flu as a proton-sensitive marker on the surface and φOH as a soluble excited-state proton emitter, the dynamics of the acid-base equilibration between the surface and the bulk was measured in the time-resolved domain. The results were analyzed by using a rigorous kinetic analysis that is based on numeric integration of coupled nonliner differential rate equations in which the rate constants are used as adjustable parameters. The analysis of 11 independent measurements, carried out under various initial conditions, indicated that the protonation of the Flu proceeds through multiple pathways involving diffusion-controlled reactions and proton exchange among surface groups. The surface of the protein carries an efficient system made of carboxylate and histidine moieties that are sufficiently close to each other as to form a proton-collecting antenna. It is the passage of protons among these sites that endows cytochrome c oxidase with the capacity to pick up protons from the buffered cytoplasmic matrix within a time frame compatible with the physiological turnover of the enzyme.
Hydrogen-bonded molecules can exchange protons among them at a very high rate. In small structures, the reaction can be monitored as the continuum infrared absorption that was termed by Zundel as proton polarizability (1). In macroscopic systems, proton transfer through H-bonded networks can be quantitated by the percolation model of Careri (2), in which a semi-dried protein exhibits high proton conductivity. The surface conductivity is the only pathway for protons in the absence of bulk water. On the surface of the fully hydrated structure, the protons propagate both in the bulk and on the surface (3). The quantitation of the relative contribution of proton transfer among surface groups to the overall rate in well-hydrated proteins is the subject of this study. Previous experiments with bacteriorhodopsin indicated that, over a very short range (≈10 Å), the proton exchange among surface groups exceeds the rate of “through the bulk” proton diffusion (4, 5). The present contribution expands our studies to more complex protein systems, the redox-linked proton-pump enzymes by using cytochrome c oxidase (COX) as a model system.
The terminal heme-copper oxidases are a group of enzymes that catalyze reduction of dioxygen to water. These enzymes successively transfer four electrons to O2 while four protons (defined as “substrate protons”) are picked up to form H2O. During turnover of COX from Rhodobacter sphaeroides, electrons from cytochrome c are transferred first to copper A (CuA; in subunit II) and then consecutively through heme a, to the binuclear center heme a3/copper B (CuB; in subunit I), where bound dioxygen is reduced to water. Some of the free energy released by the redox reaction is conserved by pumping protons (≈1 H+/electron) across the membrane. The direction of the proton pump is antipodal to the electron flux (for a recent review, see ref. 6). Thus, the overall reaction catalyzed by COX is associated with removal of eight protons from the inner space, four by the formation of water, and another four by the pumping machinery.
The crystal structures of COX from Paracoccus denitrificans (7) and bovine heart (8, 9) have been recently determined to atomic resolution. The amino acid sequence of the R. sphaeroides enzyme (three subunits) is highly homologous (≈70% similarity) to that of the bovine enzyme and the kinetic, spectral, and proton-pumping characteristics of the two enzymes are the same (10, 11). Consequently, the P. denitrificans and bovine enzyme structures are used as adequate models of the R. sphaeroides enzyme.
Two proton-input pathways in subunit I have been proposed. One of them, defined as the D-pathway, includes aspartate 132 [D(I-132)]§ and glutamate 286 [E(I-286)]. There is evidence that this pathway is used for uptake of both substrate and pumped protons during reaction of the fully reduced enzyme with O2 (12–15). Therefore, to avoid reduction of O2 (and uptake of substrate protons) without the uptake of pumped protons, the flux of protons through the pump must be at least as fast as the binding of protons to dioxygen as it is getting reduced. The overall turnover activity of the R. sphaeroides enzyme is ≈1,800 s−1 (10). Because two protons per electron are taken up, the average proton-uptake rate from the proton-input side is ≈3,600 s−1. This rate implies that protons must be kept available for the intra-protein processes for a time period of 280 μs. Considering the high buffer capacity of the cytoplasmic matrix, the enzyme has to overcome two dynamic limitations: to abstract a proton from the buffered medium and to keep it on the surface. These demands can be met by the combination of negative charges as electrostatic attractors for protons and relatively high pK moieties, which will retain the proton on the protein.
In the present study, we attached a pH-sensitive, surface-bound pH probe, fluorescein (Flu), to a fortuitous site, Cys-223 of subunit III, that is located on the proton-input side of the protein ≈25Å from D(I-132) (see Fig. 1A). The dynamics of its protonation was measured by subjecting the preparation to short, reversible, proton pulses (16, 17). The kinetic analysis of the results was carried out in correspondence with the projected structure of the protein. The outcome of this structural-kinetic analysis is that the protonation of the bound Flu is assisted by a nearby carboxylate and a single histidine moieties. We propose that the same mechanism is operating in the delivery of protons to the physiological sites of proton entry to the protein (18). These results imply that the surface of the protein operates as an efficient proton collecting antenna; the carboxylates pick the protons from the bulk and rapidly transfer them to the histidine moieties that keep them, as covalently bound protons, for a period compatible with the turnover time of COX.
Figure 1.
(A) Model of the R. sphaeroides COX structure. The model structure was calculated from the bovine heart enzyme structure (ref. 9; 1OCC.PDB) by using the program modeller (31). The enzyme subunits I, II, and III are color coded in magenta, red, and yellow, respectively. The positions of D(I-132), the entry point to the D-pathway (see text) and Cys(III-223), where fluorescein is bound, are shown. (B) Detailed structure around C(III-223). Acidic (Asp/Glu), basic (Arg/Lys), and His residues are marked in red, blue, and yellow, respectively. Acidic, basic, or His residues within ≈10 Å from C(III-223) are H(III-152), H(III-237), H(III-248) (not shown), E(III-241), and R(III-226). The radii of the spheres drawn around the atoms are 0.8 Å.
MATERIALS AND METHODS
Preparation of Enzyme.
The enzyme was prepared as described (19). The turnover activity was measured as described (19). Both the unlabeled and labeled enzyme displayed a turnover activity of ≈1,800 s−1 at pH 6.5.
Binding of Flu to COX.
A solution of the enzyme at a concentration of ≈10 μM in 0.1% n-dodecyl-β-d-maltoside (Anatrace), 100 mM KCl, was supplemented with fluorescein-5-maleimide at a molar excess of 1–10 per enzyme molecule. The mixture was incubated overnight at 4°C, and the unbound Flu was removed on a Sephadex G-25 column (PD10, Pharmacia) or by dialysis against 100 mM KCl and 0.1% n-dodecyl-β-d-maltoside at pH ≈7.5. The concentration of the enzyme was determined by using an absorption coefficient of 24 mM−1 cm−1 for the reduced-minus-oxidized enzyme at 605 nm (20), whereas Flu was determined from its absorbance at 496 nm at pH ≈8.5, using an absorption coefficient of 63 mM−1 cm−1. Within the indicated molar excess ratio, the stoichiometry of bound Flu was found to be 0.8 ± 0.1.
Gel electrophoresis of the labeled COX indicated that the Flu label was bound only to subunit III. Of the three cysteins in this subunit, two (C143 and C146) are buried deeply inside the membrane-spanning part of the protein and one C(III-223) is exposed. We assume C(III-223) to be the Flu-binding site.
Proton Pulse Technology.
Each protein sample was monitored under a set of varying initial conditions: the pH of the solution, which alters the ratio of the protonation state of all proton-binding sites, and the φOH concentration (9 and 27 μM). The dynamics were measured at two time scales (30 and 300 μs). The transient absorbencies were recorded at 458 nm and 496 nm. The transients were converted to concentrations by using the differential (alkaline minus acidic) extinction coefficients of φO− and Flu of 24 and 50 mM−1 cm−1, respectively (21).
Mode of Analysis.
The analysis was carried out by numeric simulation of the observed transients by using a set of coupled nonlinear differential rate equations that correspond to all acid-base reactions proceeding in the perturbed space (for details, see refs. 16 and 17). The shape of the computed curves was modulated by the rate constants that were used as adjustable parameters (16, 17, 21–27). The simulation was taken as valid if the dynamics, computed with one set of rate constant, were superposition over the transients, measured under varying initial conditions, within the limits of the electronic noise of the measuring system.
RESULTS
Titration of the Covalently Bound Flu.
The pK of the bound dye was measured by recording the absorption spectrum of the protein. The measured pK (7.55) is significantly higher than that of the free dye (6.3). Considering that the titration was carried out in 100 mM KCl solution, the pK shift suggests that the dye is bound in a hydrophobic environment that favors the protonated state of the indicator.
Pulse Protonation of the Flu-Labeled COX.
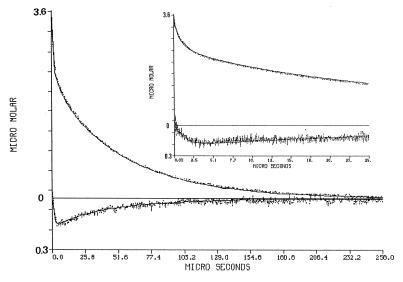
The excitation of the φOH molecule by the laser pulse causes a transient shift of its pK, from pK0 = 7.7, down to pK* = 1.4. During the brief period in which the molecule is in the excited state (≈6 ns), it dissociates to a pair of a solvated proton and an excited anion. When φO−* relaxes to its ground state, the system is in a temporary disequilibrium, in which both protons and φO− are above the equilibrium level while the φOH population is slightly depleted. Upon excitation, there is a rapid, unresolved, rise of the absorbance at 458 nm (Fig. 2, upper curves). Its magnitude corresponds with the amount of φO− ions and the discharged protons. The relaxation of the transient at 458 nm is characterized by an initial fast decay, lasting ≈1 μs, in which the φO− ions react, in a diffusion-controlled reaction with the free protons. During that period, all other proton-binding sites compete for the free protons, and their incremental protonation is proportional to their concentration, state of ionization, and the rate constant of the reaction (23, 24). The fraction of the protons bound to the protein can be estimated from the amplitude of the φO− signal at the time point of its slow down. As seen in Fig. 2, at the end of the rapid phase of reprotonation, only ≈20% of the φO− ions regained their φOH state. Thus, the residual ≈80% of the protons had reacted with other sites. Close examination of the Flu transients (Fig. 2. bottom curves; please note that the Y scale of the lower part of the figure is drawn on a 10-fold-expanded scale) reveal that the protonation of the Flu proceeds well after the time point in which the protonation of φO− had slowed down, suggesting that the Flu is supplied by proton, which were already bound to some surface sites of the protein. This feature is the subject we wish to quantitate.
Figure 2.
Dynamics of proton transfer between bulk and surface of cytochrome oxidase. The protein, (3.5 μM labeled by Flu, 85% efficiency) was suspended in 0.5% n-dodecyl-β-d-maltoside (pH 7.1) in the presence of 27 μM φOH. The solution was subjected to a train of laser pulses (2.1 mJ/pulse) at a repetition rate of 10 Hz. The transient absorbance after each pulse was monitored either at 458 nm (top curve) or at 496 nm (bottom curve). The transients were converted to molar concentrations of the φO− and the protonated Flu species as detailed in the text. Please note that the Flu signal is drawn on a 10-fold scale. The Inset depicts the dynamics as measured at a faster sweep rate of the oscilloscope. The solid lines in the figure are the reconstructed dynamics calculated by the numeric integration of the differential rate equations by using the parameters listed in Table 1.
The Kinetic Model Used for Simulation the Reaction.
The three-dimensional structure of R. sphaeroides COX was modeled, and the number of exposed carboxylates and histidine moieties was determined. On the cytoplasmic side there are 16 carboxylates and 14 histidine moieties. On the extracellular face, there are 30 carboxylates, some of them are in close proximity to Lys or Arg groups, which reduce their proton affinity. The two faces of the protein are separated by a hydrophobic band that is covered by a “collar” of the suspending detergent. All of these moieties contribute to the buffer capacity of the protein and thus modulate the rate of re-protonation of the φO− ion, which, as a free ion in solution, has a direct access to all of these sites.
The dynamics of the Flu moiety is controlled not only by its reaction with free protons but also through rapid proton transfer reactions among the proton-binding sites at the immediate vicinity of the Flu. Accordingly, for the modeling of the protonation of the Flu attached to COX, one must account for the proton-binding sites at a distance of ≈10 Å from the Cys-223 residue of subunit III. Fig. 1B depicts the projected domain where the Flu is bound. From this structure, we estimated that only one carboxylate [E(III-241)] and up to three histidine moieties [H(III-152), H(III-237), and H(III-248)] might affect the dynamics of the bound Flu.
The kinetic model used for the simulation of the dynamics describes the protein as made of three populations of proton-binding sites:
1. All sites present on the extracellular space of the protein were treated as a single population (bufferEC) of proton-binding sites, all characterized by the same pK value and the same rate constant of reaction with the soluble reactants. Because of the presence of the detergent collar, this population could not be engaged in rapid proton-transfer reaction with the Flu-labeled side of the protein. Consequently, this population affects only the dynamics of the φO− signal.
2. The cytoplasmic proton-binding sites made up the second population. It interacts with the free diffusing φO−; yet, because of proton exchange with the Flu-binding domain, it also affects the Flu signal. This population consists of carboxylates and histidine moieties, each characterized by average kinetic and thermodynamic properties (COO−av and Hisav, respectively). The number of sites was first assumed to equal that of the surface-exposed groups on the cytoplasmic side of the protein. The simulations indicated that the full quota of exposed binding sites endowed the protein with a buffer capacity too high to fit the measurements. Accordingly, the number of the histidine and carboxylates was reduced to a level where the dynamics could be reproduced. The two constituents of the second population were characterized by their rate of reactions with the soluble reactants (H+,φO−) and their rate of proton transfer with the Flu-binding domain.
3. The third population was made of the Flu moiety, the E241 carboxylate, and either 1, 2, or 3 histidine moieties.
To simulate the observed dynamics, we linked the φOH, the Flu, and the proton-binding populations by a set of equilibrium equations, introduced a temporal perturbation in the state of ionization of φOH, and propagated the perturbation to all other reactants by a set of coupled, nonlinear differential rate equations that were linked by the detailed balance principle (16, 17, 24, 27). The numeric integration of the equations, using the rate constant as adjustable parameters, reconstructed the dynamics with the accuracy shown by the continuos lines overlaying the experimental curves as in Fig. 2.
The simulation of the dynamics gains accuracy with the number of independent measurements, carried out under varying boundary conditions. The experiment, as in Fig. 2, was repeated within the pH range 6.8–7.7. For each pH value, we analyzed eight independent experiments, and all of them were fitted, within the limits set by the electronic noise, by the same set of rate constants. The fit of the φO− signal was insensitive to the number of histidine moieties at the vicinity of the Flu. On the other hand, the Flu signal could be fitted if only one histidine was located within the distance of a fast proton transfer. The rate constants and the pK values of the reactive moieties are listed in Table 1.
Table 1.
The kinetic and equilibrium parameters characterizing the dynamics of proton transfer between bulk and the surface of cytochrome oxidase
| pH | 6.82 | 7.1 | 7.31 | 7.7 |
| pK(Flu) | 7.55 | 7.55 | 7.55 | 7.55 |
| pK(BufferEC) n = 12 | 4.85 | 4.85 | 4.85 | 4.85 |
| pK(COO−near) n = 1 | 5.05 | 5.05 | 5.05 | 5.05 |
| pK(Hisnear) n = 1 | 6.35 | 6.35 | 6.35 | 6.35 |
| pK(COO−av) n = 15 | 4.4 | 4.4 | 4.4 | 4.4 |
| pK(Hisav) n = 10 | 6.35 | 6.35 | 6.35 | 6.35 |
| Flu + H+ | 1.5 ± 0.25 E 10 | 1.75 ± 0.25 E 10 | 1.5 ± 0.25 E 10 | 1.5 ± 0.25 E 10 |
| Buffer−EC + H+ | 2.0 ± 0.3 E 10 | 1.5 ± 0.3 E 10 | 2.0 ± 0.3 E 10 | 1.75 ± 0.3 E 10 |
| Flu + φO− | 1.0 ± 0.05 E 9 | 1.0 ± 0.05 E 9 | 1.0 ± 0.05 E 9 | 1.0 ± 0.05 E 9 |
| COO−near + H+ | 2.0 ± 0.3 E 10 | 2.0 ± 0.3 E 10 | 1.5 ± 0.3 E 10 | 1.5 ± 0.3 E 10 |
| COO−near + Flu | 1.0 ± 0.1 E 12 | 0.7 ± 0.1 E 12 | 0.4 ± 0.1 E 12 | 0.25 ± 0.1 E 12 |
| Hisnear + H+ | 0.5 ± 0.4 E 10 | 0.5 ± 0.4 E 10 | 0.5 ± 0.4 E 10 | 0.5 ± 0.4 E 10 |
| Hisnear + Flu | 3.5 ± 0.3 E 10 | 1.5 ± 0.25 E 10 | 1.2 ± 0.25 E 10 | 0.3 ± 0.3 E 10 |
| Hisnear + COOnear | 0.5 ± 0.4 E 10 | 0.5 ± 0.4 E 10 | 0.5 ± 0.4 E 10 | 0.5 ± 0.4 E 10 |
| COO−av + H+ | 3.0 ± 0.5 E 10 | 3.0 ± 0.5 E 10 | 3.0 ± 0.5 E 10 | 3.0 ± 0.5 E 10 |
| COO−av + Flu | <1.0 E 7 | <1.0 E 7 | <1.0 E 7 | <1.0 E 7 |
| COO−av + COOnear | <1.0 E 9 | <1.0 E 9 | <1.0 E 9 | <1.0 E 9 |
| COO−av + Hisnear | <1.0 E 9 | <1.0 E 9 | <1.0 E 9 | <1.0 E 9 |
| Hisav + H+ | 1.0 ± 0.3 E 10 | 1.0 ± 0.3 E 10 | 1.0 ± 0.3 E 10 | 1.0 ± 0.3 E 10 |
| Hisav + Flu | 5.0 ± 0.5 E 8 | 5.0 ± 0.5 E 8 | 5.0 ± 0.5 E 8 | 5.0 ± 0.5 E 8 |
| Hisav + φOH | 3.5 ± 0.2 E 8 | 4.0 ± 0.2 E 8 | 3.5 ± 0.2 E 8 | 1.1 ± 0.2 E 8 |
| Hisav + COO−near | 2.0 ± 0.5 E 10 | 2.0 ± 0.5 E 10 | 1.0 ± 0.5 E 10 | 1.0 ± 0.5 E 10 |
| Hisav + Hisnear | 7.5 ± 0.25 E 9 | 7.5 ± 0.25 E 9 | 7.5 ± 0.25 E 9 | 7.5 ± 0.25 E 9 |
| Hisav + COO−av | 2.5 ± 0.5 E 10 | 3.0 ± 0.5 E 10 | 4.0 ± 0.5 E 10 | 4.0 ± 0.5 E 10 |
n, number of reactive groups in each type of reactants.
The bold face lines denote the reactions which are the main pace makers of the overall process; the italic lines denote the reactions between reactants bound to the surface and the rate constants are of virtual second order reactions.
DISCUSSION
The Kinetic Model.
The simulations presented in this study were based on a set of assumptions that were derived from the structural model of the protein as shown in Fig. 1. According to the projected structure, residue C(III-223) is not fully exposed. Consequently, the binding of Flu may distort the domain. Considering these arguments, the number of proton-binding sites, which assist in the protonation of the Flu, has to be deduced from the kinetics whereas the projected structure serves only as a guideline. The results of the simulations were very explicit; the reconstruction of the Flu dynamics could be attained only with the presence of one carboxylate and one histidine at a proton-transfer distance from the Flu moiety. Omitting either the carboxylate or the histidine forfeited the quality of the fit. Similarly, having more than one histidine in the site generated Flu signals that could not be matched with the experimental one.
The rate constants given in Table 1 are pH independent, except for the proton transfer between the Flu and the two accessory sites COO−near and Hisnear. Both rates appeared to decrease steadily with increasing pH. Considering the fact that the Flu moiety is involved in the two reactions, it is tempting to attribute the deceleration to some changes in the exposure of the Flu. This explanation seems to be inadequate because the rates of the reaction of the Flu with free protons and with the φO− are pH independent. An alternative explanation to the phenomenon is local rearrangement of the amino acid residues near the C(III-223) site. Until now, we have encountered only twice the case in which the kinetic behavior of one moiety on a protein exhibits a pH dependence while all others parameters were constant. One case was Cytochrome c (tuna) in which the protonation of His-26 was pH dependent (Y. Marantz, unpublished results.). The second case was bacteriorhodopsin, whose C-terminal peptide was removed by tryptic digestion, in which the Coulombic overlap of two carboxylates was found to vary around pH = 7.3 (S. Checover, unpublished results).
Quantitative Evaluation of the Rate Constants.
Some of the rate constants given in Table 1 are printed in bold face. The corresponding reactions were found to be the most critical for defining the magnitude and the shape of the curves. Any variation in their values forfeit the quality of the fit to an extent that it cannot be ameliorated by changing the values of all other rate constants. The other constants were somewhat less stringent as seen by their larger limits of variation. The distortion of the simulation curves caused by a change in one of these rates could be adjusted by varying some rate constants, all within the limits given in Table 1. This high level of coherence between the rate constants is the consequence of the detailed balance principle that couples the state of protonation of all reactants through the constancy of total proton content. Because of these internal restrictions, the limit of confidence is as high as given in Table 1.
The reaction of well exposed moieties with free protons should have the magnitude of diffusion-controlled reactions, as given by the Debye–Smulochovski equation (16, 17, 24–27). For well exposed single proton-binding sites on a protein or a membrane, the value is 1–2 1010 M−1 s−1. The rate of the reaction of the Flu with the free protons has a value of 1.5 × 1010 M−1 s−1. Similar rates had been measured for indicators adsorbed to micelles (23) or bound to bacteriorhodopsin (4, 5). The collisional deprotonation of the Flu-H+ by the φO− also is indicative to an unrestricted access of φO− to the bound dye. These rate constants of reaction with free-diffusing species implies that although cysteine 223 might have a limited exposure, the bound Flu is well exposed. The rate constants of the protonation of the COO−near and Hisnear as well as COO−av and Hisav, all fall in the range of diffusion-controlled reactions.
The exchange of protons among surface groups (marked by italics in Table 1) is quantitated by a virtual second order rate constant (22, 24, 25). This term quantitates a reaction in which a proton dissociates from one site and is immediately taken by a nearby acceptor. In the case that the donor–acceptor distance is shorter than that of a homogeneous distribution of the same reactants, the magnitude of the virtual rate constants is much larger than that of a diffusion-controlled reaction and values as high as 1012 M−1 s−1 may be obtained. Recently, Sacks et al. (21, 22) reported that the passage of a proton from the carboxylate group, at position 5 of the dicarboxy-Flu, to the oxy-anion of the chromophore had a virtual rate constant of 6 × 1012 M−1 s−1. The rate constant of proton transfer between the COO−near and Flu has a virtual second order rate constant of 1.2 × 1012 M−1 s−1. This value is indicative of a very close proximity of the carboxylate to the Flu. On the other hand, the proton transfer from COO−near to Hisnear is much slower. This observation implies that these two moieties are more apart of each other than from the Flu.
The other rates for the proton transfer among the surface groups vary from 107, like the proton transfer from the COO−AV to the bound Flu, up to ≈3 × 1010 as measured for the proton transfer between the averaged carboxylates and histidine populations. The low values are interpreted as a proton transfer between remote sites or because a positive charge is located between the donor and the acceptor (21, 22). Fast rates, like the one between COOHav and Hisav are equated with the dense packing of the carboxylates and the histidine moieties on the cytoplasmic surface of the protein. The fast reaction, together with the high abundance of these groups on the surface, endows the enzyme with an efficient mechanism for picking up protons from the bulk.
The Mechanism of Proton Transfer on the Protein’s Surface.
Examination of the traces in Fig. 2 reveal that the protonation of the Flu proceeds past the time point in which the reprotonation of φO− has been slowed, a phase of the reaction in which the released protons were taken up by the various surface groups. This incremental protonation of the Flu is attributed to reshuffling of protons among the surface groups, ending by the protonation of the Flu. This delayed proton transfer among the surface groups can be reconstructed by the differential equations that simulate the reaction.
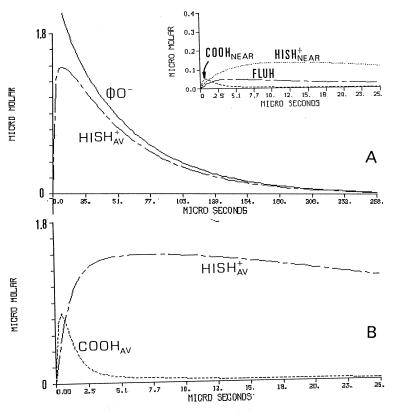
The temporal protonation of each subpopulation of proton-binding sites is presented in Fig. 3. Fig. 3A depicts the dynamics of the φO− and Hisav. During the first few microseconds, Hisav undergoes a phase of rapid protonation, functioning as the main proton-binding sites of the protein. This property is evident from the comparison with the φO− signal some 30 μs after the pulse, the two curves are of comparable amplitude. This similarity indicates that most of the released protons found their way to the exposed histidines. The dynamics of the cytoplasmic carboxylates population (COOHav) is presented in Fig. 3B, where the tracings are shown on an expanded time scale. The protonation of the carboxylates is very rapid, much faster than the protonation of the histidines (Fig. 3A), and relax to an almost prepulse level within the period in which the histidines are protonated. This kind of dynamic is typical for a proton-shuttle group that picks up protons from the bulk and delivers them to a stronger base in its vicinity.
Figure 3.
Detailed scenario of the protonation dynamics of the reacting constituents corresponding with the protonation of cytochrome oxidase. The curves correspond with the experiment presented in Fig. 2 and depict the dynamics of each of the reacting elements incorporated in the simulation. The dynamics of the φO− and the averaged histidine population (HISHav+) are shown in A. The Inset to A depicts the protonation of the Flu moiety (FLUH) and the nearby histidine and carboxylate. (B) The most initial events of the protonation of the averaged populations of the histidine moieties and the carboxylates The parameters used for the reconstruction are those generating the fitted lines in Fig. 2.
The dynamics of COO−near, Hisnear, and the Flu are shown in Fig. 3A Inset. The dynamic feature of COO−near is also of a shuttling group, it binds protons very rapidly, but immediately looses them to the two bases, the Flu and the histidine. The preferential protonation of the histidine is caused by its higher availability for binding protons; at the pH of the measurements, 85% of Hisnear is in its deprotonated state whereas the Flu is only 30%.
The Role of the Partial Reactions in Controlling the Overall Dynamics.
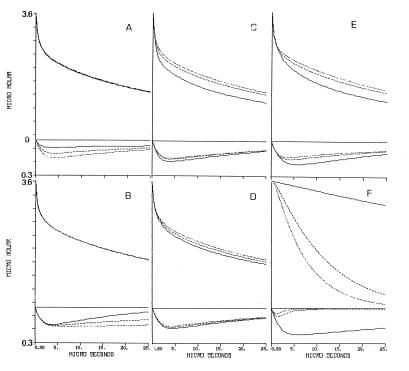
The proton exchange among nearby proton-binding sites affects their dynamics by two modes: one is the accelerated proton delivery by the shuttling groups and the second one is elongation of the proton’s dwell time on the surface by covalent binding to medium pK moieties. The effect of these terms on the dynamics of the reaction is exemplified in Fig. 4. In each frame, the magnitude of one kinetic parameter was reduced to 55% (dotted line) and 10% (solid line) of the value given in Table 1 (dashed line), and the projected dynamics were drawn. As clearly seen, each of the parameters affects the shape of the curves in its own mode; some affect mostly the Flu dynamics, the φO−, or both.
Figure 4.
A graphical presentation of the effect of the kinetic parameters on the dynamics of proton transfer between bulk and cytochrome oxidase. The tracings given in each frame correspond with the transients of the φOH and the Flu anions under conditions in which one of the rate constants characterizing the system is slowed down. Note the different scales of the Upper and Lower parts of the figure. The dotted line in each frame was drawn by using the value given in Table 1. The dashed and solid lines were calculated for the same parameter reduced to 55% and 10%, respectively. (A) The rate of protonation of the nearby carboxylate. (B) The rate of proton transfer from the near histidine to the Flu. (C) The rate of bulk proton uptake by the averaged carboxylate population. (D) The rate of bulk proton uptake by the averaged histidine population. (E) The rate of proton transfer between the averaged carboxylates and the averaged histidine populations. (F) The effect of adding buffer pK = 7.7 at concentrations of 27 μM, (solid line), 1.3 mM (dashed line), and 2.7 mM (dotted line).
Fig. 4A exhibits the effect of the rate of proton uptake by the nearby carboxylate, demonstrating its crucial role in the protonation of the Flu. Slowing the reaction effects the amplitude and dynamics of the Flu, indicating that the direct reaction of the dye with free protons is not the only path for its protonation. When the rate of protonation of the nearby carboxylate is slower than the rate of the reaction of the Flu with bulk proton, the amount of protons reaching the Flu diminished by ≈75%. This outcome demonstrates that the accessory carboxylate expands the size of the proton reactive surface of the indicator molecule. On the other hand, this pathway has a negligible effect on the φO− signal; most of the protons are stored by the surface histidine moieties so that the contribution of the Flu proton-binding capacity to the total proton balance is marginal.
The second aspect of the antenna is demonstrated in Fig. 4B, where the rate of proton transfer between Hisnear and Flu is reduced with respect to the value given in Table 1. The protonation of Flu is insensitive to the variation in the rate constant, but its subsequent deprotonation is accelerated when the rate is reduced. The slower relaxation at high rate of the surface proton transfer is caused by constant replenishment of the Flu with protons released from Hisnear (the estimated dwell time of proton on Hisnear is (≈300 μs, ref. 21). The storage of the proton on the moiety, together with the rapid exchange with the Flu, renders the histidine to be a local proton reservoir with respect to the Flu moiety. As expected, the φOH dynamics is totally independent of the proton transfer between the Hisnear and the Flu.
Fig. 4 C, D, and E demonstrate the dynamics role of the proton-binding sites, which are not in the immediate vicinity of the Flu. These moieties, which makes most of the protein’s buffer capacity, affect both the dynamics of the Flu and the φO−. Fig. 4C demonstrates the role of the carboxylates in the gathering of protons to the surface. When their rate of protonation is reduced, the reprotonation of the bulk indicator φO− is accelerated. The rapid protonation of the surface carboxylates is the main pathway for the protonation of the histidine moieties which, because of the lack of attractive charge, has an inherent slower reaction with free protons (see Fig. 3B). We have found a minor coupling between the COOav− population and the dynamics of the Flu. That coupling is because the Flu is not marking a catalytically active domain. In the case of bacteriorhodopsin, we had noted that the protonation of the orifice of the channel was assisted much by the surface carboxylates (5). Fig. 4D demonstrates that the average histidine population is not involved in the initial proton binding to the surface. Reduction of the rate of their protonation within the ranged predicted by the Debye–Smoluchowski equation (1010–109 M−1 s−1) hardly affects the dynamics.
The high number of carboxylates and histidine moieties on the surface lead to an efficient proton transfer among them, which is the most crucial reaction on the enzyme’s surface. Initially, the protons preferentially react with the carboxylates. With time they are gradually transferred to the histidine moieties which, because of their higher pK, have a slower rate of proton transfer to φO−. When the rate of inter-surface proton transfer is reduced (Fig. 4E, continuos line), there is an acceleration of proton pick-up by the φO−. The dynamics of the Flu exhibit an interesting feature; as the rate of proton transfer among the surface groups is slowed, more protons accumulate on Flu. This feature is evidence for the dynamic state of the protons on the enzyme’s surface. When the proton transfer from COO−av to Hisav is slowed, the flux of protons via COO−near and Hisnear to Flu increase.
The Effect of Buffer on the Surface-Bulk Proton Transfer.
During its catalytic cycle, COX picks protons from the well buffered cytoplasmic matrix of the cell and either pump them across the membrane or use them for the production of H2O. The progressive slowing of the enzyme’s steady-state activity at high pH values indicates that proton availability can restrict the turnover of the enzyme. The slowing of the proton-coupled electron transfers during the reaction of the reduced enzyme with O2 (28) or the enzyme’s reduction in the absence of O2 (29, 30) indicates that the proton must be available at the point of entry for a period long enough so that the stepping-in will materialize. Consequently, the presence of proton must be considered not only in terms of average occupation but also in terms of the length of its dwell time.
Although the average state of protonation of the surface is independent of the buffer concentration, the dwell time on the surface is definitely buffer controlled; at low concentration, the dissociation of the proton from a surface group is a function of its pK (24). In the presence of buffer, the collisional proton transfer becomes the dominating pathway and the dwell time becomes very short. The effect of the buffer concentration on the dwell time of a proton on the surface of COX is shown by the simulation given in Fig. 4F. The simulation corresponds to a situation in which a buffered solution of the protein is subjected to a brief proton pulse. Normally the protons will be taken both by the protein and the soluble buffer; in the present case, we let the protons react exclusively with the protein while the buffer (pK = 7.7) gains its protons only from the protein. At zero time, the protons were released to the bulk and the deprotonation of the protein’s surface by the buffer is given by the top curves. At low buffer concentrations (27 μM), only 20% of the protons bound to the protein have been lost to the buffer within 25 μs (Fig. 4F, top curves, solid line). At higher buffer concentrations, the proton population on the protein dwindles very rapidly, and in the presence of 2.7 mM, the protons are lost with a time constant of 10 μs. The bottom curves in Fig. 4F depicts the dynamics of the Flu. At low buffer concentration the Flu retains its proton for >150 μs, but as the buffer concentration increases to the mM range, the incremental protonation of Flu becomes a brief event not more than few microseconds. Consequently, for an efficient functioning under physiological conditions, COX must have the mechanism to attract protons from the bulk and to retain them in a buffer-inaccessible form. This mechanism must be an innate property of the protein.
The results we have presented rely on observations centered on at a single Flu moiety, attached on a fortuitous site on the cytoplasmic surface of COX. It should be stated that the labeled site does not have any proven physiological functioning, yet being located on the surface of a protein that must compete for protons, it bears the properties of its environment. It reveals, through its dynamics, the capacity of the surface to act as a proton collecting antenna. Experiments with better placement of the Flu are under way and may reveal whether the pH dependence of proton exchange is a local effect or a more general property of the protein.
Acknowledgments
P.B. is grateful for a travel grant from the Federation of European Biochemical Societies.
ABBREVIATIONS
- COX
cytochrome c oxidase
- Flu
fluorescein
- φOH
pyranine
- φO−
pyranine anion
- nomenclature of amino acid residues
i.e., D(I-132) represents aspartate 132 of subunit I
Footnotes
The amino acid numbering is based on the R. sphaeroides COX sequence.
References
- 1.Zundel G. J Mol Struct. 1994;322:33–42. [Google Scholar]
- 2.Rupley J A, Careri G. Adv Protein Chem. 1991;41:37–172. doi: 10.1016/s0065-3233(08)60197-7. [DOI] [PubMed] [Google Scholar]
- 3.Gutman M, Nachliel E, Tsfadia Y. In: Permeability and Stability of Lipid Bilayers. Disalvo E A, Simon S A, editors. Boca Raton, FL: CRC; 1995. pp. 259–276. [Google Scholar]
- 4.Nachliel E, Gutman M, Kiryati S, Dencher N A. Proc Natl Acad Sci USA. 1996;93:10747–10752. doi: 10.1073/pnas.93.20.10747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yaniv S, Nachliel E, Dencher N A, Gutman M. Biochemistry. 1997;36:13919–13928. doi: 10.1021/bi9717542. [DOI] [PubMed] [Google Scholar]
- 6.Ferguson-Miller S, Babcock G T. Chem Rev. 1996;96:2889–2907. doi: 10.1021/cr950051s. [DOI] [PubMed] [Google Scholar]
- 7.Iwata S, Ostermeier C, Ludwig B, Michel H. Nature (London) 1995;376:660–669. doi: 10.1038/376660a0. [DOI] [PubMed] [Google Scholar]
- 8.Tsukihara T, Aoyama H, Yamashita E, Tomizaki T, Yamaguchi H, Shinzawa-Itoh K, Nahashima R, Yaono R, Yoshikawa S. Science. 1995;269:1069–1074. doi: 10.1126/science.7652554. [DOI] [PubMed] [Google Scholar]
- 9.Tsukihara T, Aoyama H, Yamashita E, Tomizaki T, Yamaguchi H, Shinzawa-Itoh K, Nahashima R, Yaono R, Yoshikawa S. Science. 1996;272:1136–1144. doi: 10.1126/science.272.5265.1136. [DOI] [PubMed] [Google Scholar]
- 10.Hosler J P, Ferguson-Miller S, Calhoun M W, Thomas J W, Hill J, Lemieux L, Ma J, Georgiou C, Fetter J, Shapleigh J, et al. J Bioenerg Biomembr. 1993;25:121–136. doi: 10.1007/BF00762854. [DOI] [PubMed] [Google Scholar]
- 11.Calhoun M W, Thomas J W, Hill J, Hosler J P, Shapleigh J, Tecklenburg M M J, Ferguson-Miller S, Babcock G T, Alben J O, Gennis R B. Biochemistry. 1993;32:10905–10911. doi: 10.1021/bi00091a046. [DOI] [PubMed] [Google Scholar]
- 12.Ädelroth P, Ek M S, Mitchell D M, Gennis R B, Brzezinski P. Biochemistry. 1997;36:13824–13829. doi: 10.1021/bi9629079. [DOI] [PubMed] [Google Scholar]
- 13.Konstantinov A A, Siletski S, Mitchel D, Kaulen A, Gennis R B. Proc Natl Acad Sci USA. 1997;94:9085–9090. doi: 10.1073/pnas.94.17.9085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ädelroth P, Gennis R B, Brzezinski P. Biochemistry. 1997;37:2470–2476. doi: 10.1021/bi971813b. [DOI] [PubMed] [Google Scholar]
- 15.Brzezinski, P. & Ädelroth, P. (1998) J. Bioenerg. Biomembr., in press. [DOI] [PubMed]
- 16.Gutman M. Methods Biochem Anal. 1984;30:1–103. doi: 10.1002/9780470110515.ch1. [DOI] [PubMed] [Google Scholar]
- 17.Gutman M. Methods Enzymol. 1986;127:522–538. doi: 10.1016/0076-6879(86)27042-1. [DOI] [PubMed] [Google Scholar]
- 18.Marantz, Y., Nachliel, E., Aagaard, A., Brzezinski, P. & Gutman, M. (1998) Biochim. Biophys. Acta., in press. [DOI] [PMC free article] [PubMed]
- 19.Mitchell D M, Gennis R B. FEBS Lett. 1995;368:148–150. doi: 10.1016/0014-5793(95)00626-k. [DOI] [PubMed] [Google Scholar]
- 20.Vanneste W H. Biochemistry. 1966;5:838–848. doi: 10.1021/bi00867a005. [DOI] [PubMed] [Google Scholar]
- 21.Sacks V. M.Sc. thesis. Ramat Aviv, Israel: Tel Aviv University; 1997. [Google Scholar]
- 22.Sacks, V., Marantz, Y., Aagaard, A., Checover, S., Nachliel, E. & Gutman, M. (1998) Biochim. Biophys. Acta, in press.
- 23.Gutman M, Nachliel E. Biochemistry. 1985;24:2941–2946. doi: 10.1021/bi00333a020. [DOI] [PubMed] [Google Scholar]
- 24.Gutman M, Nachliel E. Biochim Biophys Acta. 1990;1015:391–414. [Google Scholar]
- 25.Gutman M, Nachliel E. Annu Rev Phys Chem. 1997;48:329–356. doi: 10.1146/annurev.physchem.48.1.329. [DOI] [PubMed] [Google Scholar]
- 26.Yam R, Nachliel E, Gutman M. J Am Chem Soc. 1988;110:2636–2640. [Google Scholar]
- 27.Gutman M, Nachliel E. Biochim Biophys Acta. 1995;1231:123–138. [Google Scholar]
- 28.Oliveberg M, Brzezinski P, Malmström B G. Biochim Biophys Acta. 1989;977:322–328. doi: 10.1016/s0005-2728(89)80087-8. [DOI] [PubMed] [Google Scholar]
- 29.Ädelroth P, Sigurdson H, Hallén S, Brzezinski P. Proc Natl Acad Sci USA. 1996;93:12292–12297. doi: 10.1073/pnas.93.22.12292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Brzezinski P. Biochemistry. 1996;35:5611–5615. doi: 10.1021/bi960260m. [DOI] [PubMed] [Google Scholar]
- 31.Sali A, Blundell T L. J Mol Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]