Clines of nuclear DNA markers suggest a largely Neolithic ancestry of the European gene pool

Abstract

Comparisons between archaeological findings and allele frequencies at protein loci suggest that most genes of current Europeans descend from populations that have been expanding in Europe in the last 10,000 years, in the Neolithic period. Recent mitochondrial data have been interpreted as indicating a much older, Paleolithic ancestry. In a spatial autocorrelation study at seven hypervariable loci in Europe (four microsatellites, two larger, tandem-repeat loci, and a sequence polymorphism) broad clinal patterns of DNA variation were recognized. The observed clines closely match those described at the protein level, in agreement with a possible Near Eastern origin for the ancestral population. Separation times between populations were estimated on the basis of a stepwise mutation model. Even assuming low mutation rates and long generation times, we found no evidence for population splits older than 10,000 years, with the predictable exception of Saami (Lapps). The simplest interpretation of these results is that the current nuclear gene pool largely reflects the westward and northward expansion of a Neolithic group. This conclusion is now supported by purely genetic evidence on the levels and patterns of microsatellite diversity, rather than by correlations of biological and nonbiological data. We argue that many mitochondrial lineages whose origin has been traced back to the Paleolithic period probably reached Europe at a later time.

According to Ammerman and Cavalli-Sforza’s demic-diffusion model (1), current European populations are descended largely from ancestors who expanded from the Near East in the Neolithic age. Their westward and northward expansion, a consequence of demographic increase, spread their genes over the entire continent, along with the novel technologies for farming and animal breeding. In the process, Neolithic farmers mixed very little with the preexisting hunting–gathering communities; the genes of the latter, therefore, should represent only a small fraction of the present European gene pool. The Neolithic demic-diffusion model rests on three main classes of arguments, namely: (i) the presence of extensive allele frequency clines, encompassing much of Europe and the Levant (2–5); (ii) the correlation between the allele frequencies in those clines and the dates of origin of agriculture inferred from the archaeological record (2, 5–7); and (iii) the overlapping between the boundaries of those clines, and linguistic barriers whose onset is placed by linguists at the Neolithic period or later (8–10).

Computer simulations have shown that a Neolithic expansion is the simplest, but not the only, possible cause of the continentwide clines of allele frequencies. Paleolithic population dispersal may have been accompanied by founder effects, resulting in clines under successive short-distance gene flow (11). At the same time, some recent studies on mtDNA did not identify simple, clinal patterns in Europe (12, 13). Although these studies are based on a single nonnuclear marker, the suspicion was raised that, in general, protein polymorphisms may fail to represent faithfully the underlying DNA diversity. If the correspondence between gene frequency and linguistic patterns is regarded as largely coincidental, a different evolutionary hypothesis on European ancestry may be put forward. According to this hypothesis, the current European gene pool was established in the Paleolithic age, relatively few Near Eastern genes were incorporated in the Neolithic age, and the farming technologies mostly spread through cultural transmission, rather than by population movements (13).

In this study we looked for molecular evidence supporting either of these views on the origin and evolution of the European gene pool. We described patterns of geographical variation at seven hypervariable nuclear loci, and we applied a recently proposed method for inferring dates of population divergence from microsatellite diversity. To validate the time estimates thus obtained, we quantified the possible confounding effect of recent gene flow, using a birth–death process to represent the dynamics of foreign alleles brought by immigration into an expanding population. The clinal patterns of molecular diversity across populations, and the conservative estimates of times since population divergence we obtained jointly suggest that the current structure of the European population is unlikely to have been established before the Neolithic age.

MATERIALS AND METHODS

The Database.

The data of this study have been collected through an extensive search of published literature and unpublished sources. We are confident that they represent most, if not all, information available by mid-1997 about seven hypervariable nuclear loci in Europe (Table 1). The number of samples ranged between 18 and 64 with a mean of 44 samples per locus, and a total of 308. Overall, 130,560 chromosomes (or 65,280 individuals) were studied, for an average of 424 chromosomes per sample. The number of chromosomes analyzed at each locus varied between 8,568 and 28,000. In almost all cases we had allele, rather than genotype, frequencies, and therefore all comparisons had to be made separately for each locus considered.

Table 1.

A summary of the database analyzed

	Type of marker*	Chromosome	No. of Samples	No. of chromosomes	No. of alleles†
ApoB3′	Mini (15)	2	23	13,412	28  (28–55)
D1S80	Mini (8)	1	50	17,572	28  (14–41)
DQα	α-chain	6	54	16,148	6
FES/FPS	Micro (4)	15	44	22,250	10  (6–15)
FXIIIA	Micro (4)	6	18	8,568	18  (2–19)
HUMTH01	Micro (4)	11	55	28,000	9  (3–10+)
VWA31A	Micro (4)	12	64	24,610	12  (11–22)

^*Length of the repeated motif in parentheses. 

^†Minimum and maximum allele length in parentheses. 

Four loci are tetranucleotide microsatellites (HUMTH01, FES/FPS, FXIIIA, VWA31A), and two are minisatellites (ApoB_3′, D1S80). DQα is a gene coding for the α-chain of the highly polymorphic HLA-DQ molecule. Polymorphism of the mini- and microsatellite loci can be described by variation in the number of repeats of a core sequence (their range of variation is in Table 1). For DQα, the six alleles considered (usually referred to as DQA1.1, -A1.2, -A1.3, -A2, -A3, and -A4) differ by known nucleotide substitutions (14).

Geographical Coordinates.

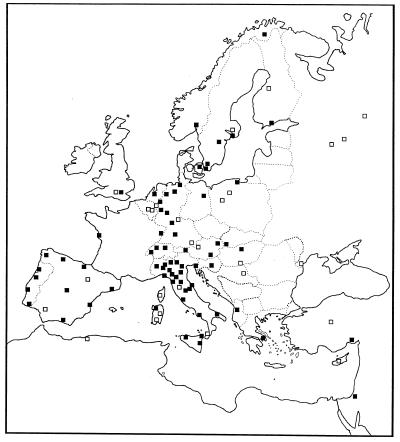
The spatial location of the samples generally could be determined without ambiguity by using information given in the original papers. Samples that came from a broad region were assigned the geographical coordinates of the main town in the region. The distances between samples were such that inaccuracies at this stage could hardly affect the results of the subsequent analysis. A few samples were impossible to locate exactly in space and were discarded. All the results refer to the 97 localities in Fig. 1.

Figure 1.

Spatial distribution of the 97 samples considered. Open squares, localities where one marker was typed; solid squares, localities where two or more markers were typed.

Autocorrelation Analysis.

Patterns of sequence variation in the geographical space were summarized by II (15), a spatial autocorrelation statistic designed for the treatment of DNA data. II was calculated independently at each locus, by comparing all possible pairs of chromosomes available. These comparisons were carried out in arbitrary distance classes, e.g., at distances = 0, between 1 and 100 km, between 101 and 200 km, etc. (see legends to Tables 2 and 3). In practice, within each distance class, length differences were transformed into measures of genetic resemblance. Alleles of similar length (i.e., both longer or both shorter than average) contributed positively to the value of II, alleles of dissimilar length contributed negatively, and large length differences had a greater weight than small differences. Alleles present more than once enter repeatedly into the computations, and therefore II quantifies both frequency and allele length differences among localities. II may vary between −1 and +1 and has an expectation of 0 when alleles are randomly distributed. Significant positive values indicate overall DNA resemblance between samples separated by that distance, and significant negative values indicate molecular dissimilarity. DNA diversity at the DQα locus was described in a similar way, but on the basis of the number of mutational steps separating alleles. The minimum differences were thus 0 (between chromosomes carrying the same allele) and 1 (between chromosomes with the alleles DQA-1.1 and DQA-1.2); the maximum difference was 30 (between DQA-1.3 and DQA-3).

Table 2.

Spatial autocorrelation analysis of molecular variation at seven loci

	Distance class limits, km
	0	1–500	501–1,000	1,001–1,500	1,501–2,000	2,001–2,500	2,501–3,000	>3,000
ApoB3′	0.66**	0.27**	−0.00	−0.20**	−0.15**	−0.33†**
D1S80	0.25**	0.06**	−0.07**	0.04**	−0.03	−0.10**	0.19**	−0.35**
DQα	0.37**	0.10**	0.01	−0.06*	−0.13**	0.04	−0.07*	−0.10*
FES/FPS	0.42**	0.03	0.02	−0.03	−0.09**	0.02	−0.30**	−0.28**
FXIIIA	0.18**	−0.03	−0.01	−0.03	−0.05‡**
HUMTH01	0.36**	0.09**	0.04**	−0.11**	−0.07**	0.07*	−0.06**	−0.20**
VWA31A	0.23**	0.06*	0.01	0.04	−0.03	−0.04	−0.24**	−0.61**

II values are ×100. 

^*P < 0.05. 

^**P < 0.01. 

^†This class corresponds to >2,000 km. 

^‡This class corresponds to >1,500 km. 

Table 3.

Short-distance spatial autocorrelation of molecular variation at six loci

	Distance class limits, km
	0	1–100	101–200	201–500
ApoB3′	0.66**	0.26**		0.28**
D1S80	0.25**	0.18**	0.17**	0.02
DQα	0.37**	0.27**	0.11*	0.08**
FES/FPS	0.42**	0.39**	0.26**	−0.10**
HUMTH01	0.36**	0.21**	0.01	0.09**
VWA31A	0.23**	0.14**	0.13**	0.03

II values are ×100. 

^*P < 0.05. 

^**P < 0.01. 

Statistical significance of the estimated II was assessed by comparison with the values expected if the geographical distribution of chromosomes is random. Seven expected distributions, one for each locus, were constructed independently by extracting without replacement random pairs of alleles irrespective of their geographic location. When the number of allele pairs reached a critical value chosen under conservative criteria (see ref. 15), a pseudovalue of II was calculated. By repeating this procedure 200 times, empirical distributions of pseudovalues were generated under the null hypothesis of no spatial structuring, and the observed II statistics were compared with them (15). Such a randomization process was extremely time-consuming, and that is why it was repeated only 200 times for each locus. As a consequence, the levels of significance could not be less than 0.01 (two-tailed tests), although in several cases the observed values exceeded by far the extreme pseudovalues obtained by randomization.

The pattern of genetic variation shown by each locus is described objectively by the plot of autocorrelation coefficients versus distance (correlogram). A spatially random distribution results in a series of insignificant II values, at all distances. A decreasing set of II coefficients, from positive significant to negative significant, describes a cline, whereas a decreasing correlogram from positive significant to insignificant at large distances is expected for allele frequencies under isolation by distance, i.e., when genetic diversity reflects only genetic drift and short-range gene flow (16).

Dating Population Separation.

Goldstein et al.’s (17) measure of genetic distance for microsatellites was used to approximately locate in time the main episodes of population divergence. Under a stepwise mutation model, the times since population splits are expected to be proportional to the squared difference in average allele lengths (δμ)² between populations. Two underlying assumptions are that gene flow is negligible, and that genetic drift contributes less than mutation to population divergence; thus, divergence times essentially are unaffected by population size (see, however, ref. 18). In humans, a widely accepted estimate of the mutation rate for dinucleotides is u = 5.6 × 10⁻⁴ (19, 20); Chakraborty et al. (21) calculated that values for tetranucleotides are 1.5–2 times as low. Therefore, we used u = 3.73 × 10⁻⁴ and u = 2.80 × 10⁻⁴ and generation times of 20 and 25 years for estimating a range of values. To reduce statistical errors, samples were preliminarily pooled according to their country, and the average allele lengths considered (μ) were calculated within such composite samples.

RESULTS

Autocorrelation.

The coefficients of autocorrelation of Table 2 are based on 111 alleles, 53 of them occurring at a frequency greater than 0.01 across Europe. Although differences exist among loci, all seven correlograms depart significantly from randomness and share some common features. First, despite II values being small, much smaller indeed than classical autocorrelation indices, they often achieve a high statistical significance. Second, spatial autocorrelation is positive and significant for all loci at distance zero, i.e., for comparisons between chromosomes of the same sample. Third, positive II values, not all of them significant, are observed at short distances for all loci except FXIIIA (Table 3). Fourth, autocorrelation is basically 0 at intermediate distances. Finally, all loci exhibit negative values beyond 2,000 km, most of them significant.

Because of the spatial distribution of samples, the last distance class considered for FXIIIA lumps all comparisons beyond 1,500 km. A more detailed analysis of population relationships was possible for the other markers. At large distances most II values were negative and highly significant up to 3,500 km and more. However, positive autocorrelation occasionally is observed, even beyond 2,000 kilometers, e.g., for HUMTH01 and D1S80. Conversely, geographically near samples show a clear genetic resemblance (Table 3), which tends to decline with distance toward insignificant values beyond 200 or 500 km.

In synthesis, molecular gradients spanning much of Europe are evident. They are the main expected genetic consequence of a directional population expansion. Single loci show occasional autocorrelation peaks at intermediate distances, which may be the signatures of other less important demographic events. However, the overall pattern of variation of the seven markers considered is clearly clinal, with populations at the extremes of the geographical range showing the highest DNA divergence and intermediate samples showing intermediate characteristics.

Time Estimates.

The groups currently dwelling in the extreme North and West, and in the Levant, can reasonably be expected to have the deepest genealogical relationships, i.e., to be descended from populations that separated first. In addition, because of geographical isolation, genetic differences between these groups are unlikely to have been blurred much by local gene flow. Therefore, the dates of their split, approximate though they must be, allow one to locate in time the evolutionary phenomenon that led to the establishment of continentwide gradients in Europe. It is only by analyzing many loci that an accurate evolutionary tree can be inferred (22). Sufficient molecular information is available so far for only four microsatellite loci, and hence the estimates obtained in this study are admittedly, but inevitably, approximate.

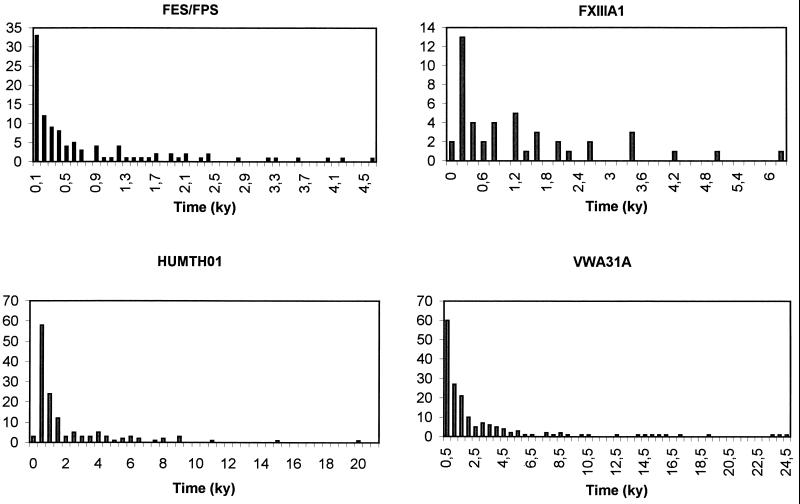
The time estimates evaluated for individual loci vary from virtually 0 to 25,000 (Fig. 2). Fifteen estimates of population splits out of 467 were greater than 10,000 years; all of them involved Saami (Lapps), or Turks, or both. On average, times estimated from FXIIIA and FES/FPS variation are shorter. Note that neither Saami nor Near Eastern/Turkish samples were available at the former locus, nor had Saami been typed for FES/FPS, and yet clines are apparent for these markers as well. This is an indirect proof that the gradients described in this study are not simply a result of the presence of highly differentiated outliers at the extremes of the area studied.

Figure 2.

Distribution of estimated pairwise times since separation of populations, based on Goldstein et al.’s (δμ)² measure of genetic distance, with u = 2.80 × 10⁻⁴, generation time = 25 years. Maximum estimates were: 4,511 years (France vs. Sardinia) for FES/FPS (no Saami samples available); 6,042 years (Italy vs. Switzerland) for FXIIIA (neither Saami nor Near Eastern samples available); 19,537 years (Saami vs. Turkey) for HUMTH01; and 24,481 (Saami vs. Spain) for VWA31A.

All estimates of times since separation of populations other than Saami, but including Sardinians and Basques, were below 10,000 years (Fig. 2). These dates are rather recent, and so hereafter we only give upper bounds of their estimates. We do not believe any of these figures should be taken at its face value; clearly, it is the trend of the data that contains useful information, and not the exact numerical estimates. However, the overall pattern emerging is one in which, even using a long generation time (25 years) and the lowest mutation rate, there is no evidence of European population splits predating the diffusion of Neolithic technologies, as inferred from archaeological evidence. Using the mutation rates recently estimated from pedigrees for Y chromosome tetranucleotide microsatellites (23) would further reduce the time elapsed since population separations.

Possible Effects of Recent Gene Flow.

Divergence times are estimated assuming complete isolation of two populations after their split, which is probably unrealistic. The possible effect of successive gene flow is difficult to quantify, but some recent derivations can prove useful. Using a birth–death process (24), which provides a good approximation for the dynamics of a rare allele, Slatkin and Rannala (25) showed that with mutants arising according to a Poisson process with parameter θ (the average number of mutants per unit of time), the probability of observing i copies of a rare mutation in a sample after t units of time is given by

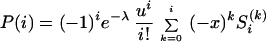where S is the Stirling number of the first kind, and u, x, and λ are functions of the birth and death rates (B and D, respectively) and of time.

After setting B = 0.5 and D = 0.5 − r to model a population increasing exponentially in size at rate r (25), and rescaling the time in units of generations, the same expression can be used to find the probability that i copies of a gene introduced by immigration (rather than by mutation) are observed in a sample.

A Paleolithic origin of the European gene pool might potentially be reconciled with the findings of the present study if the apparent divergence times of less than 10,000 years were a result of the presence in our samples of genes that recent gene flow introduced. If we assume that the population of a European country increased from a size of 5,000 individuals 50,000 years ago (see ref. 26) to its present size of 50 million, the rate of exponential demographic growth is about r = 0.0037. Suppose now the population began exchanging migrants very early, say, about 40,000 years ago, with an average rate of one immigrant per generation (θ = 2). The expression above predicts that the number of sequences of immigrant origin (i.e., immigrants, and their descendants in the sample), in a present-day sample of 1,000, will be less than or equal to 19, with a probability of >95%. In other words, had Eastern and Western European populations separated 50,000 years ago, and had they consistently exchanged one migrant per generation for 40,000 years, in 95% of the samples less than 2% of the chromosomes would be descended from these migrants. It is hard to imagine that such a small fraction of immigrant chromosomes may have distorted the overall pattern of genetic diversity we obtained. Higher values of θ (Table 4) alter the picture only slightly. The short divergence times estimated in this study, even between spatially distant populations, appear unlikely to result from the confounding effect of gene flow occurring after the major population splits.

Table 4.

Estimated number (n) of sequences of foreign origin in a present-time sample of 1,000 sequences, as a function of θ, the average number of immigrants per generation over the last 40,000 years

θ	n with maximum probability	95% upper confidence limit of n
1	2	12
2	6	19
5	19	37
10	41	65
15	64	92

DISCUSSION

The autocorrelation coefficients estimated in this study never exceed 0.01. These low figures reflect the large diversity within populations. Only less than 6 percent of the overall human DNA diversity occurs among samples of the same continent, the largest share by far being represented by individual differences among members of the same population (27). Therefore, two random sequences extracted from the same sample can be only slightly more similar than random sequences extracted anywhere in the geographical space. Even so, however, these small interpopulation differences determine significant departures from randomness, as shown by the high statistical significance of all correlograms.

Aside from recent gene flow, two confounding factors, homoplasy and selection, may have affected our results. Homoplasy results in underestimation of population differences. That does not seem a major source of error in within-species studies (28), but sufficient data about humans are not available yet. At any rate, by using the stepwise mutation model we took into account the possibility that an already-existing allele could be generated by loss or gain of a repeat. This possibility is not considered under alternative models, such as the infinite allele model (29).

In principle, one cannot rule out the effects of selection either. However, parallel patterns of geographic variation at several loci are regarded as evidence for the effect of factors affecting the entire genome rather than single genes, that is to say, for gene flow rather than for selection (30). Also, to the best of our knowledge, no correlation has been found so far between allele lengths of the microsatellites we considered and pathological phenotypes, although two of these loci map close to genes coding for proteins involved in the coagulation process. Therefore, although length variation may not be totally neutral, selection is unlikely to have played any major role in the establishment of these multilocus gradients across Europe.

Broad genetic gradients in Europe have long been known for allozyme systems, blood groups, and HLA loci (5). Similar gradients were described recently for the frequencies of DNA variants (31, 32). The present study demonstrates that even at the DNA sequence level the population of Europe is structured, with Northern and Western populations showing the highest divergence from Near Eastern populations, and intermediate situations in between. This cannot be a consequence of isolation by distance, because distant populations are not expected to differ significantly under that process (16, 33). Hence, previous studies based on non-DNA markers did not misrepresent the basic patterns of genetic variation. Such patterns seem only compatible with a directional demographic expansion affecting much of Europe.

When did that expansion take place? It is simplistic to regard the evolutionary history of a species as a succession of population splits, because short-range gene flow must have occurred, somewhat reducing levels of population differentiation. However, the rates of gene flow probably have been minimal between the most distant localities. Therefore, by estimating the dates of separation between Northern, Eastern, and Western European populations one can have an idea of the moment at which the gradients began to be established. Such dates estimate what Stoneking et al. (34) termed an “effective separation time”; in other words, these figures are accurate only if the populations remained completely isolated from each other after their split. But the calculations we carried out using the birth–death process suggest that plausible amounts of local gene flow do not dramatically alter the picture.

Even if we take the maximum values of our estimates, the populations at the extremes of the European clines seem to have separated less than 10,000 years ago. The only exception, and a reasonable one, is represented by Saami, who speak a non-Indo-European language, and who also differ from the other Europeans at the mitochondrial level (35). Their remote separation from most other Europeans had to be expected. The absolute dating we obtained is evidence of a Neolithic demographic expansion in Europe based only on genetic data, and not on correlation between biological and nonbiological data. Of course, a Neolithic population split does not imply that the entire pre-Neolithic population of Europe was replaced by expanding agriculturists. The amount of admixture among those groups cannot be estimated from our data, but these results, and the calculations carried out modeling gene flow in terms of a birth–death process, do not seem consistent with the notion that a large share of the European gene pool is derived from local Paleolithic ancestors.

A recent origin of European populations is also suggested by their limited genetic differentiation, observed in many studies based on allozymes (reviewed in ref. 5), mtDNA (12, 36), or hypervariable nuclear loci (this study). Low differentiation is expected if populations separated recently, as in the model of Neolithic demic diffusion. Alternatively, an ancient separation might be consistent with limited interpopulation differences, but only under unlikely evolutionary circumstances. If current Europeans descend largely from groups that settled Europe in the Paleolithic age, either these groups were small, but they extensively exchanged genes (which requires the further assumption that they were poorly isolated), or they were large, large enough indeed to maintain the preexisting genetic diversity (37, 38). Although quantitative statements are difficult in this domain, both scenarios conflict with widely accepted models of Paleolithic populations (39).

The hypothesis of a major role of the Neolithic expansion in the peopling of Europe has been challenged recently by a study based on mitochondrial allele genealogies. Richards et al. (13) showed that most European mitochondrial lineages coalesce in the Upper Paleolithic age. They concluded that current Europeans are descended largely from ancestors who entered Europe at that time, implying that allele frequency clines were established at that time. That view underrates the case that the depth of a gene genealogy is not mechanically related to the age of the population from which the genes come (38, 40). If the group colonizing an area already contains some genetic variation, the coalescence times of its genes will consistently overestimate the age of the population until equilibrium is reached. That many European mitochondrial alleles have been generated by mutations occurring in the Paleolithic age does not imply that they spread in Europe at the same time (41).

In conclusion, the geographical patterns of DNA variation described here for seven nuclear loci agree with the results of previous non-DNA studies. These patterns, and the time estimates we calculated of their origin, suggest that the main demographic process affecting the current European gene pool occurred in the Neolithic age, and that that process may have led to the diffusion of alleles whose genealogy dates back to even very remote periods. Mitochondrial diversity may be distributed differently, perhaps for its maternal mode of inheritance (42), or perhaps for founder effects occasionally affecting the maternally transmitted genes of some populations (43). Alternatively, mitochondrial patterns of variation may need more sensitive statistical tools to be recognized. However, the Southeast–Northwest gradients of frequencies described for mitochondrial haplogroup H (44) lends further support to the view that a large fraction of genetic diversity in Europe reflects the consequences of a Neolithic demic diffusion from the Levant.