Abstract
We analyze the local structure of model and empirical food webs through the statistics of three-node subgraphs. We study analytically and numerically the number of appearances of each subgraph for a simple model of food web topology, the so-called generalized cascade model, and compare them with 17 empirical community food webs from a variety of environments, including aquatic, estuarine, and terrestrial ecosystems. We obtain analytical expressions for the probability of appearances of each subgraph in the model, and also for randomizations of the model that preserve species' numbers of prey and number of predators; their difference allows us to quantify which subgraphs are over- or under-represented in both the model and the empirical food webs. We find agreement between the model predictions and the empirical results. These results indicate that simple models such as the generalized cascade can provide a good description not only of the global topology of food webs, as recently shown, but also of its local structure.
Keywords: Food webs, Motifs, Complex networks, Network structure
1. Introduction
Food web theory seeks to understand the functioning of ecosystems by studying the trophic relations among its species (Cohen et al., 1990). To this end, in the last years great effort has been devoted to the compilation of comprehensive empirical food webs (see for instance Dunne et al., 2002). The statistical treatment of these data has revealed several regularities among food webs belonging to quite diverse habitats, such as deserts, lakes and islands, suggesting that some robust mechanism common to most ecosystems is at work (Williams and Martinez, 2000; Camacho et al., 2002b; Stouffer et al., 2005).
Several models have been proposed to describe the structure of food webs and clarify the origin of these patterns. They differ in the mechanisms underlying them and in the level of description. Some of them describe the dynamics of the network according to evolutionary rules (Amaral and Meyer, 1999; Rossberg et al., 2005; Rossberg et al., 2006a,b), population biology (Yodzis, 1981), or mixtures of both (Caldarelli et al., 1998; Lassig et al., 2001). Other so-called static models do not contain the explicit dynamics of the ecosystem, but provide some mechanistic rules aiming to generate food webs with a statistically similar structure to the empirical ones (Cohen and Newman, 1985; Williams and Martinez, 2000; Cattin et al., 2004; Stouffer et al., 2005).
Two of these static models, the niche model (Williams and Martinez, 2000) and the nested-hierarchy model (Cattin et al., 2004), yield good predictions for a wide number of statistical measures of empirical food webs. Indeed, it has been demonstrated analytically that the two models yield the same distributions for the number of prey and number of predators (Stouffer et al., 2005), which imply, for example, the same fractions of top and basal species or the standard deviations of generality and vulnerability, just as observed numerically (Cattin et al., 2004). Remarkably, these distributions are in good agreement with most of the highest quality empirical food webs in the literature, providing a general pattern of food web topology (Camacho et al., 2002a,b; Stouffer et al., 2005).
It has also been demonstrated that much of the success of these models relies in the fact that they satisfy two basic conditions (Stouffer et al., 2005): (i) the species' niche values form a totally ordered set, and (ii) each species has a specific exponentially decaying probability of preying on a given fraction of the species with lower niche values. Any model which satisfies these conditions will reproduce the distributions of number of prey and number of predators observed empirically. For instance, the generalized cascade model (Stouffer et al., 2005)—a generalization of Cohen and Newman's (1985) cascade model to satisfy condition (ii)—exhibits the same distributions. Those two conditions can thus be interpreted as fundamental mechanisms shaping food web structure.
Aside few exceptions (Melián and Bascompte, 2004; Bascompte and Melian, 2005), the studies of these models, however, mainly characterize the global structure of food web topology. Here, in contrast, we focus on the analysis of the local structure of food webs through the study of the so-called food web subgraphs or motifs (Fig. 1). This methodology has been applied successfully to a number of empirical networks, including biological, technological and sociological systems, to uncover the underlying structure at a scale in between the entire community and single or pairwise population dynamics (Milo et al., 2002, 2004). Let us note that some authors have attempted to gain insight into the dynamics and stability of natural ecosystems in terms of small sub-webs containing species strongly connected, the so-called “community modules” (Holt, 1997; Holt and Hochberg, 2001). Our perspective is complementary: whereas the latter approach is dynamical and considers only strong links, we focus on structural properties of the food webs; to do so we consider all links, and not only the strong ones. Our perspective is thus similar to the one followed by Bascompte and Melian (2005), though it differs in several aspects, such as the theoretical approach and our systematic analysis of all three-node subgraphs.
Fig. 1.
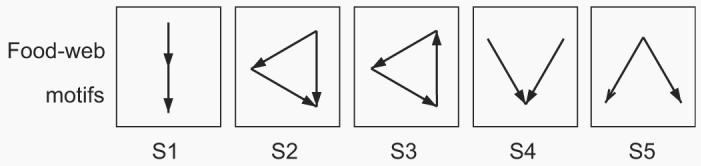
Three-species motifs containing only single links. Notice that each of these motifs has a clear ecological relevance and is additionally related to some community modules. Motif S1 describes the simple food chain, S2 simple omnivorism, S3 a trophic loop involving three species, S4 isolated exploitative competition, and S5 isolated generalist predation.
The purpose of this work is to study the statistics of subgraphs in model and empirical food webs in order to check if the two basic ingredients for food web construction specified above can satisfactorily describe not only the global properties of empirical food webs, such as the distributions of number of prey, of predators and related quantities, but also its local structure. Because it allows for analytical treatment, we will focus here on the generalized cascade model, the simplest model obeying those ingredients. Specifically, we study analytically and numerically the subgraph probabilities for the generalized cascade model and find agreement between the analytical expressions and the empirical results. We conclude that the model is able to capture the basic properties of the local structure of food webs. Therefore, simple static models as the generalized cascade provide a good unifying description of food web structure both at the global and local levels.
The paper is organized as follows. In the second section, we study the statistics of subgraphs for the generalized cascade model. This analysis is twofold: we first evaluate the number of appearances for each subgraph and secondly we study their patterns of over/under-representation. In the third section, we perform the same analysis for the completely random model, as a basis for comparison. Section 4 compares the model predictions with the results obtained for 17 empirical food webs.
2. The generalized cascade model
The original cascade model (Cohen and Newman, 1985; Cohen et al., 1990) is based on two rules: (1) species make up an ordered set according to their niche value n drawn uniformly in the interval [0, 1], and (2) any species j with nj<ni becomes a prey of i with fixed probability x0 = 2CS/(S − 1); here S is the number of species in the food web, L the number of trophic connections, and C ≡ L/S2 the directed connectance. Williams and Martinez (2000) demonstrated that this model is not able to reproduce the properties of real food webs.
Stouffer et al. (2005) demonstrated, however, that it can be easily generalized to provide similar agreement to the niche (Williams and Martinez, 2000) or the nested-hierarchy (Cattin et al., 2004) models as compared to many empirical food webs. The generalization consists in that the probability x with which a species i feeds on species j with nj≤ni is not the same for every predator i, but it is drawn at random from a probability distribution p(x) given by
| (1) |
the so-called beta-distribution (see Fig. 2). Parameter β is related with the directed connectance of the empirical food web by C = 1/2(β + 1) (Williams and Martinez, 2000).
Fig. 2.
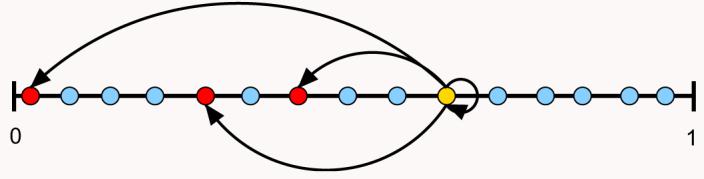
The generalized cascade model of Stouffer et al. (2005). In the generalized cascade model species make up an ordered set according to their niche value n, 0<n<1. Each species i then consumes species j with nj≤ni with a probability x drawn at random from a probability distribution p(x) given by the beta-distribution Eq. (1). In this example the predator (the yellow species) can consume any of the species to its left on the axis, including itself. In this case, x ≈ 0.2 and the yellow predator consumes itself and three other species.
2.1. Subgraph probabilities
Neglecting cannibalism or self-links, there are two possible unique subgraphs comprising a pair of species: (i) single links, A → B, i.e. species A eats species B but not conversely, and (ii) double links, A↔B. With three species, there are 13 unique subgraphs possible. Since predators in the generalized cascade model cannot feed on species having a larger niche value, no trophic loops of any size can exist. As a consequence there is no mutual predation and none of the eight unique motifs which contain double links will be observed in the generalized cascade model. Therefore, our study focusses on the five subgraphs S1–S5 (Fig. 1), while the analysis of the motifs containing double links will be dealt with elsewhere. The present analysis is nonetheless meaningful since single connections account for the vast majority of the links in empirical food webs (see Appendix A). Notice that these motifs have a clear ecological relevance and are additionally related to some proposed community modules; in particular, motif S1 describes the simple food chain, S2 simple omnivorism, subgraph S3 a trophic loop involving three species, S4 isolated exploitative competition, and S5 isolated generalist predation.
The probability pi of subgraph i is related to the number of appearances of the subgraph Ni by
| (2) |
where the denominator is the total number of possible triplets of species. We choose the probability p, instead of the number of appearances N because, as we will later demonstrate, the probability is not a function of S, and instead depends on a single variable, the directed connectance C. This property is a very interesting one because it allows a unified description of food webs of different size.
Recall that no trophic loops are possible within the generalized cascade model. Motif S3 is therefore forbidden and
| (3) |
We next derive expressions for the remaining motifs, S1, S2, S4, and S5. The probability for a given motif to appear is equivalent to the probability for three arbitrary species to be connected in the specified fashion. Let us now consider three arbitrary species, A, B, and C, with nA>nB>nC. We call xi the probability of species i consuming each species with lower niche values. It then follows that
| (4) |
| (5) |
and
| (6) |
where 〈…〉 indicates the average over the probability distribution p(x). In addition, because xA and xB are independent random variables, Eqs. (4)-(6) can be rewritten as
| (7) |
| (8) |
and
| (9) |
These expressions are valid for arbitrary distributions p(x). Substituting the beta-distribution, Eq. (1) (see Appendix B) becomes
| (10) |
| (11) |
and
| (12) |
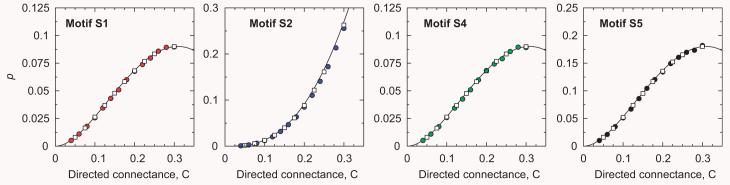
In Fig. 3, we compare the analytical predictions, Eqs. (10)-(12), with simulations of the generalized cascade model—in these simulations and throughout the paper, subgraphs have been directly enumerated using dynamic programming, as in the mfinder software for network motif detection. It becomes visually apparent that the expressions we derived compare quite well with the model-generated data. Notice that the probabilities p only depend on the connectance C.
Fig. 3.
Comparison between analytical expressions, Eqs. (10)-(12), and simulations of the generalized cascade model for motifs S1, S2, S4, and S5. We exclude motif S3 because, by definition, pS3 = 0. It is visually apparent that the analytical predictions agree with the model-generated data. Filled circles are for food webs with S = 50 and open squares for food webs with S = 100. Each data point represents an average over 1000 model-generated food webs.
2.2. Patterns of over/under-representation of subgraphs
As a second test of the generalized cascade model, we analyze which subgraphs are typically over- or under-represented as compared to the corresponding randomized networks (Milo etal., 2002,2004). The randomized networks are obtained by preserving the number of prey ki and of predators mi of each species i as in the generalized cascade model, but rewiring their trophic links randomly using the Markov-chain Monte Carlo switching algorithm (Maslov and Sneppen, 2002; Itzkovitz et al., 2004).
By virtue of the randomization a species in the randomized network may feed on a species with a higher niche value than itself, a possibility that is excluded in the model. However, because of the formulation of the Markov-chain Monte Carlo switching algorithm, no double links are produced in the randomization and the resulting networks only contain subgraphs S1–S5 (Maslov and Sneppen, 2002; Itzkovitz et al., 2004). Notice, however, that, by construction, the distributions of number of prey or of number of predators are the same ones as in the original network. Then, one must not confuse these randomized networks with completely random networks, whose distributions are different from the original ones. We deal with the latter ones in the next section, as a null model for comparison with the predictions of the generalized cascade model.
Note that, since randomized food webs possess the same degree distributions as the original ones, the occurrence of patterns of over/under-representation of subgraphs in empirical food webs would require an explanation. One can think of two principle arguments for their existence: either they are a consequence of the mechanism generating the network (Artzy-Randrup et al., 2004) or they provide some ecological advantage and have arisen as a result of selection pressure. Here we show that the generalized cascade model yields well-defined patterns of over/under-representation of motifs. If these predictions compare well with empirical food webs, one might conclude that the second hypothesis is not required and all patterns arise as the result of the food web generating mechanisms.
We thus next evaluate the probabilities of subgraphs in randomized networks of the generalized cascade model. Itzkovitz et al. (2003) derived expressions for the mean number of appearances of each subgraph for randomized networks with an arbitrary degree distribution. In Appendix B, we calculate the probabilities for the three-species motifs in the randomizations of the generalized cascade model yielding
| (13) |
| (14) |
| (15) |
| (16) |
and
| (17) |
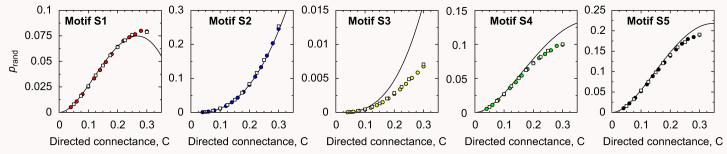
Fig. 4 compares the analytical predictions for the randomizations, Eqs. (13)-(17), with simulations of the generalized cascade model finding good agreement. The small discrepancies observed have their origin in that some of the expressions derived in Itzkovitz et al. (2003) are approximate.
Fig. 4.
Comparison between analytical expressions, Eqs. (13)-(17), and randomizations of the generalized cascade model for motifs S1–S5. It is visually apparent that the analytical predictions compare well with the model-generated data. Filled circles are for food webs with S = 50 and open squares for food webs with S = 100 Each data point represents an average over 1000 model-generated food webs.
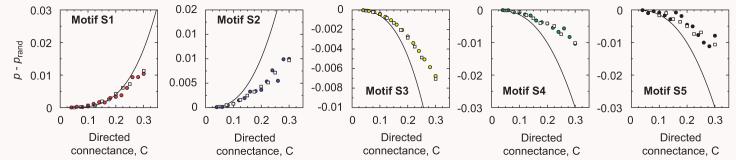
Finally, we obtain the differences by subtracting the probability of motifs appearing in the model, Eqs. (10)-(12), and in their randomizations, Eqs. (13)-(17). Table 1 summarizes these results. We show comparisons between the expressions for p − prand and simulations of the generalized cascade model in Fig. 5. Our analytical derivations thus predict that food webs generated by the generalized cascade model have over-expression of motifs S1 (a food chain) and S2 (simple omnivorism) and under-representation of motifs S3 (a trophic loop), S4 (isolated exploitative competition), and S5 (isolated generalist predation). The percentage of under/over-representation is, however, rather small, generally under 10%. These predictions make up our second check of the generalized cascade model.
Table 1.
Analytical expressions for appearance probability of motifs S1–S5 in the generalized cascade model
| Three-node motif | p – prand | Representation |
|---|---|---|
| S1 | Over | |
| S2 | Over | |
| S3 | under | |
| S4 | under | |
| S5 | under |
The right column states the prediction of over- or under-representation of each motif according to the model.
Fig. 5.
Comparison between analytical expressions for p − prand and simulations of the generalized cascade model for motifs S1–S5. The model predicts over-representation of motifs S1 and S2 and under-representation of motifs S3–S5. The analytical predictions compare well with the model-generated data, though they generally overestimate the differences due to the approximate character of the expressions used to evaluate prand. Filled circles are food webs with S = 50 and open squares food webs with S = 100. Each data point represents an average over 1000 model-generated food webs.
3. The completely random model
In the following section, we will compare the analytical expressions derived for the generalized cascade model with empirical data. However, we calculate them now for a different model, a fully random network, in order to determine whether the probability functions for the subgraphs depend significantly on the mechanisms underlying the generation of the network.
In a completely random (Erdos–Renyi) network, each species has the same probability x to be connected to any other species in the network. According to this definition, the average number of prey per species is z ≡ L/S = Sx, and the directed connectance yields C ≡ z/S = x.
Let us consider three arbitrary species in = the network, say A, B, and C. They are connected through subgraph S1 if, for instance, A eats B, and B eats C with no further links among them; this happens with probability x2(1 − x)4. Of course, there exist other options to build this subgraph by A, B, and C exchanging their roles, which amounts to a total of six different configurations. As a consequence, we have
| (18) |
Similarly, considering the number of configurations for every subgraph and the probability for each of them, one finds
| (19) |
| (20) |
and
| (21) |
Finally, since these networks are completely random, their randomization provides equally random networks, so that the probabilities for subgraphs S1–S5 in the randomized networks of this model are exactly the same ones, namely Eqs. (18)-(21). The differences between them are obviously zero.
4. Subgraphs statistics in empirical food webs
One interesting observation from Figs. 3-5 is that the probabilities generated by model food webs depend on a single variable, the directed connectance C, and very weakly on the size of the food web. This indicates that our representation of the probabilities versus C can be adequate to provide a unified description of empirical data, since it allows us to include in the same plot food webs with different sizes. If empirical food webs behave as model food webs, one expects a common trend for the probabilities as functions of C despite having different S values.
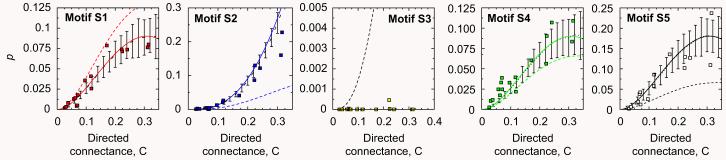
In this section we compute the fraction of appearances for each subgraph S1–S5 for 17 empirical food webs (see Appendix A for details). Figs. 6-8 show the results for the empirical food webs, their randomizations, and the differences, and also the comparison with the generalized cascade and the fully random models. One observes that the analytical expressions obtained for the generalized cascade model provide a reasonable agreement with empirical data for p and prand with no adjustable parameters; in contrast, the completely random model provides remarkably poorer fits to the empirical values in most cases.
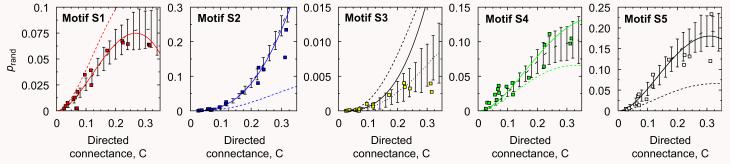
Fig. 6.
Fraction of appearances of motifs for empirical food webs (symbols) compared to the analytical predictions for the generalized cascade model (solid lines) and the random model (dashed lines). Numerical simulations for the generalized cascade model with S = 50 are shown by the dotted line where the error bars are two standard deviations. It is visually apparent that the generalized cascade model fits rather well the empirical data for all the motifs, whereas the random model provides much poorer fits. Note that there are no fitting parameters in model estimates.
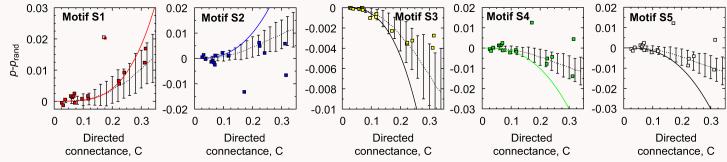
Fig. 8.
Differences between actual appearances of motifs and the corresponding randomized food webs for 17 empirical food webs (symbols) as compared to the analytical predictions for the generalized cascade model (solid line) and the random model (dashed lines). Numerical simulations for the generalized cascade model with S = 50 are shown by the dotted line, where the error bars are two standard deviations. Motifs S1 and S2 are typically over-represented and motifs S3–S5 are under-represented, in agreement with the qualitative predictions of the model. The two noticeable deviations correspond to Bridge Brook (C = 0:17) and Skipwith Pond (C = 0:32). Quantitatively, the analytical curves generally overestimate the differences at larger values of C for both the empirical values and the numerical simulations of the generalized cascade model.
In the plots for the differences, the data generally appear more noisy. This is due to the fact that the empirical values for p and prand are in general quite similar in magnitude; they commonly differ by less than 10%, in agreement with the model predictions. The general trend, however, is that motifs S1 and S2 are typically over-represented and motifs S3–S5 are under-represented, in agreement with the qualitative predictions of the model as expressed in Table 1. Quantitatively, the theoretical curves generally over-estimate the empirical values, while the numerical simulations of the model provide reasonable estimates.
There exists, however, more noise in the empirical data than exhibited by the model, in particular for motif S2. To explore this issue further, let us note that it is the same two food webs which seem to deviate from the general trend in the plots of Fig. 8: they are Bridge Brook (with C = 0:17) and Skipwith Pond (C = 0.32). Why exactly those two food webs behave differently from the others is interesting but unclear. We can note that they are the smallest food webs of the ones studied, each with 25 trophic species (see Table 2). Although statistical fluctuations grow with decreasing size, they do not seem enough to explain this behaviour. Note, on the other hand, that they match rather well with the predictions for p and prand separately (Figs. 6 and 7).
Table 2.
Empirical food webs studied
| Food web | S | L | Single links |
Double links |
Cannibal links |
Reference |
|---|---|---|---|---|---|---|
| Benguela | 29 | 203 | 186 | 5 | 7 | Yodzis (1998) |
| Bridge Brook Lake | 25 | 106 | 102 | 1 | 3 | Havens (1992) |
| Caribbean Reef | 50 | 556 | 471 | 32 | 21 | Opitz (1996) |
| Chesapeake Bay | 31 | 68 | 67 | 0 | 1 | Baird and Ulanowicz (1989) |
| Coachella Valley | 29 | 262 | 199 | 22 | 19 | Polis (1991) |
| Grassland | 61 | 97 | 97 | 0 | 0 | Martinez et al. (1999) |
| Little Rock Lake | 92 | 997 | 936 | 24 | 13 | Martinez (1991) |
| Northeast US Shelf | 79 | 1400 | 1363 | 7 | 25 | Link (2002) |
| Scotch Broom | 85 | 223 | 219 | 0 | 4 | Hawkins et al. (1997) |
| Skipwith Pond | 25 | 197 | 181 | 4 | 8 | Warren (1989) |
| St. Marks Seagrass | 48 | 221 | 218 | 0 | 3 | Christian and Luczkovich (1999) |
| St. Martin Island | 42 | 205 | 205 | 0 | 0 | Goldwasser and Roughgarden (1993) |
| Ythan Estuary (1) | 83 | 395 | 389 | 1 | 4 | Hall and Raffaelli (1991) |
| Ythan Estuary (2) | 174 | 579 | 573 | 1 | 4 | Hall and Raffaelli (1993) |
| Canton Creek | 102 | 697 | 696 | 0 | 1 | Townsend et al. (1998) |
| Stony Stream | 109 | 829 | 827 | 0 | 2 | Townsend et al. (1998) |
| El Verde Rainforest | 155 | 1509 | 1369 | 69 | 2 | Waide and Reagan (1996) |
S is the number of trophic species in the food web and L is the number of trophic predator-prey interactions.
Fig. 7.
Fraction of appearances of motifs for randomizations of the empirical food webs (symbols) compared to the analytical predictions for the generalized cascade model (solid line) and the random model (dashed lines). Numerical simulations for the generalized cascade model with S = 50 are shown by the dotted line where the error bars are two standard deviations. It is visually apparent that the generalized cascade model fits rather well the empirical data for all the motifs, whereas the random model provides much poorer fits. Note that there are no fitting parameters in model estimates.
In summary, the behaviour of the two models indicates that the behaviour observed in the empirical data is not a trivial one: not any model would yield a similar behaviour for the quantities analyzed. Furthermore, we observe remarkable agreement between the local structure in the generalized cascade model and the empirical data.
5. Concluding remarks
The predictions of the generalized cascade model for the appearances of subgraphs S1–S5 provide good comparison to the empirical results, in contrast to those for a completely random model. This generalized cascade model was recently shown to fit empirical data for a number of global quantities, including the distributions of the number of prey and predators. Here we show that it also describes the local structure of empirical food webs. This suggests that many features of food web structure could be explained by considering the two principle ingredients inside the model, namely (i) the species' niche values form a totally ordered set, and (ii) each species has a specific exponentially decaying probability of preying on a given fraction of the species with lower niche values. These could then be considered as basic mechanisms actually shaping food webs.
It is an interesting ecological question to determine why these appear to be such important ingredients to explain food web structure. Recently, Rossberg et al. have devised a couple of dynamic models, the speciation model (Rossberg et al., 2005, 2006a) and the matching model (Rossberg et al., 2006b) that seem to provide the dynamical explanation. By starting from an ordered set of species, the dynamic evolutionary rules of speciation, extinction, and migration lead to distributions of number of prey and number of predators similar to the ones obtained through the static models. Indeed, the matching model fits remarkably the empirical data, improving in some cases the predictions of the niche model at the expense of a number of adjustable parameters. From the result of an extensive analysis, the authors conclude that the tendency of newly created species to avoid competition with their relatives is indeed the fundamental mechanism responsible of food web structure.
Empirical and model food webs predict over-representation of motifs S1 and S2, and under-representation of motifs S3–S5. Empirical data are rather noisy, and the over-representation of subgraph S2 predicted by the generalized cascade model is unclear in the empirical data. This is also the result found by Bascompte and Melian (2005), who also analyzed the under/over-representation of a number of ecologically relevant subgraphs, among them, our motifs S1 (food chain) and S2 (simple omnivory). Our methodology, however, differs from theirs in several aspects. On the one hand, we consider trophic species instead of taxonomic ones; on the other hand, we count motifs only once (for instance, we do not count the food chains included in motifs S2 in the evaluation of S1). Despite the different analysis, we still do not find an unambiguous over-representation of omnivorism, in contrast to what one may expect according to its stabilizing role in trophic interactions (McCann and Hastings, 1997).
Finally note that, from the quantitative point of view, the percentage of under/over-representation of motifs is generally small, usually less than a 10%; curiously, this is also the order of magnitude predicted by the generalized cascade model. This high similarity between the number of subgraphs in empirical food webs and in their randomizations indicates that there may be no overwhelming evolutionary trend toward under/over-representation of any motif, and that the small differences observed are more likely a consequence of the mechanisms generating the food web.
Acknowledgements
We thank R. Guimerà and M. Sales-Pardo for stimulating discussions and helpful suggestions. JC thanks the Spanish CICYT (FIS2006-12296-C02-01) and the Direcció General de Recerca (2005 SGR 000 87) for support. DBS acknowledges the NU ChBE Murphy Fellowship and NSF-IGERT “Dynamics of Complex Systems in Science and Engineering” (DGE-9987577). LANA acknowledges a Searle Leadership Fund Award, National Institute of General Medical Sciences/National Institutes of Health K25 Career Award, the J.S. McDonnell Foundation, and the W.M. Keck Foundation.
Appendix A. Empirical food webs
Table 2 provides the list of food webs analyzed as well as some topological parameters characterizing them. They range between 25 and 92 trophic species, and the average connectivity varies from 2.19 to 17.72. It also contains the number of single links, double links, and cannibal links for each empirical food web. One observes that the frequency of double links is generally small, with only one case, Coachella Valley, close to 10%.
Appendix B. Motif probabilities in the generalized cascade model
We calculate here the subgraph probabilities for the randomizations of the generalized cascade model. Itzkovitz et al. (2003). derived general expressions for the average number of appearances Ni of motifs in randomized networks. The fraction of motifs is obtained dividing Ni by the total number of possible triplets of species, ST ≡ S(S-1)(S-2)/6. For subgraphs S1–S5, these can be cast as
| (22) |
with
| (23) |
where z ≡ L/S is the average connectivity, ki and mi denote the number of prey and number of predators of species i, respectively, and 〈…〉 is the average over all species in the randomized network. Since these networks have the same distributions of in- and out-links that the original networks, these averages can be calculated directly from the latter ones.
From expressions (23), and can be rewritten as
| (24) |
Therefore, can be evaluated if one knows p1, p4, and p5. In order to calculate these quantities, let us note that they have a direct interpretation. (i) is the number configurations where species A eats B, and B eats C, independently if there is a trophic connection between species A and C (i.e. it is like a generalization of motif S1); therefore, p1 = N1 / ST is just the probability for this configuration, namely 〈xAxB〉 = 〈x〉2 , since xA and xB are independent random variables. (ii) is the number of configurations where species A feeds on C and species B feeds on C, independently if A and B are connected (i.e. like a generalization of motif S4); then, p4 is the probability 〈xAxB〉 = 〈x〉2 . (iii) Similarly, p5 is the probability of A eating species B and C, independently of the eventual connection of B and C, namely .
By replacing these results in Eqs. (22)-(24), one finds
| (25) |
Finally, the beta-function (1) yields
| (26) |
The substitution of these expressions into (25) supplies Eqs. (13)-(17).
References
- Amaral LAN, Meyer M. Environmental changes, coextinction, and patterns in the fossil record. Phys. Rev. Lett. 1999;82:652–655. [Google Scholar]
- Artzy-Randrup Y, Fleisman SJ, Ben-Tal N, Stone L. Comment on “network motifs: simple building blocks of complex networks”. Science. 2004;305:1107. doi: 10.1126/science.1099334. [DOI] [PubMed] [Google Scholar]
- Baird D, Ulanowicz RE. The seasonal dynamics of the Chesapeake Bay ecosystem. Ecol. Monogr. 1989;59:329–364. [Google Scholar]
- Bascompte J, Melian CJ. Simple trophic modules for complex food webs. Ecology. 2005;86(11):2868–2873. [Google Scholar]
- Caldarelli G, Higgs PG, McKane AJ. Modeling coevolution in multispecies communities. J. Theor. Biol. 1998;193:345. doi: 10.1006/jtbi.1998.0706. [DOI] [PubMed] [Google Scholar]
- Camacho J, Guimerà R, Amaral LAN. Analytical solution of a model for complex food webs. Phys. Rev. E. 2002a;65 doi: 10.1103/PhysRevE.65.030901. art. no. 030901(R) [DOI] [PubMed] [Google Scholar]
- Camacho J, Guimerà R, Amaral LAN. Robust patterns in food web structure. Phys. Rev. Lett. 2002b;88 doi: 10.1103/PhysRevLett.88.228102. art. no. 228102. [DOI] [PubMed] [Google Scholar]
- Cattin M-F, Bersier L-F, Banašek-Richter C, Baltensperger R, Gabriel J-P. Phylogenetic constraints and adaptation explain food-web structure. Nature. 2004;427:835–839. doi: 10.1038/nature02327. [DOI] [PubMed] [Google Scholar]
- Christian RR, Luczkovich JJ. Organizing and understanding a winter's seagrass foodweb network through effective trophic levels. Ecol. Modelling. 1999;117:99–174. [Google Scholar]
- Cohen JE, Newman CM. A stochastic theory of community food webs I. Models and aggregated data. Proc. R. Soc. B. 1985;224:421–448. [Google Scholar]
- Cohen JE, Briand F, Newman CM. Community Food Webs: Data and Theory. Springer; Berlin: 1990. [Google Scholar]
- Dunne JA, Williams RJ, Martinez ND. Food-web structure and network theory: the role of connectance and size. Proc. Natl Acad. Sci. USA. 2002;99:12917–12922. doi: 10.1073/pnas.192407699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldwasser L, Roughgarden J. Construction of a large Caribbean food web. Ecology. 1993;74:1716–1733. [Google Scholar]
- Hall SJ, Raffaelli D. Food-web patterns: lessons from a species-rich web. J. Anim. Ecol. 1991;60:823–842. [Google Scholar]
- Hall SJ, Raffaelli D. Food webs: theory and reality. Adv. Ecol. Res. 1993;24:187–239. [Google Scholar]
- Havens K. Scale and structure in natural food webs. Science. 1992;257:1107–1109. doi: 10.1126/science.257.5073.1107. [DOI] [PubMed] [Google Scholar]
- Hawkins BA, Martinez ND, Gilbert F. Source food webs as estimators of community food web structure. Int. J. Ecol. 1997;18:575–586. [Google Scholar]
- Holt RD. Community modules. In: Gange AC, Brown VK, editors. Multitrophic interactions in Terrestrial Ecosystems, 36th Symposium of the British Ecological Society. Blackwell Science; 1997. pp. 333–350. [Google Scholar]
- Holt RD, Hochberg ME. Indirect interactions, community modules and biological control: a theoretical perspective. In: Waijnberg E, Scott JK, Quimby PC, editors. Evaluation of Indirect Ecological Effects of Biological Control. CAB International; 2001. pp. 13–37. [Google Scholar]
- Itzkovitz S, Milo R, Kashtan N, Ziv G, Alon U. Subgraphs in random networks. Phys. Rev. E. 2003;68 doi: 10.1103/PhysRevE.68.026127. art. no. 026177. [DOI] [PubMed] [Google Scholar]
- Itzkovitz S, Milo R, Kashtan N, Newman MEJ, Alon U. Reply to “Comment on ‘Subgraphs in random networks’”. Phys. Rev. E. 2004;70 doi: 10.1103/PhysRevE.68.026127. art. no. 058102. [DOI] [PubMed] [Google Scholar]
- Lassig M, Bastolla U, Manrubia SC, Valleriani A. Shape of ecological networks. Phys. Rev. Lett. 2001;86:4418–4421. doi: 10.1103/PhysRevLett.86.4418. [DOI] [PubMed] [Google Scholar]
- Link J. Does food web theory work for marine ecosystems? Marine Ecology Progr. Ser. 2002;230:1–9. [Google Scholar]
- Martinez ND. Artifacts or attributes? effects of resolution on the Little Rock Lake food web. Ecol. Monogr. 1991;61:367–392. [Google Scholar]
- Martinez ND, Hawkins BA, Dawah HA, Feifarek BP. Effects of sampling effort on characterization of food-web structure. Ecology. 1999;80:1044–1055. [Google Scholar]
- Maslov S, Sneppen K. Specificity and stability in topology of protein networks. Science. 2002;296:910–913. doi: 10.1126/science.1065103. [DOI] [PubMed] [Google Scholar]
- McCann K, Hastings A. Re-evaluating the omnivory–stability relationship in food webs. Proc. R. Soc. of London B. 1997;264:1249–1254. [Google Scholar]
- Melián CJ, Bascompte J. Food web cohesion. Ecology. 2004;85(2):352–358. [Google Scholar]
- Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: simple building blocks of complex networks. Science. 2002;298:824–827. doi: 10.1126/science.298.5594.824. [DOI] [PubMed] [Google Scholar]
- Milo R, Itzkovitz S, Kashtan N, Levitt R, Shen-Orr S, Ayzenshtat I, Sheffer M, Alon U. Superfamilies of designed and evolved networks. Science. 2004;303:1538–1542. doi: 10.1126/science.1089167. [DOI] [PubMed] [Google Scholar]
- Opitz S. Trophic interactions in caribbean coral reefs. ICLARM Technical Reports. 1996;43:341. [Google Scholar]
- Polis GA. Complex trophic interactions in deserts: an empirical critique of food-web theory. Am. Nat. 1991;138:123–155. [Google Scholar]
- Rossberg AG, Matsuda H, Amemiya T, Itoh K. An explanatory model for food-web structure and evolution. Ecol. Complexity. 2005;2:317–321. [Google Scholar]
- Rossberg AG, Matsuda H, Amemiya T, Itoh K. Some properties of the speciation model for food web structure—mechanisms for degree distributions and intervality. J. Theor. Biol. 2006a;238(2):401–415. doi: 10.1016/j.jtbi.2005.05.025. [DOI] [PubMed] [Google Scholar]
- Rossberg AG, Matsuda H, Amemiya T, Itoh K. An explanatory model for food-web structure and evolution. J. Theor. Biol. 2006b;241:552–563. [Google Scholar]
- Stouffer DB, Camacho J, Guimerà R, Ng CA, Nunes Amaral LA. Quantitative patterns in the structure of model and empirical food webs. Ecology. 2005;86:1301–1311. [Google Scholar]
- Townsend CR, Thompson RM, McIntosh AR, Kilroy C, Edwards E, Scarsbrook MR. Disturbance, resource supply, and food-web architecture in streams. Ecol. Lett. 1998;1:200–209. [Google Scholar]
- Waide RB, Reagan WB, editors. The Food Web of a Tropical Rainforest. University of Chicago Press; Chicago, IL: 1996. [Google Scholar]
- Warren PH. Spatial and temporal variation in a freshwater food web. Oikos. 1989;55:299–311. [Google Scholar]
- Williams RJ, Martinez ND. Simple rules yield complex food webs. Nature. 2000;404:180–183. doi: 10.1038/35004572. [DOI] [PubMed] [Google Scholar]
- Yodzis P. The stability of real ecosystems. Nature. 1981;289:674–676. [Google Scholar]
- Yodzis P. Local trophodynamics and the interaction of marine mammals and fisheries in the Benguela cosystem. J. Anim. Ecol. 1998;67:635–658. [Google Scholar]