Experimental Parameterization of an Energy Function for the Simulation of Unfolded Proteins

Abstract

The determination of conformational preferences in unfolded and disordered proteins is an important challenge in structural biology. We here describe an algorithm to optimize energy functions for the simulation of unfolded proteins. The procedure is based on the maximum likelihood principle and employs a fast and efficient gradient descent method to find the set of parameters of the energy function that best explain the experimental data. We first validate the method by using synthetic reference data, and subsequently apply the algorithms to data from nuclear magnetic resonance spin-labeling experiments on the Δ131Δ fragment of Staphylococcal nuclease. A significant strength of the procedure that we present is that it directly uses experimental data to optimize the energy parameters, without relying on the availability of high resolution structures. The procedure is fully general and can be applied to a range of experimental data and energy functions including the force fields used in molecular dynamics simulations.

INTRODUCTION

Studies of unfolded proteins are becoming increasingly important in molecular biology. For example, residual structure in the unfolded states of globular proteins may affect the stability and folding of these proteins. Further, it is becoming clear that the native states of many proteins are highly dynamic and resemble unfolded proteins more than globular folds (1,2). While the precise prevalence of such disordered proteins is difficult to determine experimentally (3,4), it has been predicted (5) that up to 30% of eukaryotic proteins contain regions of more than 50 amino acids that are completely disordered. These regions thus have a native state characterized by increased dynamics and short-lived conformations and interactions. In addition, it is known that some proteins display such increased dynamics throughout their entire amino-acid sequences (1,2,5). These so-called intrinsically unfolded proteins are also predicted to be abundant in eukaryotic genomes (5), and have been suggested to play a central role in protein interaction networks (6), and to be implicated in a range of human diseases including Alzheimer's, Parkinson's, and cardiovascular diseases as well as cancer (7–9).

Despite the immense interest in disordered and unfolded proteins, a molecular description and understanding of their function is in general lacking (1). This is in particular due to the fact that structural studies of disordered proteins are highly challenging due to their increased dynamical properties (10,11). Recently, however, nuclear magnetic resonance spectroscopy (NMR) methods have been used extensively to obtain structural and dynamic information about unfolded and intrinsically disordered proteins (12). Together with other methods including x-ray scattering techniques (13), such studies have provided important information about the prevalence of residual structure in unfolded proteins. In particular these studies have shown that nonrandom long-range hydrophobic interaction are often present (14–19). Detailed structural interpretations of NMR and scattering experiments on disordered proteins are complicated by the fact that the experimental data are averages over very broad ensembles of conformations (20). However, when such dynamic averaging is taken into account, the experimental data can provide important restraints that can be used to obtain structural models of unfolded proteins (13,18,19,21).

One experimental method that has proven particularly well suited for structural studies of unfolded proteins is paramagnetic relaxation enhancement (PRE) NMR experiments (15,17,22,23). In these experiments, paramagnetic spin-labels are introduced at specific sites throughout the amino-acid sequence, and the resulting broadening of the backbone amide NMR signals is measured. The observed effects, which may extend to >20 Å, are directly related to the average distance between the spin-label and the amide proton. PRE experiments can therefore be used to probe long-range interactions present in unfolded states that could not be determined using, for example, NOE experiments. Provided that appropriate attention is given to the ensemble averaging that is implicit in these experimental data, the distance information can be used as restraints to determine ensembles of conformations that represent unfolded proteins (18,19,24).

Computational methods such as all-atom molecular dynamics simulations provide a complementary strategy to study the structural and dynamical properties of unfolded proteins (14,25). This approach has the distinct advantage that it does not require experimental data as input, and thus when properly validated provides the opportunity to predict the structural features of disordered proteins. A recurring problem in computer simulations of proteins is, however, the fact that highly accurate simulations are also very computationally demanding. Due to the large conformational space sampled by disordered and unfolded proteins, efficient sampling of the unfolded states using all-atom models requires very large amounts of computational power (25).

Coarse-grained protein models provide an alternative simulation methodology that attempts to overcome this sampling problem (26). By reducing the number of particles to be simulated, as well as using simplified energy functions, efficient sampling becomes feasible. One significant problem in this approach is, however, that it is not always clear how to derive the energy functions to be used in conjunction with the coarse-grained model. Physics-based parameter estimation is in general not possible because of the use of coarse-grained models. Statistical potentials provide one possible method to derive energy functions for coarse-grained models (27), and this approach has recently been very successful in the study of native proteins (28). However, large databases of reference structures are needed to derive such potentials and these are not available for unfolded proteins.

The parameter learning technique is a more general strategy toward optimizing parameters in energy functions and force fields. For example, Fain et al. parameterized a very general energy function by requiring that the energy of a conformation and the RMSD to the native state be correlated (29). Also, the energy parameters in a molecular dynamics force field have been optimized by requiring that the native state is stable (30). More recently, Winther et al. (31) used a gradient descent parameter optimization scheme to ensure that the probability of the native state was higher, and hence its free energy lower, than that of other conformations. However, while such approaches are highly promising when energy functions for prediction of protein structure are considered, they require a set of well-defined reference conformations to be used in the target function that is optimized. Since disordered proteins are characterized by broad ensembles of conformations and do not have a single well-defined native state conformation, the structural similarity to such a reference conformation cannot be used to derive energy functions for unfolded proteins.

To overcome the problem in parameterizing energy functions from single reference conformations, Groth et al. (32) devised a procedure that uses an ensemble of conformations in an optimization procedure for solvation parameters. They used a set of conformations derived from experimental NMR data, and optimized the force-field parameters to match the statistical weights of the conformations in the ensemble. Alternatively, inverse Monte Carlo procedures have been used to parameterize effective energy functions based on full knowledge of radial density functions (33).

In this study, we extend the ideas described above to develop a framework to optimize energy parameters for the simulation of unfolded proteins. In particular, our algorithm uses experimental data directly in the target function for optimization. Thus, the parameters that are obtained are not biased by the prior use of a particular structure determination scheme. In short, the iterative algorithm that we propose involves cycles of 1), sampling of conformations using an initial guess of energy parameters; 2), back-calculation of experimentally observable quantities from the simulated structures; 3), comparison with experimental data; and 4), an efficient gradient-based optimization scheme to obtain improved energy parameters, which are in better agreement with experiments. We here describe the framework of the algorithm and apply it to PRE experiments on unfolded proteins. We first test and validate the method using synthetic experimental data, and subsequently apply the procedure to experimental PRE data on the Δ131Δ fragment of Staphylococcal nuclease (15).

Our results show that it is possible to optimize energy parameters directly against experimental data, and that the procedure therefore provides a strategy to parameterize energy functions without having to rely on the availability of suitable reference conformations. The method is generally applicable to a range of types of experimental data, and we therefore also expect it to be useful for optimizing other types of energy functions including those used in molecular dynamics simulations.

METHODS

In our simulations, we use a C_α model with monomers of a uniform hard-sphere radius (2.5 Å). All bond lengths are fixed to 3.8 Å. Conformations were obtained via Metropolis Monte Carlo sampling using both larger pivot moves and local crankshaft moves in a ratio 1:9. In the parameter learning algorithm described in Results, each ensemble consists of 20,000 conformations, and was generated by performing 10⁸ Monte Carlo moves and saving a conformation every 5000 moves.

The HP-model

To create the HP-model of the Acyl Coenzyme-A Binding Protein (ACBP), we divided the amino acids in to two equally large groups according to their hydrophobicity. The amino acids that were classified as polar were Lys, Asp, Glu, Asn, Gln, Pro, Ser, Arg, Gly, and Thr, and the ones classified as hydrophobic were Ala, Tyr, His, Val, Trp, Cys, Leu, Ile, Met, and Phe.

Energy function

The energy function that we use consists of a local sequence-independent term, and a nonlocal contact energy term. The nonlocal energies are implemented as pairwise contact (square-well) potentials. These include a hard core clash distance of 5 Å C_α center-to-center distance, and an outer cutoff (interaction distance) of 8.5 Å. Residue pairs that are within these two limits contribute to the total energy with a pairwise energy, ε_ij, that depends on the amino-acid types (i and j) of the two residues. Interactions between pairs of residues separated by less than three amino acids are excluded.

The local energy function is a sequence-independent backbone potential that we use to ensure that the C_α bond angles (θ) and dihedral angles (τ) conform to a distribution that is representative of unfolded structures. To create such a potential, we analyzed all atom structures obtained with the program RCG, which generates structures that model unfolded ensembles well (21). Inspection of the distributions of θ- and τ-angles showed smooth, bi-modal distributions of both θ and τ, which to a first approximation could be considered independent. As the simplest starting point, we therefore chose to model these distributions independently using a sequence-independent energy function that consisted of the sum of two von Mises functions:

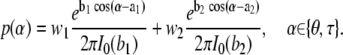(1)

The parameters a₁, b₁, a₂, and b₂ in this equation are given in Table 1 and were obtained by fitting against the distributions obtained from RCG. I₀ is the modified Bessel function of order zero.

TABLE 1.

Parameters for the backbone θ and τ potentials

	w1	a1	b1	w2	a2	b2
Angles (θ)	0.012052	2.0168	59.393	0.0025810	1.7149	439.31
Dihedrals (τ)	0.011481	−2.7311	4.2100	0.0059725	4.8657	−1.7150

The total energy is obtained by combining the local and nonlocal energies as

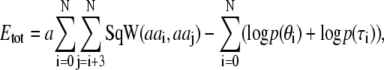(2)

where SqW(aa_i, aa_j) is the square-well function described above. In the parameter optimization algorithm that we describe here, we only optimize the interaction parameters in the nonlocal energy whereas we keep the local energy terms and the interaction radii constant. The overall energy scale is determined by the simulation temperature which we here choose by setting kT = 1. The parameter a determines the relative weight between the local and the nonlocal energy function. For the generation of synthetic data we determined the value of a so as to reproduce the scaling between the radius of gyration and the chain length as determined experimentally (34). In the HP-model we therefore used a = 0.45. In the 20-parameter model described in more detail in Results we used a = 2.8 together with the values of q_i determined previously (35) (with q ranging from 0.333 for leucine to 0.125 for lysine). The same value of a = 2.8 was used in the optimization against the experimental data.

Paramagnetic relaxation enhancement data

In the calculations, we use a coarse-grained C_α model for the polypeptide chain. For the back-calculation of PRE data from the conformations, we therefore used the distances between pairs of C_α-atoms to estimate the intensity ratios. However, the experimentally determined PRE effects arise from the interaction between the amide proton and a paramagnetic nitroxide group attached through the side chain of engineered cysteine residues. To minimize bias arising from this difference we excluded residue pairs separated by less than seven residues in the calculation of χ². This value was obtained by visual inspection of simulated intensity ratio profiles, but agrees with the length scale over which residue stiffness extends in unfolded proteins (36). In the experimental study of Δ131Δ, the spin-label introduced at position 105 was suspected to perturb the structure significantly (15), and we therefore left out the data from this spin-label from our analysis.

RESULTS

A data-driven optimization algorithm

Our goal is to develop a procedure that is able to define an energy function for the simulation of unfolded proteins. We here consider energy functions of fixed functional forms, although the methods described are also applicable to more generally shaped energy functions (29). Instead of relying on the availability of a set of suitable reference conformations, we optimize the energy function directly against experimental data. Thus, for a given choice of a functional form, the goal is to determine a set of energy parameters that are most compatible with (i.e., has the highest posterior probability for) a set of experimental data. The iterative algorithm that we have developed is schematically shown in Fig. 1, and the mathematical framework for the method is described in detail in the Supplementary Material. While the procedures involved are completely general, we here describe their application in optimizing energy parameters for a coarse-grained C_α model to match experimental PRE data from experiments on unfolded proteins.

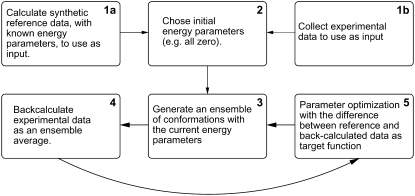
FIGURE 1.

An iterative algorithm for optimization of energy parameters from experimental data. The algorithm begins with either block 1a or 1b, and then proceeds to block 2. It then consists of multiple cycles of blocks 3–5. Resort to the main text for a discussion of the individual steps.

In the PRE experiments used here, the intensity of the NMR signals of the backbone amide protons is recorded with spin-labels attached, one at a time, at specific sites throughout the amino-acid sequence. When the spin-label is in its oxidized paramagnetic state the NMR cross-peaks are broadened in a distance-dependent manner and hence the measured peak intensity (I_ox) is lower than the intensity measured (I_red) when the spin-label is reduced to its diamagnetic state. The observed intensity ratio, I_ox/I_red, is directly related to the distances between the spin-label and amide proton through the equations (15,23):

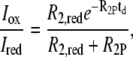(3)

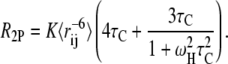(4)

In these equations, R_2P is the paramagnetic contribution to the transversal relaxation rate, 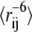is the (weighed) ensemble-averaged distance between spin-label and amide proton and K, τ_C, ω_H, R_2,red, and t_d are known constants or experimentally measured values (23).

The first step of the algorithm (boxes 1a or 1b in Fig. 1) consists of the collection of a set of experimentally determined values of I_ox/I_red (or synthetic data for method validation). Also, in the first round of optimization an initial guess of energy parameters is needed, and we here typically set all interaction parameters to zero (Box 2 in Fig. 1). Then, because the experimental data represent ensemble averages from a large set of conformations, we generate heterogeneous ensembles of protein conformations in each iteration of the algorithm (Step 3 in Fig. 1). The ensembles are here generated by Metropolis Monte Carlo simulations, and each round uses a different set of energy function parameters.

From the ensemble of conformations generated in the Monte Carlo sampling we calculate the ensemble-averaged distances, 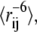and use Eqs. 3 and 4 to back-calculate the I_ox/I_red values one would have observed if this ensemble had been studied experimentally (Step 4 in the algorithm). To quantify how well the generated ensemble represents the experimental data, the calculated and experimentally determined intensity ratios are compared using a χ² score:

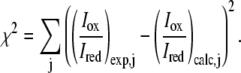(5)

Low values of χ² indicate a good agreement between experiment and simulation whereas high values mean that the simulated structures do not represent the experimentally determined data well. In the initial rounds of our algorithm the energy parameters may not be realistic, and hence the calculated χ² values are typically high.

The purpose of the optimization algorithm is to maximize the likelihood of the experimental data given the energy parameters or, equivalently, to minimize the χ² score by changing the energy parameters. In principle, this could be performed by first changing one or more energy parameters, and then to perform a Monte Carlo simulation with the changed energy parameters. From the ensemble obtained, one could estimate a new χ² score which could be used to judge whether the new parameter set is better or worse than the original (30). However, this approach is computationally extremely demanding and currently not feasible, as each small step in the multidimensional parameter space involves a complete resampling of conformations.

Instead, we devised a highly efficient approximate method to estimate the effect on χ² when energy parameters are changed. The idea is that for small steps in parameter space we can assume that the previous Monte Carlo sample provides a reasonable ensemble of conformations, and that the change in energy parameters corresponds only to a reweighing of the individual conformations (37,38). Since we know the probability distribution according to which the ensemble was sampled, we can estimate the reweighed quantity 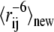for a new set of energy parameters from (37,39):

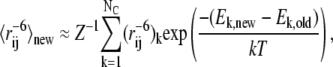(6)

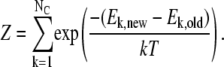(7)

Here, the sums extend over the N_C conformations in the ensemble, and E_k,new is the energy of the k^th conformation, as calculated with the new parameters. E_k,old is the energy of the same conformation calculated with the old set of parameters that were used to generate the ensemble of conformations, and 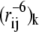is the pairwise distance between spin-label and amide proton in the conformation. The approach is analogous to Zwanzig's free-energy perturbation method (37), and allows us to estimate the average distances one would expect to obtain if the energy parameters are changed slightly, without having to resort to a full resampling of conformations. Alternatively, the idea can be viewed as a particular implementation of the umbrella-sampling method (38) in which ΔE = E_new − E_old is the biasing potential, and Eqs. 6 and 7 are used to remove the bias in the simulations.

From the updated set of distances obtained in Eq. 6 we can calculate a new set of intensity ratios, and thereby estimate the χ² score obtained with the modified parameters. Since this procedure is computationally very efficient, we can use standard nonlinear optimization methods such as the Levenberg-Marquardt procedure (40) to optimize the set of energy parameters (Step 5 in Fig. 1).

Since the approach described above is only applicable to local changes in parameter and conformation space (37,41), our algorithm includes periodic resampling of conformations with the modified energy parameters. In practice, this is performed after the Levenberg-Marquardt optimization procedure has converged locally in parameter space. After local convergence we therefore perform a full Monte Carlo sampling of conformations using the updated energy parameters. We then use this ensemble for the next iteration in the full algorithm (Fig. 1) and continue until the obtained parameters converge. In the applications described below, the parameters converge within <20 iterations of the algorithm.

Testing the algorithm with synthetic data

To test and validate the parameter learning algorithm described above we found it useful initially to generate synthetic reference data and use this as input to the algorithm. Such synthetic reference data ensure that the data we use as reference are consistent with the protein model and local energy function that we employ. Importantly, since the synthetic reference data were generated with known energy parameters we can examine to what extent our optimization procedure can be used to recover these parameters. Furthermore, synthetic reference data are free from experimental noise, allowing for the analysis of experimental data with different levels of pseudo-random noise.

As an initial test case we chose to start with the off-lattice C_α HP-model (H, hydrophobic; P, polar) which is a simple yet reasonably realistic model for unfolded proteins (42). Importantly, the HP-model is designed to capture the hydrophobic interactions that are known to be important in unfolded proteins (16).

For our studies we chose the 86-residue bovine Acyl Coenzyme-A Binding Protein (ACBP) whose unfolded state has been studied extensively (18,23,24,43) using NMR spectroscopy. We used the wild-type sequence of ACBP and divided the amino acids into two groups, hydrophobic (H) and polar (P), as described in Methods. The energy function that we use is a contact potential in which hydrophobic interactions are favored (ε_HH = −1) and all other interactions are neutral (ε_HP = ε_PP = 0). Using this model we performed a long Monte Carlo simulation (2.4 × 10⁹ steps) at a temperature where the chain expansion matches experimental data on unfolded proteins (34), and extracted 2.4 × 10⁵ conformations. From these conformations we calculated synthetic experimental PRE data using Eqs. 3 and 4. To mimic the experimental studies of ACBP (23) we used positions 17, 36, 46, 65, and 86 for the spin-labels.

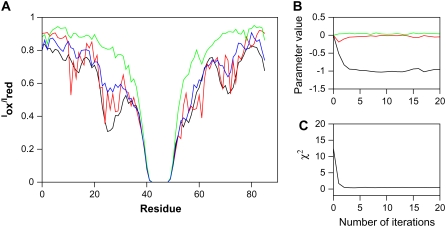
We then tested how well the algorithm could recover the known HP parameters using only the knowledge of the synthetic experimental data. As initial guess for parameters we used values that represent a protein with no global attractive forces, i.e., ε_HH = ε_HP = ε_PP = 0. The progress through the first few steps of the algorithm is shown in Fig. 2 A. In this plot the black curve represents the synthetic intensity-ratio data for a spin-label placed at position 46. The green curve in the plot is the intensity-ratios calculated from the first ensemble generated using the initial energy parameters. Not surprisingly, the curve is very different from the black curve, indicating that the initial set of conformations does not represent the data well, but instead resembles the ratios expected for a random coil. The noise in the green curve arises from the relatively small ensemble size (20,000 conformations) used in the calculations.

FIGURE 2.

(A) Development of the intensity ratio profiles during the first few steps of the optimization algorithm. The data correspond to a spin-label introduced at position 46 in the ACBP sequence. (Black) Synthetic reference data generated using an HP-model (Step 1A in Fig 1). (Green) Back-calculated data from the initial energy parameters (Step 4, first round). (Red) Intensity ratios obtained after parameter optimization (Step 5, first round). (Blue) Intensity ratios obtained after resampling using the optimized parameters (Step 3, second round). (B) Development of the energy parameters through 20 iterations of the algorithm. (Black, ε_HH; red, ε_HP; green, ε_PP.) It can be seen that the parameters converge to the values corresponding to the HP-model after a few iterations of the algorithm. (C) Development of the χ² score during 20 iterations of the algorithm. It can be seen that the score drops concomitantly with the convergence of the parameters.

The next step in the algorithm is the approximate gradient descent optimization method in which each conformation in the sampled ensemble is reweighed and the updated intensity ratio is estimated using Eq. 6. The red curve in Fig. 2 A shows the data after convergence of the optimization algorithm. This curve is more noisy because the optimization algorithm acts via stabilizing more relevant conformations, thereby in practice reducing the effective size of the ensemble. Nevertheless, it is clear that the red curve is significantly closer to the black reference data. This is reflected by a drop in the calculated χ² from 12.4 to 3.5, and the optimized energy parameters (ε_HH = −0.5, ε_HP = −0.2, ε_PP = 0.0) are also much closer to the true values of the HP-model than the initial guess. In the next iteration of the algorithm we begin by resampling conformations using the updated energy parameters, and the resulting calculated intensity ratios are shown as the blue curve in Fig. 2 A. This ensemble is then used as starting point for the next round of parameter optimization, and the algorithm is continued until convergence.

We completed 100 iterations of the algorithm and the resulting parameter values and χ² scores from the first 20 cycles are shown in Fig. 2, B and C, respectively. It is seen that the χ² score rapidly drops to a low value of ≈0.27 within a few optimization steps and then stays constant throughout the rest of the calculations. Simultaneously, it can be seen that the parameters also quickly move toward values around ε_HH ≈ −1, ε_HP ≈ 0, and ε_PP ≈ 0, and that the values are well converged and stable. The nonzero value of χ² and the fluctuations of the energy parameters are here mainly caused by statistical noise from the finite size of the ensembles both generated during the iterations but also used to define the synthetic data. By averaging over steps 5–100 in the algorithm, we obtain ε_HH = −1.01 ± 0.03, ε_HP = −0.007 ± 0.03, and ε_PP = 0.025 ± 0.02 (mean and standard deviation). The parameters recovered from the parameter learning procedure are thus in excellent agreement with the HP parameters that were used to generate the synthetic reference data. The fact that there is an uncertainty, albeit small, in the calculated parameters can be understood from the mathematical framework described in the Supplementary Material. In particular, Eq. 22 in the Supplementary Material shows that there are two contributions to the inverse variance in the estimated parameters with a common scale given by (kTσ_d)⁻². In this context, σ_d represents the uncertainty of the synthetic data as a consequence of using a finite sample. The first term in Eq. 22 is a product of covariances, C·C, between the energy variation in parameter space and the calculated experimental data. It provides a measure of how sensitive the data is to changes of the parameters and must, for physical reasons, be bounded from above. The second term, which we found to be negligible for synthetic data (not shown), takes into account the fact that it may not always be possible to match the experimental data perfectly.

To test the robustness against the initial guess for the energy parameters we repeated the calculations using either an overall attractive (ε_HH = ε_HP = ε_PP = −0.5) or repulsive (ε_HH = ε_HP = ε_PP = 0.5) potential as starting point. In both cases the optimized parameters were within error the same as those obtained above, demonstrating that the parameter learning algorithm is highly robust with respect to the initial guess of the parameters.

Optimization of a 20-parameter model

With success for the optimization of three parameters from synthetic reference data, we proceeded to test a more realistic model able to capture the full sequence variability of proteins. A full 20 × 20 matrix with pairwise interaction energies for a contact potential has 210 independent parameters, and we judged this to be too large a change from three parameters. One possibility to reduce the number of parameters is, as in the HP-model, to divide the 20 amino acids into separate groups and use a reduced alphabet of representative amino acids (44). However, we instead chose to use a model inspired by the observation (35) that a full interaction energy matrix for native proteins (27) can be well described by a single dominant eigenvector of the matrix. That is, for native proteins the 210 interaction energy parameters (ε_ij) in a statistical potential can be very well approximated from a per-amino-acid property, q_i, using the relationship ε_ij ≈ −q_iq_j (35). In native proteins, q_i is related to the hydrophobicity of the i^th amino acid, and this approximation to estimate the pairwise interaction energies is therefore expected to be particularly suitable in situations where nonspecific hydrophobic interactions are dominant.

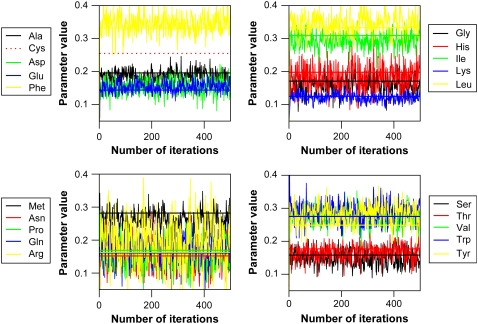
Again, we decided to test the algorithm using synthetic data. As reference values of q_i for the 20 amino acids we used the values obtained by diagonalizing the interaction potential for native proteins (27,35), but carried out the simulations at an increased temperature where the chain is unfolded. We generated synthetic data for ACBP, and used our optimization algorithm on the synthetic data. The resulting evolution of the 20 energy parameters during 500 cycles of the algorithm is shown in Fig. 3. In that figure the horizontal lines indicate the target q_i values that were used to generated the synthetic data. While the fluctuations here are larger than for the HP-model, it is clear that the algorithm is still able to recover the underlying energy parameters well. For example, the Pearson correlation coefficient is 0.99 between the input parameters and those recovered after optimization. Again the errors in the estimated parameters can be understood in terms of the equations in the Supplementary Material (Eq. 24). Our results show that it is possible to encode an energy function with at least 20 energy parameters using spin-label data of this type. As for the HP-model, multiple independent runs of the algorithm gave average parameter values that were identical within error.

FIGURE 3.

Parameter optimization using a 20-parameter model. Parameters were optimized against synthetic data, and the plots show the development of the 20 energy parameters during 500 iterations of the algorithm. The parameters are shown in four plots for better visualization. In each box, the horizontal lines indicates the parameter values that were used to generate the synthetic reference data. There are no cysteine residues present for ACBP, so we are unable to optimize a parameter value for Cys. It is seen that the parameters converge after a few iterations and then fluctuate closely around their optimal values (Pearson correlation coefficient of 0.99 between input and average of optimized parameters).

Effects of experimental noise, amount of data, and ensemble size

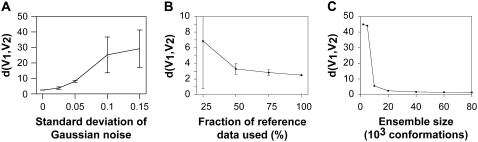
The use of synthetic data allows us to examine in detail the effects of changing different parameters in the optimization algorithm. First, since the synthetic data is inherently free from experimental error, we study the effect of different levels of experimental noise. We thus prepared four sets of synthetic data with increasing amounts of noise by adding random numbers from Gaussian distributions with standard deviations: 0.025, 0.05, 0.10, and 0.15. We then applied the optimization algorithm to each of these four data sets and calculated the average energy parameters from each run. For the lowest levels of noise the parameters converged well, whereas for the highest levels the obtained values are averages over highly fluctuating values of q_i. We observed that the quality of the parameters obtained decreased monotonously as increasing amounts of noise was added. To quantify this observation, we calculated the force-field metric described previously (45) between the optimized parameters and the ideal reference values used to generate the synthetic data. A low value of this score indicates that two energy functions are very similar. As seen in Fig. 4 A, the energy-function distance between the true underlying energy function and the one obtained after parameter optimization increases gradually with the amount of noise added. This observation is in qualitative agreement with the error analysis detailed in the Supplementary Material. In particular, Eq. 11 in the Supplementary Material shows that the inverse covariance matrix of the estimated parameters depends linearly on the inverse of the square value of the noise level. Note also that the obtained distance in the absence of noise is approximately the same as that obtained by adding Gaussian noise with a standard deviation of 0.025.

FIGURE 4.

Analysis of the effect of noise, amount of data, and ensemble size. (A) Synthetic data were generated with different levels of noise by adding random Gaussian noise with zero mean and varying standard deviation. The energy parameters were subsequently optimized against this data. The similarity between the ideal and the optimized parameters was quantified using an energy-function metric (45), d(V₁, V₂), between two potential energy functions V₁ (reference) and V₂ (optimized parameters). The results show that there is an approximately linear dependence between the accuracy of the optimized energy function and the noise level (standard deviation of Gaussian noise). (B) We sampled different subensembles using only a fraction of the full dataset. These subensembles were then used as input to the optimization algorithm, and the optimized parameters were then compared to the reference parameters. (C) Effect of using different ensemble sizes during the optimization. In all plots are the values showing the mean and standard deviation over independent runs.

An additional complication in real experiments is the lack of complete sets of data. We therefore analyzed how robust the algorithm is when part of the full spin-label dataset is missing. For these calculations we randomly selected only a fraction (25%, 50%, or 75%) of the full synthetic dataset and repeated the optimization using only these reduced sets of data. We again quantified the agreement to the ideal energy function using the force-field metric (45) (Fig. 4 B). The plot clearly shows that the algorithm is robust against missing data points and can achieve essentially the same accuracy using only half of the experimental data. Interestingly, comparison to Fig. 4 A shows that the effects of missing data points is minor compared to that of high levels of experimental noise.

Finally, we analyzed the effect of using different ensemble sizes during the optimization algorithm. The calculated intensity ratios depend on the averages 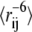in the simulated ensembles. These averages are most sensitive to short distances, and it is therefore essential to have a sufficiently broad ensemble in order not to bias the interpretation of the data (18). In the optimizations described above, each ensemble consists of 20,000 conformations. To ensure that this was sufficiently large, we repeated the optimization calculations using ensembles consisting of between 2000 and 80,000 conformations (Fig. 4 C). The results clearly show that the energy function can be recovered efficiently if the ensemble size is larger than 10,000 conformations. Presumably, for ensembles smaller than this, the tails of the distributions are not sampled sufficiently well for the optimization to be efficient.

Application to experimental PRE data

Given the ability to recover parameters well from synthetic ACBP data we then applied the algorithm to experimentally determined PRE data. Initially we used data obtained from experiments on ACBP at a series of different denaturant concentrations and pH values (18,23,24). However, we found that the parameters displayed large fluctuations during the optimization and did not give converged results in independent runs, suggesting that the information contents in these experimental data sets were not sufficient to determine a set of energy parameters using the algorithm described. A more detailed analysis of these optimizations suggests that parameter fluctuations are more pronounced when using data obtained at more denaturing conditions, and hence are likely to arise at least in part because there is less residual structure under these conditions (results not shown). Further, we note that there is approximately the same amount of data available at all sets of conditions (18,24), corresponding approximately to 65% or larger in the context of Fig. 4 B. In contrast to the case of synthetic data, the optimization against experimental data may be hampered both by random experimental errors as well as systematic errors arising from the approximate energy function and the use of a coarse-grained model. In the framework of the Supplementary Material (Eqs. 11 and 24), this means that not only the finite covariances (first term), but also the fact that it is not possible to match the experiments perfectly (second term), gives rise to parameter uncertainties.

Instead we turned to experimental data from the Δ131Δ fragment of Staphylococcal nuclease (15,46). Δ131Δ is an unfolded form of Staphylococcal nuclease that has been obtained by deleting residues 4–12 and 141–149 of the wild-type protein sequence (47). The experimental data that we used contained 676 intensity ratio values distributed among 13 different spin-label probes. Application of the algorithm on this data gave rise to a set of well-determined energy parameters (Table 2). In principle it is possible to evaluate the convergence of these parameters using Eq. 20 in the Supplementary Material. However, this requires good estimates of the experimental uncertainties which were not available. We have therefore taken a more pragmatic approach in which we made sure that multiple independent optimization runs gave results that were identical within the errors in the individual runs. The resulting energy parameters are thus able to describe the unfolded state of the Δ131Δ fragment well, and as we describe below are not the result of overfitting the data. However, inspection of the obtained parameters does not reveal any simple pattern and, for example, the interaction parameters are not significantly correlated to the hydrophobicity of the amino acids.

TABLE 2.

Energy parameters (q_i) obtained from optimization against spin-label data on Δ131Δ

Amino acid	Parameter	SD	Amino acid	Parameter	SD
ALA	0.122	0.004	GLY	0.193	0.001
CYS	ND	ND	HIS	−0.61	0.02
ASP	−0.05	0.02	ILE	0.615	0.008
GLU	−0.108	0.004	LYS	0.291	0.004
PHE	0.126	0.01	LEU	0.291	0.006
MET	0.243	0.004	SER	0.440	0.006
ASN	0.184	0.004	THR	0.031	0.008
PRO	0.382	0.008	VAL	0.425	0.003
GLN	0.214	0.002	TRP	0.084	0.006
ARG	0.43	0.01	TYR	0.293	0.005

The parameters are calculated as the average and standard deviations over three independent runs.

Cross-validation of optimized parameters

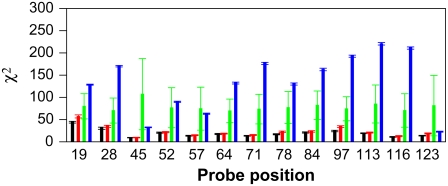
As the parameters in Table 2 were obtained by optimizing against all data from a single protein it is conceivable that the obtained values suffer from overfitting. To test whether this is the case we carried out a full cross-validation study. We generated 13 different data sets by leaving out the data from each of the 13 spin-label probes one at a time. For each of these 13 data sets we carried out a full parameter optimization. We then, for each data set in turn, calculated the intensity ratios for the spin-label probes that were not included in the optimization. For example, in the first cross-validation data set we included all but the first spin-label probe in the optimization, and finally we calculated the intensity ratios for the first probe. The accuracy of the calculated values was then quantified by calculating the χ² value to the experimental data. The resulting 13 χ² values are shown as the red bars in Fig. 5. For comparison, the black bars show the χ² values for each probe when all probes were used in the optimization. Not surprisingly, the cross-validated χ² values are all slightly higher than those obtained from the full data sets. However, the increase in χ² is in general very small, and often within error the same as that obtained from 20 individual runs as indicated by the error bars in Fig. 5. Thus, these results show that the parameters obtained do have predictive value and are not seriously affected by overfitting.

FIGURE 5.

Validation of the parameters optimized from experimental reference data. Each bar corresponds to the χ² value calculated between the experimental intensity ratios for a particular spin-label probe, and the values calculated using different energy parameters. (Black) Values obtained when parameters were optimized against all spin-label data. The bar shows the mean and standard deviation over 10 independent runs. (Red) Values obtained in a cross-validation where the spin-label data for the probe for which the χ² is calculated were left out of the optimization algorithm. The bar shows the mean and standard deviation over 10 independent runs. (Green) χ² values obtained using permuted parameters. The bar shows the mean and standard deviation of the values obtained from 40 runs, each using a different set of permuted energy parameters. (Blue) Values obtained when the energy function only consists of the local backbone potential, i.e., in the absence of any long-range attractive interactions.

In principle, the observed effects might be the result of a heteropolymer collapse rather than the result of any sequence-specific effects. To test whether the optimized parameters do in fact contain any amino-acid-specific information we carried out 40 additional Monte Carlo simulations. In each of these we permuted the 19 energy parameters in Table 2 (no cysteine in Δ131Δ) to generate 40 different energy functions. By permuting the energy parameters we ensure that the average interaction energy between two residues is conserved while we scramble any sequence-specific effects in the parameters. The green bars in Fig. 5 show the average and standard deviation of the χ² values for each probe obtained in this way. It is clear that permutation of the energy parameters gives rise to χ² values that are significantly larger than those obtained either in the full optimization or from the cross-validation calculations. Finally, we carried out 40 independent simulations in which there was no interaction potential at all (q_i = 0). The resulting χ² values (blue bars in Fig. 5) are in general much higher than those obtained from the optimized and permuted parameters. Together, these results clearly show that the parameters obtained both contain a contribution from a sequence-independent collapse and from sequence-specific interactions that are not captured by the permuted parameters. We are therefore confident that the parameters we have found using all 13 probes are not the result of over-fitting, and that the optimized parameters reflect inherent properties of the spin-label data which, in turn, depend on the nature of the conformational preferences of Δ131Δ.

Transferability of the optimized parameters

The parameters that we have optimized using the spin-label data for Δ131Δ correspond to effective interaction parameters under the conditions (pH 5.3, 305 K) at which the experiments were performed (15). It is known that varying solvent conditions can affect the presence of residual structure and thereby the measured spin-label intensity ratios as demonstrated, for example, for acid and denaturant unfolded ACBP (18,24). With this caveat in mind, we carried out simulations of ACBP using the parameters that we optimized from Δ131Δ in order to evaluate any potential transferability of the optimized parameters. Table 3 shows the χ² values that we calculate when we compare the predictions to each of the six different sets of experimental data for ACBP. For comparison, we carried out a set of calculations in which all interaction parameters were set to zero, corresponding to an excluded volume random coil chain. Finally, we carried out a set of calculations where we permuted the energy parameters that we optimized from the Δ131Δ data. The results are summarized in Table 3 and reveal that the optimized parameters in general have a better prediction capability than the other parameter sets. Only at the most strongly denaturing conditions (pH 2.3 and 3.0 M GuaHCl), which are also most dissimilar to the conditions at which the Δ131Δ data were obtained, is a simple random coil model a better predictor. Also, it is noteworthy that permutations of the parameters that were optimized for Δ131Δ lead to worse predictions, in line with the conclusions above that it is not just the overall scale of the parameters that have been optimized.

TABLE 3.

Prediction of ACBP spin label data using either the optimized parameters or different sets of control parameters

ACBP Dataset	Optimized	Random coil	Permuted
1.6 M GuaHCl	13.6 ± 0.2	47.8 ± 0.5	29 ± 14
1.9 M GuaHCl	13.3 ± 0.2	38.9 ± 0.5	37 ± 23
3.0 M GuaHCl	14.8 ± 0.3	12.1 ± 0.3	47 ± 36
pH 2.3	35.3 ± 0.6	25.7 ± 0.4	73 ± 48
pH 2.8	16.8 ± 0.4	45.4 ± 0.6	50 ± 29
pH 3.0	22.8 ± 0.4	53.2 ± 0.3	50 ± 23

Values shown are the χ² values to previously determined experimental data (18,24) under the conditions indicated. Values are the means and standard deviations over 10 runs. In the case of the permuted parameters, each run was carried out using a different permutation.

DISCUSSION

We have here described the development of a computational algorithm for the parameterization of energy functions. The algorithm is distinguished from earlier work by not requiring a reference conformation or ensemble, but instead takes, as experimental input, observables such as PRE data. One advantage of this approach is that it is applicable to systems such as disordered proteins where the similarity to a reference conformation is not easily defined. An additional strength of this approach is that it is not biased by any prior structural interpretation of the experimental data. For example, a set of experimental PRE values on unfolded proteins can be compatible with both compact and expanded ensembles of conformations (11,18,19), and it may not always be clear which description is the most appropriate. Similarly, it has been observed that widely different structures may be compatible with the same set of NOE or x-ray scattering data (48,49). By avoiding reliance upon a prior structural interpretation of a set of experimental data, the algorithm may be able to recover more realistic sets of parameters.

Using synthetic, but realistic, PRE data we have shown that it is in principle possible to parameterize energy functions using results obtained from NMR experiments on unfolded proteins. Further, application of the method to experimental data on Δ131Δ shows that the approach can yield reproducible and internally consistent results from experimental data. However, the parameters obtained from the analysis of Δ131Δ do not seem to conform to an easily identifiable general pattern. We believe that the parameters obtained include properties that are specific to Δ131Δ in addition to more general properties of unfolded proteins. Nevertheless, in a test of the transferability of the optimized parameters to ACBP, we find that the parameters give better predictions than both a simple random coil model and a model in which the optimized parameters were permuted. To improve the optimized parameters we suggest to apply the algorithm to multiple proteins and experimental data sets simultaneously, thus minimizing effects that are specific to a single protein. For example, the algorithm can be directly applied to multiple proteins by extending the sum in the calculation of χ² (Eq. 5) to multiple data sets. However, as the parameters that are optimized are effective interaction parameters under the experimental conditions, this approach requires that multiple data sets have been measured under similar conditions, which to our knowledge is not the case for PRE data. As an alternative method to obtain transferable energy parameters, experiments from different experimental conditions can be combined by specifically including a dependency on the conditions in the energy function.

Finally, we note that our method is applicable to a range of experimental data, and that it can be applied to multiple types of experiments simultaneously. For example, it should be possible to combine PRE data from unfolded proteins with other types of data such as scalar couplings, residual dipolar couplings, and x-ray scattering data (13,21,34,50) to parameterize a more detailed energy function that include a sequence-dependent local energy function.

Also, while the method that we describe has been developed with heterogenous states in mind, it is also applicable to the native states of globular proteins. For example, it is clear that native states of proteins may be highly dynamic (51–53) and that the level of such dynamics can be determined experimentally (54). The methods described here may therefore be used to refine energy functions for exploring native states, including force fields used in molecular dynamics simulations, by optimizing these against NMR observables that probe the structure as well as the dynamics in native proteins.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.