A Correlative Analysis of Actin Filament Assembly, Structure, and Dynamics

Abstract

The effect of the type of metal ion (i.e., Ca²⁺, Mg²⁺, or none) bound to the high-affinity divalent cation binding site (HAS) of actin on filament assembly, structure, and dynamics was investigated in the absence and presence of the mushroom toxin phalloidin. In agreement with earlier reports, we found the polymerization reaction of G-actin into F-actin filaments to be tightly controlled by the type of divalent cation residing in its HAS. Moreover, novel polymerization data are presented indicating that LD, a dimer unproductive by itself, does incorporate into growing F-actin filaments. This observation suggests that during actin filament formation, in addition to the obligatory nucleation– condensation pathway involving UD, a productive filament dimer, a facultative, LD-based pathway is implicated whose abundance strongly depends on the exact polymerization conditions chosen. The “ragged” and “branched” filaments observed during the early stages of assembly represent a hallmark of LD incorporation and might be key to producing an actin meshwork capable of rapidly assembling and disassembling in highly motile cells. Hence, LD incorporation into growing actin filaments might provide an additional level of regulation of actin cytoskeleton dynamics. Regarding the structure and mechanical properties of the F-actin filament at steady state, no significant correlation with the divalent cation residing in its HAS was found. However, compared to native filaments, phalloidin-stabilized filaments were stiffer and yielded subtle but significant structural changes. Together, our data indicate that whereas the G-actin conformation is tightly controlled by the divalent cation in its HAS, the F-actin conformation appears more robust than this variation. Hence, we conclude that the structure and dynamics of the Mg–F-actin moiety within the thin filament are not significantly modulated by the cyclic Ca²⁺ release as it occurs in muscle contraction to regulate the actomyosin interaction via troponin.

Since it has been generally believed that actin filaments provide the physical basis for the structure and dynamic properties of the cell cytoskeleton and the muscle sarcomere, a wealth of biochemical, cell biological, and structural studies using different approaches concerning this issue have been performed during the past 25 years. It has become apparent that several effector molecules, such as metal ions; the state of hydrolysis of the bound nucleotide; and small drugs and actin-binding proteins strongly influence the functional properties of monomeric (G) as well as filamentous (F) actin in vitro. For instance, depending on whether Ca²⁺ or Mg²⁺ is bound to the high-affinity divalent cation binding site (HAS)¹ of the G-actin molecule, its biochemistry is significantly altered. Accordingly, at least three effects have emerged from various observations: (a) Replacement of the divalent cation under low-salt conditions (micromolar range) causes a conformational change of the G-actin monomer (Cooper et al., 1983a ; Carlier et al., 1986b ; Estes et al., 1987; Mejean et al., 1988; Strzelecka-Golaszewska et al., 1993); (b) Mg– G-actin nucleates F-actin polymerization much more efficiently than Ca–G-actin (Selden et al., 1983; Tobacman and Korn, 1983; Cooper et al., 1983a ; Gershman et al., 1984; Newman et al., 1985; Mozo-Villarias and Ware, 1985; Carlier et al., 1986b ); and (c) the rate of filament elongation is similar for both Ca– and Mg–G-actin and independent of the different high-salt (millimolar range) polymerization conditions used (Selden et al., 1983, 1986; Gershman et al., 1984; Zimmerle and Frieden, 1988; Carlier et al., 1986b ).

Interestingly, Orlova and Egelman (1993) found that F-actin filaments may exist in two distinct states of flexural rigidity, which they termed “flexible” and “rigid.” Evidently, the transition from flexible to rigid could be induced by variation of the bound divalent cation and/or the nucleotide (see also Egelman and Orlova, 1995). In addition, corresponding three-dimensional (3-D) reconstructions from electron micrographs revealed large structural changes, from which these authors concluded that the modulation of actin's flexibility and structure by Ca²⁺ and Mg²⁺ may play an important physiological role within the cell (e.g., in motility-based processes). At variance with Egelman and co-workers, Isambert et al. (1995) and Scharf and Newman (1995) found the flexural rigidity of Ca– and Mg–F-actin filaments to be very similar. Most recently, Yasuda et al. (1996) reported that the torsional rigidity of Ca–F-actin was about three times as large as that of Mg–F-actin, whereas the flexural rigidity was practically independent of the kind of divalent cation bound to the HAS. Additional investigations have suggested that F-actin may also exhibit long-range cooperativity propagating via the intersubunit bonds through the entire filament so as to have physiological implications (Orlova et al., 1995; Egelman and Orlova, 1995; Prochniewicz et al., 1996; Orlova and Egelman, 1997).

Taken together, these findings imply that actin filaments may play more dynamic or active roles in muscle and nonmuscle cells than hitherto assumed. In accordance, a still growing number of reports have been attempting to identify and characterize the parameters and factors that may modulate actin filament dynamics. Since in vitro there are many ways to polymerize G-actin monomers into F-actin filaments, finding a consensus concerning the ion and nucleotide composition used for actin polymerization is far from obvious, and hence renders direct comparison of the different findings reported in the literature rather difficult. This situation is further complicated by the observation that mono- and divalent cations compete for binding to multiple lower-affinity sites that, however, are poorly characterized in terms of their cation selectivity and binding affinities.

In an attempt to overcome some of these ambiguities, we have decided to investigate more systematically the effect of the divalent cation bound to the single HAS of the G-actin molecule (for review see Estes et al., 1992). To establish a direct correlation between biochemical, structural, and mechanical data, we investigated the polymerization behavior of G-actin as well as the 3-D structure and mechanical properties of the resulting F-actin filaments. For this purpose, three distinct G-actin moieties (i.e., in terms of the divalent cation bound to the HAS) were prepared. Polymerization was assayed by the fluorescence enhancement of pyrenated actin (c.f., Kouyama and Mihashi, 1981). To probe for the formation of distinct oligomers during the early stages of actin polymerization, an intermolecular cross-linking assay was used (c.f., Millonig et al., 1988). Moreover, F-actin filament formation and maturation were followed by time-resolved electron microscopy. After reaching steady state, the dynamic properties of the resulting filaments were evaluated from electron micrographs of negatively stained specimens by measuring their crossover spacing and maximal crossover width frequency distributions (Bremer et al., 1991) and their apparent persistence length (Orlova and Egelman, 1993). To assess the subunit conformation and intersubunit contact pattern of the respective F-actin filaments, refined and averaged 3-D helical reconstructions were computed (Bremer et al., 1994). In combination with the different divalent cations bound to the HAS of the actin molecule, the effect of phalloidin, a bicyclic heptapeptide toxin of the toadstool Amanita phalloides (c.f., Wieland and Faulstich, 1978), was investigated on the course of actin filament polymerization, 3-D structure, and dynamics.

This correlative analysis has led to a deeper insight into actin filament assembly, structure, and mechanics. Besides the obligatory nucleation–condensation-based filament formation, it has identified a second, facultative actin assembly pathway involving formation of a dimer that is unproductive by itself but does, however, incorporate into growing filaments and hence could be of relevance to regulate actin filament assembly, dynamics, and turnover in vivo.

Materials and Methods

Materials

Unless specified otherwise, all chemicals were of analytical or best available grade. ATP (A-2383, sodium salt, grade I), phalloidin from Amanita phalloides (P-2141), and dimethylformamide (DMF) were purchased from Sigma Chemical Co. (St. Louis, MO). N,N′-1,4-phenylenebismaleimide (1,4-PBM) was obtained from Aldrich Chemical Co. (Milwaukee, WI), and N-(1-pyrenyl)-iodoacetamide (pyrene) was a product of Molecular Probes (Eugene, OR). Uranyl formate was obtained from BDH Chemicals Ltd. (Poole, England). Electron image film SO-163 and developer D-19 were products of Eastman Kodak Co. (Rochester, NY). For all experiments, NANOpure deionized water was used (Skan AG, Basel-Allschwil, Switzerland).

Preparation of G-actin and Polymerization into F-actin

Actin was prepared by previously described protocols (Millonig et al., 1988; Bremer et al., 1994). Briefly, rabbit skeletal muscle actin was isolated from an acetone powder (Spudich and Watt, 1971) and further purified by gel filtration on a 2.5 × 100–cm Sephadex G-200 column (Pharmacia Biotech, Inc., Piscataway, NJ). The resulting fractions (typically 1–2 mg/ml) were stored in buffer A (2.5 mM imidazole, 0.2 mM CaCl₂, 0.2 mM ATP, 0.005% NaN₃, pH 7.4) at 4°C and used within 1–2 wk. This preparation method yields ATP–G-actin with Ca²⁺ bound to the HAS of the molecule (i.e., Ca-ATP–G-actin). To produce EGTA-ATP–G-actin (i.e., divalent cation–free actin; see Valentin-Ranc and Carlier, 1991), immediately before use Ca-ATP–G-actin was incubated with 1 mM EGTA for 10 min on ice. Mg-ATP–G-actin was obtained as for EGTA-ATP–G-actin, but in the presence of 0.05 mM MgCl₂. G-actin at a protein concentration of 1 mg/ml (i.e., 24 μM) was polymerized to F-actin by adding KCl to 100 mM at room temperature. Phalloidin-treated filaments were polymerized in the presence of a twofold molar excess of the toxin relative to actin. Protein concentration was determined by the BCA assay (a protein assay reagent from Pierce [Rockford, IL]) or spectrophotometrically using an extinction coefficient of 0.617 cm²/mg at 290 nm and a molecular mass of 42 kD for actin.

Pyrene Fluorescence Measurements and Intermolecular Cross-Linking Assay

Fluorescent actin was obtained by covalently coupling Cys374 of the protein with N-(1-pyrenyl)iodoacetamide (pyrene) using the method of Tellam and Frieden (1982) with the following modifications: (a) actin (1 mg/ml) was polymerized by addition of 2 mM MgCl₂ and 50 mM KCl; and (b) the pyrene/actin molar ratio in the reaction mixture was 2:1. After dialysis over 3 d against several changes of buffer A and after a clear spin at 100,000 g for 2 h, the labeling efficiency was determined as described by Kouyama and Mihashi (1981) and amounted typically to 80%. In each polymerization experiment, actin was used at a concentration of 1 mg/ml with about 4% of the total protein being pyrenated. Fluorescence intensity was measured at 407 nm after excitation at 365 nm.

Monitoring actin polymerization by intermolecular cross-linking with 1,4-PBM was carried out as described by Millonig et al. (1988). A 5 mM stock solution of 1,4-PBM dissolved in 100% DMF was freshly prepared and kept on ice during the experiment. Polymerization was initiated at room temperature by the addition of KCl to 100 mM to a specific G-actin moiety at a protein concentration of 1 mg/ml. Aliquots were removed at different time points and incubated with 1,4-PBM (previously diluted with 10 mM Na-Borate, 100 mM KCl, pH 9.2, supplemented with the appropriate amount and type of divalent cation [i.e., 0.2 mM Ca²⁺, or 0.05 mM Mg²⁺, or 1 mM EGTA] so that the concentration of DMF during cross-linking was always <0.5%) at a cross-linker/protein ratio of 0.5:1 at room temperature. The reaction was quenched after 2 min by the addition of 3× SDS-PAGE sample buffer (i.e., containing 5% β-mercaptoethanol). The presence of cross-linked actin oligomers was visualized by SDS-PAGE with Coomassie blue staining. The nominal 0-min time point in each experiment was the time needed to cross-link the first aliquot after the addition of salt (typically 5–10 s).

Specimen Preparation and EM Data Acquisition

Polymerized material (i.e., incubation of 100–200 μl of 1 mg/ml G-actin in the presence of 100 mM KCl for 1 h at room temperature) was centrifuged for 15 min at 100,000 g. The supernatant was discarded, and the pellet was resuspended in the original volume of polymerization buffer (i.e., buffer A + 100 mM KCl), immediately fivefold diluted before a 5-μl aliquot was applied to a weakly glow-discharged, carbon-coated, 400-mesh/inch copper grid. The sample was allowed to adsorb for 30 s, washed, and negatively stained with 0.75% (wt/vol) uranyl formate (pH 4.25), as described before (Bremer and Aebi, 1994). Specimens were examined in a conventional transmission electron microscope (CTEM) (model H-7000; Hitachi Ltd., Tokyo, Japan) operated under low-dose conditions at an accelerating voltage of 100 kV and at a nominal magnification of 30,000× for low-magnification overviews (see Fig. 5). Micrographs were recorded on electron image film (S0-163; Eastman Kodak Co.), which was developed for 6 min at room temperature in developer (D-19; Eastman Kodak Co.) diluted threefold with water. Magnification calibration was performed according to Wrigley (1968) using negatively stained catalase crystals. High-magnification images of the same negatively stained specimens were recorded by scanning transmission electron microscopy (STEM) using a Vacuum Generator (East Grinstead, England) STEM HB5 operated at an accelerating voltage of 80 kV and at a nominal magnification of 500,000×, as described by Bremer et al. (1994). Data recording was performed with an annular dark-field (ADF) detector interfaced to a custom-built, digital data acquisition system (Müller et al., 1992).

Figure 5.

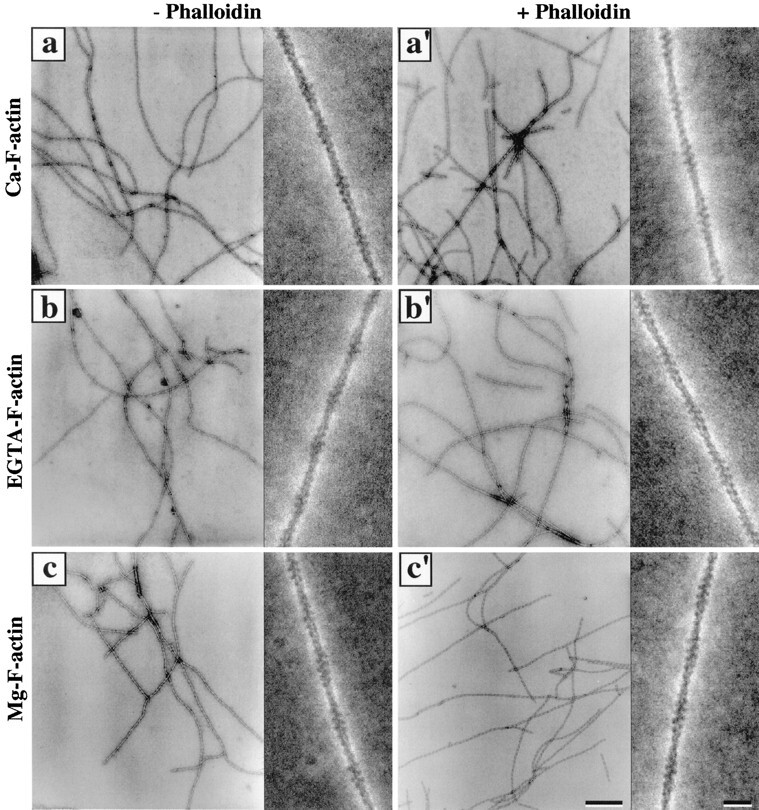
Negatively stained F-actin filaments imaged by CTEM at a nominal magnification of 30,000× (overviews) and by STEM at a nominal magnification of 500,000× (insets) using an ADF detector. Ca–G-actin (a and a′), EGTA–G-actin (b and b′), and Mg–G-actin (c and c′) were allowed to polymerize for 60 min at room temperature with 100 mM KCl in the absence (a–c) and presence (a′–c′) of a 2:1 molar excess of phalloidin over actin. Samples were centrifuged for 15 min at 100,000 g, and the pellets were resuspended in polymerization buffer and applied to a lightly glow-discharged carbon-coated copper EM grid (see Materials and Methods). Bars: (overviews) 250 nm; (insets) 20 nm.

Determination of Crossover Spacings and Maximum Crossover Widths and Evaluation of Filament Flexibility

The analysis of single crossovers (i.e., spacing and width) was facilitated by the increased contrast of the STEM ADF over CTEM bright-field images (see Fig. 5). The general procedure was as follows (for details see Bremer et al., 1991): STEM ADF images of negatively stained F-actin filaments were first digitally unbent using a routine implemented in the SEMPER 6 image processing package (Synoptics, Ltd., Cambridge, UK) (Saxton, 1996) run on a DEC VAX workstation (Digital Equipment Corp., Maynard, MA). The resulting images were Fourier-filtered so that the spatial frequencies above (30 nm)⁻¹ and those below (250 nm)⁻¹ were masked out. Projection of such images normal to the helix axis revealed the crossover points unequivocally as local maxima. Corresponding maximum crossover width measurements were carried out by projecting image sections of unbent filaments of about one and a half crossovers in length parallel to the filament axis. Gaussian filtering of the resulting radial mass density profile yielded two maxima, which reflected the maximum crossover width. Finally, the coordinates of these maxima were determined by a computational peak search and used to compute crossover spacings and widths along individual F-actin filaments. Frequency distributions were represented as histograms (using CricketGraph) with Gaussian curves fitted. For each filament condition, 240 crossover spacing and 120 crossover width data points were collected. Knowing that the crossover spacing corresponds to a 180° turn of each of the two long-pitch helical strands, and assuming an axial raise of 2.75 nm per actin subunit (c.f., Aebi et al., 1986), the screw angle ψ (i.e., the rotational angle between the two adjacent subunits along the left-handed genetic helix; Aebi et al., 1986) can be calculated.

Flexibility measurements of negatively stained actin filaments were quantified by the persistence length λ, which reflects a statistical relationship between the contour length, L, along a rope–like structure and the end-to-end distance, R, of the same segment by the following equation (Landau and Lifshitz, 1958; see also Orlova and Egelman, 1993):

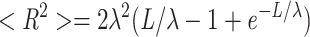
To accurately trace the contour length of smoothly curved filament segments selected for being break- and kink-free, 2.5-fold enlarged prints were produced from low-magnification CTEM images of negatively stained specimens (see Fig. 5). In doing so, we considered the possibility that adsorption of the filaments to a weakly glow-discharged carbon support film might alter their effective persistence length by “forcing” them from a truly 3-D configuration into a 2-D environment (i.e., by the interaction of the filaments with the support film). Hence only “apparent” persistence lengths could be determined; however, given the occurrence of such preparation-induced alterations, these should be approximately the same for each sample, so that direct comparison between different filament preparations was justified (see also Orlova and Egelman, 1993). To calculate the apparent persistence length λ_app, the contour length L and the end-to-end distance R of selected filament segments were measured from low-magnification CTEM micrographs. Least-squares fits to the data were performed using the program SIGMA PLOT, and these yielded values for the apparent persistence length λ_app (Orlova and Egelman, 1993). For each filament condition, 150 data points were collected. We tested the sensitivity of this method by subdividing single data sets into subsets and comparing the resulting persistence lengths (data not shown). By doing so, we found that values differing by a factor of less than 1.7 were not statistically significantly different.

Digital Image Processing and 3-D Helical Reconstruction

All image processing work was carried out on a DEC VAX server or a DEC VAX workstation following the semiautomated protocol developed by Bremer et al. (1994). The systematic analysis of single crossovers (see above) from F-actin filament stretches recorded by STEM ADF at high magnification (see Fig. 5) allowed us to select well-preserved, uniformly stained F-actin filament segments yielding reasonably even crossover spacings and widths. Since most of these filament segments were always slightly curved, digital unbending was performed using a routine implemented in the SEMPER 6 image processing package (see above). Subsequently, the straightened filament images were subjected to 3-D helical reconstruction using the Micrograph Data Processing Program MDPP (Smith and Gottesman, 1996). More specifically, unbent filament segments were D(Z,k)-filtered (Smith and Aebi, 1974) using the integer helical selection rule l = −6n + 13m (screw angle ψ = −166.15°) over exactly two helical repeats (i.e., 26 subunits), whereby the helical repeat length and radial position of the filament axis were optimized in a 3-D helical parameter search. We decided not to refine the helical selection rule since most of them would have required longer filament segments. For instance, the integer helical selection rules l = −19n + 41m, l = −20n + 43m, and l = −25n + 53m required helical repeat lengths comprising 41, 43, and 53 subunits, respectively. We found that processing over short segments (e.g., 26 subunits) preserved structural information of the F-actin filament reconstruction the best (e.g., in terms of the concavity of the cleft separating the inner from the outer domain of the subunit; Bremer et al., 1991, 1994). Processing over longer filament segments (i.e., >40 subunits), often resulted in a loss of structural detail even after refining the helical selection rule. Among the processing artifacts evaluated by Bremer et al. (1994), the use of a suboptimal helical selection rule did not significantly affect the 3-D reconstruction over short segments (e.g., 26 subunits). For example, at the 25 Å resolution level, ±1.5° difference in the screw angle ψ did not reveal a significant change of the pronounced concavity of the cleft separating the inner from the outer domain of the subunit, and it resulted in only a very small loss of structural detail of the contact pattern between the two long-pitch helical strands (see Fig. 8, a and b, of Bremer et al., 1994). Moreover, from our crossover spacing measurements (see above and Results), we did not expect a change in the screw angle ψ by more than ±1° within our selected images. Hence, we decided to keep the helical selection rule and the filament segment length constant (i.e., l = −6n + 13m; two helical repeats). All two-crossover-long filament segments that were helically processed from each STEM ADF data set of our different F-actin preparations with the highest transmitted power upon D(Z,k)-filtration (usually ∼75 ± 5%) were Fourier-transformed, and their equator and the 1st, 2nd, 5th, 6th, 7th, 8th, 13th, and 14th layerlines were extracted. Layerline correlation with a reference was used to align single filaments (Smith et al., 1976) to build an average. Three cycles of an iterative alignment procedure were enough to obtain stable averages. 3-D reconstructions were computed (DeRosier and Moore, 1970; Smith et al., 1976) and surface-rendered using the program MapView (Henn et al., 1996) implemented on a Silicon Graphics (Mountain View, CA) Crimson graphics computer equipped with a Reality Engine graphics subsystem. Contouring levels were chosen so as to include the nominal molecular volume of the 42-kD actin subunit or fractions of it, taking into consideration the calculated cylindrical radius of gyration of the respective reconstructions. As a control and to eliminate the possibility that the resulting averages from individual filament populations were biased, we randomly divided each data set into subsets consisting of five reconstructions each, averaged these separately, and compared the resulting averages with the overall average (data not shown). No significant bias was observed for all data sets tried.

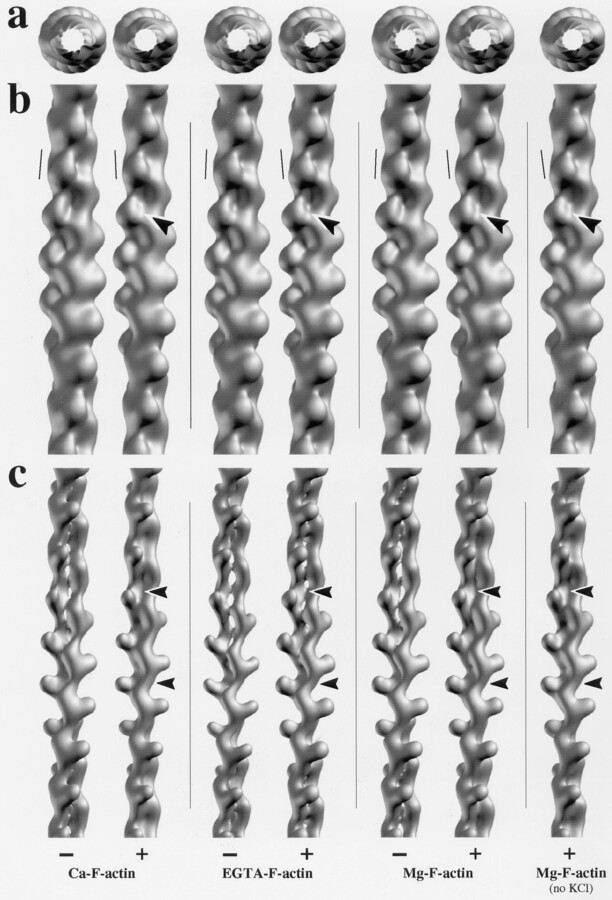
Figure 8.

Refined and averaged 3–D helical reconstructions of Ca–F-actin, EGTA–F-actin, and Mg–F-actin filaments polymerized with 100 mM KCl each in the absence (−) and presence (+) of a 2:1 molar excess of phalloidin over actin. The refined and averaged 3-D reconstruction displayed at the far right is of F-actin filaments polymerized from Mg-ATP–G-actin by adding a 2:1 molar excess of phalloidin over actin in the absence of any KCl. In each case, 10 two–crossover repeat–long F-actin filament segments were 3-D helically reconstructed and refined, aligned, and averaged. The resulting refined and averaged reconstructions are shown aligned relative to each other and surface rendered to include either 100% ([a] end-on and [b] side views) or 30% (c) of the nominal molecular volume, taking into consideration the calculated cylindrical radius of gyration of the respective reconstructions. The near-vertical lines drawn in b close to one actin subunit of each reconstruction represent the inclination of the long axis of the outer domain (i.e., subdomains 1 and 2) of the actin subunit. The arrowheads in b point to the interface where the two long-pitch helical strands come to lie side by side, thereby defining a distinct groove. The arrowheads in c point to the intersubunit contacts between (contoured arrowheads) and along (smaller arrowheads) the two long-pitch helical strands.

Results

We have prepared the following ATP–G-actin moieties (for details see Materials and Methods): Ca-ATP–G-actin (i.e., 0.2 mM CaCl₂; standard in vitro preparation); EGTA-ATP–G-actin (i.e., Ca-ATP–G-actin treated with 1 mM EGTA for 10 min at 4°C immediately before the onset of polymerization, to produce divalent cation–free G-actin; see Valentin-Ranc and Carlier, 1991); and Mg-ATP–G-actin (i.e., prepared from EGTA-ATP–G-actin in the presence of 0.05 mM MgCl₂). The protein concentration was kept at 1 mg/ml for all experiments. In each case, polymerization was initiated by adding KCl to 100 mM to a particular G-actin moiety and continued for at least 1 h to yield ADP–F-actin filaments. These three well-defined metal ion compositions allowed direct comparison since only the divalent cation (i.e., Ca²⁺, Mg²⁺, or no metal ion) bound to the HAS was varied. K⁺ essentially binds to several moderate and lower-affinity cation binding sites of the actin molecule and hence cannot compete for binding to the HAS (for reviews see Carlier, 1991; Estes et al., 1992).

The Course of Polymerization Depends on the Type of Divalent Cation Bound to the HAS of G-actin

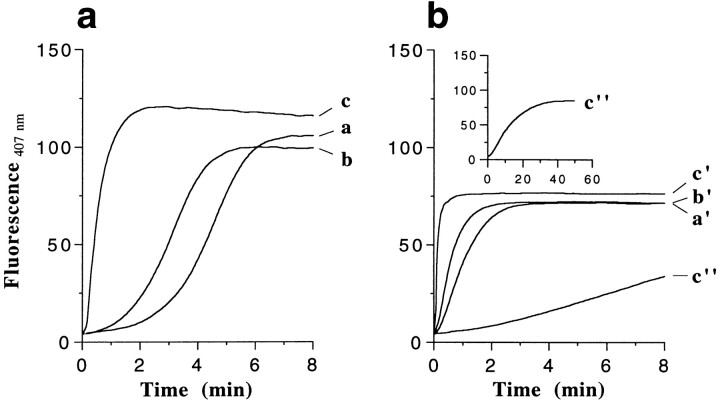
We have employed the widely used method of N-(1-pyrenyl)iodoacetamide (pyrene) fluorescence enhancement to monitor the polymerization reaction of G- to F-actin (Kouyama and Mihashi, 1981; Tellam and Frieden, 1982; Cooper et al., 1983b ). Fig. 1 documents that upon addition of 100 mM KCl, the length of the lag phase observed at the beginning of the polymerization reaction strongly depends on the divalent cation bound to the HAS of the G-actin moiety. The lag phase was relatively short with Mg–G- actin (i.e., <15 s; Fig. 1 a, trace c), whereas it became significantly longer with EGTA- (i.e., ∼2 min; Fig. 1 a, trace b) and even longer with Ca–G-actin (i.e., ∼3.5 min; Fig. 1 a, trace a). The elongation rate, which is defined by the slope of the polymerization reaction time curve, remained rather similar with Ca– and EGTA–G-actin but was approximately three to four times slower than with Mg–G-actin. Hence, divalent cation–free G-actin behaves somewhat in between Mg– and Ca–G-actin, but as judged by the length of the lag phase and the slope of the reaction time curve, it shares more similarities to Ca–G-actin than to Mg–G–actin. As a quantitative measure, the time t _1/2 that is required for half-maximum assembly (as judged by the length to reach half of the fluorescence intensity plateau) was determined for each time course of polymerization. These values are summarized in Table I.

Figure 1.

Actin polymerization monitored by the fluorescence time course of pyrene-labeled actin. Ca–G-actin (traces a and a′), EGTA–G-actin (traces b and b′), and Mg–G-actin (traces c and c′) at a protein concentration of 1 mg/ml each were polymerized with 100 mM KCl in the absence of phalloidin (a), and in the presence of a 2:1 molar excess of phalloidin over actin (b). Trace c′′ of b: Mg–G-actin (1 mg/ml) polymerization induced by phalloidin without the addition of any KCl (see also inset for a display of the same data on a different time scale). For these fluorescence time course experiments, 4% of the total actin was pyrenated; λ_excitation = 365 nm, λ_emission = 407 nm.

Table I.

Comparison of Ca–G-actin, EGTA–G-actin, and Mg–G-actin Polymerized with 100 mM KCl in the Absence (−) and Presence (+) of a 2:1 Molar Excess of Phalloidin over Actin

Conditions		Polymerization of G-actin								Mechanical properties and flexibility of F-actin												3-D reconstructions
		Pyrene fluorescence t 1/2				Cross-linking shift from LD to UD
										Crossover Spacing				Crossover Width				Persistence length λapp
																						Radius of gyration
		−		+		−		+		−		+		−		+		−		+		−		+
		s				s				nm				nm				nm				Å
Ca–G-actin		260		55		750		90		35.2 ± 2.20 (Ψ = 166.19)		37.1 ± 2.18 (Ψ = 166.90)		9.81 ± 0.57		9.11 ± 0.86		2.3		6.3		25.6 ± 0.61		24.2 ± 0.81
EGTA–G-actin		180		30		600		60		35.1 ± 1.96 (Ψ = 166.15)		37.0 ± 2.56 (Ψ = 166.86)		9.73 ± 0.49		8.50 ± 0.72		2.9		5.2		25.1 ± 0.90		24.3 ± 0.58
Mg–G-actin		30		8		45		45		35.4 ± 1.98 (Ψ = 166.27)		37.3 ± 2.31 (Ψ = 166.97)		9.10 ± 0.60		9.03 ± 0.62		2.3		6.1		25.1 ± 0.81		24.9 ± 0.78
Mg–G-actin(no KCl)		–		780		–		1200		–		37.0 ± 2.36 (Ψ = 166.86)		–		8.91 ± 0.55		–		7.2		–		24.1 ± 0.52

As illustrated in Fig. 1 b, when the three different G-actin moieties were polymerized with 100 mM KCl in the presence of a 2:1 molar excess of phalloidin over actin, the time courses were affected in two ways: (a) Ca– and EGTA–G-actin revealed a drastically shortened lag phase (i.e., <30 s; compare traces a′ and b′ of Fig. 1 b with traces a and b of Fig. 1 a), whereas virtually no lag phase was observed with Mg–G-actin (i.e., <5 s; compare trace c′ of Fig. 1 b with trace c of Fig. 1 a). (b) In both cases, the respective elongation rates increased approximately by a factor of two. Comparing native with phalloidin polymerization conditions, Mg–G-actin again revealed the fastest half time t _1/2, followed by EGTA– and Ca–G-actin (see Table I). We noted that for all three actin moieties, polymerization in the presence of phalloidin yielded an ∼30% decrease in fluorescence intensity at steady state compared to polymerization under native conditions (compare Fig. 1 b with Fig. 1 a). Apparently, this attenuation was due to a phalloidin-induced quenching of the fluorescence signal.

Rather unexpectedly, polymerization of Mg–G-actin (1 mg/ml) into filaments could also be induced by stoichiometric amounts of phalloidin in the absence of KCl (trace c′′ of Fig. 1 b). Under these conditions, steady state was reached within 1 h (Fig. 1 b, inset). EM revealed that the resulting negatively stained F-actin filaments appeared indistinguishable from those formed upon addition of salt (see Fig. 8 for a 3-D reconstruction). Under identical conditions, neither Ca- nor EGTA–G-actin (1 mg/ml) produced any significant amount of filaments in the presence of stoichiometric amounts of phalloidin alone (data not shown). Polymerization of Ca-ATP–G-actin in the presence of the toxin was achieved at an increased protein concentration (2 mg/ml) but at a very slow rate (∼4 h; data not shown).

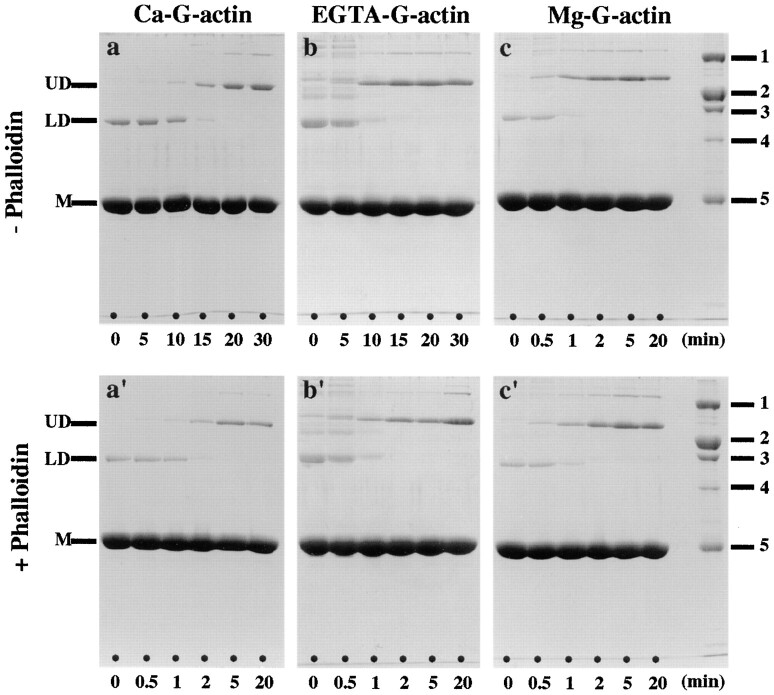
To complement the pyrene fluorescence measurements, we also used intermolecular cross-linking with 1,4-PBM (a bifunctional sulfhydryl cross-linking reagent) to monitor actin polymerization (Millonig et al., 1988). More specifically, this cross-linking assay probes the oligomeric state of actin during the early stages of its polymerization into filaments. As illustrated with Ca–G-actin in Fig. 2 a, immediately after adding 100 mM KCl to initiate polymerization (t = 0 min), a single major “lower dimer” band (LD; see Mockrin and Korn, 1981, 1983; Millonig et al., 1988) with an apparent molecular mass of 86 kD was observed by SDS-PAGE in addition to the monomer band (i.e., 42 kD). During the course of the polymerization reaction, LD gradually disappeared concomitant with the appearance of increasing amounts of a second major “upper dimer” band (UD; Knight and Offer, 1978; Mockrin and Korn, 1981, 1983; Elzinga and Phelan, 1984; Millonig et al., 1988) with an apparent molecular mass of ∼130 kD (Fig. 2 a, t = 5–30 min). Since the time required to shift from LD to UD is related to the course of polymerization, it was used to qualitatively compare different polymerization conditions with each other (Millonig et al., 1988). At steady state (Fig. 2 a, t > 20 min), additional higher molecular mass bands that probably represent F-actin trimers and higher oligomers were observed beside the UD band (Knight and Offer, 1978; Elzinga and Phelan, 1984; Millonig et al., 1988).

Figure 2.

Actin polymerization monitored by 1,4–PBM cross-linking. Ca– G-actin (a and a′), EGTA–G-actin (b and b′), and Mg–G-actin (c and c′) at a protein concentration of 1 mg/ml each were assayed. Polymerization was initiated by addition of 100 mM KCl in the absence (a–c) and presence (a′–c′) of a 2:1 molar excess of phalloidin over actin. Aliquots were removed at the times indicated and cross-linked with 1,4-PBM at a cross-linker/protein molar ratio of 0.5:1 (see Materials and Methods). Cross-linked aliquots were analyzed by SDS-PAGE (10.5% gels). Gel standards: myosin heavy chain, 200 kD (1); β-galactosidase, 116.25 kD (2); phosphorylase B, 92.5 kD (3); BSA, 66.2 kD (4); and ovalbumin, 45 kD (5).

Fig. 2 b illustrates the time course of the cross-linking pattern with EGTA–G-actin upon addition of 100 mM KCl. As can be depicted from the time point t = 0 min, immediately after the onset of the polymerization reaction a wide range of distinct cross-linked species was observed in addition to the monomer and LD bands by SDS-PAGE. On the other hand, these additional bands were absent with Ca–G-actin (Fig. 2 a). In fact, we noticed that at least some of these cross-linked species (including LD) were already present upon incubation of Ca–G-actin with 1 mM EGTA on ice before polymerization (data not shown). Concomitant with the appearance of UD (t = 10 min), most of these cross-linked species slowly disappeared and were completely absent at steady state (t > 15 min). In agreement with the results obtained by the pyrene fluorescence assay (Fig. 1 a), Mg–G-actin made the fastest shift from LD to UD (Fig. 2 c), followed by EGTA–G-actin (Fig. 2 b) and finally by Ca–G-actin (Fig. 2 a; see also Table I).

Fig. 2, a′–c′, documents the effect of a 2:1 molar excess of phalloidin over actin on the course of polymerization. The time required to shift from LD to UD was drastically shortened for both Ca– and EGTA–G-actin (i.e., from 10– 15 min without phalloidin to 1–2 min with phalloidin), whereas virtually no change was noticed with Mg–G-actin (compare Fig. 2 c with Fig. 2 c′; see also Table I). No significant amount of LD was detectable when Mg–G-actin polymerization was induced by stoichiometric amounts of phalloidin alone (i.e., without KCl; see above), indicating that this reaction step was strongly attenuated.

In summary, both pyrene fluorescence and intermolecular cross-linking with 1,4-PBM confirmed independently that the rate of the polymerization reaction is strongly controlled by the particular divalent cation bound to the HAS of G-actin. Most interestingly, phalloidin alone (i.e., without KCl; data not shown) was able to induce slow polymerization of G-actin into F-actin filaments via UD formation without, however, formation of significant amounts of LD.

LD Interacts with Growing F-actin Filaments during the Early Stages of Polymerization

Millonig et al. (1988) suggested a correlation between the time required to shift from LD to UD and t _1/2 of the corresponding pyrene fluorescence measurement. As documented in Table I, we found that this correlation was rather good for Mg–G-actin. However, Ca– and EGTA– G-actin revealed a LD to UD shift that was up to three times slower than the corresponding t _1/2. In addition, significant amounts of LD were still present after the pyrene fluorescence signal reached steady state (compare Fig. 1 a with Fig. 2, a–c). This observation suggested an active participation of LD during the course of F-actin polymerization.

To gain more insight into the mechanism of actin polymerization, we monitored F-actin filament formation and maturation by EM. Fig. 3 displays CTEM micrographs of negatively stained F-actin filaments 0 (Fig. 3 a), 5 (Fig. 3 b), 10 (Fig. 3 c), and >30 min (Fig. 3 d) after the onset of polymerization by adding 100 mM KCl to Ca–G-actin. Comparison of the corresponding time points of Fig. 2 a (i.e., t = 5 and 10 min) with the apparently ragged and branched filaments displayed in Fig. 3, b and c, indicates that LD might incorporate into growing filaments during the elongation phase. Gradually, the surplus bound material dissociates from the “partially decorated” filaments to yield smooth, bona fide mature F-actin filaments at steady state (Fig. 3 d).

Figure 3.

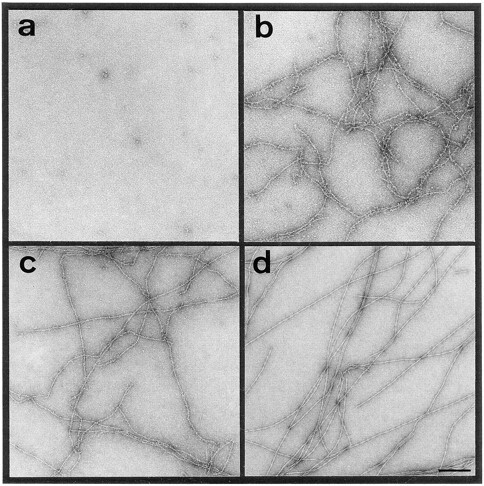
Negatively stained F-actin filaments imaged by CTEM after 0 (a), 5 (b), 10 (c), and >30 min (d) after onset of the polymerization reaction by addition of KCl to 100 mM to Ca–ATP–G-actin (1 mg/ml). At each time point, 5 μl aliquots were directly applied for 15 s to an EM grid, washed, and negatively stained with uranyl formate (for details see Materials and Methods). Bar, 200 nm.

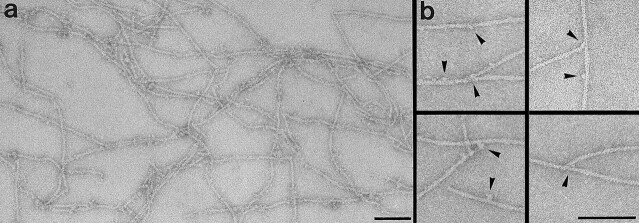
To further confirm our findings, we polymerized F-actin filaments in the presence of 1,4-PBM cross-linked LD and phalloidin to render the filaments static (i.e., to suppress monomer release from bound LDs, subunit exchange, and filament turnover, and to preserve LD-dependent filament branching). In this case, the filaments remained ragged and branched even at steady state (i.e., after 1 h incubation) and after performing a centrifugation step at 100,000 g (Fig. 4, a and b), as one would expect if covalently cross-linked LDs would stably incorporate into growing F-actin filaments. SDS-PAGE analysis of the corresponding F-actin filament pellet confirmed the presence of a significant amount of cross-linked LD at steady state (data not shown). Visual inspection of 20 electron micrographs of F-actin filaments polymerized in the presence of cross-linked LD yielded an ∼25–fold higher probability for branching (Fig. 4 b) than 20 respective electron micrographs of control filaments did (i.e., polymerized in the absence of cross-linked LD; c.f., Fig. 3 d). Moreover, control F-actin filaments (Fig. 3 d) completely lacked the striking ragged appearance revealed by F-actin filaments polymerized in the presence of cross-linked LD (Fig. 4 a).

Figure 4.

Negatively stained ragged and branched F-actin filaments polymerized in the presence of covalently cross-linked LD and imaged by CTEM. (a) Overview and (b) gallery of selected examples of branched filament segments. Ca-ATP–G-actin (1 mg/ml) was cross-linked with 1,4-PBM (see Materials and Methods) 3 min after onset of the polymerization reaction with 100 mM KCl. After 2 min, the polymerization reaction was allowed to ensue for another hour in the presence of stoichiometric amounts of phalloidin and after readjustment of the pH to 7.4. Filaments were collected by centrifugation for 15 min at 100,000 g, resuspended in buffer A supplemented with 100 mM KCl, and applied to an EM grid (for details see Materials and Methods). Bars, 100 nm.

The Gross Morphologies of Negatively Stained Native and Phalloidin-stabilized F-actin Filaments Are Indistinguishable

Our protocol to polymerize F-actin filaments from a given G-actin moiety and prepare them for CTEM or STEM by negative staining yielded well-preserved and evenly distributed filaments with a very low background of unpolymerized actin (Fig. 5).

We noticed that low-magnification CTEM micrographs recorded from Ca– and EGTA–F-actin filaments (Fig. 5, a and b) displayed fewer filament ends (i.e., on average longer filaments) than corresponding micrographs recorded from either Mg–F-actin (Fig. 5 c) or the different types of phalloidin-stabilized filaments (Fig. 5, a′–c′). This finding was not unexpected since polymerization conditions yielding a high nucleation rate (i.e., Mg–G-actin or polymerization in the presence of phalloidin; see Fig. 1) should produce a large number of relatively short filaments compared to a small number of relatively long filaments under conditions giving rise to a low nucleation rate (i.e., Ca– or EGTA–G-actin; see Fig. 1). Besides this, neither the divalent cation bound to the HAS (Fig. 5, a–c) nor the presence of phalloidin (Fig. 5, a′–c′) revealed any obvious differences in the gross morphology of the corresponding F-actin filaments when imaged by either CTEM at 30,000× or STEM ADF at 500,000×. As will be detailed in the following sections, more quantitative assessment was necessary to depict any significant mechanical or structural differences among the different filament species.

The Mechanical Properties of F-actin Filaments Do Not Depend on the Divalent Cation Bound to their HAS

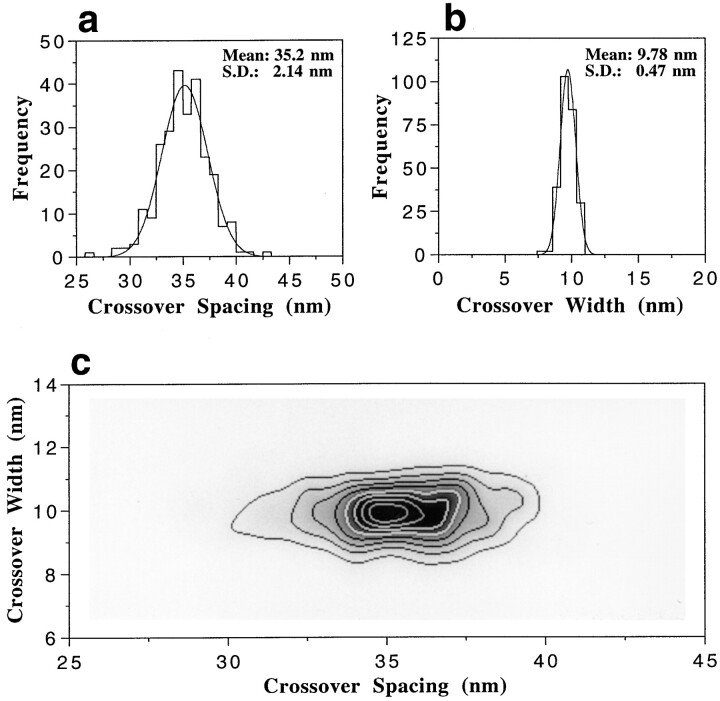
The crossover spacing, i.e., the axial spacing between two subsequent crossovers of the two long-pitch helical strands as revealed from projection images of negatively stained F-actin filaments, has been determined (Bremer et al., 1991) from high magnification STEM ADF micrographs (see Fig. 5). For each one-crossover-long filament segment evaluated, its maximum width was determined from its radial mass density profile (Steven et al., 1988). Fig. 6, a and b, yields the crossover spacing and the corresponding maximum crossover width frequency distributions for Ca–F-actin polymerized with 100 mM KCl. In Fig. 6 c, we also plotted the crossover spacings against the corresponding maximum crossover widths for the data set displayed in Fig. 6, a and b. As documented in Table I, all native filament types (i.e., those polymerized in the absence of phalloidin) yielded virtually the same crossover spacing (35.2 ± 2.1 nm for the overall mean) and maximum crossover width (9.5 ± 0.5 nm for the overall mean) distributions. The calculated screw angle ψ is −166.19 ± 0.83° (for details see Materials and Methods). These mean values (i.e., the crossover spacing and screw angle) correspond to a mean integer helical selection rule l = −6n + 13m and are in good agreement with previously published data (Aebi et al., 1986; Bremer et al., 1991, 1994; Orlova and Egelman, 1992).

Figure 6.

Statistical analysis of crossover spacing (a) and maximum crossover width (b) of negatively stained Ca–F-actin filaments imaged by STEM ADF (see Fig. 5 a). The axial spacing and maximum width of 240 filament crossovers were evaluated and the corresponding values were histogrammed in a and b. Gaussian fits have been superimposed onto the histograms, and the corresponding means and standard deviations are displayed. In c, the 240 crossover spacings/crossover widths are plotted against each other and displayed as a gray level representation with eight discrete contouring levels (i.e., corresponding to two to nine occurrences, respectively).

In contrast to the values obtained with the native filament types, we found that in the presence of a 2:1 molar excess of phalloidin over actin, the crossover spacing increased significantly to an overall mean value of 37.1 ± 2.4 nm (see Table I), thus yielding a screw angle ψ = −166.90 ± 0.85°. Hence, stabilization of F-actin filaments with phalloidin produces a change of the mean rotation angle ψ per subunit by −0.7°. Concomitant with the increase of the crossover spacing was a decrease in the maximum crossover width to an overall mean value of 8.9 ± 0.6 nm (see Table I). As depicted in Fig. 6 c for Ca–F-actin with 100 mM KCl, none of the conditions analyzed (including those in the presence of phalloidin) revealed any significant correlation between the crossover spacing and its corresponding maximum crossover width, indicating the absence of any long-range coupling of the subunit–subunit interactions within the filament.

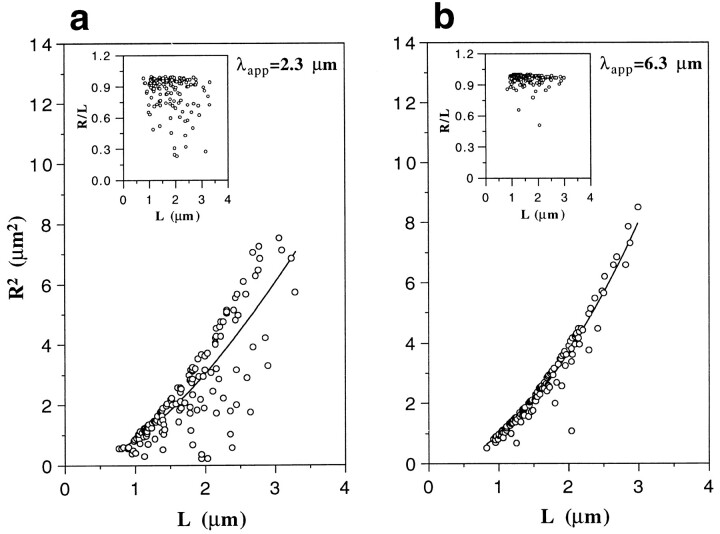
To evaluate the flexibility of the different F-actin filament types more quantitatively, we determined their persistence length λ (Landau and Lifshitz, 1958; Orlova and Egelman, 1993). The persistence length is a mechanical parameter that describes the statistical relationship between the contour length L along a filament stretch and the end-to-end distance R of the same filament stretch (for details see Materials and Methods). Both the persistence length λ and the mean ratio R/L are good measures for the flexibility of a ropelike structure such as an actin filament (Landau and Lifshitz, 1958): the stiffer a filament is, the larger its persistence length λ is, and the closer the R/L value gets to 1. As an example, Fig. 7 illustrates L versus R ² and the corresponding L versus R/L plots (insets) determined from images of negatively stained Ca–F-actin filaments recorded by CTEM (see Fig. 5, a and a′) in the absence (a) and presence (b) of stoichiometric amounts of phalloidin. A least-squares fit to the data of the L versus R ² plots, such as displayed in Fig. 7, yielded the apparent persistence length λ_app (Orlova and Egelman, 1993) for the different F-actin filament preparations with the corresponding values listed in Table I.

Figure 7.

Evaluation of the apparent persistence length of negatively stained Ca–F-actin filaments imaged by CTEM (see Fig. 5, a and a′) in the absence (a) and presence (b) of a 2:1 molar excess of phalloidin over actin. The measured data (150 data points per plot) are represented as L versus R ² plots or as L versus R/L plots (insets). A least squares fit to the L versus R ² plots (solid curves) using the equation of Landau and Lifshitz (1958; see also Materials and Methods) yielded the apparent persistence length λ_app for a given data set.

By evaluating the sensitivity of this method, we found that persistence lengths that differed by a factor of less than 1.7 were statistically indistinguishable (see Materials and Methods). Hence, as shown in Table I, no significant differences were depicted among the different types of native filaments (i.e., their apparent persistence length varied between 2.3 and 2.9 μm). In contrast, compared to native F-actin, filaments polymerized in the presence of stoichiometric amounts of phalloidin revealed a significant increase in their apparent stiffness (i.e., it varied between 5.2 and 7.2 μm). Compared to published persistence lengths determined from negatively stained F-actin filaments recorded by CTEM (Orlova and Egelman, 1993), these values appeared to be typical and reasonable.

3-D Helical Reconstructions Reveal Subtle but Reproducible Structural Differences between Native and Phalloidin-stabilized F-actin Filaments

To take advantage of the increased contrast and the linear contrast transfer characteristics of STEM ADF over CTEM bright-field images (for review see Engel and Colliex, 1993), we recorded digital STEM ADF images of the different types of negatively stained F–actin filaments (see Fig. 5, high-magnification views) and subjected them to 3-D helical reconstruction. In agreement with Bremer et al. (1994), whereas the overall size and shape of individual F-actin filament reconstructions looked invariant within a given type of native or phalloidin-stabilized F-actin filaments, their intersubunit contact patterns along and between the two long-pitch helical strands revealed subtle differences among reconstructions. Contouring the reconstructions at 30% of their total volume yielded at least three distinct types of reconstructions with characteristic intersubunit contact patterns (for details see Bremer et al., 1994): Type A, those with a strong intersubunit contact along the two long-pitch helical strands and little if any contact between them; type B, those with a discontinuous intersubunit contact between the two long-pitch helical strands; and type C, those with a strong intersubunit contact between the two long-pitch helical strands. Individual reconstructions computed from native (i.e., with Ca²⁺, Mg²⁺, or no divalent cation residing in the HAS) filament populations revealed predominantly the A and B type intersubunit contact patterns (data not shown). Their calculated cylindrical radii of gyration were very similar and varied on average from 25.1 to 25.6 Å (see Table I), values that are in good agreement with previously published values (Hartt and Mendelson, 1980; Egelman and Padron, 1984; Smith et al., 1984; Bremer et al., 1991). In contrast, individual reconstructions computed from phalloidin-stabilized filaments exhibited predominantly the B and C type intersubunit contact patterns (data not shown). Compared with those of native filaments, their radii of gyration were clearly smaller and ranged on average from 24.1 to 24.9 Å (see Table I). These findings show that compared to native filaments, phalloidin-stabilized F-actin filaments yield a tighter packing of their subunits.

Fig. 8 displays refined and averaged 3-D helical reconstructions, each averaged over 10 individual, two-crossover repeat–long F-actin filament segments. They were all surface-rendered to include either 100% (Fig. 8 a for end-on views, and Fig. 8 b for side views) or 30% (Fig. 8 c) of the nominal molecular volume (for details see Materials and Methods). Comparison among refined and averaged native type filament reconstructions exhibited no significant differences in their overall morphology and dimensions, in the fine structural features of their subunits, or in their intersubunit contact patterns (Fig. 8). In contrast, compared to their native counterparts, the phalloidin-stabilized filament reconstructions consistently revealed two subtle structural differences when contoured at 100% of their nominal molecular volume: (a) The groove appearing at larger filament radii and residing between the two long-pitch helical strands appears “padded” with additional mass and hence is less pronounced than in native filaments (Fig. 8 b, arrowheads); and (b) the outer domain (i.e., subdomains 1 and 2) of the actin subunit is tilted outward by ∼5–10° (see near-vertical lines drawn close to one actin subunit in Fig. 8 b). Moreover, contouring the phalloidin-stabilized reconstructions at 30% of their nominal molecular volume revealed more massive intersubunit contacts both along and between the two long-pitch helical strands (Fig. 8 c, arrowheads). Also, we found that Mg-ATP–G-actin that was polymerized with phalloidin only revealed the same structural features as phalloidin-KCl polymerized filaments (see Fig. 8).

Taken together, these results document that the type of divalent cation bound to the HAS does not modulate the mechanical and structural properties of the corresponding F-actin filaments to a recognizable extent at the 25 Å resolution level. Phalloidin-stabilized filaments, on the other hand, appear stiffer and exhibit a subtly yet reproducibly altered conformation.

Discussion

F-actin Polymerization Involves a Facultative, LD-based Pathway

In agreement with earlier findings, we confirmed that Mg– G-actin exhibits a faster nucleation and elongation rate than Ca–G-actin when polymerized with KCl (Maruyama, 1981; Tobacman and Korn, 1983; Selden et al., 1983, 1986; Carlier et al., 1986a ,b; Pollard, 1986; Gershman et al., 1989; Valentin-Ranc and Carlier, 1991). Moreover, removal of the divalent cation preserves the ability of actin to polymerize into normal-looking filaments. We also demonstrated that the time required to shift from the LD to the UD was the fastest with Mg²⁺ bound to the HAS.

Polymerization of G-actin monomers into F-actin filaments is commonly believed to involve three distinct steps: (a) fast monomer activation; (b) rate-limiting nucleation; and (c) moderately fast elongation (for review see Pollard, 1990; Carlier, 1991; Estes et al., 1992). This obligatory, UD-based (c.f., Millonig et al., 1988) activation–nucleation– condensation process implies a pseudo-first order assembly kinetics leading to a steady state (Engelborghs et al., 1976; Johnson and Borisy, 1977). Millonig et al. (1988) showed that under a wide variety of polymerization conditions, the first detectable step was dimerization of a significant fraction of the actin monomer pool into LD. Based on earlier observations, they proposed an antiparallel, twofold symmetrical configuration for the LD resembling the unit cell geometry of Gd-induced crystalline actin sheets (Aebi et al., 1981), a molecular architecture apparently incompatible with the helical symmetry specifying the polar F-actin filament. However, comparison of our results obtained from three independent polymerization assays (i.e., pyrene fluorescence, intermolecular cross-linking with 1,4-PBM, and time-resolved EM) implies a direct participation of the LD in the process of F-actin filament growth.

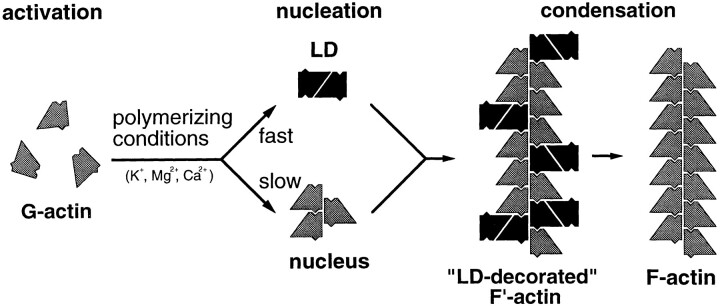
LD consumption during F-actin filament polymerization may occur by two routes: (a) Similar to the ring formation occurring during the oscillating cycle of microtubule assembly/disassembly (Mandelkow et al., 1988, 1991), LD formation is in equilibrium with the actin monomer pool and hence does not directly participate in F-actin filament formation. (b) LD represents a true filament precursor and thus directly participates in F-actin filament growth. In accord with the second route, time-resolved EM of F-actin filament formation has revealed LD directly incorporating into growing filaments by one of its subunits, thereby producing ragged filaments that frequently branch (Fig. 3, b and c). After maturation, the filaments appear smoother and less branched, suggesting that the second, unincorporated subunit of the LD gradually dissociates (e.g., upon switching of the LD from a G- to an F-like conformation) to eventually yield bona fide F-actin filaments at steady state (Fig. 3 d). In contrast, filaments polymerized in the presence of previously cross-linked LD remain ragged and branched at steady state (Fig. 4, a and b), indicating that the apparent partial decoration of the actin filaments observed during the early stages of the polymerization reaction is indeed due to direct LD incorporation. The observed filament branching (Fig. 4 b) is suggestive of potential nucleation of new filaments by LDs incorporated into growing filaments (i.e., by the unincorporated LD subunits).

As illustrated schematically in Fig. 9, taken together our polymerization data suggest that during actin filament formation, in addition to the obligatory, UD-based nucleation-condensation pathway, a facultative, LD-based pathway is implicated whose abundance is strongly dependent on the polymerization conditions chosen. Whereas LD-induced branching of polymerizing actin filaments might be a prerequisite for the rapid formation of actin meshworks within distinct compartments (e.g., at the leading edge) of motile cells, stabilization of these filament meshworks is more likely achieved by the concerted action of actin cross-linking proteins. The functional significance of LD is further supported by several recent findings with the actin-binding proteins gelsolin (Hesterkamp et al., 1993) and actobindin (Bubb et al., 1994a ,b) and the actin-binding molecule swinholide A (Bubb et al., 1995), all of which appear to stabilize an LD-type actin dimer. In this context, one may also speculate that during dynamic reorganization of the actin cytoskeleton, a substantial amount of actin is present in the form of an LD pool in the cell. However, more detailed studies are now necessary to clarify the exact role of the LD during actin filament assembly and turnover.

Figure 9.

Schematic representation of F-actin filament polymerization involving the obligatory, UD-based nucleation–condensation pathway and a facultative, LD-based pathway leading to stochastic incorporation of LDs (i.e., via one of their subunits) into growing F-actin filaments. This polymerization course transiently yields partially “LD-decorated” filaments. Probably in response to switching of the filament-bound LDs from a G-like to an F-like conformation, their unincorporated actin subunits are released into the monomer pool, thus yielding normal-looking F-actin filaments at steady state.

Phalloidin Unveils New Insights into the Mechanism of Actin Polymerization

It came as a surprise to us that phalloidin by itself (i.e., in the absence of salt) was capable of promoting polymerization of Mg–G-actin into bona fide filaments, although at a much slower rate. Whereas polymerization induced by stoichiometric amounts of phalloidin exhibited the same three characteristic phases (a lag phase, an elongation phase, and a steady state; see inset of Fig. 1 b) as observed for K⁺-induced polymerization, LD formation was apparently suppressed by the underlying polymerization mechanism.

Reaction scheme 1 describes the standard polymerization mechanism that occurs upon addition of K⁺ (e.g., 100 mM KCl) to an ATP–G-actin–containing solution: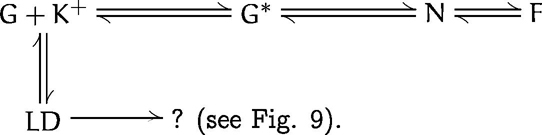

The equilibrium at the beginning of the reaction scheme Indicates that the cation (K ⁺) acts directly on the G-actin monomer (G) by binding to its multiple lower-affinity cation binding sites (Carlier et al., 1986a ; Pollard, 1990; Carlier, 1991). This activation step yields accumulation of G* concomitant with the rapid formation of LD (Millonig et al., 1988; and Results), and it is followed by the somewhat slower formation of UD-based nuclei (N), which promote elongation into F-actin filaments (F) by further addition of G*. As discussed above, LD incorporates into growing filaments and hence represents a direct participant in the F-actin polymerization reaction (see Fig. 9).

Reaction scheme 2 describes the situation for G-actin in buffer A under low-salt conditions (i.e., 0.2 mM CaCl₂ or 0.05 mM MgCl₂):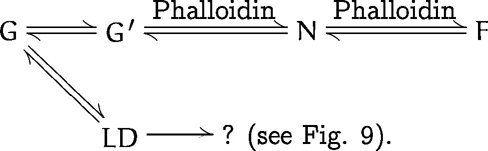

G′ stands for a spontaneously activated (i.e., without addition of salt) monomer (e.g., by thermal fluctuations) that always occurs at very low frequency and may not necessarily be identical to G*. In this case, virtually all actin is present in the G form, and hence no polymerization into F-actin filaments takes place. Also, by the cross-linking assay no significant amount of LD is depicted in this case.

Reaction scheme 3 describes the situation for the phalloidin-induced (i.e., without KCl) slow actin polymerization monitored by the fluorescence time course of pyrenated actin (see Fig. 1 b, trace c′′):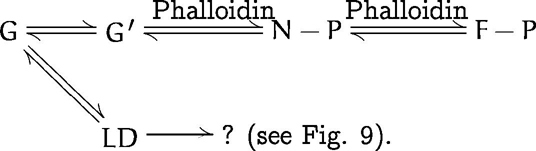

As indicated by the two forward reaction steps, phalloidin stabilizes UD-based nuclei (N-P) and growing filaments (F-P) by a “locking-in” mechanism (see also Estes et al., 1981; Coluccio and Tilney, 1984). By inhibiting the backward reaction the toxin acts like a ratchet, thus shifting the net equilibrium toward F-actin filament formation. Since LD formation appears to be strongly suppressed as in the case of G-actin in buffer A (see reaction scheme 2), this phalloidin-induced polymerization pathway appears to be dominated by a simple nucleation–condensation mechanism.

Taken together, actin polymerization in the presence of both KCl and phalloidin implies a synergistic effect of K⁺ and phalloidin on the overall course of polymerization. As documented in Fig. 1, such a synergism is indeed observed experimentally. Moreover, with K⁺ alone (reaction scheme 1) and with phalloidin alone (reaction scheme 3), polymerization of Mg–G-actin was significantly more efficient than that of EGTA– or Ca–G-actin. Hence, the overall course of the polymerization reaction is strongly controlled by the type of divalent cation bound to the HAS. These findings support and extend the notion that the conformational state of Mg-ATP–G-actin is the most appropriate to adopt a stable F-actin conformation (c.f., Strzelecka–Golaszewska et al., 1993, 1996; Kim et al., 1995).

F-actin Filament Conformation Determines Its Mechanical Properties

The structural disorder of the F-actin filament is manifested by the variable crossover spacing and width along its length and has been the subject of many investigations. This disorder is now generally accepted to represent an intrinsic dynamic feature of the actin filament (Aebi et al., 1986). Attempts to quantify and parametrize this dynamic behavior of F-actin have produced two models: (a) “random twist with cumulative angular disorder” (Egelman et al., 1982; Stokes and DeRosier, 1987); and (b) “compensatory lateral slipping” (Bremer et al., 1991; Censullo and Cheung, 1993). Consistent with the lateral slipping model of Bremer et al. (1991), we found that the axial spacing and corresponding maximum width of individual filament crossovers appeared uncorrelated for all polymerization conditions assayed (including stabilization of the filaments by phalloidin; see Fig. 6 c). This finding further suggests that cumulative lateral slipping or angular disorder may indeed occur locally over short filament segments (i.e., 2–6 subunits), but not over longer segments where filament distortions compensate each other so that there is no net propagation of structural or mechanical perturbation through an entire actin filament. These observations, however, are in conflict with results proposing a long-range cooperative effect within F-actin that could be induced by the binding of a single gelsolin molecule to the barbed end of an actin filament (Orlova et al., 1995; Prochniewicz et al., 1996) or by rigor binding of two-headed myosin to an actin filament (Orlova and Egelman, 1997).

Our determination of the apparent persistence length λ_app of negatively stained filaments revealed statistically indistinguishable values for Mg–, EGTA–, and Ca–F-actin. In contrast, we did find an approximately twofold increase in the apparent persistence length of F-actin when the filaments were polymerized in the presence of stoichiometric amounts of phalloidin. These findings are qualitatively in good agreement with results derived from thermal fluctuation (Isambert et al., 1995) and dynamic light scattering (Scharf and Newman, 1995) of F-actin filaments in solution.

In contrast, Orlova and Egelman (1993) evaluated electron micrographs of negatively stained filament preparations and reported that under certain conditions, F-actin yielded a fourfold increase in flexibility depending on whether Mg²⁺ or Ca²⁺ was bound to the HAS. Direct correlation of these data with ours is difficult because of subtle differences in the polymerization conditions (i.e., in terms of nucleotide and cation compositions and/or concentrations) chosen by these authors. For example, Orlova and Egelman (1993) used 50 mM KCl instead of 100 mM, as in our experiments, to polymerize Mg-ATP–G-actin. Moreover, some of their polymerization conditions involved the presence of millimolar amounts of divalent cations that, in addition to the HAS, are known to also bind to some of the lower-affinity cation binding sites on G-actin (for review see Estes et al., 1992). In this context, we have observed a significant increase of the apparent persistence length when Ca-ATP–G-actin was polymerized with 2 mM MgCl₂/50 mM KCl (data not shown), indicating that activation of lower-affinity sites on G-actin by divalent cations does indeed affect the flexural rigidity of the resulting F-actin filaments. In agreement with apparent persistence length measurements from electron micrographs of corresponding filaments (our unpublished data), Mg– and Ca– F-actin filaments polymerized in the presence of 2 mM MgCl₂ or 2 mM CaCl₂ appeared mechanically indistinguishable (Scharf and Newman, 1995). Last but not least, according to Gordon et al. (1997) the presence of millimolar amounts of Ca²⁺ had no effect on the movement of unregulated Mg–F-actin in an in vitro motility assay (see also Homsher et al., 1996).

It therefore came as no surprise to us that the refined and averaged 3-D reconstructions from filaments with different occupancies of their HAS revealed no significant structural differences at the 25 Å resolution level, e.g., in terms of their overall filament morphology, their fine structure of the F-actin subunit, intersubunit contact pattern, and inclination of the DNase I binding loop relative to the filament axis. Moreover, they all looked very similar to the consensus filament reconstructions of negatively stained (Bremer et al., 1994) as well as frozen-hydrated (Milligan et al., 1990) F-actin filaments representing their near-physiological conformation (i.e., Ca–G-actin polymerized with 2 mM MgCl₂ and 50 mM KCl). A recently published NMR spectroscopy-based structural analysis of F-actin assembled in the presence of different divalent cations at the HAS (i.e., Ca²⁺ versus Mg²⁺) revealed changes in the mobility of the first 21 NH₂-terminal amino acids within subdomain 1 (Heintz et al., 1996). However, these changes seem too small to be detected by EM at the 25 Å resolution level and most likely do not significantly affect the flexibility of the F-actin polymer.

Compared to native F-actin filaments, all phalloidin-stabilized filaments (including those polymerized without KCl) yielded refined and averaged 3-D reconstructions with a subtle yet significant increase in the mass density of their intersubunit contact pattern, both along and between the two long-pitch helical strands. Besides these changes, the F-actin subunit conformation and overall filament morphology remained highly conserved upon stoichiometric binding of phalloidin. Since the standard deviations of crossover spacing and width frequency distributions of phalloidin-stabilized F-actin preparations did not differ significantly from those of native filaments (Table I), we interpreted this higher mass density as stronger physical contacts between subunits within the polymer, a situation being consistent with the increased stiffness of phalloidin-stabilized F-actin filaments.

Lorenz et al. (1993) reported similar structural changes of atomic models based on x–ray fiber diffraction to 8 Å resolution from oriented gels of native and phalloidin-stabilized F-actin filaments. They also found a similar rotation of subdomain 2, thereby stabilizing the DNase I binding loop so as to increase the long-pitch helical intersubunit contact and to decrease the cylindrical radius of gyration of the phalloidin-stabilized F-actin polymer. These structural changes of F-actin upon stoichiometric binding of phalloidin are sufficient to qualitatively explain the observed twofold increase in filament stiffness. They also support the model proposed by Orlova and Egelman (1993) for the modulation of actin flexibility that appears to involve a rotation of subdomain 2. Moreover, comparison of our native F-actin filament 3-D reconstructions with our refined and averaged phalloidin-stabilized 3-D reconstructions revealed that a distinct groove on native filaments that resides between the two long-pitch helical strands becomes padded with additional mass in the presence of phalloidin (Fig. 8 b, arrowheads). In fact, exactly this groove has been previously proposed by Bremer et al. (1991) and Lorenz et al. (1993) to represent the phalloidin binding site.

In conclusion, we applied a variety of analytical methods to evaluate actin filament polymerization, structure, and dynamics in the presence of different reagents. Most importantly, our systematic approach revealed for the first time that actin polymerization involves a facultative, LD-based pathway besides the obligatory, UD-based nucleation–condensation pathway. The overall reaction courses and equilibria of these two pathways are tightly controlled by the type of divalent cation bound to the HAS of the G-actin molecule. These findings may have important consequences for the assembly of F-actin filaments, and in particular, on the formation of actin filament meshworks within living cells. Despite the different polymerization courses, the respective structures of the resulting F-actin filaments at the 25 Å resolution level are very similar and rather insensitive to the type of divalent cation bound to the HAS of the actin molecule. We therefore expect that the F-actin conformation of microfilaments and thin filaments is insensitive to intracellular Ca²⁺ release (i.e., 0.1– 10 μM) in actin-based motility processes and muscle contraction. In contrast, the conformation and/or mechanical properties of the F-actin filament may be modulated significantly by actin-associated proteins such as, for example, tropomyosin (i.e., via troponin in a Ca²⁺-dependent manner; Isambert et al., 1995), myosin (Yanagida and Oosawa, 1978; Orlova and Egelman, 1997), α-actinin (McGough et al., 1994), or scruin (Owen and DeRosier, 1993).

Abbreviations used in this paper

1,4-PBM,N,N′-1,4-phenylenebismaleimide; 2-D

two-dimensional

3-D

three-dimensional

ADF

annular dark-field

CTEM and STEM

conventional and scanning transmission electron microscopy

DMF

dimethylformamide

HAS

high-affinity divalent cation binding site

LD and UD

lower and upper dimer